有理数减法学案2
2.2.有理数的减法(1)(学案)
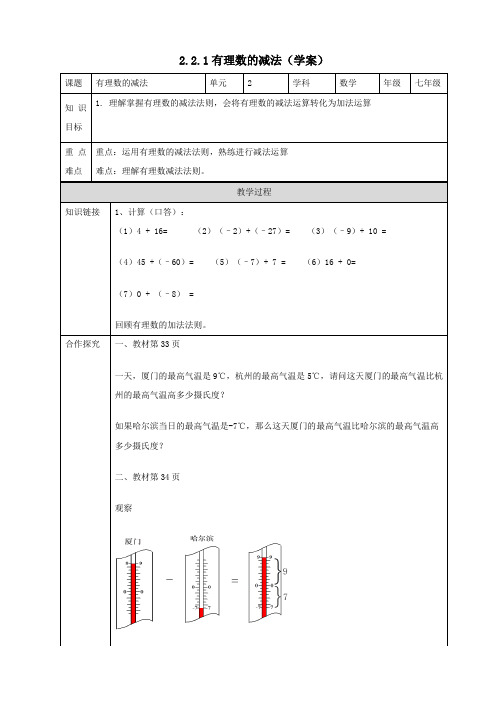
2.2.1有理数的减法(学案)一、教材第33页一天,厦门的最高气温是9℃,杭州的最高气温是5℃,请问这天厦门的最高气温比杭州的最高气温高多少摄氏度?如果哈尔滨当日的最高气温是-7℃,那么这天厦门的最高气温比哈尔滨的最高气温高多少摄氏度?二、教材第34页观察A. -3B. -2C. -1D. 32.如图所示为某县十二月份某一天的天气预报,则该天最高气温比最低气温高( )A. -7 ℃B. 7 ℃C. -3 ℃D. 3 ℃3.若b<0,则在a,a-b,a+b三个数中,最大的是(B)A. aB. a-bC. a+bD. 不能确定【方法宝典】根据有理数的减法法则进行计算.1.下列计算结果正确的是()A. (-14)-5=-9B. 0-(-3)=3C. (-3)-(-3)=-6D. |5-3|=-22.点A,B,C在同一条数轴上,其中点A,B表示的数分别为-3,1.若点B,C之间的距离为2,则点A,C之间的距离为( )A. 3B. 2C. 3或5D. 2或63.在足球循环赛中,红队与黄队的比分为4∶1,黄队与蓝队的比分为2∶1,蓝队与红队的比分为1∶0,则下列关于三个队净胜球数的说法,正确的是()A. 红队2,黄队-2,蓝队0B. 红队2,黄队-1,蓝队1C. 红队3,黄队-3,蓝队1D. 红队3,黄队-2,蓝队04.已知表示数a,b的点在数轴上的位置如图所示,则在a+b,b-2a,|a-b|,|b|-|a|中,负数的个数是()A. 1B. 2C. 3D. 45.计算:(1)|1-6|=____.。
《2.6 有理数的加减混合运算》第二课时 学案3

《 有理数的加减混合运算(2)》学案【学习目标】 1.掌握有理数加减混合运算的技能,进行熟练运算; 2.通过解决简单实际问题过程的反思,获得解决问题的经验; 【学习方法】自主探究与合作交流相结合。
【学习重难点】重点:熟练进行有理数的加减混合运算,能应用运算律简化运算 难点:培养初步的数感及对数学活动的兴趣 【学习过程】 模块一 预习反馈 一、学习准备1.有理数加减混合运算的方法和步骤:①运用______法则把有理数的混合运算中的_______转化成________。
②应用加法运算律__________________________和加法法则进行简便计算。
2.请同学们阅读教材p45—p46,预习过程中请注意:⑴不懂的地方要用红笔标记符号;⑵完成你力所能及的习题和课后作业。
二、教材精读 3.省略加号和括号例1 一架飞机进行特技表演,起飞后的高度变化如下(上升记为正,下降记为负): +5.5km;—3.7km ; +1.3km;—1.6km;—1km 求此时飞机的比起飞点高了多少? 解法一:所有数相加:解法二:+5.5—3.7+1.3—_____________=发现:+5.5+(—3.7)+(1.3)+(—1.6)+(—1)=+5.5—3.7+1.3—1.6—1 归纳:在和式里,通常把各个加数的括号和它前面的加号省略不写,写成省略加号的和的形式。
如:_________________)5()6()7()8(=++-+-+-; 读法一:按这个式子表示的意义读作:“负8、负7、负6、正5的和”; 读法二:按运算意义读作:“负8减7减6加5”。
实践练习:将下列各式写成省略加号的和的形式,并合理交换加数的位置。
(1)(+16)+(-29)-(+11)+(+9)= ;(2)(-2.6)-(4.7)-(+0.5)+(+2.4)+(-3.2)= ; (3)(+21)-5+(-31)-(+41)+(-32)= ;归纳:方法:(1)括号前是“+”号,括号内的数的符号不变;(2)括号前是“—”号,括号内的数的符号改变。
2020年人教版数学七年级上册精品学案1.3.2 第2课时 有理数加减混合运算(含答案)

第一章 有理数1.3 有理数的加减法1.3. 2 有理数的减法第2课时 有理数的加减混合运算学习目标:1、能把有理数的加、减法混合运算的算式写成几个有理数的和式,并能正确地进行有理数加减混合运算。
2、能体会数学中的转化思想。
学习难点:有理数加减法的混合运算及其应用。
教学过程一、情境引入1.有理数的加法法则,有理数的减法法则。
2.一架飞机做特技表演,它起飞后的高度变化情况为:上升4.5千米,下降3.2千米,上升1.1千米,下降1.4千米,求此时飞机比起飞点高了多少千米?3.(-8)-(-10)+(-6)-(+4),这是有理数的加减混合运算题,你会做吗?请同学们思考练习。
根据有理数减法法则,有理数的加减混合运算可以统一为二、探索新知1.加法、减法统一成加法由于减法可以改写成加法进行运算,因此所有加法、减法的运算在有理数范围内都可以统一成加法运算。
如:(-12)+(-5)-(-8)-(+9)可以改写成 (-12)+(-5)+(+8)+(-9) 做一做:(1) (-9)-(+5)-(-15)-(+9)(2) 2+5-8(3) 14-(-12)+(-25)-172.有理数加法运算中,加号可以省略如: 12+(-8)=12-8; (-12)+(-8)=(-12)-(+8)=(-12)-8(-9)+(-5)+(+15)+(-20)= -9-5+15-20练一练:将(-15)-(+63)-(-35)-(+24)+(-12)先统一成加法,再省略加号。
3.加、减混合运算中“+”“—”号的理解(1)可以看作是运算符号(第一个数除外)如:-5-3+8-7可读作负5减去3加上8减去7(2)可以看作是一个数的本身的符号如:-5-3+8-7可以看作是(-5)+(-3)+(+8)+(-7),可读作负5、负3、正8、负7的和4.省略加号的加法算式的运算练一练: (1)-3-5+4 (2)-26+43-24+13-46三、 问题问题1.计算(1)(-4)+9-(-7)-13(2)11-39.5+10-2.5-4+19(3)54)1.3()53(4.2+-+--问题2.寻道员沿东西方向的铁路进行巡视维护。
人教版数学七年级上册1-3-2有理数的减法学案2

人教版数学七年级上册1-3-2有理数的减法学案2教学过程一、自主学习(一)、自学课文 P (二)、导学练习1. 一架飞机作特技表演,起飞后的高度变化如下表:此时飞机所飞高度比起飞点高了多少千米?2. 回顾小学数学中加减法混合运算的顺序.(从左到右,依次计算)•以教材第28页例6(计算(-20)+(+3)-(-5)-(+7)的值)为例来说明.计算:(-20)+(+3)-(-5)-(+7)怎样读这个算式?这个式子中有加法,也有减法,我们可不可以利用有理数的减法法则,•把这个算式改变一下?再给算一算,你发现了什么?3.通过上面的问题,我们可以归纳“减法可以”.加减混合运算可以统一为,用字母表示为: a+b-c=.上面那个算式还可以怎样读?教师引导:式子(-20)+(+3)十(+5)+(一7)是-20,+3,+5,-7的和,为了书写简单,可以省略式中的括号和加号,把它写为-20+3+5-7,读作:“负20正3正5负7的和”,或读作“负20加3加5减7",鼓励学生使用第一种读法;并让学生体会两种读法的区别.再根据教科书,规范书写例6的运算过程.(三)自学疑难摘要:组长检查等级:组长签名:二合作探究例1 计算:(1)(-7)-(+5)+(-4)-(-10)(2)-+(-)-(-)-1解:(1)(-7)-(+5)+(-4)-(-10)=-7-5-4+10=-6(2)-+(-)-(-)-1=--+-1=-教师点评:我们解题时要注意书写过程例2 计算:-5.13+4.62+(-8.47)-(-2.3)解:-5.13+4.62+(-8.47)-(-2.3)=-5.13+4.62-8.47+2.3=-6.68三、展示提升1、每个同学自主完成二中的练习后先在小组内交流讨论。
2、每个组根据分配的任务把自己组的结论板书到黑板上准备展示。
3、每个组在展示的过程中其他组的同学认真听作好补充和提问。
四、反馈与检测1.计算:(1)10十(十4)十(一6)一(一5);(2)(一8)一(十4)十(一7)一(十9)。
江苏省无锡市蠡园中学七年级数学上册《有理数的加法与减法》学案(2)(无答案) 苏科版

课型:新课学习目标(学习重点):1.理解并掌握有理数的减法法则,会将有理数的减法运算转化成加法运算. 2.能正确地进行有理数的减法运算. 3.体会“化归”的数学思想.4.能运用有理数的减法运算解决简单的问题. 补充例题:例2.填空:(1)比-10℃低5℃的温度是_____;(2)比0小3的数是_____;-8比_____大4;(3)-123的绝对值的相反数与213的差为 ;(4)a =8,b =3,且a >0,b <0,则a -b = _____.(5)求出数轴上两点之间的距离:①表示数10的点与表示数4的点 ;②表示数2的点与表示数-4的点 ; ③表示数-1的点与表示数-6的点 .(B )已知A 、B 在数轴上分别表示a 、b (1)对照数轴填写下表:a6 ﹣6 ﹣6 ﹣6 2 ﹣1.5 b4 04﹣4﹣10﹣1.5A 、B 两点的距离(2) 若A 、B 两点间的距离记为d ,试问d 和a 、b 有何数量关系?(3)在数轴上标出所有符合条件的整数点P ,使它到10和﹣10的距离之和为20,并求所有这些整数的和.(4)找出(3)中满足到10和﹣10的距离之差大于1而小于5的整数的点P .(5)若点C 表示的数为x ,当点C 在什么位置时,|x +1|+|x +2|取得的值最小?自我检测题1、(1)有理数的减法法则:减去一个数,等于 . (2)9-(-4)=9+ =_______; (-4)-2=(-4) + =_______; -8-0=-8+ =______; 0-8=________+ =; 0-(-8)=0+ =________.(3)13℃比5℃高__________℃,12℃比-3℃高__________℃. 2.计算:(1)8-(-7); (2)-7-2; (3)0-5; (4)0-(-4.5).3.计算:(1)(-312 )-(+514 ); (2)(-13 )-14; (3)(—12)-(—18)(4)6.25 —(—734) (5)-(-312 )-(+56)-(-234).补充训练题1.算式是5—7看成减法运算,减数是 ,看成加法运算,第一个加数是5,第二个加数是 . 2.0-(-3)= ; -3-(-7.5)= ; 0-2=______; (-3)-2=______; (-3)-(-5)=______; (-5)-(+6)=____; (+3)+(___)= -1. 3. +2比-3大______;-5比3小_______;-8比_______小2. 4.比-8的相反数多2的数是 . 5.若a -(-b )=0,则a 与b 的关系是 .6.在下列等式:2-(-2)=0, (-3)-(+3)=0,(-3)-|-3|=0, 0-(-1)=1, 其中正确的算式有( ) A .1个B .2个C .3个D .4个7.下列说法中错误的有( )①若两数的差是正数,则这两个数都是正数;②若两个数是互为相反数,则它们的差为零;③零减去任何一个有理数,其差是该数的相反数A .0个B .1个C .2个D .3个 8.列式并计算:(1)3cm 比7cm 短多少?(2)海拔-50m 比海拔200m 低多少?(3)学校正东2km 的地方与学校正西1km 的地方相距多远?9.(1)5-(-5) (2)0-7-5 (3)(-1.3)-(-2.1)(4)113-212 (5)(1-2)-(-5-2) (6)(-34)-(-23)(7)(-312 )-(+514 ); (8)(-13 )-14 ; (9)(+16 )-(+13 )-(-112 ); (10)-16 -14 -(-13).10.2005年4月10日,哈尔滨等5个城市的最高气温与最低气温记录如下表(单位℃) 哪个城市的温差最大?哪个城市的温差最小?拓展提高题:(B )已知有理数a 、b 在数轴上的对应点位置如图所示: ׀ ׀ ׀ b o a化简:①│a │—a = ③│a │+│b │= ②│a +b │= ④│b —a │=。
【人教版】初一七年级数学上册《1.3.2 第1课时 有理数的减法法则》学案

第一章 有理数1.3 有理数的加减法1.3.2 有理数的减法第1课时 有理数的减法法则学习目标:1.理解有理数减法法则, 能熟练进行减法运算.2.会将减法转化为加法,进行加减混合运算,体会化归思想.学习难点有理数的减法法则的理解,将有理数减法运算转化为加法运算.自主学习:一、情境引入:1.昨天,国际频道的天气预报报道,南半球某一城市的最高气温是5℃,最低气温是-3℃,你能求出这天的日温差吗?(所谓日温差就是这一天的最高气温与最低气温的差)2.珠穆朗玛峰和吐鲁番盆地的海拔高度分别是8848米和-155米,问珠穆朗玛峰比吐鲁番盆地高多少?探索新知:(一) 有理数的减法法则的探索1.我们不妨看一个简单的问题: (-8)-(-3)=?也就是求一个数“?”,使 (?)+(-3)=-8根据有理数加法运算,有 (-5)+(-3)= -8所以 (-8)-(-3)= -5 ①2.这样做减法太繁了,让我们再想一想有其他方法吗?试一试做一个填空:(-8)+( )= -5容易得到 (-8)+(+3 )= -5 ②思考: 比较 ①、②两式,我们有什么发现吗?3.验证:(1)如果某天A 地气温是3℃,B 地气温是-5℃,A 地比B 地气温高多少?3-(-5)=3+ ;(2)如果某天A 地气温是-3℃,B 地气温是-5℃,A 地比B 地气温高多少?(-3)-(-5)=(-3)+ ;(2)如果某天A 地气温是-3℃,B 地气温是5℃,A 地比B 地气温高多少?(-3)-5=(-3)+ ;(二)有理数的减法法则归纳1.说一说:两个有理数减法有多少种不同的情形?2.议一议:在各种情形下,如何进行有理数的减法计算?3.试一试:你能归纳出有理数的减法法则吗?由此可推出如下有理数减法法则:减去一个数,等于加上这个数的相反数。
字母表示:)(b a b a -+=-由此可见,有理数的减法运算可以转化为加法运算。
【思考】:两个有理数相减,差一定比被减数小吗?说明:(1)被减数可以小于减数。
有理数的减法教案

课题有理数减法主讲教师赵燕课标要求能熟练运用法则进行有理数的减法运算和解决生活实际问题。
教材分析《有理数的减法》这节的内容远接小学阶段关于非负有理数的减法运算,近承本章第四节有理数的加法运算。
为后期有理数的混合运算、实数、整式、方程等运算的学习奠定了坚实的基础。
学生分析:小学学习了整数的减法运算,在生活中他们也经常会进行同类量的比较,因此学生对减法的应用并不陌生。
但初中学习了有理数后,将对减法运算有进一步的认识和理解。
目标:经历探索有理数的减法法则的过程,理解有理数的减法法则,并能熟练运用法则进行有理数的减法运算和解决生活实际问题。
教学重点及解决措施:有理数的减法法则的理解和应用,及学生合作意识和探究能力的培养。
让学生通过不同性质的减法运算来验证结果来掌握难点。
教学难点及解决措施:法则中减法到加法的转变过程,在实际情境中体会减法运算的意义并利用有理数的减法法则解决实际问题。
通过补充一些生活实例的计算问题和提高题,帮助学生提高运算能力和思维能力。
突破难点。
教学环节一复习旧知识复习有理数加法法则(复习旧知识,为本节课做一个基础。
)二创设情境,设疑导入本章引言(可以让学生体会到“数学源于现实,扎根于现实。
”激发学生的学习兴趣)三探索规律,形成法则Array就算式3-(-3)=6与3+3=6有理数减法法则:减去一个数,等于加上这个数的相反数。
(强调运用法则时:被减数不变,减号变加号,减数变成其相反数)四典型例子例子1、课本第22页例4 (让学生熟练掌握法则)观察上面题思考:当a大于b时,a-b差的符号?当a小于b时,a-b差的符号?例子2、(补充)导学案26页第7题(强调如何把语言文字转化成数学式子)例3、(补充)(让学生运用减法解决生活实际问题)全班学生分为五个组进行游戏,每组的基本分为100分,答对一题加50分,答错一题扣50分,游戏结束时,各组的分数如下:(1)第一名超出第二名多少分?(2)第一名超出第五名多少分?第一组第二组第三组第四组第五组100 150 -400 350 -100(三)课堂练习完成课本23页1,2 25页6学案24页自主测评1,2基础反思第4题(四)布置课后作业:课本25页第3题;第4题,第6题导学案25页基础反思第1题第2题第3题(五)、课堂小结(3分钟)1.有理数的减法运算法则:减去一个数,等于加上这个数的相反数2.转化的思想方法:减法运算转化成加法进行计算。
《2.7有理数的减法》学案

《2.7有理数的减法》学案设计:姚栋祥一、教学目标:1、掌握有理数减法的法则。
2、会进行有理数减法的运算。
3、学会把加法转化为减法的这种思想。
二、导学计算下列各式:50-20=__________,50+(-20)=____;50-10=__________,50+(-10)=________;比较每横行的两个算式,你能得出什么结论?50-20______50+(-20),50-10________50+(-10)20是-20的,10是-10的。
于是我们不难得到:有理数的减法法则:减去一个数,等于加上这个数的。
a-b=a+三、课堂研讨:注意:减法在运算时有个要素要发生变化。
1、口算:(1)3-5=___;(2)3-(-5)=___;(3)(-3)-5=______;(4)(-3)-(-5)=____;(5)-6-(-6)=______;(6)-7-0=___;(7)0-(-7)=______;(8)(-6)- 6=_____;(9) 9 -(-11)=___;3、填空⑴-9+( )=16;⑵42+( )=-25;⑶( )-(-18)=35; ⑷( )-87=-21例1 世界上最高的山峰是珠穆朗玛峰,其海拔高度是 8848 米,吐鲁番盆地的海拔高度是–155 米,两处高度相差多少米?解:答:两处高度相差米。
四、课堂练习:1、计算:(1) 18-(-3) (2) (-3)-18(3) (-18)-(-3) (4) (-3)-[16-(-2)](5) 18-(6-9).2、课堂达标(1)3-(-3)=___;(2)(-11)-2=______;(3)0-(-6)=___; (4)(-7)-(+8)=_____;(5)-12-(-5)=______;(6)3比5大_______;(7)-8比-2小______;(8)-4-()=10;(9)如果 a>0,b<0,则 a-b 的符号是 ______;(10)A地的海拔高度是34米,B地的海拔高度是-10米,A B两地海拔高度相差_______米五、小结与反思:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
永和学校 六年级数学 主 备 人 王海涛 王杨 审阅人 使用时间 班级 姓名
1 有理数的减法第二课时学案
学习目标:(1分钟)
1、 掌握有理数的减法法则;熟练进行有理数的加减混合运算
2、 初步掌握数学学习中转化的思想方法;
3、 了解加与减两种运算的对立统一关系,掌握数学学习中转化的思想。
导入新课:(1分钟)今天我们学习有理数的加减混合运算 自主预习:(7分钟)(自学教材23到24页内容,回答下列问题,)
1、 计算:一架飞机做特技表演,起飞后的高度变化如下:上升4.5千米,下降3.2千米,上升
1.1千米,下降1.4千米.此时飞机所飞高度比起飞点高了多少千米? 列示: ,结果是 2、 计算:
(一8)一(一10)+(一6)一(+4).
(1)请你把上式写成和的形式:原式= .(减法化成加法) (2)为了书写方便,可以省略各式中的括号和加号,把它写成 这个式子读作 ,也可以读作 (3)请你用不同的方法写出该题的解题过程. 方法一: 方法二:
注意:由于加减混合运算是同级运算,按式子的顺序进行运算,也可适当运用加法交换律、结合律,在运用交换律交换加数的位置时,要连同前面的符号一起交换. 反馈交流(教师提问每组5号)(3分钟) 合作探究:(10分钟)
1、例:计算:(-20)+(+3)-(-5)-(+7)
2、引入相反数后,加减混合运算可以统一位加法运算,其算式为a+b-c=a+b+(-c)
3、计算:
(1)1-4+3-0.5 (2)-2.4+3.5-4.6+3.5
(3)(-7)-(+5)+(-4)-(-10) (4)43-27+(-6
1)-(-
3
2
)-1
4、河里的水位第一天上升了8cm ,第二天下降了7cm ,第三天下降了9cm ,则第三天 河水水位比刚开始的水位高 cm .
5、一l0—3+5—2可以看成 的和。
6、计算
(1)(-8)+10+2+(-1) (2)5+(-6)+3+9+(-4)+(-7)
(3)(-0.8)+1.2+(-0.7)+(-2.1)+0.8+3.5 (4)
21+(-32)+54+(-2
1)+(-
3
1
)
展示提升(每组1号板演)(10分钟) 教师精讲点拨(5分钟) 课堂小结,整理笔记(4分钟) 达标测试(4分钟)计算下列各题:
(4)2.7+(一8.5)一(+1.5)一(一6.3).。
