运筹学期末考试试卷(B)卷
运筹学考试题b卷附标准答案

运筹学期末考试题( b 卷)注意事项:1、答题前,考生务必将自己的姓名、班级填写在答题卡上。
2、答案用钢笔或圆珠笔写在答题卡上,答在试卷上不给分。
3、考试结束,将试卷和答题卡一并交回。
一、单项选择题(每小题 1 分,共 10分) 1:下列关于运筹学的缺点中,不正确的是()A.在建立数学模型时,若简化不慎,用运筹学求得的最优解会因与实际相差大而失去意义B.运筹学模型只能用借助计算机来处理C.有时运筹学模型并不能描述现实世界D.由于运筹学方法的复杂性使一些决策人员难以接受这些解决问题的方法2:在下面的数学模型中,属于线性规划模型的为()max S 4X Y min S 3X Y max S X2Y2min S 2XYA. s.t. XY 3B. s.t. 2X Y 1 C. s.t. XY2 D. s.t. XY3X,Y 0 X,Y 0 X,Y 0 X,Y 03.线性规划一般模型中,自由变量可以用两个非负变量的()代换。
A.和 B .商 C.积 D.差4:以下关系中,不是线性规划与其对偶问题的对应关系的是()。
A.约束条件组的系数矩阵互为转置矩阵B.一个约束条件组的常数列为另一个目标函数的系数行向量C.两个约束条件组中的方程个数相等D.约束条件组的不等式反向 5.对偶问题的对偶是()A.原问题 B .解的问题 C.其它问题 D.基本问题 6:若原问题中x i0 ,那么对偶问题中的第i 个约束一定为()A.等式约束 B .“≤”型约束矚慫润厲钐瘗睞枥庑赖。
C.“≥”约束D .无法确定7:若运输问题已求得最优解,此时所求出的检验数一定是全部()A .小于或等于零B .大于零C.小于零D .大于或等于零8:考虑某运输问题,其需求量和供应量相等,且供应点的个数为 m,需求点的个数是 n。
若以西北角法求得其初始运输方案,则该方案中数字格的数目应为()聞創沟燴鐺險爱氇谴净。
A.( m+n)个B.( m+n-1 )个C.( m-n)个D. ( m-n+1)个9:关于动态规划问题的下列命题中错误的是()A、动态规划分阶段顺序不同,则结果不同B、状态对决策有影响C、动态规划中,定义状态时应保证在各个阶段中所做决策的相对独立性D、动态规划的求解过程都可以用列表形式实现10:若 P为网络 G 的一条流量增广链,则 P中所有逆向弧都为 G 的()A .非零流弧B .饱和边C .零流弧D .不饱和边 残骛楼諍锩瀨濟溆塹籟。
运筹学B卷复习题

《运筹学》B卷复习题一、判断题1.任何线性规划问题一定有最优解.(×)2.若运输问题中的产量和销量为整数,则其最优解也一定为整数.(×)3.整数规划的可行解集合是离散型集合.(√)4.求网络最大流的问题可归结为求解一个线性规划模型.(√)5.在动态规划模型中,问题的阶段数等于问题中子问题的数目.(√)6.若到达排队系统的顾客为泊松流,则依次到达的两名顾客之间的间隔时间服从负指数分布.(√)7.风险情况下采用EMV决策准则的前提是决策应重复相当大的次数.(√)8.根据决策者对物体之间两两相比的关系,主观做出比值的判断,这样得到的矩阵称作判断矩阵.(√)二、单选题1.图解法通常用于求解有( B )个变量的线性规划问题。
A. 1B. 2C. 4D. 52.当某供给地与某需求地之间不允许运输时,它对应的运价为( B )。
A. 零B. 充分大C. 随便取D. 以上都不对3.关于指派问题决策变量的取值,下列说法正确的是( B )。
A. 不一定为整数B. 不是0就是 1C. 只要非负就行D. 都不对4.四个棋手单循环比赛,采用三局两胜制必须决出胜负,如果以棋手为节点,用图来表示比赛结果,则是个( C )。
A. 树B. 任意两点之间有线相连的图C. 任意两点之间用带箭头的线相连的图D. 连通图5.下列正确的结论是( C )。
A. 顺推法与逆推法计算的最优解可能不一样B. 各阶段所有决策组成的集合称为决策集C. 第k阶段所有状态构成的集合称为第k段状态集D. 状态sk的决策就是下一阶段的状态6.设有一单人打字室,顾客的到达为普阿松流,平均到达时间间隔为20分钟,打字时间服从指数分布,平均时间为15分钟,顾客在打字室内平均逗留时间为( B )。
A.2小时B. 1小时C. 4小时D.3小时7.以下哪项不属于按环境分类的决策( D )。
A. 确定型B. 不确定型C. 风险型D. 单项决策型8.判断矩阵中元素 a ij=1表示i因素与j因素( A )。
运筹学试卷及参考问题详解
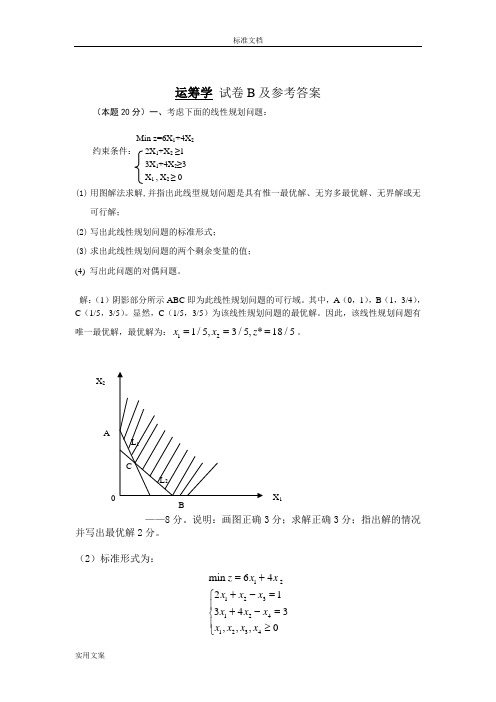
运筹学 试卷B 及参考答案(本题20分)一、考虑下面的线性规划问题:Min z=6X 1+4X 2约束条件: 2X 1+X 2 ≥13X 1+4X 2≥3 X 1 , X 2 ≥ 0(1) 用图解法求解,并指出此线型规划问题是具有惟一最优解、无穷多最优解、无界解或无可行解;(2) 写出此线性规划问题的标准形式; (3) 求出此线性规划问题的两个剩余变量的值; (4) 写出此问题的对偶问题。
解:(1)阴影部分所示ABC 即为此线性规划问题的可行域。
其中,A (0,1),B (1,3/4),C (1/5,3/5)。
显然,C (1/5,3/5)为该线性规划问题的最优解。
因此,该线性规划问题有唯一最优解,最优解为:121/5,3/5,*18/5x x z ===。
——8分。
说明:画图正确3分;求解正确3分;指出解的情况并写出最优解2分。
(2)标准形式为:121231241234min 6421343,,,0z x x x x x x x x x x x x =++-=⎧⎪+-=⎨⎪≥⎩ X 1 X 2 AB——4分 (3)两个剩余变量的值为:340x x =⎧⎨=⎩——3分(4)直接写出对偶问题如下:12121212max '323644,0z y y y y y y y y =++≤⎧⎪+≤⎨⎪≥⎩——5分(本题10分)二、前进电器厂生产A 、B 、C 三种产品,有关资料下表所示:学模型,不求解)解:设生产A 、B 、C 三种产品的数量分别为x 1,x 2和x 3,则有:——1分123123123123123max 810122.0 1.5 5.030002.0 1.5 1.21000200250100,,0z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤⎪⎨≤⎪⎪≤⎪≥⎪⎩ ——14分,目标函数和每个约束条件2分(本题10分)三、某电子设备厂对一种元件的年需求为2000件,订货提前期为零,每次订货费为25元。
运筹学教材编写组《运筹学》期末考试试卷(B)

《运筹学》期末考试试卷(B)学院 班级 姓名 学号考生注意∶1.本试题共 七 题,共 3 页,请考生认真检查;一、用单纯形法求解下述线性规划问题(20分)⎧⎨⎪⎪⎩⎪⎪0,824424m ax 2121212121≥≤-≤-≤+-+=x x x x x x x x x x z二、设一线性规划问题为(25分)⎧⎨⎪⎩⎪m a x ,,z x x x x x x x x x j j =-+++≤-+≤≥=27624013123121232 目标函数变为max z x x x =++23123;3 约束条件右端项由(6,4)T 变为(3,5)T;4 增加一个约束条件-+≥x x 1322三、某种产品今后四周的需求量分别为300,700,900,600件,必须得到满足。
已知每件产品的成本在起初两周是10元,以后两周是15元。
工厂每周能生产这种产品700件,且在第二、三周能加班生产。
加班后,每周可增产200件产品,但成本每件增加5元。
产品如不能在本周交货,则每件每周存贮费是3元。
问如何安排生产计划,使总成本最小,要求建立运输问题数学模型求解。
(25分)四、某校蓝球队准备从以下6名预备队员中选拔3名为正式队员,并使平均身高尽可能高,这6名预备队员情况如下表所示,试建立数学模型。
(20分)队员的挑选要满足下列条件:2少补充一名后卫队员;3大李或小田中间只能入选一名;4最多补充一名中锋;5如果大李或小赵入选,小周就不能入选。
五、某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知,每周星期一至星期五不能出席某一讲座的学生数如下表:(20分)学生总数。
六、某飞行队有5名正驾驶员和5名副驾驶员。
由于种种原因,某些正、副驾驶员不能同机飞行,某些则可以,如下表所示。
每架飞机出航时需正,副驾驶员各一人。
问最多能有几架飞机同时出航?应如何安排正,副驾驶员?用图论方法求解。
(20分)七、填空:(20分)1.某工程公司拟从四个项目中选择若干项目,若令11,2,3,40i i i ix ìïï==íïïïî,第个项目被选中;,第个项目未被选中;用i x 的线性表达式表示下列要求:(1)从1,2,3项目中至少选2个: ;(2)只有项目2被选中,项目4才能被选中: ;2.用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经济意义是 ,若从该空格出发进行调整,设调整量为2,则调后可使总运费下降 ;3. 动态规划中的Bellman 最优性原理是。
运筹学期末试题及答案

运筹学期末试题及答案一、选择题(每题2分,共20分)1. 线性规划问题的基本解是:A. 唯一解B. 可行域的顶点C. 可行域的内部点D. 可行域的边界点2. 以下哪项不是运筹学中的常用数学工具?A. 线性代数B. 微积分C. 概率论D. 量子力学3. 单纯形法是解决哪种类型问题的算法?A. 整数规划B. 非线性规划C. 线性规划D. 动态规划4. 以下哪个是网络流问题中的术语?A. 节点B. 弧C. 流量D. 所有以上5. 以下哪个不是运筹学中的优化问题?A. 最大化问题B. 最小化问题C. 等值问题D. 线性规划问题...(此处省略其他选择题)二、简答题(每题10分,共30分)1. 简述线性规划问题的基本构成要素。
2. 解释单纯形法的基本思想及其在解决线性规划问题中的应用。
3. 描述网络流问题中的最短路径算法,并简述其基本原理。
三、计算题(每题25分,共50分)1. 给定以下线性规划问题:Max Z = 3x1 + 5x2s.t.2x1 + x2 ≤ 10x1 + 3x2 ≤ 15x1, x2 ≥ 0请找出该问题的最优解,并计算最大值。
2. 考虑一个网络流问题,其中有三个节点A、B、C,以及四条边。
边的容量和成本如下表所示:| 起点 | 终点 | 容量 | 成本 ||||||| A | B | 10 | 2 || A | C | 5 | 3 || B | C | 8 | 1 || C | B | 3 | 4 |假设从节点A到节点B的需求量为8,从节点A到节点C的需求量为5。
使用最小成本流算法求解此问题,并计算总成本。
四、论述题(每题30分,共30分)1. 论述运筹学在现代企业管理中的应用,并给出至少两个实际案例。
运筹学期末试题答案一、选择题答案:1. B2. D3. C4. D5. C...(此处省略其他选择题答案)二、简答题答案:1. 线性规划问题的基本构成要素包括目标函数、约束条件和变量。
运筹学期末考试试题

运筹学期末考试试题一、选择题(每题2分,共20分)1. 以下哪项不是线性规划问题的基本特征?A. 线性目标函数B. 线性约束条件C. 非线性约束条件D. 可行域2. 单纯形法中,如果某个基解的系数矩阵的某一列的所有元素都是负数,这意味着什么?A. 该基解是最优解B. 该基解不可行C. 该基解是退化解D. 该基解是可行解但不是最优解3. 在网络流问题中,若某条路径的流量超过了其容量限制,这将导致:A. 问题无解B. 问题有无穷多解C. 问题有唯一解D. 问题有多个可行解4. 动态规划用于解决的问题通常具有以下哪种特性?A. 线性性B. 递归性C. 非线性性D. 随机性5. 以下哪个算法不是用于解决整数规划问题的?A. 分支定界法B. 割平面法C. 单纯形法D. 贪心算法二、简答题(每题10分,共30分)1. 解释什么是敏感性分析,并简述其在运筹学中的应用。
2. 描述网络流问题中的最小费用流问题,并给出一个简单的实例。
3. 简述如何使用动态规划解决资源分配问题。
三、计算题(每题25分,共50分)1. 给定以下线性规划问题,求解其最优解:\[ \text{Maximize } Z = 3x_1 + 2x_2 \]\[ \text{Subject to: } \]\[ 2x_1 + x_2 \leq 10 \]\[ x_1 + 3x_2 \leq 15 \]\[ x_1, x_2 \geq 0 \]2. 考虑一个生产问题,工厂需要生产两种产品A和B。
产品A的生产需要机器X工作2小时,机器Y工作1小时,利润为每单位500元。
产品B的生产需要机器X工作1小时,机器Y工作3小时,利润为每单位300元。
机器X每天最多工作8小时,机器Y每天最多工作12小时。
如何安排生产计划以最大化利润?四、案例分析题(共30分)1. 某公司计划在不同地区开设新的销售点,需要考虑运输成本、市场需求和竞争对手的情况。
请使用运筹学方法分析该公司应该如何决定销售点的位置和数量,以实现成本最小化和市场覆盖最大化。
《管理运筹学》考试试卷A,B卷及答案

《管理运筹学》考试试卷A,B卷及答案一、选择题(每题2分,共20分)1. 运筹学的英文全称是:A. Operation ResearchB. Operation ManagementC. Operational ResearchD. Operations Management2. 线性规划问题的标准形式中,目标函数是:A. 最大化B. 最小化C. 既可以是最大化也可以是最小化D. 无法确定3. 在线性规划中,约束条件可以用以下哪个符号表示?A. ≤B. ≥C. =D. A、B、C都对4. 简单线性规划问题中,如果一个变量在任何解中都不为零,则称这个变量为:A. 基变量B. 非基变量C. 独立变量D. 依赖变量5. 以下哪个方法可以用来求解线性规划问题?A. 单纯形法B. 拉格朗日乘数法C. 对偶理论D. A、B、C都可以二、填空题(每题3分,共15分)6. 在线性规划中,如果一个约束条件的形式为“≥”,则称这个约束为______约束。
7. 在线性规划问题中,若决策变量为非负整数,则该问题为______规划问题。
8. 在目标规划中,目标函数通常表示为______。
9. 在运输问题中,如果产地和销地的数量相等,则称为______。
10. 在排队论中,顾客到达的平均速率通常表示为______。
三、计算题(每题10分,共30分)11. 某工厂生产甲、乙两种产品,甲产品每件利润为200元,乙产品每件利润为150元。
工厂每月最多生产甲产品100件,乙产品150件。
同时,生产甲产品每件需要3小时,乙产品每件需要2小时,工厂每月最多可利用工时为300小时。
试建立该问题的线性规划模型,并求解。
12. 某公司有三个工厂生产同一种产品,分别供应给四个销售点。
各工厂的产量和各销售点的需求量如下表所示。
求最优的运输方案,并计算最小运输成本。
工厂\销售点 A B C D产量 20 30 50需求量 10 20 30 4013. 设某商店有三个售货员,负责四个收款台。
管理运筹学期末试卷B

一、填空题(每小题4分,共20分)1、设原LP问题为则它的标准形和对偶规划问题分别为: 和。
2、用分枝定界法求整数规划的解时,求得放松问题的解为x1=18/11,x2=40/11,则可将原问题分成如下两个子问题与求解.3、右图的最小支撑图是。
4、右边的网络图是标号算法中的图,其中每条弧上的数表示其容量和流量。
该图中得到的可行流的增广链为:,在其上可增的最大流量为。
5、则其最优解为:,最优值。
二、单项选择题(每小题2分,共10分)1、下列表格是对偶单纯形表的是(A )ABCD2A 、可行域必有界; B 、可行域必然包括原点; C 、可行域必是凸的; D 、可行域内必有无穷多个点.3、在运输问题中如果总需求量大于总供应量,则求解时应( ) A 、虚设一些供应量; B 、虚设一个供应点; C 、根据需求短缺量,虚设多个需求点; D 、虚设一个需求点。
4、下列规划问题不可用动态规划方法求解的是( ) A 、背包问题; B 、最短路径问题 C 、线性规化: D 、5、下列关于图的论述正确地是( ) A 、有向图的邻接矩阵是对称矩阵;B 、图G 是连通的,当且仅当G 中的任意两点之间至少存在一条链;C 、任何一个连通图,都存在唯一的最小支撑树;D 、若图是图一个支撑子图,则。
三、判断题(每小题2分,共10分)( )1、若原始问题是利润最大化的生产计划问题,则对偶问题是资源定价问题,对偶问题的最优解称为原始问题中资源的影子价格。
影子价格越大说明这种资源越是相对紧缺,影子价格越小说明这种资源相对不紧缺.( )2、对max 型整数规划,若其松弛问题最优解对应的目标函数值为Z c ,而其最优整数解对应的目标值为Z d ,那么一定有Z c ≤Z d .( )3、任何一个无圈的图G 都是一个树图。
( )4、一个可行流满足平衡条件是指:所有中间结点处流出量=流入量,收点流出量=0, 发点流入量=0,收点流入量=发点流出量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建农林大学考试试卷 ( B )卷
学年 第 学期
课程名称: 运 筹 学 考试时间 120分钟
专业 年级 班 学号 姓名
1. 目标规划模型中,目标约束ax d d g -
+
+-=中的g 称为 目标值 。
2. 线性规划问题的单纯形法中,有最优解的判别准则是 所有检验数非负且最优值为常数 。
3. 如果流{}
ij f f =中所有0ij f =,则称f 是 零 流。
4. 如果001020(,,...,)m B P P P =,t B 为最优基,则1
t B -为01020(,,...,)t
t
t
m P P P 。
5. 无向图中的环是 端点重合的边 。
二、单项选择题(选择正确答案的字母填入空格处,每小题2分,共10分)
1.线性规划的非对称形式的原问题和对偶问题数学模型中,互补松弛性的描述式为 C 。
A. **
**0,0s s y x y x == B. **
0s y x = C. **0s y x = D .**
0y x =
2. 若11(,)V V 为最大截集,则 C 。
A. 11(,)c V V 为最小截量
B. 11(,)c V V 为最大流流量
C. 11(,)c V V 为11(,)V V 的截量
D. 11(,)c V V 为最小截量 3. 最短路求解的主要内容是 D 。
A. 关键路线
B. 最短路线
C. 最短路长
D. 最短路线和最短路长 4. 线性规划问题的价值系数变化后,当最优表中 B 不发生变化。
A. 非基变量检验数
B. 限定常数、技术系数和基变量检验数
一、填空题(每空2分,共10分)
C. 检验数
D. 目标函数值的相反数 5. 网络计划中关键工序a ij 的TF ij C 。
A.>0
B.<0
C.=L j -E i -T ij
D.=L j
三、判断题(正确打“√”;错误打“×”;每小题2分,共10分)
1. 在增广链上确定的流量调整量只能是负的。
( × )
2. 目标规划模型中必须有目标约束。
( √ )
3. 线性规划问题有最优解。
( × )
4. 网络计划中,非关键路线上工序的施工时间延长可能导致工期延长。
( √ )
5. 树中可能存在环。
( × )
四、问答题(每小题5分,共20分)
1. 闭回路的定义及应用。
m ×n 表可以划分为m ×n 个格,一个格也可以称为一个点,在不同的 m ×n 表中,格或点代表不同的含义。
取产销平衡表来介绍闭回路定义。
在产销平衡表中取偶数个点jp ip j i j i x x x ,1,10,0,...,,,若这些点满足
,10i i = 21j j =
,32i i = 43j j = ……
,)1(ip p i =-0j jp = 或满足
,10j j = 21i i =
,32j j = 43i i =
……
,)1(jp p j =-0i ip = 则称这些点构成一条闭回路。
闭回路用来进行方案调整,计算检验数,判断可行解是否基本解等等。
2. 最大流问题的线性规划模型。
max ()
0()..0
1,2,,()sj js ij ij ij sj js a A a v f f c a A v f i s s t f f i n v f i t ∈≤≤∈⎧
⎪
=⎧⎪
⎨⎪
-==⎨⎪⎪⎪-=⎩⎩
∑∑ 3. 线性规划模型的特点。
略。
4. 目标规划模型中目标约束的结构。
略。
五、(第一小题5分,第二小题3分,第三小题2分,共10分) 对)(P :要求:
1.()()12,1,1c c c ==,用单纯形法求解;
2.画出可行域;
3.指出()12,c c c =变动下的最优解。
1122
121212
min 10():
..5,0z c x c x x x P s t x x x x =++≤⎧⎪-≥⎨⎪≥⎩
解: ⑴ 单纯形法求解如下:
**(5,0,5,0,0),5T x z ==。
2.可行域如下:
说明:P c =-。
六、(10分)
用破圈法或避圈法求图1的最大生成树,并指出其权重和(10分)
解:⑴避圈法:首先确定应选的边数为顶点数减1,即应选7条边。
所选的边染上红色,旁边标明选边序号,结果如下图所示。
最大生成树权为85. ⑵避圈法略。
七、(10分) 对)(OP ,要求
1.求解
2.给出一个合理的实际意义。
11122
12111222121122
min ()10
():..25
,,,,,0z P d d P d x x d d OP s t x x d d x x d d d d +-+
-+-+
-+-+=++⎧++-=⎪++-=⎨⎪≥⎩
解:⒈⑴单纯形法
求解过程见下表,据下表得。
}
5,0{,)0,10(
T **
⑵图解法
相关图形见图2。
⑴ 考虑硬约束,可行域为第一限象; ⑵ 考虑P 1,最优解在直线AB 上; ⑶ 考虑P 2,最优解在点A 上。
因此,。
}
5,0{,)0,10(2P z x T ==**
x1
+
1
图2
⒉略。
八、(10分)
(教材P155例7)有某种机床,可以在高低两种不同的负荷下进行生产,在高负
荷下生产时,产品的年产量为g,与年初投入生产的机床数量u
1的关系为g=g(u
1
)=8u
1,
这时,年终机床完好台数将为au
1
,(a为机床完好率,0<a<1,设a=0.7).在低负荷下
生产时,产品的年产量为h,和投入生产的机床数量u
2的关系为h=h(u
2
)=5u
2
,相应的
机床完好率为b(0<b<1,设b=0.9),一般情况下a<b。
假设某厂开始有x=1000台完好的机床,现要制定一个五年生产计划,问每年开始时如何重新分配完好的机床在两种不同的负荷下生产的数量,以使在5年内产品的总产量为最高。
解:首先构造这个问题的动态规划模型。
⑴变量设置
①设阶段变量k表示年度,因此,阶段总数n=5。
②状态变量s k表示第k年度初拥有的完好机床台数,同时也是第k-1年度末时
的完好机床数量。
③决策变量u k ,表示第k 年度中分配于高负荷下生产的机床台数。
于是s k - u k
便为该年度中分配于低负荷下生产的机床台数。
这里u k 与u k 均取连续变量,当它们有非整数数值时.可以这样理解:如sk =0.6,就表示一台机器在k 年度中正常工作时间只占6/10;u k =0.4时,就表示一台机床在k 年度只有4/10的时间于高负荷下工作。
⑵ 状态转移方程为
⑶ 允许决策集合,}{k k k k k s u u s D ≤≤=0)(
⑷ 目标函数。
设v k (s k ,u k )为第k 年度的产量,则v k (s k ,u k )=8u k +5(s k -u k ),因此,目标函数为
),(),(),()(555111,u s v u s v u s v s v k k k k k k k n k +++=+++
⑸ 递推方程。
令f k (s k )表示由第k 年的状态s k 出发,采取最优分配方案到第5年度结束这段时间的产品产量,根据最优化原理有以下递推关系:
}{)(),(max )(11)
(++∈+=k k k k k s D u k k s f u s v s f k k k 1,2,3,4,5=k
0)(66=s f
⑹ 边界条件:s 1=1000,s 6≥0。
分阶段求解见下表。
)
(9.07.0)(1k k k k k k k u s u u s b au s -+=-+=+
由表5可得最优策略:}{397,567,810,0,0)1000(1=p 。
目标函数最优值:
2.23691)1000(1=f 个。
九、(10分)
对表1,用表上作业法求解。
表1
'解:根据产销平衡可知表1中不限应取为2,—应取为M ,因此问题的基础数据表等价与表2: 表2
⑴关于0
x 的计算
用伏格尔法确定0
x
说明:决定,A II 和,A IV 两个数字格,后者是补零的格。
x检验数为零,但取它为入基变量时调整量为零,所以最优解唯一,为注意空格
11
z=⨯+⨯+⨯+⨯=
x,最优值*534425513106
位势(0)
检验数(0)。
