11年研究生试卷(答案)
2011考研试题及评分标准.

(D) α 2 , α 3 , α 4
(7) 设 F1 ( x) 与 F2 ( x ) 为两个分布函数,其相应的概率密度 f1 ( x ) 与 f 2 ( x) 是连续函数,则必 为概率密度的是 (A) f1 ( x ) f 2 ( x) 则 E (UV ) = (A) EU ⋅ EV (B) EX ⋅ EY (C) EU ⋅ EY (D) EX ⋅ EV (B) 2 f 2 ( x ) F1 ( x) (C) f1 ( x ) F2 ( x ) (D) f1 ( x ) F2 ( x) + f 2 ( x ) F1 ( x) (8) 设随机变量 X 与 Y 相互独立, 且 EX 与 EY 存在, 记 U = max{ X , Y } , V = min{ X , Y } ,
T (6) 设 A = (α1 , α 2 , α 3 , α 4 ) 是 4 阶矩阵, A 为 A 的伴随矩阵。 若 (1, 0,1, 0) 是方程组 Ax = 0 *
的一个基础解系,则 A* x = 0 的基础解系可为 (A) α1 , α 3 (B) α1 , α 2 (C) α1 , α 2 , α 3
(B) I < K < J (C) J < I < K (D) K < J < I
(5) 设 A 为 3 阶矩阵,将 A 的第 2 列加到第 1 列得矩阵 B ,再交换 B 的第 2 行与第 3 行得
1 0 0 1 0 0 单位矩阵。记 P1 = 1 1 0 , P2 = 0 0 1 ,则 A = 0 0 1 0 1 0 −1 (A) P1P2 (B) P1 P2 (C) P2 P1 (D) P2 P1−1
D
计算二重积分 I =
2011年考研数学二真题及答案解析

0
0
1
,则
A
(
)
0 0 1
0 1 0
(A) P1P2 .
(B) P11P2 .
(C) P2P1 .
(D) P2 P11 .
(8) 设 A (1,2 ,3,4 ) 是 4 阶矩阵, A* 为 A 的伴随矩阵,若 (1, 0,1, 0)T 是方程组
数学(二)试题 第 1 页 (共 13 页)
2x 2 cxk 1
cos2
x
3
lim x0
2 cos2 x 1 cxk 1
2 cos2
x
lim
x0
4 4 cos2 cxk 1
x
lim
x0
4 sin 2 cxk 1
x
lim
x0
4 cxk 3
1.
所以 c 4, k 3 ,故答案选(C).
(2)【答案】(B).
x2 f x2 f x3
图1
(21) (本题满分 11 分)
已知函数 f (x, y) 具有二阶连续偏导数,且 f (1, y) 0 , f (x,1) 0 ,
f (x, y)dxdy a ,其中 D (x, y) | 0 x 1,0 y 1 ,计算二重积分
D
I
xy
f
xy
(
x,
y)dxdy
.
D
(22) (本题满分 11 分)
1 )
连接而成的.
2
2
(I) 求容器的容积;
(II) 若将容器内盛满的水从容器顶部全部抽出,至少需要做多少功?(长度单位: m
,重力加速度为 gm / s2 ,水的密度为103 kg / m3 ).
y
西安石油大学研究生数值分析10 11年试题

一、填空题(每题2分,共20分) 1.近似数 x =0.231关于真值x=0.229有
位有效数字。 。
n
2.求方程 f ( x) 0 的根时,对应的牛顿切线法迭代公式为 3.设 l i ( x) (i=0,1,2,…,n)是n次拉格朗日插值基函数,则
4 0 x1 5 2 3 1 1 x 2 9 2 2 0 x 3 3
四、(12分)写出解线性方程组
4 x1 2 x3 4 x1 4 x 2 2 x3 1 的高斯—赛德尔迭代法的迭代格式,并判断其收敛性。 3 x 5 x x 2 2 3 1
l ( x) =
i 1 i
。
4.求解微分方程初值问题
y ' f ( x, y ) 时,设x节点步长为h,则欧拉预估— y ( x0 ) y 0
迭代法和
校正方法的局部截断误差为 。 5.若线性方程组AX=b的系数矩阵A为严格对角占优矩阵,则 迭代法收敛。 6.差商与向前差分满足关系: 差商与向后差分满足关系: 7.用数值方法求积分 。 。
五、(12分)已知一组观察数据为 i 0 1 2 2 3 3 4
xi
1
yi
0
-5
-6
3
试用此组数据构造3次牛顿插值多项式 N 3 ( x) ,并计算 N 3 (1.5) 的值。 六、(12分)试确定经验公式 y ae 中的参数a和b(a为正数),使该函数曲线与下列数
bx
据按最小二乘原则相拟合(至少保留ห้องสมุดไป่ตู้位小数)。 1 2
xi
3 20
管理学815考研试题(最终)

安徽财经大学2 0 11 年攻读硕士学位研究生入学测验试题〔答案必需写在答题纸上,写在试卷上无效〕测验科目:办理学一、概念辨析题〔在阐述概念的根底上,比拟两者的区别和联系。
每题1 0 分,小计50分〕1.X理论,Y理论2.程序性方案,非程序性方案3.正强化,负强化4.前馈控制,反应控制5.集权式带领,民主式带领一、判断阐述题〔每题25 分,小计 1 00 分〕1.选择一项你近期做出并赐与你重大影响的决策,如:是否兼职、是否报考公务员等,阐发说明:(1) 做出决策的根本过程。
(2) 如何从不同的备选方案做出选择。
2.假定你筹办创办一家经济型酒店,规模在 1 5 0 人摆布,并担任该酒店总经理,主要经营餐饮、小型购物中心和住宿业务,请你别离设计两种组织布局方案,比拟其优势与劣势。
3.“目光远大的公司的核心价值不雅不需要理性的或者外在的理由,它们不随趋势和时尚的变化而变化,甚至也不随市场;状况的变化而变化〞。
你同意上述看法吗?请说明理由。
4.比拟拟于通用电气、中国石化等这样的大企业而言,为什么那些小型软件企业会更容易实现其组织文化变化呢?安徽财经大学20 1 2 年攻读硕士学位研究生入学测验试题〔答案必需写在答题纸上,写在试卷上无效〕测验科目:办理学一、简述题〔每题 1 2 分,共60 分〕1.办理的一个著名定义是:“通过别人并和别人一道实现组织目标。
〞说明办理者如何才能有效地做到这一点。
2.办理者在道德方面的带领作用应表达在哪些方面?3.当办理者越来越经常地使用电脑和软件东西时,他们将台皂够制定更理性的决策,你是否同意这种说法?为什么?4.带领生命周期理论的主要不雅点是什么?在现实办理实践中如何运用这种理论?5.“每位员工在组织控制工作中都起到了作用〞,或者“控制仅仅是办理者的责任〞。
你同意吗?请说明你的不雅点。
二、阐述题〔每题30 分,共9 0 分〕1.随着环境的复杂性和变更性的增强,办理决策中的不确定性因素也大为增加,只有那种与外部环境相适应的组织布局才可能成为有效的组织布局。
安财811西方经济学--考研试题(11--14)

(2)商品市场和货币市场同时均衡时的利率与收入。 安徽财经大学 2012 年攻读硕士学位研究生入学考试试题 (答案必须写在答题纸上,写在试卷上无效) 考试科目:西方经济学 微观部分 一、名词解释(每小题 6 分,共 30 分) 1.需求函数 2 显性成本. 3.替代效应 4.规模报酬 5.引致需求 二、简答题(每小题 10 分,共 30 分) 1.简述基数效用论消费者效用最大化的均衡条件。 2.简述边际报酬递减规律内容。 3.简述完全竞争厂商短期均衡时几种可能的情况。 三、论述题(每小题 1 5 分,共 30 分) 1.论述垄断造成市场失灵的原因及其解决措施。 2.论述短期产量曲线与短期成本曲线之间的关系。 四、计算题(每小题 15 分,共 15 分) 1.假定有两个相互竞争的公司分别生产 x 和 Y 产品,两个公司的需 求曲线分别为:PX=1000-5X;PY=1600 - 4Y 这两家公司目前的销售量分别为 1 00 单位和 250 单位,求: (1)X 和 Y 当前的需求价格弹性: (2)如果 Y 降价,并使 Y 的销售量增加到 300 单位,同时导致 X 的销售量 下降到 75 单位,请计算 X 商品的交叉价格弹性; (3)假定生产 Y 的公司目标是销售收入最大化,其降低价格的策略是否符合 其目标? 宏观部分 一、简答题(每题 8 分,共 24 分)
安
徽
财经Βιβλιοθήκη 大学2013 年攻读硕士学位研究生入学考试试题 (答案必须写在答题纸上,写在试卷上无效) 考试科目:西方经济学 微观部分
一、名词解释(每小题 7 分,共 35 分) 1.帕累托最优与帕累托改进; 2.边际替代率与边际转换率; 3.规模经济与自然垄断; 4.脊线与扩展线; 5.边际收益产品与边际要素成本。 二、简答题(每小题 10 分,共 20 分) 1.解释“谷贱伤农”的原因。 2.为什么竞争厂商有短期供给曲线,而垄断厂商没有? 三、论述题(每小题 15 分,共 30 分) 1.简述个别劳动供给曲线向后弯曲与市场劳动供给曲线向右上方倾斜的原因。
东南大学结构力学考研真题及答案11年2003~2013
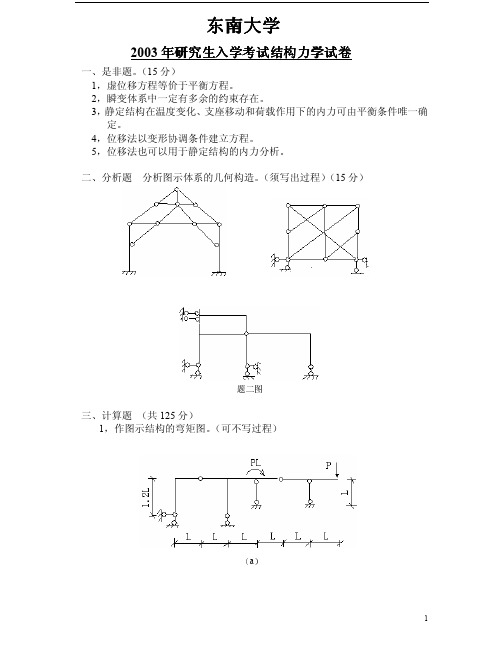
个多余约束。 d)m=16,n=19,r=8,可知 W=2.故体系几何可变。
280 + 0.875 − 70 = 210.875kN ⋅ m
放松结点 2,等于在结点 2 加一与约束力矩反向的力偶荷载 −210.875kN ⋅ m ,21 端的
分配弯矩为
23 端的分配弯矩为
−210.875× 4 = −120.5kN ⋅ m 7
杆端 12 的传递弯矩为
−210.875× 3 = −90.375kN ⋅ m 7
-70 15.063 1.076 0.077 0.006
280 -140 -140
-60.25 30.125 30.125
-4.304 2.152 2.152
-0.308 0.154 0.154
-0.022 0.011 0.011
280
-70 -120.5
15.063 -8.607
-90.375 -6.456
2
4¥¦§¨©¢¢£EI ¥ !"#$%&¤
5,图示结构 A 支座处的弹簧刚度为 k,用位移法作图示结构在 A 支座下沉 c 和 50kN 水平影响下的弯矩图。(需写出计算过程)
6,用力矩分配法作图示结构的弯矩图。(需写出分析过程)
3
东南大学
2004 年研究生入学考试结构力学试卷
一, 分析图示结构的几何稳定性(须写出分析过程)(20 分)
二,作图示结构的弯矩图(无须写出分析过程)
2011年432统计学真题及答案

2011年432统计学真题及答案浙江⼯商⼤学2011年硕⼠研究⽣⼊学考试试卷(B )卷招⽣专业:应⽤统计硕⼠考试科⽬:432统计学总分:(150分)考试时间:3⼩时⼀. 单项选择题(本题包括1—30题共30个⼩题,每⼩题2分,共60分。
在每⼩题给出的四个选项中,只有⼀个符合题⽬要求,把所选项前的字母填在答题纸上)。
1.为了调查某校学⽣的购书费⽤⽀出,从各年级的学⽣中分别抽取100名学⽣,组成样本进⾏调查,这种抽样⽅法属于()。
A. 简单随机抽样B. 分层抽样C. 系统抽样D. 整群抽样2.已知某⼯⼚⽣产的某零件的平均厚度是2厘⽶,标准差是0.25厘⽶。
如果已知该⼚⽣产的零件厚度为正态分布,可以判断厚度在 1.5厘⽶到 2.5厘⽶之间的零件⼤约占()。
A. 95% B. 89% C. 68% D. 99%3.某校⼤⼆学⽣统计学考试的平均成绩是70分,标准差是10分,从该校⼤⼆学⽣中随机抽取100个同学作为样本,则样本均值的数学期望和抽样分布的标准误差分别为()。
A. 70,10 B. 70,1 C. 70,4 D. 10,104.根据⼀个具体的样本,计算总体均值的置信⽔平为90%的置信区间,则该区间()。
A. 以90%的概率包含总体均值 B. 有10%的可能性包含总体均值 C. 绝对包含总体均值D. 绝对包含总体均值或绝对不包含总体均值5.某企业计划投资2万元的⼴告费以提⾼某种新产品的销售量,企业经理认为做了⼴告可使每天销售量达100吨。
实⾏此计划9天后经统计知,这9天的⽇平均销售量为99.32吨。
假设每天的销售量服从正态分布),(2σµN ,在05.0=α的显著性⽔平下,检验此项计划是否达到了该企业经理的预计效果,建⽴的原假设和备择假设为()。
A .100:,100:10≠=µµH H B. 100:,100:10>≤µµH H C . 100:,100:10<≥µµH H D .100:,100:10≤>µµH H 6. 在回归分析中,因变量的预测区间估计是指()。
11年川大高等代数及答案

四川大学2011年攻读硕士学位研究生入学考试题一、(本题满分20分)1. (5分)设V 是数域F 上的线性空间,V s ∈ααα,,,21 .令}{1F k k W i si i i ∈=∑=α.证明:W 是V的子空间(称为由s ααα,,,21 生成的子空间). 证明:取W ∈βα,且∑==si ii k 1αα,∑==si ii k 1ββ∑∑∑===+=+=+si i i i s i i i si i i k k k 111)(βαβαβα,则W ∈+βα ①∑∑====si i i s i i i k k k k k 11)(ααα,则W k ∈α ②由①、②,得W 是V 的子空间2. (15分)设)(2F M 是数域F 上的2阶方阵组成的线性空间,设V 是由如下的4个矩阵生成的)(2F M 的子空间:⎥⎦⎤⎢⎣⎡-=02411A ,⎥⎦⎤⎢⎣⎡=30152A ,⎥⎦⎤⎢⎣⎡--=41233A ,⎥⎦⎤⎢⎣⎡--=54924A ,(1)求V dim 并写出V 的一个基. (2)设映射f:F f →为:)()(A tr A f =,其中)(A tr 表示矩阵A 的迹. 求fkerdim 并写出fker的一个基.解:(1)取)(2F M 的一个基11E 、12E 、21E 、22E ,VF M →)(2在这个基下对应的矩阵是B有),,,(),,,(432122211211A A A A B E E E E =,则⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=5430410292142351B⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----00003618005430235154300510011021023515430410292142351则3dim =V ,故V的一个基为1A 、2A 、3A(2)取矩阵C ,使得0)(=C f ,根据题意,有02211=+c c由332211A x A x A x C++=,有方程048321=++-x x x此方程的基础解系由2个线性无关的向量构成,即)'1,0,7(、)'8,7,0(-⎥⎦⎤⎢⎣⎡-==413264)'1,0,7)(,,(3211A A A C ,⎥⎦⎤⎢⎣⎡-=-=1182311)'8,7,0)(,,(3212A A A C则有2kerdim =f ,故fker 的一个基为1C 、2C二、(本题满分20分)设F ,K 都是数域且K F ⊆.1.(5分)设s ααα,,,21 是F 上的n 维列向量.证明:s ααα,,,21 在F 上线性相关当且仅当s ααα,,,21 在K 上线性相关.证明:取s ααα,,,21 的极大无关组为F r ∈γγγ,,,21必要性:s ααα,,,21 在F 上线性相关,则方程i r X αγγγ=),,,(21 有解(s i ,,2,1 =)有K X ∈,则方程i r X αγγγ=),,,(21 在K 上有解故s ααα,,,21 在K 上线性相关 充分性:s ααα,,,21 在K 上线性相关,则方程i r X αγγγ=),,,(21 在K 上有解在K 上有),,,,(),,,(2121i r r r r αγγγγγγ =由F ir ∈αγγγ,,,,21 ,则在F 上也有),,,,(),,,(2121i r r r r αγγγγγγ =故方程i r Xαγγγ=),,,(21 在F 上有解故s ααα,,,21 在F 上线性相关 2.(5分)设A ,B 为F 上的n 阶方阵.证明:A ,B 在F 上相似当且仅当A ,B 在K 上相似.证明:必要性: 由A ,B 在F 上相似,存在可逆矩阵)(F M P n ∈,使得B AP P =-1又)(K M P n ∈,则A ,B 在K 上相似充分性: 由A ,B 在K 上相似,则在K 上A ,B 有相同的行列式因子)(λk D (n k ,,2,1 =) 由A ,)(F MB n ∈,有)(λk D 属于F则在F 上A ,B 也有相同的行列式因子)(λk D故A ,B 在F 上相似3.(5分)设F 上的n 次多项式)(x f 在K 上有n 个根n x x x ,,,21 .证明:∏≤<≤-112)(j i j i x x 属于F . 证明:令0111)(a x a x a x a x f n n n n ++++=-- (F a a a n n ∈-01,,, )由根与系数的关系,有n n x x x a +++=-- 211、n n n x x x x x x a 121212--+++= 、……由∏≤<≤-112)(j i j i x x 为对称多项式,则可由01,,,a a a n n -表示 故∏≤<≤-112)(j i j i x x 属于F4.(5分)证明:关于数的加法和乘法K 是F 上的线性空间. 证明:取K 上的元素α、β,数a 、F b ∈ 由K F⊆, αββα+=+,有αβ+为K 上的元素βαβαβαb b a a b a +++=++))((,βαβαb b a a +++为K 上的元素则关于数的加法和乘法K 是F 上的线性空间 三、(本题满分20分)给定任意的可逆矩阵A .请说出4种求1-A 的方法(使用计算机程序的方法除外),并简要说明理由.解:法1:通过初等变换由行变,有()()1-→A E E A ;由列变,有⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛-1A E E A法2:通过伴随矩阵由E A AA =*,有⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==-nn n nn n A A A A A AA A A A A A A21222121211111*1法3:通过H-C 定理 令A 的特征多项式为0111)(a a a A E f n n n ++++=-=--λλλλλ如00=a ,有)()(1211a a f n n n +++=--- λλλλ,则A 含特征值0,A 不可逆 故00≠a ,则O E a A a A a A A f n n n =++++=--0111)(有E a a A a a A a A n n n 012011011----=---- 法4:通过A 的最小多项式令A 的最小多项式0111)(a a a m m m m ++++=--λλλλ同上,有00≠a ,则O E a A a A a A A m m m m =++++=--0111)( 有E a a A a a A a A m m m 012011011----=----四、(本题满分20分)设1)(121++++=--x x x x f p p ,p 是素数.1.(10分)证明)(x f 在有理数域Q 上不可约.2.(10分)令})()({O A f C M A n =∈=M ,其中)(C M n 是全体n 阶复矩阵组成的集合.把M 中的矩阵按相似关系分类,即A ,B 属于同一类当且仅当存在可逆的复矩阵C 使得1-=CBC A .问M 中的全部矩阵可以分成几类?说明理由.1.证明:11)(--=x x x f p ,令1+=y x ,有yy C y y y f pk kk p p 11)1()1(0-=-+=+∑=1221111)1(p p p p p p p p pk k k p C y C y C y C y C y f ++++==+---=-∑由艾森斯坦判别法,p 为素数,121,,,-p p p p C C C p 、p 不能整除p p C 、2p 不能整除1p C故)1(+y f 在有理数域不可约,即)(x f 在有理数域不可约.2.证明: 由O A f =)(,又1)0(=f ,则0不是A 的特征值由)(C M A n ∈,则A 有n 个特征值0≠i λ(n i ,,2,1 =)则存在可逆矩阵P ,使得JAP P =-1J 除去排列次序外是由A 唯一确定的,则J 可能为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡n λλλ11121 ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡n λλλ11021 ,……,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡n λλλ00021共有n 种,则M 中的全部矩阵可分为n 类五、(本题满分20分)设V 是数域F 上的n 维线性空间,)(V End 表示V 上的全体线性变换组成的线性空间. 1.(10分)求)(dim V End 并写出)(V End 的一个基. 2.(10分)设)(V End ∈A ,设A 的特征多项式为)(x f .证明:如果V 可以分解为非平凡的-A 不变子空间的直和,那么,)(x f 在F 上可约.问:此结论的逆命题是否成立?说明理由.1.解:设nn E E E ,,,1211 是n n⨯P的一组基,n n⨯P是2n 维的,可知V 的全体线性变换与n n⨯P同构, 故V 的全体线性变换组成的线性空间是2n 维的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五.(10分)今有赵、钱、孙、李、周五位教师,要承担语文、数学、物理、化学、英语五门课程。已知赵熟悉数学、物理、化学三门课程,钱熟悉语文、数学、物理、英语四门课程,孙、李、周都只熟悉数学、物理两门课程。问能否安排他们都只上他们熟悉的一门课程,使得每门课程都有人教(用图论方法求解)。
3.设 是图 的推广邻接矩阵,则 的 行 列元 等于由 中顶点 到顶点 的长度为_n_途径数目。
4.完全图 的邻接矩阵的最大特征值为_n_。
5.不同构的3阶单图共有___4___个。
6.设 阶图 是具有 个分支的森林,则其边数 。
7. 阶树( )的点连通度为___1___;边连通度为____1___;点色数为__2___; 若其最大度为 ,则边色数为___ __。
8.图 是 连通的,则 中任意点对间至少有_k__条内点不交路。
9.5阶度极大非哈密尔顿图族为___ ___和__ _____。
10.完全图 能够分解为 个边不相交的一因子之并。
11. 设连通平面图 具有5个顶点,9条边,则其面数为__6_; ( )阶极大平面图的面数等于__ ___; ( )阶极大外平面图的顶点都在外部面边界上时,其内部面共有 个。
A1: LA, S ; A2: MA, LA, G ; A3: MA, G, LA;
A4: G, LA, AC ; A5: AC, LA, S ; A6: G, AC;
A7: GT, MA, LA ; A8: LA,GT, S ; A9: AC, S, LA;
A10: GT, S。人只上一门自己所熟悉的课程。
六.(6分)设 是赋权完全偶图G=(V,E)的可行顶点标号,若标号对应的相等子图 含完美匹配 ,则 是G的最优匹配。
七.(6分)求证:在n阶简单平面图G中有 ,这里 是G的最小度。
证明:若不然,设G是6连通图,
由惠特尼定理得:
所以
即
与G是简单图矛盾
八、(10分)课程安排问题:某大学数学系要为这个夏季安排课程表。所要开设的课程为:图论(GT),统计学(S),线性代数(LA),高等微积分(AC),几何学(G),和近世代数(MA)。现有10名学生(学生用Ai表示,如下所示)需要选修这些课程。根据这些信息,确定开设这些课程所需要的最少时间段数,使得学生选课不会发生冲突。(要求用图论方法求解)
电子科技大学研究生试卷
(考试时间:至,共__2_小时)
课程名称图论及其应用教师学时60学分
教学方式讲授考核日期_2011__年___月____日成绩
考核方式:(学生填写)
一.填空题(每空1分,共22分)
1.若n阶单图G的最小度是 ,则其补图的最大度 = 。
2.若图 , ,则它们的积图 的顶点数= ;边数= 。
(A)必要条件;(B)充分条件;(C)充分必要条件。
5.下列说法正确的是(A)
(A) 非平凡树和 方体都是偶图;
(B) 任何一个3正则图都可1-因子分解;
(C) 可1-因子分解的3正则图中一定存在哈密尔顿圈;
(D) 平面图 的对偶图的对偶图与 是同构的。
三、 (10分)设无向图 有12条边,且度数为3的结点有6个,其余结点的度数小于3,求G的最少结点个数。
解:建立图论模型,设A, B, C, D, E分别代表赵、钱、孙、李、周五位教师。
a,b, c, d, e分别代表语文、数学、物理、化学、英语五门课程。得模型图如下:
A B C D E
问题转化为是否存在饱和A,B,C,D,E的匹配存在。
取顶点子集合 ,因 ,所以
由霍尔定理知:不存在饱和A,B,C,D,E,的匹配。
12. 完全偶图 的点独立数等于___2___,点覆盖数等于 。
13. 完全 元根树有 片树叶, 个分支点,则其总度数为 或 。
14.对具有 条边的单图定向,能得到 个不同的定向图。
二.单项选择(每题3分,共15分)
1.下面给出的序列中,不是某图的度序列的是(C)
(A) (1,3,5,4,7); (B) (2,2,2,2,2); (C) (3,2,3,3); (D) (1,5,7,1).
解:设G的最少结点个数x,其余结点平均度数为d,则得
当d=2时,x取最小值3,满足 。
所以……
四,(12分)在下面边赋权图中求:(1)每个顶点到点 的距离(只需要把距离结果标在相应顶点处,不需要写出过程); (2) 在该图中求出一棵最小生成树,并给出最小生成树权值(不需要中间过程,用波浪线在图中标出即可).
GT
MA
LA S
2.下列无向图 一定是树的是(D)
(A) 连通图;
(B)无回路但添加一条边后有回路的图;
(C) 每对结点间都有路的图;
(D) 连通且 。
3.以下必为欧拉图的是(C)
(A) 顶点度数全为偶数的连通图;
(B)奇数顶点只有2个的图;
(C) 存在欧拉迹的图;
(D) 没有回路的连通图。
4.设 是 ( )阶单图,则其最小度 是 为哈密尔顿图的(B)
