人教版小学五年级数学《梯形的面积》课件
人教版小学五年级数学上册《梯形的面积》教案
梯形的面积教学目标1.理解和掌握梯形的面积计算公式，能运用公式正确地计算梯形的面积，并能运用公式解决实际问题。
2.理解梯形面积计算公式的推导过程，培养学生的自我探索精神。
3.提高学生运用知识解决问题的能力，培养分析概括和思考的能力。
重点：理解并掌握梯形的面积计算公式，能运用公式解决实际问题。
难点：理解梯形面积计算公式的推导过程。
教具准备：PPT课件教学过程一、复习导入1．导入：这一单元我们已经学习了三角形和平行四边形的面积计算，谁来说一说它们的计算公式？（平行四边形的面积＝底×高，用字母表示是S=ah；三角形面积＝底×高÷2，用字母表示是S＝ah ÷2。
）让学生回忆它们的面积的计算方法是怎么推导出来的？（把它转化成已经学过的图形来研究面积的。
）2．揭题：生活中的图形除了三角形和平行四边形外，还有梯形，这节课我们就利用转化的方法来研究梯形的面积计算公式。
（板书课题：梯形的面积）二、创设情境，探索新知1、计算面积（单位厘米）（第1题图）（第2题图）2、计算面积（单位厘米）怎么计算呢？能不能运用转换的思想，变成已经学过的图形。
已学过的图形，三角形，平行四边形，长方形。
）讨论梯形面积推导过程。
转化为两个三角形。
从这里可以看出两个三角形的高与梯形的高都、两个一样的梯形拼成一个平行四边形。
平行四边形的底为梯形的（上底+下底），高为梯形的高。
那么梯形的面积=（上底+下底）×高÷2剪切拼接成长方形，长为梯形的中位线，宽为梯形的高。
那么：梯形的面积=（上底+下底）×高÷23、如果用 S 表示梯形的面积，梯形面积的计算公式可以写成：S=(a+b)h÷2三、学以致用1．出示教材第96页例3。
教师：什么是横截面？请学生独立解决，全班核对答案。
教师：因为我们刚刚开始学梯形的面积公式，对公式不熟，所以计算时可以先写上公式，再列算式。
等以后熟练了，公式可以省略。
小学五年级数学《梯形的面积》课件【三篇】
【导语】课件是根据教学⼤纲的要求，经过教学⽬标确定，教学内容和任务分析，教学活动结构及界⾯设计等环节，⽽加以制作的课程软件。
它与课程内容有着直接联系。
使⽤课件能够吸引学⽣注意⼒，提⾼学习情绪,从⽽诱发学⽣学习的兴趣。
下⾯是整理分享的⼩学五年级数学《梯形的⾯积》课件，欢迎阅读与借鉴，查看更多请点击课件频道。
⼩学五年级数学《梯形的⾯积》课件篇⼀ 教学⽬标： 1让学⽣在实际情境中，认识计算梯形⾯积的必要性。
2在⾃主探索活动中，让学⽣经历推导梯形⾯积公式的过程。
3能运⽤梯形⾯积的计算公式，解决相应的实际问题。
教学重难点： 理解梯形⾯积公式的推导过程，帮助学⽣形成思考问题的习惯。
教学准备： 梯形纸⽚、多媒体课件、剪⼑。
教学过程： ⼀复习引⼊回顾平⾏四边形、三⾓新的⾯积公式，想⼀想：三⾓型⾯积的公式是怎么推导出来的 ⼆探究新知 实际操作，⾃主探究。
电脑演⽰地24页的情境图，启发学⽣思考：如何把体型转化成我们已经学过的图形呢? 1独⽴操作，⾃主探索。
学⽣⽤事先准备的学具⾃⼰进⾏剪拼，在探索的过程中，逐步形成特有的思考问题的习惯。
2⼩组讨论。
四⼈⼩组继续运⽤转化的⽅法将梯形转化成前⾯学过的图形，进⽽求出梯形的⾯积。
3交流汇报，发现规律。
(1)引导观察，转化后的图形与原来的梯形有什么关系?请学⽣⽤语⾔描述梯形⾯积的推导过程。
(2)联系三⾓形的⾯积公式，分析理解：为什么梯形和三⾓形的⾯积计算公式都要除以2? (3)经观察分析后，引导学⽣得出结论，并⽤字母公式来表⽰。
三看书质疑，交流感想 阅读第24页内容，回顾⾃⼰探索梯形⾯积公式的过程，并与同伴谈谈⾃⼰的想法。
完成课前提出的问题 四巩固应⽤，拓展提⾼ 完成25页习题 五全课总结与反思 通过本课的学习，你⼜有哪些收获?你在学习⽅法上⼜有了那些提⾼⼩学五年级数学《梯形的⾯积》课件篇⼆ 【教学内容】 九年义务教育⼩学《数学》教科书(⼈教版)第九册。
《梯形的面积》说课(课件)人教版五年级上册数学
第二环节：自主探究梯形面积的公式推导过程。 设计意图：这一环节的设计，让学生通过小组合作和动
手操作自主研究，验证猜想，最终得出结论，让学生主动参 与到教学活动的同时感受转化的数学思想，这一环节我利用 动画演示与信息技术手段相结合，起到画龙点睛的作用，课 件在学生迷惑不解之时呈现，每次都适时引导学生理解、领 会，真正达到了辅助教学的目的。
根据对数学课程标准的研读，首先，我来说一说对教材的分析。
本节课的内容属于空间与图形这块领域，它是学生已经认识了梯形、知道 了梯形的特征、会画梯形的高，并经历了平行四边形和三角形面积计算的推导过 程，已有了转化思想的基础上进行教学的，为学习组合图形的面积奠定了基础。
基于以上分析，结合学生的认知规律，我制定了以下的教学目标。
知识与技能目标：利用多媒体动画演示和动手操作活动，让学生经历梯形 面积计算公式的推导过程，掌握梯形面积的计算方法，并能灵活运用方法解决相 关问题。
过程与方法目标：在经历多种活动的探索过程中，培养学生自主探究、合 作交流的能力。
情感态度与价值观目标：进一步感受转化的数学思想，发展学生的空间观 念、推理能力。
这一阶段的学生具有一定的学习能力，对生活中常见的 现象能够进行正确的分析与判断，但学生的概括能力较弱， 推理能力也有待发展，很大程度上依赖具体形象的经验材料 来理解抽象逻辑关系，因此，本节课在学生已经了解三角形 面积公式的推导过程的基础上，以独立思考、自主探索、合 作交流、动手操作等多种形式达到本节课的教÷2 =26 × 20÷2
软
=10530（平方米） 答：它的面积是10530平方米。
=260（平方米）
板
答：这个花坛的面积是260平方
米。
件
块
提出问题：你能根据 已有的经验，借助手 中的学具推导出梯形 的面积计算公式吗？
人教版五年级上册数学(新插图) 第3课时 梯形的面积 教学课件
二、创设情境，探究新知
给一个长2.4m、宽0.8m的长方形宣 传栏刷油漆，每平方米要用油漆0.9kg。 一共需要多少千克油漆？
规范解答 2.4×0.8 ＝ 1.92（m2） 1.92×0.9 ＝ 1.728（kg）
答：一共需要1.728 kg油漆。
计算下面各题。 [教材P5 做一做]
6.7×0.3 = 2.01
[教材P8 练习二 第5题]
1.28×30=38.4（万千米） 答：月球到地球约有38.4万千米。
四、课堂练习，个别指导
1.计算下面各题。[教材P8 练习二 第1题]
1.8×23 = 41.4
0.37×0.4 = 0.148
1.8 × 23
54 36
4 1.4
0. 3 7 × 0.4
0.1 4 8
1.计算下面各种商品的总价。 [教材P8 练习二 第2题]
19.00×2.7= 51.30（元）
7.50×3.4= 25.50（元）
3.60×7.5= 27.00（元）
易错点：在读台秤上的千克数时，要弄清每一小格代表的千克数。
2.判断下面各个积的小数位数有没有错误。
[教材P8 练习二 第3题]
56.7 × 38 = 2 1 5 4.6
高
= (三角形的底+平行四边形的底×2)×高÷2
下底
=[平行四边形的底+(三角形的底+平行四边形的 底)]×高÷2
=(梯形的上底+梯形的下底)×高÷2
所以，梯形的面积=(上底+下底)×高÷2
方法2 梯形的面积 = 三角形①的面积+三角形②的面积
上底 ①
= 上底×高÷2+下底×高÷2 =(上底+下底)×高÷2
五年级数学上册课件 梯形的面积课件6 人教新课标版
练习一
计算下面每个梯形的面积。
1米
2.5米 10 米
12
米
3米
16米
例题 3 我国三峡水电大坝的横截面的一部分是梯形 （如下图），求它的面积。
36米
s = (a + b ) h ÷ 2 =(36+120)×135÷2 =156×135÷2 =10530(m ) 答：它的横截面面积是10530平方米。
底
上底 + 下底
×
高
梯形的面积=（上底+下底）×高 ÷ 2
上底
中点 .
高 下底
. 中点
下底 上底
平行四边形的面积 =
底
×
高
梯形的面积=（上底+下底）×高 ÷ 2
上底 a 高
.中点
h
高 下底 上底
下底 b
三角形的面积 =
底
×
高 ÷ 2
梯形的面积= （上底+下底）×高 ÷ 2
S
=
(a+ b)×
h÷ 2
2
个梯形的上底、下底的和是12厘米，高是 是10厘米，它的面积是60平方厘米。 （ ） 2、两个面积相等的梯形一定能拼成一个平行 四边形。 （ ）
练习三
它们的面积分别是多少？
40cm 45cm
一辆汽车侧面的两块玻璃是梯形（如下图），
40cm
71cm
65cm
练 习 四 计算梯形的面积
40
35
42
思考题：
用篱笆围成一块养鸡场（如下图的梯形），一面利 用房屋的墙壁，篱笆长65米，求养鸡场的面积。
15米
高 底
平行四边形的面积= 底 × 高
s=ah
小学五年级数学-第十七讲 梯形的面积
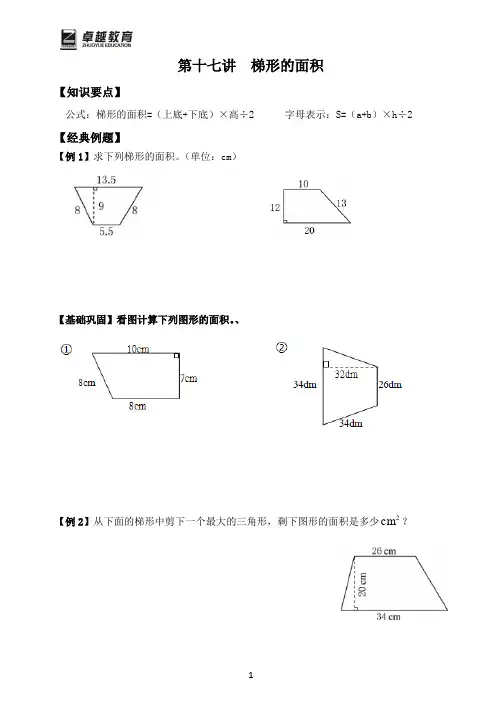
第十七讲梯形的面积【知识要点】公式：梯形的面积=（上底+下底）×高÷2 字母表示：S=（a+b）×h÷2 【经典例题】【例1】求下列梯形的面积。
（单位：cm）【基础巩固】看图计算下列图形的面积。
、cm？【例2】从下面的梯形中剪下一个最大的三角形，剩下图形的面积是多少2【基础巩固】填表。
【例3】一块梯形广告牌的上底是12m，下底是16m，高是2m。
涂这块广告牌一共用油漆56kg，平均每平方米用多少千克油漆？【基础巩固】一块梯形麦田，上底是105米，下底是145米，高是60米，这块麦田共收小麦4800千克。
平均每公顷收小麦多少千克？【自我检测】一、填空题。
1.两个（）的梯形可以拼成一个平行四边形，拼成的平行四边形的底等于梯形的（）和（）的和；拼成的平行四边形的高等于原梯形的（）。
2. 一个梯形的面积是6.3平方米，高是1.5米，上底是2.4米，则下底是（）米。
3.梯形的上底、下底和高都扩大10倍，高不变，那么梯形的面积扩大（）倍。
4.一个梯形，在它的同一侧给上底和下底都增加4cm，它增加的图形是（）形；若梯形的高是7.5cm，那么梯形的面积增加（）。
5.一个平行四边形和一个梯形的面积相等，高也相等，这个梯形的上、下底之和是这个平行四边形底边的（）。
6.一个梯形上底12米，比下底短6米，高6.5米，它的面积是（）。
7.一个梯形的上下底之和是56厘米，高是12厘米，面积是（）。
8.一个梯形的面积是 6.5平方分米，上下底之和是13厘米，这个梯形的高是（）。
二、选择题。
1. 一个梯形的高扩大3倍，上、下底不变，它的面积（）。
A.不变B.扩大3倍C.扩大9倍cm。
2.一个梯形的上底是12cm，下底是18cm，高是上底的一半，它的面积是（）2A.7.5B.135C.90三、判断题。
1.梯形的面积等于平行四边形的面积的一半。
（）2.只有一组对边平行的四边形是梯形。
（）3.梯形的面积等于上底加下底的和乘以高。
人教版五年级数学上册梯形的面积 (课件)(共15张PPT)
s=Байду номын сангаасh s=ah÷2
你能用学过的方法推导出梯 形的面积公式吗？
上底(a)
腰
腰
高(h)
下底(b)
独立思考：
借助你们手中的梯形纸片，先独立思考，可以用拼一拼，画一画，剪一剪，看看能不能把 梯形转化成我们学习过的图形，并找到转化前后图形间的联系，把你找到的联系在纸上写 一写，让别人一眼就能看出你是如何推导出梯形面积计算方法的，学具不够用可以找老师 领取。
合作学习：
1、思考完后，四人小组交流，先选出一名组长，让组员依次说出自己的方法。 2、说的同学说清楚，要能说服自己的组员，待说完后组员也可以发表自己的想法。 3、小组内推选出你觉得可行的方法，待会展示交流（可以是一种、两种等多种方法）。
展示交流
上底 高
下底
上底 高
下底
梯形的面积＝（上底＋下底）×高÷2
2个梯形的面积 （上底＋下底） 高 平行四边形的面积＝ 底 × 高
上底 高
下底
展示交流
上底 高
下底
梯形的面积＝（上底＋下底）×高÷2
2个梯形的面积 （上底＋下底） 高 平行四边形的面积＝ 底 × 高
展示交流
上底 高
下底
梯形的面积＝小三角形的面积＋大三角形的面积
＝上底×高÷2＋下底×高÷2
＝（上底＋下底）×高÷2
展示交流
上底 高
下底
梯形的面积＝平行四边形的面积＋三角形的面积 ＝上底×高＋（下底－上底)×高÷2 ＝（上底＋下底）×高÷2
你知道吗？
倍积
等积
上底+下底
上底 下底
通过今天的学习你有什么收获？
一个堤坝的横截面是梯形（如下图），求横截 面的面积。
最新梯形的面积教学课件15篇
梯形的面积教学课件15篇梯形的面积教学课件15篇梯形的面积教学课件(1)《梯形的面积计算》教学反思口前镇中心校赵艳秋今天上了《梯形的面积计算》这节课，反思整堂课的教学，自我感觉较为满意的是，突出了以下几个方面：一、体现了自主探究教学的特点。
本课的教学充分让学生动手实践——用学具剪一剪、拼一拼，进行了自主探索，并组织了小组合作交流。
体现了探究性教学的特点。
放手让学生自己利用已有的学习经验，动手把梯形转化成已经学过的图形，并让学生通过找图形之间的联系，从不同的途径探索出梯形的面积计算方法。
在这一环节的教学中，我十分注意突出学生主体作用的发挥，让学生主动操作、讨论，在充分感知、理解的基础上总结出梯形面积的计算方法。
学生出现了多种操作方法，如：一部分学生把两个完全一样的梯形通过旋转、平移转化成一个平行四边形，推导出梯形的面积公式；一部分学生用一个梯形沿中位线剪开，翻转180度，拼成一个平行四边形，推导出公式；还有一部分学生用一个梯形沿梯形的右上角到对腰的中点剪下，翻转180度，拼成一个三角形，推导出面积公式。
尤其突出的是充分发挥了学生的自主性，实实在在地给了学生进行探究、发现、创新的时间和空间！真正体现了“学生是学习的主人，教师是组织者、引导者和参与者”。
发展了学生的创新能力。
学生的创新能力不是一节课就能培养起来的。
这节课学生能够想出那么多种方法，有以前几节课的探究平行四边形和三角形的面积为基础，学生的自主探究能力要经过一定量的积累，而不是一蹴而就的。
但是如果长期这样得到训练，学生探究所需要的时间就会越来越短，创新能力也会越来越强。
尤其突出的是充分发挥了学生的自主性，实实在在地给了学生进行探究、发现、创新的时间和空间！真正体现了“学生是学习的主人，教师是组织者、引导者和参与者”。
发展了学生的创新能力。
值得指出的是：这当中还蕴含了数学思想方法的教学：让学生把陌生的知识自主地转化为已有的知识经验，体现了迁移、转化思想。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9
8 （单位：㎝）
×A、（14+8）×9÷2 ×B、（15+9）×8 √C、（15+9）×8÷2
√D、 12×8
中位线 ×高
操作探究
上底
中位线
高
下底 中位线的长度与梯形上下底之间的关系？
中位线=（上底+下底）÷2
m=(a+b)÷2
中位线＝（上底＋下底）÷２
?
25㎝
中位线
28㎝
25×2-28
用割补的方法推导
梯形的面积
本节课我们来继续学习梯形的面积，在掌握 用拼、割两种方法推导梯形的面积公式的基础上 我们来探究梯形的中位线和梯形的面积的关系， 同学们要理解并掌握用梯形的中位线表示梯形面 积的方法，并能解决实际的问题。
判断
两个上底、下底和高分别相等
的 梯形 ，形状也相等。
×
两个面积相等的梯形可以拼成
× 一个平行四边形。
× 梯形不是轴对称图形。
回顾 用拼的方法推导
梯形的面积= (上底+下底)×高÷2
S=(a+b)h÷2
上底
上底
下底
下底
用割的方法推导
上底
高
高
+
高
下底
S1=ah÷2 S2=bh÷2
S梯 =S1+S2 =ah÷2 +bh÷2
=(a+b)h÷2
运用 计算这个梯形面积的正确算式是 （C、D ）。
14
15 12
上底
中位线
高
下底
梯形面积=中位线×高
S=mh
归纳
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2 S=(a+b)÷2×h
梯形的面积= 中位线 ×高
S=mh
运用(求梯形的中位线)单位:厘米
3
5.5 6
7 解：m=(a+b)÷2
=(3+7)÷2 =5（㎝）
运用(求梯形的中位线)单位:厘米
22
18
10
20
解：m=(a+b)÷2 =(18+10)÷2 =14（㎝）
填表（单位：cm）
图形底Βιβλιοθήκη 高 中位线 面积梯形
a 14 7.5 10
75
b6
a8
梯形
b 4？ 5
6
30
梯形 a 10
8 6 48
b2
本节课我们主要学习了用梯形的 中位线来求梯形的面积，你学习的怎 么样？和同桌说一说这一节课你都掌 握了哪些内容？