第3章 连接-2
第3章 平面连杆机构
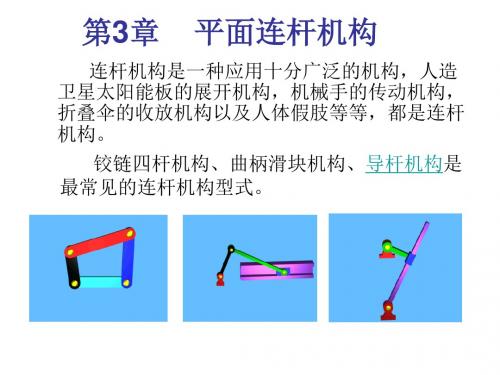
↓ ∞ 曲柄摇杆机构 曲柄滑块机构 偏心曲柄滑块机构
s =l sin φ
φ
l
→∞
对心曲柄滑块机构
双滑块机构
正弦机构
• 正弦机构应用 • 从动件3的位移与原动件转角的正弦成正比
缝纫机针杆机构
• 转动副C→移动副
• 转动副B→移动副
• • • •
转动副A→移动副(杆1 → 块) 椭圆仪: 当滑块1和3沿机架的十字槽滑动时, 连杆2上的各点便描绘出长、短径不同的椭圆 •
广义曲柄存在的条件
• 铰链四杆机构 • A、B为整周转动副的 条件是构件1上的B点 能够通过B1和B2点 • 形成三角形B1DC1和 三角形B2DC2
l2 l3 l4 l1 l3 l2 l4 l1
l2 l1 l3 l4 l3 l1 l2 l4
l4 l1 l2 l3
• 曲柄摇杆机构
平面铰链四杆机构的两个连架杆一个为曲柄,另 一个为摇杆的机构
• 曲柄的连续转动 ↔ 摇杆的连续往复摆动
曲柄摇杆机构的应用
• 抽油机
曲柄摇杆机构的应用
• 牛头刨床横向自动 进给机构 • 调整雷达天线仰角 的曲柄摇杆机构
3.1.2 由曲柄摇杆机构改变机架得到的机构
• 1、双曲柄机构 • 两连架杆均为曲柄 的铰链四杆机构
• 曲柄较短时,通常做成偏心轮 • 增大轴颈的尺寸,提高偏心轴的强度和刚度 • 广泛应用于传力较大的剪床、冲床、颚式破碎 机、内燃机等机械中
多杆机构
• 几个四杆机构组成 多杆机构 • 惯性筛驱动机构 • 两个四杆机构组成 六杆机构 • 原动曲柄2、连杆3 、 从动曲柄4和机架1 组成双曲柄机构 • 曲柄4(原动件)、连 杆5 、滑块6(筛子) 和机架1组成曲柄滑 块机构
第3章2 低压配电系统运行方式

单相接地时,由于短路电流较小,不易检测出故 障,保护装置可能不动作。
单相接地时,另两相电压升高,对绝缘不利,可 能会损坏设备,且增加触电危险。
1.4 安全措施:
绝缘监视
在不接地配电网中,发生一相故障接地时,其 他两相对地电压升高,可能接近相电压,这会增 加绝缘的负担、增加触电的危险。这时,如某设 备另一相漏电,即使该设备上有合格的保护接地, 也不可能将其故障电压限制在安全范围以内。而 且,不接地配电网中一相接地的接地电流很小, 线路和设备还能继续工作,故障可能长时间存在。 这对安全是非常不利的。因此,在不接地配电网 中,需要对配电网进行绝缘监视 ( 接地故障监视 ), 并设置声光双重报警信号。
其中第二个字母表示电气设备外露导电部分 接地方式:T表示独立于电源接地点的直接接地; N为法文Neutre的首字母,表示直接与电源系统接 地点或该点引出的导体相连接。
后续字母表示中性线与保护线的关系:C是法 文Combinaison的首字母,表示中性线与保护线合 并为一根导体;S是法文Separateur的首字母,表 示中性线与保护线分开为两根相互独立的导体。
如不计及带电体与外壳之间的过渡电阻,其大小
为
IE
U RN
RE
由于RE和RN都是欧姆级的电阻,因此,IE 不可能太 大。这种情况下,一般的过电流保护装置不起作 用,不能及时切断电源,使故障长时间延续下去。
2.3 TT系统安全评价:
1)当电气设备的金属外壳带电(相线碰壳或设备绝 缘损坏而漏电)时,由于有接地保护,可以大大 减少触电的危险性。但是,低压断路器(自动开 关)不一定能跳闸,造成漏电设备的外壳对地电 压高于安全电压,属于危险电压。
TT 系统
2.2 TT系统安全原理:
高中数学第三章函数的概念与性质3-2函数的基本性质3-2-1函数的单调性与最值学生用书湘教必修第一册

3.2 函数的基本性质 3.2.1 函数的单调性与最值教材要点要点一 函数最大(小)值设D 是函数f (x )的定义域,I 是D 的一个非空的子集.(1)如果有a ∈D ,使得不等式f (x )≤f (a )对一切x ∈D 成立,就说f (x )在x =a 处取到最大值M =f (a ),称M 为f (x )的最大值,a 为f (x )的最大值点;(2)如果有a ∈D ,使得不等式f (x )≥f (a )对一切x ∈D 成立,就说f (x )在x =a 处取到最小值M =f (a ),称M 为f(x )的最小值,a 为f (x )的最小值点.状元随笔 最大(小)值必须是一个函数值,是值域中的一个元素,如函数y =-x 2(x ∈R )的最大值是0,有f (0)=0.要点二 增函数与减函数的定义状元随笔 定义中的x 1,x 2有以下3个特征(1)任意性,即“任意取x 1,x 2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;(2)有大小,通常规定x 1<x 2; (3)属于同一个单调区间. 要点三 单调性与单调区间如果函数y =f (x )在区间I 上是增函数或减函数,那么就说函数y =f (x )在这一区间上具有(严格的)________,区间I 叫作y =f (x )的________.状元随笔 一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”连接.如函数y =1x 在(-∞,0)和(0,+∞)上单调递减,却不能表述为:函数y =1x 在(-∞,0)∪(0,+∞)上单调递减.基础自测1.思考辨析(正确的画“√”,错误的画“×”) (1)函数f (x )≤1恒成立,则f (x )的最大值是1.( )(2)函数y =f (x )在[1,+∞)上是增函数,则函数的单调递增区间是[1,+∞).( ) (3)函数y =1x 的单调递减区间是(-∞,0)∪(0,+∞).( )(4)如果函数y =f (x )在区间[a ,b ]上单调递减,在区间[b ,c ]上单调递增,则函数y =f (x )在区间[a ,c ]上在x =b 处有最小值f (b ).( )2.函数y =-2x 2+3x 的单调递减区间是( ) A .[0,+∞) B .(-∞,0) C .(−∞,34]D .[34,+∞)3.(多选)如果函数f (x )在[a ,b ]上是增函数,对于任意x 1,x 2∈[a ,b ](x 1≠x 2),则下列结论中正确的是( )A .f (x 1)−f (x 2)x 1−x 2>0B .(x 1-x 2)[f (x 1)-f (x 2)]>0C .f (a )≤f (x 1)<f (x 2)≤f (b )D .f (x 1)>f (x 2)4.函数f (x )在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是________.题型1 利用图象求函数的单调区间例1 已知函数f(x)=x2-4|x|+3,x∈R.(1)将函数写成分段函数的形式;(2)画出函数的图象;(3)根据图象写出它的单调区间.方法归纳(1)求函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等,可根据其单调性写出函数的单调区间,若函数不是上述函数且函数图象容易作出,可作出其图象,根据图象写出其单调区间.(2)一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接.跟踪训练1 (1)已知函数y=f(x)的图象如图所示,则该函数的减区间为( )A.(-3,1)∪(1,4)B.(-5,3)∪(−1,1)C.(-3,-1),(1,4)D.(-5,-3),(-1,1)(2)函数y=-x2+2|x|+3的单调递增区间是__________,递减区间是__________________.题型2 函数的单调性判断与证明例2 用定义证明函数f(x)=x+k(k>0)在(0,+∞)上的单调性.x方法归纳利用定义证明函数单调性的步骤注:作差变形是解题关键.跟踪训练2 已知函数f (x )=xx 2+4,判断并用定义证明f (x )在(0,+∞)上的单调性.题型3 函数单调性的应用 角度1 比较大小例3 已知函数y =f (x )在[0,+∞)上是减函数,则( ) A .f (34)>f (a 2-a +1) B .f (34)<f (a 2-a +1)C .f (34)≥f (a 2-a +1) D .f (34)≤f (a 2-a +1)状元随笔 利用单调性比较函数值或自变量的大小时,要注意将对应的自变量转化到同一个单调区间上.角度2 解不等式例4 f (x )是定义在(-2,2)上的减函数,若f (m -1)>f (2m -1),则实数m 的取值范围是( )A .m >0B .0<m <32 C .-1<m <3D .-12<m <32状元随笔 利用单调性解不等式,就是根据单调性去掉函数的对应法则,构造不等式(不等式组)求解,注意函数的定义域,所有自变量都必须在函数的定义域内.角度3 利用函数的单调性求参数的取值范围例5 若f(x)=-x2+4mx与g(x)=2m在区间[2,4]上都是减函数,则m的取值范围x+1是( )A.(-∞,0)∪(0,1] B.(−1,0)∪(0,1]C.(0,+∞) D.(0,1]方法归纳“函数的单调区间为I”与“函数在区间I上单调”的区别单调区间是一个整体概念,说函数的单调递减区间是I,指的是函数递减的最大范围为区间I,而函数在某一区间上单调,则指此区间是相应单调区间的子区间.所以我们在解决函数的单调性问题时,一定要仔细读题,明确条件含义.角度4 求函数的最值例6 已知函数f(x)=2(x∈[2,6]),求函数的最大值和最小值.x−1方法归纳1.利用单调性求函数的最大(小)值的一般步骤(1)判断函数的单调性.(2)利用单调性求出最大(小)值.2.函数的最大(小)值与单调性的关系(1)若函数f(x)在区间[a,b]上是增(减)函数,则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).(2)若函数f(x)在区间[a,b]上是增(减)函数,在区间[b,c]上是减(增)函数,则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.跟踪训练3 (1)已知函数f (x )=x 2+bx +c 图象的对称轴为直线x =2,则下列关系式正确的是( )A .f (-1)<f (1)<f (2)B .f (1)<f (2)<f (-1)C .f (2)<f (1)<f (-1)D .f (1)<f (-1)<f (2)(2)函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),则实数m 的取值范围是( ) A .(-∞,-3) B .(0,+∞)C .(3,+∞)D .(-∞,-3)∪(3,+∞)(3)已知函数f (x )=|2x -a |的单调递增区间是[3,+∞),则a 的值为________. (4)已知函数f (x )=32x−1,求函数f (x )在[1,5]上的最值.易错辨析 忽视函数的定义例7 已知函数f (x )={−x 2−ax −5(x ≤1),ax(x >1),是R 上的增函数,则a 的取值范围是( )A .-3≤a <0B .a ≤-2C .a <0D .-3≤a ≤-2解析:函数f (x )={−x 2−ax −5(x ≤1),ax (x >1),是R 上的增函数,则f (x )=-x 2-ax -5(x ≤1)单调递增,故它的对称轴-a 2≥1,即a ≤-2,此时f (x )=ax (x >1)也单调递增,所以a <0,要保证在R 上是增函数.还需在x =1处满足-12-a ×1-5≤a1,即a ≥-3.综上所述,-3≤a ≤-2.答案:D 易错警示课堂十分钟1.(多选)如图所示的是定义在区间[-5,5]上的函数y =f (x )的图象,则下列关于函数f (x )的说法正确的是( )A .函数在区间[-5,-3]上单调递增B .函数在区间[1,4]上单调递增C .函数在区间[-3,1]∪[4,5]上单调递减D .函数在区间[-5,5]上没有单调性 2.函数y =1x−1的单调减区间是( )A .(-∞,1),(1,+∞)B .(-∞,1)∪(1,+∞) C{x ∈R |x ≠1}D .R3.函数y =2x+1在[2,3]上的最小值为( ) A .1B .13 C .23D .124.设关于x 的函数y =(k -2)x +1是R 上的增函数,则实数k 的取值范围是________. 5.已知f (x )是定义在[-1,1]上的增函数,且f (x -2)<f (1-x ),求x 的取值范围.3.2 函数的基本性质3.2.1 函数的单调性与最值新知初探·课前预习要点二f(x1)<f(x2) f(x1)>f(x2) 增函数减函数要点三单调性单调区间[基础自测]1.答案:(1)×(2)×(3)×(4)√,+∞).2.解析:借助图象得y=-2x2+3x的单调减区间是[34答案:D3.解析:由函数单调性的定义可知,若函数y=f(x)在给定的区间上是增函数,则x1-x2与f(x1)-f(x2)同号,由此可知,选项A,B正确;对于C,D,因为x1,x2的大小关系无法判断,则f(x1)与f(x2)的大小关系也无法判断,故C、D不正确.故选AB.答案:AB4.解析:由图象知点(1,2)是最高点,点(-2,-1)是最低点,∴y max=2,y min=-1.答案:-1,2题型探究·课堂解透例1 解析:(1)f (x )=x 2-4|x |+3={x 2−4x +3,x ≥0,x 2+4x +3,x <0.(2)如图.(3)由图象可知单调递增区间为[-2,0),[2,+∞),单调递减区间为(-∞,-2),[0,2).跟踪训练1 解析:(1)在某个区间上,若函数y =f (x )的图象是上升的,则该区间为增区间,若是下降的,则该区间为减区间,故该函数的减区间为(-3,-1),(1,4).(2)y =-x 2+2|x |+3={−x 2+2x +3,x ≥0,−x 2−2x +3,x <0.画出函数图象如图,由图可知函数y =-x 2+2|x |+3的单调递增区间是:(-∞,-1],(0,1].递减区间是:[-1,0],[1,+∞).答案:(1)C (2)(-∞,-1],(0,1] [-1,0],[1,+∞) 例2 证明:设x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 1)-f (x 2)=(x 1+k x 1)−(x 2+k x 2)=(x 1-x 2)+(k x 1−k x 2)=(x 1-x 2)+k ·x 2−x1x 1x2=(x 1-x 2)-k ·x 1−x 2x 1x 2=(x 1-x 2)·x 1x 2−k x 1x 2,因为0<x 1<x 2,所以x 1-x 2<0,x 1x 2>0.当x 1,x 2∈(0,√k ]时,x 1x 2-k <0⇒f (x 1)-f (x 2)>0,此时函数f (x )为减函数; 当x 1,x 2∈(√k ,+∞)时,x 1x 2-k >0⇒f (x 1)-f (x 2)<0,此时函数f (x )为增函数. 综上,函数f (x )=x +kx (k >0)在区间(0,√k ]上为减函数,在区间(√k ,+∞)上为增函数.跟踪训练2 解析:f (x )在(0,2)上单调递增,在(2,+∞)上单调递减. 证明如下:∀x 1,x 2∈(0,+∞),且x 1<x 2,有f (x 1)-f (x 2)=x 1x +124-x2x +224=x 1(x +224)-x2(x +124)(x +124)(x +224)=(x 2−x 1)(x 1x 2−4)(x +124)(x +224),因为0<x 1<x 2,所以x 2−x 1>0,(x +124)(x 22+4)>0.当x >2时,x 1x 2−4>0,(x 2−x 1)(x 1x 2−4)(x +124)(x +224)>0,f (x 1)-f (x 2)>0,即f (x 1)>f (x 2),此时f (x )单调递减. 当0<x <2时,x 1x 2−4<0,(x 2−x 1)(x 1x 2−4)(x +124)(x +224)<0,f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),此时f (x )单调递增.所以,f (x )在(0,2)上单调递增,在(2,+∞)上单调递减.例3 解析:∵a 2-a +1=(a −12)2+34≥34.又∵函数y =f (x )在[0,+∞)是减函数,∴f (a 2-a +1)≤f (34).故选C.答案:C例4 解析:由题意知{−2<m −1<2,−2<2m −1<2,m −1<2m −1,解得0<m <32.故选B.答案:B例5 解析:函数f (x )=-x 2+4mx 的图象开口向下,且以直线x =2m 为对称轴,若在区间[2,4]上是减函数,则2m ≤2,解得m ≤1,g (x )=2m x+1的图象由y =2m x 的图象向左平移一个单位长度得到的,若在区间[2,4]上是减函数,则2m >0,解得m >0.综上可得m 的取值范围是(0,1].故选D.答案:D例6 解析:∀x 1,x 2∈[2,6],且x 1<x 2,则f (x 1)-f (x 2)=2x 1−1−2x 2−1=2[(x 2−1)−(x 1−1)](x 1−1)(x 2−1)=2(x 2−x 1)(x 1−1)(x 2−1). 由2≤x 1<x 2≤6,得x 2-x 1>0,(x 1-1)(x 2-1)>0,于是f (x 1)-f (x 2)>0,即f (x 1)>f (x 2).所以,函数f (x )=2x−1在区间[2,6]上单调递减.因此,函数f (x )=2x−1在区间[2,6]的两个端点处分别取得最大值与最小值.在x =2时取得最大值,最大值是2;在x =6时取得最小值,最小值是0.4.跟踪训练3 解析:(1)因为该二次函数的图象开口向上,对称轴为直线x =2,所以f (x )在(-∞,2]上单调递减,因为2>1>-1,所以f (2)<f (1)<f (-1).故选C.(2)因为函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),所以2m >-m +9,即m >3.故选C.(3)f (x )=|2x -a |={2x −a ,x ≥a 2−2x +a ,x <a 2, 所以f (x )=|2x -a |的单调递减区间是(−∞,a 2),单调递增区间是[a 2,+∞), 若函数f (x )=|2x -a |的单调递增区间是[3,+∞),则a 2=3,解得a =6.(4)先证明函数f (x )=32x−1的单调性,设x 1,x 2是区间(12,+∞)上的任意两个实数,且x 2>x 1>12, f (x 1)-f (x 2)=32x1−1−32x 2−1=6(x 2−x 1)(2x 1−1)(2x 2−1). 由于x 2>x 1>12,所以x 2-x 1>0,且(2x 1-1)·(2x 2-1)>0,所以f (x 1)-f (x 2)>0,即f (x 1)>f (x 2),所以函数f (x )=32x−1在区间(12,+∞)上是单调递减的,所以函数f (x )在[1,5]上是单调递减的,因此,函数f (x )=32x−1在区间[1,5]的两个端点上分别取得最大值与最小值,即最大值为f (1)=3,最小值为f (5)=13.答案:(1)C (2)C (3)6 (4)见解析 [课堂十分钟]1.解析:若一个函数出现两个或两个以上的单调性相同的区间,不一定能用“∪”连接.故选ABD.答案:ABD2.解析:单调区间不能写成单调集合,也不能超出定义域,故C ,D 不对,B 表达不当.故选A.答案:A3.解析:∵函数y =2x+1在[2,3]上单调递减,∴当x =3时,y =2x+1有最小值12. 故选D.答案:D4.解析:f (x )为R 上的增函数,则k -2>0,k >2.答案:(2,+∞)5.解析:∵f (x )是定义在[-1,1]上的增函数,且f (x -2)<f (1-x ),∴{−1≤x −2≤1,−1≤1−x ≤1,x −2<1−x ,解得1≤x <32, 所以x 的取值范围为1≤x <32.。
第三章约束受力分析示力图

BⅠ Ⅱ
FA
FCy F K
A
FCx
C
F BD
BⅠ
Ⅱ G
G
★理论力学电子教案
第3章 约束 受力分析示力图
46
谢 谢!
汇报结束
谢谢大家! 请各位批评指正
17
吊臂:
结构的简化 约束的简化1 约束的简化2 荷载的简化 标注尺寸 计算简图
★理论力学电子教案
第3章 约束 受力分析示力图
18
三、 示力图
在确定的考察对象上画上别的物体作用于它的力(包括主动力和约 束力),这样构成的图形称为示力图或受力图,有时也叫隔离体图 。
作示力图是解答力学问题的第一步工作,也是很重要的一步工作,不 能省略,更不容许有任何错误。正确作出示力图,可以清楚表明物体受力 情况和必需的几何关系,有助于对问题分析和所需数学方程的建立,因而 也是求解力学问题的一种有效的手段。如果不画示力图,求解将会发生困 难,乃至无从着手。如果示力图错误,必将导致错误结果,在实际工作中 就会造成生产建设的损失,有时甚至会造成极严重的危害。因此,在学习 力学时,必须一开始就养成良好习惯,认真地、一丝不苟地作示力图,再 据以作进一步的分析计算。
解: 1.物块 B 的受力图。 FD
2. A 的受力图。
FE E A F G1
FI
D
B
HG
C
G2
E
D
A
B
I
G1
G2
★理论力学电子教案
第3章 约束 受力分析示力图
22
3.滑轮 C 的受力图。
J H
FH FCx
G C
FCy
FG
E
A
I
G1
HG C
(完整版)第三章__连接的构造与计算习题及答案
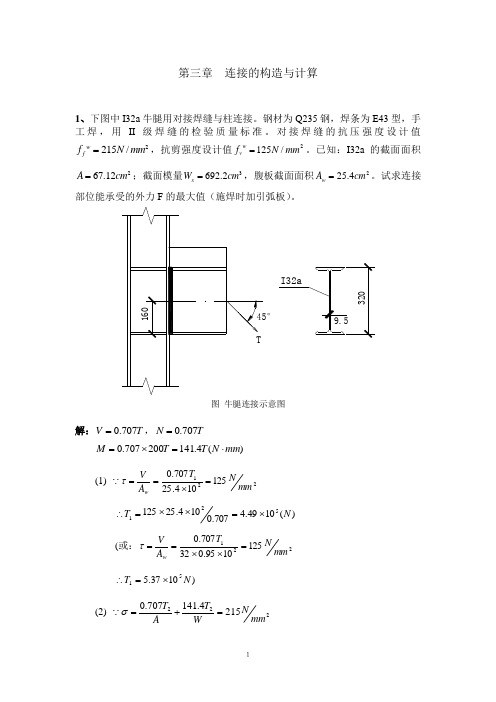
第三章 连接的构造与计算1、下图中I32a 牛腿用对接焊缝与柱连接。
钢材为Q235钢,焊条为E43型,手工焊,用II 级焊缝的检验质量标准。
对接焊缝的抗压强度设计值2215/w f f N mm =,抗剪强度设计值2125/w v f N mm =。
已知:I32a 的截面面积267.12A cm =;截面模量3692.2x W cm =,腹板截面面积225.4w A cm =。
试求连接部位能承受的外力F 的最大值(施焊时加引弧板)。
°图 牛腿连接示意图解:T V 707.0=,T N 707.0=)(4.141200707.0mm N T T M ⋅=⨯=(1) 221125104.25707.0mm N T A V w =⨯==τ )(1049.4707.0104.25125521N T ⨯=⨯⨯=∴(或:2211251095.032707.0mm N T A Vw =⨯⨯==τ )1037.551N T ⨯=∴(2) 2222154.141707.0mm N WT A T =+=σ2232215)102.6924.1411012.67707.0(mm N T =⨯+⨯∴ )(1094.652N T ⨯=∴(3) 折算应力(在顶部中点亦可)()2151.11.1000555.0000278.03000276.03)000233.0104.30707.0( 000278.0104.25707.0000276.01605.26160102.6924.1411012.67707.03322212133213321333231⨯=≤=⨯+=+=⨯==⨯==-⨯⨯+⨯=w f f T T T T T T T T T τσττσ或得:)(1.4263KN T ≤ (KN T f T 3wf 33.484 1.10.000488≤≤或)由T 1、T 2、T 3中取最小值,得T =426.1(KN )m KN M Nmm ⋅=⨯⨯=4104105 N V 5104⨯=f ff f h h W M 6.4283.93331046=⨯==σ22.1=f β, f ff f h h A V 6.14282801045=⨯==τ 2002.1471)6.1428()22.16.428()(2222≤=+=+ff f f f f h h h τβσ mm h f 4.7≥,取mm h f 8=.3、如图所示的牛腿用角焊缝与柱连接。
第3章2 流体动力学基础-伯努利方程的应用

30
2
4
V2 A2 V1 A1
V12 p 1 0.198 H 2 1 1.5 2.72 4.22m水柱 2g V12 5.26m水柱 2g
列断面0-0和真空室断面1-1的能量方程
p0
V12 H1 H 2 2g p1
V12 H1 H 2 2.72 5.26 1.5 1.04m 2g 上述计算中没有考虑管道中的能量损失,而实际上若要用 射流泵产生上述真空,水箱应? p1
p1
p真
0.2 13.6 2.72m水柱
出水口通大气,水池液面通大气,p2=p0=0。 对断面1-1、2-2列能量方程:
p1
V12 p2 V22 H2 2g 2g
A d 50 V22 V12 1 V12 1 V12 0.198V12 A2 d 2 75
27
A 2 p A pC V A 1 2 g AC
2 A
因为AA>AC,上式左端为正值,即PC<PA,而AC越小则PC值越 低。当PC比大气压还要低时,若在C处把管子开一小孔,管内 液体并不会漏出来,而外面的空气却反而会被大气压压进管子。 若在小孔上接一根管子,其下端浸在液箱中,则管内液面在大 气压的作用下会上升。 当
现取水流进入喷嘴前的A断面和水流流出喷嘴时的C断面列能 量方程(暂时不考虑能量损失)
pA
2 VA pC VC2 2g 2g
移项
p A pC
VC2 VA2 2g
p A pC
VA2 AA 1 2 g AC
03.2.铆钉和螺栓连接的计算
§3.3.3 铆钉和螺栓连接的计算
第3章 剪切
铆钉连接主要有三种方式:1.搭接(图a),铆钉受单剪;2.单盖 板对接(图b),铆钉受单剪;3.双盖板对接(图c),铆钉受双剪。
第1页,共10页。
第1页
建筑组铆钉来传力,在此情况下, 由于铆钉和被连接件的弹性变形,所以铆钉组中位于两端的铆钉 所传递的力要比中间的铆钉所传递的力大。
第3页,共10页。
第3页
建筑工程学院
第3章 剪切
例题 8-8 某钢桁架的一个节点如图a所示。斜杆A由两根63 mm×6 mm的等边角钢组成,受轴向力F =140 kN作用。该斜杆用直径为d =16 mm螺栓连接在厚度为10 mm的结点板上,螺栓按单行排列。已知角钢、
结点板和螺栓材料均为Q235钢,许用应力为[s ]=170 MPa,[t ]=130
MPa,[sbs]=300 MPa。试选择所需的螺栓个数并校核角钢的拉伸强度。
第4页,共10页。
第4页
建筑工程学院
第3章 剪切
解:1.按剪切强度条件选择螺栓个数
由于此连接中各螺栓的材料和直径相同,且斜杆上的轴向力 其作用线通过该组螺栓的截面形心,故认为每个螺栓所传递的力 相等,为F/n,此处 n为螺栓个数。
斜杆上三个螺栓按单行 排列(图b)。图c示出了该 斜杆(含两角钢)的受力图 和轴力FN图。
该斜杆在图c中所示的 m-m截面上轴力最大,而净 截面面积又最小,故为危险 截面。
第9页,共10页。
第9页
建筑工程学院
该截面上:
第3章 剪切
FN,max=F=140 kN
由型钢规格表可查得每根 63 mm×6 mm 等边角钢的横截面面积为 7.29 cm2,故危险截面的净面积为
人教版高中生物选择性必修3第3章第2节课时练习含答案
第3章第2节[基础达标]题组一目的基因的筛选与获取1.在基因工程的基本操作程序中,目的基因的获取途径不包括()A.从基因文库中获取目的基因B.利用PCR技术扩增目的基因C.人工合成目的基因D.利用DNA分子杂交技术,获取目的基因【答案】D【解析】可以从基因文库中获取目的基因,A不符合题意;获取目的基因的方法之一是PCR技术,B不符合题意;可以通过人工合成的方法获取目的基因,C不符合题意;DNA 分子杂交技术不能用于获取目的基因,D符合题意。
2.(2023·广东广州阶段练习)PCR是一种体外迅速扩增DNA片段的技术。
PCR过程一般经历下述30多次循环:95 ℃下使模板DNA变性、解链→55 ℃下复性(引物与DNA模板链结合)→72 ℃下引物链延伸(形成新的DNA链)。
下列有关PCR过程的叙述中不正确的是() A.变性过程中破坏的是DNA分子内碱基对之间的氢键B.复性过程中引物与DNA模板链的结合是依靠碱基互补配对原则完成C.延伸过程中需要DNA聚合酶、A TP、四种核糖核苷酸D.PCR与细胞内DNA复制相比所需酶的最适温度较高【答案】C【解析】变性是DNA分子解旋,该过程中破坏的是DNA分子内碱基对之间的氢键,A 正确;复性过程中引物与DNA模板链的结合是依靠碱基互补配对原则完成的,B正确;延伸是合成DNA的子链,所以该过程中需要DNA聚合酶、A TP、四种脱氧核糖核苷酸,C错误;PCR与细胞内DNA复制相比所需酶的最适温度较高,因为PCR过程需要高温变性,即使在复性时的温度也比较高,D正确。
题组二基因表达载体的构建3.下列对基因表达载体构建的叙述,不正确的是()A.需要限制酶和DNA连接酶等特殊工具B.基因表达载体中有的含有启动子和密码子C.标记基因不一定是抗生素抗性基因D.基因表达载体的构建是基因工程的核心【答案】B【解析】基因表达载体是目的基因与载体的结合,在此过程中通常用同一种限制酶切割目的基因与载体,用DNA连接酶将相同的末端连接起来,A正确;基因表达载体含有启动子、终止子、标记基因和目的基因,密码子位于mRNA上,B错误;抗生素抗性基因可作为标记基因,但标记基因不都是抗生素抗性基因,C正确;基因表达载体的构建是基因工程的核心,在细胞外进行,使目的基因在受体细胞中稳定存在并且可以遗传给下一代并表达和发挥作用,D正确。
运动控制_第3章____转速、电流双闭环直流调速系统
第3章 转速、电流双闭环直流调速系统
当U*n一定时,转速n将稳定在U*n /α数值上。当 n<U*n /α,在突加负载TL时,其自动调节过程如下:
TL↑→n↓→Un↓→ΔUn↑→U*i↑→ΔUi↑ →Uct↑→Ud↑→n↑
最终保持转速稳定。当负载减小,转速上升时,也有类似的 调节过程。
第3章 转速、电流双闭环直流调速系统
最终使转速保持恒定,即ΔUn=U*n-Un=0,
n
U
* n
,如图3-5
中的CA段虚线所示。
第3章 转速、电流双闭环直流调速系统
但是由于转速环是外环,起主导作用,而电流环的作用 只相当于转速环内部的一种扰动作用,因而只要转速环的开 环放大倍数足够大,最终靠ASR的积分作用,可以消除转速 偏差。因此,双闭环系统的稳态特性具有近似理想的“挖土 机特性”(如图3-5中实线所示)。
Un* Un n n0
(3-1)
n
n0
U
* n
(3-2)
第3章 转速、电流双闭环直流调速系统
Ui* Ui I d I dL
(3-3)
Uc
Ud0 Ks
Cen IdR Ks
CeUn* / IdLR
Ks
(3-4)
第3章 转速、电流双闭环直流调速系统
第3章 转速、电流双闭环直流调速系统
此时,电流
I
d
U
* im
I dm
,Idm为最大电流,是由设
计者选定的,取决于电动机的容许过载能力和拖动系统允许
的最大加速度,一般选择为额定电流IdN的1.5~2倍。 注意,图3-5中的AB段下垂特性只适合于n<n0(n0为电动
计算机通信与网络_第3章习题解答
第三章习题解答3.1 简述数据链路层的功能。
答:数据链路层是在物理层提供的比特流传送服务的基础上,通过一系列的控制和管理,构成透明的、相对无差错的数据链路,向网络层提供可靠、有效的数据帧传送的服务。
其主要功能包括:链路管理,帧定界,流量控制,差错控制,数据和控制信息的识别,透明传输,寻址。
3.2 试解释以下名词:数据电路,数据链路,主站,从站,复合站。
答:数据电路是一条点到点的,由传输信道及其两端的DCE构成的物理电路段,中间没有交换节点。
数据电路又称为物理链路,或简称为链路。
数据链路是在数据电路的基础上增加传输控制的功能构成的。
一般来说,通信的收发双方只有建立了一条数据链路,通信才能够有效地进行。
在链路中,所连接的节点称为“站”。
发送命令或信息的站称为“主站”,在通信过程中一般起控制作用;接收数据或命令并做出响应的站称为“从站”,在通信过程中处于受控地位。
同时具有主站和从站功能的,能够发出命令和响应信息的站称为复合站。
3.3 数据链路层流量控制的作用和主要功能是什么?答:流量控制简称“流控”,是协调链路两端的发送站、接收站之间的数据流量,以保证双方的数据发送和接收达到平衡的一种技术。
在计算机网络中,由于接收方往往需要对接收的信息进行识别和处理,需要较多的时间,通常发送方的发送速率要大于接收方的接收能力。
当接收方的接收处理能力小于发送方的发送能力时,必须限制发送方的发送速率,否则会造成数据的丢失。
流量控制就是一种反馈机制,接收方随时向发送方报告自己的接收情况,限制发送方的发送速率。
保证接收方能够正常、有序地接收数据。
3.4 在停止-等待协议中,确认帧是否需要序号?为什么?答:在停止-等待协议中,由于每次只确认一个已经发送的帧,确认帧可以不需要序号。
但在一些特殊情况下会出现问题。
如果发送方在超时重发一个帧后又收到了迟到的确认,就不能确定该应答是对哪一个帧的确认,并可能导致随后的传送过程重新差错。
3.5 解释为什么要从停止-等待协议发展到连续ARQ协议。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a max
Mya 27.2 106 68.9 143.6N/mm2 ft w 300N/mm 2 Iw 13.05 106
b max
Myb 27.2 106 (190 12 68.9) Iw 13.05 106 277.4 N/mm 2 f cw 350 N/mm 2
V S w1 240 103 2.032 106 1 16.8 N/mm 2 Iw tw 2898 106 10
eq 1 31
2
2
173.92 3 16.82 176.3N/mm 2
1.1 f t w 1.1185 203.5N/mm 2,满足。
§3.3 角焊缝的构造和计算
4 3
5
F
200
200
第3章
Chapter 3
连
接
Connections
2. 焊缝截面上的有效应力
把F分解成两个分力并移至焊缝形心O处,焊缝实际受力为: 水平轴心力 剪力 弯矩
焊缝有效截面上应力分量为: N 0.6F N = =1.40F 10-4 N/mm 2 Ae 43.01102
f f w 160 N/mm 2 角焊缝设计强度值
K1=0.7,K2=0.3,lw3=b=125mm
§3.3
角焊缝的构造和计算
第3章
Chapter 3
连
接
Connections
正面角焊缝所能承受的内力N3为:
§3.3
角焊缝的构造和计算
第3章
Chapter 3
连
接
Connections
例3.10验算图示双面角焊缝连接的强度。已知连接承受动荷载,钢 材为Q235BF,焊条为E43。f w 160N/mm 2 f F1=180kN 【解】 将外力F1,F2 移向焊缝形心O,得:
板书讲解
第3章
Chapter 3
连
接
Connections
【例题3.5】 验算如图所示牛腿与柱的对接焊缝连接。F=170kN,钢材 Q390,E55焊条,手工焊,质量等级为三级,不采用引弧板。
160 F a
—120×12
96 12 10 190
a M
max
b
—200×10
b M
§3.2
对接焊缝的构造和计算
max
V 170 103 89.5N/mm2 f vw 205N/mm2,满足。 Aw 1900
b eq M 2 3 max 2 277.42 3 89.52
317.8N/mm 2 1.1 f t w 1.1 300 330 N/mm 2,满足。
2
160 104 F 580 103 N=580kN 2.76
当e=0,M=0,焊缝强度应满足:
fN 2 4 1.40 f F 10 1.862 f f w 160N/mm2 f 1.22
2
2
160 10 4 F 731103 N=731kN 2.19
max
VS w I wt
240 103 2.032 106 2898 106 10 27.2 N/mm 2 f vw 125N/mm 2,满足。
1000 h0 179.5 173.9 N/mm 2 1032 h
max
1
max
1
1 max
250 10323 240 10003 Iw 2898 106 mm 4 12 Iw 2898 106 Ww 5.6163 106 mm 3 ymax 516
S w1 250 16 508 2.032 106 mm 3
S w S w1 500 10 250 3.282 106 mm 3
§3.2 对接焊缝的构造和计算
第3章
Chapter 3
连
接
Connections
2. 焊缝强度计算
w 查表,f t w 185N/mm 2 , f V 125N/mm 2 M 1008 106 max 179.5N/mm 2 f t w 185N/mm 2 , 满足。 Ww 5.6163 106
h 构造要求:f max 1.2tmin 1.2 8 9.6mm hfmin 1.5 tmax 1.5 10 4.74mm 取 hf =6mm
连接承受动力荷载: f 1.0
N 180 10 3 f 94 .0 N / mm 2 0.7h f lw 2 0.7 6 240 2 6 V 240 10 3 f 125 .3 N / mm 2 0.7h f lw 2 0.7 6 240 2 6
第3章
Chapter 3
连
96
接
x yc x0
Connections
【解】
1. 截面几何特征值计算
12 96 6 10 190 (95 12) yc 68.9mm 12 96 10 190
12
190
Aw 10 190 1900 mm 2
10
96 123 190 103 190 2 2 Iw 96 12 (68.9 6) 190 10 (190 12 68.9 ) 12 12 2 13.05 106 mm 4
第3章
Chapter 3
连
接
Connections
1. 焊缝有效截面的几何性质
取
hf 8mm hf max 1.2t min 1.2 8 9.6mm hfmin 1.5 t max 1.5 20 6.7 mm
两条竖向焊缝的有效截面面积:
Ae 2 0.7 8 38 2 1.5 2 0.8 37.4cm2
第3章
Chapter 3
连
接
Connections
【例题3.4】 计算三块钢板焊成工字形截面的对接焊缝(如图所示)。已 知截面尺寸为:翼缘板宽度b1=100mm, 厚度t1=12mm ,腹板 高度h=200mm,厚度t=8mm。轴向拉力N=200kN,作用在焊 缝上的弯矩M=40kN.m ,作用在焊缝上的剪切力V=240kN 。 钢材为Q345钢,采用手工焊,焊缝质量为二级,焊条E50, 施焊时用引弧板。
3 N F 0.6 F 5 4 V F 0.8F 5 3 M Fe F 50 30 F 5
(e=5cm)
M
M 30F = =1.09F 10-4 N/mm2 We 275 103
V 0.8F f = =1.86F 10-4 N/mm 2 Ae 43.01102
§3.3 角焊缝的构造和计算
可见当连接存在偏心时将较大的降低其承载力
第3章
Chapter 3
连
接
Connections
例3.12 试设计如图a所示牛腿和柱连接的角焊缝。已知F=420kN(静 力荷载),钢材为Q235B,焊条为E43,手工焊。
F
fB
fA
fB
【解】 (a)
(b)
(c)
采用如图b所示沿牛腿周边围焊的角焊缝,且再转角处连续施焊。为 避免焊缝相交的不利影响,将牛腿的上下角切去r=15 mm的弧形缺口, 因此可取焊缝的有效截面如图c所示。 力F在角焊缝形心处引起的剪力:V=420kN 弯矩:M=Fe=420×0.3=126kN.m,由于牛腿翼缘竖向刚度低,故一般 考虑剪力由腹板上两条竖向焊缝承受,弯矩则由全部焊缝承受。
板书讲解
第3章
Chapter 3
连
接
Connections
例题3.9 试确定图3.3.15所示承受静态轴心力的三面围焊连接 的承载力及肢尖焊缝的长度。已知角钢2∟125×10,与厚度 为8mm的节点板连接,其搭接长度为300mm,焊脚尺寸 hf=8mm,钢材为Q235-B,手工焊,焊条为E43型。 解:
焊缝的有效截面面积:
Ae 2 0.7 0.8 40 2 0.8 43.01cm2
1 0.7 0.8 38.43 5285cm4 12 Iw 5285 截面模量: We 275 cm3 20 h f 20 0.8
惯性矩: I w 2
板书讲解
第3章
Chapter 3
连
接
Connections
【例题3.3】
验算如图所示的钢板对接焊缝的连接。M=1008kN.m,V=240KN, 钢材Q235,E43焊条,手工焊,质量等级为三级,采用引弧板。
16 M V 10
max
1
1
250
1000 16
max
1
【解】
1. 截面几何特征值计算
M 180 120 240 90 0
N F1 180kN V F2 240kN
240
120 t=8 90 F2=240kN t=10
f f
§3.3
角焊缝的构造和计算
2 94.0 2 2 w 2 2 125 .3 156 .6 N / mm f f 160 N / mm f 1.0 强度满足要求
角焊缝的构造和计算
第3章
Chapter 3
连
接
Connections
例题3.7 条件同例题3.6,现改为三面围焊,试设计该拼 lw 接板。 N
B lw
’
Chapter 3
连
接
Connections
例题3.8 试验算如图所示直角角焊缝的强度。已知焊缝承受的 斜向静力荷载设计值F=280kN,θ=60°,角焊缝的焊角尺寸hf = 8mm ,实际长度l =155mm,钢材为Q235B,手工焊,焊条为 E43 型。
