数学建模模拟题,图论,回归模型,聚类分析,因子分析等 ()
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (10)

(利用聚类分析对省、自治区分类)摘要本题旨在通过聚类分析将这些省、自治区进行分类。
我们利用spss软件,对数据进行分类。
通过对其所包含的信息量的比重来选择应该分为几类。
关键词:聚类分析Ⅰ问题重述1.1 表49 是1999 年中国省、自治区的城市规模结构特征的一些数据,试通过聚类分析将这些省、自治区进行分类。
表49城市规模结构特征数据Ⅱ模型假设Ⅲ符号说明Ⅳ模型建立及求解5.1.问题分析本题通过给出1999 年中国省、自治区的城市规模结构特征的一些数据,让我们利用聚类分析的方法,将这些省、自治区进行分类。
5.2.模型建立及求解我们可以利用spss软件对该问题进行求解。
在计算过程当中,我们不妨先检验其是否能包含题中数据信息的85%以上。
所以,我们先检验其是否符合因子分析,经验证P 值为0,适合做因子分析(详见表一)。
所以我们开始验证能分几组就能包含总信息的85%以上。
经验证,当分为三类时,其所包含的信息量为90.274%(详见表二)。
所以,我们不妨将省、自治区分为3类。
通过应用spss软件16.0版本,得到问题的求解。
具体为表三所示。
即其具体的分类为:Ⅴ模型评价与改进该题应用聚类分析将这些省、自治区进行分类。
通过图表的形式呈现较为简便。
但是在分类的过程中,由于我们只将其分为3类,不能包含题中数据所呈现的全部内容。
所以不具有普遍性。
对此,我们应尽量的多分几组,使得其涵盖的内容更为全面。
参考文献[编号] 作者,书名,出版地:出版社,出版年。
[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
[编号] 作者,资源标题,网址,访问时间(年月日)。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (5)

(习题11.1 单样本方差分析——关于抗生素与血浆蛋白质结合有无显著性差异的研究)摘要将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象,以致减少了药效。
所以,通过研究5种常用的抗生素注入到牛的体内时,抗生素与血浆蛋白质结合的百分比,来对其进行相关的研究。
本题利用单样本方差分析的方法,研究在样本服从正态分布且方差相等的情况下,各类抗生素与血浆蛋白质结合的百分比的均值有无显著性的差异。
通过建立模型以及求解得知,P值为6.7398e-08小于α(α的取值为0.05)。
所以我们认为各类抗生素与血浆蛋白质结合的百分比的均值有显著性的差异。
关键词:单样本方差分析描述分布特征的统计量Ⅰ问题重述1.1将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象,以致减少了药效。
所以该题研究了5种常用的抗生素注入到牛的体内时,抗生素与血浆蛋白质结合的百分比。
试在水平α= 0.05 下检验这些百分比的均值有无显著的差异。
设各总体服从正Ⅱ模型假设假设一:该样本数据真实可靠。
能够反映真实情况。
假设二:各样本总体服从正态分布,且方差相同。
假设三:所选的牛的体质是一样的。
忽略其他因素对实验数据的影响。
Ⅲ符号说明1μ表示青霉素1x 的均值。
2μ表示四环素2x 的均值。
3μ表示链霉素3x 的均值。
4μ表示红霉素4x 的均值。
5μ表示氯霉素5x 的均值。
IV 模型建立及求解3.1对该问题的分析对于该问题,是研究抗生素与血浆蛋白质结合的百分比的均值有无显著性的差异。
即只考虑血浆蛋白质对抗生素的影响,而其他影响因素都保持不变。
3.2模型建立及求解假设各总体服从正态分布,且方差相同。
即各类抗生素均服从总体i x 的正态分布2(,)i N μσ,1,2,3,4,5i =。
又设j n 为第j 次试验,1,2,3,4j =。
所以我们不妨提出原假设0H :12345μμμμμ====;112345:,,,,H μμμμμ不全相等。
故其模型为:()51200,,1,2,3,4,5;1,2,3,4ij i ij i i ij x N i j μαεαεα=⎧=++⎪⎪=⎨⎪⎪==⎩∑ 注:μ为总均值。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (44)
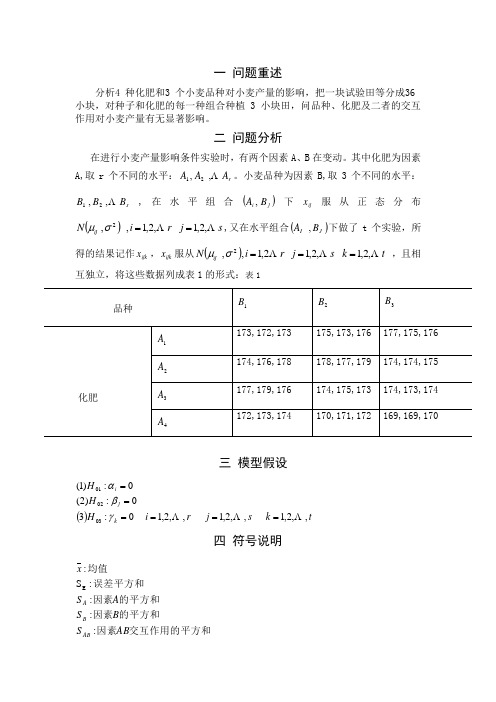
一 问题重述分析4 种化肥和3 个小麦品种对小麦产量的影响,把一块试验田等分成36 小块,对种子和化肥的每一种组合种植 3 小块田,问品种、化肥及二者的交互作用对小麦产量有无显著影响。
二 问题分析在进行小麦产量影响条件实验时,有两个因素A 、B 在变动。
其中化肥为因素A,取r 个不同的水平:r A A A ,,21。
小麦品种为因素B,取3个不同的水平:sB B B ,,21,在水平组合()jiB A ,下ij x 服从正态分布()s j r i N ij ,2,1,2,1,,2==σμ,又在水平组合()J I B A ,下做了t 个实验,所得的结果记作ijk x ,ijk x 服从()t k s j r i N ij ,2,1,2,12,1,,2===σμ ,且相互独立,将这些数据列成表1的形式:表1三 模型假设()tk s j r i H H H kj i ,,2,1,,2,1,,2,10:30:)2(0:)1(030201 ======γβα四 符号说明交互作用的平方和因素的平方和因素的平方和因素误差平方和均值AB S B S A S x AB B A ::::S :E五 模型建立将ijk x 分解为:t k s j r i x ijk ij ijk ,2,1,2,12,1,===+=εμ 其中 ()2,0~σεN ijk ,且相互独立,记∑∑∑====r i s j tk ijk x rs x 1111∑∑∑∑∑====∙∙∙∙=∙===s j r i tk ijk tk j ijk i t k ijk ij x rt x x st x x t x 111111,1,1 将全体数据对x 的偏差平方和 ()∑∑∑===-=ri sj tk ijk T x x S 1112进行分解得:AB B A E T S S S S S +++= 其中 ()∑∑∑===∙-=ri sj tk ij ijk E x x S 1112()∑=∙∙-=ri i Ax x st S12()∑=∙∙-=sj j B x x rt S 12()∑=∙∙∙∙∙+--=ri j i ij AB x x x x st S 12x x x x xx j ij i -=-=-=∙∙∙∙∙γβα建立模型s.t.()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧=====+++=∑∑∑===tk s j r i N x x ijktk k sj j ri i k j i ijk ,2,1,2,1,,2,1,,0~002111σεγβαγβα六 模型求解利用spss13.0软件通过编写程序(程序见)得出:由表可知:化肥对小麦的产量影响较大,品种次之,交互作用对产量基本没有影响。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等(74)

利用主成分分析法建立多元回归模型一问题重述对某种商品的销量y 进行调查,并考虑有关的四个因素:—居民可支配收入,-该商品的平均价格指数,-该商品的社会保有量,-其它消费品平均价格指数。
表16是调查数据。
利用主成分方法建立y 与的回归方程。
二问题分析该问题要求我们利用主成分分析法建立的回归方程,首先我们从题目条件可知该问题属于回归分析方面的问题。
因此,我们先从题目所给的数据入手,首先对原始数据进行标准化处理,即利用标准化公式将观测值化为标准值;接着我们求出相关系数矩阵,从而求出该相关系数矩阵的特征值和特征向量;然后我们得到主成分,从而得到主成分回归方程;最后根据以上过程建立回归模型。
三模型假设四符号说明五模型建立与求解5.1对数据进行标准化处理标准化处理[1]:所谓标准化处理,是指对数据同时进行中心化——压缩处理,即将的n次观测值分别记作,,然后利用公式;其中根据以上公式得到标准化数据。
同理,将的观测值也进行标准化处理,并记作5.2根据标准化数据计算相关系数矩阵R相关系数矩阵R=,其中。
5.3根据相关系数矩阵计算特征值和特征向量编写相应的程序,利用matlab7.0.1运行程序(程序见附录)求的相关系数矩阵的4个特征值分别为它们对应的四个标准正交化特征向量分别为因此求得的四个主成分分别为:从而求得前两个主成分的贡献率为,所以我们剔除第三个和第四个主成分,只取第一个和第二个主成分。
综上得到关于主成分的回归方程为化为关于标准数据的回归方程最后得到关于观测值的回归模型为并且该模型的剩余标准差为参考文献[1] 司守奎,数学建模算法与程序:国防工业出版社,2011年8月1日。
附录利用matlab7.0.1编写的程序clc,clearload sn.txt[m,n]=size(sn);X0=sn(:1:n-1);y0=sn(:,n);r=corrcoef(x0);xb=zscore(x0);yb=zscore(y0);[c,s,t]=princomp(xb)Contr=cumsum(t)/sum(t)Num=input(‘qingxuanzezhuchengfendegeshu:’)Hg=s(:,1:num)ybhg=c(:,1:num)*hghg2=[mean(y0)-std(y0)*mean(x0)./std(x0)*hg,std’(y0)*hg’./std(x0)] fprintf(‘y=%f,hg2(1));for i=1:n-1fprintf(+%f*x%d,hg2(i+1),i);endfprintf(‘\n’)rmse2=sqrt(s um((x0*hg2(2:end)’+hg2(1)-y0).^2)/(m-num-1))。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (32)

第五章第八题摘要关键词:Ⅰ问题重述某公司计划推出一种新型产品,需要一系列完成的工作(详见图表)问题一:根据所给表格及其各个作业的相关关系画出产品的计划网络图问题二:求完成新产品的最短时间,列出各项作业的最早开始时间、最迟开始时间和计划网络的关键路线问题三:假定公司计划在17 周内推出该产品,各项作业的最短时间和缩短1 周的费,求产品在17 周内上市的最小费用问题四:如果各项作业的完成时间并不能完全确定,而是根据以往的经验估计出来的,其估计值如表所示。
试计算出产品在21 周内上市的概率和以95%的概率完成新产品上市所需的周数。
Ⅱ问题分析Ⅲ模型假设Ⅳ符号说明(1)x是事件i的开始时间,i(2)1为最初事件,n为最终事件(3)t是作业()j i,的计划时间ijⅤ模型建立Ⅵ模型求解根据图表所给紧前作业与作业的先后顺序我们可以画出如图示的计划网图图一计划网络图x是事件i的开始时间,1为最初事件,n为最终事件。
希望总的工期最设i短,即极小化1x x n -。
设ij t 是作业()j i ,的计划时间,因此,对于事件i 与事件j 有不等式设 i x 是事件i 的开始时间,1为最初事件,n 为最终事件。
希望总的工期最短,即极小化1x x n -。
设ij t 是作业()j i ,的计划时间,因此,对于事件i 与事件j 有不等式ij i j t x x +≥由此得到相应的数学规划问题1min x x n -..t s ()⎩⎨⎧∈≥∈∈+≥Vi x Vj i A j i t x x i ij i j ,0,,,, 其中V 是所有的事件集合,A 是所有的作业集合。
根据题目要求用lingo11.0编写程序(见附录)得到问题的解:图二 新产品最短时间根据图示结果可得:01=x ,则作业B A ,的开工时间均是第0天,62=x 作业C 的开工时间是第6天;03=x 则作业F 的工时间是第6天;等等。
每个作业只要按规定的时间开工,整个项目的最短工期为20天Ⅶ模型评价与改进参考文献[编号] 作者,书名,出版地:出版社,出版年。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (51)

第11章第3题摘要商品的销售量与商品销售点所在的地理位置、销售点处的广告和销售点的装潢,服务态度,售后服务等多种因素有关,本题考察了销售点所在地理位置、销售点处得广告和销售点的装潢三个因素对销售量得影响。
需进行多因素方差分析,从而判断三因素的显著性。
关键词:显著性三因素方差分析不同水平一.问题重述某集团为了研究商品销售点所在的地理位置、销售点处的广告和销售点的装潢这三个因素对商品的影响程度,选择了三个位置,分别为市中心黄金地段、非中心的地段、城乡结合部,两种不同的广告形式,两种不同的装潢档次在四个城市进行了搭配试验。
表1是试验的销售量的数据。
问:在显著水平0.05下,检验不同地理位置、不同广告、不同装潢下的销售量是否有显著差异?二.问题分析本题为了研究商品销售点所在的不同地理位置、销售点处的广告和销售点的装潢这三个因素对商品的影响程度,所以将地理位置、销售点处的广告和销售点的装潢作为三个因素。
市中心黄金地段、非中心的地段、城乡结合部这三个位置看作是地理位置的三个水平,两种广告形式视为销售点处的广告的两个不同水平,两种不同装潢档次视为销售点装潢的两个不同水平。
要求三个因素是否存在显著性差异,就是对三个因素进行多因素方差分析,可得三个因素的显著性。
三.模型假设1.假设只考虑商品销售点所在的地理位置、销售点处的广告和销售点的装潢这三个因素,不存在其他因素对结果构成影响。
2.假设试验时数据真实,没有记录错误。
3.假设试验中所有产品质量等各因素相同。
四.符号说明A1——市中心黄金地段A2——非中心的地段A3——城乡结合部B1,B2——两种不同的广告形式C1,C2——两种不同的装潢档次五.模型建立根据题意,想要分析销售点所在的地理位置、销售点处的广告和销售点的装潢这三个因素对销售量的影响,就是进行显著性差异分析。
将表1的数据转化整理得到表2如下:异。
六.模型求解通过spss软件求解,得到结果如下表:表3表4由表4可以知道,三个不同的地理位置、两种不同的广告形式和两个不同的装潢档次的p值均为0,小于显著水平0.05,所以都存在显著性差异。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (7)

(习题12.2)关于样本点距离与该点处某金属含量的回归关系摘要本文通过建立回归模型,运用进行多曲线拟合,对距离样本点的距离与该点处某金属的含量建立线性回归关系。
对于题中所给的有限组数据,我们编写程序,运用MATLAB8.1.0软件对其先做散点图分析,通过观察图示,初步定性的得出,二者之间的确存在着某种线性关联。
然后,根据经验,确定满足条件的若干条曲线,运用spss16.0软件,对其进行多曲线拟合,由所得结果确定最佳拟合曲线为二次曲线,然后建立二次曲线线性回归模型2210y a x a x a =++,最后求解出参数,模型为20.00280.1692108.8969y x x =-++。
该模型在建立时,进行多次定性定量的分析,具有较高的可行性,所得结果具有一定的科学性和较高的可信度,对于解决实际问题具有较大的参考价值。
关键词:线性回归模型、散点图、曲线拟合、定性分析、定量分析一 问题重述一矿脉有13个相邻样本点,人为地设定一原点,现测得各样本点对原点的距离x ,与该样本点处某种金属含量y 的一组数据如表1,画出散点图观测二者的关系,试建立合适的回归模型,如二次曲线、双曲线、对数曲线等。
表1二 问题分析由题意可得,x 和y 存在某种线性回归关系。
在表1中所给的13组数据中,可先画出散点图,对两者的关系做一个定性的判断,然后,模拟多种模型,从中选择出模拟效果最好的一个,建立模型,最后求解模型系数,确定二者之间的线性关系。
三 模型假设3.1 该题中所给的13组数据具有一定的代表性和概括性。
3.2 所求解的模型基于人工设定的该原点的条件下。
四 符号说明4.1 210,,:a a a 模拟方程的系数。
五 模型建立与求解5.1 模型的分析我们对表1中的数据进行录入,编写程序(源程序见附件程序1)用MATLAB8.1.0软件,得出x 与y 的散点图(图1)图1.散点图由图1可知,x与y的确存在某种线性关系。
进而,我们又用spss16.0软件,假定存在多种曲线关系,根据经验,我们选定一次曲线、二次曲线、对数曲线对图1上的点进行拟合,得到如下结果以及图2的拟合效果曲线。
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (27)

(用二人非常数和对策解决两人摸三张牌问题)摘要该题讲有三张牌,点数分别为1,2,3,大小顺序按照3>2>1,通过对两人摸牌原则和给谁钱原则的分析,该问题总结为二人非常数和对策纯策略问题。
首先就问题进行分析,要设置局中人A 和B 的赢得矩阵,设局中人A 有m 个策略m αα ,1,局中人B 有n 个策略n ββ ,1,分别记为{}m s αα ,11=,{}n s ββ ,12=。
所谓的常数和对策是指局中人A 和局中人B 所赢得的值之和为一常数,二人非常数和对策问题也称为双矩阵对策,也有纯策略对策和混策略对策两种,在这里要用纯策略对策,要用Nash 平衡点来求最优纯策略和策略值。
问题一:说明A ,B 各有多少纯策略,首先要分析A 的摸牌情况和A 喊大或喊小,在逐个列出B 的摸牌情况和是否选择翻牌或弃权,列出各种情况,在分析A,B 各有多少纯策略。
问题二:根据优超原则淘汰具有劣势的策略,并列出A 的赢得矩阵,要再解决问题一的基础上,根据A,B 的纯策略找到A 的赢得矩阵。
问题三:求解双方的最优策略和对策值,要在问题一和问题二的基础上,列出A 和B 的赢得矩阵,在赢得矩阵中交叉部分即为对策值,最优策略转化成用Nash 平衡点来求。
我们通过大量不同模型的筛选,发现二人非常数和对策纯策略模型很好的解决该问题。
关键词: 二人非常数和对策 纯策略 赢得矩阵 最优策略 对策值Ⅰ 问题重述1.1所谓的常数和对策是指局中人A 和局中人B 所赢得的值之和为一常数,二人非常数和对策问题也称为双矩阵对策,也有纯策略对策和混策略对策两种,在这里要用纯策略对策。
1.2首先要解决A,B 有多少个纯策略,再按照优超原则淘汰具有劣势的策略,列出A 和B 的赢得矩阵,从中找出A 的赢得矩阵,找到对策值,把最优策略的求解转化成用Nash 平衡点来求。
Ⅱ 问题分析这是一个二人非常数和对策问题从题中分析,A 可能摸牌的情况有三种,分别为1,2,3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4) 为产品 在加班的时间内生产的件数。
Ⅴ
利用LINGO编写程序(见附录)
求得 =40 =0 =10 =4 =0 =0 =1即产品I生产50件,产品II生产4件时,总的利润最大,最大利润为413元。
附录
model:
sets:
level/1..2/:p,z,goal;
二十一章第三题
摘要
建立目标规划模型,先找出目标函数和约束条件,然后建立模型,利用Lingo程序求解。
关键词:
Ⅰ
某工厂生产两种产品,每件产品I可获利10元,每件产品II可获利8元。每生产一件产品I,需要3小时;每生产一件产品II,需要2.5小时。每周总的有效时间为120小时。若加班生产,则每件产品I的利润降低1.5元;每件产品II的利润降低1元。决策者希望在允许的工作及加班时间内取得最大利润,试建立该问题的目标规划模型并求解
c=3 2.5 0 0 3 2.5 3 2.5 10 8 8.5 7;
wminus=1 1 1;
enddata
min=@sum(level:p*z);
p(ctr)=1;
@for(level(i)|i#ne#ctr:p(i)=0);
@for(level(i):z(i)=@sum(obj(i,j):wminus(i,j)*dminus(j)));
@for(s_con_num(i):@sum(variable(j):c(i,j)*x(j))+dminus(i)=g(i));
@for(level(i)|i #lt# @size(level):@bnd(0,z(i),goal(i)));
@for(variable:@gin(x));
end
variable/1..4/:x;
s_con_num/1..3/:g,dminus;
s_con(s_con_num,variable):c;
obj(level,s_con_num)/1 1,1 2,2 3/:wminus;
endsets
a:
ctr=?;
goal=? 0;
g=120 160 640;
Ⅱ
建立目标规划模型前,先找出目标函数和约束条件,然后建立模型,利用Lingo程序求解。
由题可知,无论生产产品Ⅰ或Ⅱ每小时的盈利不超过4元,每周的生产时间不超过160小时,因而最大利润不超过640。
Ⅲ
(1)生产过程中没有出现其他问题;
Ⅳ
(1) 为产品 在允许的时间内生产的件数;
(2) 为产品 在允许的时间内生产的件数;
