人教A版高中数学必修四《三角函数的图像与性质》学案
人教A版高中数学必修四三角函数的图象与性质学案(1)

三角函数的性质【学习目标】1. 通过三角变换后,得到求最值、单调性及周期的基本型sin()y A x ωϕ=+进行求解了解函数的周期性2. 以极度的热情投入学习,体会成功的快乐。
【学习重点】三角函数的性质,特别是单调性和周期性以及最值是重中之重。
【学习难点】三角函数的性质,特别是单调性和周期性以及最值是重中之重。
[自主学习]2.函数y =sinx 的对称性与周期性的关系.⑴ 若相邻两条对称轴为x =a 和x =b ,则T = .⑵ 若相邻两对称点(a ,0)和(b ,0) ,则T = .⑶ 若有一个对称点(a ,0)和它相邻的一条对称轴x =b ,则T = . 注:该结论可以推广到其它任一函数.[典型例析]例1. 已知函数)12(sin 2)62sin(3)(2ππ-+-=x x x f )(R x ∈;(1)求函数f(x)的最小正周期;(2)求使函数f(x)取得最大值的x 的集合.例2. 已知函数f (x)=21log (sinx -cosx)⑴ 求它的定义域和值域; ⑵ 求它的单调区间; ⑶ 判断它的奇偶性;⑷ 判定它的周期性,如果是周期函数,求出它的最小正周期.例3.某港口水的深度y(米)是时间t(0≤t<24,单位:时)的函数,记作y=f(t),下面是某日水深的数据:经过长期观察,y=f(t)的图象.(1)试根据以上数据,求出函数y=f(t)的近似表达式;(2)一般情况下,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底中需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米,如果希望该船在一天内安全进出港,请问,它至多在港里停留多长时间(忽略进出港所需的时间)?[当堂检测] ⒈函数sin 2sin(2)3cos 2cos(2)3x x y x x ππ++=++的最小正周期为_____________________ ⒉直线y a =与曲线sin y x x =+在(0,2)x π∈内有两个不同的交点,则实数a 的取值范围是____________________;3若函数2()sin 2(2)cos 2f x a x a x =+-的图象关于直线8x π=-对称,则a 的值等于_______________________________ 4.已知函数2()2cos sin()sin cos 3f x x x x x x π=+-+(I ) 求函数()f x 的最小正周期; (II ) 求函数()f x 的最大值及最小值; (III )写出()f x 的单调递减区间.[学后反思]____________________________________________________ _________________________________________________________________________________________________________________________________。
人教A版高中数学必修四人教三角函数的图象与性质教案(3)
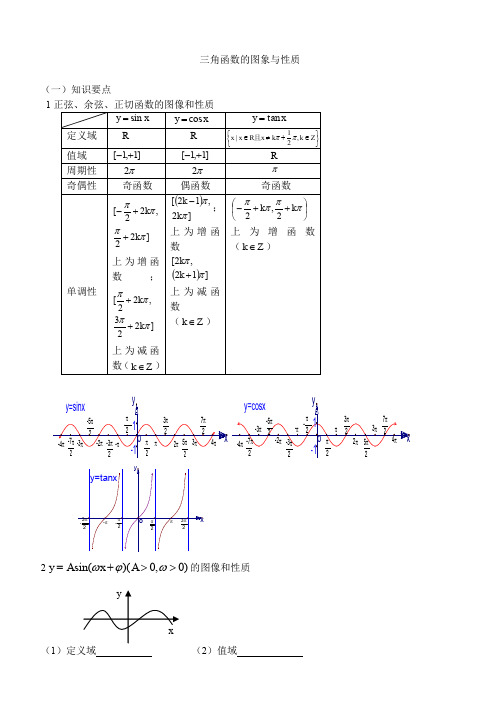
三角函数的图象与性质(一)知识要点12sin()(0,0)y A x A ωϕω=+>>的图像和性质(1)定义域 (2)值域(3)周期性 (4)奇偶性 (5)单调性 (二)学习要点 1会求三角函数的定义域 2会求三角函数的值域3会求三角函数的周期 :定义法,公式法,图像法。
如x y sin =与x y cos =的周期是π. 4会判断三角函数奇偶性 5会求三角函数单调区间6对sin()(0,0)y A x A ωϕω=+>>函数的要求 (1)五点法作简图(2)会写sin y x =变为sin()(0,0)y A x A ωϕω=+>>的步骤 (3)会求sin()y A x ωϕ=+的解析式(4)知道cos()y A x ωϕ=+,tan()y A x ωϕ=+的简单性质 7知道三角函数图像的对称中心,对称轴 8能解决以三角函数为模型的应用问题 (三)例题讲解例1求函数3tan(2)4y x π=--的定义域,周期和单调区间。
例2已知函数()2sin(2)4f x x π=-(1)求函数的定义域; (2) 求函数的值域; (3) 求函数的周期; (4)求函数的最值及相应的x 值集合; (5)求函数的单调区间; (6)若3[0,]4x π∈,求()f x 的取值范围; (7)求函数()f x 的对称轴与对称中心;(8)若()f x ϕ+为奇函数,[0,2)ϕπ∈,求ϕ;若()f x ϕ+为偶函数,[0,2)ϕπ∈,求ϕ。
例3.(1)将函数1sin(2)24y x π=-的图象向______平移_______个单位得到函数1sin 22y x =的 图象(只要求写出一个值)(2)要得到1cos(2)24y x π=-的图象,可以把函数sin()cos()66y x x ππ=--的图象向______平移_______个单位(只要求写出一个值). 例 4.设x R ∈,函数21()cos ()2f x x ωϕ=+-(0,)2o πωϕ><<,已知()f x 的最小正周期为π,且1()84f π=. (1)求ω和ϕ的值; (2)求的单调增区间.例5.如下图,某地一天从6时到14时的温度变化曲线近似满足函数y =A sin(ωx +φ)+b (1)求这段时间的最大温差(2)写出这段曲线的函数解析式(四)练习题 一、选择题1.将函数sin (0)y x ωω=>的图象向左平移6π个单位,平移后的图象如图所示,则平移后的图象所对应函数的解析式是 A .sin()6y x π=+ B .sin()6y x π=- C .sin(2)3y x π=+D .sin(2)3y x π=- 2.设0a >,对于函数()sin (0)sin x af x x xπ+=<<,下列结论正确的是A .有最大值而无最小值B .有最小值而无最大值C .有最大值且有最小值D .既无最大值又无最小值 3.函数y =1+cos x 的图象(A )关于x 轴对称 (B )关于y 轴对称 (C )关于原点对称(D )关于直线x =2π对称 4.已知函数f (x )=2sin ϖx(ϖ>0)在区间[3π-,4π]上的最小值是-2,则ϖ的最小值等于 A.32 B.23C.2D.35.设点P 是函数x x f ωsin )(=的图象C 的一个对称中心,若点P 到图象C 的对称轴上的距离的最小值4π,则)(x f 的最小正周期是 A .2π B . π C.2π D . 4π 6.已知R a ∈,函数R x a x x f ∈-=|,|sin )(为奇函数,则a =( )(A )0 (B )1 (C )-1 (D )±17为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数R x x y ∈=,sin 2的图像上所有的点(A )向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) (B )向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变)(C )向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)(D )向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)8.已知函数11()(sin cos )sin cos 22f x x x x x =+--,则()f x 的值域是(A)[]1,1- (B) 2⎡⎤-⎢⎥⎣⎦(C)1,2⎡-⎢⎣⎦(D)1,2⎡--⎢⎣⎦9.函数1|sin(3)|2y x =+的最小正周期是( )A.π2B.π C.2π D.4π10.函数()tan 4f x x π⎛⎫=+⎪⎝⎭的单调增区间为 A .,,22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭B .()(),1,k k k Z ππ+∈C .3,,44k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭ D .3,,44k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭11.下列函数中,图象的一部分如右图所示的是(A )sin 6y x π⎛⎫=+⎪⎝⎭(B )sin 26y x π⎛⎫=-⎪⎝⎭(C )cos 43y x π⎛⎫=-⎪⎝⎭(D )cos 26y x π⎛⎫=-⎪⎝⎭12.已知函数x b x a x f cos sin )(-=(a 、b 为常数,0≠a ,R x ∈)在4π=x 处取得最小值,则函数)43(x f y -=π是( ) A .偶函数且它的图象关于点)0,(π对称 B .偶函数且它的图象关于点)0,23(π对称 C .奇函数且它的图象关于点)0,23(π对称 D .奇函数且它的图象关于点)0,(π对称 13设ππ22αβ⎛⎫∈- ⎪⎝⎭,,,那么“αβ<”是“tan tan αβ<”的( ) A.充分而不必要条件B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件14.函数y=21sin2+4sin 2x,x R ∈的值域是 (A)[-21,23] (B)[-23,21] (C)[2122,2122++-] (D)[2122,2122---] 二、填空题 15.sin()4y x π=-+在[0,2]x π∈的增区间是16.2cos 0()x x R ≥∈的x 的集合是17.8sin()48x y π=-的振幅,初相,相位分别是 18.tan 1x ≤,且x 是直线的倾斜角,则x ∈19.已知函数()2sin (0)f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-,则ω的最小值是____。
新人教A版高中数学(必修4)1.4《三角函数的图象与性质》教案2课时

1.4.1正弦函数、余弦函数的图象教学目的:1、用单位圆中的正弦线画出正弦函数的图象;2、用五点法作正弦函数和余弦函数的简图;3、正弦函数图象与余弦函数图象的变换关系。
教学重点、难点重点:会用单位圆中的三角函数线画出正弦函数的图像,并在此基础上由诱导公式画出余弦函数的图像难点:用单位圆中的正弦线作正弦函数的图象教学过程:一、复习引入:正弦线、余弦线:设任意角α的终边与单位圆相交于点P(x ,y),过P 作x 轴的垂线,垂足为M ,则有 MP r y ==αsin ,OM r x ==αcos向线段MP 叫做角α的正弦线,有向线段OM 叫做角α的余弦线.二、讲授新课:1、正弦函数图象的几何作法采用弧度制, x 、y 均为实数,步骤如下:(1)在 x 轴上任取一点 O 1 ,以 O l 为圆心作单位圆;(2)从这个圆与 x 轴交点 A 起把圆分成 12 等份;(3)过圆上各点作x 轴的垂线,可得对应于0、6π、3π、、2π的正弦线;(4)相应的再把 x 轴上从原点 O 开始,把这0~2π这段分成 12 等份;(5)把角的正弦线平移,使正弦线的起点与 x 轴上对应的点重合;(6)用光滑曲线把这些正弦线的终点连结起来。
2、五点法作图 描点法在要求不太高的情况下,可用五点法作出,y sin x,x [0,2]=∈π的图象上有五 点起决定作用,它们是 描出这五点后,其图象的形状 基本上就确定了。
因此,在精确度要求不太高时,我们常常先描出这五个点,然后用平滑的曲线将它们连3(0,0),(,1),(,0),(,1),(2,0)22πππ-π接起来,就得到在相应区间内正弦函数的简图,这种方法叫做五点法。
注意:(1)描点法所取的各点的纵坐标都是查三角函数表得到的数值,不易描出对应点的精确位置,因此作出的图象不够精确。
(2)几何法作图较为精确,但画图时较繁。
(3)五点法是我们画三角函数图象的基本方法,要切实掌握好。
(4)作图象时,函数自变量要用弧度制,这样自变量与函数值均为实数,因此在 x 轴、 y 轴上可以统一单位,作出的图象正规,便于应用。
高中数学必修4《三角函数的图象与性质》教案

高中数学必修4《三角函数的图象与性质》教案高中数学必修4《三角函数的图象与性质》教案【一】教学准备教学目标1、知识与技能(1)了解周期现象在现实中广泛存在;(2)感受周期现象对实际工作的意义;(3)理解周期函数的概念;(4)能熟练地判断简单的实际问题的周期;(5)能利用周期函数定义进行简单运用。
2、过程与方法通过创设情境:单摆运动、时钟的圆周运动、潮汐、波浪、四季变化等,让学生感知周期现象;从数学的角度分析这种现象,就可以得到周期函数的定义;根据周期性的定义,再在实践中加以应用。
3、情感态度与价值观通过本节的学习,使同学们对周期现象有一个初步的认识,感受生活中处处有数学,从而激发学生的学习积极性,培养学生学好数学的信心,学会运用联系的观点认识事物。
教学重难点重点: 感受周期现象的存在,会判断是否为周期现象。
难点: 周期函数概念的理解,以及简单的应用。
教学工具投影仪教学过程【创设情境,揭示课题】同学们:我们生活在海南岛非常幸福,可以经常看到大海,陶冶我们的情操。
众所周知,海水会发生潮汐现象,大约在每一昼夜的时间里,潮水会涨落两次,这种现象就是我们今天要学到的周期现象。
再比如,[取出一个钟表,实际操作]我们发现钟表上的时针、分针和秒针每经过一周就会重复,这也是一种周期现象。
所以,我们这节课要研究的主要内容就是周期现象与周期函数。
(板书课题)【探究新知】1.我们已经知道,潮汐、钟表都是一种周期现象,请同学们观察钱塘江潮的图片(投影图片),注意波浪是怎样变化的?可见,波浪每隔一段时间会重复出现,这也是一种周期现象。
请你举出生活中存在周期现象的例子。
(单摆运动、四季变化等)(板书:一、我们生活中的周期现象)2.那么我们怎样从数学的角度研究周期现象呢?教师引导学生自主学习课本P3——P4的相关内容,并思考回答下列问题:①如何理解“散点图”?②图1-1中横坐标和纵坐标分别表示什么?③如何理解图1-1中的“H/m”和“t/h”?④对于周期函数的定义,你的理解是怎样?以上问题都由学生来回答,教师加以点拨并总结:周期函数定义的理解要掌握三个条件,即存在不为0的常数T;x必须是定义域内的任意值;f(x+T)=f(x)。
高中数学1.4.1三角函数图像与性质(1)学案新人教A版必修4

福建省泉州市唯思教育高中数学 1.4.1 三角函数图像与性质(1)学案 新人教A 版必修4【学习目标】1、能借助正弦线画出正弦函数的图象,并在此基础上由平移正弦曲线的方法画出余弦函数的图象;2、会用五点法画出正弦曲线和余弦曲线在一个周期上的草图;3、借助图象理解并运用正、余弦函数的定义域和值域。
【重点难点】五点法作正、余弦函数的图象;正、余弦函数的定义域和值域。
一、预习指导(一) 平移正弦线画出正弦函数的图象:1、 在单位圆中,作出对应于11,,,6326ππππ…的角及对应的正弦线; 2、 作出sin y x =在[0,2]π区间上的图象:(1)平移正弦线到相应的位置;(2)连线 3、 作出sin y x =在R 上的图象(二) 用五点法画出正弦函数在[0,2]π区间上的简图(三) 平移正弦曲线的方法画出余弦函数的图象: 思考:1、sin ,cos y x y x ==的图象有什么关系?为什么?2、由sin y x =的图象怎样作出cos y x =的图象?请在下图中画出cos y x =的图象。
(四)用五点法画出余弦函数在[0,2]π区间上的简图(四) 仔细观察正弦曲线和余弦曲线,总结正弦函数与余弦函数的性质: (1)定义域: (2)值域:对于sin y x =:当且仅当x = 时, max y = ;当且仅当x = 时,min y = ;对于cos y x =;当且仅当x = 时,max y = ;当且仅当x = 时,min y = 。
二、典型例题例1、 画出下列两组函数的简图:(1)cos ,y x x R =∈ ; 2cos ,y x x R =∈ (2)sin ,y x x R =∈ ; sin 2,y x x R =∈例2、 求下列函数的最大值及取得最大值时的自变量x 的集合: (1)cos 3xy = (2)2sin 2y x =-例3、 求函数y =的定义域。
例4、 求函数27sin 4sin 4y x x =-++的值域。
人教A版高中数学必修四 《三角函数的图像与性质》学案

三角函数的图象与性质学习目标:结合图像,理解并掌握正弦函数、余弦函数的性质。
②正弦曲线:正弦函数x y sin =,R x ∈的图像叫做正弦曲线。
作函数x y sin =,[]π2,0∈x 的简图的五个关键点是_______________________.正弦函数x y sin =,R x ∈是周期为_____ ________函数,它的值域是__________;当x=______________时,函数有最大值,是_____;当x=______________时,函数有最小值,是______;正弦函数x y sin =,R x ∈的单调递增区间是_______________,单调递减区间是________________.正弦曲线关于直线___________________对称,又关于点_____________对称。
2.余弦曲线:余弦函数x y cos =,R x ∈的图像叫做余弦曲线。
余弦曲线关于直线__________________对称,又关于点_____________对称。
余弦函数x y cos =,R x ∈是周期为______的________函数,它的值域是__________;当x=______________时,函数有最大值,是_____;当x=______________时,函数有最小值,是______;余弦函数x y cos =,R x ∈的单调递增区间是_______________,单调递减区间是________________. 作函数x y cos =,[]π2,0∈x 的简图的五个关键点是________________________________________. 。
的值求已知ααπ2cos ,53)sin()4(=-已知.)4cos(2cos),40(135)4sin(απαπααπ+<<=-求已知αααcossin,32tan+=求(1);化简:(1)cos3cos sin3sin αααα+;(2)cos()cos()66ππαα++-;(3)cos15cos75-已知 sin +cos =53 ① , cos +s in =54 ②,求sin (+).已知, 且, 求cos ,sin αα的值。
人教A版高中数学必修四三角函数的图象与性质学案新(4)

三角函数性质与图像知识清单: 备注:以上性质的理解记忆关键是能想象或画出函数图象........... 函数sin()y A x ωϕ=+的图像和性质以函数sin y x =为基础,通过图像变换来把握.如①sin y x=−−−−→图例变化为②sin()y A x ωϕ=+(A >0,ω>0)相应地,①的单调增区间2,222k k ππππ⎡⎤-++⎢⎥⎣⎦−−−→变为2222k x k πππωϕπ-+++≤≤的解集是②的增区间.注:⑴)sin(ϕω+=x y 或cos()y x ωϕ=+(0≠ω)的周期ωπ2=T ;⑵sin()y x ωϕ=+的对称轴方程是2x k ππ=+(Z k ∈),对称中心(,0)k π;cos()y x ωϕ=+的对称轴方程是x k π=(Z k ∈),对称中心1(,0)2k ππ+; )tan(ϕω+=x y 的对称中心(0,2πk ). 课前预习1.函数sin cos y x x =-的最小正周期是 .2. 函数1π2sin()23y x =+的最小正周期T = .3.函数sin2xy =的最小正周期是 4.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是5.函数22cos()()363y x x πππ=-≤≤的最小值是 6.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象向 平移 个单位长度7.将函数sin y x =的图象上各点的横坐标扩大为原来的2倍,纵坐标不变,再把所得图象上所有点向左平移3π个单位,所得图象的解析式是 .8. 函数sin y x x =+在区间[0,2π]的最小值为______.9.已知f (x )=5sin x cos x -35cos 2x +325(x ∈R ) ⑴求f (x )的最小正周期; ⑵求f (x )单调区间;⑶求f (x )图象的对称轴,典型例题例1、三角函数图像变换 将函数12cos()32y x π=+的图像作怎样的变换可以得到函数cos y x =的图像? 变式1:将函数cos y x =的图像作怎样的变换可以得到函数2cos(2)4y x π=-的图像?例2、已知简谐运动ππ()2sin 32f x x ϕϕ⎛⎫⎛⎫=+<⎪⎪⎝⎭⎝⎭的图象经过点(01),,则该简谐运动的最 小正周期T 和初相ϕ分别为 例3、三角函数性质求函数34sin(2)23y x ππ=+的最大、最小值以及达到最大(小)值时x 的值的集合变式1:函数y =2sin x 的单调增区间是 变式2、下列函数中,既是(0,2π)上的增函数,又是以π为周期的偶函数是( ) (A)y =lg x 2 (B)y =|sin x | (C)y =cos x (D)y=x 2sin 2变式3、已知⎥⎦⎤⎢⎣⎡∈2,0πx ,求函数)125cos()12cos(x x y +--=ππ的值域变式4、已知函数12()log (sin cos )f x x x =-⑴求它的定义域和值域;⑵求它的单调区间;⑶判断它的奇偶性; ⑷判断它的周期性.例4、三角函数的简单应用如图,某地一天从6时至14时的温度变化曲线近似满足函数y =A sin (ωx +ϕ)+b .(Ⅰ)求这段时间的最大温差; (Ⅱ)写出这段曲线的函数解析式.例5、三角恒等变换 函数y =xx cos sin 21++的最大值是 .变式1:已知cos 2π2sin 4αα=-⎛⎫- ⎪⎝⎭,求cos sin αα+的值. 变式2:已知函数2π()2sin 24f x x x ⎛⎫=+-⎪⎝⎭,ππ42x ⎡⎤∈⎢⎥⎣⎦,.求()f x 的最大值和最小值. 实战训练1.函数x x f 2sin 21)(-=的最小正周期为2. 函数f x x x x ()cos sin cos =-223的最小正周期是____ 3.函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于4.若函数()2sin()f x x ωϕ=+,x ∈R (其中0ω>,2ϕπ<)的最小正周期是π,且(0)f =,则5.若函数()y f x =的图象按向量a 平移后,得到函数(1)2y f x =--的图象,则向量a = 6.函数5tan(21)y x =+的最小正周期为 7.将π2cos 36xy ⎛⎫=+⎪⎝⎭的图象按向量π24⎛⎫=-- ⎪⎝⎭,a 平移,则平移后所得图象的解析式为 8.若函数21()sin ()2f x x x R =-∈,则f(x)是最小正周期为 的 函数 9.已知函数()sin (0)f x x ωωπ⎛⎫=+> ⎪3⎝⎭的最小正周期为π,则该函数的图象( ) A .关于点0π⎛⎫ ⎪3⎝⎭,对称 B .关于直线x π=4对称 C .关于点0π⎛⎫ ⎪4⎝⎭,对称 D .关于直线x π=3对称 10.下列函数中,周期为2π的是( ) A .sin2x y = B .sin 2y x = C .cos 4xy = D .cos 4y x =11.函数()sin ([,0])f x x x x π=-∈-的单调递增区间是( ) A .5[,]6ππ-- B .5[,]66ππ-- C .[,0]3π- D .[,0]6π-12.设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ,则()f x ( ) A .在区间2736ππ⎡⎤⎢⎥⎣⎦,上是增函数B .在区间2π⎡⎤-π-⎢⎥⎣⎦,上是减函数 C .在区间84ππ⎡⎤⎢⎥⎣⎦,上是增函数D .在区间536ππ⎡⎤⎢⎥⎣⎦,上是减函数13.要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=-⎪3⎝⎭的图象( )A .向右平移π6个单位 B .向右平移π3个单位 C .向左平移π3个单位D .向左平移π6个单位14.(07年全国卷二理2).函数sin y x =的一个单调增区间是( ) A .ππ⎛⎫- ⎪44⎝⎭, B .3ππ⎛⎫ ⎪44⎝⎭,C .3π⎛⎫π ⎪2⎝⎭,D .32π⎛⎫π⎪2⎝⎭, 15.函数()sin 2cos2f x x x =-的最小正周期是16.已知函数)2sin(42cos 2ππ+⎪⎭⎫ ⎝⎛-x x 。
人教A版高中数学必修4第一章 三角函数1.4 三角函数的图象与性质导学案

1.4三角函数的图象与性质1.4.1 正弦函数、余弦函数的图象学习目标1、会用“五点法”和“几何法”画正弦函数、余弦函数的图,体会“几何法”作正弦函数图象的过程,提高动手能力;2、通过函数图象的应用,体会数形结合在解题中的应用;3、三角函数图象和图象的应用;自主梳理1. 正弦函数(或余弦函数)的概念 任意给定一个实数x ,有唯一确定的值x sin (或x cos )与之对应,由这个对应法则所确定的函数x y sin =(或x y cos =)叫做正弦函数(或余弦函数),其定义域为 。
2. 正弦曲线或余弦曲线正弦函数的图象和余弦函数的图象分别叫做 和 。
3. 用五点法作正弦函数和余弦函数的简图(描点法):(1)正弦函数[]π2,0,sin ∈=x x y 的图象中,五个关键点是: , , , 。
(2)余弦函数[]π2,0,cos ∈=x x y 的图象中,五个关键点是: , , , 。
预习检测1、函数)3sin(π+=x y 的定义域为____________________;值域为____________________;2、函数)3cos(2π-=x y 的定义域为__________________;值域为____________________;互动课堂 问题探究1:【例】 作出函数x y cos 31-1=在]2,2[ππ-上的图像;【变式】)23sin(π+=x y ;问题探究2:【例】已知]23,2[ππ-∈x ,解不等式23sin -≥x ;【变式】已知R x ∈,解不等式23sin -≥x ;问题探究3:【例】求下列函数的值域: (1)x x y sin |sin |+= (2)]6,6[),32sin(2πππ-∈+=x x y(3)1cos 2cos --=x x y【变式】求函数],3[,1sin 4sin 32ππ∈+-=x x x y 的值域;问题探究4: 【例】(1)讨论方程x x sin lg =解的个数;(2)若函数]2,0[|,sin |2sin )(π∈+=x x x x f 与直线k y =有且仅有两个不同的交点,求k 的取值范围;【变式】当k 为何值时,方程k x x =+|sin |2sin 有一解、三解、四解?课堂练习1、在同一坐标系内的函数x y sin =与x y cos =的图象的交点坐标是 ( ) A . Z k k ∈),0,(π B Z k k ∈+),1,22(ππC Z k k k∈-+),)1(,2(ππ D Z k k k∈-+),2)1(,4(ππ2、下面有四个判断:① 作正、余弦函数的图象时,单位圆的半径长与x 轴上的单位长可以不一致; ② []π2,0,sin ∈=x x y 的图象关于)0,(πP 成中心对称; ③ []π2,0,cos ∈=x x y 的图象关于直线π=x 成轴对称; ④ 正、余弦函数的图象不超过两直线1,1-==y y 所夹的范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省怀仁中学2014高中数学《三角函数的图象与性质》学案 新人
教A 版必修4
学习目标:
1.能借助图象理解正、余弦函数的定义域、值域、周期性、奇偶性、单调性;
2.能熟练写出形如sin(2)6y x π=+、cos(2)3y x π
=-等的单调区间. 学习重点:正、余弦函数的性质.
学习过程: 一.问题情境:我们已经作出了正、余弦函数的图象;
那么,利用图象可以得到正、余弦函数的哪些性质呢?
二.建构数学:如图:
正弦函数、余弦函数的主要性质:
(1)定义域:__________.
(2)值域:__________.
当且仅当_________x =时,sin ,y x x R =∈取得最大值为______;
当且仅当_________x =时,sin ,y x x R =∈取得最小值为______;
当且仅当_________x =时,cos ,y x x R =∈取得最大值为______;
当且仅当_________x =时,cos ,y x x R =∈取得最小值为______;
(3)周期性:____.T =
(4)奇偶性:正弦函数是___函数,其图象关于____对称;
余弦函数是___函数,其图象关于____对称.
(5) 单调性:当x ∈
_____________________时,sin y x =单调递增; 当x ∈_____________________时,sin y x =单调递减;
当x ∈_____________________时cos y x =单调递增;
当x ∈_____________________时cos y x =单调递减.
三.数学运用:
例1 求下列函数的最大值及取得最大值时自变量x 的集合: (1)cos
;3
x y = (2)2sin 2.y x =-
例2 求函数sin(2)3y x π
=+的单调增区间.
四.课堂练习:
1. 求下列函数的最大值及取得最大值时自变量x 的集合:
(1)1cos ;y x =+ (2)2cos .3x y =- 2. 求下列函数的单调区间:
(1) sin();4y x π=+ (2) 3cos .2
x y = 3.不求值,分别比较下列各组中两个三角函数值的大小: (1)0sin 250与0sin 260; (2)15cos 8π与14cos .9
π 4.
五.课堂小结:
六:课后反思。
