大小图形组合
五年级组合图形的面积精选32题
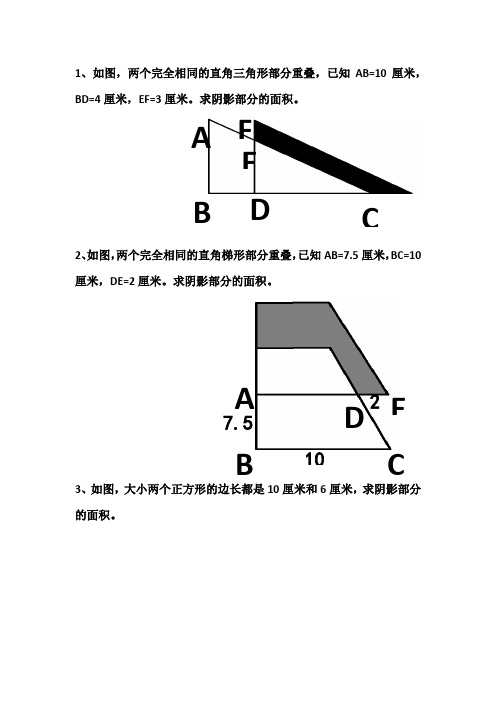
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。
中班数学活动《图形组合》

汇报人:
202X-01-05
• 引言 • 图形组合基础知识 • 活动实施 • 活动效果评估 • 活动改进建议
01 引言
活动背景
图形组合是中班数学教育的重要内容 之一,旨在培养幼儿的观察力、想象 力和创造力。
通过图形组合活动,幼儿可以了解基 本图形的特点,学习如何将不同的图 形进行组合,从而培养他们的空间思 维能力和解决问题的能力。
04 活动效果评估
评估标准
知识掌握程度
动手操作能力
创新思维能力
参与度和兴趣
评估幼儿对图形组合的理解 和运用能力,包括对基本图 形(如圆形、三角形、正方 形等)的认知,以及图形组 合后产生的新的图形(如椭 圆形、不规则图形等)的认 知。
评估幼儿在活动过程中动手 操作的能力,包括是否能正 确地剪裁、拼接、组合图形 等。
结合生活实际
可以将图形组合的教学内容与生活中的实际物品相结合,如用组合 图形来描述动物、植物或建筑的结构。
教学方法改进
互动式教学
通过互动游戏、问答等方式,引 导学生主动思考和参与,提高学
生的学习积极性。
分组合作
将学生分成小组,让他们共同完 成图形组合的任务,培养他们的
团队协作能力。
个性化教学
根据学生的学习进度和理解程度 ,进行个性化指导,确保每个学
活动目标
01
02
03
知识目标
幼儿能够掌握基本图形的 名称、特点及形状。
能力目标
幼儿能够运用图形组合的 技巧,创造出新的图形。
情感目标
培养幼儿对数学的兴趣和 热爱,提高他们的自信心 和创造力。
02 图形组合基础知识
图形分类
三角形
组合图形(一)

三角形面积:
S ah 2
阴影部分的面积:
(19.625-12.5)×2=14.25(平方厘米)
答:阴影部分的面积是14.25平方厘米。
点击关注,学习更多知识!
2 2
练习三
主讲:拓老师
已知下面图形的两条线段长2厘米,并互相 垂直,求阴影部分的面积。
正方形的面积: 2×2=4(平方厘米) 四分之一圆面积: 3.14×22÷4=3.14(平方厘米) 阴影部分的面积: 4-3.14=0.86(平方厘米) 答:阴影部分的面积是0.86平方厘米。
主讲:拓老师
组合图形(一)
点击关注,学习更多知识!
例题一
主讲:拓老师
如图,长方形的面积是8平方厘米,长方 形的长宽比是2:1,求这个组合图形的面积。
解:设宽为x厘米,长为2x厘米, 2x×x=8 x=2
·宽为2厘米,长为4厘米,
长方形面积:
S ab
半圆面积:
S r2 2
3.14×(4÷2)2÷2+8 =14.28(平方厘米)
117.75-60°÷360°×3.14×(15-7)2 ≈84.26(平方厘米) 答:阴影部分的面积是84.26平方厘米。
扇形面注,学习更多知识!
主讲:拓老师
总结
先把组合图形分成几个简单的图形,再 把每个简单图形的面积相加或相减,就是所 求的组合图形的面积;或将组合图形添补成 基本图形再进行求解。
半圆面积:
S r2 2
组合图形的面积:
9+14.13=23.13(平方厘米)
答:这个组合图形的面积是23.13
平方厘米。
点击关注,学习更多知识!
例题二
主讲:拓老师
求下面图形阴影部分的面积。(单位:厘米)
正方形组合图形
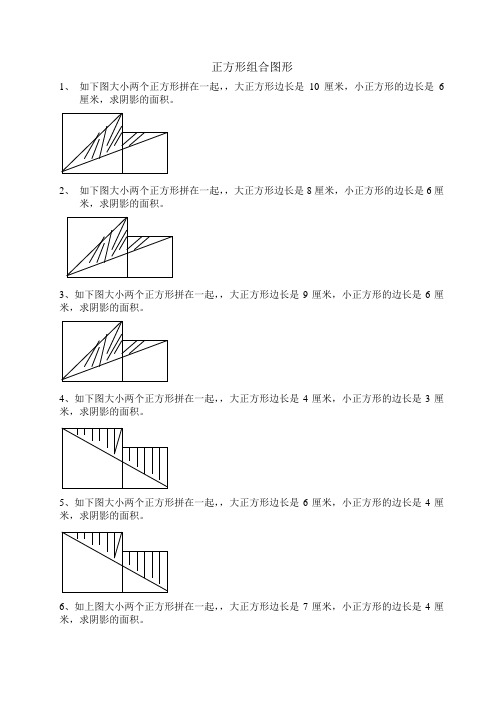
正方形组合图形
1、如下图大小两个正方形拼在一起,,大正方形边长是10厘米,小正方形的边长是6
厘米,求阴影的面积。
2、如下图大小两个正方形拼在一起,,大正方形边长是8厘米,小正方形的边长是6厘
米,求阴影的面积。
3、如下图大小两个正方形拼在一起,,大正方形边长是9厘米,小正方形的边长是6厘米,求阴影的面积。
4、如下图大小两个正方形拼在一起,,大正方形边长是4厘米,小正方形的边长是3厘米,求阴影的面积。
5、如下图大小两个正方形拼在一起,,大正方形边长是6厘米,小正方形的边长是4厘米,求阴影的面积。
6、如上图大小两个正方形拼在一起,,大正方形边长是7厘米,小正方形的边长是4厘米,求阴影的面积。
7、如下图大小两个正方形拼在一起,,大正方形边长是6厘米,小正方形的边长是4厘米,求阴影的面积。
8、如下图大小两个正方形拼在一起,,大正方形边长是5厘米,小正方形的边长是4厘米,求阴影的面积。
9、如下图大小两个正方形拼在一起,,小正方形边长是4厘米,阴影部分的面积是28平方厘米,空白部分的面积。
10、如下图大小两个正方形拼在一起,,小正方形边长是6厘米,阴影部分的面积是72平方厘米,空白部分的面积。
11、如下图大小两个正方形拼在一起,,大正方形边长是5厘米,小正方形的边长是4厘米,求阴影的面积。
12、如上图大小两个正方形拼在一起,,大正方形边长是16厘米,小正方形的边长是12厘米,求阴影的面积。
图形的拆分和组合

图形的拆分和组合
汇报人:XXX
目录
CONTENTS
01 图形的拆分
02 图形的组合
03 图形的拆分与组合 的应用
04 图形的拆分与组合 的技巧
05 图形的拆分与组合 的注意事项
图形的拆分
拆分定义
拆分:将图形分解 成多个部分或元素
目的:便于理解和 处理图形
方法:使用几何工 具或算法进行分解
拆分实例
圆形拆分:将圆形 分为两个半圆
正方形拆分:将正 方形分为四个等边 三角形
长方形拆分:将长 方形分为两个矩形
三角形拆分:将三 角形分为三个等边 三角形
提高图形的灵活性和可塑性
拆分意义
便于对图形进行修改和优化
增强图形的视觉效果和表现力
便于对图形进行复制和粘贴,提高工作效率
图形的组合
图形的拆分与组合的技 巧
色彩搭配
色彩对比:使用对比色来突出重点,如红绿、蓝黄等 色彩协调:使用相近色或同色系来保持整体和谐,如蓝绿、红橙等 色彩平衡:注意色彩的分布和比例,避免过于单调或杂乱 色彩渐变:使用渐变色来增加层次感和立体感,如从浅到深、从冷到暖等
旋转:将图形围绕某个点 旋转一定角度
形状变化
基本概念:点、 线、面、体、颜 色、纹理等
技术方法:几何建 模、光照模型、纹 理映射、动画技术 等
艺术创作
抽象画:通过图形的拆分与组合, 创造出独特的艺术风格
拼贴画:将不同的图形进行拆分 与组合,形成独特的视觉效果
插画设计:利用图形的拆分与组 合,设计出独特的插画作品
海报设计:通过图形的拆分与组 合,设计出独特的海报作品
遵循美学原则
保持图形的简洁性和统一性 注意图形的比例和布局 避免过度装饰和复杂化 考虑图形的色彩搭配和视觉效果
小学美术《图形组合》教案

在本次《图形组合》的教学过程中,我发现学生们对图形组合的概念和方法的掌握程度参差不齐。有的学生能够迅速理解并创造出有趣的图形组合,而有的学生在如何平衡画面、选择合适的颜色等方面遇到了一些困难。这让我意识到,在今后的教学中,我需要更加关注学生的个体差异,提供更多的个性化指导。
在理论讲授环节,我尝试用生动的案例和简洁的语言解释图形组合的基本概念,从学生的反馈来看,这种方法是有效的。他们能够通过案例感受到图形组合的魅力,并在实践中尝试运用所学知识。但同时,我也注意到,对于一些抽象的概念,如“画面平衡”,学生理解起来还是有难度。我考虑在下次课中,加入更多的互动环节,让学生在动手实践中更好地理解这些概念。
小学美术《图形组合》教案
一、教学内容
本节课选自小学美术教材四年级下册《图形组合》章节。教学内容主要包括:1.学习图形组合的基本方法,如并置、重叠、嵌套等;2.了解不同图形组合后的视觉效果,提高学生的审美能力;3.运用所学图形组合方法,创作一幅富有创意的画作。本章节内容旨在培养学生对图形的观察力、想象力和创造力,激发学生对美术学习的兴趣。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了图形组合的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对图形组合的理解。我希望大家能够掌握这些知识点,并在日常生活和美术创作中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
二、核心素养目标
1.培养学生图形观察与想象能力,提高审美素养,使学生能够发现生活中的图形组合,感悟美术与生活的紧密联系。
组合图形-小学数学课件

33m
35m
12m
6.4 组合图形
2、一面中国少年先锋队中队旗的面积是多少?
30cm
20cm
30cm
80 cm
6.4 组合图形
6.4 组合图形
3 下面是一块正方形空心地砖,它实际占地面积是多少?
13cm
30cm
6.4 组合图形
4 在一块梯形的地中间有一个长方形的游泳池,其余的
地方是草地。草地的面积是多少平方米?
化为学过的图形进行
估算。
6.4 组合图形
图中每个小方格的面积为 1m2,计算阴影部分面积。
6.4 组合图形
三角形+梯形
5×4÷2 + (5+2) ×4÷2
= 10 + 14
= 24(m2)
6.4 组合图形
近似转化成长方形
8×4 = 32(m2)
答:阴影部分面积大约是 32 m2。
6.4 组合图形
三种方法,就是分、拼、挖。
解决不规则图形的面积可
以用估算法。
6.4 组合图形
方是草地。草地的面积是多少平方米?
6.4 组合图形
挖的方法
(70+40) ×30÷2-30×15
= 110×30÷2-450
= 3300÷2-450
= 1650-450
= 1200(m2)
答:草地的面积是 1200 平方米。
6.4 组合图形
用不同的方法计算下图的面积。(单位:厘米)
(用四种方法)
(2)请你也设计一种方案,用上我们学过的图形,并计算
出每种植物的种植面积。
ห้องสมุดไป่ตู้
绿草的面积占长方形面积的一半
绿草的种植面积:
第二课图形的魔术组合(教案)

1.理论介绍:首先,我们要了解图形组合的基本概念。图形组合是指通过拼接、重叠等手法,将简单图形组合成新的、复杂的图形。它是几何学中的重要组成部分,可以帮助我们更好地理解图形的性质和空间结构,同时也能激发我们的创造力和想象力。
案例分析:接下来,我们来看一个具体的案例。通过将两个等腰三角形组合,我们可以得到一个正方形。这个案例展示了图形组合在实际中的应用,以及它如何帮助我们解决问题。
这些核心素养目标与新教材要求相符,有助于学生在掌握知识的同时,提升综合素养。
三、教学难点与重点
1.教学重点
(1)掌握图形的基本组合方法:教师需引导学生掌握三角形、正方形、长方形等基本图形的组合方法,如拼接、重叠等,以便于创作出新的图形。
举例:通过将两个三角形组合成一个正方形,或用一个长方形和一个三角形组合成一个梯形。
还有一点值得反思的是,课堂总结环节的时间安排。今天的时间有些紧张,导致总结不够充分。在以后的教学中,我需要注意时间分配,确保课堂总结环节能够让学生充分消化所学知识,巩固学习成果。
五、教学反思
在今天的教学中,我发现学生们对图形的组合有着浓厚的兴趣。他们积极参与到课堂讨论和实践中,这让我感到很欣慰。通过这节课的学习,我看到了一些值得反思的地方。
首先,关于教学内容的安排,我觉得将图形组合与现实生活相结合的做法很受学生欢迎。他们在动手操作的过程中,不仅掌握了基本概念,还学会了如何将所学知识应用到实际问题中。在今后的教学中,我将继续关注学生的兴趣点,将生活实例融入课堂,提高他们的学习积极性。
3.运用所学的图形组合知识,解决实际问题,培养学生的创新意识和动手操作能力。
本节课将通过实际操作、小组合作、讨论交流等形式,让学生在轻松愉快的氛围中掌握图形组合的技巧,激发他们对几何图形的兴趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本组合图形练习
1如图,△DAC 和△EBC 都是等边三角形,AE 、BD 分别与CE 、CE 交于点M 、N ,AE 、DB 交于点H ,其中A 、C 、B 三点共线。
求证:(1)△ACE≌△DCB
(2)△AMC ∽△DMH (3) 求∠DHM
(4)CM=CN (5)△CMN 是等边三角形
(6)MN ∥AB (7)连接CH,证明CH 平分∠AHB
H
H
2.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于点G,连结BE. (1)下列结论中:① CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④ CD·AE=EF·CG;一定正确的结论有()
A.1个 B 2个 C 3个D.4个
3.如图,点C为线段AB上任意一点(不与A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接PC.
(1)求证:△ACE≌△DCB;
(2)请你判断△AMC与△DMP的形状有何关系并说明理由;
(3)求证:∠APC=∠BPC.
4,如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C 为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y 轴于点E.①△OBC与△ABD全等吗?判断并证明你的结论;
②随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.
5.如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE 是平行四边形,连接CE 交AD 于点F ,连接BD 交CE 于点G ,连接BE .下列结论中:
①CE=BD ;②△ADC 是等腰直角三角形;③∠ADB=∠AEB ;④CD •AE=EF •CG ; 一定正确的结论有( )
A .1个
B .2个
C .3个
D .4个
6.如图,四边形ABCD 、CEFG 都是正方形,点G 在线段CD 上,连接BG 、DE ,DE 和FG 相交于点O ,设AB=a ,CG=b (a >b ).下列结论:①△BCG ≌△DCE ;②BG ⊥DE ;③
=;④(a ﹣b )
2
•S △EFO =b 2•S △DGO .其中结论正确的个数是( )
A .4个
B .3个
C .2个
D .1个
7.如图1, 正方形OABC 与正方形ODEF 放置在直线l 上,连结AD 、CF ,此时AD=CF .AD ⊥CF 成立.
(1)正方形ODEF 绕O 点逆时针旋转一定的角度,如图2,试判断AD 与CF 还相等吗?若成立,
请证明;若不成立,请说明理由.
(2)正方形ODEF 绕O 点逆时针旋转,使点E 旋转至直线l 上,如图3,求证:AD ⊥CF . (3)在(2)小题的条件下, AD 与OC 的交点为G ,当AO =3,OD =2时,求线段CG 的长.
图2
图
1
8.如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.(1)线段BE与AF的位置关系是,= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(90°<a<180°),延长FC交AB于点D,如果AD=6﹣2,求旋转角a的度数.
9.(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.。
