高三数学三模考试质量分析及对策(理)
高三数学三模考试质量分析及对策(理)
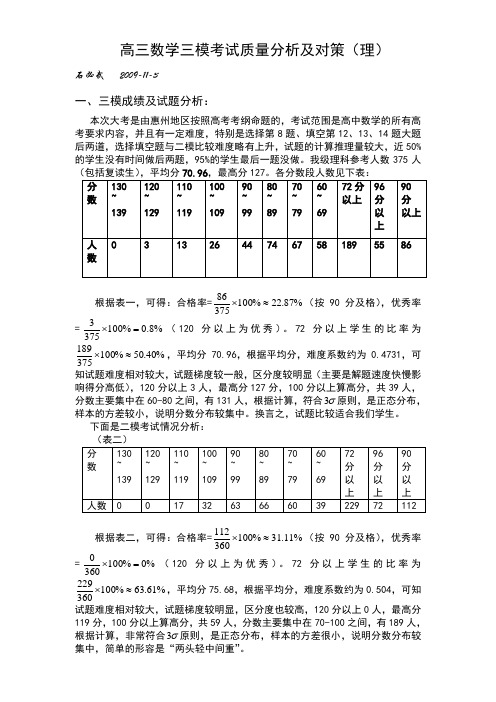
高三数学三模考试质量分析及对策(理)石必武 2009-11-3一、三模成绩及试题分析:本次大考是由惠州地区按照高考考纲命题的,考试范围是高中数学的所有高考要求内容,并且有一定难度,特别是选择第8题、填空第12、13、14题大题后两道,选择填空题与二模比较难度略有上升,试题的计算推理量较大,近50%的学生没有时间做后两题,95%的学生最后一题没做。
我级理科参考人数375人根据表一,可得:合格率=%87.22%10037586≈⨯(按90分及格),优秀率=%8.0%1003753=⨯(120分以上为优秀)。
72分以上学生的比率为%40.50%100375189≈⨯,平均分70.96,根据平均分,难度系数约为0.4731,可知试题难度相对较大,试题梯度较一般,区分度较明显(主要是解题速度快慢影响得分高低),120分以上3人,最高分127分,100分以上算高分,共39人,分数主要集中在60-80之间,有131人,根据计算,符合σ3原则,是正态分布,样本的方差较小,说明分数分布较集中。
换言之,试题比较适合我们学生。
下面是二模考试情况分析: 根据表二,可得:合格率=%11.31%100360112≈⨯(按90分及格),优秀率=%0%1003600=⨯(120分以上为优秀)。
72分以上学生的比率为%61.63%100360229≈⨯,平均分75.68,根据平均分,难度系数约为0.504,可知试题难度相对较大,试题梯度较明显,区分度也较高,120分以上0人,最高分119分,100分以上算高分,共59人,分数主要集中在70-100之间,有189人,根据计算,非常符合σ3原则,是正态分布,样本的方差很小,说明分数分布较集中,简单的形容是“两头轻中间重”。
从结果看,三模的尖子生有所回升(120分以上的由0人减为3人),110分以上人数持平但及格人数减少了26人,平均分也下降了4.69。
尽管平均分有所下降,但毕竟是外面来的考题(题目的实际难度未减,计算推理量较大),我们有理由相信,只要一如既往,坚持不懈,一定有一个好收成。
2024年成都七中高三数学(理)三模考试卷附答案解析

2024年成都七中高三数学(理)三模考试卷时间:120分钟满分:150分2024.04一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若向量(),4a x = 与向量()1,b x = 是共线向量,则实数x 等于()A .2B .2-C .2±D .02.复数3i1iz +=-(其中i 为虚数单位)的共轭复数为()A .12i+B .12i -C .12i-+D .12i--3.已知全集{}02πU x x =≤≤,集合sin A x x ⎧⎪=≥⎨⎪⎪⎩⎭,{}sin cos B x x x =≥,则A B ⋂等于()A .π3π,44⎡⎤⎢⎥⎣⎦B .π2π,33⎡⎤⎢⎥⎣⎦C .ππ,43⎡⎤⎢⎥⎣⎦D .2,43ππ⎡⎤⎢⎥⎣⎦4.2nx⎛⎝的展开式中,第5项为常数项,则正整数n 等于()A .8B .7C .6D .55.三棱锥A BCD -的三视图如图所示,则该三棱锥的各条棱中,棱长最大值为()AB C .D .26.已知3sin 2cos 21αα+=,则tan α=()A .3B .13C .13或0D .3或07.已知圆22:1C x y +=,直线:0l x y c -+=,则“0c ≥”是“圆C 上任取一点(),x y ,使0x y c -+≤的概率小于等于12”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要8.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:优秀非优秀甲班10b乙班c30附:()()()()22()n ad bc K a b c d a c b d -=++++(n a b c d =+++),()20P K k ≥0.050.0250.0100.0050k 3.8415.0246.6357.879已知在全部105人中随机抽取1人,成绩优秀的概率为27,则下列说法正确的是()A .甲班人数少于乙班人数B .甲班的优秀率高于乙班的优秀率C .表中c 的值为15,b 的值为50D .根据表中的数据,若按97.5%的可靠性要求,能认为“成绩与班级有关系”9.若ln 1,ln3b a e c =-==,则,,a b c 的大小关系为()A .a c b >>B .b c a >>C .c b a>>D .a b c>>10.已知函数()cos f x x x =-,若()()12πf x f x +=,则()12f x x +=()A .π1-B .π1+C .πD .011.已知双曲线C :22221x y a b-=(0a >,0b >)的左、右焦点分别为1F ,2F ,左、右顶点分别为1A ,2A ,P 为双曲线上一点,且直线1PA 与2PA 的斜率之积等于3,则下列说法正确的是()A .双曲线的渐近线方程为3y x =±B .双曲线CC .若12PF PF ⊥,则12PF F △的面积为2aD .以1F 为半径的圆与渐近线相切12.设函数()3f x x x =-,正实数,a b 满足()()2f a f b b +=-,若221a b λ+≤,则实数λ的最大值为()A .2+B .4C .2D .二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.13.某班男女生的比例为3:2,全班的平均身高为168cm ,若女生的平均身高为159cm ,则男生的平均身高为cm .14.抛物线22y px =(0p >)的焦点为F ,过F 的直线l 与抛物线相交于A ,B 两点(A 在第一象限),分别过A ,B 作准线的垂线,垂足分别为C ,D ,若CD AF BF =-,则直线l 的倾斜角等于.15.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sin cos 0c A C =,则22sin sin sin sin A B A B ++=.16.在三棱柱111ABC A B C -中,1AA ⊥平面1,90,1,2,ABC ABC BA BC BB P ∠=︒===是矩形11BCC B 内一动点,满足223PA PC +=,则当三棱锥-P ABC 的体积最大时,三棱锥-P ABC 的外接球的表面积为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.某保险公司为了给年龄在20~70岁的民众提供某种疾病的医疗保障,设计了一款针对该疾病的保险,现从10000名参保人员中随机抽取100名进行分析,这100个样本按年龄段[)[)[)[)[]20,30,30,40,40,50,50,60,60,70分成了五组,其频率分布直方图如下图所示,每人每年所交纳的保费与参保年龄如下表格所示.(保费:元)据统计,该公司每年为该项保险支出的各种费用为一百万元.年龄[)20,30[)30,40[)40,50[)50,60[]60,70保费x2x3x4x5x(1)用样本的频率分布估计总体的概率分布,为使公司不亏本,则保费x 至少为多少元?(精确到整数)(2)随着年龄的增加,该疾病患病的概率越来越大,经调查,年龄在[)50,60的老人中每15人就有1人患该项疾病,年龄在[]60,70的老人中每10人就有1人患该项疾病,现分别从年龄在[)50,60和[]60,70的老人中各随机选取1人,记X 表示选取的这2人中患该疾病的人数,求X 的数学期望.18.已知数列{}n a 的前n 项和为,342n n n S S a =-.(1)证明:数列{}n a 是等比数列,并求出通项公式;(2)设函数()21ln 2f x x x ⎛⎫=⋅-⎪⎝⎭的导函数为()f x ',数列{}n b 满足()n n b f a =',求数列{}n b 的前n 项和n T .19.如图,在三棱柱111ABC A B C -中,1AA ⊥平面1,90,2,ABC ABC BA AA D ∠=︒==是棱AC 的中点,E 在棱1BB 上,且1AE A C ⊥.(1)证明://BD 平面1AEC ;(2)若四棱锥111C AEB A -的体积等于1,求二面角11C AE A --的余弦值.20.在平面直角坐标系xOy 中,椭圆22221x y a b+=(0a b >>)过点()2,0A ,直线l 与椭圆相交于不同于A 点的P ,Q 两点,N 为线段PQ 的中点,当直线ON 斜率为14-时,直线l 的倾斜角等于4π(1)求椭圆的方程;(2)直线AP ,AQ 分别与直线3x =相交于E ,F 两点.线段E ,F 的中点为M ,若M 的纵坐标为定值12,判断直线l 是否过定点,若是,求出该定点,若不是,说明理由.21.已知函数()()()e sin 1,0,πxf x ax x x x =---∈.(1)若12a =,证明:()0f x >;(2)若函数()f x 在()0,π内有唯一零点,求实数a 的取值范围.请考生在第22,23题中任选择一题作答,如果多做,则按所做的第一题记分.作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.选修4-4:坐标系与参数方程22.在直角坐标系xOy 中,直线l 的参数方程1010x ty t =+⎧⎨=-⎩(为参数),以O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2sin cos ρθθ=,且直线l 与曲线C 相交于,M N 两点.(1)求直线l 的普通方程和曲线C 的直角坐标方程;(2)设点()00,P x y 是直线l 上一点,满足20PM PN +=,求点P 的直角坐标.选修4-5:不等式选讲23.已知函数()1f x x =-.(1)求不等式()32f x x ≥-的解集;(2)若函数()()5g x f x x =+-的最小值为m ,正数a ,b 满足a b m +=,求证:224a bb a+≥.1.C【分析】根据向量共线列方程,解方程即可.【详解】因为a 与b共线,所以41x x ⋅=⨯,解得2x =±.故选:C.2.B【分析】先对复数z 化简,再根据共轭复数的概念求解.【详解】()()()()3i 1i 3i 24i12i 1i 1i 1i 2z ++++====+-+-,所以复数z 的共轭复数为12i -.故选:B.3.B【分析】先利用三角函数知识化简两个集合,结合交集运算可得答案.【详解】因为3sin 2x ≥,02x π≤≤,所以π2π33x ≤≤;因为sin cos x x ≥,所以πsin cos sin 04x x x ⎛⎫--≥ ⎪⎝⎭,所以π2π2ππ4k x k ≤-≤+,解得π5π2π+2π44k x k ≤≤+,Z k ∈;因为02x π≤≤,所以π5π44x ≤≤,所以π2π,33A B ⎡⎤⎢⎥⎣=⎦.故选:B 4.C【分析】利用二项式定理求出展开式通项,由条件列方程求n .【详解】二项式2n x⎛ ⎝的展开式的第1r +为()1C 2rn r rr n T x -+⎛= ⎝,所以()4444465C 2C 2n n n nn T x x---⎛== ⎝,由已知6n =,故选:C.5.A【分析】根据给定的三视图作出原三棱锥,再求出各条棱长即可得解.【详解】依题意,三视图所对三棱锥A BCD -如图,其中AB ⊥平面BCD ,BC CD ⊥,1,2AB CD BC ===,则AC ==,BD ==,AD ==故选:A 6.D【分析】将条件等价转化为()sin 3cos sin 0ααα-=,再利用等式性质得到结果.【详解】由于()23sin 2cos 26sin cos 12sin 2sin 3cos sin 1αααααααα+=+-=-+,故条件3sin 2cos21αα+=等价于()sin 3cos sin 0ααα-=,这又等价于sin 0α=或sin 3cos αα=,即tan 0α=或tan 3α=,所以D 正确.故选:D.7.C【分析】由事件从圆C 上任取一点(),x y ,使0x y c -+≤的概率小于等于12,求c 的范围,结合充分条件和必要条件的定义判断结论.【详解】直线0x y c -+=的斜率为1,在x 轴上的截距为c -,在y 轴上的截距为c ,当c >C 上不存在点(),x y ,使0x y c -+≤,所以事件圆C 上任取一点(),x y ,使0x y c -+≤的概率为0,当c =C 上有且仅有一个点(),x y ,使0x y c -+≤,所以事件圆C 上任取一点(),x y ,使0x y c -+≤的概率为0,若0c <,如图,圆C 上满足条件0x y c -+≤点为劣弧AB (含,A B )上的点,设劣弧AB 的长度为t ,则0πt <<,所以事件圆C 上任取一点(),x y ,使0x y c -+≤的概率12π2t P =<,若0c =,如图,圆C 上满足条件0x y c -+≤点为直线l 上方的半圆上的点,所以事件圆C 上任取一点(),x y ,使0x y c -+≤的概率π12π2P ==,若0c <<,如图,圆C 上满足条件0x y c -+≤点为优弧CD (含,C D )上的点,设优弧CD 的长度为s ,则π2πs <<,所以事件圆C 上任取一点(),x y ,使0x y c -+≤的概率12π2t P =>,若c ≤C 上所有点满足条件0x y c -+≤,所以事件圆C 上任取一点(),x y ,使0x y c -+≤的概率2π12πP ==,所以“圆C 上任取一点(),x y ,使0x y c -+≤的概率小于等于12”等价于“0c ≥”,所以“0c ≥”是“圆C 上任取一点(),x y ,使0x y c -+≤的概率小于等于12”的充要条件,故选:C.8.D【分析】根据条件解出45b =,20c =,然后直接计算即可判断A ,B ,C 错误,使用2K 的计算公式计算2K ,并将其与5.024比较,即可得到D 正确.【详解】对于C ,由条件知1030105b c +++=,1021057c +=,故65b c +=,1030c +=.所以45b =,20c =,故C 错误;对于A ,由于甲班人数为10104555b +=+=,乙班人数为3020305055c +=+=<,故A 错误;对于B ,由于甲班优秀率为1025511=,乙班优秀率为202250511=>,故B 错误;对于D ,由于()2210545201030 6.109 5.024********K ⋅⨯-⨯=≈>⋅⋅⋅,故D 正确.故选:D.9.A【分析】由题设ln e a e =,ln 2ln 424b ==,ln 33c =,构造ln ()xf x x=(0)x >,利用导数研究其单调性,进而判断,,a b c 的大小.【详解】由题设知:ln e a e =,ln 2ln 424b ==,ln 33c =,令ln ()xf x x=(0)x >,则21ln ()x f x x -'=,易知(0,)e 上()f x 单调递增,(,)e +∞上()f x 单调递减,即()(3)(4)(2)f e f f f >>=,∴a c b >>.故选:A.【点睛】关键点点睛:构造ln ()xf x x=(0)x >,利用导数研究其单调性,进而比较函数值的大小.10.B【分析】先利用导数证得()f x 在R 上单调递增,再利用条件得到()()12πf f x x =-,结合单调性即知12πx x +=,最后代入求值即可.【详解】因为()cos f x x x =-,所以()1sin 0f x x '=+≥.所以()f x 在R 上单调递增.因为()()12πf x f x +=,所以()()()()()1122222ππcos f x f x f x f x f x x x =-++-=-=()()222πcos ππf x x x =----=,结合()f x 在R 上单调递增,知12πx x =-,即12πx x +=.所以()()12ππππ1cos f x x f +===+-.故选:B.11.D【分析】通过123PA PA k k =求得22b a ,从而求得双曲线的渐近线方程,由此判断A ;进而可求得双曲线的离心率判断B ;求得三角形的面积判断C ;求得1F 到渐近线的距离可判断D.【详解】对于A ,设点(,)P x y ,则2222)1(x y b a-=,因为12(,0),(,0)A a A a -,所以1222222PA PA y y y b k k x a x a x a a ===+-- ,又123PA PA k k =,得223b a =,所以ba=y =,故A 错误;对于B,因为2c a ==,所以双曲线C 的离心率为2,故B 错误;对于C ,因为12PF PF ⊥,所以2221212||||||PF PF F F +=,又12||||||2PF PF a -=,所以22121212(||||||)2|||||||PF PF PF PF F F -+=,所以2212(2)2|||||(2)a PF PF c +=,所以212||||2PF PF b =,所以12121||||2PF F S PF PF ==2b ,故C 错误;对于D ,由B 选项可得2c a =,以1F到渐近线方程为y =的距离为:222a d ===,又1F,所以以1F为半径的圆与渐近线相切,故D 正确.故选:D.12.A【分析】依题意可得33a b a b +=-,从而得到222211a b b a b a b ba λ+⎛⎫ ⎪⎝⎭+-≤=-,再令()1at t b =>,最后利用基本不等式计算可得.【详解】因为()3f x x x =-,所以()3f a a a =-,()3f b b b =-,又()()2f a f b b +=-,所以332a a b b b -+-=-,即33a b a b +=-,因为0a >,0b >,所以330a b +>,所以0a b >>,所以331a b a b+=-,又221a b λ+≤,即3322a b a b a bλ++≤-,所以322b ba b a b λ≤+-,所以222211a b b a b a b ba λ+⎛⎫ ⎪⎝⎭+-≤=-,令at b=,则1t >,所以2221112211111a t t b b a t t t t ++-+===++-⎛⎫ ⎪⎝⎭---()2121t t =-++-22≥+=+,当且仅当211t t -=-,即1t时取等号,所以)22min221b a b a b ⎛⎫+=+ ⎪-⎝⎭,所以2λ≤+,则实数λ的最大值为2+.故选:A【点睛】关键点点睛:本题关键是推导出331a b a b +=-,从而参变分离得到222b a a b b λ≤+-,再换元、利用基本不等式求出222b a b b a +-的最小值.13.174【分析】设出男生的平均身高,然后根据条件列方程求解即可.【详解】设男生的平均身高为cm x ,则根据题目条件知321591683232x +⋅=++,即3318840x +=,所以84031852217433x -===.故答案为:174.14.4π##45︒【分析】由已知结合抛物线的定义分别表示CD ,AF ,BF ,求出直线l 的斜率,即可求解.【详解】抛物线22y px =的准线为:2p x =-,设()11,A x y ,()22,B x y ,则1,2p C y ⎛⎫- ⎪⎝⎭,2,2p D y ⎛⎫- ⎪⎝⎭,又A 在第一象限,所以10y >,20y <,所以12CD y y =-,由抛物线定义可得12pAF x =+,22p BF x =+,所以121222p pAF BF x x x x -=+--=-,又CD AF BF =-,所以12CD x x =-,所以1212x x y y -=-,故直线AB 的斜率12121y y k x x -==-,所以直线l 的倾斜角为π4.故答案为:π4.15.34##0.75【分析】由正弦定理可得sin sin cos 0C A A C =,可求得C ,由余弦定理可得222c a b ab =++,再结合正弦定理可得222sin sin sin sin sin A B A B C ++=,可求结论.【详解】由sin cos 0c A C =,结合正弦定理可得sin sin cos 0C A A C =,因为sin 0A ≠,所以sin 0C C =,所以tan C =因为(0,π)C ∈,所以2π3C =,由余弦定理可得2222cos c a b ab C =+-,可得222c a b ab =++,结合正弦定理可得2223sin sin sin sin sin 4A B A B C ++==.故答案为:34.16.73π##73π【分析】根据给定条件,确定点P 的位置,再结合球的截面小圆性质确定球心并求出球半径即得.【详解】显然三棱柱111ABC A B C -为直三棱柱,过P 作1//PQ AA 交BC 于Q ,连接AQ ,令,PQ x CQ y ==,显然PQ ⊥平面ABC ,,AQ BC ⊂平面ABC ,则,PQ AQ PQ BC ⊥⊥,而90ABC ∠=︒,则222222221(1),PA PQ AQ x y PC x y =+=++-=+,又223PA PC +=,于是22221(1)3x y y ++-+=,整理得2213()24x y =--+,当12y =时,max x 三棱锥-P ABC 的底面ABC 面积为12,要其体积最大,当且仅当x 最大,因此2PQ =,即1PC PB BC ===时,三棱锥-P ABC 的体积最大,PBC 的外接圆圆心2O 为正PBC 的中心,令三棱锥-P ABC 的外接球球心为O ,半径为R ,则2OO ⊥平面PBC ,显然AC 的中点1O 是ABC 的外接圆圆心,则1OO ⊥平面ABC ,由AB BC ⊥可得AB ⊥平面PBC ,于是21//O Q OO ,而1//O Q AB ,则1O Q ⊥平面PBC ,21//OO O Q ,四边形12OOQO 是平行四边形,因此121336OO O Q PQ ===,而11222O C AC ==,则22211712R OO O C =+=,所以三棱锥-P ABC 的外接球的表面积27π4π3S R ==.故答案为:7π3【点睛】关键点点睛:解决与球有关的内切或外接问题时,关键是确定球心的位置,再利用球的截面小圆性质求解.17.(1)30元(2)16【分析】(1)根据小矩形面积和为得到关于a 的方程,解出a 值,再列出不等式,解出即可;(2)首先分析出X 的取值为0,1,2,再列出对应概率值,利用期望公式计算即可.【详解】(1)()0.0070.0160.0250.02101a ++++⨯=,解得0.032a =,保险公司每年收取的保费为:()100000.070.1620.3230.2540.2510000 3.35x x x x x x +⨯+⨯+⨯+⨯=⨯,所以要使公司不亏本,则10000 3.351000000x ⨯≥,即3.35100x ≥,解得10029.853.35x ≥≈,即保费30x =元;(2)由题意知X 的取值为0,1,2,()14912601510150P X ==⨯=,()1914123115101510150P X ==⨯+⨯=,()11121510150P X ==⨯=,列表如下:X12P126150231501150()1262312510121501501501506E X ∴=⨯+⨯+⨯==.18.(1)证明见解析,212n n a -=(2)12520ln24399n n T n +⎤⎡⎫⎛⎫=⋅-+⎥ ⎪⎪⎢⎝⎭⎣⎭⎦【分析】(1)根据11,1,2n nn S n a S S n -=⎧=⎨-≥⎩分两步求解即可;(2)方法一:根据题意,结合导数运算与212n n a -=得()ln2214nn b n =⋅-⋅,进而将{}n b 通项公式变形为125211ln2443939n n n b n n +⎡⎤⎛⎫⎛⎫=⋅--- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再根据裂项求和求解即可.方法二:根据题意,结合导数运算与212n n a -=得()ln2214nn b n =⋅-⋅,再根据错位相减法求和即可.【详解】(1)解:342n n S a =- ,()11342,2n n S a n --∴=-≥,相减得1344n n n a a a -=-,即14n n a a -=,∴数列{}n a 是以4为公比的等比数列,又1113423S a a =-=,解得12a =121242n n n a --=⋅=.(2)解:方法一:()212ln 2ln f x x x x x x x x'=+⋅-= ,()n n b f a =',212n n a -=,()212122ln2ln2214n n n n b n --∴=⋅=⋅-⋅,()125211ln2214ln2443939n n n n b n n n +⎡⎤⎛⎫⎛⎫=⋅-⋅=⋅--- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ ,∴1231n n nT b b b b b -=+++++ 21324357137ln244ln244ln24499999191⎡⎤⎡⎤⎡⎤=⋅⨯+⨯+⋅⨯-⨯+⋅⨯-⨯+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦11252112520ln244ln243939399n n n n n n ++⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫+⋅---=⋅-+ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦∴12520ln24399n n T n +⎡⎤⎛⎫⋅-+ ⎪⎢⎝⎭⎣=⎥⎦.方法二:()212ln 2ln f x x x x x x x x'=+⋅-= ,()n n b f a =',212n n a -=,()212122ln2ln2214n n nn b n --∴=⋅=⋅-⋅∴()()2311ln214ln234ln254ln2234ln2214n nn T n n -+++++=⋅⋅⋅⋅⋅⋅⋅-⋅⋅-⋅ ()()12344ln214ln234ln254ln2234ln2214n n n T n n +++++=⋅⋅⋅⋅⋅⋅⋅-⋅⋅-⋅+ ,两式相减得:()11233ln214ln224ln224ln224ln2214n n n T n +-=⋅⋅⋅⋅⋅⋅⋅++⋅-⋅-⋅++ ()()1231ln2142ln2444ln2214n n n ++++=⋅⋅-⋅⋅+- ()()21114ln2142ln2ln22141414n n n +-=⋅⋅-+⋅⋅---()111ln2142ln2ln22414163n n n ++--⋅-⋅+=⋅⋅()()11165412ln22ln23ln221433ln 220432ln 2n n n n n +++⎡⎤-⋅+⋅⋅-=--⋅⎣=-⎦-∴()()1116546542520ln249939ln 220ln 2209n n n n n n T n +++⎡⎤⎡⎤-⋅-⋅⎡⎤⎛⎫⎣⎦⎣⎦===⋅-+ ⎪⎢⎥---⎭⎣+⎝⎦∴12520ln24399n n T n +⎡⎤⎛⎫⋅-+ ⎪⎢⎝⎭⎣=⎥⎦19.(1)证明见解析(2)12【分析】(1)先利用线面垂直的判定与性质定理证得1AE A B ⊥,再利用平行线分线段成比例的推论证得//BD FG ,从而利用线面平行的判定定理即可得证;(2)利用四棱锥111C AEB A -的体积求出11B C ,建系并写出相关点的坐标,求出两个平面的法向量,利用空间向量的夹角公式计算即得.【详解】(1)如图,连接1A B 交AE 于F ,连接1A D 交1AC 于G ,连接FG ,1AA ⊥ 平面ABC ,BC ⊂平面ABC ,1AA BC ∴⊥,又因11,,,BC AB AB AA A AB AA ⊥⋂=⊂平面ABE,故BC ⊥平面ABE,又AE ⊂平面ABE,则BC AE ⊥,又111,,,AE A C A C BC C A C BC ⊥=⊂ 平面1,A BC 则⊥AE 平面1,A BC 又1A B ⊂平面1A BC ,1AE A B ∴⊥,在1Rt A AB △中,由12AB AA ==知1A B =,2111AA A F A B ==即12A F BF =,又因1111//,2AD A C A C AD =,可得12A G GD =,即在1A BD 中,112AG A F GD FB==,,BD FG ∴∥FG ⊂ 平面1AEC ,BD ⊄平面1AEC//BD ∴平面1AEC ;(2)设11B C x =,四棱锥111C AEB A -的体积为()1121132⨯+=,解得x =,由(1)知11190,90AA B A BA EAB A BA ∠+∠=︒∠+∠=︒,所以1AA B EAB ∠=∠,又11tan tan AB BE AA B EAB AA AB ∠==∠==,则1BE =,所以E 为棱1BB 的中点.以1,,BC BA BB 分别为,,x y z轴建立空间直角坐标系,如图,则()())()11,0,0,1,2,0,A E C A ,则1(0,AE EC == ,设平面1AEC 的法向量为(),,n x y z =,由1n AE n EC ⎧⊥⎪⎨⊥⎪⎩,得00z z ⎧+=⎪⎨+=⎪⎩,令z =(n =- ,因BC ⊥平面11ABB A ,故可取平面1AEA 的法向量()1,0,0m =,1cos ,||||2n m n m n m ⋅〈〉==-,因为二面角11C AE A --为锐二面角,所以二面角11C AE A --的余弦值为12.20.(1)2214x y +=;(2)直线l 过点()2,1-.【分析】(1)根据点A 得到2a =,然后利用点差法得到2144b -=-,即可得到1b =,然后写椭圆方程即可;(2)设,P Q 的坐标,根据直线,AP AQ 的方程得到点,E F 的坐标,然后将α,β转化为方程sin 2cos x y kx x -=-的两根,根据M 的纵坐标和韦达定理得到00121422k kx y -⋅=-+,最后根据M 的纵坐标为定值得到0x ,0y ,即可得到直线l 过定点.【详解】(1)由已知得2a =,设()11,P x y ,()22,Q x y ,PQ 中点为()00,N x y 由22112222221414x y b x y b ⎧+=⎪⎪⎨⎪+=⎪⎩相减得222221212121221212044x x y y y y y y b b x x x x ---++=⇒⋅=--+,∴221144b b -=-⇒=,即1b =.所以椭圆方程为2214x y +=.(2)设()2cos ,sin P αα,()2cos ,sin Q ββ,所以AP l :()sin 22cos 2y x αα=--,即()122tan 2y x α=--,∴13,2tan 2E α⎛⎫ ⎪ ⎪ ⎪-⎝⎭,同理13,2tan 2F β⎛⎫ ⎪ ⎪ ⎪-⎝⎭,设直线l 过点()00,x y ,∴α,β是方程sin 2cos x y k x x -=-的两根.即20022002tantan 2222tan tan 22x x y y k x xx x --=---,整理得()200002tan2tan 2022x xy k kx y kx k ---+-+=,∴002tantan 222y k kx αβ+=--,00002tan tan 222y k kx y k kx αβ+-=--,∴00tantan1121224422tan tan 22M y k kx y αβαβ+=-=-⋅=-+,∴02x =,01y =-,所以直线l 过点()2,1-.【点睛】关键点睛:本题解题关键在于M 的纵坐标为定值,对于定值的问题关键在于与参数无关,本题中M 的纵坐标为定值可得与参数k 无关,即可得到02x =,然后求0y 即可.21.(1)证明见解析;(2)1,2⎛⎫+∞ ⎪⎝⎭【分析】(1)对()f x 求导后构造函数()()11e sin cos 122xg x f x x x x =-'=--,通过求导得出()f x '的单调性和范围得出函数()f x 的单调性,进而得出结论;(2)分类讨论参数a 与12的关系,并通过构造函数和多次求导来探究函数()f x 的单调性,即可得出满足函数在()0,π内有唯一零点的实数a 的取值范围.【详解】(1)由题意,在()()()e sin 1,0,πxf x ax x x x =---∈中,当12a =时,不等式()0f x >等价于1e sin 102xx x x --->,则()11e sin cos 122xf x x x x '=---,令函数()()g x f x =',则()1e cos sin 2xg x x x x +'=-,()10,π,e cos 1cos 0,sin 02x x x x x x ∈∴->->> ,所以函数()g x 在()0,π上单调递增,且()00g =,()()0g x f x '∴=>在()0,π上恒成立,即函数()f x 在()0,π上单调递增,且()00f =,所以()0,πx ∈时,不等式()0f x >成立;(2)由题意及(1)得,在()()()e sin 1,0,πxf x ax x x x =---∈中,当12a ≤时,()1e sin 1e sin 12x xf x ax x x x x x =---≥---,由(1)可知此时()0f x >,所以此时函数()f x 没有零点,与已知矛盾,12a ∴>,()()e sin cos 1xf x a x x x =-+-',令函数()()h x f x =',所以()()e sin 2cos xh x a x x x =-'+,令函数()()u x h x =',()()3sin cos x u x e a x x x ∴=++',①若()()π0,,e 3sin cos 02xx u x a x x x ⎛⎫∈=++'> ⎪⎝⎭,所以函数()()u x h x ='在π0,2⎛⎫ ⎪⎝⎭上递增,且()π2ππ0120,022u a u e a ⎛⎫=-=+ ⎪⎝⎭,0π0,2x ⎛⎫∴∃∈ ⎪⎝⎭,使函数()h x 在()00,x 上递减,在0π,2x ⎛⎫ ⎪⎝⎭上递增,②若π,π2x ⎡⎫∈⎪⎢⎣⎭时,显然()()e sin 2cos 0xh x a x x x =-'+>,所以函数()h x 在()00,x 上递减,在()0,πx 上递增,且()()0π0e 10,ππ10h h e a =-==+->()10,πx x ∴∃∈,使函数()f x 在()10,x 上递减,在()1,πx 上递增,又()()00e 10,πe π10f f π=-==--> ,()10f x ∴<,且()21,πx x ∃∈,使得()20f x =,综上得,当12a >时,函数()f x 在()0,π内有唯一零点,∴a 的取值范围是1,2∞⎛⎫+ ⎪⎝⎭.【点睛】关键点点睛:本题考查构造函数,多次求导,函数的单调性,函数的导数求零点,考查学生分析和处理问题的能力,计算的能力,求导的能力,具有很强的综合性.22.(1)200x y +-=,2y x=(2)()22,2-或()191,.【分析】(1)直线的参数方程消去参数t ,得到直线l 的普通方程,再利用直角坐标与极坐标的转化公式求得曲线C 的直角坐标方程;(2)将直线l 的参数方程,代入曲线C 中,得到韦达定理,利用直线参数方程中参数的几何意义求解.【详解】(1)由1010x t y t =+⎧⎨=-⎩,消去参数t ,得20x y +=,即直线l 的普通方程为200x y +-=,.由2sin cos ρθθ=得:22sin cos ρθρθ=,∵cos x ρθ=,sin y ρθ=,∴2y x =,即曲线C 的直角坐标方程为2y x =.(2)设直线l的参数方程为00222x x y y t ⎧=-⎪⎪⎨⎪=+⎪⎩,代入2y x =得:220001222t t y x t +=-,整理得(22000220t t y x +++-=,设点M ,N 对应的参数分别为1t ,2t,120t t +=-2120022t t y x =-,因为20PM PN +=u u u u r u u u r r ,可得1220t t +=且0020x y +=.解得022x =,02y =-,或019x =,01y =,经验证均满足0∆>,所以求点P 的直角坐标为()22,2-或()19,1.23.(1){4|3x x ≥或23x ⎫≤-⎬⎭;(2)证明见解析.【解析】(1)根据()32||f x x - ,可得3131x x -⎧⎨>⎩ 或1301x x +⎧⎨⎩ 或3130x x -+⎧⎨<⎩ ,然后解不等式组即可得到解集;(2)先利用绝对值三角不等式求出()g x 的最小值,再利用基本不等式求出22a b b a+的最小值即可.【详解】解:(1)当1x ≥时,得41323x x x -≥-⇒≥,∴43x ≥;当01x <<时,得1322x x x -≥-⇒≥,∴无解;当0x ≤时,得21323x x x -≥+⇒≤-;综上,不等式的解集为{4|3x x ≥或23x ⎫≤-⎬⎭.(2)∵()()()15154g x x x x x =-+-≥---=,∴4m =,即4a b +=,又由均值不等式有:22a b a b+≥,22b a b a +≥,两式相加得2222a b b a a b b a ⎛⎫⎛⎫+++≥+ ⎪ ⎪⎝⎭⎝⎭,∴224a b a b b a +≥+=.【点睛】本题考查了绝对值不等式的解法,绝对值三角不等式和基本不等式,考查了转化思想和分类讨论思想,属于中档题.。
高三数学三模考试情况分析

高三数学三模考试情况分析1.考试成绩分析:理科平均分43.7,最高50.3,最,32.7文科平均分34.9,最高44.3,最,28.1学生个人,理科,最高96,最低10;文科,最高93,最低02.学情分析:绝大多数学生学习状态较好,上课比较认真,对复习教学十分有利。
但是由于学习强度大,出现疲劳,急需进行心理疏导。
3. 答卷情况、得分情况总体上与高考难易程度一致,但是为了全面考察知识,我们有意识在一些题目设置了一些障碍,扫描一下学生对知识真正掌握情况,发现复习中存在的问题。
结果学生感觉不太适应,大题有些也不太常规,知识点多,综合性强,文科比理科难。
绝大多数学生主要靠客观题(选择,填空)得分,但是由于这次一些小题不常规,导致靠小题拿分的同学吃了亏,大题得分率较低,文理18题能做上的同学较多,而且阅卷发现一些学生的书写杂乱无章,字迹潦草,偶然做对的地方还看不清楚。
4.存在问题:总体感觉:基本功太差,免疫力低下。
由于要全面考察知识的掌握,设置的点较多。
小题中中档题较多,知识点多,学生上手困难,尤其是文科试题,没有难题,但也没有很容易的题目,这次考试成绩普遍较低,发现学生考试心态影响了发挥,好多学生由于前几个题做得不顺,导致心慌意乱,后面的大题尽管简单,也不能平静作答,出现较大失误。
这次考试充分暴露出很多问题,虽然成绩不理想,但提前发现这些问题,及早预防,也是复习备考中很大的收获。
总体上文理都存在的最大问题是基础掌握不牢,概念不清,记不住东西,运算能力差,运算速度慢,书写不规范,从这次考试还发现,学生基础不牢固,一些基本公式依然没记熟,不会应用。
比如文理科的第一题学生审题不严做对的很少,理科的20题做对的也没有几个人。
文科14题,考差等比数列,只要将公式代入,就可解决问题,但就这个题目,全年级作对的不到20人,17题考查等差数列,也都是用基本公式代入求解的基本问题,但得分很低。
这都提醒我们最后阶段依然要重视回归基础,带着学生一起梳理知识点,熟记概念公式。
完整)高三数学考试质量分析

完整)高三数学考试质量分析建议:教师应该注重基础训练,加强对基础技能的训练和巩固。
可以通过讲解解题思路、分析解题方法等方式来提高学生的技能水平。
同时,要注重培养学生的逻辑思维能力,让学生能够理清思路,正确推理,做到严谨、准确。
第三类是应用方面,学生对于数学的应用场景理解不深,无法将数学知识运用到实际问题中去解决问题。
建议:教师要注重培养学生的应用能力,通过多样化的应用题目训练,让学生能够熟练运用数学知识解决实际问题。
同时,也要注重培养学生的数学建模能力,让学生能够将实际问题转化为数学问题,进而解决问题。
2、试卷难易度分析本次试卷整体难度适中,难度与期中考试相当。
试卷采取了一系列措施来控制试卷的难度,如控制入口题的难度、分步设问等。
同时,试卷也注重考查学生的数学思维能力和应用能力,体现了数学的应用价值和选拔功能。
建议:在今后的试卷设计中,可以进一步注重对学生数学思维能力和应用能力的考查,让试卷更加贴近实际应用,更加全面地考查学生的数学素养和能力。
3、试卷评价本次试卷整体质量较高,试题设计合理,难度适中,注重考查学生的数学思维能力和应用能力,体现了数学的应用价值和选拔功能。
同时,试卷也存在一些问题,如学生对于概念、定理、公式、法则的理解不透,技能方面的薄弱,以及应用能力的不足等。
针对这些问题,教师可以加强基础训练,注重培养学生的数学思维能力和应用能力,让学生能够更好地掌握数学知识,提高数学素养和能力。
建议:针对学生技能与训练的问题,老师应该加强对训练的指导,定时进行针对性训练和小专题训练。
针对学生数学方法、数学思想运用不自如的问题,老师在教学时应该暴露自己的思维过程,尤其是遇到障碍时,让学生去体会、琢磨。
要在问题的分析、思路的发展中运用数学思维想方法进行思维导向,并且从数学思想方法的角度对做过的题目进行比较、分析、鉴别、归类;编结知识之网。
针对学生缺乏应试技巧的问题,老师应该加强与学生的情感的沟通和交流,让学生有成就感,增强研究的兴趣,激发进一步研究的兴趣。
高三数学三模考试试卷分析

银海区福成中学 宁加荣
ห้องสมุดไป่ตู้ 一、试题分析
本次试题题型、形式与高考及前两次模拟考试卷一致,是传统题型,主要考查学生掌握数学基础知识,应用知识的能力,大部分考题是常见常考内容,也是对各章中重点要求掌握的知识点,试题前易后难,相比前两次难易梯度稍明显。各类题型中后面一、二题较难,前几题相对简单,大部分同学都能做一些。试卷整体难度比前两次模拟考小一点。
(1)引导学生对本次考试做好订正和小结,对常考知识点和易错点加强练习和检查。
(2)加强选择题的练习,传授给同学一些应对选择题的技巧、方法。
(3)引导学生在考试时合理安排时间,重点做好1-10题、13、14题,解答题前三题,进行专题训练。
如17题三角函数题,由CotC= ,求sinA的值,绝大多数计算不出,导致整道题失分,其他题就更难得分了。
(2)数学基础知识,灵活应用能力不够。
(3)逻辑思维,解读题能力低。
(4)解答过程马虎,运算能力差等。
三、教学设想
针对本次考试中出现的情况,后阶段要着重做好如下几个方面的教学工作:
二、试卷分析
1、考试结果
经统计分析,我校文科50人参考,最高分52分,平均30分,理科29人参加考试,最高93分,平均分34分,大部分同学靠选择题得分,填空题、解答题得分率非常低,平均不到10%。
2、存在的问题
这次考试反映出的问题大多是一些老问题,比如:
(1)知识不全面,顾此失彼
(完整)高三数学考试质量分析

高三数学考试质量剖析试卷剖析1、要点全面观察三基:试题要点观察高中数学基础知识和基本方法和基本的思想方法,2、控制试卷的难度控制了试卷的整体难度,难度基本与期中考试持平,试卷采纳了以下的举措控制试卷难度:(1)控制试卷的进口题的难度;(2)控制每种题型进口题的难度;(3)较难的解答题采纳分步设问,分步给分的设计方法;(4)控制新题型的比率;(5)控制较难题的比率。
基本上做到了试卷难度的起点和梯度设置适合;3、控制试题的运算量,重视对数学能力的观察。
本试卷适合地降低了试题运算量,降低了对运算能力,特别是数值计算的要求,要点观察代数式化简和变形的能力以及思想方法和计算方法,重视对学生思想能力的观察,要点观察了学生思想能力:直观感知、察看发现、归纳类比、抽象归纳、符号表示、运算求解、数据办理、演绎证明、反省与建构等中心数学能力,要点观察了数形联合、简单的分类议论、化归等数学基本思想方法.3、持续保持应用性题目据有必定的比率;表现数学的应用价值,发展学生的应意图识是新课程的基本理念,也是新课程教材的突出特点,此刻大家也广泛认同经过设置应用题来观察学生应用数学的意识,创建新的问题情形使考生在新的情形中实现知识迁徙,创建性地解决问题,更能表现考生的数学素质和能力,突出了高考的选拔功能,真实观察出考生的学习潜力.试卷保持了应用性题目占必定的比率.4、重视对数学通性通法的观察。
试卷突出要点、重在通性通法、淡化特别技巧。
整张试卷以惯例题为主,综合题目分步设问,由浅入深,有条有理,有益于广大考生获得基安分,稳固考生情绪,发挥出最正确水平。
存在的主要问题及建议1. 从答题状况看,主要存在三类问题:第一类是观点、定理、公式、法例的理解不透,掌握不牢。
建议:教师在平时教课中,增强研究高中数学课程标准,与时俱进的认识三基,重视对三基的教课,并实时复习训练增强、确实夯实三基。
教课中应环绕知识点,将其与其余知识点的联系及联系的方式,全面集中地显现出来,让学生领会到什么是深入观点,理解到什么程度才能驾轻就熟,对你的解题帮助最大。
高三数学模拟试题分析及今后备考措施(多套整理)

高三数学模拟考试分析高三数学组一、试卷总体分析:本次高三数学模拟试题从整体看,既注重了对基础知识的重点考查,也注重了对能力的考查。
从考生的反映看,试题难度适中,最后两道大题考查深入,有较好的梯度和区分度;坚持重点内容重点考,考潜能,考数学应用,在“知识的交汇处命题”有新的突破,反映了新课程的理念,试卷注重对常规数学思想方法以及通性、通法的考查,注重认识能力的考查,注重创新意识,稳中求新,新中求活,活中凸显能力。
——深化能力立意,在知识的交汇点处命制试题试题在利用选择题、填空题和解答题的前四道考查基础知识的同时,设置了几道把关的数学解答题,试题中较容易的是17题、18题、19题和20题,考查的内容分别是三角、概率、空间几何和导数与函数,重点考查了降低要求的概率和空间几何。
试卷的两道题难度较大,第21题是数列题,第22题是圆锥曲线题。
本次摸拟考试数学试题注重综合性、应用性、探索性、开放性等能力型题目的考查,充分体现了能力立意,在考查学生数学基础知识、数学思想和方法的基础上,以逻辑思维能力为核心,同时考查了学生的学习能力、运算能力、空间想像能力、应用能力、探究能力、分析和解决问题的能力和创1新能力,同时加强对思维品质的考查。
试卷在考查基础知识的同时,注重对数学思想和方法的考查,注重对数学能力的考查。
试题强调了知识间的内在联系,注意从学科的整体高度出发,注重各部分知识的综合性、相互联系及在各自发展过程中各部分知识间的纵向联系,在知识网络交汇点设计试题是本次模拟考试的又一道风景线,如试题很多涉及到两个或两个以上的知识点,第17题为向量与三角函数的交汇,第18题为概率与复数的交汇,第21题为数列与推理与证明的交汇,第22题为向量与解析几何的交汇。
本次模拟考试抓住知识网络的交汇点,设计出具有综合性的新颖试题,以达到较全面的考查考生的数学基础和数学素养的目标。
体现了倡导在高中数学中推广研究性学习、强化素质教育的导向。
高三模考数学试卷反思

一、试卷整体分析本次高三模考数学试卷涵盖了高中数学的所有知识点,难度适中,题型丰富。
通过对试卷的仔细分析,我发现自己在以下几个方面存在不足。
二、具体问题分析1. 基础知识掌握不牢固在试卷中,有很多基础题我未能正确解答。
这说明我在基础知识掌握方面存在较大漏洞。
具体表现在以下几个方面:(1)三角函数、解三角形、数列等基础知识掌握不扎实,导致解题时出现错误。
(2)立体几何中的空间想象能力和计算能力不足,导致空间几何题得分率较低。
(3)概率统计中的计算和推理能力有待提高。
2. 解题技巧不足在解题过程中,我发现自己在以下方面存在不足:(1)审题不仔细,导致解题思路混乱。
(2)解题过程中,对于一些较复杂的题目,缺乏有效的解题方法,导致解题时间过长。
(3)在选择题和填空题中,由于粗心大意,导致部分题目失分。
3. 时间分配不合理在本次模考中,我未能合理分配时间,导致部分题目在规定时间内未能完成。
具体表现在:(1)对于一些较难的题目,花费过多时间,导致后面的题目无法按时完成。
(2)在解答题目时,缺乏时间观念,导致部分题目未能得到完整解答。
三、改进措施1. 加强基础知识的学习针对基础知识掌握不牢固的问题,我将采取以下措施:(1)回顾教材,对基础知识进行系统梳理。
(2)多做练习题,巩固基础知识。
(3)请教老师,针对自己的薄弱环节进行针对性学习。
2. 提高解题技巧为了提高解题技巧,我将:(1)多做典型题目,总结解题方法。
(2)参加数学竞赛,锻炼自己的解题能力。
(3)向优秀同学学习,借鉴他们的解题思路。
3. 合理分配时间为了提高时间利用率,我将:(1)制定学习计划,合理安排时间。
(2)在考试前进行模拟训练,提高时间观念。
(3)在考试过程中,学会放弃,确保得分率。
四、总结通过本次高三模考数学试卷的反思,我认识到自己在基础知识、解题技巧和时间分配方面存在不足。
在今后的学习中,我将认真总结经验教训,努力提高自己的数学水平。
相信在老师和同学的帮助下,我一定能够在高考中取得优异成绩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学三模考试质量分析及对策(理)高三数学三模考试质量分析及对策(理)
石必武 2009-11-3 一、三模成绩及试题分析:
本次大考是由惠州地区按照高考考纲命题的,考试范围是高中数学的所有高考要求内容,并且有一定难度,特别是选择第8题、填空第12、13、14题大题后两道,选择填空题与二模比较难度略有上升,试题的计算推理量较大,近50%的学生没有时间做后两题,95%的学生最后一题没做。
我级理科参考人数375人(包括复读生),平均分70.96,最高分127。
各分数段人数见下表: 分130 120 70 110 100 90 8060 72 分 96 90数 ~ ~ ~ ~ 以上分分 ~ ~~~
139 129119 109 99 89 7969 以以上
上人13 26 44 74 67 58 189 55 86 0 3
数
86根据表一,可得:合格率=(按90分及格),优秀率,100%,22.87%375
3=(120分以上为优秀)。
72分以上学生的比率为,100%,0.8%375
189,平均分70.96,根据平均分,难度系数约为0.4731,可,
100%,50.40%375
知试题难度相对较大,试题梯度较一般,区分度较明显(主要是解题速度快慢影
120分以上3人,最高分127分,100分以上算高分,共39人,响得分高低),
分数主要集中在60-80之间,有131人,根据计算,符合原则,是正态分布,3,
样本的方差较小,说明分数分布较集中。
换言之,试题比较适合我们学生。
下面是二模考试情况分析:
(表二)
分130 120 72 9690110 10090 80 70 60
数 ~ ~~ ~~ ~ ~ 分分分 ~
139 129 119 109 99 8979 69 以以以
上上上人数0 0 1732 63 66 60 39 229 72 112
112根据表二,可得:合格率=(按90分及格),优秀率,100%,31.11%360
0=(120分以上为优秀)。
72分以上学生的比率为,100%,0%360
229,平均分75.68,根据平均分,难度系数约为0.504,可知,
100%,63.61%360
试题难度相对较大,试题梯度较明显,区分度也较高,120分以上0人,最高
分119分,100分以上算高分,共59人,分数主要集中在70-100之间,有189
人,根据计算,非常符合原则,是正态分布,样本的方差很小,说明分数分布较3, 集中,简单的形容是“两头轻中间重”。
从结果看,三模的尖子生有所回升(120分以上的由0人减为3人),110分以
上人数持平但及格人数减少了26人,平均分也下降了4.69。
尽管平均分有所下
降,但毕竟是外面来的考题(题目的实际难度未减,计算推理量较大),我们有理由相信,只要一如既往,坚持不懈,一定有一个好收成。
二、对考试结果的分析
从学生答题情况看,我们发现了如下问题:第一,选择题较简单,只要概念清楚,基本计算准确就能拿到较好的分数(只有第8题计算量较难,很多学生难以想
到换元法);填空题主要是第12、13、14三题容易失分,其余5个题相对较简单,
失分的原因有:不能理论联系实际,把实际问题转化成数列问题;不能用分类讨论的方法解绝对值不等式等;大题的前四道属中档题,也是主要得分点,如果计算不
准、方法不当、分类不全、理解不到位,得分率也不会高,后两道题很少有学生做或做对;第二,解基础题的规范性不够,有丢三落四现象,失分严重;第三,计算推理能力不强,解题速度太慢;第四,学生审题能力不强,没有弄懂题目意思就下笔,(比如第20题)有的找不到解题思路;第五,由于试题的难度不大,尖子班学生略显优势。
三、今后的对策
第一:继续开展学法指导,结合每一个学生的具体特点针对性地帮助、指导;
第二:继续加大检查力度、辅导力度,要主动出击,深入了解学生之所想,了解学生之所需;
第三:抓基础,要求大部分学生“双基”过关,抓答题规范;
第四:抓解题速度,通过限时训练提高解题速度。
第五:认真备好每一节课,继续提高课堂效率;同时做好课后总结反思。
四、今后的具体作法:
实验班——由于数学基础相对较好,解题能力较强,思维也较积极,所以下一阶段除抓解题的准确率外,还要抓解题速度(通过利用固定的110分钟每周一套完整的高考模拟题训练,并做认真批改讲评)
理科A层——由于A层有尽70%的学生基础和能力都很一般,这类学生群的数量大,是我们教学的主体对象,所以我们应一如既往地做好:教学中很抓基本知识(包括定义、公式、定理等)和基本技能(包括解题方法、解题规范),部分章节也注意能力的培养,围绕考试内容,结合大纲要求,认真制定教学案,让学生明确每一章节的学习目标;同时加强每天的限时训练(老师继续全批全改,及时讲评);结合学生实际情况,一周的六份训练题有三张题跟进度,三张题综合)
理科B层——理科B层的学生是一种混合体(含体育生),有基础特差的,有反映特慢的,有不遵守纪律的,有好出风头的,当然到现在也有不少学生想学,并且
想学好,因此给这类学生上课时,要尽量挖掘他们的闪光点,以表扬为主,教学内容可限制在数学概念和基本知识上,主要进行基础题的训练。
力争完成每天一份限时训练题(大约40分钟完成)。
三个层次的教学要求明显不同,力争使各个层次的学生都有收获。
要求学生每天都做一份限时训练题,除级组大测外,每周三测试一次,巩固复习效果。
每一次训练和测试,都全部批改,并选择性地及时评讲,同时要求学生对错误问题及时纠正,并在纠错本上规范性地改正。
大力抓好学生对知识的复习整理工作,使学生形成习惯。
