卵形曲线参数计算1

卡西尼卵形线二级结论

卡西尼卵形线二级结论概述卡西尼卵形线是指由卡西尼椭圆函数描述的一个曲线，其形状类似于椭圆，却有一端延伸得更加细长，如同一个鸟巢的形状。

该曲线的特殊性质引起了科学家的极大兴趣，并且在多个研究领域中发现了相关的二级结论。

本文将对卡西尼卵形线的二级结论进行全面、详细、完整的探讨。

卡西尼椭圆曲线的定义卡西尼椭圆曲线的数学表达式为：(x^2 + y^2)^2 = a^2 * (x^2 - y^2)其中，(x, y)为曲线上任意一点的坐标，a为常数。

卡西尼椭圆曲线具有一个特殊的性质，即曲线上任意一点到两个焦点的距离的乘积等于常数的平方：PF1 * PF2 = a^2卡西尼卵形线的性质卡西尼卵形线具有以下几个重要性质：1.中点切线平行于传方向曲线：卡西尼卵形线的中点切线与焦线的夹角等于传方向曲线与焦线的夹角。

2.对角线交点处切线垂直于传方向曲线：卡西尼卵形线的对角线交点处的切线与传方向曲线垂直。

3.曲线外端点处切线过焦点：卡西尼卵形线的曲线外端点处的切线经过焦点，即焦点是曲线上所有切线的一个公共点。

卡西尼卵形线的二级结论二级结论一：焦点与极限在卡西尼卵形线上，焦点有以下重要性质：1.焦点是曲线的对称中心：任意取曲线上一点P和其对称点P’，则P和P’到焦点的距离之积相等。

2.焦点与曲线的对称轴上有垂直关系：曲线的对称轴与曲线上任意一点到焦点的距离的乘积为常数。

3.曲线上离焦点越远的点，其到焦点的距离趋近于曲线的半径：即当P到焦点的距离无限增大时，这个距离与曲线的半径趋于相等。

二级结论二：卡西尼卵形线与力学在力学领域中，卡西尼卵形线也有一些相关的二级结论：1.卡西尼卵形线的轨迹：如果一个质点被两个力限制在卡西尼卵形线上，那么该质点的轨迹将是卡西尼卵形线。

2.卡西尼卵形线的稳定性：在某些力学系统中，卡西尼卵形线是一个稳定的平衡位置，当质点偏离卡西尼卵形线时，力将会将其拉回。

3.卡西尼卵形线与天体运动的关系：天体的运动轨迹中存在一类特殊情况，即当天体被两个引力中心所限制时，其运动轨迹将形成卡西尼卵形线。

卵形曲线计算原理

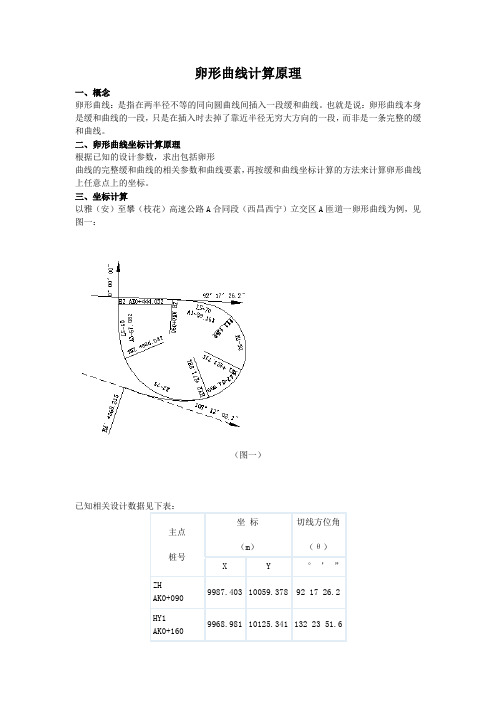
卵形曲线计算原理一、概念卵形曲线：是指在两半径不等的同向圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：1、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ'-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

缓和曲线计算方法

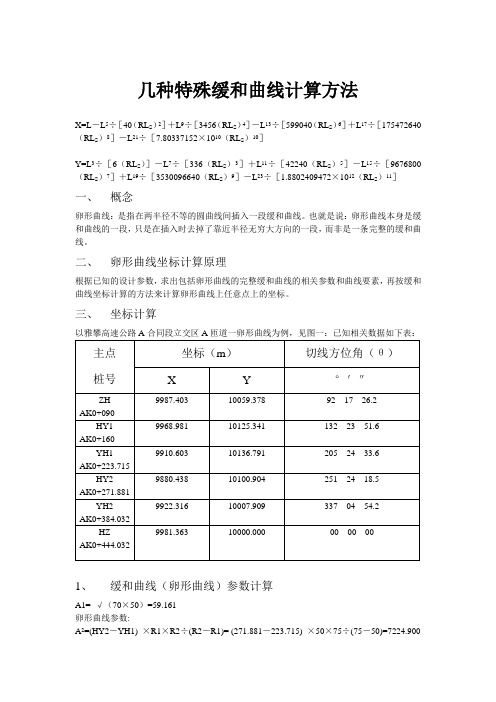
几种特殊缓和曲线计算方法X=L－L5÷［40（RL S）2］＋L9÷［3456（RL S）4］－L13÷［599040（RL S）6］＋L17÷［175472640（RL S）8］－L21÷［7.80337152×1010（RL S）10］Y=L3÷［6（RL S）］－L7÷［336（RL S）3］＋L11÷［42240（RL S）5］－L15÷［9676800（RL S）7］＋L19÷［3530096640（RL S）9］－L23÷［1.8802409472×1012（RL S）11］一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅攀高速公路A合同段立交区A匝道一卵形曲线为例，见图一：已知相关数据如下表：1、缓和曲线（卵形曲线）参数计算A1= √（70×50）=59.161卵形曲线参数:A2=(HY2－YH1) ×R1×R2÷(R2－R1)= (271.881－223.715) ×50×75÷(75－50)=7224.900A2=√（7224.900）=84.999A3=√（60×75）=67.0822、卵形曲线所在缓和曲线要素计算卵形曲线长度L F由已知条件知：L F=HY2－YH1=271.881－223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度L S，由此找出HZ｀点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）L M=L S（YH1至HZ｀的弧长）=A2÷R1=7224.9÷50=144.498∴HZ｀桩号=YH1+L M=223.715+144.498=368.213L E=HY2至HZ｀的弧长=A2÷R2=7224.9÷75=96.332或L E=L M－L F=144.498－48.166=96.332卵形曲线长度L F=L M－L E=144.498－96.332=48.166（校核）HY2=HZ｀－L E=368.213－96.332=271.881（校核）以上说明计算正确3．HZ｀点坐标计算（见图2）㈠用缓和曲线切线支距公式计算，缓和曲线切线支距通式：Xn=［（－1）n+1×L4n－3］÷［（2n-2）！×22n－2×（4n－3）×（RL S）2n－2］Yn=［（－1）n+1×L4n－1］÷［（2n-1）！×22n－1×（4n－1）×（RL S）2n－1］公式中符号含义：N——项数序号（1、2、3、……n）！——阶乘R——圆曲线半径LS——缓和曲线长度㈡现取公式前6项计算（项数越多精度越高，可根据工程精度需求取项数），带入公式后计算如下：X=L－L5÷［40（RL S）2］＋L9÷［3456（RL S）4］－L13÷［599040（RL S）6］＋L17÷［175472640（RL S）8］－L21÷［7.80337152×1010（RL S）10］Y=L3÷［6（RL S）］－L7÷［336（RL S）3］＋L11÷［42240（RL S）5］－L15÷［9676800（RL S）7］＋L19÷［3530096640（RL S）9］－L23÷［1.8802409472×1012（RL S）11］公式中L为计算点至ZH ｀或HZ｀的弧长HZ｀：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ｀－YH1=368.213-223.715=144.498将L=LS带入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2＋Y2）=131.5301偏角a1=arctg（Y÷X）=27°5′0.2″偏角计算用反正切公式，不要用其他公式。

卵形曲线的坐标计算

… 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】 … 】Ｈ
表１（续）
８９１０
ｌｌ
Ｈ；第一阶扭转振动频率为１９Ｈ；第一阶扭弯ｚ．５ｚ８
拱梁（称）弯对竖拱梁（对称）弯反竖拱梁（对称）弯反侧
摘要：卵形曲线是路线设计中几种复杂的曲线之一，但与其相关内容的介绍很少，因此根据卵形曲线的定义及设计参数给出其坐标的计算过程很有实际意义关键词：卵形曲线；坐标；计算中图分类号：Ｕ１、４２３文献标识码：Ａ文章编号：１０ — ７６２０）２０ — １９００２４８（０７０、３０２ — ２
／
～ —
、
件和有关标准规范要求，也是评定桥梁运营荷载等
＼Ｌ／
ｊ，
级最直接和有效的手段。动载试验通过测试桥梁在
动载作用下的响应，分析桥梁的频率、阻尼和振型
ＤｒｃｙＵｄｒＣｉｅｅＰｏｌＳＡｍｄＰｌｅＦｒｅｅｉ００９ｈｎ）ｉｔｎｅｈｎｓｅｐｅｒｅｏｃｏｃ，Ｂｉｎ１０２，Ｃｉａｅｌｉｊｇ
Ａｂｔａｔｓｒｃ：Ｔｅｅｇｓａｅｃｒｅｓｏｅｏｈｏｌｘｃｒｅｏｅｉｎｏｄｌｅ，ｂｔｔｅｒｌｔｄｈｇ — ｈｐｄｕｖｓｉｎｆｔｅｃｍｐｅｕｖｓｆｒｄｓｇｒａｉｎｕｈｅａｅｃｎｅｄｓｖｒａｅｏ，ｔｅｅｒｍｕｈｒｃｉａｍｅｎｎｓｏｇｖｎｔｅｏｐｅｆｏｕａｉｎｏｒｏｔｎｉｅｙｒｒ．Ｓｈｒａｅｃｐａｔｌｃａｉｇｆｒｉｉｇｈｃｕｏｃｍｐｔｔｃｏ－ｏｄｎｔｓｏｇ — ｈｐｄｃｒｅｃｏｄｎｏｔｅｄｆｉｏｆｅ－ｈｐｄｃｒｅｎｔｅｉｎｐｒｍｅｅ．ｉａｅｆｅｇｓａｅｕｖｓａｃｒｉｇｔｈｅｎｔｎｏｇｓａｅｕｖｓａｄｉｄｓ — ａａｔｒｉｉｓｇＫｅｒｓｅｇｓａｅｕｖｓｏｒｉａｅ；ｃｍｐｔｔｎｙｗｏｄ：ｇ — ｈｐｄｃｒｅ；ｃｏｄｎｔｓｏｕａｉｏ

笛卡尔卵形线求参数

笛卡尔卵形线求参数笛卡尔卵形线（Cartesian oval）是一种在笛卡尔坐标系中的二维曲线，由法国数学家笛卡尔于17世纪提出。

它的数学表达式为：（x²/a²） + （y²/b²） = 1其中，a和b分别是椭圆的长轴和短轴的长度。

笛卡尔卵形线是一种非常有特殊形状的曲线，它既有椭圆的特点，又有双曲线的特点。

从数学上来说，它是一个椭圆和一个双曲线的交点，因此也被称为交点曲线。

这种曲线在几何学和物理学中有着广泛的应用。

笛卡尔卵形线在几何学中有着重要的地位。

它的形状独特，可以用来描述一些特殊的几何问题。

例如，在光学中，当光线从一个焦点射入椭圆，经过反射后又汇聚到另一个焦点上，这个路径就可以用笛卡尔卵形线来描述。

另外，在天文学中，行星的轨道和彗星的轨道也可以用笛卡尔卵形线来近似描述。

笛卡尔卵形线在物理学中也有着重要的应用。

例如，在电磁学中，当一个带电粒子在两个电荷之间运动时，其路径也可以用笛卡尔卵形线来描述。

另外，在力学中，当一个质点在一个中心力场中运动时，其轨迹也可以是笛卡尔卵形线。

这些应用都是基于笛卡尔卵形线的数学性质和几何形状的特点。

笛卡尔卵形线还在工程学和计算机图形学中有着广泛的应用。

例如，在计算机图形学中，通过控制椭圆的长轴和短轴的长度，我们可以绘制出各种各样的卵形线，从而实现复杂的图形效果。

另外，在工程学中，通过研究笛卡尔卵形线的性质，可以设计出一些具有特殊功能的曲线，用于解决一些实际问题。

笛卡尔卵形线是一种具有特殊形状和重要应用的曲线。

它在几何学、物理学、工程学和计算机图形学等领域都有着广泛的应用。

通过研究笛卡尔卵形线的性质和应用，我们可以深入理解这个曲线的数学本质，同时也可以将它应用于解决实际问题。

希望通过本文的介绍，读者对笛卡尔卵形线有更加深入的了解。

卵形曲线要素及其上任意点坐标的严密算法

线角为、弦ＹＨ１－ＨＹ２的长度Ｓ以及弦
求得卵形曲线要素（切线角、切线增量ｑ、圆曲线内
移值、切线长Ｔ等）。
１．１卵形曲线要素推证完整缓和曲线计算公式为：
标为（Ｘ，Ｙ），交点２高斯坐标为（ｘ：，
Ｙ：）。设ＩＰ２处圆曲线ＨＹ２－ＹＨ２圆心位置为Ａ，过
Ａ点作垂线Ａ — Ｖ垂直线段２一ＨＺ于、／ｒ，作垂线Ａ．Ｖ。垂直线段ＩＰ１一ＩＰ２于Ｖ。；连接Ａ与ＩＰ２点，由
２０／３５６７ — ６ ຫໍສະໝຸດ ．．．。． — —
—
．
．．
．
．．
—
—
ＣＮ２２＿１３Ｚ３／Ｎ
卵形曲线要素及其上任意点坐标的严密算法
任克林
（四川省冶金地质勘查局测绘工程大队，成都６１０２１２）
摘要：针对公路中线（平曲线）卵形曲线测设与计算，将卵形曲线补全为完整缓和曲线，并利用其几何性质
图１中以Ｒ＞Ｒ：右转路线为例，设卵形线ＹＨＩ－ＨＹ２缓和曲线切线角（以下简称切线角）为２处后缓和曲线切线角为，弦ＹＨ１－ＨＹ２与
，
ＹＨ２一ＨＺ为ＩＰ２处后缓和曲线，长度为Ｌ，卵形线（ＩＰ２处前缓和曲线）ｙＨ１＿ＨＹ２曲线长度为Ｌ＾，起

卵形曲线计算(1)

2、卵形曲线计算本设计由于12~JD JD 之间的距离偏小，又都为右偏，直线长度很难满足要求，同时也为适应地形条件的变化，所以此处敷设卵形曲线。

卵形曲线设计计算如下：运用纬地软件设计卵形曲线，系将卵形曲线看做是两个同向基本型平曲线的组合对接，首先给定小圆半径以及小圆的前缓和曲线长度：1700R =，1100S L =，这个前缓和曲线的起点半径为无穷大，而后缓和曲线长度为0。

然后切换到交点2，给定前缓和曲线长100F L =，后缓和曲线长2100S L =，由于中间过渡段曲线的半径变化是从12~R R ，所以第二段曲线的前缓和曲线F L 起点给定半径为小圆半径700，终点半径即大圆曲线半径2R 采用纬地软件的“T1+Rc+S2”或“T1+S1+Rc ”反算模式，计算结果为1451.22。

卵形曲线设计参数宜满足如下三个条件： ①112F R A R ≤≤ ②120.20.8R R ≤≤ ③10.0030.03D R ≤≤已知：1212700,1451.22,100S S F R R L L L ===== 计算：（如图2.1）图2.1 卵形曲线示意图[11]122112122212121212120.27001451.220.480.8,,,242422F F F F F F F F R R D R R O O O O L L L L P P q q R R ≤==≤=--=====2212122211221221212112212112111,()1001451.22700135227.231451.22700350367.737002135227.23135227.23193.18,93.187001451.2224F F F F F F F F F F F F F F F F F F A A L L R R A R R L L L R R L R R A R R A R A R A A L L R R L P R ==-=-==-⨯⨯==-=≤=≤========反推：22222121212211293.18193.182.22,0.252470024241451.22193.1893.1896.59,46.592222749.011451.22700F F F F F F L P R L L q q O O D R R O O =====⨯⨯==========--=-1749.01 2.210.003 2.217000.00310.03D R -=≤==≤综上计算，本设计卵形曲线设计满足《公路路线设计规范》要求。

卵型曲线计算方法

文档名
3）卵型曲线计算方法
M
(R 1p 1)ta 2 1 n(R 2p2)ta 2 2 nAB
（1）中间缓和曲线计算
回旋线参数：A424DR3 4 24PFR13R23
(R1R2)3
必须检查参数A是否在规定范围：R2/2<A<R2。
中间缓和曲线段长度LF ：
LFR A 2 2A R 1 2R R 11 R R 22A2
M点坐标： x M x Y1H x /co cso M s 1( 8)0 y M y Y1H x /co ss iM n 1 ( 8)0
式中：x,y——中间缓和曲线R1处切线支距值；
δ——中间缓和曲线R1处弦角，
arctan
y x
l1 —— 曲率半径为R1处的缓和曲线长度，
法粗定出沿线应穿应避的一系列中间控制点，拟定路线轮廓方案。（二）放坡，定导向线
现场放均坡线。仪器：坡度仪或手水准仪、花杆。
第四节直接定线
一、直接定线的工作步骤
（一）分段安排路线在选线布局定下的主要控制点之间，沿拟定方向用试坡方
法粗定出沿线应穿应避的一系列中间控制点，拟定路线轮廓方案。（二）放坡，定导向线
2．虚交点
▪ ①切基线法：
▪ ②离、割基线法：
③曲线起终点法：
R A1 A2 2 sin 2
3．回头曲线
▪ 大头回头曲线布设：主曲线
▪
两条辅助曲线
▪ 半径确定同虚交点法。
3．回头曲线
▪ 大头回头曲线布设：主曲线
▪
两条辅助曲线横断面检查。
谢谢大家
（3）中间缓和曲线起点M坐标计算：
②当R1<R2时：回旋线起点M位于HY2点前方。由YH1坐标推算M坐标：