求解AOE网关键路径例题详解3页word
关键路径问题
1）将项目中的各项活动视为有一个时间属性的结点，从项目起点到终点进行排列；
2）用有方向的线段标出各结点的紧前活动和紧后活动的关系，使之成为一个有方向的网络图；
3）用正推法和逆推法计算出各个活动的最早开始时间，最晚开始时间，最早完工时间和最迟完工时间，并计算出各个活动的时差；
void seekkeyroot()//求关键路径的主函数
{
int projectnumber,activenumber,totaltime=0;
printf("\n");
printf("输入符合标准，欢迎进入求关键路径的系统!\n");
printf("\n");
printf("请输入这个项目的AOE-网的节点数: ");
{
int projectname;//顶点域
int id;//顶点的入度信息
edgenode *link; //边表头指针
}vexnode;
void CreateGraphic(vexnode* Graphicmap,int projectnumber,int activenumber)//创建图
{
CreateGraphic(Graphicmap,projectnumber,activenumber);//创建邻接图
SearchMapPath(Graphicmap,projectnumber,activenumber,totaltime);//求出最大路径，并打印出关键路径
printf("\n");
edgenode *p; //边表头的指针
totaltime=0; //存放整个工程的最短时间
《信息系统监理师》难点--关键路径
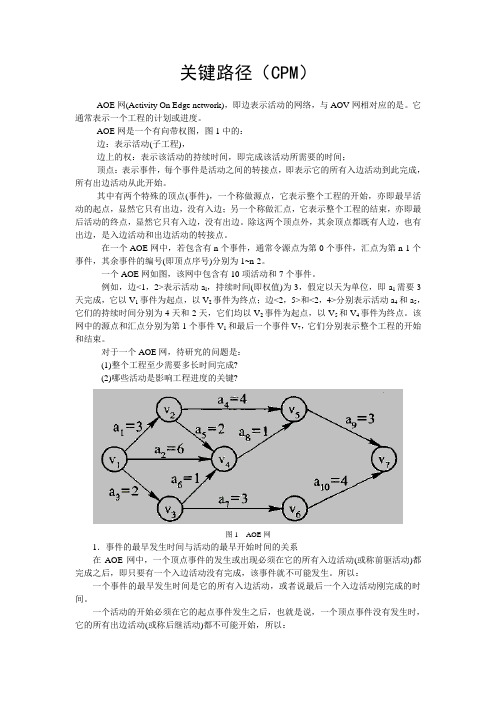
关键路径（CPM）AOE网(Activity On Edge network)，即边表示活动的网络，与AOV网相对应的是。
它通常表示一个工程的计划或进度。
AOE网是一个有向带权图，图1中的：边：表示活动(子工程)，边上的权：表示该活动的持续时间，即完成该活动所需要的时间；顶点：表示事件，每个事件是活动之间的转接点，即表示它的所有入边活动到此完成，所有出边活动从此开始。
其中有两个特殊的顶点(事件)，一个称做源点，它表示整个工程的开始，亦即最早活动的起点，显然它只有出边，没有入边；另一个称做汇点，它表示整个工程的结束，亦即最后活动的终点，显然它只有入边，没有出边。
除这两个顶点外，其余顶点都既有人边，也有出边，是入边活动和出边活动的转接点。
在一个AOE网中，若包含有n个事件，通常令源点为第0个事件，汇点为第n-1个事件，其余事件的编号(即顶点序号)分别为1~n-2。
一个AOE网如图，该网中包含有10项活动和7个事件。
例如，边<1，2>表示活动a l，持续时间(即权值)为3，假定以天为单位，即a1需要3天完成，它以V1事件为起点，以V2事件为终点；边<2，5>和<2，4>分别表示活动a4和a5，它们的持续时间分别为4天和2天，它们均以V2事件为起点，以V5和V4事件为终点。
该网中的源点和汇点分别为第1个事件V1和最后一个事件V7，它们分别表示整个工程的开始和结束。
对于一个AOE网，待研究的问题是：(1)整个工程至少需要多长时间完成?(2)哪些活动是影响工程进度的关键?图1AOE网1．事件的最早发生时间与活动的最早开始时间的关系在AOE网中，一个顶点事件的发生或出现必须在它的所有入边活动(或称前驱活动)都完成之后，即只要有一个入边活动没有完成，该事件就不可能发生。
所以：一个事件的最早发生时间是它的所有入边活动，或者说最后一个入边活动刚完成的时间。
一个活动的开始必须在它的起点事件发生之后，也就是说，一个顶点事件没有发生时，它的所有出边活动(或称后继活动)都不可能开始，所以：一个活动的最早开始时间是它的起点事件的最早发生时间。
软件设计师重点难点-关键路径
软件设计师重点难点——关键路径关键路径这个知识点在软件设计师考试中，是一个难点。
说到关键路径这个概念，大家应该多少有些印象，可能都知道它是“最长路径”而不是“最短路径”，但说到它为什么是最长路径，提出这个概念的用意何在，它有什么应用，在计算机中关键路径是如何求的等问题却没有几个人能真正搞清楚，甚至书上给出了完整的例子，都有很多人看不懂。
下面我先会简单的说明基本概念，然后以一个例子，结合平时希赛教育学员的疑问，对这个知识点进行详细的分析。
在AOV网络中，如果边上的权表示完成该活动所需的时间，则称这样的AOV为AOE 网络。
例如，图1表示一个具有10个活动的某个工程的AOE网络。
图中有7个顶点，分别表示事件1～7，其中1表示工程开始状态，7表示工程结束状态，边上的权表示完成该活动所需的时间。
下面我们来理解一下关键路径的思想，图1虽节点不多，但是为了让问题变得更为简单、直观，我们画另一个AOE网络，如图2所示。
从图2中我们可以看出，关键路路径实际上是从源点到目的地的最长路径。
为什么是最长路径呢?因为图中的某些事件是可以并发执行的。
如图2所示，当到达V1后，可以同时往V2，V3，V4三个方向走，而V2，V3，V4都有到Vk的路径，且长度都为1，并且Vk 是终点，则关键路径是V1->V2->Vk。
因为这条路径最长，只要这条路径到目的地Vk时其他的都已经到达Vk。
而在这条关键路径上的活动a2，a5称为关键活动。
为了找出给定的AOE网络的关键活动，从而找出关键路径，先定义几个重要的量：V e(j)、Vl(j) ：顶点j事件最早、最迟发生时间。
e(i)、l(i)：活动i最早、最迟开始时间。
从源点V1到某顶点Vj的最长路径长度称为事件Vj的最早发生时间，记为Ve(j)。
Ve(j)也是以Vj为起点的出边<Vj，Vk>所表示的活动ai的最早开始时间e(i)。
在不推迟整个工程完成的前提下，一个事件Vj允许的最迟发生时间记为Vl(j)。
关于AOE网中关键路径求解算法的研究
ｌ 相关概念
在 Ａ Ｅ网 中有 些活 动可 以并行 地进 行 ， 以完 Ｏ 所
第三步 ， Ａ Ｅ网所有活动的最早开始时间 ｅ 求 Ｏ 。
如 果活 动 ａ 由 ＜ ， 表 示 ， 用公 式 （ ） 解 ： （） ｋ＞ 利 ３求
ｅ ｉ ＝ｖ（） （ ） ｅｊ （） ３
Ｖ（） Ｍ ｘ ｖ（） ｄ ｔｉ ） ， 中 ２＜＝ ｅｊ ＝ ａ ｛ ｉ ＋ ｕ（， ｝其 ｅ ＜
＝ｎ （） １
第 二 步 ， Ａ Ｅ 网所 有 时 间 的最 迟 发 生 时 间 求 Ｏ ｖ。利用 公式 （ ） ｖ（ ）＝ ｖ（ ） ｌ ２ 从 ｌｎ ｅ ｎ 开始 向后递推 Ｖ（）＝ ｎ｛ｆ（）一ｄｔｉ ） ， 中 １＜ ＝ｉ １ｉ Ｍｉ ｅ ｕ（， ｝其 ＜
第六步 ， 找出所有 ｚ ｅ ０的关键路径。 —＝
作者简 介 ： 常友渠（ ９９一） 讲师 ， 士学位 ， １７ ， 硕 主要研究方 向： 计算机应用 。
３ ８
重 庆 电 力 高 等 专 科 学 校 学 报
第１ ５卷
２２ 基于 Ｐ 阵的求解方法 ． 矩
基于 Ｐ 矩阵的求关键路径的算法 ： 第 一 步 ， 造 图 Ｇ 的 ／阶 Ｐ邻 接 矩 阵 Ｍ。 构 ７ ， ＝ （ ， ｏ） 其中， 如果 邻接 ｖ， ， （ ）＞， ｊ口 ＝＜ Ｌ ｉ ｊ 否则 ０＝ ０的值 ； ， 其中 Ｌ ｉ 的值为 到 边上的权 ； （） ｊ 第 二步 ， 据 构 造 ： 根 将 中所 有 路删 去
【 关键词】 Ｏ Ａ Ｅ网； 关键路径； 算法 ； 广度优先搜索遍历（Ｆ ） Ｂ Ｓ 【 中图分类号］Ｐ １．２ Ｔ ３１１ 【 文献标识码】 Ａ 【 文章编号】０８ ０２ ２ｌ） １ Ｏ７ １０— ３ （０００ ＿ ３ ３ ８ ｏ
(整理)AOE关键路径.
显然，对于关键活动而言，e(i)= l(i)。对于非关键活动，l(i)－e(i)的值是该工程的期限余量，在此范围内的适度延误不会影响整个工程的工期。
一个活动ai的最晚开始时间l(i)和最早开始时间e(i)的差值l(i)－e(i)是该活动完成的时间余量。它是在不增加完成整个工程所需的总时间的情况下，活动ai可以拖延的时间。当一活动的时间余量为零时，说明该活动必须如期完成，否则就会拖延整个工程的进度。所以称l(i)－e(i)=0，即l(i)=e(i)时的ai是关键活动。
(4)根据各顶点的ve和vl值，求每条弧（活动）ai的最早开始时间e(i)和最迟开始时间l(i)。
(5)找出e(i)=l(i)的活动，则为关键活动。由关键活动形成的由源点到汇点的每一条路径就是关键路径，关键路径有可能不止一条。
三、关键路径算法的实现
由于每个事件的最早发生时间ve(i)和vl(i)要在拓扑序列的基础上进行计算，所以关键路径算法的实现要基于拓扑排序算法，我们仍采用邻接表做有向图的存储结构。
if(vl[k]<vl[j]－p->weight) vl[k]= vl[j]－p->weight;
(6)从源点开始，对于每个顶点i，用指针p依次指向i的每个邻接顶点，取得每个顶点的序号j=p->adjvex，分别计算活动<vi，vj>的最早发生时间和最迟发生时间e和l。
e=ve[i]；l=vl[j]－p->weight;
图6.22一个AOE网
和AOV-网不同，对AOE-网有待研究的问题是：
(1)完成整项工程至少需要多少时间?
(2)哪些活动是影响工程进度的关键?
由于在AOE-网中有些活动可以并行地进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度(这里所说的路径长度是指路径上各活动持续时间之和，不是路径上弧的数目)。路径长度最长的路径叫做关键路径(Critical Path)。假设开始点是v0，从v0到vi的最长路径长度叫做事件vi的最早发生时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间。我们用e(i)表示活动ai的最早开始时间。还可以定义一个活动的最迟开始时间l(i)，这是在不推迟整个工程完成的前提下，活动ai最迟必须开始进行的时间。两者之差l(i)-e(i)意味着完成活动ai的时间余量。我们把l(i)=e(i)的活动叫做关键活动。显然，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快工程的进度。因此，分析关键路径的目的是辨别哪些是关键活动，以便争取提高关键活动的工效，缩短整个工期。
数据结构程序设计实验～AOE图的关键路径
数据结构课程设计报告专业网络工程班级姓名学号指导老师评分计算AOE网的关键路径AOE网即边表示活动的网络。
通常，可用AOE网来估算工程计划的完成时间。
如下所示的AOE网包括11项活动，9个事件，每个事件都有所需的完成时间。
我们现在要解决的是：（1）完成整项工程至少需要多少时间（最短时间）；（2）哪些活动是影响工程进度的关键（关键活动）。
用e(i)表示活动最早开始时间，l(i)表示活动的最迟开始时间，则l(i)-e(i)为完成该活动的时间余量。
对于本例列表如下：下图就是上述AOE网的关键路径：请编程完成下列工作：1、输入：（1）顶点的信息和入度；（2）AOE网的边（始点、终点和权值）。
2、输出：（1） AOE网的邻接表（按“顶点入度：—>顶点权值”的格式输出）如a 0：-->4 5-->3 4-->2 6（2）输出关键活动每行所显示的分别为开始事件、结束事件、最早开始时间、最迟开始时间和完成活动的时间余量：当l(i)-e(i)=0时，在该行注明为关键活动。
如：a b 0 0 0 关键活动源程序#include<stdio.h>#include<stdlib.h>#include<iomanip.h>#include <process.h>//#define PROJECTNUMBER 9//10//#define PLANNUMBER 11//13typedef struct node{int adjvex;int dut;struct node *next;}edgenode;typedef struct{int projectname;int id;edgenode *link;}vexnode;//vexnode Graphicmap[PROJECTNUMBER];void CreateGraphic(vexnode* Graphicmap,int projectnumber,int activenumber){int begin,end,duttem;edgenode *p;for(int i=0;i<projectnumber;i++){Graphicmap[i].projectname=i;Graphicmap[i].id =0;Graphicmap[i].link =NULL;}printf("某项目的开始到结束在图中的节点输入<vi,vj,dut>\n");printf("如：3,4,9 回车表示第三节点到第四节点之间的活动用了9个单位时间\n"); for(int k=0;k<activenumber;k++){scanf("%d,%d,%d",&begin,&end,&duttem);p=(edgenode*)malloc(sizeof(edgenode));p->adjvex =end-1;p->dut =duttem;Graphicmap[end-1].id ++;p->next =Graphicmap[begin-1].link ;Graphicmap[begin-1].link =p;}}int SearchMapPath(vexnode* Graphicmap,int projectnumber,int activenumber,int& totaltime){int i,j,k,m=0;int front=-1,rear=-1;int* topologystack=(int*)malloc(projectnumber*sizeof(int));//用来保存拓扑排列int* vl=(int*)malloc(projectnumber*sizeof(int));//用来表示在不推迟整个工程的前提下，VJ允许最迟发生的时间int* ve=(int*)malloc(projectnumber*sizeof(int));//用来表示Vj最早发生时间int* l=(int*)malloc(activenumber*sizeof(int));//用来表示活动Ai最迟完成开始时间 int* e=(int*)malloc(activenumber*sizeof(int));//表示活动最早开始时间edgenode *p;totaltime=0;for(i=0;i<projectnumber;i++) ve[i]=0;for(i=0;i<projectnumber;i++){if(Graphicmap[i].id==0){topologystack[++rear]=i;m++;}}while(front!=rear){front++;j=topologystack[front];m++;p=Graphicmap[j].link ;while(p){k=p->adjvex ;Graphicmap[k].id --;if(ve[j]+p->dut >ve[k])ve[k]=ve[j]+p->dut ;if(Graphicmap[k].id ==0)topologystack[++rear]=k;p=p->next ;}}if(m<projectnumber){printf("\n本程序所建立的图有回路不可计算出关键路径\n");printf("将退出本程序\n");return 0;}totaltime=ve[projectnumber-1];for(i=0;i<projectnumber;i++)vl[i]=totaltime;for(i=projectnumber-2;i>=0;i--){j=topologystack[i];p=Graphicmap[j].link ;while(p){k=p->adjvex ;if((vl[k]-p->dut )<vl[j])vl[j]=vl[k]-p->dut ;p=p->next ;}}i=0;printf("| 起点 | 终点 | 最早开始时间 | 最迟完成时间 | 差值 | 备注 |\n");for(j=0;j<projectnumber;j++){p=Graphicmap[j].link;while(p){k=p->adjvex ;e[++i]=ve[j];l[i]=vl[k]-p->dut;printf("| %4d | %4d | %4d | %4d | %4d |",Graphic map[j].projectname +1,Graphicmap[k].projectname +1,e[i],l[i],l[i]-e[i]);if(l[i]==e[i])printf(" 关键活动 |");printf("\n");p=p->next ;}}return 1;}void seekkeyroot(){int projectnumber,activenumber,totaltime=0;system("cls");printf("请输入这个工程的化成图形的节点数:");scanf("%d",&projectnumber);printf("请输入这个工程的活动个数:");scanf("%d",&activenumber);vexnode* Graphicmap=(vexnode*)malloc(projectnumber*sizeof(vexnode)); CreateGraphic(Graphicmap,projectnumber,activenumber);SearchMapPath(Graphicmap,projectnumber,activenumber,totaltime);printf("整个工程所用的最短时间为：%d个单位时间\n",totaltime);system("pause");}int main(){char ch;for(;;){do{system("cls");printf("| 欢迎进入求关键路径算法程序 |");for(int i=0;i<80;i++)printf("*");printf("%s","(S)tart开始输入工程的节点数据并求出关键路径\n"); printf("%s","(E)xit退出\n");printf("%s","请输入选择:");scanf("%c",&ch);ch=toupper(ch);}while(ch!='S'&&ch!='E');switch(ch){case'S':seekkeyroot(); break; case'E':return 1; }}}。
关键路径AOE网及其如何求关键路径步骤
关键路径AOE网及其如何求关键路径步骤一、关键路径（一）AOE网在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成活动所需的时间），称之为用边表示活动的网络，简称AOE网(Activity On Edge NetWork)AOE⽹具有以下两个性质：①只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始；②只有在进入某顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。
另外，有些活动是可以并行进行的在AOE网中仅有一个入度为0的顶点，称为开始顶点（源点），它表示整个工程的开始；也仅有一个出度为0的顶点，称为结束顶点（汇点），它表示整个工程的结束。
（二）关键路径从源点到汇点的有向路径可能有多条，所有路径中，具有最大路径长度的路径称为关键路径，⽽把关键路径上的活动称为关键活动完成整个工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程的完成时间就会延迟。
活动ai的时间余量d(i)=l(i)-e(i)，表⽰在不增加完成整个工程所需总时间的情况下，活动ai 可以拖延的时间若一个活动的时间余量为零，则说明该活动必须要如期完成，d(i)=0即l(i)=e(i)的活动ai是关键活动由关键活动组成的路径就是关键路径（三）求关键路径的步骤（四）求所有事件的最早发生时间1.求所有事件的最早发生时间ve()（五）求所有事件的最迟发生时间1.求所有事件的最迟发生时间vl()1.求所有活动的最早发生时间e()1.求所有活动的最迟发生时间l()（八）求所有活动的时间余量（九）关键活动、关键路径的特性若关键活动耗时增加，则整个工程的工期将增长缩短关键活动的时间，可以缩短整个工程的工期当缩短到一定程度时，关键活动可能会变成非关键活动可能有多条关键路径，只提高⼀条关键路径上的关键活动速度并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
关键路径AOE介绍
10 0
2018/11/5 2018/11/5
2018/10/31 2018/11/1
15 2018/11/15 1 2018/11/16
2018/11/16 2018/11/20
8 2018/11/24 4 2018/11/28
2018/10/26 A3
2018/10/31 B4
2018/11/16 C3
数据挖掘 数学建模 智能分析
项目关键路径分析
1
关键路径解决的问题 关键路径法用于在进度模型中估算项目最短工期，确定逻辑网络路径的进度灵活 性大小。这种进度网络分析技术在不考虑任何资源限制的情况下，沿进度网络路 径使用顺推与逆推法，计算出所有活动的最早开始、最早结束、最晚开始和最晚 完成日期。 项目的关键路径说明，缩短项目的非关键路径的周期无法缩短项目的周期。只有 有效的缩短关键路径周期才可以缩短项目的周期。
9
没有计划开始时间下的情况
活动名称 项目准备 需求1 需求2 需求3 开发1 开发2 开发3 开发4 测试1 测试2 测试3 版本发布1 版本发布2 现场实施
活动ID S A1 A2 A3 B1 B2 B3 B4 C1 C2 C3 D1 D2 E
2 6 4 10 16 13 12 15 10 11 8 12 14 14
2018/10/26 A3
2018/10/31 B4
2018/11/16 C3
8
项目关键路径
项目关键路径为S->A2->B3->C2->D2->E. 说明： 1、如果活动C2的计划开始时间提前1天，那么整个项目可以提前一天完成，也就是说2018/10/23开始至 2018/12/27结束，历史63天。 2、非关键路径可以在浮动范围内完成就可以。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
☆求解AOE网关键路径例题
【例7-1】下表给出了某工程各工序之间的优先关系和各工序所需的时问（其中“一”表示无先驱工序），请完成以下各题：
(1) 画出相应的AOE网。
(2) 列出各事件的最早发生时间和最迟发生时间。
(3) 求出关键路径并指明完成该工程所需的最短时间。
【例题分析】
·试题考核AOE网和关键路径问题。
要求熟悉AOE网的概念和如何求关键路径的方法及步骤。
【例题解答】
(1) 根据表的数据，可得AOE网，如图所示。
(2) 所有事件的最早发生时间ve，如下所示：
ve（v1）＝ 0 ve（v2）＝
3 ve（v3）＝ 2
ve（v4）＝ Max{ ve（v2）+2，ve（v3）+4}＝ 6
ve（v5）＝ ve（v2）＋3 ＝ 6
ve（v6）＝ Max{ ve（v3）+3，ve（v4）+2，ve（v5）+1}＝ 8
所有事件的最迟发生时间vl，如下所示：
vl（v6）＝ 8 vl（v5）＝vl（v6）－1＝ 7 vl（v4）
＝vl（v6）－2 ＝ 6
vl（v3）＝ Min{ vl（v4）－4，vl（v6）－3}＝ 2
vl（v2）＝ Min{ vl（v4）－2，vl（v5）－3}＝ 4
vl（v1）＝ Min{ vl（v2）－3，vl（v3）－2}＝ 0
(3) 求所有活动的最早发生时间e、最迟发生时间l和时
间余量l-e。
e（A）＝ve（v1）＝ 0 l（A）＝vl（v2）－3＝ 1 l（A）
－e（A）＝ 1
e（B）＝ve（v1）＝ 0 l（B）＝vl（v3）－2＝ 0 l（B）
－e（B）＝ 0
e（C）＝ve（v2）＝ 3 l（C）＝vl（v4）－2＝ 4 l（C）
－e（C）＝ 1
e（D）＝ve（v2）＝ 3 l（D）＝vl（v5）－3＝ 4 l（D）
－e（D）＝ 1
e（E）＝ve（v3）＝ 2 l（E）＝vl（v4）－4＝ 2 l（E）
－e（E）＝ 0
e（F）＝ve（v3）＝ 2 l（F）＝vl（v6）－3＝ 5 l（F）
－e（F）＝ 3
e（G）＝ve（v4）＝ 6 l（G）＝vl（v6）－2＝ 6 l（G）
－e（G）＝ 0
e（H）＝ve（v5）＝ 6 l（H）＝vl（v6）－1＝ 7 l（H）
－e（H）＝ 1
所以，关键路径为：B、E、G。
完成该工程最少需要8天时间。
希望以上资料对你有所帮助，附励志名3条：
1、积金遗于子孙，子孙未必能守；积书于子孙，子孙未必能读。
不如
积阴德于冥冥之中，此乃万世传家之宝训也。
2、积德为产业，强胜于美宅良田。
3、能付出爱心就是福，能消除烦恼就是慧。