江岸区八十一中2013-2014学年上学期九年级数学期中考试压轴题详解
江岸区九年级

江岸区九年级(上)数学期中试题(命题人:汪金龙 考试时间:120分钟 满分:120分)一、选择题(共12小题,每题3分,共36分) 1的值为( )A 、3B 、-3C 、3或-3D 、6 2、已知x = -1是方程x 2 + mx – 1 = 0解,则m 的值为( ) A 、-1 B 、0 C 、2 D 、-2 34中自变量x 的取值范围是( )A 、x ≥5B 、x ≤5C 、x >5D 、x <-55、在平面直角坐标系中,点P (2,—3)关于原点对称的点的坐标是( ) A 、(2,3) B 、(-2,3) C 、(-2,-3) D 、(-3,2)6、如图,AB 是⊙O 的直径,C 是⊙O 上一点,且∠A=45°, 则下列结论中正确的是( ) A 、BC =12AB B 、 BC =ACC 、 BC <ACD 、 BC >AC 7、不解方程,判别方程x 2– 4x + 4 = 0的解的情况( )A 、两个不相等的实数根B 、两个相等的实数根C 、无实数根D 、一个实数根8、武汉市2009年中考数学数与代数、空间与图形、统计与概率三个领域在试题中所占的比重分别为45%、40%、15%,小明同学绘制成扇形统计图如图所示,其中空间与图形部分在扇形统计图中所占的圆心角为( ) A 、40° B 、54° C 、120° D 、144°9、下列图形给我们很多圆的形象,其中两圆没有 的位置关系是( )A 、外离B 、内含C 、外切D 、内切 10、“国庆”期间,小李和同学一起到中山公园游玩大型摩天轮,摩天轮的半径为20m ,匀速转动一周需要12min ,小李乘座最底部的车厢(离地面1m ),经过2min 后到达Q 点(如图所示),则此时他离地面的高度是( )A 、10mB 、11mC 、D 、(10)mAB OC45°ABCD11、2008年奥运会游泳馆又叫“水立方”,是奥运会标致性场馆之一,其府视图是一个边长为170m 的正方形ABCD ,正中间是一个矩形泳池,其面积占正方形ABCD 面积的15/289(如图),泳池到AB 、CD 的距离都是x m ,到AD 、BC 的距离都是(x +10)m.求得x 应为( )A 、50mB 、60mC 、70mD 、100或60m12、如图,正方形ABCD 中,点E 、F 、H 分别是AB 、BC 、CD 的中点,CE 、DF 交于G ,连结AG 、HG .下列结论:①CE ⊥DF ;②AG =AD ;③∠CHG =∠DAG ;④12H G AD=.其中正确的有( ) A 、①②B 、①②④C 、①③④D 、①②③④第10题图 第11题图 第12题图二、填空题(共4小题,每题3分,共12分)。
2013-2014学年人教版九年级上期中测试数学试题(含答案)

湖北省宜城市2013-2014学年第一学期期中测试一、选择题 (本大题有12个小题,每小题3分,共36分.)1.下列二次根式中,的取值范围是3x≥的是()B. C.2. 下列二次根式中,是最简二次根式的是()A. C.3. 下列各式计算正确的是()A.63238=- B. 5102535=+C. 222224=÷ D. 682234=⨯4. 下列方程中,一元二次方程共有().①432=-xx②04322=+-xyx③412=-xx④42=x⑤0332=+-xxA. 2个 B.3个 C.4个 D. 5个5. 关于关于x的一元二次方程1352+=-xxx的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法判断6. 某种商品零售价经过两次降价后的价格为降价前的81%,则平均每次降价()A.19% B.10% C.9.5% D.20%7.下列命题中是真命题的是( )A.经过两点不一定能作一个圆B.经过三点不一定能作一个圆C.经过四点一定不能作一个圆D.一个三角形有无数个外接圆8.四边形ABCD的对角线相交于点O,且AO=BO=CO=DO,则这个四边形()A.仅是轴对称图形B.仅是中心对称图形C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形,又不是中心对称图形 9.如图所示,在正方形ABCD 中,AB=4,点O 在AB 上,且OB=1,点P 是BC 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转90°得到线段OQ.要使点Q 恰好落在AD 上,则BP 的长是( )A .3B .2C .1D .无法确定10. 如图所示,如果AB 为⊙O 的直径,弦CD ⊥AB ,垂足为E ,那么下列结论中,错误的是( )A.CE=DEB.弧BC=弧BDC.∠BAC=∠BADD.AC ﹥AD11.下列四个命题:①顶点在圆心的角是圆心角;②两个圆心角相等, 它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中正确的有( ) A.0个 B.1个 C.2个 D.3个12. 已知⊙O 的半径为5cm ,点P 到⊙O 的最近距离是2,那么点P 到⊙O 的最远距离是( ) A.7cm B.8cm C. 7cm 或12cm D.8cm 或12cm二、填空题 (本大题有5个小题,每小题3分,共15分.)13.计算(236)(236)+-=14. 已知方程x 2-x -1=0有一根为m ,则m 2-m +2013的值为____.15.如图,已知正方形ABCD 的边长为3,E 为CD 边上一点,DE=1.以点A 为中心,把△ADE 顺时针旋转90︒,得△ABF ,连接EF ,则EF 的长等于 .16. 如图,AB 为⊙O 的直径,弦CD ⊥AB ,E 为弧BC 上一点,若∠CEA=28o,则∠ABD=°.ABCDE O · 第10题图A第16题图 17.已知等腰△的三个顶点都在半径为5cm 的⊙上,如果底边的长为8cm ,则边上的高为 .三、解答题(本大题共9个小题,计69分.)18.(本题满分5分)计算:4832426-÷+⨯.19.(本题满分7分)先化简,再求值:(a -1+12+a )÷(212+a ),其中a =2-1.20.(本题满分6分)已知方程2(1)140x m x m +-+-=的一个根是3,求m 的值及方程的另一个根.21.(本题满分7分)已知关于x 的一元二次方程04222=-++k x x 有两个不相等的实数根(1)求k 的取值范围;(2)若k 为正整数,且该方程的根都是整数,求k 的值。
武汉市江岸区九年级上期中数学试题及答案(扫描版).doc

江岸区2015~2016学年度第一学期期中考试九年级数学试卷参考答案 一、选择题(共10小题,每小题3分,共30分)题号1 2 3 4 5 6 7 8 9 10 答案 A CD B C D C B D D 二、填空题(共6小题,每小题3分,共18分) 11.3、-2、-1 12.(1,-2) 13.-214.2217 15.x <-1或x >3 16.416.提示:根据共顶点等腰三角形的旋转模型 △AEC ≌△ADB (SAS )∴∠ADB =∠AEC =150°∴∠BDE =150°-60°=90°连接CD∵∠CED =360°-150°-60°=150°∴∠CED =∠CEA∴△AEC ≌△DEC (SAS )∴CA =CD∴CE 为AD 的垂直平分线延长CE 交AD 于F ,则∠AEF =30°∴AF =3,EF =3在△ACF 中,522=-=AF AC CF∴CE =BD =5-3=2在Rt △BED 中,422=+=BD DE BE三、解答题(共8题,共72分)17.解:2131±-=x18.解:(1) y =x 2-2x -3;(2) x <-1或x >319.证明:易证:△AOF ≌△COE∴CE =AF由垂径定理得:CE =21CD ,AF =21AD∴AD =CD20.解:(3) 145+π21.解:设横彩条宽为2x cm ,则竖彩条宽为3x cm ,由题意得(20-4x )(30-6x )=2516×600,解得x 1=1,x 2=9当x =9时,宽为18∵18×2>20(舍去)∴x =1答:使横彩条宽为7 cm ,竖彩条宽为3 cm22.解:(1) 由题意得⎪⎩⎪⎨⎧≥+-≥=+12401500202012121x x x x x ,解得10≤x 1≤13即共有四种进货方案(2) 设利润为W ,则W =[1760-(-20x 1+1500)]x 1+[1700-(-10x 2+1300)]x 2=30x 12-540x 1+12000 =30(x 1-9)2+9570当x 1=13时,W 有最大值为10050即采购高级羽绒服13件时,总利润最大为10050件23.解:(1) AF =BM +MF(2) 过点A 作AG ⊥CM 于G ,反向延长GA 交EN 于H ∴四边形GMNH 为矩形∴AH ⊥EN根据三垂直得:△CMB ≌△AGC ,△AEH ≌△EDN ∴CM =AG ,EN =AH∴MN =GH =GA +AH =CM +EN(3) 中线倍长CP ,则△BCP ≌△DGP∴BC =DG ,BC ∥DG可证:△CAE ≌△GDE∴CE =EG ,CE ⊥EG∴△CPE 为等腰直角三角形∴CP =PE ,CP ⊥PE24.解:(1) D (2,-3)(2) 作D 关于AB 对称的点D ′必在AE 上A (-m ,0)、B (3m ,0),C (0,-3am 2),D (2m ,-3am 2) ∴D ′(2m ,3am 2)∵抛物线过点C∴-3am 2=-3,am 2=1∴直线AD ′的解析式为11+=x my 联立⎪⎩⎪⎨⎧--=+=)32(1122m mx x a y x m y ,整理得x 2-3mx -4m 2=0解得x 1=4m ,x 2=-m (舍去)∴E (4m ,5)∴E 在y =5上运动(3) F (m ,-4)、E (4m ,5)、A (-m ,0)、D (2m ,-3) 设P (b ,0)∴PF 2=(m -b )2+16,AD 2=9m 2+9,AE 2=25m 2+25∴(m-b)2+16+9m2+9=25m2+25,解得b1=-3m,b2=5m ∴P(-3m,0)或(5m,0)。
湖北省武汉市十一滨江初级中学2014届九年级数学上学期期中试题(含答案)

湖北省武汉市十一滨江初级中学2014届九年级上学期期中考试数学试题新人教版一、选择题(本大题共10小题,每小题3分,共30分) 姓名: 1.式子3+x 在实数范围内有意义,则x 的取值范围是( ) A.3-≥x B.x>-3 C.3≥x D.x>32.下列图形中,是中心对称图形但不是轴对称图形的是( )A .B .C .D .3.如图①,图形旋转一定角度后能与自身重合,则旋转的角度可能是( ) A .45° B .60° C .72° D .90° 4.下列计算①1553=⨯; ②1031003=;③322723=;④16=4.其中错误的是( ) A .① B .② C .③ D .④5.若x 1,x 2是方程x 2-3x -4=0的两根,则x 1·x 2的值是( ) A .-4 B .4 C .3 D .-3 6.用配方法解方程01102=--x x ,正确的变形是( )A .26)5(2=-xB .26)5(2=+xC .1)5(2=-x D .24)5(2=-x7.如图②所示,在平行四边形ABCD 中,E 为DC 边的中点,AE 交BD 于点Q ,若△DQE 的面积为9,则△AQB 的面积为( ) A .18 B .27 C .36 D .458.如图③,AB是⊙O 的直径,C 是半圆弧AB 的中点,D 是⋂BC 上(异于B 、C )的任意一点,则∠CDB 等于( )A .100°B .120°C .150°D .135°9.下面每个正方形中的四个数之间都具有某种相同的规律,由此可推断x 的值应是( ).589573275314531A .90B .92C .94D .9610.如图④, ⊙P 过O 、()6,0A 、()0,2C ,半径PB ⊥PA ,双曲线(0)ky x x=< 恰好经过B 点,则k 的值是( ). A .-1 B .-2 C .-3 D .-4 二、填空题(每小题3分,共18分) 11.计算:62⋅=_________;12.在平面直角坐标系中有三个点A(1,2),B(-1,2)和C(1,-2),其中关于原点O 的对称两点为点________与点________;13.某班x 名学生,同学们两两互相赠送贺卡,共送贺卡1560张,则可列方程: ; 14.如图⑤,A(2,3)是双曲线(0)ky x x=>上的一点,P 为x 轴正半轴上一点,将A 点绕 P 点顺时针旋转90°,恰好落在双曲线上的另一点B ,则P 点的坐标为 ; 15.△ABC 在直角坐标系中的位置如图⑥所示,点P 为边AC 上一点,且P( a ,b ),现将△ABC 绕点(-1 ,0 )逆时针旋转180°,那么点P 的对应点P ′的坐标为 ;16.如图所示,在Rt △ABC 中,∠ACB=90°,AC=4,BC=3,D 为斜边AB 上一点,以CD 、CB 为边作平行四边形CDEB ,当AD= ,平行四边形CDEB 为菱形。
2013-2014学年度九年级第一学期期中测试数学试卷分析

2013-2014学年度第一学期九年级数学期末考试试卷分析
栽麻中学
一、考试概况
试卷满分为150分.全卷共三个大题,共25小题.其中选择题10小题,填空题8小题,解答题6小题。
二、存在问题
1、我校学生基础差,在选择题中丢分太多。
2、选择题出题较好。
3、11题书写不规范,不注意书写未知数。
4、12题我校学生理解能力差,导致丢分较多。
5、15题学生答案不全。
6、19题学生总是出现一步到位,导致步骤分丢掉。
7、20题的第二小题学生书写不规范。
8、概率题学生都能理解,得分比较多。
9、22题漏写坐标。
10、23,24,25题丢分较多。
三、补救措拖
1、加强基础知识的教学,重视双基,平时的教学面向全体学生。
2、关注学生的计算,严抓计算,在课堂教学中多展示计算过程,少一带而过,另外加强板书解题步骤的示范作用,以提高学生的计算能力。
3、加强综合题的训练,提高学生综合应用能力。
4、培养学生良好的书写习惯,引导学生规范答题;
5、讲解选择题的正确填涂方式,并说明其原因。
6、重视课堂教学中的板书,分析解答题解答的关键步骤与评分标准,让学生明白解答题的关键步骤,让学生学会正确的作答的方法;
7、分析讲评正确的看题习惯,要求学生要认真审题,在弄清题意后方可着手解答,减少过失性的失分;
8、加强对学生思想教育端正学生的学习态度,对一些基础比较好,但是较为散漫的男生要多督促,多开导,改变散漫的状态,积极起;
9、要多鼓励学生,激发他们学习的信心,让她们从思想上认同数学学习。
2013、2014武汉中考数学试卷分析
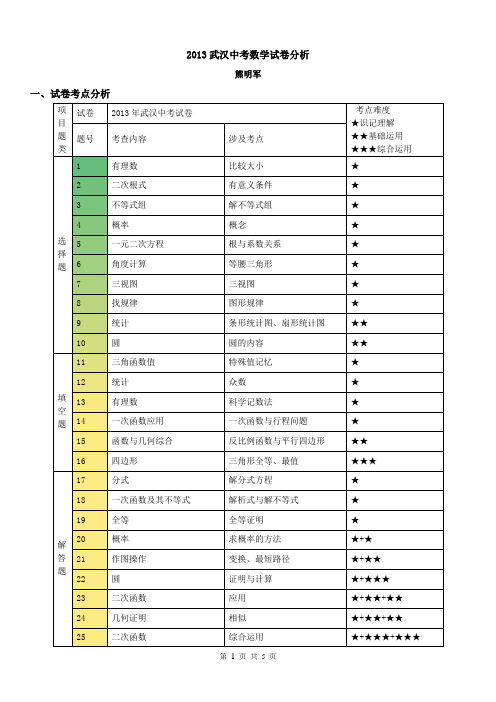
2013武汉中考数学试卷分析熊明军一、试卷考点分析项目题类试卷2013年武汉中考试卷考点难度★识记理解★★基础运用★★★综合运用题号考查内容涉及考点选择题1 有理数比较大小★2 二次根式有意义条件★3 不等式组解不等式组★4 概率概念★5 一元二次方程根与系数关系★6 角度计算等腰三角形★7 三视图三视图★8 找规律图形规律★9 统计条形统计图、扇形统计图★★10 圆圆的内容★★填空题11 三角函数值特殊值记忆★12 统计众数★13 有理数科学记数法★14 一次函数应用一次函数与行程问题★15 函数与几何综合反比例函数与平行四边形★★16 四边形三角形全等、最值★★★解答题17 分式解分式方程★18 一次函数及其不等式解析式与解不等式★19 全等全等证明★20 概率求概率的方法★+★21 作图操作变换、最短路径★+★★22 圆证明与计算★+★★★23 二次函数应用★+★★+★★24 几何证明相似★+★★+★★25 二次函数综合运用★+★★★+★★★二、试卷分析:2013年武汉中考数学试题考点完全按照考纲要求,没有出现超出考试范围的题目。
本套试卷整体难度偏大,计算要求偏高,体现在16题,22题第二问和25题第二问,对学生知识的综合运用能力要求很高。
1-9题和四调、五调考点和顺序完全一致,难度也没有任何变化,主要考察学生相应知识点的识记与简单应用。
第10题和四调、五调考察的几何最值问题有所不同,改为用字母表示弧长的题目。
而将最值问题移到填空题第16题,取代了之前调考中的多解几何题。
对于字母运算与表示结果与高中要求接轨,是今后数学学习的一个方向。
填空题11-15题也和调考中的考察顺序一致,11-13考察学生对特殊三角函数值的识记,12题考察数据的收集与整理中众数的概念,13题考察比较基础的科学记数法。
14题考察学生对于一次函数的理解与应用,看懂题目加以分析,对大部分学生来讲都不是难题。
15题依旧考察反比例函数与四边形的综合题目,利用设未知点坐标来求解是这道题目的关键。
初三九年级上册数学 压轴解答题中考真题汇编[解析版]
![初三九年级上册数学 压轴解答题中考真题汇编[解析版]](https://img.taocdn.com/s3/m/8776aed2a45177232e60a21c.png)
初三九年级上册数学 压轴解答题中考真题汇编[解析版]一、压轴题1.如图1,△ABC 中,AB=AC=4,∠BAC=100,D 是BC 的中点.小明对图1进行了如下探究:在线段AD 上任取一点E ,连接EB .将线段EB 绕点E 逆时针旋转80°,点B 的对应点是点F ,连接BF ,小明发现:随着点E 在线段AD 上位置的变化,点F 的位置也在变化,点F 可能在直线AD 的左侧,也可能在直线AD 上,还可能在直线AD 的右侧.请你帮助小明继续探究,并解答下列问题:(1)如图2,当点F 在直线AD 上时,连接CF ,猜想直线CF 与直线AB 的位置关系,并说明理由.(2)若点F 落在直线AD 的右侧,请在备用图中画出相应的图形,此时(1)中的结论是否仍然成立,为什么?(3)当点E 在线段AD 上运动时,直接写出AF 的最小值.2.如图,在四边形ABCD 中,9054ABC BCD AB BC cm CD cm ∠=∠=︒===,,点P 从点C 出发以1/cm s 的速度沿CB 向点B 匀速移动,点M 从点A 出发以15/cm s 的速度沿AB 向点B 匀速移动,点N 从点D 出发以/acm s 的速度沿DC 向点C 匀速移动.点P M N 、、同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为ts . (1)如图①,①当a 为何值时,点P B M 、、为顶点的三角形与PCN △全等?并求出相应的t 的值; ②连接AP BD 、交于点E ,当AP BD ⊥时,求出t 的值; (2)如图②,连接AN MD 、交于点F .当3883a t ==,时,证明:ADF CDF S S ∆∆=.3.已知:如图1,在O 中,弦2AB =,1CD =,AD BD ⊥.直线,AD BC 相交于点E .(1)求E ∠的度数;(2)如果点,C D 在O 上运动,且保持弦CD 的长度不变,那么,直线,AD BC 相交所成锐角的大小是否改变?试就以下三种情况进行探究,并说明理由(图形未画完整,请你根据需要补全).①如图2,弦AB 与弦CD 交于点F ; ②如图3,弦AB 与弦CD 不相交: ③如图4,点B 与点C 重合.4.如图,已知矩形ABCD 中,BC =2cm ,AB =23cm ,点E 在边AB 上,点F 在边AD 上,点E 由A 向B 运动,连结EC 、EF ,在运动的过程中,始终保持EC ⊥EF ,△EFG 为等边三角形.(1)求证△AEF ∽△BCE ;(2)设BE 的长为xcm ,AF 的长为ycm ,求y 与x 的函数关系式,并写出线段AF 长的范围;(3)若点H 是EG 的中点,试说明A 、E 、H 、F 四点在同一个圆上,并求在点E 由A 到B 运动过程中,点H 移动的距离.5.如图1,有一块直角三角板,其中AB 16=,ACB 90∠=,CAB 30∠=,A 、B 在x 轴上,点A 的坐标为()20,0,圆M 的半径为33,圆心M 的坐标为(5,33-,圆M 以每秒1个单位长度的速度沿x 轴向右做平移运动,运动时间为t 秒;()1求点C 的坐标;()2当点M 在ABC ∠的内部且M 与直线BC 相切时,求t 的值;()3如图2,点E 、F 分别是BC 、AC 的中点,连接EM 、FM ,在运动过程中,是否存在某一时刻,使EMF 90∠=?若存在,直接写出t 的值,若不存在,请说明理由.6.(2015秋•惠山区期末)如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=.(1)若点Q是线段BC上一点,且点Q的横坐标为m.①求点Q的纵坐标;(用含m的代数式表示)②若点P是⊙A上一动点,求PQ的最小值;(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A 随着点A的运动而移动.①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.7.如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.(1)若ED=BE,求∠F的度数:(2)设线段OC=a,求线段BE和EF的长(用含a的代数式表示);(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.8.如图,在▱ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O 交BD 于E .(1)如图1,当PB =3时,求PA 的长以及⊙O 的半径; (2)如图2,当∠APB =2∠PBE 时,求证:AE 平分∠PAD ;(3)当AE 与△ABD 的某一条边垂直时,求所有满足条件的⊙O 的半径.9.如图,函数y=-x 2+bx +c 的图象经过点A (m ,0),B (0,n )两点,m ,n 分别是方程x 2-2x -3=0的两个实数根,且m <n .(1)求m ,n 的值以及函数的解析式;(2)设抛物线y=-x 2+bx +c 与x 轴的另一交点为点C ,顶点为点D ,连结BD 、BC 、CD ,求△BDC 面积;(3)对于(1)中所求的函数y=-x 2+bx +c , ①当0≤x ≤3时,求函数y 的最大值和最小值;②设函数y 在t ≤x ≤t +1内的最大值为p ,最小值为q ,若p-q =3,求t 的值.10.如图,抛物线2()20y ax x c a =++<与x 轴交于点A 和点B (点A 在原点的左侧,点B 在原点的右侧),与y 轴交于点C ,3OB OC ==.(1)求该抛物线的函数解析式.(2)如图1,连接BC ,点D 是直线BC 上方抛物线上的点,连接OD ,CD .OD 交BC 于点F ,当32COFCDFSS=::时,求点D 的坐标.(3)如图2,点E 的坐标为(03)2-,,点P 是抛物线上的点,连接EB PB PE ,,形成的PBE △中,是否存在点P ,使PBE ∠或PEB ∠等于2OBE ∠?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,直线l分别交x轴、y轴于点A,B,∠BAO = 30°.抛物线y = ax2 + bx + 1(a < 0)经过点A,B,过抛物线上一点C(点C在直线l上方)作CD∥BO交直线l于点D,四边形OBCD是菱形.动点M在x轴上从点E( -3,0)向终点A匀速运动,同时,动点N在直线l上从某一点G向终点D匀速运动,它们同时到达终点.(1)求点D的坐标和抛物线的函数表达式.(2)当点M运动到点O时,点N恰好与点B重合.①过点E作x轴的垂线交直线l于点F,当点N在线段FD上时,设EM = m,FN = n,求n 关于m的函数表达式.②求△NEM面积S关于m的函数表达式以及S的最大值.12.矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).(1)如图1,当点G落在AD边上时,直接写出AG的长为;(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)//CF AB ,证明见解析;(2)成立,证明见解析;(3)AF 的最小值为4 【解析】 【分析】(1)结合题意,根据旋转的知识,得BE EF =,80BEF ∠= ,再根据三角形内角和性质,得50BFD ∠=;结合AB=AC=4,D 是BC 的中点,推导得CFD BAD ∠=∠,即可完成解题;(2)由(1)可知:EB=EF=EC ,得到B ,F ,C 三点共圆,点E 为圆心,得∠BCF=12∠BEF=40°,从而计算得ABC BCF ∠=∠,完成求解; (3)由(1)和(2)知,CF ∥AB ,因此得点F 的运动路径在CF 上;故当点E 与点A 重合时,AF 最小,从而完成求解. 【详解】(1)∵将线段EB 绕点E 逆时针旋转80°,点B 的对应点是点F ∴BE EF =,80BEF ∠= ∴180502BEFEBF BFE -∠∠=∠== ,即50BFD ∠=∵AB=AC=4,D 是BC 的中点 ∴BD DC =,AD BC ⊥∴BF CF =,ABD ACD △≌△ ∴FBD FCD △≌△,1005022BAC BAD CAD ∠∠=∠=== ∴50BFD CFD ∠=∠= ∴50CFD BAD ∠=∠= ∴//CF AB(2)如图,连接BE 、EC 、BF 、EF由(1)可知:EB=EF=EC∴B ,F ,C 三点共圆,点E 为圆心 ∴∠BCF=12∠BEF=40°∵50BAD ∠=,AD BC ⊥ ∴9040ABC BAD ∠=-∠= ∴ABC BCF ∠=∠∴//CF AB ,(1)中的结论仍然成立 (3)由(1)和(2)知,//CF AB ∴点F 的运动路径在CF 上 如图,作AM ⊥CF 于点M∵8090BEF ∠=<∴点E 在线段AD 上运动时,点B 旋转不到点M 的位置 ∴故当点E 与点A 重合时,AF 最小 此时AF 1=AB=AC=4,即AF 的最小值为4. 【点睛】本题考查了旋转、等腰三角形及底边中线、垂直平分线、全等三角形、三角形内角和、平行线、圆心角、圆周角的知识;解题的关键是熟练掌握等腰三角形、旋转、垂直平分线、平行线、圆心角和圆周角的知识,从而完成求解.2.(1)① 2.5t =, 1.1a =或2t =,0.5a =;②1t =;(2)见解析 【解析】 【分析】(1)①当PBM PCN ≅△△时或当MBP PCN ≅△△时,分别列出方程即可解决问题; ②当AP BD ⊥时,由ABP BCD ≅△△,推出BP CD =,列出方程即可解决问题; (2)如图②中,连接AC 交MD 于O 只要证明AOM COD ≅△△,推出OA OC =,可得ADO CDO S S ∆∆=,AFO CFO S S ∆∆=,推出ADO AFO CDO CFO S S S S ∆∆∆∆-=-,即ADF CDF S S ∆∆=;【详解】解:(1)①90ABC BCD ∠=∠=︒,∴当PBM PCN ≅△△时,有BM NC =,即5t t -=①5 1.54t at -=-②由①②可得 1.1a =, 2.5t =.当MBP PCN ≅△△时,有BM PC =,BP NC =,即5 1.5t t -=③ 54t at -=-④,由③④可得0.5a =,2t =.综上所述,当 1.1a =, 2.5t =或0.5a =,2t =时,以P 、B 、M 为顶点的三角形与PCN △全等;②AP BD ⊥, 90BEP ∴∠=︒,90APB CBD ∴∠+∠=︒,90ABC ∠=︒,90APB BAP ∴∠+∠=︒, BAP CBD ∴∠=∠,在ABP △和BCD 中,BAP CBD AB BCABC BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ABP BCD ASA ∴≅△△,BP CD ∴=, 即54t -=, 1t ∴=;(2)当38a =,83t =时,1DN at ==,而4CD =,DN CD ∴<,∴点N 在点C 、D 之间, 1.54AM t ==,4CD =, AM CD ∴=,如图②中,连接AC 交MD 于O , 90ABC BCD ∠=∠=︒, 180ABC BCD ∴∠+∠=︒, //AB BC ∴,AMD CDM ∴∠=∠,BAC DCA ∠=∠, 在AOM 和COD △中, AMD CDM AM CDBAC DCA ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()AOM COD ASA ∴≅△△,OA OC ∴=,ADO CDO S S ∆∆∴=,AFO CFO S S ∆∆=,ADO AFO CDO CFO S S S S ∆∆∆∆∴-=-, ADF CDF S S ∆∆∴=.【点睛】本题考查三角形综合题、全等三角形的判定和性质、等高模型等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.3.(1)60E ∠=︒(2)①结论:直线AD 、BC 相交所成锐角的大小不发生改变,依然是60︒;证明过程见详解.②结论:直线AD 、BC 相交所成锐角的大小不发生改变,依然是60︒;证明过程见详解.③结论:直线AD 、BC 相交所成锐角的大小不发生改变,依然是60︒;证明过程见详解. 【解析】 【分析】(1)根据AD BD ⊥得到AB 是直径,连接OC 、OD ,发现等边三角形,再根据圆周角定理求得30EBD ∠=︒,再进一步求得E ∠的度数;(2)分别画出三种图形,图2中,根据圆周角定理和圆内接四边形的性质可以求得;图3中,根据三角形的外角的性质和圆周角定理可以求得;图4中,根据切线的性质发现直角三角形,根据直角三角形的两个锐角互余求得. 【详解】解:(1)连接OC 、OD ,如图:∵AD BD ⊥ ∴AB 是直径 ∴1OC OD CD === ∴OCD 是等边三角形 ∴60COD ∠=︒ ∴30DBE ∠=︒ ∴60E ∠=︒(2)①结论:直线AD 、BC 相交所成锐角的大小不发生改变依然是60︒ 证明:连接OD 、OC 、AC ,如图:∵1OD OC CD === ∴OCD 为等边三角形 ∴60COD ∠=︒ ∴30DAC ∠=︒ ∴30EBD ∠=︒ ∵90ADB ∠=︒ ∴903060E ∠=︒-︒=︒②结论:直线AD 、BC 相交所成锐角的大小不发生改变依然是60︒ 证明:连接OC 、OD ,如图:∵AD BD ⊥ ∴AB 是直径 ∴1OC OD CD === ∴OCD 是等边三角形 ∴60COD ∠=︒ ∴30DBE ∠=︒∴903060BED ∠=︒-︒=︒③结论:直线AD 、BC 相交所成锐角的大小不发生改变依然是60︒ 证明:如图:∵当点B 与点C 重合时,则直线BE 与O 只有一个公共点 ∴EB 恰为O 的切线∴90ABE ∠=︒∵90ADB ∠=︒,1CD =,2AD =∴30A ∠=︒∴60E ∠=︒.故答案是:(1)60E ∠=︒(2)①结论:直线AD 、BC 相交所成锐角的大小不发生改变,依然是60︒;证明过程见详解.②结论:直线AD 、BC 相交所成锐角的大小不发生改变,依然是60︒;证明过程见详解.③结论:直线AD 、BC 相交所成锐角的大小不发生改变,依然是60︒;证明过程见详解.【点睛】本题考查了圆周角定理、等边三角形的判定、圆内接四边形的性质.此题主要是能够根据圆周角定理的推论发现AB 是直径,进一步发现等边COD △,从而根据圆周角定理以及圆内接四边形的性质求解.4.(1)详见解析;(2)21y 2x =-,302AF ≤≤;(3)3. 【解析】【分析】(1)由∠A =∠B =90°,∠AFE =∠BEC ,得△AEF ∽△BCE ;(2)由(1)△AEF ∽BCE 得AF AEBE BC =,y x =,即212y x =-+,然后求函数最值;(3)连接FH ,取EF 的中点M ,证MA =ME =MF =MH ,则A 、E 、H 、F 在同一圆上;连接AH ,证∠EFH =30°由A 、E 、H 、F 在同一圆上,得∠EAH =∠EFH =30°,线段AH 即为H 移动的路径,在直角三角形ABH 中,60AH sin AB =︒=,可进一步求AH. 【详解】解:(1)在矩形ABCD 中,∠A =∠B =90°,∴∠AEF +∠AFE =90°,∵EF ⊥CE ,∴∠AEF +∠BEC =90°,∴∠AFE =∠BEC ,∴△AEF ∽△BCE ;(2)由(1)△AEF ∽BEC 得AF AE BE BC =,y x =,∴212y x =-+,∵2132y x x =-+=213(3)22x --+, 当3x =时,y 有最大值为32, ∴302AF ≤≤; (3)如图1,连接FH ,取EF 的中点M ,在等边三角形EFG 中,∵点H 是EG 的中点, ∴∠EHF =90°,∴ME =MF =MH ,在直角三角形AEF 中,MA =ME =MF ,∴MA =ME =MF =MH ,则A 、E 、H 、F 在同一圆上;如图2,连接AH ,∵△EFG 为等边三角形,H 为EG 中点,∴∠EFH =30°∵A 、E 、H 、F 在同一圆上∴∠EAH =∠EFH =30°,如图2所示的线段AH 即为H 移动的路径,在直角三角形ABH 中,360AH sin AB =︒=, ∵AB =23∴AH =3, 所以点H 移动的距离为3.【点睛】此题主要考查圆的综合问题,会证明三角形相似,会分析四点共圆,会运用二次函数分析最值,会分析最短轨迹并解直角三角形是得分的关键.5.(1)(C 8,43;(2)t=18s ;(3)t 1513=【解析】【分析】(1)如图1中,作CH ⊥AB 于H .解直角三角形求出CH ,OH 即可.(2)如图1﹣1中,设⊙M 与直线BC 相切于点N ,作MH ⊥AB 于H .求出OH 的长即可解决问题.(3)设M(﹣5+t,33),EF12=AB=8,由∠EMF=90°,可得EM2+MF2=EF2,由此构建方程即可解决问题.【详解】(1)如图1中,作CH⊥AB于H.∵A(20,0),AB=16,∴OA=20,OB=4.在Rt△ABC中,∵∠ACB=90°,AB=16,∠CAB=30°,∴BC12=AB=8,CH=BC•sin60°=43,BH=BC•cos60°=4,∴OH=8,∴C(8,43).(2)如图1﹣1中,设⊙M与直线BC相切于点N,作MH⊥AB于H.∵MN=MH=33,MN⊥BC,MH⊥BA,∴∠MBH=∠MBN=30°,∴BH3=MH=9,∴点M的运动路径的长为5+4+9=18,∴当点M在∠ABC的内部且⊙M与直线BC相切时,t的值为18s.(3)∵C(8,43),B(4,0),A(20,0).∵CE=EB,CF=FA,∴E(6,23),F(14,23),设M(﹣5+t,33),EF12=AB=8.∵∠EMF=90°,∴EM2+MF2=EF2,∴(6+5﹣t)2+(3)2+(14+5﹣t)2+(3)2=82,整理得:t2﹣30t+212=0,解得:t=15±13.【点睛】本题是圆的综合题,考查了平移变换,解直角三角形,切线的判定和性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考压轴题.6.(1)①﹣m+8;②PQ最小=OQ最小﹣1=3.8;(2)①t=时,⊙A与直线BC相切;②<t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.【解析】试题分析:(1)①根据正切的概念求出BC=10,OC=8,运用待定系数法求出直线BC的解析式,根据函数图象上点的坐标特征解得即可;②作OQ⊥AB交⊙A于P,则此时PQ最小,根据三角形面积公式计算即可;(2)①根据切线的性质和相似三角形的性质计算即可;②结合图形、运用直线与圆的位置关系定理解答.解:(1)①∵点B的坐标为(6,0),tan∠OCB=,∴BC=10,OC=8,设直线BC的解析式为y=kx+b,,解得,∵点Q的横坐标为m,∴点Q的纵坐标为﹣m+8;②如图1,作OQ⊥AB交⊙A于P,则此时PQ最小,×AB×OQ=×BO×CO,解得,OQ=4.8,∴PQ最小=OQ最小﹣1=3.8;(2)①如图2,⊙A与直线BC相切于H,则AH⊥BC,又∠BOC=90°,∴△BHA∽△BOC,∴=,即=,解得,BA=,则OA=6﹣=,∴t=时,⊙A与直线BC相切;②由(2)①得,t=时,⊙A与直线BC相切,当t=5时,⊙A经过点B,当t=7时,⊙A经过点B,当t=15时,⊙A经过点C,故<t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.考点:圆的综合题.7.(1)30°;(2)EF=;(3)CO的长为或时,△PEB为等腰三角形.【解析】试题分析:(1)利用圆周角定理以及三角形内角和定理得出即可;(2)首先证明△HBO≌△COD(AAS),进而利用△COD∽△CBF,得出比例式求出EF的长;(3)分别利用①当PB=PE,不合题意舍去;②当BE=EP,③当BE=BP,求出即可.试题解析:(1)如图1,连接EO,∵∴∠BOE=∠EOD,∵DO∥BF,∴∠DOE=∠BEO,∵BO=EO,∴∠OBE=∠OEB,∴∠OBE=∠OEB=∠BOE=60°,∵CF⊥AB,∴∠FCB=90°,∴∠F=30°;(2)如图1,作HO⊥BE,垂足为H,∵在△HBO和△COD中,∴△HBO≌△COD(AAS),∴CO=BH=a,∴BE=2a,∵DO∥BF,∴△COD∽△CBF,∴∴,∴EF=;(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,∴∠COD=∠DOE,∴C关于直线OD的对称点为P在线段OE上,若△PEB为等腰三角形,设CO=x,∴OP=OC=x,则PE=EO-OP=4-x,由(2)得:BE=2x,①当PB=PE,不合题意舍去;②当BE=EP,2x=4-x,解得:x=,③当BE=BP,作BM⊥EO,垂足为M,∴EM=PE=,∴∠OEB=∠COD,∠BME=∠DCO=90°,∴△BEM∽△DOC,∴,∴,整理得:x2+x-4=0,解得:x=(负数舍去),综上所述:当CO的长为或时,△PEB为等腰三角形.考点:圆的综合题.8.(1)PA13O的半径为393;(2)见解析;(3)⊙O的半径为2或477【解析】【分析】(1)过点A作BP的垂线,作直径AM,先在Rt△ABH中求出BH,AH的长,再在Rt△AHP中用勾股定理求出AP的长,在Rt△AMP中通过锐角三角函数求出直径AM的长,即求出半径的值;(2)证∠APB=∠PAD=2∠PAE,即可推出结论;(3)分三种情况:当AE⊥BD时,AB是⊙O的直径,可直接求出半径;当AE⊥AD时,连接OB,OE,延长AE交BC于F,通过证△BFE∽△DAE,求出BE的长,再证△OBE是等边三角形,即得到半径的值;当AE⊥AB时,过点D作BC的垂线,通过证△BPE∽△BND,求出PE,AE的长,再利用勾股定理求出直径BE的长,即可得到半径的值.【详解】(1)如图1,过点A作BP的垂线,垂足为H,作直径AM,连接MP,在Rt△ABH中,∠ABH=60°,∴∠BAH=30°,∴BH=12AB=2,AH=AB•sin60°=3∴HP=BP﹣BH=1,∴在Rt△AHP中,AP22AH HP+13∵AB是直径,∴∠APM=90°,在Rt△AMP中,∠M=∠ABP=60°,∴AM=APsin60︒133239,∴⊙O的半径为3,即PA⊙O(2)当∠APB=2∠PBE时,∵∠PBE=∠PAE,∴∠APB=2∠PAE,在平行四边形ABCD中,AD∥BC,∴∠APB=∠PAD,∴∠PAD=2∠PAE,∴∠PAE=∠DAE,∴AE平分∠PAD;(3)①如图3﹣1,当AE⊥BD时,∠AEB=90°,∴AB是⊙O的直径,∴r=12AB=2;②如图3﹣2,当AE⊥AD时,连接OB,OE,延长AE交BC于F,∵AD∥BC,∴AF⊥BC,△BFE∽△DAE,∴BFAD =EFAE,在Rt△ABF中,∠ABF=60°,∴AF=AB•sin60°=BF=12AB=2,∴28,∴EF,在Rt△BFE中,BE5,∵∠BOE=2∠BAE=60°,OB=OE,∴△OBE是等边三角形,∴r;③当AE⊥AB时,∠BAE=90°,∴AE为⊙O的直径,∴∠BPE=90°,如图3﹣3,过点D 作BC 的垂线,交BC 的延长线于点N ,延开PE 交AD 于点Q , 在Rt △DCN 中,∠DCN =60°,DC =4,∴DN =DC •sin60°=23,CN =12CD =2, ∴PQ =DN =23,设QE =x ,则PE =23﹣x ,在Rt △AEQ 中,∠QAE =∠BAD ﹣BAE =30°,∴AE =2QE =2x ,∵PE ∥DN ,∴△BPE ∽△BND ,∴PE DN =BP BN , ∴2323x -=BP 10, ∴BP =10﹣533x , 在Rt △ABE 与Rt △BPE 中,AB 2+AE 2=BP 2+PE 2,∴16+4x 2=(10﹣533x )2+(23﹣x )2, 解得,x 1=63(舍),x 2=3,∴AE =23,∴BE =22AB AE +=224(23)+=27,∴r =7,∴⊙O 的半径为2或47或7.【点睛】此题主要考查圆与几何综合,解题的关键是熟知圆的基本性质、勾股定理及相似三角形的判定与性质.9.(1)m =﹣1,n =3,y =﹣x 2+2x +3;(2)S=3;(3)①y 最大值=4;当x =3时,y 最小值=0;②t =﹣1或t =2【解析】【分析】(1)首先解方程求得A 、B 两点的坐标,然后利用待定系数法确定二次函数的解析式即可;(2)根据解方程直接写出点C 的坐标,然后确定顶点D 的坐标,根据两点的距离公式可得BDC ∆三边的长,根据勾股定理的逆定理可得90DBC ∠=︒,据此求出 △BDC 面积; (3)①确定抛物线的对称轴是1x =,根据增减性可知:1x =时,y 有最大值,当3x =时, y 有最小值;②分5种情况:1、当函数y 在1t x t +内的抛物线完全在对称轴的左侧;2、当11t +=时;3、当函数y 在1t x t +内的抛物线分别在对称轴的两侧;4、当1t =时,5、函数y 在1t x t +内的抛物线完全在对称轴的右侧;分别根据增减性可解答.【详解】解:(1)m ,n 分别是方程2230x x --=的两个实数根,且 m n <,用因式分解法解方程:(1)(3)0x x +-=,11x ∴=-,23x =,1m ∴=-,3n =,(1,0)A ∴-,(0,3)B ,把(1,0)-,(0,3)代入得, 103b c c --+=⎧⎨=⎩,解得23b c =⎧⎨=⎩, ∴函数解析式为2y x 2x 3=-++.(2)令2230y x x =-++=,即2230x x --=,解得11x =-,23x =,∴抛物线2y x 2x 3=-++与x 轴的交点为 (1,0)A -,(3,0)C ,1OA ∴=,3OC =,∴对称轴为1312x -+==,顶点(1,123)D -++,即 (1,4)D ,∴BC = BD ==DC ==222CD DB CB =+,BCD ∴∆是直角三角形,且90DBC ∠=︒,∴112322S BCD BD BC ==⨯⨯=; (3)∵抛物线y =﹣x 2+2x +3的对称轴为x =1,顶点为D (1,4),①在0≤x ≤3范围内,当x =1时,y 最大值=4;当x =3时,y 最小值=0;②1、当函数y 在1t x t +内的抛物线完全在对称轴的左侧,当x t =时取得最小值 223q t t =-++,最大值2(1)2(1)3p t t =-++++,令22(1)2(1)3(23)3p q t t t t -=-++++--++=,即 213t -+=,解得1t =-.2、当11t +=时,此时4p =,3q =,不合题意,舍去;3、当函数y 在1t x t +内的抛物线分别在对称轴的两侧,此时4p =,令24(23)3p q t t -=--++=,即 2220t t --=解得:11t =),21t = );或者24[(1)2(1)3]3p q t t -=--++++=,即 t =4、当1t =时,此时4p =,3q =,不合题意,舍去;5、当函数y 在1t x t +内的抛物线完全在对称轴的右侧,当x t =时取得最大值 223p t t =-++,最小值2(1)2(1)3q t t =-++++,令2223[(1)2(1)3]3p q t t t t -=-++--++++=,解得 2t =.综上,1t =-或2t =.【点睛】本题是二次函数的综合题型,其中涉及到的知识点有利用待定系数法求抛物线的解析式,抛物线的顶点公式,直角三角形的性质和判定,勾股定理的逆定理,最值问题等知识,注意运用分类讨论的思想解决问题.10.(1)2y x 2x 3=-++;(2)点D 的坐标为(14),或(2)3,;(3)点P 的坐标为:(14),或17()24-,或13209()24--,或. 【解析】【分析】(1)由3OB OC ==及图像可得B 、C 两点坐标,然后利用待定系数法直接进行求解即可;(2)由题意易得35COF COD S S =,进而得到点D 、F 横坐标之间的关系为53D F x x =,设F 点横坐标为3t ,则D 点横坐标为5t ,则有直线BC 的解析式为3y x =-+,然后可直接求解;(3)分∠PBE 或∠PEB 等于2∠OBE 两种情况分别进行求解即可.【详解】解:(1)3OB OC ==,则:()()3003B C ,,,, 把B C 、坐标代入抛物线方程,解得抛物线方程为:2y x 2x 3=-++①;(2)∵32COF CDF S S =△△::, ∴35COF COD S S =,即:53D F x x =, 设F 点横坐标为3t ,则D 点横坐标为5t ,点F 在直线BC 上,而BC 所在的直线表达式为:3y x =-+,则33(3)F t t -,, 则直线OF 所在的直线表达式为:3313t t y x x t t--==, 则点55(5)D t t -,, 把D 点坐标代入抛物线解析式,解得:15t =或2 5, 则点D 的坐标为(14),或(2)3,;(3)①当2PBE OBE ∠=∠时,当BP 在x 轴上方时,如图2,设1BP 交y 轴于点E ', ∴12PBE OBE ∠=∠ , ∴E BO EBO ∠'=∠ ,又60E OB EBO BO BO ∠'=∠=︒=, ,∴()E BO EBO AAS '≌ ,∴32EO EO ==, ∴点3(20)E ',,直线1BP 过点BE '、,则其直线方程为:1322y x =-+②, 联立①②并解得:12x =- , 故点P 1的坐标为17()24-,;当BP 在x 轴下方时, 如图2,过点E 作//EF BE '交2BP 于点F ,则FEB EBE ∠=∠',∴222E BE OBE EBP OBE ∠'=∠∠=∠, ,∴FEB EBF ∠=∠ ,∴FE BF = ,直线EF 可以看成直线BE '平移而得,其k 值为12-, 则其直线表达式为:1322y x =-- ,设点13()22F m m --,,过点F 作FH y ⊥轴交于点H ,作BK HF ⊥于点K , 则点13()202H m --,,13()232K m --,, ∵EF BF =,则22FE BF =, 即:()2222331313()()22222m m m m +-++=-++, 解得:52m =, 则点511()24F -,, 则直线BF 表达式为:113322y x =-…③, 联立①③并解得:132x =-或3(舍去3), 则点213209()24P --,; ②当2PEB OBE ∠=∠时,当EP 在BE 上方时,如图3,点E '为图2所求,设BE '交3EP 于点F ,∵2EBE OBE ∠'=∠,∴3EBE P EB ∠'=∠ ,∴FE BF = ,由①知,直线BE '的表达式为:1322y x =-+, 设点13()22F n n -+,,13()232K n -+,, 由FE BF =,同理可得:12n =, 故点15()24F ,,则直线EF 的表达式为:11322y x =-④, 联立①④并解得:1n =或92- (舍去负值), ∴34(1)P , ; 当EP 在BE 下方时,同理可得:x =舍去负值),故点458(417P +-+,.故点P 的坐标为:(14),或17()24-,或13209()24--,或(54178+-+,. 【点睛】 本题主要考查二次函数的综合,关键是熟练掌握二次函数的性质与一次函数的性质,利用数形结合及分类讨论思想进行求解.11.(1)点D 的坐标为(2,12),抛物线的解析式为24 ?1?3y x =-+;(2)①1n =+;②234S m =+,S 【解析】【分析】(1)由抛物线的解析式为y = ax 2 + bx + 1,得到OB=1,根据菱形的性质结合含30度的直角三角形的性质点A 、D 、C 的坐标,再利用待定系数法即可求解;(2)①在Rt △FEA 中,FB=12FA=2,FD=FB+BD=3,根据题意设此一次函数解析式为:n km b =+,求得m =2n FB ==,m =3n FD ==,代入n km b =+,即可求解;②求得NA 3m =,过N 作NQ ⊥EA ,得到NQ=12NA=32,利用面积公式得到S 关于m 的函数表达式,再利用二次函数的性质即可求解.【详解】(1)∵抛物线的解析式为y = ax 2 + bx + 1,∴OB=1,∵∠BAO=30︒,∠BOA=90︒,∴AB=2OB=2,=ABO=60︒,∴点A 的坐标为0),又∵四边形OBCD 是菱形,且∠ABO=60︒,∴OD=CD=OB=1,∴△DOB为等边三角形,∴∠BOD=60︒,∠DOA=30︒,BD=BO=OD=DA=1,延长CD交OA于H,则CH⊥OA,∴DH=12OD=12,3CH=CD+DH=32,∴点D的坐标为312),点C的坐标为332),将A30) , C的坐标为(32,32)代入抛物线的解析式y = ax2 + bx + 1,得:3310333142a ba⎧+=⎪⎨+=⎪⎩,解得:433ab⎧=-⎪⎨⎪=⎩,∴抛物线的解析式为243?1?3y x x=-+;(2)①在Rt△FEA中,∠FAE=30︒,3FA=2AB=4,∴FB=12FA=2,FD=FB+BD=3,∵动点M、N同时作匀速直线运动,∴n关于m成一次函数,故设此一次函数解析式为:n km b=+,当点M运动到点O时,点N恰好与点B重合,∴3m=2n FB==,当点M运动到点A时,点N恰好与点D重合,∴23m=3n FD==,代入n km b =+,得:23b b⎧=+⎪⎨=+⎪⎩,解得:31k b ⎧=⎪⎨⎪=⎩,∴此一次函数解析式为:1n =+; ②NA=FA-FN=4- 33n m =-, 过N 作NQ ⊥EA ,则NQ=12NA=32,∴2133224S m m ⎛⎫==+ ⎪ ⎪⎝⎭,∵0<,当3m ==⎝⎭0m ≤≤范围内,∴1322S ⎛=-= ⎝⎭最大 【点睛】 本题主要考查了二次函数的综合应用,涉及待定系数法、菱形的性质、等边三角形的判定和性质、二次函数的性质、函数图象的交点等.本题涉及知识点较多,综合性较强,难度较大.12.(1)4﹣2)32;(3)4【解析】【分析】(1)在Rt △DCG 中,利用勾股定理求出DG 即可解决问题;(2)首先证明AH =CH ,设AH =CH =m ,则DH =AD ﹣HD =4﹣m ,在Rt △DHC 中,根据CH 2=CD 2+DH 2,构建方程求出m 即可解决问题;(3)如图,当点G 在对角线AC 上时,△OGE 的面积最小,当点G 在AC 的延长线上时,△OE′G′的面积最大,分别求出面积的最小值,最大值即可解决问题.【详解】解:(1)如图1中,∵四边形ABCD是矩形,∴BC=AD=CG=4,∠D=90°,∵AB=CD=2,∴DG=22CDCG-=2242-=23,∴AG=AB﹣BG=4﹣23,故答案为:4﹣23.(2)如图2中,由四边形CGEF是矩形,得到∠CGE=90°,∵点G在线段AE上,∴∠AGC=90°,∵CA=CA,CB=CG,∴Rt△ACG≌Rt△ACB(HL).∴∠ACB=∠ACG,∵AB∥CD∴∠ACG=∠DAC,∴∠ACH=∠HAC,∴AH=CH,设AH=CH=m,则DH=AD﹣AH=5﹣m,在Rt△DHC中,∵CH2=DC2+DH2,∴m2=22+(4﹣m)2,∴m=52,∴AH=52,GH22AH AG-22522⎛⎫-⎪⎝⎭32.(3)在Rt△ABC中,2225AC AB BC=+=,152OC AC,由题可知,G点在以C点为圆心,BC为半径的圆上运动,且GE与该圆相切,因为GE=AB 不变,所以O到直线GE的距离即为△OGE的高,当点G在对角线AC上时,OG最短,即△OGE的面积最小,最小值=12×OG×EG=12×2×(4﹣5)=4﹣5.当点G在AC的延长线上时,OG最长,即△OE′G′的面积最大.最大值=12×E′G′×OG′=12×2×(4+5)=4+5.综上所述,455【点睛】本题考查求一点到圆上点距离的最值、矩形的性质、全等三角形的判定和性质、旋转变换、勾股定理.(1)比较简单,掌握勾股定理和旋转的性质是解决此问的关键;(2)能表示Rt△DHC三边,借助方程思想是解决此问的关键;(2)理解线段GE的运动轨迹,得出面积最小(大)时G点的位置是解决此问的关键.。
第一学期武汉市八十一中学初三10月抽考数学试卷

第一学期武汉市八十一中学初三10月抽考数学试卷九年级数学试题一、选择题(每题3分,共30分)1.下列方程是一元二次方程的是( )A.x ²-4=0B.x ²+x -1=0C.x ²+xy -y ²=0D.x ²12.方程x (x -3)=0的解是( )A.x =3B.x1=0,x2=3C.x1=1,x2=3D.x1=0,x2=-33.用配方法解方程x ²-2x -3=0则方程能够变形为( )A.(x -1)²=3B.(x -2)²=4C.(x -1)²=1D.(x -1)²=44.不解方程,判定方程x ²+3x -1=0的根的情形是( )A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.没有实数根5.某校九年级学生毕业时,每个同学将自己的相片向全班其他同学各送一张留作纪念,全班共送1980张相片,假如全班有x 名学生,依照题意,列出方程为( )A.x (x -1)=1980B.x (x +1)=1980C.2x (x +1)=1980D. ()119802x x -= 6.由二次函数y =2(x -3)²+1,可知( ) A.其图像的开口向下B.其图像的对称轴为直线x =-3C.其最小值为1D.当x <3时,y 随写的增大而增大. 7.抛物线21252y x x =-+-与坐标轴的交点个数是( )A.0B.1C.2D.38.把抛物线y =x ²先向左平移2个单位,再向上平移3个单位所得抛物线为( )A.y =(x -2)²-3B. y =(x +2)²-3C. y =(x +2)²+3D. y =(x -2)²+39.已知点(-1,y1)、(-312,y2)、(12,y3)在函数y =3x ²+6x +12的图像上,则y1、y2、y3的大小关系是( )A.y1>y3>y2B.y2>y1>y3C.y2>y3>y1D.y3>y1>y210.已知:二次函数y =ax ²+c ,当x =1时,-4≤y ≤-2,当x =2时,-1≤y ≤2,则当x =3时,y 的取值范畴为( ) A.2123y ≤≤ B.2103y ≤≤ C.493y ≤≤ D.19y ≤≤二、填空题(每题3分,共18分)11.一元二次方程x2-4=0的根为______________12.若点(2,-5)、(6,-5)在抛物线y =ax2+bx +c 上,则它的对称轴是________________13.已知关于x 的一元二次方程x ²-4x -k =0的一个根为3,则另一根是____________.14.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m 处达到最高,高度为3m ,水柱落地处离池中心3m ,水管的长为_______________15.已知,三次函数y =-x ²+8x -3,当-2≤x ≤5时,y 的取值范畴是_______________16.直线y =kx +2与抛物线y =2x ²+(b -2)x -4交于A ,B 两点,抛物线y =2x ²+(b -2)x -4交y 轴于C 点,则S △ABC =_______________三、解答下列各题(共计72分)17.(本题10分)解方程①x ²-2x =0 ②x ²-2x -1=018.(本题10分)已知抛物线的顶点为(1,4),与x 轴交于点(-1,0),求抛物线的解析式.19.(本题10分)若x1、x2是一元二次方程x²-3x-5=0的两个根.①直截了当填空:x1+x2=____________,x x =_______________12②求(x1-3)(x2-3)的值.20.(本题10分)如图,一名男生推铅球,铅球行进的高度y(单位:米)与水平距离x(单位:米)之间的关系是二次函数的关系,铅球行进起米,行进到水平距离为4米时达到最高处,最大高度为3米.点的高度为35(1)求二次函数的解析式;(2)求铅球推出的距离.21.(本题10分)如图,抛物线y=ax2+2ax-3交x轴于A(-3,0)、B两点,直线y=kx交抛物线于C、D两点(1)直截了当写出:a=___________,B点的坐标为______________;死记硬背是一种传统的教学方式,在我国有悠久的历史。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图1,在平面直角坐标系中,A (0,6),P (0,4),点C 为x 轴正半轴上任一点, BP ⊥AC 于E ,交x 轴于B 点,△ABC 外接圆⊙M 交y 轴负半轴于D 点;
(1)求D 点的坐标;
(2)当点C 在x 轴正半轴上任意移动时,圆心M 的纵坐标是否改变?请写出你的结论,并说明理由;
(3)如图2,BF BC =,当点C 在x 轴正半轴上任意移动时,请问:
AE EC AF
-的值是否发生变化?若不变请求出其值;若变化,请写出变化范围.
图1 图2
解:(1)D (0,-4) 如下图,连BD ,12,345,BD BP ∠=∠∴∠=∠=∠=,又BO ⊥PD 根据等腰三角形“三线合一”的性质,OD=OP=4;
(2)点M 的纵坐标不发生改变,恒为1. 理由如下:作MH ⊥y 轴于H ,易知AH=DH ,设OH=y ,则有HD=4+y 、PH=4-y 、AP=2y ,又已知AP=2,所以y=1;
(3)1AE EC AF
-= 连接BF ,过B 作AF 的延长线的垂线,垂足为K. BF BC = ∴BF=BC
又KFB BEC ∠=∠(圆内接四边形的外角等于内对角) ∴△BKF ≌△BEC 有KF=EC ;BK=AE 易证:△BKA ≌△BEA (HL )
∴AE=AK=AF+KF=AF+EC (此题亦可用BAF BAE ∠=∠来做)
①|②
③。
