湖北武汉2010中考数学模拟试题八答案不全
2010年武汉市中考数学试卷详解(完整版)

2010年湖北省武汉市中考数学试卷参考答案与试题解析一、选择题(共12小题,每小题3分,满分36分)1.(2010•武汉)﹣2的相反数是()A.﹣2 B.﹣C.D.2考点:相反数。
分析:一个数的相反数就是在这个数前面添上“﹣”号.解答:解:﹣2的相反数是2.故选D.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号.一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.(2010•武汉)函数y=中,自变量x的取值范围是()A.x>1 B.x≥1 C.x<1 D.x≤1考点:函数自变量的取值范围;二次根式有意义的条件。
分析:本题主要考查自变量的取值范围,函数关系式是二次根式,根据二次根式的意义,被开方数是非负数就可以求解.解答:解:根据题意得:x﹣1≥0,解得x≥1.故选B.点评:函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.3.(2010•武汉)如图,数轴上表示的是某不等式组的解集,则这个不等式组可能是()A.B.C.D.考点:在数轴上表示不等式的解集。
专题:计算题。
分析:先根据数轴得到不等式的解集是﹣1<x<2,再分别把四个选项的解集求出即可判断.解答:解:根据数轴可知这个不等式的解集是﹣1<x<2.四个选项的解集分别是:A、x>2,故本选项错误;B、﹣1<x<2,故本选项正确;C、x<﹣1,故本选项错误;D、无解,故本选项错误.故选B.点评:不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.4.(2010•武汉)下列说法:①“掷一枚质地均匀的硬币一定是正面朝上”;②“从一副普通扑克牌中任意抽取一张,点数一定是6”()A.①②都正确B.只有①正确C.只有②正确D.①②都不正确考点:随机事件。
2010年中考模拟数学卷参考答案

2010年中考模拟试卷 数学参考答案及评分标准三、解答题(本题有8小题,第17~19题每题6分,第20~21题8分,第22~23题每题10分,第24题12分,共66分) 17、(本题满分6分) 解:∵方程2233x mx x -=--无解∴方程2233x mx x -=--有增根x=3------------2分∴方程两边同乘以(x-3),得:26x m -=------------2分∴当x=3时,m =分 18、(本题满分6分)解:过C 点作BA 的延长线交于点E ,------------1分∵AB =AC =10,∠B =022.5 ∴∠EAC =045∴△EAC 为等腰直角三角形------------1分设AE =EC =X,则AB =AC =10∴x =∴111022S A B E C ∆=⋅=⨯⨯=≈35.42m ------------2分又∵53.610⨯2cm =362m >35.42m ------------1分 ∴预订草皮够用------------1分19、(本题满分6分)解:答案不唯一,酌情给分。
20、(本题满分8分)解:(1)18 0.55------------各1分(2)图略--------------共4分(虚设组不设各扣1分)(3)0.55±0.1均为正确------------2分 21、(本题满分8分) 解:(1)正确的结论:①②③------------2分(2)错误理由:当a >0时,只有1x >2x >0或2x <1x <0时,1y <2y 而2x <0<1x 时,1y >2y ------------4分 改正:当a >0时,在同一象限内,函数a y x=,y 随x 增大而减小-----2分22、(本题满分10分)解:(1)如右图------------共6分(030,045角,线段a 各1分,余酌情给分)(2)设AB =x,则R t △ABC 中,OB =x ,由题意得:6+ x ------------1分得,1)x =≈8米------------2分 答:旗杆高度约为8米。
2010年武汉市中考数学试题

2010年武汉市中考数学试题亲爱的同学,在你答题前,请认真阅读下面以及“答卷”上的注意事项:1.本试卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成.全卷共6页,三大题,满分l20分.考试用时120分钟.2.答题前,请将你的姓名、准考证号填写在“答卷”相应位置,并在“答卷”背面左上角填写姓名和准考证号后两位.3.答第Ⅰ卷(选择题)时,选出每小题答案后,用2B铅笔把“答卷”上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后。
再选涂其他答案.不得答在“试卷”上.4.第Ⅱ卷(非选择题)用0.5毫米黑色笔迹签字笔书写在“答卷”上,答在“试卷”上无效.预祝你取得优异成绩!第Ⅰ卷(选择题,共36分)一、选择题(共12小题,每小题3分,共36分)下列各题中均有四个备选答案,其中有且只有一个正确,请在答卷上将正确答案的代号涂黑.1.有理数-2的相反数是()(A)2 (B)-2 (C)12(D)-122.函数y=x的取值范围是()(A)x≥1.(B)x≥-1.(C)x≤1.(D)x≤-1.3.如图,数轴上表示的是某不等式组的解集,则这个不等式组可能是()(A)x>-1,x>2 (B)x>-1,x<2(C)x<-1,x<2 (D)x<-1,x>24.下列说法:①“掷一枚质地均匀的硬币一定是正面朝上”;②“从一副普通扑克牌中任意抽取一张,点数一定是6”.(A) ①②都正确.(B)只有①正确.(C)只有②正确.(D)①②都正确.5.2010年上海世博会开园第一个月共售出门票约664万张,664万用科学记数法表示为( )(A)664×104(B)66.4×l05(C)6.64×106(D)0.664×l076.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是()(A)100°(B)80°(C)70°(D)50°7.若x1,x2是方程x2=4的两根,则x1+x2的值是( )(A)8.(B)4.(C)2.(D)0.8.如图所示,李老师办公桌上放着一个圆柱形茶叶盒和一个正方体的墨水盒,小芳从上面看,看到的图形是(A) (B) (C) (D)9.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是()(A)(13,13) (B)(―13,―13) (C)(14,14) (D)(-14,-14)10.如图,⊙O 的直径AB 的长为10,弦AC 长为6,∠AC'B 的平分线交⊙O 于D ,则CD 长为( ) (A) 7(B)(C) (D) 911.随着经济的发展,人们的生活水平不断提高.下图分别是某景点2007—2009年游客总人数和旅游收入年增长率统计图.已知该景点2008年旅游收入4500万元.下列说法:①三年中该景点2009年旅游收入最高;②与2007年相比,该景点2009年的旅游收入增加[4500×(1+29%)-4500×(1-33%)]万元;③若按2009年游客人数的年增长率计算,2010年该景点游客总人数将达到280255280(1)255-⨯+万人次。
湖北2010中考数学模拟试卷十新人教版

2010年中考数学模拟试卷(十)一、精心选一选,相信自己的判断!(本大题共12小题,每小题3分,共36分) 1.下列二次根式中,最简二次根式是( ) A .a 27B .24a +C .a1D .b a 232.小明在一天晚上帮妈妈洗三个只有颜色不同的有盖茶杯,这时突然停电了,小明只好将茶杯和杯盖随机搭配在一起,那么三个茶杯颜色全部搭配正确的概率是( )A .31B .61C .91D .271 3.已知一弧长为m 的弧所对的圆周角为120°,那么它所对的弦长为( ) A .m π233 B .m π423 C .m π433 D .m π223 4.北京2008奥运的国家体育场“鸟巢”建筑面积达25.8万平方米,用科学记数法表示应为( ) A .25.8×104m 2B .25.8×105m 2C .2.58×105m 2D .2.58×106m 25.如图,在平面直角坐标系中,点A 在第二象限,⊙A 与x 轴相切于B ,与y 轴交于C (0,1),D (0,4)两点,则点A 的坐标是( )A .(23-,25) B .(25-,2) C .(2-,25)D .(25-,23)6.方程0822=--x x 和方程02542=+-x x 的所有实根的积为( ) A .16-B .4-C .8-D .21-7.已知不等式组⎩⎨⎧>+>xx ax 465的解集是6->x ,则a 的取值范围是( )A .6-≥aB .6->aC .6-<aD .6-≤a8.如图,点A ,B ,C 都是数轴上的点,点B ,C 关于点A 对称,若点A 、B 表示的数分别是2,19,则点C 表示的数为( ) A .192-B .219-C .194-D .419-9.如图,等腰梯形ABCD 中,AD ∥BC ,以A 为圆心,AD 为半径的圆与BC 相切于点M ,与AB第5题图第8题图相交于点E ,若AD =2,BC =6,则扇形DAE 的面积为( )A .π23B .π43C .π3D .π8310.把抛物线2)1(2+-=x y 向上平移1个单位,再向左平移1个单位,得到的抛物线是( )A .122+=x yB .1)2(22++-=x yC .122--=x yD .1)2(22-+-=x y11.如图,直角梯形ABCD 中,AD ∥BC ,∠A =∠B =90°,E 是AB 的中点,连结DE 、CE ,AD +BC =CD ,以下结论:(1)∠CED =90°;(2)DE 平分∠ADC ;(3)以AB 为直径的圆与CD 相切;(4)以CD 为直径的圆与AB 相切;(5)△CDE 的面积等于梯形A BCD 面积的一半. 其中正确结论的个数为( ) A .2个B .3个C .4个D .5个12.用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x ,y 表示矩形的长和宽(x >y ),则下列关系式中不正确的是( )A .12=+y xB .2=-y xC .35=xyD .14422=+y x二、细心填一填,试试自己的身手!(本大题共6小题,每小题3分,共18分) 13.已知131-=x y ,那么2323122-+-y xy x 的值是__________. 14.如图,菱形OABC 中,∠A =120°,OA =2,将菱形OABC 绕点O 顺时针旋转90°到OA ′B ′C ′,则图中由弧BB ′,B ′A ′,弧A ′C ,CB 围成的阴影部分的面积是__________.第8题图第11题图第12题图15.如图,已知双曲线)0(>=k xky 经过Rt △OAB 斜边OB 的中点D 与直角边AB 相交于点C .若△OBC 的面积为3,则k =__________.16.如图是两个以O 为圆心的同心圆,记小圆为A 区,圆环为B 区,在图形所在区域进行撒豆试验,统计发现豆子落在A 区的概率为31,若大圆的半径OM =50cm ,那么小圆的半径ON 的长为__________cm .17.如图,将边长为2cm 的两个互相重合的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度α(0°<α<90°),若两正方形重叠部分的面积为2334cm ,则这个旋转角度为__________.18.观察下列图形:它们是按一定规律排列的,依照此规律,第16个图形共有__ __个“x ”.三、用心做一做,显显自己的能力!(本大题共7小题,满分66分) 19.(本题共两小题,每小题3分,共6分)(1)计算:1231)21(332--+----第14题图第15题图第16题图第17题图(2)先化简,再求值:)2(42442+⋅-+-x x x x ,其中3=x20.(本题满分8分)如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形.(1)使三角形的三边长分别为3,22,5,请在图(1)中画出这个三角形; (2)使三角形为钝角三角形,且面积为4,在图(2)中画出一个并标出各边的长.21.(本题满分10分)某电脑公司有A ,B ,C 三种型号的甲种品牌电脑和D ,E 两种型号的乙种品牌电脑,希望中学要从甲,乙两种品牌电脑中各选购一个型号的电脑. (1)用树状图或列表的方法写出所有购买方案;(2)如果(1)中各种选购方案的可能性相同,那么A 型号电脑被选中的概率是多少? (3)希望中学购买甲、乙两种品牌电脑共36台(价格如下表所示),恰好用了10万元人民币,其中甲品牌为A 型电脑,求购买的A 型电脑有多少台?第20题图型号 A B C D E单价(元) 6000 4000 2500 5000 200022.(本题满分10分)如图,在以点O 为圆心的两个同心圆中,AB 经过圆心O ,且与小圆相交于A ,与大圆相交于点B ,小圆的切线A C 与大圆相交于D ,O C 平分∠ACB . (1)证明直线BC 是小圆的切线; (2)试证明: AC +AD =BC ;(3)若AB =8cm ,BC =10cm ,求大圆与小圆形成的圆环的面积.23.(本题满分10分)已知关于x 的一元二次方程)0(022)23(2>=+++-m m x m mx . (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为x 1、x 2(x 1<x 2),若y 是m 的函数,且122x x y -=,求这个函数的解析式;第22题图(3)在(2)的条件下结合函数的图象回答:当自变量的取值满足什么条件时,y≤2m.24.(本题满分10分)孝感商场按标价销售某种工艺品时,每件可获利45元,按标价的八五折销售该工艺品8件与按标价降低35元销售该工艺品12件所获利润相同.(1)该工艺品每件的进价,标价分别为多少元?(2)若每件工艺品按(1)中求得的进价进货,标价售出,商场每天可售出该工艺品100件.若每件工艺品售价降低1元,则每天可多售出4件.问每件工艺品降价多少出售,每天获得的利润最大?最大利润是多少?25.(本题满分12分)如图,直角梯形COAB中,OC∥AB , 以O为原点建立平面直角坐标系,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4).点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒.(1)求直线BC的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的72? (3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设△OPD 的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围;(4)当动点P 在线段AB 上移动时,能否在线段OA 上找到一点Q ,使四边形CQPD 为矩形?如果能,请求出此时动点P 的坐标;如果不能,请说明理由.参考答案及评分标准一、精心选一选,相信自己的判断!1~5:BAACC 6~10:CDCAB ; 11~12:DD . 二、细心填一填,试试自己的身手!13.114.3238-π15.2 16.cm 335017.30°18.49三、用心做一做,显显自己的能力!19.(1)32-- (2)化简得242-x ,将3=x 代入得21-20.答案不唯一,略 21.(1)树状图如下: 甲品牌ABC乙品牌 D E D E D E (2)31(3)设购买A 型电脑x 台.① 如果乙品牌是D 型电脑,有10000)36(50006000=-+x x 台,得80-=x ,不合题意,舍去;② 如果乙品牌为E 型电脑,有10000)36(20006000=-+x x ,得x =7,所以购买A型电脑7台.22.(1)作OE ⊥BC 于E ,可证OE =OA ,所以BC 是小圆的切线. (2)连结OD ,由(1)知AC =CE ,再证△AOD ≌△EOB ,得AD =BE∴BC =AD +AC(3)由(2)可得BE =4,S 圆环=S 大圆-S 小圆=π(O B 2-OE 2) =π·BE 2=16π(cm 2)23.(1)△=[]222)2(44)22(4)23(+=++=+-+-m m m m m m∵ m > 0∴(m +2)2>0∴方程总有两个不相等的实数根 (2)解方程得x 1=1,m m x 222+=∴)0(2222212>=-+=-=m mm m x x y(3)1≥m24.(1)设进价为x 元,标价为(x +45)元x x x x 1212)3545(8885.0)45(-⨯-+=-⨯⨯+155=x进价为155元,标价为200元(2)设降价a 元,利润4500904)4100)(155200(2++-=+--=a a a a W当10)4(280=--=x a 元时4900)4(4804500)4(42=--⨯-=x x W 元降价10元出售时,获利最多4900元.25.(1)直线BC 的解析式为443+=x y (2)过点D 作DE ⊥OA 于E ,则易知DE 为梯形OABC 的中位线.S 梯形OABC =568)104(21=⨯+⨯P 点在OA 上,且四边形OPDC 的面积为167256=⨯时 8721=⋅⋅t 716=t E(3)⎪⎪⎩⎪⎪⎨⎧<≤+-<≤-<<=)2318(518458)188(244)80(27t t t t t t S(4)在OA 上不能找到一点Q ,使四边形CQPD 为矩形.理由如下:过C 作CM ⊥AB 于M ,则易知CM =OA =8,AM =OC =4. ∴B M =6在Rt △B CM 中,BC =10682222=+=+BM CM ∴CD =BD =521=BC 假设四边形CQPD 为矩形,则PQ =C D =5,且PQ ∥CD ∴∠B =∠1又∵∠BDP =∠PAQ =90° ∴Rt △PAQ ∽Rt △BDP ∴PAPQBD PB =设BP=x ,则PA =x -10 ∴xx -=1055,化简得025102=+-x x 解得5=x ,即PB =5 ∴PB =BD 假设不成立.。
湖北省武汉市2010年中考模拟数学试题4

新世纪教育网精选资料版权全部@新世纪教育网武汉市 2010 学年度九年级中考模拟试卷数学试卷一,选择题(共 12 小题,每题 3 分,共 36分)1,- 5的倒数的绝对值是()3A:-5B:5C:3D :-3 33552,函数 y=1x x 1中,自变量 x 的取值范围是()2A: x≥ -1B:x> 2C:x>-1且 x≠2 D: x≥ -1 且 x≠ 22 x3 1)3,不等式组的解集在数轴上可表示为(x 124,以下计算错误的选项是()A:14×7 =72 B :60 ÷ 5 =23C:9a+ 25a =8a D: 3 2 - 2 =35,若 x=-1是一元二次方程ax 2 +3a=-8 的解,则 a 的值为()A: 2B: -2C: 4D: -46,据相关部门统计,全国大概有1010 万考生参加今年的中考,1010万用科学记数法表示为()A:1.010 × 10 3B:1010×10 4C: 1.010×10 6D: 1.010×1077, 如图 , 四边形 ABCD为矩形纸片 , 将纸片 ABCD折叠 , 使点 B恰巧落在 CD边的中点 E 处 , 折痕为 AF, 若CD=6,则 AF=( )A:43B:33C:42D:88, 如图 1 搁置的一个机器部件, 若其主视图如图2, 则其俯视图是 ( )9, 甲乙两名学生进行射击练习, 两人在同样条件下各射靶 5 次 , 射击成绩统计以下 :命中环数 ( 单位:环 )78910甲命中相应环数的次数2201乙命中相应环数的次数1310从射击成绩的均匀数评论甲乙两人的射击水平,则( )A: 甲比乙高B:甲乙同样C:乙比甲高D:不可以确立10, 如图 , 在△ ABC中 , 已知∠ C=90° ,BC=3,AC=4, ⊙O是内切圆 ,E , F, D分别为切点,则tan ∠ OBD=( )32C:11A:B:D:3 23211,2008年武汉市建设两型社会共投资48 亿元,由四项建设工程构成, ①园林建设投资占20%,②水环境建设投资占30%,③环卫基础建设投资占 10%, ④城市建设投资占 40%,近几年每年总投资见折线图 , 依据以上信息 , 以下判断 :(1)2008 年总投资的增添率与 2006 年持平(2)2008年园林建设48×20%=9.6 亿(3) 若 2009 年 ,2010 年总投资的增添率都与2007 年同样 , 估计2010 年共投资 48× (1+ 4024)224亿元; (4) 若 2008年园林建设投资比原计划增添10%,则 2008 年园林建设 , 水环境建设两项投资同样 . 此中正确的个数是 ( )A:4 个B:3个C:2个D:1个12, 如图,在△ ABC中, CD⊥ AB,且 CD2 =AD×DB, AE均分∠ CAB交 CD于 F,CN=BE① CF=BN②∠ ACB=90°C③ FN∥ AB④ AD2 =DF× DC则以下结论正确的选项是()A:①②④ B :②③④ C :①②③ D :①③二,填空题(共 4小题 , 每题3分,共 12分 )13, 黄陂区某水晶商铺一段时间内销售了各样不一样价钱的水晶项链75 条 , 其价钱和销售数目以下表 :价钱(元)2025303540507080100150销售数目(条)139********下次进货时 , 你建议该商铺应多进价钱为_________元的水晶项链 .14, 小明按这样的规律用火柴棒搭图形,则第 10个图形需 ________根火柴棒 .15, 直线 y=mx+n和抛物线y=ax 2 +bx+c 在同一坐标系中的地点以下图, 那么不等式mx+n﹤ ax 2 +bx+c﹤ 0的解集是 _________16, 如图 , 矩形 OABC的两边 OA,OC分别在 x 轴和 y 轴的正半轴上,点G为矩形对角线的交点,经过点G的双曲线y= k在第一象限的图象与BC订交于点M,交 AB 于 N,x若 B(4, 2)则AN的值为 __________. CM三,解答以下各题(9 小题,共72 分)17,(此题6分)解方程: x 2 -x-1=018,( 此题 6分 ) 先化简,再求值:( 1-x)÷1,此中 x=1 x1x x 2200919,(此题6分)如图,四边形 ABCD中, AD∥ BC,对角线 AC, BD交于点 O,且 OA=OC,求证四边形ABCD是平行四边形。
湖北武汉2010中考数学模拟试题八答案不全--数学

武汉市2009—2010学年度九年级中考模拟测试题8姓名:__ 学号:__ 学校:__-、选择题。
(下列各题的备选答案中,只有一个是正确的,请将正确答案的序号填入题后的括号内.本题共12个小题,每小题3分,共36分) 1、-3的倒数是( )A :3B :-3C :-31 D 、31 2、在函数y=5-x 中自变量的取值范围是( ) A 、x <5 B 、x >5 C 、x ≥5 D 、x ≤5 3、若不等式组112x x ≤⎧⎨+>-⎩的解集在数轴上可表示为( )4、下列运算正确的是 ( )A .(2a 2)3=6a 6B .2a 2+3a 2=5a 4C .a 3÷a -1=a 4D .(a+2b)2=a 2+4b 25、关于x 的一元二次方程(m -1)x 2+x +m 2-1=0有一根为0,则m 的值为( )A 、1B 、-1C 、1或-1D 、216、嫦娥一号”月球探测卫星于2007年10月24日成功发射.11月26日国家航天局正式公布“嫦 娥一号”传回的第一幅月面图像.该幅月球表面图,成像区域的面积为128800平方公里.这个数据用科学记数法为 ( )A .1288×102平方公里B .128.8×103平方公里C .12.88×104平方公里D .1.288⨯105平方公里7、如图,ΔABC 与ΔA ’B ’C ’关于直线l 对称,则∠B 的度数为( )A .30°B .50°C .90°D .100°8、如图,是一组几何体,它的俯视图是( )9、为了某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:月用水量(吨)4 5 6 9 户数3421 30︒lC'B'A'B CA 50︒第7题图则关于这10户家庭的约用水量,下列说法错误的是( )A .中位数是5吨B . 极差是3吨C .平均数是5.3吨D .众数是5吨10、如图,点E 、B 、C 在⊙A 上,已知圆A 的直径为1,B E 是⊙A 上的一条弦.则COS ∠OBE =( ) A 、OB 的长 B 、BE 的长 C 、OE 的长 D 、OC 的长 11、近来年我市政府不断加大对城市绿化的经济投入,使全市绿地面积不断增加,从2006年底到2008年底城市绿地面积变化如图所示,根据图中提供的信息,下列说法:①2007年绿地面积比2006年增长9%;②2008年的年增长率比2007年的年增长率大;③这两年绿地面积的年平均增长率是10%,其中正确的个数有( ) A 、0个 B 、1个 C 、2个 D 、3个12、如图,已知平行四边形ABCD 中,45DBC =∠,DE BC ⊥BF AD ,于E ,BF CD ⊥于F ,DE BF ,相交于H ,的延长线相交于G ,下面结论: ①2DB BE =②A BHE =∠∠③AB BH =④BHD BDG △∽△.其中正确的结论是( ) A .①②③④B .①②③C .①②④D .②③④二、填空题(共4小题,每小题3分,共12分)13、若2、3、7、9、x 的平均数与众数相等,则x 的值为________。
2010年湖北各地中考数学试卷及答案集锦(12套)(WORD版)
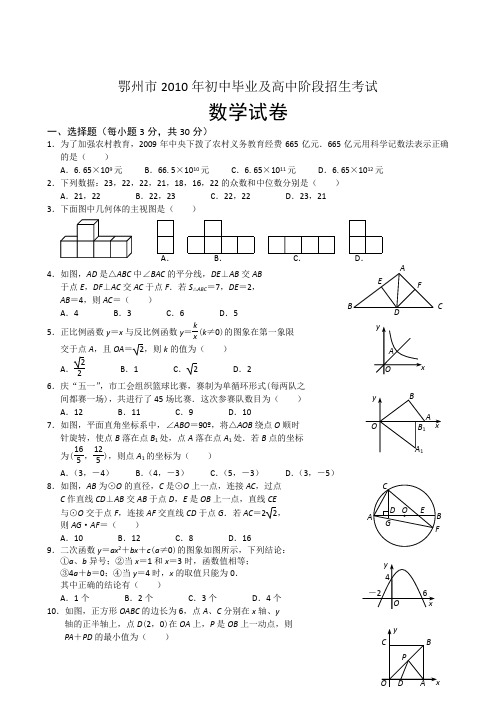
ABCF EAB C GFEDO鄂州市2010年初中毕业及高中阶段招生考试数学试卷一、选择题(每小题3分,共30分)1.为了加强农村教育,2009年中央下拨了农村义务教育经费665亿元.665亿元用科学记数法表示正确的是( )A .6.65×109元B .66.5×1010元C .6.65×1011元D .6.65×1012元 2.下列数据:23,22,22,21,18,16,22的众数和中位数分别是( ) A .21,22 B .22,23 C .22,22 D .23,21 3.下面图中几何体的主视图是( )4.如图,AD 是△ABC 中∠BAC 的平分线,DE ⊥AB 交AB 于点E ,DF ⊥AC 交AC 于点F .若S △ABC =7,DE =2, AB =4,则AC =( )A .4B .3C .6D .55.正比例函数y =x 与反比例函数y = kx (k ≠0)的图象在第一象限交于点A ,且OA =2,则k 的值为( )A .22 B .1 C . 2 D .2 6.庆“五一”,市工会组织篮球比赛,赛制为单循环形式(每两队之 间都赛一场),共进行了45场比赛.这次参赛队数目为( ) A .12 B .11 C .9 D .107.如图,平面直角坐标系中,∠ABO =90º,将△AOB 绕点O 顺时 针旋转,使点B 落在点B 1处,点A 落在点A 1处.若B 点的坐标 为( 16 5, 125),则点A 1的坐标为( ) A .(3,-4) B .(4,-3) C .(5,-3) D .(3,-5) 8.如图,AB 为⊙O 的直径,C 是⊙O 上一点,连接AC ,过点 C 作直线CD ⊥AB 交AB 于点D ,E 是OB 上一点,直线CE 与⊙O 交于点F ,连接AF 交直线CD 于点G .若AC =22, 则AG ·AF =( )A .10B .12C .8D .169.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论: ①a 、b 异号;②当x =1和x =3时,函数值相等; ③4a +b =0;④当y =4时,x 的取值只能为0. 其中正确的结论有( )A .1个B .2个C .3个D .4个 10.如图,正方形OABC 的边长为6,点A 、C 分别在x 轴、y轴的正半轴上,点D (2,0)在OA 上,P 是OB 上一动点,则A .B .C .D .A BCDDA .210B .10C .4D .6二、填空题(每小题3分,共18分)11.5的算术平方根是 .12.圆锥的底面直径是2m ,母线长4m ,则圆锥的侧面积是 m 2.13.已知α、β是方程x 2―4x ―3=0的两个实数根,则(α―3)(β―3)= .14.在一个黑色的袋子中装有除颜色外其他均相同的3个红球和6个白球,从中任意摸出1个球,摸出的球是白球的概率是 . 15.已知⊙O 的半径为10,弦AB =103,⊙O 上的点C 到弦AB 所在直线的距离为5,则以O 、A 、B 、C为顶点的四边形的面积是 .16.如图,四边形ABCD 中,AB =AC =AD ,E 是BC 的中点,AE =CE ,∠BAC =3∠CBD ,BD =62+66,则AB = .三、解答题(共72分)17.(8分)解不等式组⎪⎩⎪⎨⎧-<--≥--,,13524)2(3x x x x 并写出该不等式组的整数解.18.(8分)先化简2211112-÷⎪⎭⎫ ⎝⎛+--x x x x ,然后从-1、1、2中选取一个数作为x 的值代入求值.19.(8分)我市第四高级中学与第六高级中学之间进行一场足球比赛,邀请某校两位体育老师及两位九年级足球迷当裁判,九年级的一位足球迷设计了开球方式.(1)两位体育老师各抛掷一枚硬币,两枚硬币落地后正面朝上,则第四高级中学开球;否则,第六高级中学开球.请用树状图或列表的方法,求第四高级中学开球的概率.(2)九年级的另一位足球迷发现前面设计的开球方式不合理,他修改规则:如果两枚硬币都朝上时,第四高级中学得8分;否则,第六高级中学得4分.根据概率计算,谁的得分高,谁开球.你认为修改后的规则公平吗?若公平,请说明理由;若不公平,请你设计对双方公平的开球方式.20.(8分)春节期间,某客运站旅客流量不断增大,旅客往往需要长时间排队等候购票.经过调查发现,每天开始售票时,约有400人排队购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售A B C D EG H M A B C D E 60º30º与售票时间x (分钟)的关系如图所示,已知售票的前a 分钟只开放了两个售票窗口(规定每人只能购票一张).(1)求a 的值.(2)求售票到第60分钟时,售票厅排队等候购票的旅客人数.(3)若要在开始售票后半小时内让所有的排队旅客都能够购到票,以便后来到站的旅客随到随购,至少需要同时开放几个售票窗口?21.(8分)如图,一艘潜艇在海面下500m A 点处测得俯角为30º前下方的海底C 处有黑匣子信号发出,继续在同一深度直线航行4000m 后再次在B 点处测得俯角为60º前下方的海底C 处有黑匣子信号发出,求海底黑匣子C 点距离海面的深度(结果保留根号).22.(10分)工程师有一块长AD =12分米,宽AB =8分米的铁板,截去长AE =2分米、AF =4分米的直角三角形,在余下的五边形中,截得矩形MGCH ,其中点M 在线段EF 上. (1)若截得矩形MGCH 的面积为70平方分米,求矩形MGCH 的长与宽. (2)当EM 为多少时,矩形MGCH 的面积最大?并求此时矩形的周长.23.(10分)如图,一面利用墙,用篱笆围成的矩形花圃ABCD 的面积为S m 2,平行于墙的BC 边长为x m .(1)若墙可利用的最大长度为10m ,篱笆长为24m ,花圃中间用一道篱笆隔成两个小矩形,求S 与x 之间的函数关系式.(2)在(1)的条件下,围成的花圃的面积为45m 2时,求AB 的长.能否围成面积比45m 2更大的花圃?如果能,应该怎样围?如果不能,请说明理由.(3)若墙可利用最大长度为40m ,篱笆长77m ,中间用n 道篱笆隔成小矩形,且当这些小矩形为正方形和x 为正整数时,请直接写出一组满足条件的x 、n 的值.24.(12分)如图,在直角坐标系中,已知点A (-1,0)、B (0,2),动点P 沿过B 点且垂直于AB 的射线BM 运动,其运动的速度为每秒1个单位长度,射线BM 与x 轴交于点C . (1)求点C 的坐标.(2)求过A 、B 、C 三点的抛物线的解析式. (3)若点P 开始运动时,点Q 也同时从C 点出发,以点P 相同的速度沿x 轴负方向向点A 运动,t 秒后,以P 、Q 、C 为顶点的三角形为等腰三角形(点P 到点C 时停止运动,点Q 也同时停止运动),求t 的值.(4)在(2)(3)的条件下,当CQ =CP 时,求直线OP 与抛物线的交点坐标.A D BCA BD C…图1图22010年恩施自治州初中毕业及高中招生考试数 学 试 题注意事项:1.本试卷分试题卷和答题卡两部分,考试时间为120分钟,满分为120分.2.考生在答题前请阅读答题卡中的“注意事项”,然后按要求答题. 3.所有答案均须做在答题卡相应区域,做在其它区域无效.一、填空题:(本大题共8个小题,每小题3分,共24分) 1.9的相反数是 .2.据有关部门预测,恩施州煤炭总储量为2.91亿吨,用科学记数法表示这个数是 吨(保留两个有效数字). 3. 分解因式:=+-b ab b a 22 .4.在一个不透明的盒子里装有5个黑球,3个红球和2个白球,它们除颜色外其余都相同,从中随机摸出一个球,摸到红球的概率是 . 5.在同一直角坐标系中,正比例函数x k y 1=的图象与反比例函数xk y 2=的图象有公共点,则21k k 0(填“>”、“=”或“<”).6.如图1,在ABCD 中,已知AB=9㎝,AD=6㎝,BE 平分∠ABC 交DC 边于点E ,则DE 等 于 ㎝.7.如图2,在矩形ABCD 中,AD =4,DC =3,将△ADC 按逆时针方向绕点A 旋转到△AEF (点A 、B 、E 在同一直线上),连结CF ,则CF = .8.如图3,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依次类推,如果n 层六边形点阵的总点数为331, 则n 等于 .二、选择题:(下列各小题都给出四个选项,其中只有一项是符合题目要求的.本大题共8个小题,每小题3分,共24分) 9.()24-的算术平方根是:A. 4B. 4±C. 2D. 2± 10.下列计算正确的是:()223()3图3图2图111.用4个棱长为1的正方体搭成一个几何体模型,其主视图与左视图如图4所示,则该立方体的俯视图不可..能.是:12.不等式组⎩⎨⎧≤-<+5148x x x 的解集是:A. 5≤xB. 53≤<-xC.53≤<xD. 3-<x13.某品牌商品,按标价九折出售,仍可获得20%的利润.若该商品标价为28元,则商品的进价为:A. 21元B. 19.8元C. 22.4元D. 25.2元 14.如图5,EF 是△ABC 的中位线,将△AEF 沿中线AD 方向平移到△A 1E 1F 1的位置,使E 1F 1与BC 边重合,已知△AEF 的面积为7,则图中阴影部分的面积为: A. 7 B. 14 C. 21 D. 2815.某班随机抽取6名同学的一次地生测试成绩如下:82,95,82,76,76,82.数据中的众数和中位数分别是:A. 82,76B. 76,82C. 82,79D. 82,82 16.如图6, 已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是A .24πB .30πC .48πD .60π 三、解答题(本大题共8个小题,满分72分) 17.(6分) 计算:2+()()()121212010-++--313⨯-18.(8分)解方程:14143=-+--xx x19.(8分)如图7,已知,在ABCD 中,AE=CF ,M 、N 分别是DE 、BF 的中点.求证:四边形MFNE 是平行四边形 .20.(8分)2010年4月14日青海玉树发生7.1级地震,地震灾情牵动全国人民的心.某社区响应恩施州政府的号召,积极组织社区居民为灾区人民献爱心活动.为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图8所示的不完整统计图.已知A、B两组捐款户数直图7 图4图6图5⑴ A 组的频数是多少?本次调查样本的容量是多少? ⑵ 求出C 组的频数并补全直方图.⑶ 若该社区有500户住户,请估计捐款不少于300元的户数是多少?21.(10分) 如图9,已知,在△ABC 中,∠ABC=090,BC 为⊙O 的直径, AC 与⊙O 交于点D,点E 为AB 的中点,PF ⊥BC 交BC 于点G,交AC 于点F. (1)求证:ED 是⊙O 的切线. (2)如果CF =1,CP =2,sinA =54,求⊙O 的直径BC.22.(10分) 恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.(1)若存放x 天后,将这批香菇一次性出售,设这批香菇的销售总金额为y 元,试写出y 与x 之间的函数关系式.(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少? 图8 图923.(10分)(1)计算:如图10①,直径为a 的三等圆⊙O 1、⊙O 2、⊙O 3两两外切,切点分别为A 、B 、C ,求O 1A 的长(用含a 的代数式表示).(2)探索:若干个直径为a 的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中n 层圆圈的高度n h和(用含n 、a 的代数式表示). (3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米.用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?(3≈1.73)24.(12分) 如图11,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.②③①图11图10数学试题卷注意事项:1. 本试卷分为试题卷和答题卷两部分。
2010年武汉市中考数学试卷及答案

2010湖北武汉市中考数学试卷第Ⅰ卷 (选择题,共36分)一、选择题 (共12小题,每小题3分,共36分)下列各题中均有四个备选答案,其中有且只有一个正确,请在答卷上将正确答案的代号涂黑。
1. 有理数-2的相反数是(A) 2 (B) -2 (C) 21 (D) -212. 函数y=1-x 中自变量x 的取值范围是(A) x ≥1 (B) x ≥ -1 (C) x ≤1 (D) x ≤ -1 3. 如图,数轴上表示的是某不等式组的解集,则这个不等式组可能是(A) x> -1,x>2 (B) x> -1,x<2 (C) x< -1,x<2 (D) x<-1,x>24. 下列说法: “掷一枚质地均匀的硬币一定是正面朝上”; “从一副普通扑克牌中任意抽取 一张,点数一定是6”;(A) 都正确 (B) 只有 正确 (C) 只有 正确 (D) 都错误 。
5. 2010年上海世博会开园第一个月共售出门票664万张,664万用科学计数法表示为 (A) 664⨯104 (B) 66.4⨯105 (C) 6.64⨯106 (D) 0.664⨯1076. 如图,△ABC 内有一点D ,且DA=DB=DC ,若∠DAB=20︒,∠DAC=30︒,则∠BDC 的大小是(A) 100︒ (B) 80︒ (C) 70︒ (D) 50︒ 7. 若x 1,x 2是方程x 2=4的两根,则x 1+x 2的值是 (A) 8 (B) 4 (C) 2 (D) 0 。
8. 如图所示,李老师办公桌上放着一个圆柱形茶叶盒和一个正方体的墨水盒,小芳从上面看,看到的图形是9. 如图,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行。
从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是 (A) (13,13) (B) (-13,-13) (C) (14,14) (D) (-14,-14) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
武汉市2009—2010学年度九年级中考模拟测试题8
姓名:__ 学号:__ 学校:__
-、选择题。
(下列各题的备选答案中,只有一个是正确的,请将正确答案的序号填入题后的括号内.本
题共12个小题,每小题3分,共36分) 1、-3的倒数是( )
A :3
B :-3
C :-
31 D 、3
1
2、在函数y=5-x 中自变量的取值范围是( ) A 、x <5 B 、x >5 C 、x ≥5 D 、x ≤5
3、若不等式组1
12x x ≤⎧⎨
+>-⎩
的解集在数轴上可表示为( )
4、下列运算正确的是 ( )
A .(2a 2)3=6a 6
B .2a 2+3a 2=5a 4
C .a 3÷a -1=a 4
D .(a+2b)2=a 2+4b 2
5、关于x 的一元二次方程(m -1)x 2+x +m 2-1=0有一根为0,则m 的值为( )
A 、1
B 、-1
C 、1或-1
D 、
2
1
6、嫦娥一号”月球探测卫星于2007年10月24日成功发射.11月26日国家航天局正式公布“嫦 娥一号”传回的第一幅月面图像.该幅月球表面图,成像区域的面积为
128800平方公里.这个数据用科学记数法为 ( )
A .1288×102平方公里
B .128.8×103平方公里
C .12.88×104平方公里
D .1.288⨯105
平方公里
7、如图,ΔABC 与ΔA ’B ’C ’关于直线l 对称,
则∠B 的度数为( )
A .30°
B .50°
C .90°
D .100°
8、如图,是一组几何体,它的俯视图是( )
9、为了某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:
月用水量(吨)
4 5 6 9 户数
3
4
2
1
30︒
l
C'
B'A'B C
A 50︒
第7题图
则关于这10户家庭的约用水量,下列说法错误的是( )
A .中位数是5吨
B . 极差是3吨
C .平均数是5.3吨
D .众数是5吨
10、如图,点E 、B 、C 在⊙A 上,已知圆A 的直径为1,B E 是⊙A 上的
一条弦.则COS ∠OBE =( )
A 、O
B 的长 B 、BE 的长
C 、OE 的长
D 、OC 的长
11、近来年我市政府不断加大对城市绿化的经济投入,使全市绿地面积不断增加,从2006年底到2008年底城市绿地面积变化如图所示,根据图
中提供的信息,下列说法:①2007年绿地面积比2006年增长9%;②2008年的年增长率比
2007年的年增长率大;③这两年绿地面积的年平均增长率是10%,其中正确的个数有( ) A 、0个 B 、1个 C 、2个 D 、3个
12、如图,已知平行四边形ABCD 中,45DBC =∠,
DE BC ⊥BF AD ,于E ,BF CD ⊥于F ,DE BF ,相
交于H ,的延长线相交于G ,下面结论: ①2DB BE =
②A BHE =∠∠③AB BH =
④BHD BDG △∽△.其中正确的结论是( ) A .①②③④
B .①②③
C .①②④
D .②③④
二、填空题(共4小题,每小题3分,共12分)
13、若2、3、7、9、x 的平均数与众数相等,则x 的值为________。
14、不等式组8.下列三种化合物的结构式及分子式,请按其规律,写出第n 种化合物的分子式:__ ___
H H H H H H
|
| |
| | |
H -C -H
H —C — C —H H —C —C — C —H …… | | |
| | |
H
H H
H H H 分子式: CH 4
C 2H 6
C 3H 8
15、直线y=kx+3经过点A (-3,2),不等式-2x-4≤kx+3<3的解集是 ________。
B A
C
E
O
A
B C
D
E
F H
G
-2
-1 -2
-1
2 2
1
1 3
x
y
y 1 y 2 O
16、如图,一次函数y=-3
3
x+1的图象与x 轴、y 轴分别交于点A 、B ,以线段AB•为边在第一象限内作等边△ABC .则△ABC 的面积是________。
三、解答下列各题(共九小题,共72分) 17、(本题满分6分)x²+4x -1=0
18、(本题满分6分)先化简,再求值:⎪⎭
⎫
⎝⎛--÷-+x x x x x 1211,其中2=x .
19、(本题满分6分)已知:如图4,在直角梯形ABCD 中,AD//BC ,∠A=90°,BC=CD ,BE ⊥DC 于点E.求证:△ABD ≌△EBD
20、(本题满分7分)宝宝和贝贝是一对双胞胎,他们参加奥运志愿者选拔并与甲、乙、丙三人都进入了前5名.现从这5名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出:(1)宝宝和贝贝同时入选的概率;(2)宝宝和贝贝至少有一人入选的概率.
21、(本题满分7分)如图,抛物线y 1=-x 2+2向右平移1个单位得到
抛物线y 2,回答下列问题:
(1)抛物线y 2的顶点坐标_____________; (2)阴影部分的面积S =___________;
(3)若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3, 求抛物线y 3的解析式.
第16题图
第19题图
第15题图
22、如图,C 为线段AB 上一点,以BC 为直径作⊙O,再以AO 为直径作⊙M 交⊙O 于D 、B 作AB 的垂线交AD 的延长线于F ,连结CD 。
若AC =2,且AC 与AD 的长是关于x 的方22(15)0x x k -++=的两个根。
①求证:AD 是⊙O 的切线; ②求线段DF 的长;
23、施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM 为12米.现以O 点为原点,OM 所在直线为x 轴建立直角坐标系(如图1所示).
⑴求出这条抛物线的函数解析式,并写出自变量x 的取值范围;
⑵隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
⑶施工队计划在隧道门口搭建一个矩形“脚手架”CDAB ,使A 、D 点在抛物线上。
B 、C 点在地面OM 线上(如图2所示).为了筹备材料,需求出“脚手架”三根木杆AB 、AD
、DC 的长度之和....的最大值是多少,请你帮施工队计算一下.
图2
24、(本题满分10分)如图①,已知△ABC 中,AB=AC ,点P 是BC 上的一点,PN ⊥AC 于点N ,PM ⊥AB 于点M ,CG ⊥AB 于点G 点。
(1)则CG 、PM 、PN 三者之间的数量关系是_________。
(2)如图②,若点P在BC的延长线上, 则PM、PN、CG三者是否还有上述关系,若有,请说明理由,若没有,猜想三者之间又有怎样的关系,并证明你的猜想;
D
y
P
x
O
M
A B
C
第23题图
第22题图
第21题图
(3)如图③,AC 是正方形ABCD 的对角线,AE=AB, 点P 是BE 上任一点, PN ⊥AB 于点N ,PM ⊥AC
于点M ,猜想PM、PN、AC有什么关系;(直接写出结论)
25、(本题满分12分)已知,建立如图所示平面直角坐标系,点B 在第一象限内,将Rt△AB O 沿OB 折叠后,点A 落在第一象限内的点C 处.
(1)求点C 的坐标;
(2)若抛物线()2
0y ax bx a =+≠经过C 、A 两点,求此抛物线的解
析式;
(3)若上述抛物线的对称轴与OB 交于点D,点P 为线段DB 上一动点,
过P 作y 轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM 为很等腰梯形?若存在,请求出此时点P 的坐标;若不存在,请说明理由
.
第24题图
第25题图
答案
一、选择题(每小题3分,共24分)
1. C
2.C
3.A
4.C
5.B
6.D
7.D
8.B
9.B 10.C 11.D12.B。
