建筑力学课件8复习课程
合集下载
建筑力学(完整版)ppt课件

精品课件
第一章 静力学基础
第一节 基本概念 一、力 1.力的定义 力是物体之间相互的机械作用。由于力的作用 ,物体的机械运动状态将发生改变,同时还引起物 体产生变形。前者称为力的运动效应(或外效应) ;后者称为力的变形效应(或内效应)。 在本课程中,主要讨论力对物体的变形效应。
精品课件
2.力的三要素 力的大小、方向(包括方位和指向) 和作用点,这三个因素称为力的三要素。 实际物体在相互作用时,力总是分布在 一定的面积或体积范围内,是分布力。如 果力作用的范围很小,可看成是作用在一 个点上,该点就是力的作用点,建筑上称 这种力为集中力。
作为施工技术及施工管理人员,也要求必须掌握建筑力学知识。知道 结构和构件的受力情况,什么位置是危险截面,各种力的传递途径以及 结构和构件在这些力的作用下会发生怎样的破坏等等,才能很好地理解 图纸设计的意图及要求,科学地组织施工,制定出合理的安全和质量保 证措施;在施工过程中,要将设计图纸变成实际建筑物,往往要搭设一 些临时设施和机具,确定施工方案、施工方法和施工技术组织措施。如 对一些重要的梁板结构施工,为了保证梁板的形状、尺寸和位置的正确 性,对安装的模板及其支架系统必须要进行设计或验算;进行深基坑( 槽)开挖时,如采用土壁支撑的施工方法防止土壁坍落,对支撑特别是 大型支撑和特殊的支撑必须进行设计和计算,这些工作都是由施工技术 人员来完成的。因此,只有懂得力学知识才能很好地完成设计及施工任 务,避免发生质量和安全事故,确保建筑施工正常进行。
精品课件
构件的强度、刚度和稳定性统称为构件的承载能力。其高低 与构件的材料性质、截面的几何形状及尺寸、受力性质、工 作条件及构造情况等因素有关。在结构设计中,如果把构件 截面设计得过小,构件会因刚度不足导致变形过大而影响正 常使用,或因强度不足而迅速破坏;如果构件截面设计得过 大,其能承受的荷载过分大于所受的荷载,则又会不经济, 造成人力、物力上的浪费。因此,结构和构件的安全性与经 济性是矛盾的。建筑力学的任务就在于力求合理地解决这种 矛盾。即:研究和分析作用在结构(或构件)上力与平衡的 关系,结构(或构件)的内力、应力、变形的计算方法以及 构件的强度、刚度和稳定条件,为保证结构(或构件)既安 全可靠又经济合理提供计算理论依据。
第一章 静力学基础
第一节 基本概念 一、力 1.力的定义 力是物体之间相互的机械作用。由于力的作用 ,物体的机械运动状态将发生改变,同时还引起物 体产生变形。前者称为力的运动效应(或外效应) ;后者称为力的变形效应(或内效应)。 在本课程中,主要讨论力对物体的变形效应。
精品课件
2.力的三要素 力的大小、方向(包括方位和指向) 和作用点,这三个因素称为力的三要素。 实际物体在相互作用时,力总是分布在 一定的面积或体积范围内,是分布力。如 果力作用的范围很小,可看成是作用在一 个点上,该点就是力的作用点,建筑上称 这种力为集中力。
作为施工技术及施工管理人员,也要求必须掌握建筑力学知识。知道 结构和构件的受力情况,什么位置是危险截面,各种力的传递途径以及 结构和构件在这些力的作用下会发生怎样的破坏等等,才能很好地理解 图纸设计的意图及要求,科学地组织施工,制定出合理的安全和质量保 证措施;在施工过程中,要将设计图纸变成实际建筑物,往往要搭设一 些临时设施和机具,确定施工方案、施工方法和施工技术组织措施。如 对一些重要的梁板结构施工,为了保证梁板的形状、尺寸和位置的正确 性,对安装的模板及其支架系统必须要进行设计或验算;进行深基坑( 槽)开挖时,如采用土壁支撑的施工方法防止土壁坍落,对支撑特别是 大型支撑和特殊的支撑必须进行设计和计算,这些工作都是由施工技术 人员来完成的。因此,只有懂得力学知识才能很好地完成设计及施工任 务,避免发生质量和安全事故,确保建筑施工正常进行。
精品课件
构件的强度、刚度和稳定性统称为构件的承载能力。其高低 与构件的材料性质、截面的几何形状及尺寸、受力性质、工 作条件及构造情况等因素有关。在结构设计中,如果把构件 截面设计得过小,构件会因刚度不足导致变形过大而影响正 常使用,或因强度不足而迅速破坏;如果构件截面设计得过 大,其能承受的荷载过分大于所受的荷载,则又会不经济, 造成人力、物力上的浪费。因此,结构和构件的安全性与经 济性是矛盾的。建筑力学的任务就在于力求合理地解决这种 矛盾。即:研究和分析作用在结构(或构件)上力与平衡的 关系,结构(或构件)的内力、应力、变形的计算方法以及 构件的强度、刚度和稳定条件,为保证结构(或构件)既安 全可靠又经济合理提供计算理论依据。
《建筑力学课件-第一章课件》

静力学基础
1
平衡条件
建筑物在静力平衡状态下,合力和合力矩均为零。
2
受力分析
通过受力分析,确定建筑物各个构件的内力和外力。
3
应力与变形
建筑物在受力作用下,会产生应力和变形。
弹性力学基础
胡克定律
弹性材料的应力与应变成正比。
梁的挠度
通过弹性力学理论计算梁的挠度以评估结构的 性能。
弹性模量
衡量材料抵抗应力的能力。
建筑结构的施工安全与质量控 制
施工过程中需要重视结构的施工安全和质量控制,确保建筑物的结构稳定和 耐久性。
美观性
建筑物外观应具备美观性和艺术 性。
可持续性
建筑物设计应考虑本流程
1
建立模型
2
根据建筑物的实际情况,建立结构分析
的数学模型。
3
收集数据
收集建筑物的相关数据,包括荷载、材 料性质等。
求解
使用数学方法对模型进行求解,得到结 构的力学性能。
建筑物荷载分析
自重荷载
使用荷载
• 建筑物本身的重量 • 包括结构构件、装修材料等
• 建筑物使用过程中产生 的荷载
• 包括人员、设备、家具等
环境荷载
• 建筑物所处的环境条件 • 包括风荷载、地震荷载等
建筑物结构的设计与优化
设计
根据使用需求和结构要求,进行结构设计,满足建筑物的功能和安全性。
优化
通过调整结构参数和使用优化方法,提高结构的性能和效率。
应力分布
弹性力学理论可以计算建筑物中各点的应力分 布情况。
塑性力学基础
塑性力学基础研究了材料在超过弹性限度后的变形和破坏行为,对于设计可 靠的建筑结构至关重要。
稳定性理论
建筑力学完整版全套ppt课件

2 、均匀 料性 的假 力 ,设 学 任 小块材 同料的力
3 、各 材项 料 同
沿不同 相 方 同 向 , 砖 的 如 素混凝土
本教性 材材 中料
工程实 全 际 是 中 各 材 的 向 钢筋混凝土
三在 、 产 一 弹
荷载 失撤 , , 这
失的 如) , 变 :
四、 超塑 过 载 一部 部分 分 体
杆件 现, 为 错
F F
三、扭转 一对 杆 相 件 反 的
杆件 发 的 生 相 对 邻
四、弯曲 对方 于相 杆 通 体轴的平面) 杆件曲 的线 轴线由
工各 程当 种 中
起本 主组 变 要 题( 98) 1 4 建筑力学的任 建究 筑 , 结 力 作度 用 。 , 下 证常 结 材 工 构
使设 靠 计 又 的 经 结构 足的 强 的 一、 坏张 的 求 是件 要发 在 求
结构都抽象为刚
2、强度问题
主要研 本 究 变 构 形 算 件 形 理论和方法。 要便结 , 构 应 满 保 满 足 问 决 结 题 如 识 解 问 决 结 题 如 4 、超静 算定结构 介法 绍 法 , 求 连求 续 是 解 梁
静定问 结题 构。 对强 5、稳定性问题 这里 件 只 下 研 直 在 2 5 问 上 情 题 面 所 定 研 构 性 究 理想变形体。
如:设 结备 构的 活荷 结 载 构 : 上
如: 的 风 材 、 料 雪
三、 可 按 分 其特点 构 是 上 加 各 显 载 点 荷载达最后 值后 衡 , 状 结 态 如:机 地 器 震 转 时 压 动 的 动荷载特点
由于 点荷 有 , 时间而变。
q
F1
F2
第二章
静力学基本概念和物体的 受力分析
3 、各 材项 料 同
沿不同 相 方 同 向 , 砖 的 如 素混凝土
本教性 材材 中料
工程实 全 际 是 中 各 材 的 向 钢筋混凝土
三在 、 产 一 弹
荷载 失撤 , , 这
失的 如) , 变 :
四、 超塑 过 载 一部 部分 分 体
杆件 现, 为 错
F F
三、扭转 一对 杆 相 件 反 的
杆件 发 的 生 相 对 邻
四、弯曲 对方 于相 杆 通 体轴的平面) 杆件曲 的线 轴线由
工各 程当 种 中
起本 主组 变 要 题( 98) 1 4 建筑力学的任 建究 筑 , 结 力 作度 用 。 , 下 证常 结 材 工 构
使设 靠 计 又 的 经 结构 足的 强 的 一、 坏张 的 求 是件 要发 在 求
结构都抽象为刚
2、强度问题
主要研 本 究 变 构 形 算 件 形 理论和方法。 要便结 , 构 应 满 保 满 足 问 决 结 题 如 识 解 问 决 结 题 如 4 、超静 算定结构 介法 绍 法 , 求 连求 续 是 解 梁
静定问 结题 构。 对强 5、稳定性问题 这里 件 只 下 研 直 在 2 5 问 上 情 题 面 所 定 研 构 性 究 理想变形体。
如:设 结备 构的 活荷 结 载 构 : 上
如: 的 风 材 、 料 雪
三、 可 按 分 其特点 构 是 上 加 各 显 载 点 荷载达最后 值后 衡 , 状 结 态 如:机 地 器 震 转 时 压 动 的 动荷载特点
由于 点荷 有 , 时间而变。
q
F1
F2
第二章
静力学基本概念和物体的 受力分析
建筑力学课件8
成反比。
三铰拱的计算
2、内力的计算
计算图a所示三铰拱K截面的内力 取隔离体如图b
M [ FAV x F1 ( x a1 )] FH y
相应简支梁K截面的弯矩为M 0 相应简支梁K截面的剪力为FS0 相应简支梁K截面的轴力为FN0 相应简支梁
M M 0 FH y
FS FS0 cos FH sin FN FS0 sin FH cos 压力为正
Mk1
FNK1 FQK1
4m
5.33kN 1.33kN
FNK1 1.33sin (5.33 q y1 ) cos 0.72kN
FQK 1 1.33cos (5.33 q y1 ) sin 1.95kN y12 M K 1 1.33x1 5.33y1 q 3.80kN m 2
练习: 作图示结构弯矩图
Pl / 2 Pl / 2 l/2
P
P
P
l
l/2
l l
Pl / 2
l
2 Pl
P
l/2 l/2
Pl
Pl
P
l l
l
练习: 作图示结构弯矩图
P
l l l l
P
l
l
P
l
l
拱的内力分析
一般指杆的轴线为曲线形状, 并且在竖向荷载作用下会产 生水平支座反力的结构。
重要特点: 竖向荷载产生水平推力(与梁相比) 优点: M减小,FN为主 ——便于使用抗压材料:砖、石、混凝土 缺点: 水平反力要求 ——地基、支承结构、(墙、柱、墩等) 更坚固。 ——可称拱式结构或推力结构
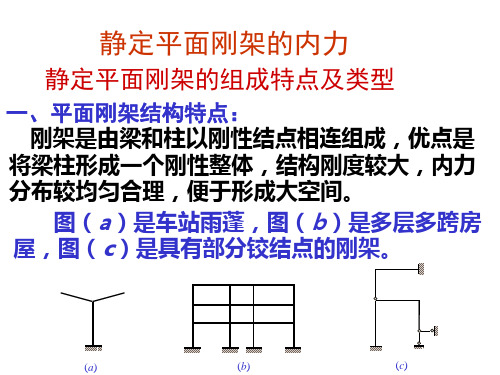
刚架的内力: 刚架的内力是指各杆件中垂直于杆轴的横 截面上的弯矩、剪力和轴力。在计算静定刚 架时,通常应由整体或某些部分的平衡条件 ,求出各支座反力和各铰接处的约束力,然 后逐杆绘制内力图。
三铰拱的计算
2、内力的计算
计算图a所示三铰拱K截面的内力 取隔离体如图b
M [ FAV x F1 ( x a1 )] FH y
相应简支梁K截面的弯矩为M 0 相应简支梁K截面的剪力为FS0 相应简支梁K截面的轴力为FN0 相应简支梁
M M 0 FH y
FS FS0 cos FH sin FN FS0 sin FH cos 压力为正
Mk1
FNK1 FQK1
4m
5.33kN 1.33kN
FNK1 1.33sin (5.33 q y1 ) cos 0.72kN
FQK 1 1.33cos (5.33 q y1 ) sin 1.95kN y12 M K 1 1.33x1 5.33y1 q 3.80kN m 2
练习: 作图示结构弯矩图
Pl / 2 Pl / 2 l/2
P
P
P
l
l/2
l l
Pl / 2
l
2 Pl
P
l/2 l/2
Pl
Pl
P
l l
l
练习: 作图示结构弯矩图
P
l l l l
P
l
l
P
l
l
拱的内力分析
一般指杆的轴线为曲线形状, 并且在竖向荷载作用下会产 生水平支座反力的结构。
重要特点: 竖向荷载产生水平推力(与梁相比) 优点: M减小,FN为主 ——便于使用抗压材料:砖、石、混凝土 缺点: 水平反力要求 ——地基、支承结构、(墙、柱、墩等) 更坚固。 ——可称拱式结构或推力结构
刚架的内力: 刚架的内力是指各杆件中垂直于杆轴的横 截面上的弯矩、剪力和轴力。在计算静定刚 架时,通常应由整体或某些部分的平衡条件 ,求出各支座反力和各铰接处的约束力,然 后逐杆绘制内力图。
《建筑力学》PPT课件(最全版)

为拉力。
§3–1约束与约束反力
A
§3–1约束与约束反力
光滑接触面约束
§3–1约束与约束反力
光滑支承接触对非自由体的约束力,作用在 接触处;方向沿接触处的公法线并指向受力
物体,故称为法向约束力,用FN表示。
§3–1约束与约束反力
光滑铰链约束 此类约束简称铰链或铰 径向轴承、圆柱铰链、固定铰链支座等 (1) 、径向轴承(向心轴承)
§2–1 力的概念
四、力系、合力与分力 力 系——作用于同一物体或物体系上的一群力。
等效力系——对物体的作用效果相同的两个力系。
平衡力系——能使物体维持平衡的力系。 合 力——在特殊情况下,能和一个力系等效
的一个力。
分 力——力系中各个力。
§2–2 静力学公理
公理一 (二力平衡公理) 要使刚体在两个力作用下维持平衡状态,
杆的受力图能否画为 图(d)所示?
若这样画,梁AB的受力 图又如何改动?
§3–2物体的受力分析及受力图
例1-4
不计三铰拱桥的自重与摩擦,画 出左、右拱AC,CB的受力图与 系统整体受力图。
解: 右拱CB为二力构件,其受力 图如图(b)所示
§3–2物体的受力分析及受力图
取左拱AC ,其受力图如图(c)
第三章
物体的受力分析 结构的计算简图
§3–1约束与约束反力 §3–2物体的受力分析及受力图 §3–3 结构的计算简图
§3–1约束与约束反力
自由体:位移不受限制的物体。 非自由体:位移受到限制的物体。 约束:限制非自由体运动的其他物体 。 约束反力:约束对被约束体的反作用力 主动力:约束力以外的力。
解:画出简图 画出主动力
画出约束力
§3–2物体的受力分析及受力图
§3–1约束与约束反力
A
§3–1约束与约束反力
光滑接触面约束
§3–1约束与约束反力
光滑支承接触对非自由体的约束力,作用在 接触处;方向沿接触处的公法线并指向受力
物体,故称为法向约束力,用FN表示。
§3–1约束与约束反力
光滑铰链约束 此类约束简称铰链或铰 径向轴承、圆柱铰链、固定铰链支座等 (1) 、径向轴承(向心轴承)
§2–1 力的概念
四、力系、合力与分力 力 系——作用于同一物体或物体系上的一群力。
等效力系——对物体的作用效果相同的两个力系。
平衡力系——能使物体维持平衡的力系。 合 力——在特殊情况下,能和一个力系等效
的一个力。
分 力——力系中各个力。
§2–2 静力学公理
公理一 (二力平衡公理) 要使刚体在两个力作用下维持平衡状态,
杆的受力图能否画为 图(d)所示?
若这样画,梁AB的受力 图又如何改动?
§3–2物体的受力分析及受力图
例1-4
不计三铰拱桥的自重与摩擦,画 出左、右拱AC,CB的受力图与 系统整体受力图。
解: 右拱CB为二力构件,其受力 图如图(b)所示
§3–2物体的受力分析及受力图
取左拱AC ,其受力图如图(c)
第三章
物体的受力分析 结构的计算简图
§3–1约束与约束反力 §3–2物体的受力分析及受力图 §3–3 结构的计算简图
§3–1约束与约束反力
自由体:位移不受限制的物体。 非自由体:位移受到限制的物体。 约束:限制非自由体运动的其他物体 。 约束反力:约束对被约束体的反作用力 主动力:约束力以外的力。
解:画出简图 画出主动力
画出约束力
§3–2物体的受力分析及受力图
建筑力学课件第八章

n
上一页 下一页
返回
8.2 轴心拉压直杆横截面的应力
K称为理论应力集中系数,它反映了应力集中的程度,是一个大于1 的系数。试验和理论分析结果表明构件的截面尺寸改变越急剧,构件 的孔越小,缺口的角越尖,应力集中的程度就越严重。因此,构件上 应尽量避免带尖角、小孔或槽,在阶梯形杆的变截面处要用圆弧过渡, 并尽量使圆弧半径大一些。 各种材料对应力集中的反应是不相同的。塑性材料(如低碳钢)具有 屈服阶段,当孔边附近的最大应力到达屈服极限时,该处材料首先屈 服,应力暂时不再增大,若外力继续增大,增大的内力就由截面上尚 未屈服的材料所承担,使截面上其他点的应力相继增大到屈服极限, 该截面上的应力逐渐趋于平均,如图8-5(c)所示。因此,用塑性材 料制作的构件,在静荷载作用下可以不考虑应力集中的影响。而对于 脆性材料制成的构件,情况就不同了。因为材料不存在屈服,当孔边 最大应力的值达到材料的强度极限时,该处首先产生裂纹。所以用脆 性材料制作的构件,应力集中将大大降低构件的承载力。
上一页
返回
8.2 轴心拉压直杆横截面的应力
8.2.1 轴心拉压直杆横截面正应力
前已述及,轴心拉压直杆横截面上只有一个内力分量——轴力。轴力 是横截面连续分布的内力的合力。轴向拉压杆横截面上的分布内力是 均匀分布的,其方向都沿杆轴方向。下面以一个简单演示试验予以说 明。 用一根均质、等截面直杆,并在其表面均匀地画上一些与杆轴线平行 的纵向线和与之垂直的横向线,如图8-2(a)所示。当在杆上施加轴 向拉力后,如图8-2(b)所示,可以看到所有纵向线都伸长了,其伸 长量相等,所有横线仍保持为与杆轴线垂直。 根据上述现象可作如下假设: (1)平面假设。若将各条横线看作一个横截面,则杆的横截面位移 后依然保持平面,且依然垂直于杆的轴线。 (2)设想杆件是由许多等截面的纵向纤维组成,纵向纤维间无挤压。
建筑力学通用课件(完整版)

近似解法
用近似的数学表达式来表示每个单元 的物理量,如位移、应力等。
平衡方程
根据物理平衡原理,建立每个单元的 平衡方程,通过求解这些方程得到每 个单元的近似解。
集成
将各个单元的近似解集成整个系统的 近似解。
有限元方法在建筑力学中的应用
结构分析
利用有限元方法可以对建筑结构进行静力、动力、稳定性等分析 ,预测结构的承载能力和安全性。
刚体平衡
刚体的定义
刚体是指在力的作用下,其形状和大小均不发生变化的物体。
刚体的平衡条件
对于刚体,如果它在某个方向上受到的力矩为零,那么这个刚体就处于平衡状 态。即∑M=0。
03
材料力学
应力与应变
应力
材料在单位面积上所承受的力,表示为σ,公式为σ=F/A,其中F为作用在材料上 的力,A为受力面积。
相对运动与绝对运动
介绍相对运动与绝对运动的区别和联系,以及在动力学中的重要应 用。
动能与势能
01
02
03
动能
描述物体由于运动而具有 的能量,与物体的质量和 速度平方成正比。
势能
描述物体由于位置而具有 的能量,如重力势能、弹 性势能等。
动能与势能的转换
介绍动能与势能之间的相 互转换,以及在动力学中 的重要应用。
建筑力学通用课件(完 整版)
xx年xx月xx日
• 引言 • 静力学基础 • 材料力学 • 结构力学 • 动力学基础 • 弹性力学 • 有限元方法
目录
01
引言
建筑力学的重要性
确保结构安全
优化设计方案
建筑力学是确保建筑物安全的重要基 础,通过合理的设计和计算,可以避 免结构失效和倒塌。
建筑力学可以帮助设计师更好地理解 结构的性能和限制,从而优化设计方 案,提高建筑的功能性和经济性。
《建筑力学》PPT课件(最全版)

§2–1 力的概念
1、平衡——平衡是物体机械运动的特殊形式,是 指物体相对地球处于静止或匀速直线运动 状态。
2、刚体——在外界的任何作用下形状和大小都始 终保持不变的物体。或者在力的作用下, 任意两点间的距离保持不变的物体。
刚体是一种理想化的力学模型。
一个物体能否视为刚体,不仅取决于变 形的大小,而且和问题本身的要求有关。
F
=
= B
F1
F F2
B
F1
A
A
A
§2–2 静力学公理
公理三 (力平行四边形公理)
作用于物体上任一点的两个力可合成为作用
于同一点的一个力,即合力。合力的矢由原两
力的矢为邻边而作出的力平行四边形的对角矢
来表示。
R
即,合力为原两力的矢量和。
矢量表达式:R= F1+F2
A
F1
§2–2 静力学公理
推论 (三力汇交定理)
力是物质间的一种相互作用,机械运动状态的变化是由这种相互作 用引起的。静止和运动状态不变,都意味着各作用力在某种意义上的平 衡。力学,可以说是力和(机械)运动的科学。
第二章
静力学基本概念
§2–1 力的概念 §2–2 静力学公理 §2–3 力矩与力偶 §2–4 力在坐标轴上的投影 §2–5 力的平移定理
§2-3 力矩与力偶
五、力矩的性质: 1、力沿作用线移动时,对某点的矩不变 2、力作用过矩心时,此力对矩心之矩等于零 3、力矩的值与矩心位置有关,同一力对不同 的矩心,其力矩不同。
§2-3 力矩与力偶
4、力矩的解析表达式
y B
A
y
Ox
x
力对某点的矩等于该力沿坐标轴的分力对 同一点之矩的代数和
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
W Tp 1.510π6D1N 3 mm51MPa
16
D13161π.5 5110M 6P N amm53.1mm
2、在两轴长度相等、材料相同的情况下, 两轴重量之比等于两轴横截面面积之比,即:
A空 A实
π(D2 d2) 4
π4D12
902 852 53.12
0.31
讨论:由此题结果表明,在其它条件相同的情况 下,空心轴的重量只是实心轴重量的31%,其节 省材料是非常明显的。
例题7.1 图示传动轴,转速 n300r min,A轮为
主动轮,输入功率 NA10 kW,B、C、D为从动 轮,输出功率分别为
NB4.5 kW, NC3.5 kW
ND2.0 kW,试求各段扭矩。
解:1、计算外力偶矩
M e A 9 5 4 9 N n A 9 5 4 9 3 0 1 0 0rk W m in 3 1 8 .3N m
制成,外径 D90 mm ,壁厚 2.5 mm ,
工作时的最大扭矩 T1.5Nm,
若材料的许用切应力 60 MPa,
试校核该轴的强度。
解:1、计算抗扭截面系数 主传动轴的内外径之比
d9022.50.944
D 90
抗扭截面系数为
W p 1 D 6 3 ( 1 4 ) 1 ( 6 9 0 ) 3 ( 1 0 .9 4 4 4 )m m 3 2 9 5 1 0 2 m m 3
7.5 等直圆轴扭转时的变形及刚度条件
7.5.1 圆轴扭转时的变形
轴的扭转变形用两横截面的相对扭转角:
d T dx GIp
d T dx GIp
当扭矩为常数,且 G
I
也为常量时,
p
相距长度为l的两横截面相对扭转角为
d T dx Tl
l
l GIp
GIp
rad
式中 G I p 称为圆轴扭转刚度, 它表示轴抵抗扭转变形的能力。
WP
IP D432D3
D/2
D 2
16
空心圆极惯性矩轴:
IP AA 2 d A 2d 2 D 23 d 3 2 (D 4 d 4 )3 D 2 4( 1 4 )
式中 d 为空心圆轴内外径之比。
D
空心圆的抗扭截面系数 WPDIP /21D 63(14)
极惯性矩的量纲是长度的四次方, 常用的单位为mm4 抗扭截面系数的量纲是长度的三次方, 常用单位为mm3
T Ip
得到圆轴扭转横截面上 任意点切应力公式
当 R 时,表示圆截面边缘处的切应力最大
max
T Ip
T Wp
R
式中 W p 称为抗扭截面系数。
它是与截面形状和尺寸有关的量。
7.3.2 极惯性矩和抗扭截面系数
实心圆截面的极惯性矩:
IPA
A 2d A2
D 2 0
3d
D 4 3 2
抗扭截面系数为:
2、分段计算扭矩,分别为
T 1M eB143.2N m (图c) T2M eBM eA 143.2N m -318.3N m -175N m(图d) T 3 M eD 6 3 .7N m (图e)
T 2 ,T 3 为负值说明实际方向与假设的相反。
3、作扭矩图 T 175Nm
max
7.3 等直圆轴扭转时横截面上的切应力
对一般传动轴
0.5 (o) m ~1.0(o) m
对于精密机器的轴
0.15 (o) m ~0.30(o) m
7.3.1 实心圆轴横截面上的应力 1、变形几何关系
⑴ 变形后,圆轴上所有的横截面均保持为平面, 即平面假设;
⑵ 横截面上的半径仍保持为直线; ⑶ 各横截面的间距保持不变。
d
dx
2、物理关系
G
G
Gd
dx
3、静力学关系
A dA T
Gd 2dAT dx A
A2dA Ip 称截面的极惯性矩
d T dx GIp
相对扭转角的正负号由扭矩的正负号确定, 即正扭矩产生正扭转角,负扭矩产生负扭转角。 若两横截面之间T有变化,或极惯性矩变化,亦 或材料不同(切变模量G变化),则应通过积分 或分段计算出各段的扭转角,然后代数相加,即:
n
Tili
i1 G i I pi
对于受扭转圆轴的刚度通常用相对扭转角沿杆
长度的变化率用 表示,称为单位长度扭转角。
建筑力学课件8
7.2 圆轴扭转时横截面上的内力及扭矩图 7.2.1 扭矩 平衡条件
M x 0
T Me
内力偶矩T称为扭矩
扭矩的单位:
N m 或 kNm
扭矩的正负号规定为:自截面的外法线向截面看, 逆时针转向为正,顺时针转向为负
扭矩图
常用与轴线平行的x坐标表示横截面的位置,以与 之垂直的坐标表示相应横截面的扭矩,把计算结果 按比例绘在图上,正值扭矩画在x轴上方, 负值扭矩画在x轴下方。这种图形称为扭矩图。
7.4 等直圆轴扭转时的强度计算
7.4.1 圆轴扭转强度条件 工程上要求圆轴扭转时的最大切应力不得超过
材料的许用切应力 ,即
max
上式称为圆轴扭转强度条件。
T Wp
max
试验表明,材料扭转许用切应力
塑性材料 0.5~0.6
脆性材料 0.8~1.0
例题7.2 汽车的主传动轴,由45号钢的无缝钢管
即:
d T
dx GIp
7.5.2 圆轴扭转刚度条件
对于建筑工程、精密机械,刚度的刚度条件:
max
在工程中 的单位习惯用(度/米)表示, ,
将上式中的弧度换算为度,得:
max
G TIp
max
180
π
对于等截面圆轴,即为:max
Tmax GIp
180
π
许用扭转角的数值,根据轴的使用精密度、 生产要求和工作条件等因素确定。
2、计算轴的最大切应力
m axW Tp12 .5 9 51 0 16 02 N m m m m 3 50.8M Pa
3、强度校核
m ax50.8M P a
主传动轴安全
例题7.3 如把上题中的汽车主传动轴改为实心 轴,要求它与原来的空心轴强度相同,试确定实 心轴的直径,并比较空心轴和实心轴的重量。
解:1、求实心轴的直径,要求强度相同,即实心 轴的最大切应力也为51 M Pa ,即
M e B 9 5 4 9 N n B 9 5 4 9 3 0 4 0 .5 rk m W in 1 4 3 .2N m
M e C 9 5 4 9 N n C 9 5 4 9 3 0 3 0 .5rk m W in 1 1 1 .4N m M e D 9 5 4 9 N n D 9 5 4 9 3 0 2 0 .0 rk m W in 6 3 .7N m
16
D13161π.5 5110M 6P N amm53.1mm
2、在两轴长度相等、材料相同的情况下, 两轴重量之比等于两轴横截面面积之比,即:
A空 A实
π(D2 d2) 4
π4D12
902 852 53.12
0.31
讨论:由此题结果表明,在其它条件相同的情况 下,空心轴的重量只是实心轴重量的31%,其节 省材料是非常明显的。
例题7.1 图示传动轴,转速 n300r min,A轮为
主动轮,输入功率 NA10 kW,B、C、D为从动 轮,输出功率分别为
NB4.5 kW, NC3.5 kW
ND2.0 kW,试求各段扭矩。
解:1、计算外力偶矩
M e A 9 5 4 9 N n A 9 5 4 9 3 0 1 0 0rk W m in 3 1 8 .3N m
制成,外径 D90 mm ,壁厚 2.5 mm ,
工作时的最大扭矩 T1.5Nm,
若材料的许用切应力 60 MPa,
试校核该轴的强度。
解:1、计算抗扭截面系数 主传动轴的内外径之比
d9022.50.944
D 90
抗扭截面系数为
W p 1 D 6 3 ( 1 4 ) 1 ( 6 9 0 ) 3 ( 1 0 .9 4 4 4 )m m 3 2 9 5 1 0 2 m m 3
7.5 等直圆轴扭转时的变形及刚度条件
7.5.1 圆轴扭转时的变形
轴的扭转变形用两横截面的相对扭转角:
d T dx GIp
d T dx GIp
当扭矩为常数,且 G
I
也为常量时,
p
相距长度为l的两横截面相对扭转角为
d T dx Tl
l
l GIp
GIp
rad
式中 G I p 称为圆轴扭转刚度, 它表示轴抵抗扭转变形的能力。
WP
IP D432D3
D/2
D 2
16
空心圆极惯性矩轴:
IP AA 2 d A 2d 2 D 23 d 3 2 (D 4 d 4 )3 D 2 4( 1 4 )
式中 d 为空心圆轴内外径之比。
D
空心圆的抗扭截面系数 WPDIP /21D 63(14)
极惯性矩的量纲是长度的四次方, 常用的单位为mm4 抗扭截面系数的量纲是长度的三次方, 常用单位为mm3
T Ip
得到圆轴扭转横截面上 任意点切应力公式
当 R 时,表示圆截面边缘处的切应力最大
max
T Ip
T Wp
R
式中 W p 称为抗扭截面系数。
它是与截面形状和尺寸有关的量。
7.3.2 极惯性矩和抗扭截面系数
实心圆截面的极惯性矩:
IPA
A 2d A2
D 2 0
3d
D 4 3 2
抗扭截面系数为:
2、分段计算扭矩,分别为
T 1M eB143.2N m (图c) T2M eBM eA 143.2N m -318.3N m -175N m(图d) T 3 M eD 6 3 .7N m (图e)
T 2 ,T 3 为负值说明实际方向与假设的相反。
3、作扭矩图 T 175Nm
max
7.3 等直圆轴扭转时横截面上的切应力
对一般传动轴
0.5 (o) m ~1.0(o) m
对于精密机器的轴
0.15 (o) m ~0.30(o) m
7.3.1 实心圆轴横截面上的应力 1、变形几何关系
⑴ 变形后,圆轴上所有的横截面均保持为平面, 即平面假设;
⑵ 横截面上的半径仍保持为直线; ⑶ 各横截面的间距保持不变。
d
dx
2、物理关系
G
G
Gd
dx
3、静力学关系
A dA T
Gd 2dAT dx A
A2dA Ip 称截面的极惯性矩
d T dx GIp
相对扭转角的正负号由扭矩的正负号确定, 即正扭矩产生正扭转角,负扭矩产生负扭转角。 若两横截面之间T有变化,或极惯性矩变化,亦 或材料不同(切变模量G变化),则应通过积分 或分段计算出各段的扭转角,然后代数相加,即:
n
Tili
i1 G i I pi
对于受扭转圆轴的刚度通常用相对扭转角沿杆
长度的变化率用 表示,称为单位长度扭转角。
建筑力学课件8
7.2 圆轴扭转时横截面上的内力及扭矩图 7.2.1 扭矩 平衡条件
M x 0
T Me
内力偶矩T称为扭矩
扭矩的单位:
N m 或 kNm
扭矩的正负号规定为:自截面的外法线向截面看, 逆时针转向为正,顺时针转向为负
扭矩图
常用与轴线平行的x坐标表示横截面的位置,以与 之垂直的坐标表示相应横截面的扭矩,把计算结果 按比例绘在图上,正值扭矩画在x轴上方, 负值扭矩画在x轴下方。这种图形称为扭矩图。
7.4 等直圆轴扭转时的强度计算
7.4.1 圆轴扭转强度条件 工程上要求圆轴扭转时的最大切应力不得超过
材料的许用切应力 ,即
max
上式称为圆轴扭转强度条件。
T Wp
max
试验表明,材料扭转许用切应力
塑性材料 0.5~0.6
脆性材料 0.8~1.0
例题7.2 汽车的主传动轴,由45号钢的无缝钢管
即:
d T
dx GIp
7.5.2 圆轴扭转刚度条件
对于建筑工程、精密机械,刚度的刚度条件:
max
在工程中 的单位习惯用(度/米)表示, ,
将上式中的弧度换算为度,得:
max
G TIp
max
180
π
对于等截面圆轴,即为:max
Tmax GIp
180
π
许用扭转角的数值,根据轴的使用精密度、 生产要求和工作条件等因素确定。
2、计算轴的最大切应力
m axW Tp12 .5 9 51 0 16 02 N m m m m 3 50.8M Pa
3、强度校核
m ax50.8M P a
主传动轴安全
例题7.3 如把上题中的汽车主传动轴改为实心 轴,要求它与原来的空心轴强度相同,试确定实 心轴的直径,并比较空心轴和实心轴的重量。
解:1、求实心轴的直径,要求强度相同,即实心 轴的最大切应力也为51 M Pa ,即
M e B 9 5 4 9 N n B 9 5 4 9 3 0 4 0 .5 rk m W in 1 4 3 .2N m
M e C 9 5 4 9 N n C 9 5 4 9 3 0 3 0 .5rk m W in 1 1 1 .4N m M e D 9 5 4 9 N n D 9 5 4 9 3 0 2 0 .0 rk m W in 6 3 .7N m
