焦点三角形面积公式
焦点三角形面积公式

椭圆焦点三角形面积公式的应用2 2 22(a -C ) 2b 1 COST 1 COST由任意三角形的面积公式得:2 eS,F 1PF 2 = b tan 2典题妙解△ F i PF 2的面积.y1 中,a =10,b =8,c =6,而 J - 60 .记 | PR几,| PF 2 |二 r 2.64点P 在椭圆上,-由椭圆的第一定义得:r 1 r 2 =2a=20.例1 若P 是椭圆100F 2是其焦点,且—FfF ? =60,求2S..R PF 2- 2 r 1r 2 Sin 71 - b1 COSTe e2sin COS — 2 2 二 b 2 2COS 2-2e tan —.2 同理可证,在椭圆 22y- —1(ba >b >0) 中,公式仍然成立.解法一:在椭圆100 即 4a 2 -2r 1r 2(1 COST ) = 4c 2.22定理 在椭圆 写•爲二1 ( a > b > 0)中,焦点分别为F 1、F 2,点P 是椭圆上任,, 2 2 2在厶F |PF2中,由余弦定理得:r ir 2 -2r i r 2cos v - (2c ).配方,得:(n 亠 r 2 )2 —3「订2 =144.256 .400 一3叩2 =144.从而 吋2二已3.Sr 1PF^b 2tan64tanBO 、6^2 3| PF i | | PF 2 |A. 3 37 ,贝y cos 二二 PF1 PF2.| PF 1 | ■〔 PF 2 |29 S.^PF ? - b tan 2 故选答案A.= 9tan30' -3.3.点 P 到 x 轴的距离为 h ,则 S.F I PF 2 二 b 2tan 寸=9tan45 =9 ,又 S FPF2解法一复杂繁冗,运算量大,解法二简捷明了, 两个解法的优劣立现!例2 已知P22是椭圆—1上25 9的点,F 1、 F 2分别是椭圆的左、右焦点,若PF 1 PF 2 则厶F 1PF 2的面积为(2 2 例3( 04湖北)已知椭圆 —•厶=1的左、右焦点分别是 16 9 F i、F 2 ,点P 在椭圆上.若P 、F 1、F 2是一个直角三角形的三个顶点,则点 P 到x 轴的距离为( 9 A.—59・7B.7C. 解:若已或F 2是直角顶点,则点P 到x 轴的距离为半通径的长 b 2若P 是直角顶点,设1S.F |PF 2 二 2「1r 2 Sin 7164.3x 2解法二:在椭圆 一1002計中,b 2=64,而—aB. 2 3解:设-F 1PF 2(2c) h = 7h,2一 9 7 .、.7h =9 , h.故答案选D.7金指点睛2 2y x1. 椭圆1上一点P 与椭圆两个焦点 F i 、F 2的连线互相垂直,则厶F 1PF 2的面积为()49 24A. 20B. 22C. 28D. 24X 22— 一2. 椭圆y = 1的左右焦点为F i 、F 2, P 是椭圆上一点,当厶F i PF 2的面积为1时,PF i 卩F 24的值为( )A. 0B. 1C. 3D. 623. 椭圆y 2 =1的左右焦点为F i 、F 2,P 是椭圆上一点,当厶F 1PF 2的面积最大时,PF i 卩F 24的值为( )A. 0B. 2C. 4D. - 2X 2 24•已知椭圆 — y -1 ( a > 1)的两个焦点为 F i 、F 2, P 为椭圆上一点,且• F i PF 2=60 ,a则| PF i | |PF 2啲值为()1 B.-3F i 、F 2为焦点,点P 在椭圆上,直线PF i 与PF 2倾斜角的差为90 , △ F 1PF 2的面积是20,离心率为PF 1 PF o16.已知椭圆的中心在原点,F 1、F 2为左右焦点,P 为椭圆上一点,且 --,△ F 1PF 2— |PF i |-|PF 2|2—4 3的面积是.3,准线方程为x,求椭圆的标准方程.3答案1.解: F 1PF 2 - v -90 ,b 2=24 ,故答案选D./a2日 日 日 皿 r --—'5.已知椭圆的中心在原点,对称轴为坐标轴,二 b tan 24tan45 = 24.22解:设•F i PF—, srw 厂tan厂1,- T45—90,卩—.故答案选A.3.解:a = 2, b = 1, c = .. 3,设/ F 1 PF 2-), S 行PF 2 = b 2 tan 三=tan ?,.当厶F 1PF 2的面积最大时,二为最大,这时点P 为椭圆短轴的端点,二=120,2.PF PF 2 =|PF 1 | |PF 2|cosv -a cos120 - -2.故答案选D.4.解:匕F 1PF 2 - )-60 , b = 1, S F 1PF 2 = b 2tantan30 = —3,2313Q PF 1| |PF 2|s 『盲1 PF 」|PF 2|,3 3才旳丹21盲'从而E |PF 2 故答案选C.5.解:设 F 1PF 2「,贝- 90 . - S * =b 2 tanf 二 b 2 tan45‘ =b 2 =20 , — c Ja 2 -b 2 <5 乂 • e =a a320a 2 解得:a 2 =45.2222所求椭圆的标准方程为 —=1或— =1.45 20 45 206.解:设 F 1PF 2 二 , cos” PF1 PF2IPF 1I IPF 2I二 b 2tan60 二、3b 22日S F1PF「b tan 22 又;— c c 2 b 2 c 21L 14J3二c 亠c 3当C 二.3时, a = b 2 c 22=2,这时椭圆的标准方程为 — y^ 1;4乂' S.F 1PF 2= 120 .当c 3时,a「b2y2二空,这时椭圆的标准方程为牢・y2=1;3 3 43 但是,此时点P为椭圆短轴的端点时,二为最大,r - 60,不合题意.2故所求的椭圆的标准方程为—y2 = 1.4211上的一点,F1、64。
椭圆的焦点三角形面积公式

椭圆的焦点三角形面积公式
1、椭圆的焦点三角形面积公式:
椭圆的焦点三角形面积公式,指的是针对椭圆的一种特殊形状的三角形,是其面积计算公式。
具体计算公式为:S=1/2ab*sqrt(1-e2),其中a、b、e分别表示椭圆长轴、短轴以及离心率,即椭圆椭圆小周长与大周
长之比,由此可以得出动态椭圆的焦点三角形面积。
2、离心率的计算方法:
离心率是指椭圆小周长与大周长之比,计算方法也很简单,通过将椭
圆的两个焦点到长轴上的距离除以长轴的长度,即可得到离心率的值。
这里要注意的是,离心率的值不能大于1,否则椭圆的小周长就大于大周长,椭圆就变成了另一种不同的形状了。
3、椭圆的焦点三角形面积计算实例:
具体计算实例,假设我们有一个椭圆,长轴长度为a=30,短轴长度为
b=20,离心率为e=0.6,则该椭圆的焦点三角形的面积计算公式为:
S=1/2ab*sqrt(1-e2),其中的a、b、e分别表示椭圆的长轴、短轴以及离
心率,则本例中的面积计算结果为S=216,即椭圆的焦点三角形的面
积为216。
有关圆锥曲线的焦点三角形面积公式的证明及其应用

圆锥曲线的焦点三角形面积问题比较常见,这类题目常以选择题、填空题、解答题的形式出现.圆锥曲线主要包括抛物线、椭圆、双曲线,每一种曲线的焦点三角形面积公式也有所不同,其适用情形和应用方法均不相同.在本文中,笔者对圆锥曲线的焦点三角形面积公式及其应用技巧进行了归纳总结,希望对读者有所帮助.1.椭圆的焦点三角形面积公式:S ΔPF 1F 2=b 2tan θ2若椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0),∠F 1PF 2=θ,则三角形ΔF 1PF 2的面积为:S ΔPF 1F 2=b 2tan θ2.对该公式进行证明的过程如下:如图1,由椭圆的定义知||F 1F 2=2c ,||PF 1+||PF 2=2a ,图1可得||PF 12+2||PF 1||PF 2+||PF 22=4a 2,①由余弦定理可得||PF 12+||PF 22-2||PF 1||PF 2cos θ=4c 2,②①-②可得:2||PF 1||PF 2(1+cos θ)=4b 2,所以||PF 1||PF 2=2b 21+cos θ,则S ΔPF 1F2=12|PF 1||PF 2|sin θ=12×2b 21+cos θsin θ,=b 22sin θ2cos 2θ22cos 2θ2=b 2tan θ2.若已知椭圆的标准方程、短轴长、两焦点弦的夹角,则可运用椭圆的焦点三角形面积公式S ΔPF 1F 2=b 2tan θ2来求椭圆的焦点三角形面积.例1.(2021年数学高考全国甲卷理科)已知F 1,F 2是椭圆C :x 216+y 24=1的两个焦点,P ,Q 为椭圆C 上关于坐标原点对称的两点,且||PQ =||F 1F 2,则四边形PF 1QF 2的面积为________.解析:若采用常规方法解答本题,需根据椭圆的对称性、定义以及矩形的性质来建立关于||PF 1、||PF 2的方程,通过解方程求得四边形PF 1QF 2的面积.而仔细分析题意可发现四边形PF 1QF 2是一个矩形,且该矩形由两个焦点三角形构成,可利用椭圆的焦点三角形面积公式求解.解:S 四边形PF 1QF 2=2S ΔPF 1F 2=b 2tan θ2=2×4×tan π2=8.利用椭圆的焦点三角形面积公式,能有效地简化解题的过程,有助于我们快速求得问题的答案.例2.已知F 1,F 2是椭圆C:x 2a 2+y 2b2=1()a >b >0的两个焦点,P 为曲线C 上一点,O 为平面直角坐标系的原点.若PF 1⊥PF 2,且ΔF 1PF 2的面积等于16,求b的值.解:由PF 1⊥PF 2可得∠F 1PF 2=π2,因为ΔF 1PF 2的面积等于16,所以S ΔPF 1F 2=b 2tan θ2=b 2tan π2=16,解得b =4.有关圆锥曲线的焦点三角形面积公式的思路探寻48的面积,2.则ΔF 1PF 如|||PF 1-|得:|||PF 2cos θ即|由②所以则S Δ夹角、例3.双曲线C 是().A.72且)设双曲F 1,F 2,离△PF 1F 2=1.本题.运用该=p 22sin θ,且与抛S ΔAOB =图3下转76页)思路探寻49考点剖析abroad.解析:本句用了“S+Vt+动名词”结构,能用于此结构的及物动词或词组有mind ,enjoy ,finish ,advise ,consider ,practice ,admit ,imagine ,permit ,insist on ,get down to ,look forward to ,put off ,give up 等。
椭圆中焦点三角形的面积公式

椭圆中焦点三角形的面积公式椭圆中的焦点三角形,是由椭圆的两个焦点和椭圆上的任意一点构成的三角形。
我们可以通过椭圆的长轴、短轴和焦距来推导出该三角形的面积公式。
首先,我们需要知道椭圆的两个焦点的坐标。
设椭圆的长轴为2a,短轴为2b,焦距为2c,椭圆的中心点为O,则左右焦点的坐标分别为(-c,0)和(c,0)。
接下来,设椭圆上任意一点的坐标为(x,y),则该点到两个焦点的距离分别为:d1 = √((x+c)² + y²) 和d2 = √((x-c)² + y²)。
由于椭圆上的点满足椭圆方程,即(x²/a²) + (y²/b²) = 1,我们可以将其转化为:y = b√(1 - x²/a²)。
将上述两个方程代入三角形面积公式S = (1/2)×b×h,其中h为三角形的高,我们有:S = (1/2)×b×(2y) = b²√(1 - (x²/a²)) (①)根据椭圆的性质,我们可以发现椭圆的长轴与短轴满足a² = b² + c²,因此,将上述公式中的b代入为√(a² - c²)后,我们有:S = a²√(1 - (x²/a²)) - c²√(1 - (x²/a²)) = a²√(1 -(x²/a²))(1 - (c²/a²)) (②)上述公式(②) 即为椭圆中焦点三角形的面积公式。
注意到其中的(1 - (c²/a²))是一个小于1的系数,因此面积公式中的主要因素是椭圆的长轴和短轴,也就是椭圆的大小。
当椭圆是一个圆形时,也就是长轴等于短轴,面积公式中的系数即为1。
抛物线的焦点三角形面积公式

抛物线的焦点三角形面积公式抛物线的焦点三角形面积公式是一个有趣的几何学概念,它可以用来计算抛物线上任意三点所组成的三角形的面积。
抛物线是一类曲线,当这类曲线经过一定变换后,它们的焦点就会凸显出来。
在抛物线上任意三点A,B,C所组成的三角形ABC的面积,可以用下面的抛物线的焦点三角形面积公式来计算:面积S=1/4[(AB²+AC²+BC²)-2(AB.AC+AB.BC+AC.BC)]其中,AB、AC、BC分别表示三角形ABC的三条边长度,AB.AC、AB.BC、AC.BC分别表示三边长之间的点乘积。
抛物线的焦点三角形面积公式可以帮助我们计算出抛物线上任意三点所构成的三角形的面积,而不需要求出抛物线的方程,这个公式比较简单,如果我们了解了它的原理,就可以很容易地计算出抛物线上任意三点所构成的三角形的面积。
抛物线的焦点三角形面积公式的原理是:如果抛物线上任意三点所构成的三角形的面积,其面积可以由抛物线的方程来求解,而抛物线的方程可以采用下面的标准形式:y=ax²+bx+c其中a,b,c是抛物线的方程中的常数。
假设抛物线上任意三点A(x1,y1)、B(x2,y2)、C(x3,y3),则把抛物线的方程代入,可以得到:y1=ax12+bx1+cy2=ax22+bx2+cy3=ax32+bx3+c这三式子可以组成一个三元二次方程组,可以求解出a,b,c的值,然后将a,b,c的值代入抛物线的面积公式,即可求出抛物线上任意三点所构成的三角形的面积。
因此,抛物线的焦点三角形面积公式的原理是:利用抛物线的方程求解出a,b,c的值,然后将a,b,c的值代入抛物线的面积公式,即可求出抛物线上任意三点所构成的三角形的面积。
总之,抛物线的焦点三角形面积公式是一个有趣的几何学概念,它可以用来计算抛物线上任意三点所组成的三角形的面积。
它的原理是:利用抛物线的方程求解出a,b,c 的值,然后将a,b,c的值代入抛物线的面积公式,即可求出抛物线上任意三点所构成的三角形的面积。
椭圆中三角形面积公式
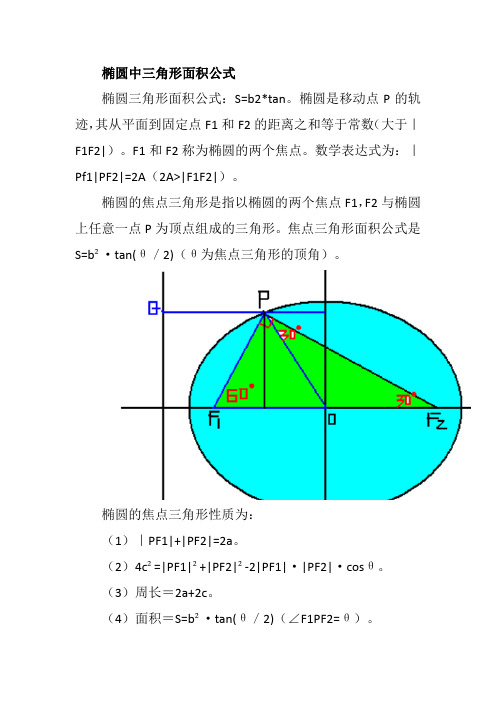
椭圆中三角形面积公式椭圆三角形面积公式:S=b2*tan。
椭圆是移动点P的轨迹,其从平面到固定点F1和F2的距离之和等于常数(大于|F1F2|)。
F1和F2称为椭圆的两个焦点。
数学表达式为:|Pf1|PF2|=2A(2A>|F1F2|)。
椭圆的焦点三角形是指以椭圆的两个焦点F1,F2与椭圆上任意一点P为顶点组成的三角形。
焦点三角形面积公式是S=b²·tan(θ/2)(θ为焦点三角形的顶角)。
椭圆的焦点三角形性质为:(1)|PF1|+|PF2|=2a。
(2)4c²=|PF1|²+|PF2|²-2|PF1|·|PF2|·cosθ。
(3)周长=2a+2c。
(4)面积=S=b²·tan(θ/2)(∠F1PF2=θ)。
椭圆三角形面积公式:S=b^2*tan(θ/2)。
1、离心率由正弦公式推导:F1P/sinα=F2P/sinβ=F1F2/sin θ,sinθ=sin(α+β),F1P+F2P=2a,F1F2=2c,e=c/a。
2、已知tan(θ/2)=sinα/(cosα+1)。
3、焦点三角形面积由余弦公式推导:∠F1PF2=θ,PF1=m,PF2=n。
4、则m+n=2a,在△F1PF2中,由余弦定理:(F1F2)^2=m^2+n^2-2mncosθ。
5、即4c^2=(m+n)^2-2mn-2mncosθ=4a^2-2mn(1+cosθ)。
6、所以mn=2b^2/(1+cosθ)。
7、S=(mnsinθ)/2=b^2*sinθ/(1+cosθ)=b^2*tan(θ/2)。
椭圆三角形表达椭圆是移动点P的轨迹,其从平面到固定点F1和F2的距离之和等于常数(大于|F1F2|)。
F1和F2称为椭圆的两个焦点。
数学表达式为:Pf1|PF2|=2A(2A>|F1F2|)。
焦点三角形面积公式是S=b²·tan(θ/2)(θ为焦点三角形的顶角)。
专题12 焦点三角形的面积公式(解析版)

A. 48 5
B. 36 5
C.16
D. 48 或 16 5
【答案】D
【详解】依题意, a 5,b 4, c 3 ,不妨设 F1 3, 0, F 3, 0 ,
对于直角三角形 MF1F2 ,
若 F1MF2
π 2
,
PF1 PF2 2a 10
由
PF1
2
PF2
2
4c
2
36
,整理得
PF1
PF2
7 7 3
3
2
33
【反思】焦点三角形问题,常规方法往往涉及到圆锥曲线的定义,利用定义,余弦定理求解,特别提醒,
在圆锥曲线中,定义是解题的重要工具.另外作为二级结论,SPF1F2
b2 tan
要特别注意记忆
F1PF2 表
2
示的是哪个角.另外利用结论 SPF1F2
b2 求解焦点三角形面积适用选择填空题,解答题需先证后用.
即为 PF1 2 PF2 2 PF1 PF2 4c2
联立可得 PF1 PF2 4c2 4a2 4b2
F1F2P 的面积为
3,
可得 1 2
PF1
PF2
sin 60 1 4b 2 2
3 2
3b2
3
解得
b
1,
a
1 2
,所以双曲线的实轴的长
2a
1.
故选:A
7.(2022
秋·湖南怀化·高二校考阶段练习)椭圆 x2 100
直线 AF 的斜率为( )
A.
1 3
B. 2 3
C.
1 2
D. 2 2
【答案】A
【详解】设双曲线右焦点为 F2 ,连接 AF2 , BF2 ,由图形的对称性知 AFBF2 为矩形,则有 | AF | AF2 2a ,
抛物线焦点三角形的面积公式

抛物线焦点三角形的面积公式
1、有一边在坐标轴上:S=1/2xa-xb×yc,有一边与坐标轴(x轴)平行:S=1/2xa-xb×yc-ya。
(得出结论)
2、抛物线是指平面内到一个定点F(焦点)和一条定直线l(准线)距离相等的点的轨迹。
它有许多表示方法,例如参数表示,标准方程表示等等。
它在几何光学和力学中有重要的用处。
抛物线也是圆锥曲线的一种,即圆锥面与平行于某条母线的平面相截而得的曲线。
(原因解释)
3、抛物线在合适的坐标变换下,也可看成二次函数图像。
(内容延伸)抛物线焦点三角形面积公式
P²/2Sina。
任意抛物线焦点F作抛物线的弦,与抛物线交于A、B两点,分别过A、B两点做抛物线的切线l1,l2相交于P点。
那么△PAB称作阿基米德三角形。
该三角形满足以下特性:
1、P点必在抛物线的准线上
2、△PAB为直角三角形,且角P为直角
3、PF⊥AB(即符合射影定理)
另外,对于任意圆锥曲线(椭圆,双曲线、抛物线)均有如下特性
抛物线焦点三角形面积公式
焦点三角形面积=b*b*tan(r/2)(其中b为短半轴长,r表示椭圆周角)设焦点为f1,f2,椭圆上任意点为a,设角f1af2为角r推导方式是设三角形另外一点是a,af1+af2=2aaf1向量-af2向量=f2f1向量。
两式都两边平方再整理得mn=2b^2/(1-cosa)(0度可以不考虑)面积就是1/2mnsina,把上面带入即得。
{注:m,n为af1和af2的长}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆焦点三角形面积公式的应用
定理 在椭圆122
22=+b
y a x (a >b >0)中,焦点分别为1F 、2F ,点P 是椭圆上任
意一点,θ=∠21PF F ,则2
tan
221θ
b S PF F =∆.
证明:记2211||,||r PF r PF ==,由椭圆的第一定义得
.4)(,2222121a r r a r r =+∴=+
在△21PF F 中,由余弦定理得:.)2(cos 22
212
22
1c r r r r =-+θ
配方得:.4cos 22)(2
2121221c r r r r r r =--+θ 即.4)cos 1(242
212
c r r a =+-θ
.cos 12cos 1)(22
2221θ
θ+=+-=∴b c a r r
由任意三角形的面积公式得:
2tan 2
cos 22cos
2
sin
2cos 1sin sin 2122
222121θθθ
θ
θ
θθ⋅=⋅=+⋅==
∆b b b r r S PF F .
.2
tan 221θ
b S PF F =∴∆
同理可证,在椭圆122
22=+b
x a y (a >b >0)中,公式仍然成立.
典题妙解
例1 若P 是椭圆
164
10022=+y x 上的一点,1F 、2F 是其焦点,且︒=∠6021PF F ,求 △21PF F 的面积.
解法一:在椭圆
1641002
2=+y x 中,,6,8,10===c b a 而.60︒=θ记.||,||2211r PF r PF == 点P 在椭圆上,
∴由椭圆的第一定义得:.20221==+a r r
在△21PF F 中,由余弦定理得:.)2(cos 22
212
221c r r r r =-+θ
配方,得:.1443)(212
21=-+r r r r
.144340021=-∴r r 从而.3
256
21=
r r .3
36423325621sin 212121=⨯⨯==
∆θr r S PF F 解法二:在椭圆
1641002
2=+y x 中,642=b ,而.60︒=θ .3
3
6430tan 642
tan
221=
︒==∴∆θ
b S PF F 解法一复杂繁冗,运算量大,解法二简捷明了,两个解法的优劣立现!
例 2 已知P 是椭圆
19252
2=+y x 上的点,1F 、2F 分别是椭圆的左、右焦点,若2
1
|
|||2121=
⋅PF PF PF PF ,则△21PF F 的面积为( ) A. 33 B. 32 C.
3 D.
3
3 解:设θ=∠21PF F ,则2
1
|
|||cos 2121=
⋅=
PF PF PF PF θ,.60︒=∴θ .3330tan 92
tan
221=︒==∴∆θ
b S PF F
故选答案A.
例3(04湖北)已知椭圆19
162
2=+y x 的左、右焦点分别是1F 、2F ,点P 在椭圆上. 若P 、1F 、2F 是一个直角三角形的三个顶点,则点P 到x 轴的距离为( )
A.
59 B. 779 C. 49 D. 4
9或77
9
解:若1F 或2F 是直角顶点,则点P 到x 轴的距离为半通径的长4
9
2=a b ;若P 是直角顶点,设点P 到x 轴的距离为h ,则945tan 92
tan
221=︒==∆θ
b S PF F ,又,7)2(2
1
21h h c S PF F =⋅⋅=
∆
97=∴h ,.7
7
9=
h 故答案选D. 金指点睛
1. 椭圆124
492
2=+x y 上一点P 与椭圆两个焦点1F 、2F 的连线互相垂直,则△21PF F 的面积为( ) A. 20 B. 22 C. 28 D. 24
2. 椭圆14
22
=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积为1时,21PF PF ⋅的值为( )
A. 0
B. 1
C. 3
D. 6
3. 椭圆14
22
=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积最大时,21PF PF ⋅的值为( )
A. 0
B. 2
C. 4
D. 2-
4.已知椭圆12
22=+y a
x (a >1)的两个焦点为1F 、2F ,P 为椭圆上一点,且︒=∠6021PF F ,
则||||21PF PF ⋅的值为( ) A .1
B .
3
1 C .
3
4 D .
3
2 5. 已知椭圆的中心在原点,对称轴为坐标轴,1F 、2F 为焦点,点P 在椭圆上,直线1PF 与2PF 倾斜角的差为︒90,△21PF F 的面积是20,离心率为
3
5
,求椭圆的标准方程. 6.已知椭圆的中心在原点,1F 、2F 为左右焦点,P 为椭圆上一点,21
|
|||212
1-=⋅PF PF ,△21PF F 的面积是3,准线方程为3
3
4±=x ,求椭圆的标准方程.
答案
1. 解:24,90221=︒==∠b PF F θ,∴2445tan 242
tan
221=︒==∆θ
b S PF F .
故答案选D.
2. 解:设θ=∠21PF F ,
12
tan
2
tan 221===∆θ
θ
b S PF F ,
∴︒=︒=90,452
θθ
,021=⋅PF PF .
故答案选A.
3. 解:3,1,2===c b a ,设θ=∠21PF F , 2
tan
2
tan
221θ
θ
==∆b S PF F ,
∴当△21PF F 的面积最大时,θ为最大,这时点P 为椭圆短轴的端点,︒=120θ,
∴2120cos cos ||||2
2121-=︒=⋅=⋅a PF PF PF PF θ.
故答案选D.
4. 解:︒==∠6021θPF F ,1=b ,3
3
30tan 2
tan
221=
︒==∆θ
b S PF F , 又 ||||4
3sin ||||21212121PF PF PF PF S PF F ⋅=⋅=
∆θ, ∴
33||||4321=⋅PF PF ,从而3
4
||||21=⋅PF PF . 故答案选C.
5. 解:设θ=∠21PF F ,则︒=90θ. 2045tan 2
tan
22221==︒==∆b b b S PF F θ
,
又 3
5
22=-=
=a b a a
c e , ∴95122=-a b ,即95
2012=-a
.
解得:452=a .
∴所求椭圆的标准方程为
1204522=+y x 或120
452
2=+x y . 6.解:设θ=∠21PF F ,∴︒=-=⋅=
120,21
|
|||cos 212
1θθPF PF PF PF .
3360tan 2
tan
22221==︒==∆b b b S PF F θ
,∴1=b .
又 33
42=c a ,即33333411222+==+=+=+c c c c c b c . ∴3=c 或3
3=
c . 当3=c 时,22
2
=+=c b a ,这时椭圆的标准方程为1422
=+y x ; 当3
3=c 时,3322
2=+=c b a ,这时椭圆的标准方程为13
422=+y x ;
但是,此时点P 为椭圆短轴的端点时,θ为最大,︒=60θ,不合题意.
故所求的椭圆的标准方程为14
22
=+y x .。
