次根式,勾股定理,平行四边形综合练习题
平行四边形与勾股定理结合-【微专题】2022-2023学年八年级数学下册常考点微专题提分精练
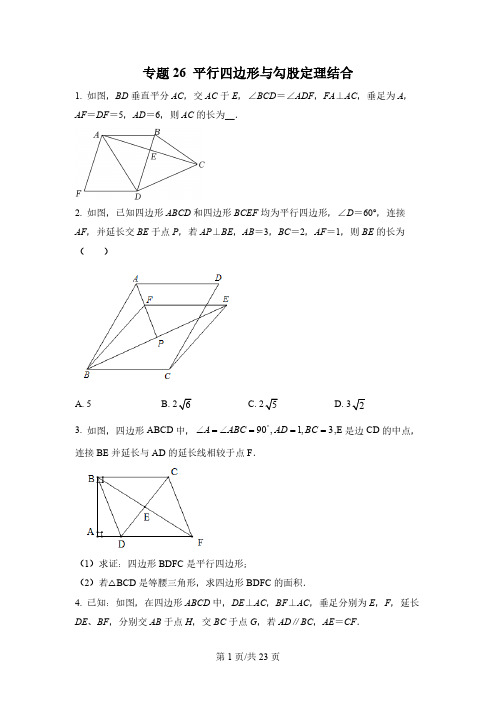
专题26 平行四边形与勾股定理结合1. 如图，BD 垂直平分AC ，交AC 于E ，∠BCD ＝∠ADF ，FA ⊥AC ，垂足为A ，AF ＝DF ＝5，AD ＝6，则AC 的长为__．2. 如图，已知四边形ABCD 和四边形BCEF 均为平行四边形，∠D ＝60°，连接AF ，并延长交BE 于点P ，若AP ⊥BE ，AB ＝3，BC ＝2，AF ＝1，则BE 的长为（ ）A. 53. 如图，四边形ABCD 中，90,1,3A ABC AD BC ︒∠=∠===,E 是边CD 的中点，连接BE 并延长与AD 的延长线相较于点F ．（1）求证：四边形BDFC 是平行四边形；（2）若△BCD 是等腰三角形，求四边形BDFC 的面积．4. 已知：如图，在四边形ABCD 中，DE ⊥AC ，BF ⊥AC ，垂足分别为E ，F ，延长DE 、BF ，分别交AB 于点H ，交BC 于点G ，若AD ∥BC ，AE ＝CF ．（1）求证：四边形ABCD 为平行四边形；（2）若∠DAH ＝∠GBA ，GF ＝2，CF ＝4，求AD 的长．5. 已知：如图所示，在平行四边形ABCD 中DE 、BF 分别是∠ADC 和∠ABC 的角平分线，交AB 、CD 于点E 、F（1）求证：四边形DEBF 是平行四边形；（2）若∠A ＝60°，AE ＝2EB ，AD ＝4，求平行四边形ABCD 的面积．6. 如图，四边形ABCD 中，AC ，BD 相交于点O ，点O 是AC 的中点，//AD BC ．（1）求证：四边形ABCD 是平行四边形；（2）若4AD BD ==，且90ADB ∠=︒，求AC 的长．7. 如图，四边形ABCD 中，BE ⊥AC 交AD 于点G ，DF ⊥AC 于点F ，已知AF =CE ，AB =CD ．（1）求证：四边形ABCD是平行四边形；（2）如果∠GBC=∠BCD，AG=6，GE=2，求AB的长．8. 如图，等边△ABC的边长是4，点D，E分别为AB，AC的中点，延长BC至BC，连接CD和EF．点F，使CF=12（1）求证：DE=CF；（2）求EF的长；（3）求四边形DEFC的面积．9. 如图，在 ABCD中，F是AD的中点，延长BC到点E，使CE=12BC，连结DE，CF．（1）求证：四边形CEDF是平行四边形；（2）若AB=4，AD=6，∠B=60°，求DE的长．10. 如图1，已知平行四边形ABCO，以点O为原点，OC所在的直线为x轴，建立直角坐标系，AB交y轴于点D，AD=2，OC=6，∠A=60°，线段EF所在的直线为OD 的垂直平分线，点P为线段EF上的动点，PM⊥x轴于点M点，点E与E′关于x轴对称，连接BP、E′M．（1）请直接写出点A的坐标为_____，点B的坐标为_____；（2）当BP +PM +ME′的长度最小时，请直接写出此时点P 的坐标为_____；（3）如图2，点N 为线段BC 上的动点且CM=CN ，连接MN ，是否存在点P ，使△PMN 为等腰三角形？若存在，请求出所有满足要求的EP 的值；若不存在，请说明理由．11. 如图，在四边形ABCD 中，//AD BC ，90B ∠=︒，16cm AD =，12cm AB =，20cm BC =，点Q 从点A 出发以2cm/s 的速度向点D 运动，点P 从点B 出发以4cm/s 的速度向点C 运动，P ， Q 两点同时出发，当点P 到达点C 时，两点同时停止运动．设运动时间为t s ．（1）当2t =时，四边形PCDQ 的面积为 ．（2）若以P ，Q ，C ，D 为顶点的四边形是平行四边形，求t 的值；（3）当05t <<时，若DQ DP ≠，则当t 为何值时，DPQ ∆是等腰三角形？12. 已知：直线y＝34x+6与x轴、y轴分别相交于点A和点B，点C在线段AO上．将△ABO沿BC折叠后，点O恰好落在AB边上点D处．（1）直接写出A、B两点的坐标：A：_____，B：______；（2）求出OC的长；（3）如图，点E、F是直线BC上的两点，若△AEF是以EF为斜边的等腰直角三角形，求点F的坐标；（4）取AB的中点M，若点P在y轴上，点Q在直线AB上，是否存在以C、M、P、Q为顶点的四边形为平行四边形？若存在，请求出所有满足条件的Q点坐标；若不存在，请说明理由．专题26 平行四边形与勾股定理结合【1题答案】【答案】9.6【解析】【分析】根据线段垂直平分线的性质得到DA =DC ，BA =BC ，根据等腰三角形的性质得到∠DAC =∠DCA ，∠BAC =∠BCA ，证明AB ∥DF ，进而得到四边形AFDB 为平行四边形，根据平行四边形的性质得到BD =AF =5，AB =DF =5，根据勾股定理列出方程，解方程得到答案．【详解】解：∵BD 垂直平分AC ，∴DA ＝DC ，BA ＝BC ，∴∠DAC ＝∠DCA ，∠BAC ＝∠BCA ，∴∠DAC ＋∠BAC ＝∠DCA ＋∠BCA ，即∠DAB ＝∠BCD ，∵∠BCD ＝∠ADF ，∴∠DAB ＝∠ADF ，∴AB ∥DF ，∵FA ⊥AC ，DB ⊥AC ，∴AF ∥BD ，∴四边形AFDB 为平行四边形，∴BD ＝AF ＝5，AB ＝DF ＝5，设BE ＝x ，则DE ＝5－x ，在Rt △AEB 中，222AB BE AE -=，在Rt △AED 中，222AD DE AE -=，∴2222AB BE AD DE -=-，即()2222565x x -=--，解得：x ＝75，∴AE 245=，∴AC ＝2AE ＝9.6，故AC 的长为9.6，故答案为：9.6．【点睛】本题考查的是平行四边形的判定和性质、线段垂直平分线的性质，掌握垂直平分线上的点到线段两端点的距离相等是解题的关键．【2题答案】【答案】D【解析】【分析】过点D 作DH ⊥BC ，交BC 的延长线于点H ，连接BD ，DE ，先证∠DHC =90º，再证四边形ADEF 是平行四边形，最后利用勾股定理得出结果．【详解】过点D 作DH ⊥BC ，交BC 的延长线于点H ，连接BD ，DE ，∵四边形ABCD 是平行四边形，AB =3，∠ADC =60º，∴CD =AB =3，∠DCH =∠ABC =∠ADC =60º，∵DH ⊥BC ，∴∠DHC =90º，∴∠ADC +∠CDH =90°，∴∠CDH =30°，在Rt △DCH 中，CH =12CD =32，DH ，∴222223(2)192BD BH DH =+=++=，∵四边形BCEF 是平行四边形，∴AD =BC =EF ，AD ∥EF ，∴四边形ADEF 是平行四边形，∴AF ∥DE ，AF =DE =1，∵AF ⊥BE ，∴DE ⊥BE ，∴22219118BE BD DE =-=-=，∴BE =故选D ．【点睛】本题考查了平行四边形的判定与性质，勾股定理，解题的关键是熟练运用这些性质解决问题．【3题答案】【答案】（1）见解析；（2）或【解析】【分析】（1）根据平行线的性质和中点的性质证明三角形全等，然后根据对角线互相平分的四边形是平行四边形完成证明；（2）由等腰三角形的性质，分三种情况：①BD=BC,②BD=CD,③BC=CD,分别求四边形的面积．【详解】解：（1）证明：∵∠A=∠ABC=90°，∴AF∥BC．∴∠CBE=∠DFE,∠BCE=∠FDE．∵E是边CD的中点，∴CE=DE．∴△BCE≌△FDE（AAS）．∴BE=EF．∴四边形BDFC是平行四边形．（2）若△BCD是等腰三角形，①若BD=BC=3 ．在Rt△ABD中，==．∴四边形BDFC的面积为S=；②若BC=DC=3，过点C 作CG ⊥AF 于G ，则四边形AGCB 是矩形，所以，AG=BC=3，所以，DG=AG-AD=3-1=2，在Rt △CDG 中，由勾股定理得， CG ===，∴四边形BDFC 的面积为S=．③BD=CD 时，BC 边上的中线应该与BC 垂直，从而得到BC=2AD=2，矛盾，此时不成立；综上所述，四边形BDFC 的面积是或．【点睛】本题考查了平行四边形的判定与性质，等腰三角形的性质，全等三角形的判定与性质，（1）确定出全等三角形是解题的关键，（2）难点在于分情况讨论．【4题答案】【答案】（1）见解析（2）5【解析】【分析】（1）根据AD ∥BC ，可得DAE BCF ∠=∠，根据，DE ⊥AC ，BF ⊥AC ，可得∠AED =∠CFB =90°，结合AE ＝CF 即可证明DAE BCF ≌△△，根据全等三角形的性质可得AD BC =，即可得证；（2）勾股定理可得CG =证明四边形DGBH 是平行四边形，可得DG HB =，继而可得AH CG =，勾股定理求得2EH =，在Rt ADE △中勾股定理即可求解．【小问1详解】证明：∵DE ⊥AC ，BF ⊥AC ，∴∠AED =∠CFB =90°，DE BF∥∵AD ∥BC ，∴∠DAE =∠BCF ，在Rt △△DAE 和△BCF 中，90DEA BFC AE CFDAE BCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，∴△DAE ≌△BCF （ASA ），∴AD =CB ，∵AD ∥BC ，∴四边形ABCD 为平行四边形；【小问2详解】DE ⊥AC ，BF ⊥AC ，∴ DH BG ∥，GBA DHA ∴∠=∠，∠DAH ＝∠GBA ，DAH DHA ∴∠=∠，AD DH =∴，在Rt GCF △中，2,4GF CF ==，CG ∴==， 四边形ABCD 是平行四边形，DC AB ∴∥，AB CD =，DG HB ∴∥，DH GB ∥ ，∴四边形DHBG 是平行四边形，DG HB ∴=，AH CG ∴==Rt AEH △中，4,AE CF AH ===，2EH ∴=，在Rt ADE △中，222AD DE AE =+，()22224AD AD =-+，解得5AD =．【点睛】本题考查了平行四边形的判定与性质，勾股定理，掌握平行四边形的性质是解题的关键．【5题答案】【答案】（1）见解析；（2）【解析】【分析】（1）证明EF 、BD 互相平分，只要证四边形DEBF 是平行四边形；利用两组对边分别平行来证明；（2）根据等边三角形的判定定理得到ADE ∆是等边三角形，求得4DE AE ==，得到2BE GE ==，过D 点作DG AB ⊥于点G ，根据直角三角形的性质得到122AG AD ==，由勾股定理得到DG ===形的面积公式即可得到结论．【详解】（1）证明： 四边形ABCD 是平行四边形，ADC ABC ∴∠=∠．又DE ，BF 分别是ADC ∠，ABC ∠的平分线，ABF CDE ∴∠=∠．//AB CD ，CDE AED ∴∠=∠，ABF AED ∴∠=∠，//DE BF ∴，//DE BF ，//DF BE ，∴四边形DEBF 是平行四边形；（2）解：60A ∠=︒ ，AB //CD ，120ADC ∴∠=︒，∵DE 是∠ADC 的角平分线，60ADE CDE ∠=∠=︒∴，ADE ∴ 为等边三角形，AE AD ∴=，4AD = ，4DE AE ∴==，过D 点作DG AB ⊥于点G ，2AE EB = ，2EB ∴=，在Rt DGE 中60DEG ∠=︒ ，30GDE ∴∠=︒，114222GE DE ∴==⨯=，224BG GE BE ∴=+=+=，在Rt ADG 中，4=AD ，60A ∠=︒，122AG AD ∴==，DG ∴==∴平行四边形ABCD 的面积6AB DG =⋅=⨯=．【点睛】本题考查平行四边形的判定和性质、等边三角形的判定和性质，勾股定理，证得ADE ∆是等边三角形是解题的关键．【6题答案】【答案】（1）见解析；（2）【解析】【分析】（1）由已知条件易证△AOD ≌△COB ，由此可得OD =OB ，进而可证明四边形ABCD 是平行四边形；（2）根据平行四边形的性质得出AC =2OA ，利用勾股定理即可解决问题．【详解】（1）证明：∵O 是AC 的中点，∴OA OC =，∵//AD BC ，∴ADO CBO ∠=∠，在AOD △和COB △中，ADO CBO AOD COB OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴AOD △≌COB △，∴OD OB =，∵OA OC =，∴四边形ABCD 是平行四边形．（2）解：∵四边形ABCD 是平行四边形，∴122OB OD BD ===，2AC OA =，∵90ADB ∠=︒，∴OA ===∴2AC OA ==【点睛】本题考查平行四边形的判定和性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是证明四边形ABCD 是平行四边形，属于中考常考题型．【7题答案】【答案】（1）见解析 （2）9【解析】【分析】（1）先证明Rt △ABE ≌Rt △CDF ，得到AB ∥CD ，即可判定平行四边形；（2）证明AB=GB ，根据勾股定理构造方程，解方程即可求解．【详解】解：（1）∵AF=CE ，∴AF-EF=CE-EF ，∴AE=CF ，∵BE ⊥AC ，DF ⊥AC ，，∴∠AEB=∠CFD=90°，∵AB=CD ，∴Rt △ABE ≌Rt △CDF ，∴∠BAE=∠DCF ，∴AB ∥CD，∵AB=CD ，∴四边形ABCD 是平行四边形；（2）∵四边形ABCD 是平行四边形，∴AD ∥BC ，∠DAB=∠BCD ，∴∠AGB=∠GBC ，∵∠GBC =∠BCD ，∴∠AGB=∠BAG ，∴AB=GB ，设AB=GB=x ，则BE=x-2，∵BG ⊥AC ，∴2222AB BE AG GE -=-，∴()2222262x x --=- ，解得x=9，∴AB =9．【点睛】本题考查了平行四边的判定与性质，勾股定理，等腰三角形判定等知识，综合性较强，熟知相关定理并根据已知条件合理选择定理是解题关键．【8题答案】【答案】（1）见解析；（2）EF=（3）．【解析】【分析】（1）利用三角形中位线定理即可解决问题；（2）先求出CD ，再证明四边形DEFC 是平行四边形即可；（3）过点D 作DH ⊥BC 于H ，求出CF 、DH 即可解决问题．【详解】解：（1）在△ABC 中，∵D 、E 分别为AB 、AC 的中点，∴DE 为△ABC 的中位线，∴DE ＝12BC ，∵CF ＝12BC ，∴DE ＝CF ；（2）∵AC＝BC，AD＝BD，∴CD⊥AB，∵BC＝4，BD＝2，∴CD∵DE∥CF，DE＝CF，∴四边形DEFC是平行四边形，∴EF＝CD＝（3）过点D作DH⊥BC于H，∵∠DHC＝90°，∠DCB＝30°，DC，∴DH＝12∵DE＝CF＝2，∴S四边形DEFC＝CF•DH＝＝【点睛】本题考查等边三角形的性质、三角形中位线定理、勾股定理、平行四边形的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，记住平行四边形的面积公式，学会添加常用辅助线，属于中考常考题型．【9题答案】【答案】（1）见解析（2【解析】【分析】（1）由“平行四边形的对边平行且相等”的性质推知AD∥BC，且AD=BC；然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等（DF=CE，且DF∥CE），即四边形CEDF是平行四边形；（2）如图，过点D作DH⊥BE于点H，构造含30度角的直角△DCH和直角△DHE．通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度．【详解】（1）证明：在▱ABCD中，AD BC，且AD=BC∵F是AD的中点AD∴DF=12BC又∵CE=12∴DF=CE，且DF CE∴四边形CEDF是平行四边形；（2）如图，过点D作DH⊥BE于点H．在▱ABCD中，∵∠B=60°，∴∠DCE=60°．∵AB=4，∴CD=AB=4，CD=2，DH∴CH=12AD=3，则EH=1．在▱CEDF中，CE=DF=12∴在Rt△DHE中，根据勾股定理知DE=．视频【10题答案】【答案】（1）（﹣2，，（4，；（2）（2；（3）EP的值为3或6或5．【解析】【分析】（1）由30°直角三角形的性质求出OD的长，再由平行四边形的性质求出BD 的长即可解决问题；（2）首先证明四边形OPME′是平行四边形，可得OP=EM，因为PM是定值，推出PB+ME′=OP+PB的值最小时，BP+PM+ME′的长度最小；（3）分三种情形画出图形分别求解即可解决问题．【详解】解：（1）如图1中，在Rt△ADO中，∵∠A=60°，∴∠AOD=30°．∵AD=2，∴OD A（﹣2，2，∵四边形ABCO是平行四边形，∴AB=OC=6，∴DB=6﹣2=4，∴B（4，；（2）如图1中，连接OP．∵EF垂直平分线段OD，PM⊥OC，∴∠PEO=∠EOM=∠PMO=90°，∴四边形OMPE是矩形，∴PM=OE∵OE=OE′，∴PM=OE′，PM∥OE′，∴四边形OPME′是平行四边形，∴OP=EM，∵PM是定值，∴PB+ME′=OP+PB的值最小时，BP+PM+ME′的长度最小，∴当O、P、B共线时，BP+PM+ME′的长度最小．∵直线OB的解析式为y，∴P（2）．故答案为（2）．（3）如图2中，当PM=PN时，∵AOCB 是平行四边形，∴∠MCN =∠A =60°．∵MC =CN ，∴△MNC 是等边三角形，∴∠CMN =∠CNM =60°．∵PM ⊥OC ，∴∠PMN =∠PNM =30°，∴∠PNF =30°+60°=90°，∵∠PFN =∠BCO =60°，∴∠NPF =30°，NF =1，∴PF =2NF =2，∵EF =2BD OC =5，∴PE =5﹣2=3．如图3中，当PM =MN 时，∵PM =MN =CM ，∴EP =OM =6如图4中，当点P 与F 重合时，NP =NM ，此时PE =EF =5．综上所述：满足条件的EP 的值为3或65．【点睛】本题考查了四边形综合题、平行四边形的性质、等腰三角形的判定和性质、最短问题等知识，解题的关键是学会利用两点之间线段最短，解决最短问题，学会用分类讨论的首先思考问题，属于中考压轴题．【11题答案】【答案】（1）2144cm ；（2）2t =；（3）83t =或74t =【解析】【分析】（1）当2t =时，算出AQ 、PB 的值，进而求出DQ 、PC 的值，由平行四边形的判定得出四边形PCDQ 为平行四边形，进而求出平行四边形的面积；（2）P 未到达C 点时，要使四边形PCDQ 是平行四边形，由平行四边形的性质得出QD PC =，列出等式解答即可；（3）分PQ PD =，QD QP =两种情况讨论计算，求出时间即可得出答案．【详解】解：（1）∵边形ABCD 中，//AD BC ，90B ∠=︒，16cm AD =，12cm AB =，20cm BC =，点Q 从点A 出发以2cm/s 的速度向点D 运动，点P 从点B 出发以4cm/s 的速度向点C 运动，当2t =时，AQ ＝4cm ，PB ＝8cm ，∴DQ ＝16－2＝12cm ，PC ＝20－8＝12cm ，∴DQ ＝PC ，∴此时四边形PCDQ 为平行四边形，四边形PCDQ 的面积为：1212=⨯2144cm ，故答案为：2144cm ；（2）P 未到达C 点时，要使四边形PCDQ 是平行四边形，则QD PC =，162204t t -=-，解得2t =．∴ 四边形PCDQ 是平行四边形时，t 的值是2．（3）①如图，若PQ PD =，过点P 作PE AD ⊥于点E ，则162QD t =-，11(162)822QE QD t t ==-=-，2(8)8AE AQ QE t t t =+=+-=+，AE BP = ，84t t ∴+=，解得：83t =．②如图，若QD QP =，过Q 作QF BC ⊥于F ，则12QF =，422FP t t t =-=，在Rt QPF ∆中，222QF FP QP +=，()()22122162t t 2∴+=-，解得74t =．∴当83t =或74t =时，DPQ ∆是等腰三角形．【点睛】本题考查了平行四边形的性质和判定，等腰三角形的判定与性质，勾股定理的应用，作辅助线利用等腰三角形三线合一的性质以及勾股定理是解题的关键．【12题答案】【答案】（1）A （-8，0），B （0，6）；（2）3；（3）（-2，2）或E （-6，-6）；（4）21(1,)4-或27(1,)4或3(7,4-【解析】【分析】（1）在直线364y x =+中，分别令x =0，y =0，可得A ，B 坐标；（2）由翻折不变性可知，OC CD =，6OB BD ==，90ODB BOC ∠=∠=︒，在Rt ADC ∆中，90ADC ∠=︒，利用222AD CD AC +=，即可求解；（3）证明()FMA ANE AAS ∆≅∆，则NE AM =，MF AN =，即可求解；（4）分MC 是边、MC 是对角线两种情况，分别求解即可．【详解】解：（1）对于直线364y x =+，令0x =，得到6y =，(0,6)B ∴，令0y =，得到8x =-，,0()8A ∴-．(8,0)A - ．(0,6)B ；（2）由（1）可得：(8,0)A -．(0,6)B ，8OA ∴=，6OB =，90AOB ∠=︒ ，10AB ∴==，由翻折不变性可知，OC CD =，6OB BD ==，90ODB BOC ∠=∠=︒，4AD AB BD ∴=-=，设CD OC x ==，在Rt ADC ∆中，90ADC ∠=︒，222AD CD AC ∴+=，2224(8)x x ∴+=-，解得3x =，3OC ∴=；（3）由点B 、C 的坐标得，直线BC 的表达式为：26y x =+，设点(,26)F m m +、(,26)E n n +，过点A 作y 轴的平行线交过点F 与x 轴的平行线于点M ，交过点E 与x 轴的平行线于点N ，AEF ∆ 为等腰直角三角形，故AE AF =，90NAE MAF ∠+∠=︒ ，90MAF MFA ∠+∠=︒，NAE MFA ∴∠=∠，90FMA ANE ∠=∠=︒ ，AE AF =，()FMA ANE AAS ∴∆≅∆，NE AM ∴=，MF AN =，即268m n --=+，268n m +=+，解得：2m =-，6n =-，故点F 的坐标为(2,2)-、点(6,6)E --；由于E 、F 的位置可能互换，故点E 的坐标为(2,2)-、点(6,6)F --；综上，点F 的坐标为(2,2)-或(6,6)E --；（4）点M 是AB 的中点，则点(4,3)M -，而点(8,0)A -，设点(0,)P n ，点3(,6)4Q m m +，①当MC 是边时，点M 向右平移1个单位向下平移3个单位得到点C ，同样点()P Q 右平移1个单位向下平移3个单位得到点()Q P ，故01m +=且3364n m -=+或01m -=且3364n m +=+，解得：1m =或1-，故点Q 的坐标为21(1,)4Q -或27(1,)4；②当MC 是对角线时，由中点公式得：43m --=且3364n m =++，解得：7m =-，故点Q 的坐标为3(7,)4-；综上，点Q 的坐标为：21(1,4-或27(1,)4或3(7,)4-．【点睛】本题考查的是一次函数综合运用，涉及到一次函数的性质、平行四边形的性质、三角形全等等，其中（4），解题的关键是要注意分类求解，避免遗漏．。
计算100题(勾股定理、二次根式、不等式)
1 _______; 2 _______; 3 _______; 4 _______; 5 _______; 6 _______; 7 _______; 8 _______; 9 _______; 10 ______; 11 _______; 12 _______; 13 _______; 14 _______; 15 _______; 16 _______; 17 _______; 18 _______; 19 _______; 20 _______; 21 _______; 22 _______; 23 _______; 24 _______; 25 _______; 26 _______; 27 _______; 28 _______; 29 _______; 30 _______; 31 _______; 32 _______; 33 _______; 34 _______; 35 _______; 36 _______; 37 _______; 38 _______; 39 _______; 40 _______; 41 _______; 42 _______; 43 _______; 44 _______; 45 _______; 46 _______; 47 _______; 48 _______; 49 _______; 50 _______; 51 _______; 52 _______; 53 _______; 54 _______; 55 _______; 56 _______; 57 _______; 58 _______; 59 _______; 60 _______; 61 _______; 62 _______; 63 _______; 64 _______; 65 _______; 66 _______; 67 _______; 68 _______; 69 _______; 70 _______; 71 _______; 72 _______; 73 _______; 74 _______; 75 _______; 76 _______; 77 _______; 78 _______; 79 _______; 80 _______; 81 _______; 82 _______; 83 _______; 84 _______; 85 _______; 86 _______; 87 _______; 88 _______; 89 _______; 90 _______; 91 _______; 92 _______; 93 _______; 94 _______; 95 _______; 96 _______; 97 _______; 98 _______; 99 _______; 100 _______;
中考数学 勾股定理综合练习(含答案)
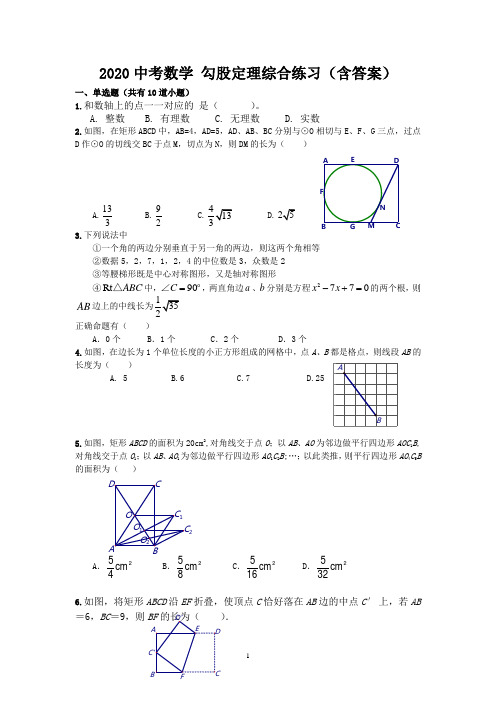
2020中考数学 勾股定理综合练习（含答案）一、单选题（共有10道小题）1.和数轴上的点一一对应的 是（）。
A. 整数B. 有理数C. 无理数D. 实数2.如图，在矩形ABCD 中，AB=4，AD=5，AD 、AB 、BC 分别与⊙O 相切与E 、F 、G 三点，过点D 作⊙O 的切线交BC 于点M ，切点为N ，则DM 的长为（ ）A.133B.92D.3.下列说法中①一个角的两边分别垂直于另一角的两边，则这两个角相等 ②数据5，2，7，1，2，4的中位数是3，众数是2 ③等腰梯形既是中心对称图形，又是轴对称图形④Rt ABC △中，90C =o ∠，两直角边a 、b 分别是方程2770x x -+=的两个根，则AB正确命题有（ ）A ．0个B ．1个C ．2个D ．3个4.如图，在边长为1个单位长度的小正方形组成的网格中，点A 、B 都是格点，则线段AB 的长度为（ ） A. 5 B.6 C.7 D.255.如图，矩形ABCD 的面积为20cm 2,对角线交于点O ；以AB 、AO 为邻边做平行四边形AOC 1B ,对角线交于点O 1；以AB 、AO 1为邻边做平行四边形AO 1C 2B ;…；以此类推，则平行四边形AO 4C 5B 的面积为（ ）A ．54cm 2B ．58cm 2C ．516cm 2 D ．532cm 26.如图，将矩形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，若AB＝6，BC ＝9，则）．FA CD E MN2A ．4B．C ．4.5D ．57.如图，两个连接在一起的菱形的边长都是1 cm ，一只电子甲虫从点A 开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行，当电子甲虫爬行2014cm 时停下，则它停的位置是( )A ．点FB ．点EC ．点AD ．点C8.如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC 中，边长为无理数的边数是（ ）A ．0B ．1C ．2D ．39.下列图形都是由边长为1厘米的小正方形连接组成的．按照图形的变化规律，第2009个图形的周长是（ ）厘米． A 、4018 B 、4020 C 、8036 D 、602710.如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE 。
中考数学平行四边形的综合题试题含答案解析
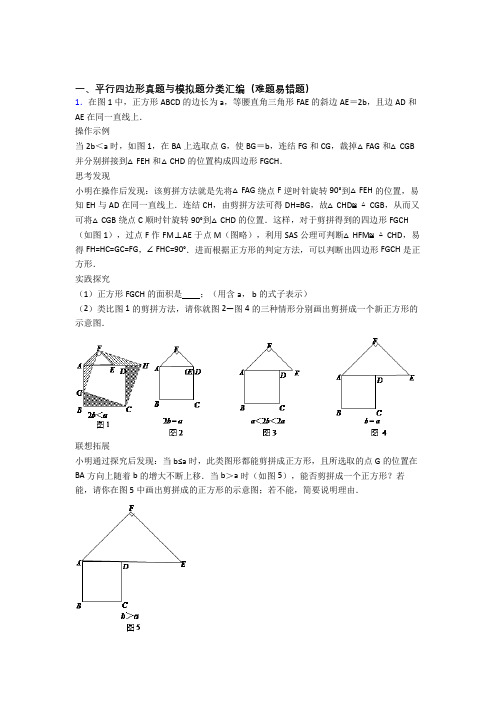
一、平行四边形真题与模拟题分类汇编（难题易错题）1．在图1中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE＝2b，且边AD和AE在同一直线上．操作示例当2b＜a时，如图1，在BA上选取点G，使BG＝b，连结FG和CG，裁掉△FAG和△CGB 并分别拼接到△FEH和△CHD的位置构成四边形FGCH．思考发现小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置，易知EH与AD在同一直线上．连结CH，由剪拼方法可得DH=BG，故△CHD≌△CGB，从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置．这样，对于剪拼得到的四边形FGCH （如图1），过点F作FM⊥AE于点M（图略），利用SAS公理可判断△HFM≌△CHD，易得FH=HC=GC=FG，∠FHC=90°．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．实践探究（1）正方形FGCH的面积是；（用含a， b的式子表示）（2）类比图1的剪拼方法，请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展小明通过探究后发现：当b≤a时，此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．当b＞a时（如图5），能否剪拼成一个正方形？若能，请你在图5中画出剪拼成的正方形的示意图；若不能，简要说明理由．【答案】（1）a2+b2；（2）见解析；联想拓展：能剪拼成正方形.见解析．【解析】分析：实践探究：根据正方形FGCH的面积=BG2+BC2进而得出答案；应采用类比的方法，注意无论等腰直角三角形的大小如何变化，BG永远等于等腰直角三角形斜边的一半．注意当b=a时，也可直接沿正方形的对角线分割．详解：实践探究：正方形的面积是：BG2+BC2=a2+b2；剪拼方法如图2-图4；联想拓展：能，剪拼方法如图5（图中BG=DH=b）．．点睛：本题考查了几何变换综合，培养学生的推理论证能力和动手操作能力；运用类比方法作图时，应根据范例抓住作图的关键：作的线段的长度与某条线段的比值永远相等，旋转的三角形，连接的点都应是相同的．2．如图，△ABC是等边三角形，AB=6cm，D为边AB中点．动点P、Q在边AB上同时从点D出发，点P沿D→A以1cm/s的速度向终点A运动．点Q沿D→B→D以2cm/s的速度运动，回到点D停止．以PQ为边在AB上方作等边三角形PQN．将△PQN绕QN的中点旋转180°得到△MNQ．设四边形PQMN与△ABC重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜3）．（1）当点N落在边BC上时，求t的值．（2）当点N到点A、B的距离相等时，求t的值．（3）当点Q沿D→B运动时，求S与t之间的函数表达式．（4）设四边形PQMN的边MN、MQ与边BC的交点分别是E、F，直接写出四边形PEMF 与四边形PQMN的面积比为2：3时t的值．【答案】（1）（2）2（3）S=S菱形PQMN=2S△PNQ=t2；（4）t=1或【解析】试题分析：（1）由题意知：当点N落在边BC上时，点Q与点B重合，此时DQ=3；（2）当点N到点A、B的距离相等时，点N在边AB的中线上，此时PD=DQ；（3）当0≤t≤时，四边形PQMN与△ABC重叠部分图形为四边形PQMN；当≤t≤时，四边形PQMN与△ABC重叠部分图形为五边形PQFEN．（4）MN、MQ与边BC的有交点时，此时＜t＜，列出四边形PEMF与四边形PQMN的面积表达式后，即可求出t的值．试题解析：（1）∵△PQN与△ABC都是等边三角形，∴当点N落在边BC上时，点Q与点B重合．∴DQ=3∴2t=3．∴t=；（2）∵当点N到点A、B的距离相等时，点N在边AB的中线上，∴PD=DQ，当0＜t＜时，此时，PD=t，DQ=2t∴t=2t∴t=0（不合题意，舍去），当≤t＜3时，此时，PD=t，DQ=6﹣2t∴t=6﹣2t，解得t=2；综上所述，当点N到点A、B的距离相等时，t=2；（3）由题意知：此时，PD=t，DQ=2t当点M在BC边上时，∴MN=BQ∵PQ=MN=3t，BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①，当0≤t≤时，S△PNQ=PQ2=t2；∴S=S菱形PQMN=2S△PNQ=t2，如图②，当≤t≤时，设MN、MQ与边BC的交点分别是E、F，∵MN=PQ=3t，NE=BQ=3﹣2t，∴ME=MN﹣NE=PQ﹣BQ=5t﹣3，∵△EMF是等边三角形，∴S△EMF=ME2=（5t﹣3）2．；（4）MN、MQ与边BC的交点分别是E、F，此时＜t＜，t=1或．考点：几何变换综合题3．图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点．（1）在图1中画出等腰直角三角形MON，使点N在格点上，且∠MON=90°；（2）在图2中以格点为顶点画一个正方形ABCD，使正方形ABCD面积等于（1）中等腰直角三角形MON面积的4倍，并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形，且正方形ABCD面积没有剩余（画出一种即可）．【答案】（1）作图参见解析；（2）作图参见解析.【解析】试题分析：（1）过点O向线段OM作垂线，此直线与格点的交点为N，连接MN即可；（2）根据勾股定理画出图形即可．试题解析：（1）过点O向线段OM作垂线，此直线与格点的交点为N，连接MN，如图1所示；（2）等腰直角三角形MON面积是5，因此正方形面积是20，如图2所示；于是根据勾股定理画出图3：考点：1.作图﹣应用与设计作图；2.勾股定理.4．（问题情境）在△ABC中，AB＝AC，点P为BC所在直线上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．当P在BC边上时（如图1），求证：PD+PE＝CF．证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．（不要证明）（变式探究）（1）当点P在CB延长线上时，其余条件不变（如图3），试探索PD、PE、CF之间的数量关系并说明理由；请运用上述解答中所积累的经验和方法完成下列两题：（结论运用）（2）如图4，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD ＝16，CF＝6，求PG+PH的值．（迁移拓展）（3）在直角坐标系中，直线l1：y＝-43x+8与直线l2：y＝﹣2x+8相交于点A，直线l1、l2与x轴分别交于点B、点C．点P是直线l2上一个动点，若点P到直线l1的距离为2．求点P的坐标．【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】（﹣1，6），（1，10）【解析】【变式探究】连接AP，同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得；【结论运用】过点E作EQ⊥BC，垂足为Q，根据勾股定理和矩形的性质解答即可；【迁移拓展】分两种情况，利用结论，求得点P到x轴的距离，再利用待定系数法可求出P的坐标．【详解】变式探究:连接AP，如图3：∵PD⊥AB，PE⊥AC，CF⊥AB，且S△ABC＝S△ACP﹣S△ABP，∴12AB•CF＝12AC•PE﹣12AB•PD．∵AB＝AC，∴CF＝PD﹣PE；结论运用:过点E作EQ⊥BC，垂足为Q，如图④，∵四边形ABCD是长方形，∴AD＝BC，∠C＝∠ADC＝90°．∵AD＝16，CF＝6，∴BF＝BC﹣CF＝AD﹣CF＝5，由折叠可得：DF＝BF，∠BEF＝∠DEF．∴DF＝5．∵∠C＝90°，∴DC2222106DF CF-=-8．∵EQ⊥BC，∠C＝∠ADC＝90°，∴∠EQC＝90°＝∠C＝∠ADC．∴四边形EQCD是长方形．∴EQ＝DC＝4．∵AD∥BC，∴∠DEF＝∠EFB．∵∠BEF＝∠DEF，∴∠BEF＝∠EFB．∴BE＝BF，由问题情境中的结论可得：PG+PH＝EQ．∴PG+PH＝8．∴PG+PH的值为8；迁移拓展:如图，由题意得：A（0，8），B（6，0），C（﹣4，0）∴AB2210，BC＝10．68∴AB＝BC，（1）由结论得：P1D1+P1E1＝OA＝8∵P1D1＝1＝2，∴P1E1＝6 即点P1的纵坐标为6又点P1在直线l2上，∴y＝2x+8＝6，∴x＝﹣1，即点P1的坐标为（﹣1，6）；（2）由结论得：P2E2﹣P2D2＝OA＝8∵P2D2＝2，∴P2E2＝10 即点P1的纵坐标为10又点P1在直线l2上，∴y＝2x+8＝10，∴x＝1，即点P1的坐标为（1，10）【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点，利用面积法列出等式是解决问题的关键．5．阅读下列材料：我们定义：若一个四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如正方形就是和谐四边形．结合阅读材料，完成下列问题：（1）下列哪个四边形一定是和谐四边形 ．A ．平行四边形B ．矩形C ．菱形D ．等腰梯形（2）命题：“和谐四边形一定是轴对称图形”是 命题（填“真”或“假”）． （3）如图，等腰Rt △ABD 中，∠BAD ＝90°．若点C 为平面上一点，AC 为凸四边形ABCD 的和谐线，且AB ＝BC ，请求出∠ABC 的度数．【答案】（1） C ；（2）∠ABC 的度数为60°或90°或150°.【解析】试题分析：（1）根据菱形的性质和和谐四边形定义，直接得出结论.（2）根据和谐四边形定义，分AD=CD ，AD=AC ，AC=DC 讨论即可.（1）根据和谐四边形定义，平行四边形，矩形，等腰梯形的对角线不能把四边形分成两个等腰三角形，菱形的一条对角线能把四边形分成两个等腰三角形够．故选C.（2）∵等腰Rt △ABD 中，∠BAD=90°，∴AB=AD.∵AC 为凸四边形ABCD 的和谐线，且AB=BC ，∴分三种情况讨论：若AD=CD ，如图1，则凸四边形ABCD 是正方形，∠ABC=90°；若AD=AC ，如图 2，则AB=AC=BC ，△ABC 是等边三角形，∠ABC=60°；若AC=DC ，如图 3，则可求∠ABC=150°.考点：1.新定义；2．菱形的性质；3．正方形的判定和性质；4．等边三角形的判定和性质；5.分类思想的应用.6．在ABC 中，AD BC ⊥于点D ，点E 为AC 边的中点，过点A 作//AF BC ，交DE 的延长线于点F ，连接CF ．()1如图1，求证：四边形ADCF 是矩形；()2如图2，当AB AC =时，取AB 的中点G ，连接DG 、EG ，在不添加任何辅助线和字母的条件下，请直接写出图中所有的平行四边形（不包括矩形ADCF ）．【答案】(1) 证明见解析；（2）四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形．【解析】【分析】（1）由△AEF ≌△CED ，推出EF=DE ，又AE=EC ，推出四边形ADCF 是平行四边形，只要证明∠ADC=90°，即可推出四边形ADCF 是矩形．（2）四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形．【详解】()1证明：∵//AF BC ，∴AFE EDC ∠=∠，∵E 是AC 中点，∴AE EC =，在AEF 和CED 中，AFE CDE AEF CED AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴AEF CED ≅，∴EF DE =，∵AE EC =，∴四边形ADCF 是平行四边形，∵AD BC ⊥， ∴90ADC ∠=，∴四边形ADCF 是矩形．()2∵线段DG 、线段GE 、线段DE 都是ABC 的中位线，又//AF BC ，∴//AB DE ，//DG AC ，//EG BC ， ∴四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形．【点睛】考查平行四边形的判定、矩形的判定、三角形的中位线定理、全等三角形的判定和性质等知识，正确寻找全等三角形解决问题是解题的关键.7．如图1，在正方形ABCD 中，AD=6，点P 是对角线BD 上任意一点，连接PA ，PC 过点P作PE⊥PC交直线AB于E．（1）求证：PC=PE;（2）延长AP交直线CD于点F.①如图2，若点F是CD的中点，求△APE的面积；②若ΔAPE的面积是21625，则DF的长为（3）如图3，点E在边AB上，连接EC交BD于点M,作点E关于BD的对称点Q，连接PQ，MQ，过点P作PN∥CD交EC于点N，连接QN，若PQ=5，MN=723，则△MNQ的面积是【答案】（1）略；（2）①8，②4或9；（3）5 6【解析】【分析】（1）利用正方形每个角都是90°，对角线平分对角的性质，三角形外角等于和它不相邻的两个内角的和，等角对等边等性质容易得证;（2）作出△ADP和△DFP的高，由面积法容易求出这个高的值.从而得到△PAE的底和高，并求出面积.第2小问思路一样，通过面积法列出方程求解即可;（3）根据已经条件证出△MNQ是直角三角形，计算直角边乘积的一半可得其面积.【详解】(1) 证明：∵点P在对角线BD上，∴△ADP≌△CDP,∴AP=CP, ∠DAP =∠DCP,∵PE⊥PC，∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP＝90°-∠DCP,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;（2）①如图2，过点P分别作PH⊥AD,PG⊥CD,垂足分别为H、G.延长GP交AB于点M.∵四边形ABCD 是正方形，P 在对角线上， ∴四边形HPGD 是正方形， ∴PH=PG,PM ⊥AB, 设PH=PG=a,∵F 是CD 中点，AD ＝6，则FD=3,ADFS =9,∵ADF S =ADP DFP SS+=1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4, 又∵PA=PE, ∴AM=EM,AE=4,∵APE S =1144822EA MP ⨯=⨯⨯=,②设HP ＝b,由①可得AE=2b,MP=6-b,∴APE S=()121626225b b ⨯⨯-=, 解得b=2.4 3.6或,∵ADF S=ADP DFP SS+=1122AD PH DF PG ⨯+⨯, ∴11166222b DF b DF ⨯⨯+⨯=⨯, ∴当b=2.4时，DF=4；当b ＝3.6时，DF ＝9, 即DF 的长为4或9; （3）如图，∵E 、Q 关于BP 对称，PN ∥CD, ∴∠1＝∠2，∠2+∠3＝∠BDC=45°, ∴∠1+∠4=45°, ∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC, ∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC, ∴∠6+∠7=90°, ∴△MNQ 是直角三角形, 设EM=a,NC=b 列方程组2227252372 3a b a b ⎧+=-⎪⎪⎨⎛⎫⎪+= ⎪ ⎪⎪⎝⎭⎩, 可得12ab=56, ∴MNQ56S=, 【点睛】本题是四边形综合题目，考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识；本题综合性强，有一定难度，熟练掌握正方形的性质，证明三角形全等是解决问题的关键.要注意运用数形结合思想.8．如图，在矩形ABCD 中，点E 在边CD 上，将该矩形沿AE 折叠，使点D 落在边BC 上的点F 处，过点F 作FG ∥CD ，交AE 于点G ，连接DG ．（1）求证：四边形DEFG 为菱形；（2）若CD=8，CF=4，求的值．【答案】（1）证明见试题解析；（2）．【解析】试题分析：（1）由折叠的性质，可以得到DG=FG，ED=EF，∠1=∠2，由FG∥CD，可得∠1=∠3，再证明 FG=FE，即可得到四边形DEFG为菱形；（2）在Rt△EFC中，用勾股定理列方程即可CD、CE，从而求出的值．试题解析：（1）由折叠的性质可知：DG=FG，ED=EF，∠1=∠2，∵FG∥CD，∴∠2=∠3，∴FG=FE，∴DG=GF=EF=DE，∴四边形DEFG为菱形；（2）设DE=x，根据折叠的性质，EF=DE=x，EC=8﹣x，在Rt△EFC中，，即，解得：x=5，CE=8﹣x=3，∴=．考点：1．翻折变换（折叠问题）；2．勾股定理；3．菱形的判定与性质；4．矩形的性质；5．综合题．9．（本题14分）小明在学习平行线相关知识时总结了如下结论：端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短．小明应用这个结论进行了下列探索活动和问题解决．问题1：如图1，在Rt△ABC中，∠C=90°，AC=4，BC=3，P为AC边上的一动点，以PB，PA为边构造□APBQ，求对角线PQ的最小值及PQ最小时的值．（1）在解决这个问题时，小明构造出了如图2的辅助线，则PQ的最小值为，当PQ最小时= _____ __；（2）小明对问题1做了简单的变式思考．如图3，P为AB边上的一动点，延长PA到点E，使AE=nPA（n为大于0的常数）．以PE，PC为边作□PCQE，试求对角线PQ长的最小值，并求PQ最小时的值；问题2：在四边形ABCD中，AD∥BC，AB⊥BC，AD＝1，AB＝2，BC＝3．（1）如图4，若为上任意一点，以，为边作□．试求对角线长的最小值和PQ最小时的值．（2）若为上任意一点，延长到，使，再以，为边作□．请直接写出对角线长的最小值和PQ最小时的值．【答案】问题1：（1）3，；（2）PQ=，=．问题2：（1）=4，．（2）PQ的最小值为．．【解析】试题分析：问题1：（1）首先根据条件可证四边形PCBQ是矩形，然后根据条件“四边形APBQ是平行四边形可得AP=QB=PC，从而可求的值．（2）由题可知：当QP⊥AC 时，PQ最小．过点C作CD⊥AB于点D．此时四边形CDPQ为矩形，PQ=CD，在Rt△ABC中，∠C=90°，AC=4，BC=3，利用面积可求出CD=,然后可求出AD=，由AE=nPA可得PE=，而PE=CQ=PD=AD-AP=，所以AP=．所以=．问题2：（1）设对角线与相交于点．Rt≌Rt．所以AD=HC，QH=AP．由题可知：当QP⊥AB时，PQ最小，此时=CH=4，根据条件可证四边形BPQH为矩形，从而QH=BP=AP．所以．（2）根据题意画出图形，当AB 时，的长最小，PQ的最小值为．．试题解析：问题1：（1）3，；（2）过点C作CD⊥AB于点D．由题意可知当PQ⊥AB时，PQ最短．所以此时四边形CDPQ为矩形．PQ=CD，DP=CQ=PE．因为∠BCA=90°，AC=4，BC=3，所以AB=5．所以CD=．所以PQ=．在Rt△ACD中AC=4，CD=，所以AD=．因为AE=nPA，所以PE==CQ=PD=AD-AP=．所以AP=．所以=．问题2：（1）如图2，设对角线与相交于点．所以G是DC的中点，作QH BC，交BC的延长线于H，因为AD//BC，所以．所以．又，所以Rt≌Rt．所以AD=HC，QH=AP．由图知，当AB时，的长最小，即=CH=4．易得四边形BPQH为矩形，所以QH=BP=AP．所以．（若学生有能力从梯形中位线角度考虑，若正确即可评分．但讲评时不作要求）（2）PQ的最小值为．．考点：1．直角三角形的性质；2．全等三角形的判定与性质；3．平行四边形的性质；4矩形的判定与性质．10．（本题满分10分）如图1，已知矩形纸片ABCD中，AB＝6cm，若将该纸片沿着过点B的直线折叠（折痕为BM），点A恰好落在CD边的中点P处．（1）求矩形ABCD的边AD的长．（2）若P为CD边上的一个动点，折叠纸片，使得A与P重合，折痕为MN，其中M在边AD上，N在边BC上，如图2所示．设DP＝x cm，DM＝y cm，试求y与x的函数关系式，并指出自变量x的取值范围．（3）①当折痕MN的端点N在AB上时，求当△PCN为等腰三角形时x的值；②当折痕MN的端点M在CD上时，设折叠后重叠部分的面积为S，试求S与x之间的函数关系式【答案】（1）AD＝3；（2）y=－其中，0＜x＜3；（3）x=；（4）S=.【解析】试题分析：（1）根据折叠图形的性质和勾股定理求出AD的长度；（2）根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式；（3）过点N作NQ⊥CD，根据Rt△NPQ 的勾股定理进行求解；（4）根据Rt△ADM的勾股定理求出MP与x的函数关系式，然后得出函数关系式.试题解析：（1）根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得：AD＝3．（2）由折叠可知AM＝MP，在Rt△MPD中，∴∴y=－其中，0＜x＜3.（3）当点N在AB上，x≥3，∴PC≤3，而PN≥3，NC≥3.∴△PCN为等腰三角形，只可能NC＝NP．过N点作NQ⊥CD，垂足为Q，在Rt△NPQ中，∴解得x=．（4）当点M在CD上时，N在AB上，可得四边形ANPM为菱形．设MP＝y，在Rt△ADM中，，即∴ y=．∴ S=考点：函数的性质、勾股定理.。
勾股定理和平行四边形好题汇总
1.完成下面题目图1 图2 图3 图4 图5 图6（2）如图2、3、4，已知，三角形ABC中，CA=CB，∠ACB=90°，D为三角形ABC外一点，且满足∠ADB=90°①如图2所示，求证：DA+DB=ξ2DC。
②如图3所示，猜想DA，DB，DC之间有怎样的数量关系，并证明你的结论。
③如图4所示，过C作CH⊥BD于H，BD=6，AD=3，求CH。
（3）如图5，点D是等边三角形△ABC外一点，若DA=13，DB=5ξ2，DC=7，试求∠BDC的度数。
（4）如图6，△ABC为等边三角形，若D为△ABC外一点，满足∠CDB=30°，求证DC2+DB2=DA2。
2.如图，在Rt△ABC中，∠B=90°，BC=5ξ3，∠C=30°，点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF.当t为何值时，△DEF为直角三角形？请说明理由3.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB, CD于E、F,连接PB､PD.若AE = 2,PF= 8.则图中阴影部分的面积是什么？4.在矩形ABCD中,点E在BC上,AE = AD,DF⊥AE,垂足为F.①求证:DF = AB;②若∠FDC = 30°,且AB = 4,求AD.5.如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD､△BCE､△ACF,请回答下列问题,并说明理由.①四边形ADEF是什么四边形?②当△ABC满足什么条件时,四边形ADEF是矩形?③当△ABC满足什么条件时,以A､D､E､F为顶点的四边形不存在6.已知，在等腰Rt△OAB中，∠OAB=90°，OA=AB，点A和B在第四象限（1）如图1，若A（1.-3），则OA=__________，点B的坐标为（______，______）（2）如图2，AD⊥y轴于点D，M为OB中点，求证：DO+DA=ξ2DM6.如图，∠AOB=40°，M和N分别在OA，OB上，且OM=2，ON=4，点P和点Q分别在OB和OA上，求MP+PQ+QN的最小值。
2018-2019学年初中数学二次根式、勾股定理、平行四边形一次函数和数据的分析中考模拟考试测试题
②该手机店购进A型、B型手机各多少部，才能使销售总利润最大？
（3）实际进货时，厂家对B型手机出厂价下调m（30＜m＜100）元，且限定商店最多购进B型手机80台．若商店保持两种手机的售价不变，请你根据以上信息及（2）中的条件，设计出使这110部手机销售总利润最大的进货方案．
24．某初中在“读书共享月”活动中．学生都从家中带了图书到学校给大家共享阅读．经过抽样调查得知，初一人均带了2册；初二人均带了3.5册：初三人均带了2.5册．已知各年级学生人数的扇形统计图如图所示，其中初三共有210名学生．请根据以上信息解答下列问题：
（1）扇形统计图中，初三年级学生数所对应的圆心角为°；
28．如图，在▱ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B，F为圆心，大于 BF的长为半径画弧，两弧交于一点P，连接AP并延长交BC于点E，连接EF．
（1）根据条件与作图信息知四边形ABEF是
A．非特殊的平行四边形
B．矩形
C．菱形
D．正方形
（2）设AE与BF相交于点O，四边形ABEF的周长为16，BF=4，求AE的长和∠C的度数．
22．随着”互联网+“时代的到来，利用网络呼叫专车的打车方式深受大众欢迎．据了解，在非高峰期时，某种专车所收取的费用y（元）与行驶里程x（km）的函数图象如图所示．请根据图象，回答下列问题：
（1）当x≥5时，求y与x之间的函数关系式；
（2）若王女士有一次在非高峰期乘坐这种专车外出，共付费47元，求王女士乘坐这种专车的行驶里程．
【详解】
∵EF∥BC，GH∥AB，
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形，
∴S△PEB=S△BGP，
平行四边形综合练习附答案
平行四边形综合练习学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列判断错误的是（）A．两组对边分别相等的四边形是平行四边形B．四个内角都相等的四边形是矩形C．四条边都相等的四边形是菱形D．两条对角线垂直且平分的四边形是正方形【答案】D【解析】【分析】分别利用平行四边形、矩形、菱形和正方形的判定定理，对选项逐一分析即可做出判断．【详解】解：A、两组对边分别相等的四边形是平行四边形，符合平行四边形的判定，故本选项正确，不符合题意；B、∵四边形的内角和为360°，四边形的四个内角都相等，∴四边形的每个内角都等于90°，则这个四边形有三个角是90°，∴这个四边形是矩形，故四个内角都相等的四边形是矩形，本选项正确，不符合题意；C、四条边都相等的四边形是菱形，符合菱形的判定，故本选项正确，不符合题意；D、两条对角线垂直且平分的四边形是菱形，不一定是正方形，故本选项错误，符合题意；故选：D．【点睛】本题考查了平行四边形、矩形、菱形和正方形的判定定理，解题的关键是正确理解并掌握判定定理．2．如图，平行四边形ABCD中，对角线AC，BD交于点O，点E是BC的中点．若OE ，则AB的长为（）6cm【答案】D【解析】【分析】根据平行四边形的性质，可得出点O 平分AC ，则OE 是三角形ABC 的中位线，则AB ＝2OE ，继而求出答案．【详解】解：∵四边形ABCD 为平行四边形，∴AO ＝CO ，∵点E 是CB 的中点，∴OE 为△ABC 的中位线，∴AB ＝2OE ，∵OE ＝6cm ，∴AB ＝12cm ．故选：D ．【点睛】本题考查了平行四边形的性质和三角形的中位线定理，关键是根据平行四边形的性质得出OE 为△ABC 的中位线．3．如图，点P 是矩形ABCD 的对角线上一点，过点P 作EF //BC ，分别交,AB CD 于,E F ，连接,PB PD ，若1,3AE PF ==，则图中阴影部分的面积为（ ）A ．3B ．6C ．9D ．12 【答案】A【解析】【分析】先根据矩形的性质证得DFP PBE SS =，然后求解即可．【详解】∴四边形AEPM 、四边形DFPM 、四边形CFPN 和四边形BEPN 都是矩形，∵ADC ABC S S =△△，AMP AEP S S =，PBE PBN S S =，PFD PDM S S =，PFC PCN S S =， ∴S 矩形DFPM =S 矩形BEPN ，∵PM =AE =1，PF =NC =3， ∴131322DFP PBE S S ==⨯⨯=△△， ∴S 阴=33+=322， 故选：A ．【点睛】本题主要考查矩形的性质、三角形的面积等知识，证得DFP PBE S S =是解答本题的关键． 4．在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的条件是（ ） A ．AC ＝BD ，AB ∥CD ，AB ＝CDB ．AD ∥BC ，∠A ＝∠C C ．AO ＝BO ＝CO ＝DO ，AC ⊥BDD ．AO ＝CO ，BO ＝DO ，AB ＝BC【答案】C【解析】【详解】试题分析：根据正方形的判定：对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案．解：A ，不能，只能判定为矩形；B ，不能，只能判定为平行四边形；C ，能；D ，不能，只能判定为菱形．故选C ．5．如图，ABC ∆中，DE BC ∥，EF AB ∥，要判定四边形DBFE 是菱形，还需要添加的条件是（ ）A ．BE 平分ABC ∠B ．AD BD =C ．BE AC ⊥D ．AB AC =【答案】A【解析】【分析】 当BE 平分∠ABC 时，四边形DBFE 是菱形，可知先证明四边形BDEF 是平行四边形，再证明BD=DE 即可解决问题．【详解】解：当BE 平分ABC ∠时，四边形DBFE 是菱形，理由：∵DE BC ∥，∴DEB EBC ∠=∠，∵EBC EBD ∠=∠，∴EBD DEB ∠=∠，∴BD DE =，∵DE BC ∥，EF AB ∥，∴四边形DBFE 是平行四边形，∵BD DE =，∴四边形DBFE 是菱形.其余选项均无法判断四边形DBFE 是菱形，故选A.【点睛】本题考查菱形的判定、平行四边形的判定和性质、角平分线的定义、等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型． 6．若一个菱形的边长为2，则这个菱形两条对角线长的平方和为( )A ．16B ．8C ．4D ．1【答案】A根据菱形的对角线互相垂直平分，即菱形被对角线平分成四个全等的直角三角形，根据勾股定理，即可求解．【详解】解：设两对角线长分别是：a ，b ． 则（12a ）2+（12b ）2=22，故有a 2+b 2=16．故选：A ．【点睛】本题主要考查了菱形的性质和勾股定理，菱形被两个对角线平分成四个全等的直角三角形，因为菱形的这个性质，使得菱形的题目一般都会和勾股定理结合起来，同学们要注意掌握．7．如图，把一张矩形纸片ABCD 按所示方法进行两次折叠，得到等腰直角三角形BEF ，若BC =1，则AB 的长度为（ ）A 2B 21+C 51+D ．43【答案】A【解析】 【分析】 先判断出∠ADE =45°，进而判断出AE =AD ，利用勾股定理即可得出结论．【详解】解：由折叠补全图形如图所示，∵四边形ABCD 是矩形，∴∠ADA '=∠B =∠C =∠A =90°，AD =BC =1，CD =AB ，由第一次折叠得：∠DAE =∠A =90°，∠ADE =12∠ADC =45°，∴∠AED =∠ADE =45°，∴AE =AD =1，在Rt △ADE 中，根据勾股定理得，DE 2AD 2，由第二次折叠可知，DC DE =【点睛】本题考查了图形的折叠和勾股定理，搞清楚折叠中线段的数量关系是解决此类题的关键．8．如图，矩形ABCD 的对角线相交于点O ，过点O 作OG AC ⊥，交AB 于点G ，连接CG ，若15BOG ∠=，则BCG ∠的度数是（ ）A ．15B ．15.5C ．20D ．37.5【答案】A【解析】【分析】 根据矩形的性质求出OCB ∠的度数，从而得到GAC ∠的度数，再根据垂直平分线的性质得到GCA GAC ∠=∠，最后求出BCG ∠的度数．【详解】解：∵OG AC ⊥，∴90COG ∠=︒，∵15BOG ∠=︒，∴901575COB COG BOG ∠=∠-∠=︒-︒=︒，∵四边形ABCD 是矩形，∴AC BD =，12OC OA AC ==，12OB OD BD ==，//AB DC ，90BCD ∠=︒， ∴OC OB =， ∴1801807552.522COB OCB OBC ︒-∠︒-︒∠=∠===︒， ∴37.5ACD BCD OCB ∠=∠-∠=︒，∵//AB CD ，∴37.5GAC ACD ∠=∠=︒，∴GO 是AC 的垂直平分线，∴AG CG =，∴37.5GCA GAC ∠=∠=︒，∴52.537.515BCG OCB GCA ∠=∠-∠=︒-︒=︒．故选：A ．【点睛】本题考查矩形的性质，垂直平分线的性质，解题的关键是熟练掌握这些性质定理，并结合题目条件进行证明．二、填空题9．正方形是有一组邻边_______，并且有一个角是_______的平行四边形，因此它既是______又是________．【答案】 相等 直角 矩形 菱形【解析】【分析】根据正方形的定义和性质填空即可．【详解】 正方形是有一组邻边相等，并且有一个角是直角的平行四边形，因此它既是矩形又是菱形．故答案为：相等，直角，矩形，菱形【点睛】本题考查了正方形的定义，解题关键是明确正方形的定义：正方形是有一组邻边相等，并且有一个角是直角的平行四边形，因此它既是矩形又是菱形．10．如图，在矩形ABCD 中，5AB =，4BC =，将矩形ABCD 翻折，使得点B 落在CD 边上的点E 处，折痕AF 交BC 于点F ，则FC =______【答案】32【分析】在Rt△ADE中，AD2+DE2=AE2，可得DE=3，CE=CD-DE=2，设FC=x，则EF=BC-FC=4-x，在Rt△ECF中，EF2=EC2+FC2，可得（4-x）2=22+x2，解方程即可．【详解】解∵△ABF≌△AEF，∴AE=AB=5，在矩形ABCD中，AD=BC=4，在Rt△ADE中，AD2+DE2=AE2，∴DE=3，CE=CD-DE=2，设FC=x，则EF=BC-FC=4-x，在Rt△ECF中，EF2=EC2+FC2，即（4-x）2=22+x2，8x=12，x=32，∴FC=32．故此答案为32．【点睛】本题考查翻折变换、矩形的性质、勾股定理等知识，解题的关键是学会利用参数构建方程解决问题．11．如图所示，在Rt△ABC中，∠C＝90°，AC＝4，将△ABC沿CB向右平移得到△DEF，若平移距离为2，则四边形ABED的面积等于_______．【答案】8【解析】【分析】形ABED 是平行四边形，最后根据平行四边形的面积公式即可得．【详解】由平移的性质得2AD BE ==，4DF AC ==，90C DFE ∠=∠=︒∴四边形ACFD 是矩形//AD CF ∴//AD BE ∴∴四边形ABED 是平行四边形（一组对边平行且相等的四边形是平行四边形） 则四边形ABED 的面积为428DF BE ⋅=⨯=故答案为：8．【点睛】本题考查了平移的性质、平行四边形的判定、矩形的判定与性质等知识点，掌握平移的性质是解题关键．12．如图，ACE ∆是以ABCD 的对角线AC 为边的等边三角形，点C 与点E 关于x 轴对称．若E 点的坐标是(7,33)-，则D 点的坐标是_____．【答案】（5，0）【解析】【分析】设CE 和x 轴交于H ，由对称性可知63CE =63AC CE ==根据勾股定理即可求出AH 的长，进而求出AO 和DH 的长，所以OD 可求，又因为D 在x 轴上，纵坐标为0，问题得解．【详解】解：点C 与点E 关于x 轴对称，E 点的坐标是(7,33)-， C ∴的坐标为(7，33)，33CH ∴=3CE =63AC ∴=，9AH ∴=，7OH =，2AO DH ∴==，5OD ∴=，D ∴点的坐标是(5,0)，故答案为：(5,0)．【点睛】本题考查了平行四边形的性质、等边三角形的性质、点关于x 轴对称的特点以及勾股定理的运用，解题的关键是综合应用以上知识点．13．如图，在矩形ABCD 中，6AB =，8AD =，P 是AD 上不与A 和D 重合的一个动点，过点P 分别作AC 和BD 的垂线，垂足为E ，F ，则PE PF +的值为______．【答案】245【解析】【分析】连接OP ，利用勾股定理列式求出BD ，再根据矩形的对角线相等且互相平分求出OA 、OD ，然后根据S △AOD =S △AOP +S △DOP 列方程求解即可．【详解】解：如图，连接OP ，∵AB=6，AD=8，∴2222.6810BD AB AD ++=，∵四边形ABCD 是矩形，∵S△AOD=S△AOP+S△DOP，∴12×12×6×8=12×5•PE+12×5•PF，解得PE+PF=245．故答案为：245．【点睛】本题考查了矩形的性质，三角形的面积，熟记性质并利用三角形的面积列出方程是解题的关键．14．如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为_____．【答案】（2，6）【解析】【分析】此题涉及的知识点是平面直角坐标系图像性质的综合应用．过点M作MF⊥CD于F，过C作CE⊥OA于E，在Rt△CMF中，根据勾股定理即可求得MF与EM，进而就可求得OE，CE的长，从而求得C的坐标．【详解】∵四边形OCDB是平行四边形,点B的坐标为(16,0)，CD∥OA，CD=OB=16，过点M作MF⊥CD于F,则182CF CD，==过C作CE⊥OA于E，∵A(20,0)，∴OA=20，OM=10，∴OE=OM−ME=OM−CF=10−8=2，连接MC,110,2MC OA==∴在Rt△CMF中，2222108 6.MF MC CF=-=-=∴点C的坐标为(2,6).故答案为(2,6).【点睛】此题重点考察学生对坐标与图形性质的实际应用，勾股定理，注意数形结合思想在解题的关键．三、解答题15．如图是某区部分街道示意图，其中AB AF⊥，E、D分别是FA和FG的中点，点C、D、E在一条直线上，点A、G、B在一条直线上，//BC FG．从B站乘车到E站只有两条路线有直接到达的公交车，路线1是B D A E⇒⇒⇒，且长度为5公里，路线2是B C F E⇒⇒⇒，求路线2的长度．【答案】5公里【解析】【分析】证明四边形BCDG是平行四边形，得到DG＝CB，再证四边形BCFD是平行四边形，根据平行四边形的性质计算，得到答案．【详解】解：∵E、D分别是FA和FG的中点，∴AB∥DE，∵BC∥GF，∴四边形BCDG是平行四边形，∴DG＝CB．∵FD＝DG，∴CB＝FD．又∵BC ∥DF ，∴四边形BCFD 是平行四边形，∴CF ＝BD ，∵AB ∥DE ，AB AF ⊥，FE ＝AE ，∴CE 垂直平分AF ，∴AE ＝FE ，FD ＝DA ，∴BC ＝DA ，∴路线2的长度：BC +CF +FE ＝AD +BD +AE ＝5（公里）．【点睛】本题考查的是平行四边形的判定和性质、线段垂直平分线的性质，掌握平行四边形的判定定理和性质定理是解题的关键．16．已知：如图，ABCD 中，5AB =，3BC =．（1）作DAB ∠的角平分线，交CD 于点E （用直尺和圆规作图，不写作法，保留作图痕迹）；（2）求CE 的长．【答案】（1）见解析；（2）CE 的长为2【解析】【分析】（1）根据尺规作图作DAB ∠的平分线即可；（2）根据平行四边形的性质和角平分线的定义，求出DE ＝DA ＝BC ＝3，再求出CE 即可．【详解】解：如图，（1）AE 即为∠DAB 的角平分线；（2）∵AE 为∠DAB 的角平分线，∴∠DAE ＝∠BAE ，在▱ABCD中，CD∥AB，∴∠BAE＝∠DEA，∴∠DAE＝∠DEA，∴DE＝DA＝BC＝3，∵DC＝AB＝5，∴CE＝CD﹣DE＝2．答：CE的长为2．【点睛】当平行线遇上角平分线时，通过角的转化，可以得到等腰三角形，这是初中几何一个很重要的数学模型，要深刻领会．17．如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF，（1）求证：AF=DC；（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．【答案】（1）见解析（2）见解析【解析】【分析】（1）根据AAS证△AFE≌△DBE，推出AF=BD，即可得出答案．（2）得出四边形ADCF是平行四边形，根据直角三角形斜边上中线性质得出CD=AD，根据菱形的判定推出即可．【详解】解：（1）证明：∵AF∥BC，∴∠AFE=∠DBE．∵E是AD的中点，AD是BC边上的中线，∴AE=DE，BD=CD．在△AFE和△DBE中，∵∠AFE=∠DBE，∠FEA=∠BED，AE=DE，∴△AFE≌△DBE（AAS）∴AF =BD ．∴AF =DC ．（2）四边形ADCF 是菱形，证明如下：∵AF ∥BC ，AF =DC ，∴四边形ADCF 是平行四边形．∵AC ⊥AB ，AD 是斜边BC 的中线，∴AD =DC ．∴平行四边形ADCF 是菱形．18．如图，四边形ABCD 是边长为13cm 的菱形，其中对角线BD 长10cm ．求：（1）对角线AC 的长度；（2）菱形ABCD 的面积．【答案】（1）24cm AC =；（2）2120cm【解析】【分析】（1）根据菱形的对角线互相垂直平分，可利用勾股定理求出AE 的长，从而求出AC 的长；（2）根据菱形的面积公式：两条对角线乘积的一半即可求得面积．【详解】解：（1）∵四边形ABCD 是菱形，AC 与BD 相交于点E ，∴90AED ∠=︒（菱形的对角线互相垂直），11105(cm)22DE BD ==⨯=（菱形的对角线互相平分）． ∴222213512(cm)AE AD DE =--=．∴221224(cm)AC AE ==⨯=（菱形的对角线互相平分）；（2）ABD BDC ABCD S S S =+菱形1122BD AE BD CE =⋅+⋅ 1()2BD AE CE =⋅+ 12BD AC =⋅ 110242=⨯⨯ 2120(cm )=．【点睛】本题主要考查了菱形的性质、菱形的面积公式、勾股定理，熟知菱形的性质是解本题的关键．19．如图，E 是▱ABCD 的边CD 的中点，延长AE 交BC 的延长线于点F ．（1）求证：△ADE ≌△FCE ．（2）若∠BAF =90°，BC =5，EF =3，求CD 的长．【答案】（1）证明过程见解析；（2）8【解析】【分析】（1）由平行四边形的性质得出AD ∥BC ，AB ∥CD ，证出∠DAE =∠F ，∠D =∠ECF ，由AAS 证明△ADE ≌△FCE 即可；（2）由全等三角形的性质得出AE =EF =3，由平行线的性质证出∠AED =∠BAF =90°，由勾股定理求出DE ，即可得出CD 的长．【详解】（1）∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ∥CD ，∴∠DAE =∠F ，∠D =∠ECF ，∵E 是▱ABCD 的边CD 的中点， ∴DE =CE ，在△ADE 和△FCE 中，DAE F D ECF DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ADE ≌△FCE （AAS ）；（2）∵ADE≌△FCE，∴AE=EF=3，∵AB∥CD，∴∠AED=∠BAF=90°，在▱ABCD中，AD=BC=5，∴DE=2222-=-=4，AD AE53∴CD=2DE=8【点睛】考点：（1）平行四边形的性质；（2）全等三角形的判定与性质20．(1)如图,纸片▱ABCD中,AD=5,S▱ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为() A．平行四边形B．菱形C．矩形D．正方形(2)如图,在(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D．①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.图1图2【答案】（1）C；（2）①证明见解析；1010【解析】【详解】试题分析：（1）如图1，纸片▱ABCD中，AD=5，S▱ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′的位置，拼成四边形AEE′D，则四边形AE E′D的形状为矩形，故选C；（2）①证明：∵纸片▱ABCD中，AD=5，S▱ABCD=15，过点A作AE⊥BC，垂足为E，∴AE=3．如图2：∵△AEF ，将它平移至△DE′F′，∴AF ∥DF′，AF=DF′，∴四边形AFF′D 是平行四边形．在Rt △AEF 中，由勾股定理，得AF=2222=34++AE EF =5，∴AF=AD=5，∴四边形AFF′D 是菱形；②连接AF′，DF ，如图3：在Rt △DE′F 中E′F=FF′﹣E′F′=5﹣4=1，DE′=3，∴DF=2222=13=10''++E D E F ，在Rt △AEF′中EF′=EF+FF′=4+5=9，AE=3，∴AF′=2222=39'++AE F E =310． 考点：①图形的剪拼；②平行四边形的性质；③菱形的判定与性质；④矩形的判定；⑤平移的性质．21．如图，在正方形ABCD 中，E 、F 分别为边AD 和CD 上的点，且AE=CF ，连接AF 、CE 交于点G ．求证：AG=CG ．【答案】证明见解析．【解析】【分析】先用SAS 证明△ADF ≌△CDE ，得∠DAF=∠DCE ，再用AAS 证明△AGE ≌△CGF 即可.【详解】∵四边形ABCD 是正方形，∴∠ADF=∠CDE=90°，AD=CD ．∵AE=CF ，∴DE=DF ，在△ADF 和△CDE 中,AD AD ADF CDE DF DE =⎧⎪∠=∠⎨⎪=⎩， ∴△ADF ≌△CDE （SAS ），∴∠DAF=∠DCE ，在△AGE 和△CGF 中，GAE GCF AGE CGF AE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AGE ≌△CGF （AAS ），∴AG=CG ．22．如图，△ABC 中，AB ＝AC ＝1，∠BAC ＝45°，△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的，连接BE ，CF 相交于点D,（1）求证：BE ＝CF ；（2）当四边形ACDE 为菱形时，求BD 的长．【答案】（1）证明见解析（22【解析】【分析】（1）先由旋转的性质得AE=AB ，AF=AC ，∠EAF=∠BAC ，则∠EAF+∠BAF=∠BAC+∠BAF ，即∠EAB=∠FAC ，利用AB=AC 可得AE=AF ，得出△ACF ≌△ABE ，从而得出BE=CF ；（2）由菱形的性质得到DE=AE=AC=AB=1，AC ∥DE ，根据等腰三角形的性质得∠AEB=∠ABE ，根据平行线得性质得∠ABE=∠BAC=45°，所以∠AEB=∠ABE=45°，于是可判断△ABE 为等腰直角三角形，所以22BD=BE ﹣DE 求解．【详解】（1）∵△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的，∴AE=AB ，AF=AC ，∠EAF=∠BAC ，∴∠EAF+∠BAF=∠BAC+∠BAF ，即∠EAB=∠FAC ，在△ACF 和△ABE 中，AC AB CAF BAE AF AE =⎧⎪∠=∠⎨⎪=⎩∴△ACF ≌△ABE∴BE=CF.（2）∵四边形ACDE 为菱形，AB=AC=1，∴DE=AE=AC=AB=1，AC ∥DE ，∴∠AEB=∠ABE ，∠ABE=∠BAC=45°，∴∠AEB=∠ABE=45°，∴△ABE 为等腰直角三角形，∴BE=2AC=2，∴BD=BE ﹣DE=21-．考点：1．旋转的性质；2．勾股定理；3．菱形的性质． 23．如图，AD 是ABC 的中线，//AE BC ，且12AE BC =，连接DE ，CE ．（1）求证：AB DE =；（2）当ABC 满足条件__________时，四边形ADCE 是矩形．【答案】（1）见解析；（2）AB =AC 或 ABC ACB ∠=∠【解析】【分析】（1）根据三角形中位线定理和平行四边形的判定和性质解答即可； （2）根据矩形的判定解答即可．【详解】（1）∵AD 是ABC 的中线，∴12BD BC =， ∵12AE BC =， ∴AE BD =，∵//AE BC ，∴四边形ABDE 是平行四边形，∴AB DE =（2）当△ABC 满足AB =AC 或ABC ACB ∠=∠时，四边形ADCE 是矩形， 11,,22BC BD AE CD BC =∴== ∴AE =CD ，∵AE ∥BC ，∴四边形ADCE 是平行四边形，∵AB =DE ，∴当AB =AC 或ABC ACB ∠=∠时，AC =DE ，∴四边形ADCE 是矩形．【点睛】此题考查了平行四边形的判定与性质、等腰三角形的性质以及矩形的判定．此题难度适中，注意掌握数形结合思想的应用．24．在边长为5的正方形ABCD 中，点E 在边CD 所在直线上，连接BE ，以BE 为边，在BE 的下方作正方形BEFG ，并连接AG ．（1）如图1，当点E 与点D 重合时，AG ＝ ；（2）如图2，当点E 在线段CD 上时，DE ＝2，求AG 的长；（3）若AG ＝5172，请直接写出此时DE 的长．【答案】（1）5（2109（3）52或152． 【解析】【分析】 （1）如图1，连接CG ，证明△CBD ≌△CBG （SAS ），可得G ，C ，D 三点共线，利用勾股定理可得AG 的长；（2）如图2，作辅助线，构建全等三角形，证明△BCE ≌△BKG ，可得AK 和KG 的长，利用勾股定理计算AG 的长；（3）分三种情况：①当点E在边CD的延长线上时，如图3，同（2）知△BCE≌△BKG （AAS），BC＝BK＝5，根据勾股定理可得KG的长，即可CE的长，此种情况不成立；②当点E在边CD上；③当点E在DC的延长线上时，同理可得结论．【详解】（1）如图1，连接CG，∵四边形ABCD和四边形EBGF是正方形，∴∠CDB＝∠CBD＝45°，∠DBG＝90°，BD＝BG，∴∠CBG＝45°，∴∠CBG＝∠CBD，∵BC＝BC，∴△CBD≌△CBG（SAS），∴∠DCB＝∠BCG＝90°，DC＝CG＝5，∴G，C，D三点共线，∴AG＝22+＝22AD DG+＝55，510故答案为：55；（2）如图2，过点G作GK⊥AB，交AB的延长线于K，∵DE＝2，DC＝5，∴CE＝3，∵∠EBG＝∠EBC＋∠CBG＝90°，∠CBG＋∠GBK＝90°，∵BE＝BG，∠K＝∠BCE＝90°，∴△BCE≌△BKG（AAS），∴CE＝KG＝3，BC＝BK＝5，∴AK＝10，由勾股定理得：AG＝22103+＝109；（3）分三种情况：①当点E在CD的延长线上时，如图3，由（2）知△BCE≌△BKG（AAS），∴BC＝BK＝5，∵AG＝5172，由勾股定理得：KG＝22517102⎛⎫-⎪⎪⎝⎭=52，∴CE＝KG＝52，此种情况不成立；②当点E在边CD上时，如图4，由（2）知△BCE≌△BKG（AAS），∵AG＝5172，由勾股定理得：KG＝22517102⎛⎫-⎪⎪⎝⎭=52，∴CE＝KG＝52，∴DE＝CD-CE=52；③当点E在DC的延长线上时，如图5，同理得CE＝KG＝52，∴DE＝5＋52＝152；综上，DE的长是52或152．【点睛】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识，本题综合性强，有一定难度，证明三角形全等是解决问题的关键．。
精品解析2022年人教版八年级数学下册第十八章-平行四边形综合测试试题(含答案及详细解析)
人教版八年级数学下册第十八章-平行四边形综合测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、已知直线:l y x =，点P 在直线l 上，点(2A ，点(2B +，若APB △是直角三角形，则点P 的个数有（ ）A ．1个B ．2个C ．3个D ．4个2、如图，四边形ABCD 是平行四边形，下列结论中错误的是（ ）A ．当▱ABCD 是矩形时，∠ABC ＝90°B ．当▱ABCD 是菱形时，AC ⊥BD C ．当▱ABCD 是正方形时，AC ＝BD D ．当▱ABCD 是菱形时，AB ＝AC3、如图所示，在矩形ABCD 中，已知AE ⊥BD 于E ，∠DBC ＝30°，BE =1cm ，则AE 的长为（ ）A．3cm B．2cm C．D4、ABCD的周长为32cm，AB：BC=3：5，则AB、BC的长分别为（）A．20cm，12cm B．10cm，6cm C．6cm，10cm D．12cm，20cm5、如图，在菱形ABCD中，AB＝5，AC＝8，过点B作BE⊥CD于点E，则BE的长为（）A．125B．245C．6 D．4856、如图菱形ABCD，对角线AC，BD相交于点O，若BD＝8，AC＝6，则AB的长是（）A．5 B．6 C．8 D．107、如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E，若∠1＝40°，则∠2的度数为（）A ．25°B ．20°C ．15°D ．10°8、平行四边形ABCD 中，60A ∠=︒，则C ∠的度数是（ ）A ．30B ．60︒C ．90︒D ．120︒9、如图，平行四边形ABCD 的周长为36，对角线AC ，BD 相交于点O ，点E 是CD 的中点，BD ＝12，则△DOE 的周长是（ ）A ．12B ．15C ．18D ．2410、如图，在四边形ABCD 中，AD BC ∥，6BC =，BDC ∆面积为21，AB 的垂直平分线MN 分别交,AB AC 于点,M N ，若点P 和点Q 分别是线段MN 和BC 边上的动点，则PB PQ +的最小值为（ ）A ．5B ．6C ．7D ．8第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图所示，正方形ABCD 的面积为6，△CDE 是等边三角形，点E 在正方形ABCD 内，在对角线BD 上有一动点K ，则KA +KE 的最小值为 _____________．2、如图，菱形ABCD的对角线AC，BD相交于点O，E为DC的中点，若2OE ，则菱形的周长为__________．3、点D、E分别是△ABC边AB、AC的中点，已知BC＝12，则DE＝_____4、判断：（1）菱形的对角线互相垂直且相等____( )____（2）菱形的对角线把菱形分成四个全等的直角三角形____( )____5、如图，在平行四边形ABCD中，∠B＝45°，AD＝8，E、H分别为边AB、CD上一点，将▱ABCD沿EH 翻折，使得AD的对应线段FG经过点C，若FG⊥CD，CG＝4，则EF的长度为 _____．三、解答题（5小题，每小题10分，共计50分）1、如图，ABCD是平行四边形，AD＝4，AB＝5，点A的坐标为（－2，0），求点B、C、D的坐标．2、如图，在Rt △ABC 中，∠ACB ＝90°．（1）作AB 的垂直平分线l ，交AB 于点D ，连接CD ，分别作∠ADC ，∠BDC 的平分线，交AC ，BC 于点E ，F （尺规作图，不写作法，保作图痕迹）；（2）求证：四边形CEDF 是矩形．3、如图，在菱形ABCD 中，点E ，F 分别是边AB 和BC 上的点，且BE ＝BF ．求证：∠DEF ＝∠DFE ．4、如图，在平行四边形ABCD 中，8cm AB =，16cm BC =．30B ∠=︒．点P 在BC 上由点B 向点C 出发，速度为每秒2cm ；点Q 在边AD 上，同时由点D 向点A 运动，速度为每秒1cm ．当点P 运动到点C 时，点P ，Q 同时停止运动．连接PQ ，设运动时间为t 秒．（1）当t为何值时，四边形ABPO为平行四边形？（2）设四边形ABPQ的面积为y，求y与t之间的函数关系式．∠的度数．（3）当t为何值时，四边形ABPQ的面积是四边形ABCD的面积的四分之三？求出此时PQD（4）连接AP，是否存在某一时刻t，使ABP△为等腰三角形？若存在，请求出此刻t的值；若不存在，请说明理由．5、如图，已知正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF DE⊥，垂足为点F，BF与CD交于点G．（1）求证：CG CE=；（2）若BE=DG=BG的长．---------参考答案-----------一、单选题1、C【解析】【分析】分别讨论90APB∠=︒三种情况，求出P点坐标即可得出答案．PAB∠=︒，90PBA∠=︒，90【详解】如图，当90PAB ∠=︒时，点A 与点P 横坐标相同，(22,0)A -2x ∴=y x =中得：2y =1(2P ∴，当90PBA ∠=︒时，点B 与点P 横坐标相同，(22,0)B +，2x ∴=代入y x =中得：2y =2(2P ∴，当90APB ∠=︒时，取AB 中点为点C ，过点P 作PM AB ⊥交于点M ，设(,)P a a ，OM a ∴=，PM a =，(22,0)A -，(2B +，2(2AB ∴=+=12AC PC AB ∴==22OC OA AC ∴=+==，2CM a ∴=-，在Rt PMC 中，222(2)a a +-=，解得：1a =，(1,1)P ∴，P ∴点有3个．故选：C ．【点睛】本题考查直角三角形的性质与平面直角坐标系，掌握分类讨论的思想是解题的关键．2、D【解析】【分析】由矩形的四个角是直角可判断A ，由菱形的对角线互相垂直可判断B ，由正方形的对角线相等可判断C ，由菱形的四条边相等可判断D ，从而可得答案.【详解】解：当▱ABCD 是矩形时，∠ABC ＝90°，正确，故A 不符合题意；当▱ABCD 是菱形时，AC ⊥BD ，正确，故B 不符合题意；当▱ABCD 是正方形时，AC ＝BD ，正确，故C 不符合题意；当▱ABCD 是菱形时，AB ＝BC ，故D 符合题意；【点睛】本题考查的是矩形，菱形，正方形的性质，熟练的记忆矩形，菱形，正方形的性质是解本题的关键.3、D【解析】【分析】根据矩形和直角三角形的性质求出∠BAE=30°，再根据直角三角形的性质计算即可．【详解】解：∵四边形ABCD是矩形，∴∠BAD=90°，∠BDA=∠DBC=30°，∵AE⊥BD，∴∠DAE=60°，∴∠BAE=30°，在Rt△ABE中，∠BAE=30°，BE=1cm，∴AB=2cm，cm)，∴AE故选：D．【点睛】本题考查了矩形的性质，含30度角的直角三角形的性质，熟记各图形的性质并准确识图是解题的关键．4、C【解析】根据平行四边形的性质，可得AB =CD ，BC =AD ，然后设3cm,5cm AB x BC x == ，可得到()23532x x += ，即可求解．【详解】解：∵四边形ABCD 是平行四边形，∴AB =CD ，BC =AD ，∵AB ：BC =3：5，∴可设3cm,5cm AB x BC x == ，∵ABCD 的周长为32cm ，∴()232AB BC += ，即()23532x x += ，解得：2x = ，∴6cm,10cm AB BC == ．故选：C【点睛】本题主要考查了平行四边形的性质，熟练掌握平行四边形的对边相等是解题的关键．5、B【解析】【分析】根据菱形的性质求得BD 的长，进而根据菱形的面积等于12AC BD CD BE ⋅=⋅，即可求得BE 的长【详解】解：如图，设,AC BD 的交点为O ，四边形ABCD 是菱形AC BD ∴⊥，142AO CO AC ===，DO BO =，5CD AB == 在Rt AOB 中，5AB =，4AO =3BO ∴26BD BO ∴== 菱形的面积等于12AC BD CD BE ⋅=⋅1168242255AC BD BE CD ⋅⨯∴==⨯= 故选B【点睛】本题考查了菱形的性质，掌握菱形的性质，求得BD 的长是解题的关键．6、A【解析】【分析】由菱形的性质可得OA =OC =3，OB =OD =4，AO ⊥BO ，由勾股定理求出AB ．【详解】解：∵四边形ABCD 是菱形，AC =6，BD =8，∴OA =OC =3，OB =OD =4，AO ⊥BO ，在Rt△AOB中，由勾股定理得：5AB=，故选：A．【点睛】本题考查了菱形的性质、勾股定理等知识；熟练掌握菱形对角线互相垂直且平分的性质是解题的关键．7、D【解析】【分析】根据矩形的性质，可得∠ABD＝40°，∠DBC＝50°，根据折叠可得∠DBC′＝∠DBC＝50°，最后根据∠2＝∠DB C′−∠DBA进行计算即可．【详解】解：∵四边形ABCD是矩形，∴∠ABC＝90°，CD∥AB，∴∠ABD=∠1＝40°，∴∠DBC＝∠ABC-∠ABD=50°，由折叠可得∠DB C′＝∠DBC＝50°，∴∠2＝∠DB C′−∠DBA＝50°−40°＝10°，故选D．【点睛】本题考查了长方形性质，平行线性质，折叠性质，角的有关计算的应用，关键是求出∠DBC′和∠DBA 的度数．8、B【解析】【分析】根据平行四边形对角相等，即可求出C∠的度数．【详解】解：如图所示，∵四边形ABCD是平行四边形，∴A C∠=∠，∴60A∠=︒，∴60∠=°．C故：B．【点睛】本题考查了平行四边形的性质，解题的关键是掌握平行四边形的性质．9、B【解析】【分析】根据平行四边形的对边相等和对角线互相平分可得，OB＝OD，又因为E点是CD的中点，可得OE是BC，所以易求△DOE的周长．△BCD的中位线，可得OE＝12【详解】解：∵▱ABCD的周长为36，∴2（BC＋CD）＝36，则BC＋CD＝18．∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD＝12，∴OD＝OB＝12BD＝6．又∵点E是CD的中点，∴OE是△BCD的中位线，DE＝12CD，∴OE＝12BC，∴△DOE的周长＝OD＋OE＋DE＝12BD＋12（BC＋CD）＝6＋9＝15，故选：B．【点睛】本题考查了三角形中位线定理、平行四边形的性质．解题时，利用了“平行四边形对角线互相平分”、“平行四边形的对边相等”的性质．10、C【解析】【分析】连接AQ，过点D作DH BC⊥，根据垂直平分线的性质得到PA PB=，再根据PB PQ AP PQ AQ+=+≥计算即可；【详解】连接AQ，过点D作DH BC⊥，∵6BC=，BDC∆面积为21，∴1212BC DH =， ∴7DH =，∵MN 垂直平分AB ，∴PA PB =，∴PB PQ AP PQ AQ +=+≥，∴当AQ 的值最小时，PB PQ +的值最小，根据垂线段最短可知，当AQ BC ⊥时，AQ 的值最小， ∵AD BC ∥，∴7AQ DH ==，∴PB PQ +的值最小值为7；故选C ．【点睛】本题主要考查了四边形综合，垂直平分线的性质，准确分析计算是解题的关键．二、填空题1【解析】【分析】根据正方形的性质可知C 、A 关于BD 对称，推出CK ＝AK ，推出EK +AK ≥CE ，根据等边三角形性质推出CE ＝CD ，根据正方形面积公式求出CD 即可．【详解】解：∵四边形ABCD 是正方形，∴C 、A 关于BD 对称，即C 关于BD 的对称点是A ，如图，连接CK ，则CK ＝AK ，∴EK+CK≥CE，∵△CDE是等边三角形，∴CE＝CD，∵正方形ABCD的面积为6，∴CD，∴KA+KE【点睛】本题考查了正方形的性质，轴对称-最短路径问题，等边三角形的性质等知识点的应用，解此题的关键是确定K的位置和求出KA+KE的最小值是CE．2、16【解析】【分析】由菱形的性质和三角形中位线定理即可得菱形的边长，从而可求得菱形的周长．【详解】∵四边形ABCD是菱形，且对角线相交于点O∴点O是AC的中点∵E为DC的中点∴OE为△CAD的中位线∴AD=2OE=2×2=4∴菱形的周长为：4×4=16故答案为：16【点睛】本题考查了菱形的性质及三角形中位线定理、菱形周长等知识，掌握这些知识是解答本题的关键．3、6【解析】【分析】根据三角形的中位线等于第三边的一半进行计算即可．【详解】解：∵D、E分别是△ABC边AB、AC的中点，∴DE是△ABC的中位线，∵BC=12，BC=6，∴DE=12故答案为6．【点睛】本题主要考查了三角形中位线定理，熟知三角形中位线定理是解题的关键．4、× √【解析】【分析】根据菱形的性质，即可求解．【详解】解：（1）菱形的对角线互相垂直且平分；（2）菱形的对角线把菱形分成四个全等的直角三角形．故答案为：（1）×；（2）√【点睛】本题主要考查了菱形的性质，熟练掌握菱形的对角线互相垂直且平分是解题的关键．5、8【解析】【分析】延长CF与AB交于点M，由平行四边形的性质得BC长度，GM⊥AB，由折叠性质得GF，∠EFM，进而得FM，再根据△EFM是等腰直角三角形，便可求得结果．【详解】解：延长CF与AB交于点M，∵FG⊥CD，AB∥CD，∴CM ⊥AB ，∵∠B =45°，BC =AD =8，∴CM由折叠知GF =AD =8，∵CG =4，∴MF =CM -CF =CM -（GF -CG ）-4，∵∠EFC =∠A =180°-∠B =135°，∴∠MFE =45°，∴EF （）故答案为：【点睛】本题主要考查了平行四边形的性质，折叠的性质，解直角三角形的应用，关键是作辅助线构造直角三角形．三、解答题1、(3,0)B 、(5,C 、(0,D【分析】根据5AB =，(2,0)A -即可求得点B ，勾股定理求得OD 即可求得点D ，再根据平行四边形的性质可得C 点坐标．【详解】解：ABCD 是平行四边形，∴CD x ∥轴，5CD AB ==，由题意可得，2OA =，90AOD ∠=︒，∴OD =，即(0,D ，∵(2,0)A -，5AB =，∴(3,0)B ，∵(0,D ，5CD AB ==，CD x ∥轴，∴(5,C ，∴(3,0)B 、(5,C 、(0,D ．【点睛】此题考查了坐标与图形，涉及了勾股定理、平行四边形的性质，解题的关键是掌握并灵活运用相关性质进行求解．2、（1）见解析（2）见解析【分析】（1）利用垂直平分线和角平分线的尺规作图法，进行作图即可．（2）利用直角三角形斜边中线性质，以及角平分线的性质直接证明CED ∠与EDF ∠都是90︒，最后加上90ACB ∠=︒，即可证明结论．【详解】（1）答案如下图所示：分别以A 、B 两点为圆心，以大于2AB 长为半径画弧，连接弧的交点的直线即为垂直平分线l ，其与AB的交点为D ，以点D 为圆心，适当长为半径画弧，分别交DA 于点M ，交CD 于点N ，交BD 于点T ，然后分别以点M ，N 为圆心，大于2MN 为半径画弧，连接两弧交点与D 点的连线交AC 于点E ，同理分别以点T ，N 为圆心，大于2TN 为半径画弧，连接两弧交点与D 点的连线交BC 于点F ． （2）证明：D 点是AB 与其垂直平分线l 的交点，D ∴点是AB 的中点，CD ∴是Rt △ABC 上的斜边的中线，2AB CD AD ∴==， DE 、DF 分别是∠ADC ，∠BDC 的角平分线，12CDE ADE ADC ∴∠=∠=∠，12CDF CDB ∠=∠， EDF CDE CDF ∠=∠+∠，11190222EDF ADC CDB ADB ∴∠=∠+∠=∠=︒ ， CD AD CDE ADE DE DE =⎧⎪∠=∠⎨⎪=⎩， ()CDE ADE SAS ∴∆∆≌，1902CED AED AEC ∴∠=∠=∠=︒， 在四边形CEDF 中，90ACB CED EDF ∠=∠=∠=︒，∴四边形CEDF 是矩形．【点睛】本题主要是考查了尺规作图、直角三角形斜边中线性质以及矩形的判定，熟练利用直角三角形斜边中线性质，找到三角形全等的判定条件，并且选择合适的矩形判定条件，是解决本题的关键．3、见解析【分析】根据菱形的性质可得AB =BC =CD =AD ，∠A =∠C ，再由BE =BF ，可推出AE =CF ，即可利用SAS 证明△ADE ≌△CDF 得到DE =DF ，则∠DEF =∠DFE ．【详解】解：∵四边形ABCD 是菱形，∴AB =BC =CD =AD ，∠A =∠C ，∵BE =BF ，∴AB -BE =BC -BF ，即AE =CF ，∴△ADE ≌△CDF （SAS ），∴DE =DF ，∴∠DEF =∠DFE ．【点睛】本题主要考查了菱形的性质，全等三角形的性质与判定，等腰三角形的性质与判定，解题的关键在于能够熟练掌握菱形的性质．4、（1）163；（2）y ＝S 四边形ABPQ ＝2t ＋32（0＜t ≤8）；（3）t ＝8，75PQD ∠=；（4）当t ＝4或ABP △为等腰三角形，理由见解析．【分析】（1）利用平行四边形的对边相等AQ ＝BP 建立方程求解即可；（2）先构造直角三角形，求出AE ，再用梯形的面积公式即可得出结论；（3）利用面积关系求出t，即可求出DQ，进而判断出DQ＝PQ，即可得出结论；（4）分三种情况，利用等腰三角形的性质，两腰相等建立方程求解即可得出结论．【详解】解：（1）∵在平行四边形ABCD中，8cmAB=，16cmBC=，由运动知，AQ＝16−t，BP＝2t，∵四边形ABPQ为平行四边形，∴AQ＝BP，∴16−t＝2t∴t＝163，即：t＝163s时，四边形ABPQ是平行四边形；（2）过点A作AE⊥BC于E，如图，在Rt△ABE中，∠B＝30°，AB＝8，∴AE＝4，由运动知，BP＝2t，DQ＝t，∵四边形ABCD是平行四边形，∴AD＝BC＝16，∴AQ＝16−t，∴y＝S四边形ABPQ＝12（BP＋AQ）•AE＝12（2t＋16−t）×4＝2t＋32（0＜t≤8）；（3）由（2）知，AE＝4，∵BC＝16，∴S四边形ABCD＝16×4＝64，由（2）知，y＝S四边形ABPQ＝2t＋32（0＜t≤8），∵四边形ABPQ的面积是四边形ABCD的面积的四分之三∴2t＋32＝34×64，∴t＝8；如图，当t＝8时，点P和点C重合，DQ＝8，∵CD＝AB＝8，∴DP＝DQ，∴∠DQC＝∠DPQ，∴∠D＝∠B＝30°，∴∠DQP＝75°；（4）①当AB＝BP时，BP＝8，即2t＝8，t＝4；②当AP＝BP时，如图，∵∠B＝30°，过P作PM垂直于AB，垂足为点M，∴BM＝4，22242BPBP⎛⎫+=⎪⎝⎭，解得：BP，∴2t，∴t③当AB＝A P时，同（2）的方法得，BP＝∴2t＝∴t＝所以，当t＝4或ABP为等腰三角形．【点睛】此题是四边形综合题，主要考查了平行四边形的性质，含30°的直角三角形的性质，等腰三角形的性质，解（1）的关键是利用AQ＝BP建立方程，解（2）的关键是求出梯形的高，解（3）的关键是求出t，解（4）的关键是分类讨论的思想思考问题．5、（1）见解析；（2）BG=【分析】（1）由正方形的性质可得BC DC=，BCG DCE∠=∠，由E∠的余角相等可得∠CBG=∠CDE，进而证明△BCG≌△DCE，从而证明CG=CE；CG BC，进而勾股定理即可求得BG的（2）证明正方形的性质可得BC DC=，结合已知条件即可求得,长【详解】（1）∵BF⊥DE∴∠BFE=90°∵四边形ABCD是正方形∴∠DCE=90°BC DC=,BCG DCE∴∠=∠∴∠CBG+∠E=∠CDE+∠E，∴∠CBG=∠CDE∴△BCG≌△DCE∴CG=CE（2）∵BC DC=，且BE=DG=∴CE CG=∵CG=CE∴CG BC=在Rt BCG中，BG=【点睛】本题考查了正方形的性质，全等三角形的性质与判定，勾股定理，掌握三角形全等的性质与判定与勾股定理是解题的关键．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ACBD E 二次根式及勾股定理和平行四边形练习题一、选择题（每小题1分，共25分） 姓名： 分数： 1.下列二次根式中，的取值范围是26x -的是（ ） =3 B. 3x ≥ C. X ≤3 D. X>32. 在ABCD 中，那么它的四个内角按一定顺序的度数比可能为（ ） A 、3:4:5:6 B 、4:5:4:5 C 、2:3:3:2 D 、2:4:3:33.下列二次根式中，是最简二次根式的是（ ）A.xy 2B.2abC.21D.422x x y + 4.下列二次根式,不能与3合并的是( )A.48B.18C.311D.75-5.如图所示, 在ABCD 中，∠D=120°，∠CAD=32°.则∠ABC 、∠CAB 的度数分别为（ ） °，120° °，28° °，120° °，32°6．下面的性质中，平行四边形不一定具有的是（ ）A.对角互补B.邻角互补C.对角相等D.对边相等.7. 如右图是一张直角三角形的纸片，两直角边AC ＝6 cm 、BC ＝8 cm ， 现将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则BE 的长为（ ） （A ）4 cm （B ）5 cm （C ）6 cm （D ）10 cm 8.下列二次根式,不能与12合并的是( ) A.48 B.18 C.311 D.75- 9.下列运算正确的是（ ） A.235=- B.312914= C.822-= D.()52522-=-10．有六根细木棒，它们的长度分别为2，4，6，8，10，12（单位：cm ），从中取出三根首尾顺次连接搭成一个直角三角形，则这根木棒的长度分别为（ ）A ．2，4，8 ,8,10 ,8,10 ,10,1211.如图,在平行四边形ABCD 中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD 的长为( )12.如图所示：是一段楼梯，高BC 是3m ，斜边AC 是5m ，如果在楼梯上铺地毯，那么至少需要地毯（ ）m m m m13.如图,在底面周长为12,高为8的圆柱体上有A,B 两点,则AB 之间的最短距离是( )A ．10 ?B ．8 ?C ．5??D ．414．如果等边三角形的边长为3，那么连结各边中点所成的三角形的周长为（ ）．第5题图第7题图第13题图第12题图1A-1-21（A ）9 （B ）6 （C ）3 （D ）9215.如右上图,在周长为20cm 的?ABCD 中,AB ≠AD,AC,BD 相交于点O,OE ⊥BD 交AD 于E,则△ABE 的周长为( ) cm cmcmcm16、把1xx -根号外的因数移到根号内，结果是（ ）A 、x B 、x -C 、x -- D 、x -17、下列根式8，12，3，21x +，33x ()x ＞0中是最简二次根式的有（ ）个。
A 、1B 、2C 、3D 、418、已知24n 是整数，正整数n 的最小值为（ ） A 、0B 、1C 、6D 、3619、直角三角形的二边长分别为3和4，则第三边是（ ）A 、5 B 、7C 、5D 、5或720、若21x y -=-，2xy =，则代数式11x y -+（）（）的值等于（ ） A 、222+ B 、222- C 、22 D 、221、下列命题中，其中正确命题的个数为（ ）个。
A 、1B 、2C 、3D 、4①Rt△ABC 中，已知两边长分别为3和4，则第三边为5； ②有一个内角等于其他两个内角和的三角形是直角三角形；③三角形的三边分别为a ，b ，c 若222a cb +=，则∠C=90° ④在△ABC 中，∠A：∠B：∠C=1：5：6，则△ABC 为直角三角形。
22、等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）64 23、三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )（A ） 等边三角形 （B ） 钝角三角形 （C ） 直角三角形 （D ） 锐角三角形.24、小刚准备测量河水的深度,他把一根竹竿插到离岸边远的水底,竹竿高出水面,把竹竿的顶端拉向岸边,竿顶和岸边的水平刚好相齐,河水的深度为( ).25、如图，数轴上的点A 所表示的数为x ，则x 2—10的立方根为（ ） A ．2-10 B ．-2-10 C ．2 D ．-2二、填空题（每小题1分，共15分）26、在□ABCD 中，∠A=︒50，则∠B = 度，∠C = 度，∠D = 度．27、如果□ABCD 的周长为28cm ，且AB ：BC=2∶5，那么AB= cm ，BC= cm ，CD= cm 28、化简:=32 ； y x 329(x>0,y>0) = .29、计算243223--)(=30、如下图，某次的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在 离树杆底部4米处，那么这棵树折断之前的高度是______米. 31、在□ABCD 中，（1）若添加一个条件_____ __，则四边形ABCD 是矩形；（2）若添加一个条件 ， 则四边形ABCD 是菱形．32、如下图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行_____米.第37题第30题 E F A DC B 第36题 第32题第33题 S3S2S1CB A D EF 33、如图，已知ABC ∆中，90ACB ∠=︒，以ABC ∆的各边为边在ABC ∆外作三个正方形，123,,S S S 分别表示这三个正方形的面积，1281,225S S ==，则3_____.S =34、对于任意不相等的两个数a ，b ，定义一种运算※如下：a※b=b a b a -+，如3※2=52323=-+． 那么12※4= 。
35、两条直角边长分别为 、，则斜边长为____ ___，面积为____ ___ .36、如图□ABCD 中AB=5，BC=9，BE ，CF 分别平分∠ABC ，∠BCD ，求EF=37、如图所示，在□ABCD 中，∠B=110°，延长AD 至F ，CD 至E ，连结EF ，则∠E+∠F=38、 计算：20102010)23()23(+-= 39、如图，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是 ．40、如图9，四边形ABCD 是正方形，P 在CD 上，△ADP 旋转后能够与△ABP ′重合，若AB ＝3，DP ＝1，则PP ′＝＿＿＿.三、解答题（共80分）41、（5分）已知04412=+-+--b b b a ，求边长为a,b 的等腰三角形的周长。
42、（5分）已知x 为奇数，且1321,96962-+++--=--x x x xx x x 求的值。
43、计算或化简（18分）① 9827527128--②)65153(1021-⨯③ )2463)(2463(+- ④ )35)(15()25(2+++-⑤ 312÷(331－23) ⑥ mm m mm m 15462-+44、（5分）已知：)57(21+=x ，)57(21-=y 求代数式22y xy x +-值。
45、（5分）如图，小红用一张长方形纸片ABCD 进行折纸，已知该纸片宽AB 为8cm ，•长BC 为10cm ．当小红折叠时，顶点D 落在BC 边上的点F 处（折痕为AE ）．想一想，此时EC 有多长？•46、（5分）一游泳池长48米，小方和小朱进行游泳比赛，从同一处(A 点)出发，小方平均速度为3米／秒，小朱为3.1米／秒．但小朱一心想快，不看方向沿斜线(AC 方向)游，而小方直游(AB 方向)，两人到达终点的位置相距14米．按各人的平均速度计算，谁先到达终点，为什么? (结果精确到 47、（5分）若x ，y 是实数，且2111+-+-<x x y ，求1|1|--y y 的值。
48、（5分）实数a ，b 在数轴上的位置如图所示，化简：(a+1)2＋2(b-1)2 -|a －b|49、（5分）已知：a ，b 为实数，且22222+-+-=a a a b．求()222ab a b ---+-的值．51、（5分）如图，在正方形ABCD 中，边AB 上有一点M,其中AM=3BM,N 是AD 上一点，且AN=ND, 判断△MNC 是否是直角三角形，并说明理由。
52、（5分）已知如图，在四边形ABCD 中，∠A=600,∠B=∠D=900,BC=2,CD=3,求AB 的长。
53、（6分）如图所示，将一矩形纸片OABC 放在直角坐标系中，O 为原点，C 在x 轴上，OA=6,OC=10,在OA 上取一点E ，将△EOC 沿EC折叠，使点O 落在AB 边上的点D 处，求点E 的坐标。
54、(6分)台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力，如图据气象观测，距某城市A 的正南方向220千米B 处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心现正以15千米/时的速度沿北偏东30o 方向往C 移动，且台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响.148-3 -2 -1 0 1 2 3 4a b xNCDM BA51题图DC AB 53题图52题图y xOCEDA B（1）该城市是否会受到这交台风的影响？请说明理由.（2）若会受到台风影响，那么台风影响该城市持续时间有多少？（3）该城市受到台风影响的最大风力为几级？。