2013西工大附中真题及答案
2013-2014年陕西省西安市西工大附中八年级(下)期中数学试卷(解析版)

2013-2014学年陕西省西安市西工大附中八年级(下)期中数学试卷一.精心选一选1.(3分)在平行四边形、等腰梯形、等腰三角形、矩形、菱形五个图形中,既是中心对称图形又是轴对称图形的有()A.1个B.2个C.3个D.4个2.(3分)下列等式从左到右的变形,属于因式分解的是()A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1C.(x+1)(x+3)=x2+4x+3D.x3﹣x=x(x+1)(x﹣1)3.(3分)如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为()A.B.C.D.4.(3分)已知多项式2x2+bx+c分解因式为2(x﹣3)(x+1),则b、c的值为()A.b=3,c=﹣1B.b=﹣6,c=2C.b=﹣6,c=﹣4D.b=﹣4,c =﹣65.(3分)如图,OP平分∠MON,P A⊥ON于点A,点Q是射线OM上的一个动点,若P A=2,则PQ的最小值为()A.1B.2C.3D.46.(3分)下列命题是真命题的是()A.如果a>b,那么ac2>bc2B.如果ab>c,那么b>C.如果a<b,那么a﹣c>b﹣c D.如果a<0,那么﹣3a>2a7.(3分)如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为()A.4cm B.5cm C.6cm D.7cm8.(3分)下列命题中正确的是()A.有两条边相等的两个等腰三角形全等B.一个锐角和一条边分别相等的两个直角三角形全等C.一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等D.两边分别相等的两个直角三角形全等9.(3分)如图所示,函数y1=|x|和的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是()A.x<﹣1B.﹣1<x<2C.x>2D.x<﹣1或x>2 10.(3分)已知,如图在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)其中正确的有()A.①②③B.②③④C.①③④D.①②③④二、填空题(共6小题,每小题3分,满分18分)11.(3分)点(﹣3,1)先向右平移2个单位,再向上平移4个单位,所得的点关于以x轴为对称点的坐标为.12.(3分)在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志,请你填出通过该桥洞的车高x(m)的取值范围是.13.(3分)在△ABC中,AB=AC,∠ABC=60°,BC=6cm,则AB=cm.14.(3分)如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A 旋转后得到△ACE,那么线段DE的长度为.15.(3分)已知x关于的不等式组恰有三个整数解,则a的取值范围是.16.(3分)如图,∠MON=30°,A在OM上,OA=2,D在ON上,OD=4,C是OM上任意一点,B是ON上任意一点,则折线ABCD的最短长度为.三.解答题17.(12分)分解因式(1)x2﹣18x+81(2)﹣9x3y2﹣6x2y2+3xy(3)a2(a﹣b)+b2(b﹣a)(4)(a2﹣3)2﹣4a2.18.(8分)解一元一次不等式及不等式组,并把它的解集在数轴上分别表示出来.(1)﹣≥x﹣(2).19.(6分)两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)20.(6分)已知关于x,y的方程组的解x,y均为负数,求m的取值范围.21.(5分)证明:等腰三角形的两腰上的中线相等.22.(5分)某工厂生产A、B两种产品共50件,其生产成本与利润如下表:若该工厂计划投入资金不超过40万元,且希望获利超过16万元,问工厂有哪几种生产方案?哪种生产方案获利润最大?最大利润是多少?23.(10分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE =BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF 的形状.2013-2014学年陕西省西安市西工大附中八年级(下)期中数学试卷参考答案与试题解析一.精心选一选1.(3分)在平行四边形、等腰梯形、等腰三角形、矩形、菱形五个图形中,既是中心对称图形又是轴对称图形的有()A.1个B.2个C.3个D.4个【解答】解:矩形、菱形是轴对称图形,也是中心对称图形,符合题意;等腰三角形、等腰梯形是轴对称图形,不是中心对称图形,不符合题意;平行四边形不是轴对称图形,是中心对称图形,不符合题意.故既是轴对称图形又是中心对称图形的是:矩形、菱形.故选:B.2.(3分)下列等式从左到右的变形,属于因式分解的是()A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1C.(x+1)(x+3)=x2+4x+3D.x3﹣x=x(x+1)(x﹣1)【解答】解:A、右边不是整式积的形式,不是因式分解,故本选项错误;B、右边不是整式积的形式,不是因式分解,故本选项错误;C、右边不是整式积的形式,不是因式分解,故本选项错误;D、符合因式分解的定义,故本选项正确;故选:D.3.(3分)如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为()A.B.C.D.【解答】解:根据题意得:,由①得:x>﹣3;由②得:x<4,则不等式组的解集为﹣3<x<4,表示在数轴上,如图所示:.故选:C.4.(3分)已知多项式2x2+bx+c分解因式为2(x﹣3)(x+1),则b、c的值为()A.b=3,c=﹣1B.b=﹣6,c=2C.b=﹣6,c=﹣4D.b=﹣4,c =﹣6【解答】解:由多项式2x2+bx+c分解因式为2(x﹣3)(x+1),得2x2+bx+c=2(x﹣3)(x+1)=2x2﹣4x﹣6.b=﹣4,c=﹣6,故选:D.5.(3分)如图,OP平分∠MON,P A⊥ON于点A,点Q是射线OM上的一个动点,若P A=2,则PQ的最小值为()A.1B.2C.3D.4【解答】解:∵垂线段最短,∴当PQ⊥OM时,PQ有最小值,又∵OP平分∠MON,P A⊥ON,∴PQ=P A=2,故选:B.6.(3分)下列命题是真命题的是()A.如果a>b,那么ac2>bc2B.如果ab>c,那么b>C.如果a<b,那么a﹣c>b﹣c D.如果a<0,那么﹣3a>2a【解答】解:A、当c=0时,如果a>b,那么ac2>bc2错误,不符合题意;B、如果ab>c,那么b>错误,不符合题意;C、如果a<b,那么a﹣c>b﹣c错误,不符合题意;D、如果a<0,那么﹣3a>2a正确,符合题意,故选:D.7.(3分)如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为()A.4cm B.5cm C.6cm D.7cm【解答】解:∵AB的垂直平分线MN交AC于D,∴AD=BD,设BD=xcm,则CD=AC﹣AD=AC﹣BD=8﹣x(cm),∵在△ABC中,∠C=90°,∴CD2+BC2=BD2,∴(8﹣x)2+42=x2,解得:x=5,∴BD=5cm.故选:B.8.(3分)下列命题中正确的是()A.有两条边相等的两个等腰三角形全等B.一个锐角和一条边分别相等的两个直角三角形全等C.一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等D.两边分别相等的两个直角三角形全等【解答】解:A、有两条边相等的两个等腰三角形全等,错误,不符合题意;B、一个锐角和一条边分别相等的两个直角三角形全等,错误,不符合题意;C、一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等,正确,符合题意;D、两边分别相等的两个直角三角形全等,错误,不符合题意,故选:C.9.(3分)如图所示,函数y1=|x|和的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是()A.x<﹣1B.﹣1<x<2C.x>2D.x<﹣1或x>2【解答】解:当x≥0时,y1=x,又,∵两直线的交点为(2,2),∴当x<0时,y1=﹣x,又,∵两直线的交点为(﹣1,1),由图象可知:当y1>y2时x的取值范围为:x<﹣1或x>2.故选:D.10.(3分)已知,如图在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)其中正确的有()A.①②③B.②③④C.①③④D.①②③④【解答】解:①∵∠BAC=∠DAE,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE.故①正确;∵△ABD≌△ACE,∴∠ABD=∠ACE.∵∠CAB=90°,∴∠ABD+∠DBC+∠ACB=90°,∴∠DBC+∠ACE+∠ACB=90°,∴∠BDC=180°﹣90°=90°.∴BD⊥CE;故②正确;③∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ABD+∠DBC=45°.∴∠ACE+∠DBC=45°,故③正确;④∵BD⊥CE,∴BE2=BD2+DE2.∵∠BAC=∠DAE=90°,AB=AC,AD=AE,∴DE2=2AD2,BC2=2AB2.∵BC2=BD2+CD2≠BD2,∴2AB2=BD2+CD2≠BD2,∴BE2≠2(AD2+AB2).故④错误.故选:A.二、填空题(共6小题,每小题3分,满分18分)11.(3分)点(﹣3,1)先向右平移2个单位,再向上平移4个单位,所得的点关于以x轴为对称点的坐标为(﹣1,﹣5).【解答】解:点(﹣3,1)先向右平移2个单位,再向上平移4个单位可得点的坐标为(﹣3+2,1+4),即(﹣1,5),所得的点关于以x轴为对称点的坐标为(﹣1,﹣5),故答案为:(﹣1,﹣5).12.(3分)在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志,请你填出通过该桥洞的车高x(m)的取值范围是0<x≤3.5.【解答】解:由题意可得:通过该桥洞的车高x(m)的取值范围是:0<x≤3.5.故答案为:0<x≤3.5.13.(3分)在△ABC中,AB=AC,∠ABC=60°,BC=6cm,则AB=6cm.【解答】解:∵在△ABC中,AB=BC,∠B=60°,∴△ABC是等边三角形,∴AB=AC=BC=6cm.故答案为6.14.(3分)如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A 旋转后得到△ACE,那么线段DE的长度为2.【解答】解:作EH⊥BC于H,如图,∵△ABC为等边三角形,∴BC=AB=4,∠B=∠ACB=60°,∵D是BC的中点,∴BD=CD=2,∵△ABD绕点A旋转后得到△ACE,∴CE=BD=2,∠ACE=∠B=60°,∴∠ECH=180°﹣∠ACB﹣∠ACE=60°,在Rt△ECH中,∵∠CEH=30°,∴CH=CE=1,EH=CH=,∴DH=DC+CH=2+1=3,在Rt△DHE中,∵EH=,DH=3,∴DE==2.故答案为2.15.(3分)已知x关于的不等式组恰有三个整数解,则a 的取值范围是1<a≤.【解答】解:解不等式+>0得:x>﹣,解不等式3x+5a+4>4(x+1)+3a得:x<2a,∵该不等式组恰好三个整数解,∴2<2a≤3,解得:1<a≤.故答案为:1<a≤.16.(3分)如图,∠MON=30°,A在OM上,OA=2,D在ON上,OD=4,C是OM上任意一点,B是ON上任意一点,则折线ABCD的最短长度为2.【解答】解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.连接DD′,AA′,OA′,OD′.∵OA=OA′,∠AOA′=60°,∴∠OAA′=∠OA′A=60°,∴△ODD′是等边三角形.同理△OAA′也是等边三角形.∴OD'=OD=4,OA′=OA=2,∠D′OA′=90°.∴A′D′==2.三.解答题17.(12分)分解因式(1)x2﹣18x+81(2)﹣9x3y2﹣6x2y2+3xy(3)a2(a﹣b)+b2(b﹣a)(4)(a2﹣3)2﹣4a2.【解答】解:(1)原式=(x﹣9)2,(2)原式=﹣3xy(3x2y+2xy﹣1),(3)原式=(a﹣b)(a2﹣b2)=(a﹣b)2(a+b),(4)原式=[((a2﹣3)+2a][(a2﹣3)﹣2a]=(a﹣1)(a+3)(a+1)(a﹣3).18.(8分)解一元一次不等式及不等式组,并把它的解集在数轴上分别表示出来.(1)﹣≥x﹣(2).【解答】(1)解:去分母,得2(x﹣2)﹣3(3x+5)≥6x﹣2(2﹣x),去括号,得2x﹣4﹣9x﹣15≥6x﹣4+2x,移项,合并同类项得﹣15x≥15,系数化为1,得x≤﹣1.在数轴上表示为:;(2)解:解不等式①得:x≥﹣2.解不等式②得:x<﹣.所以,不等式组的解集为﹣2≤x<﹣.在数轴上表示为:19.(6分)两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)【解答】解:(1)作出线段AB的垂直平分线;(2)作出角的平分线;它们的交点即为所求作的点C(2个).20.(6分)已知关于x,y的方程组的解x,y均为负数,求m的取值范围.【解答】解:两式相加得:3x=3m﹣3x=m﹣1.把x=m﹣1,代入式子得:y=﹣m﹣1∵x,y均为负数∴∴﹣1<m<1.21.(5分)证明:等腰三角形的两腰上的中线相等.【解答】已知:△ABC中,AB=AC,AD=DC,AE=EB,求证:BD=CE.证明:∵AB=AC,AD=DC,AE=EB,∴DC=BE,∠DCB=∠EBC.∵BC=CB,∴△BDC≌△CEB(SAS).∴BD=CE.即等腰三角形的两腰上的中线相等.22.(5分)某工厂生产A、B两种产品共50件,其生产成本与利润如下表:若该工厂计划投入资金不超过40万元,且希望获利超过16万元,问工厂有哪几种生产方案?哪种生产方案获利润最大?最大利润是多少?【解答】解:设生产A产品x件,则生产B产品(50﹣x)件,由题意得,投入资金不超过40万元,且希望获利超过16万元,故可得:,解得:≤x<20,∵x取整数,∴x可取17、18、19,共三种方案:①A 17件,B 33件;②A 18件,B 32件;③A 19件,B 31件.第一种方案获利:0.2×17+0.4×33=16.6万元;第二种方案获利:0.2×18+0.4×32=16.4万元;第三种方案获利:0.2×19+0.4×31=16.2万元;故可得方案一获利最大,最大利润为16.6万元.答:工厂有3种生产方案,第一种方案获利润最大,最大利润是16.6万元.23.(10分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE =BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF 的形状.【解答】证明:(1)∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,∵在△ADB和△CEA中,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)成立.∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD,∵在△ADB和△CEA中,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(3)△DEF是等边三角形.由(2)知,△ADB≌△CEA,BD=AE,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠F AE,∵BF=AF在△DBF和△EAF中,∴△DBF≌△EAF(SAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DF A+∠AFE=∠DF A+∠BFD=60°,∴△DEF为等边三角形.。
2013-2014年陕西省西安市西工大附中八年级上学期期中数学试卷及参考答案

2013-2014学年陕西省西安市西工大附中八年级(上)期中数学试卷一、选择题.1.(3分)的算术平方根是()A.B.C.±2 D.22.(3分)如图所示,△ACB∽△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°3.(3分)下列四个图形中,不是轴对称图形的是()A.B. C.D.4.(3分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°5.(3分)如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为()A.30°B.40°C.50°D.60°6.(3分)如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E.BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组 B.2组 C.3组 D.4组7.(3分)下列说法正确的是()A.带根号的数是无理数B.无限小数是无理数C.是分数D.数轴上的点与实数一一对应8.(3分)△ABC中,∠B=∠C,D为BC上一点,AB上取BF=CD,AC上取CE=BD,则∠FDE等于()A.90°﹣∠A B.90°﹣∠A C.180°﹣∠A D.45°﹣∠A9.(3分)大于且小于的整数的个数有()A.9 B.8 C.7 D.610.(3分)如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是()A.①②③B.①④⑤C.①③④D.③④⑤二、填空题.11.(3分)16的平方根是,﹣125的立方根是.12.(3分)点P(﹣2,3)关于x轴的对称点的坐标是.13.(3分)如图,△ABC中,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,∠DCB=48°,则∠A′DB的度数为.14.(3分)若,则b c+a的值为.15.(3分)如图,AD、CE均是△ABC的高,交于H,且AE=CE,若AB=17,CH=7,则AH的长为.16.(3分)如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:①AC=DE;②CD=AE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的番号有.三、解答题.17.计算题:5﹣10×﹣2﹣+|﹣2|18.如图,C在OB上,E在OA上,∠A=∠B,AE=BC.求证:AC=BE.19.尺规作图:已知线段m,n,∠α,求作△ABC,使AB=,AC=n,∠A=∠α(保留作图痕迹,不写作法)20.如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.(1)求证:△ABE≌△CAD;(2)求∠BFD的度数.21.如图,A、D、E三点在同一直线上,∠BAE=∠CAE,∠BDE=∠CDE,(1)求证:AB=AC;(2)求证:AE⊥BC.22.如图1,在正方形ABCD中,点E、F分别是BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE;②AF⊥DE.(不需要证明).(1)如图2,若点E、F不是正方形ABCD的边的中点,但满足CE=DF,则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图3,若点E、F分别在正方形ABCD的边CB的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.23.如图,已知△ABC和△DFC都是等边三角形,∠ACB=∠DCE=60°,B、C、E 在同一直线上,连接BD和AE(1)求证:AE=BD;(2)求∠AHB的度数;(3)求证:DF=GE.24.已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE.25.点P是△ABC内一点,PG是BC的垂直平分线,∠PBC=∠A,BP、CP的延长线交AC、AB于D、E,求证:BE=CD.2013-2014学年陕西省西安市西工大附中八年级(上)期中数学试卷参考答案与试题解析一、选择题.1.(3分)的算术平方根是()A.B.C.±2 D.2【解答】解:=2,2的算术平方根是.故选:B.2.(3分)如图所示,△ACB∽△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°【解答】解:∵△ACB∽△A′CB′,∴∠ACB=∠A′CB′,∴∠ACB﹣∠A′CB=∠A′CB′﹣∠A′CB,∴∠ACA′=∠BCB′,∵∠BCB′=30°,∴∠ACA′=30°,故选:B.3.(3分)下列四个图形中,不是轴对称图形的是()A.B. C.D.【解答】解:观察图形可知A、B、C都是轴对称图形;D、不是轴对称图形.故选:D.4.(3分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;故选:C.5.(3分)如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为()A.30°B.40°C.50°D.60°【解答】解:∵ED是AC的垂直平分线,∴AE=CE∴∠EAC=∠C,又∵∠B=90°,∠BAE=10°,∴∠AEB=80°,又∵∠AEB=∠EAC+∠C=2∠C,∴∠C=40°.故选:B.6.(3分)如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E.BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组 B.2组 C.3组 D.4组【解答】解:第①组满足SSS,能证明△ABC≌△DEF.第②组满足SAS,能证明△ABC≌△DEF.第③组满足ASA,能证明△ABC≌△DEF.第④组只是SSA,不能证明△ABC≌△DEF.所以有3组能证明△ABC≌△DEF.故符合条件的有3组.故选:C.7.(3分)下列说法正确的是()A.带根号的数是无理数B.无限小数是无理数C.是分数D.数轴上的点与实数一一对应【解答】解:A、带根号的数不一定是无理数,如,故本选项错误,B、无限不循环小数是无理数,故本选项错误,C、是无理数,本选项错误,D、数轴上的点与实数一一对应,故本选项正确,故选:D.8.(3分)△ABC中,∠B=∠C,D为BC上一点,AB上取BF=CD,AC上取CE=BD,则∠FDE等于()A.90°﹣∠A B.90°﹣∠A C.180°﹣∠A D.45°﹣∠A【解答】解:∵∠B=∠C,BF=CD,CE=BD,∴△BFD≌△CDE,∴∠BFD=∠CDE,∴∠FDE=180°﹣∠BDF﹣∠CDE,=180°﹣∠BDF﹣∠BFD,=∠B,=(180°﹣∠A),=90°﹣∠A.故选:B.9.(3分)大于且小于的整数的个数有()A.9 B.8 C.7 D.6【解答】解:﹣2=﹣<﹣=﹣3,3=>=4,∴大于且小于的整数有:﹣3,﹣2,﹣1,0,1,2,3,4,共八个整数.故选:B.10.(3分)如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是()A.①②③B.①④⑤C.①③④D.③④⑤【解答】解:连接CF;∵△ABC是等腰直角三角形,∴∠FCB=∠A=45°,CF=AF=FB;∵AD=CE,∴△ADF≌△CEF(SAS);∴EF=DF,∠CFE=∠AFD;∵∠AFD+∠CFD=90°,∴∠CFE+∠CFD=∠EFD=90°,∴△EDF是等腰直角三角形(故①正确).当D、E分别为AC、BC中点时,四边形CDFE是正方形(故②错误).∵△ADF≌△CEF,=S△ADF∴S四边形CEFD=S△AFC,(故④正确).∴S△CEF由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;即当DF⊥AC时,DE最小,此时DF=BC=4.∴DE=DF=4(故③错误).当△CDE面积最大时,由④知,此时△DEF的面积最小.=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8(故⑤正确).此时S△CDE故选:B.二、填空题.11.(3分)16的平方根是±4,﹣125的立方根是﹣5.【解答】解:∵(±4)2=16,∴16的平方根是±4,∵(﹣5)3=﹣125,∴﹣125的立方根是﹣5,故答案为±4,﹣5.12.(3分)点P(﹣2,3)关于x轴的对称点的坐标是(﹣2,﹣3).【解答】解:点P(﹣2,3)关于x轴的对称,即横坐标不变,纵坐标互为相反数,∴对称点的坐标是(﹣2,﹣3).故答案为:(﹣2,﹣3).13.(3分)如图,△ABC中,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,∠DCB=48°,则∠A′DB的度数为16°.【解答】解:依题意,得∠ACD=∠DCB=48°,又∠A=50°,∴在△ACD中,∠ADC=180°﹣48°﹣50°=82°,又由折叠的性质得∠A′DC=∠ADC=82°,∴∠A′DB=180°﹣∠A′DC﹣∠ADC=16°.故答案为:16°.14.(3分)若,则b c+a的值为﹣3.【解答】解:∵a﹣5≥0,5﹣a≥0,∴a=5,∴+|2c﹣6|=0,∴b+2=0,2c﹣6=0,解得b=﹣2,c=3,∴b c+a=(﹣2)3+5=﹣8+5=﹣3,故答案为﹣3.15.(3分)如图,AD、CE均是△ABC的高,交于H,且AE=CE,若AB=17,CH=7,则AH的长为13.【解答】解:∵AD、CE均是△ABC的高,∴∠AEC=∠ADC=90°,而∠AHE=∠CHD,∴∠EAH=∠HCD,在△AEH和△CEB中,∴△AEH≌△CEB,∴EH=EB,设EH=x,则EB=x,AE=AB﹣BE=17﹣x,CE=x+7,∵AE=CE,∴17﹣x=x+7,∴x=5,∴AE=12,在Rt△AEH中,AH===13.故答案为13.16.(3分)如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:①AC=DE;②CD=AE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的番号有①②④.【解答】解:∵已知DE∥BC,AB∥CD,∴四边形BCDE为平行四边形,∴CB=DE;∵∠A=∠B,∴AC=BC,∴AC=DE,即可得①正确;根据平行线等分线段性质可得AO=CO,∵AB∥CD,∴∠A=∠DCO,又∵∠AOE=∠COD,∴△AOE≌△COD(ASA),∴AE=CD,即可得②正确;OE=OD,O点是DE的中点;即可得④正确;结论③⑤无法证明.故答案填:①②④.三、解答题.17.计算题:5﹣10×﹣2﹣+|﹣2|【解答】解:原式=5×1.2﹣10×(﹣0.3)﹣2×﹣3+2﹣=6+3﹣3﹣3+2﹣=5﹣.18.如图,C在OB上,E在OA上,∠A=∠B,AE=BC.求证:AC=BE.【解答】证明:∵∠A=∠B,∠AFE=∠BFC,∴∠AEF=∠BCF,又AE=BC,∴△AEF≌△BCF,∴EF=CF,AF=BF,∴AF+CF=EF+BF,即AC=BE.19.尺规作图:已知线段m,n,∠α,求作△ABC,使AB=,AC=n,∠A=∠α(保留作图痕迹,不写作法)【解答】解:△ABC就是所求的三角形.20.如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.(1)求证:△ABE≌△CAD;(2)求∠BFD的度数.【解答】(1)证明:∵△ABC为等边三角形,∴∠BAE=∠C=60°,AB=CA,在△ABE和△CAD中,,∴△ABE≌△CAD(SAS).(2)解:∵∠BFD=∠ABE+∠BAD,又∵△ABE≌△CAD,∴∠ABE=∠CAD.∴∠BFD=∠CAD+∠BAD=∠BAC=60°.21.如图,A、D、E三点在同一直线上,∠BAE=∠CAE,∠BDE=∠CDE,(1)求证:AB=AC;(2)求证:AE⊥BC.【解答】证明:(1)∵∠BDE=∠CDE,∠BAE=∠CAE,∴∠ADB=∠ADC,又AD=AD,∴△ADC≌△ADB,∴AB=AC,(2)在△ABC中,AB=AC,∠BAE=∠CAE,∴AE⊥BC.22.如图1,在正方形ABCD中,点E、F分别是BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE;②AF⊥DE.(不需要证明).(1)如图2,若点E、F不是正方形ABCD的边的中点,但满足CE=DF,则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图3,若点E、F分别在正方形ABCD的边CB的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.【解答】解:(1)答:结论①②成立,理由如下:∵DF=CE,AD=DC,且∠ADF=∠DCE,∴△DEC≌△AFD;∴结论①、②成立(1分)(2)结论①、②仍然成立.理由:∵四边形ABCD为正方形,∴AD=DC=CB且∠ADC=∠DCB=90°,在Rt△ADF和Rt△DCE中,AD=DC,∠ADC=∠DCB,CE=DF,∴Rt△ADF≌Rt△DCE(SAS),(3分)∴AF=DE,∴∠DAF=∠CDE,∵∠ADE+∠CDE=90°,∴∠ADE+∠DAF=90°,∴∠AGD=90°,∴AF⊥DE.(5分)23.如图,已知△ABC和△DFC都是等边三角形,∠ACB=∠DCE=60°,B、C、E在同一直线上,连接BD和AE(1)求证:AE=BD;(2)求∠AHB的度数;(3)求证:DF=GE.【解答】(1)证明:∵△ABC与△DEC都是等边三角形,∴∠ACB=∠DCE=60°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴AE=BD;(2)解:由(1)得△BCD≌△ACE,∴∠CAE=∠CBD,又∵∠CBD+∠DBA=60°∴∠CAE+∠ABD=60°.在△ABH中,∠BAC+∠ABD+∠CAE+∠AHB=180°∴∠AHB=60°;(3)证明:由(1)证得:△BCD≌△ACE,∴∠BDC=∠AEC,∵∠ACB=∠DCE=60°,且B、C、E在同一直线上,∴∠ACD=60°,∵DCE是等边三角形,∴DC=CE.在△DFC和△EGC中,,∴△DFC≌△EGC(ASA)∴DF=EG,即DF=GE.24.已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE.【解答】证明:(1)∵CF平分∠BCD,∴∠BCF=∠DCF.在△BFC和△DFC中,∴△BFC≌△DFC(SAS).(2)连接BD.∵△BFC≌△DFC,∴BF=DF,∴∠FBD=∠FDB.∵DF∥AB,∴∠ABD=∠FDB.∴∠ABD=∠FBD.∵AD∥BC,∴∠BDA=∠DBC.∵BC=DC,∴∠DBC=∠BDC.∴∠BDA=∠BDC.又∵BD是公共边,∴△BAD≌△BED(ASA).∴AD=DE.25.点P是△ABC内一点,PG是BC的垂直平分线,∠PBC=∠A,BP、CP的延长线交AC、AB于D、E,求证:BE=CD.【解答】证明:作BF⊥CE于F点,CM⊥BD于M点则∠PFB=∠PMC=90°.∵PG是BC的垂直平分线,∴PB=PC.在△PBF和△PCM中,,∴△PBF≌△PCM(AAS),∴BF=CM;∵PB=PC,∴∠PBC=∠PCB=∠BPE.∵∠PBC=∠A,∴∠A=∠BPE.∴∠EPD+∠BPE=∠EPD+∠A=180°,∴∠AEP+∠ADP=180°.又∠AEP=∠BEF,∠ADP+∠CDM=180°,∴∠BEF=∠CDM.在△BEF和△CDM中,,∴△BEF≌△CDM(AAS).∴BE=CD.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
2013-2014学年陕西省西安市西工大附中七年级上学期数学期末试卷带答案

2013-2014学年陕西省西安市西工大附中七年级(上)期末数学试卷一、选择题.1.(3分)|﹣2|=()A.2B.﹣2C.D.2.(3分)在墙壁上固定一根横放的木条,则至少需要钉子的枚数是()A.1枚B.2枚C.3枚D.任意枚3.(3分)下列方程为一元一次方程的是()A.y+3=0B.x+2y=3C.x2=2x D.+y=24.(3分)下列各组数中,互为相反数的是()A.﹣(﹣1)与1B.(﹣1)2与1C.|﹣1|与1D.﹣12与1 5.(3分)下列各组单项式中,为同类项的是()A.a3与a2B.a2与2a2C.2xy与2x D.﹣3与a 6.(3分)如图,数轴A、B上两点分别对应实数a、b,则下列结论正确的是()A.a+b>0B.ab=0C.﹣<0D.+>0 7.(3分)下列各图中,可以是一个正方体的平面展开图的是()A.B.C.D.8.(3分)把两块三角板按如图所示那样拼在一起,则∠ABC等于()A.70°B.90°C.105°D.120°9.(3分)在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为()A.69°B.111°C.141°D.159°10.(3分)一件夹克衫先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是()A.(1+50%)x×80%=x﹣28B.(1+50%)x×80%=x+28C.(1+50%x)×80%=x﹣28D.(1+50%x)×80%=x+2811.(3分)轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A 港和B港相距x千米.根据题意,可列出的方程是()A.B.C.D.12.(3分)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是()A.110B.158C.168D.178二、填空题.13.(3分)﹣3的倒数是.14.(3分)单项式﹣xy2的系数是.15.(3分)若x=2是方程8﹣2x=ax的解,则a=.16.(3分)计算:15°37′+42°51′=.17.(3分)青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示为.18.(3分)已知a﹣b=2,那么2a﹣2b+5=.19.(3分)已知y1=x+3,y2=2﹣x,当x=时,y1比y2大5.20.(3分)根据图中提供的信息,可知一个杯子的原价是元.三、解答题.21.计算:(﹣1)3﹣×[2﹣(﹣3)2].22.一个角的余角比这个角的少30°,请你计算出这个角的大小.23.化简求值:(﹣4x2+2x﹣8)﹣(x﹣1),其中x=.24.解方程:﹣=1.25.一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位…(1)写出第一次移动后这个点在数轴上表示的数为;(2)写出第二次移动结果这个点在数轴上表示的数为;(3)写出第五次移动后这个点在数轴上表示的数为;(4)写出第n次移动结果这个点在数轴上表示的数为;(5)如果第m次移动后这个点在数轴上表示的数为56,求m的值.26.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.27.如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.28.某中学为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元.(1)求钢笔和毛笔的单价各为多少元?(2)①学校仍需要购买上面的两种笔共105支(每种笔的单价不变).陈老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领2447元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.②陈老师突然想起,所做的预算中还包括校长让他买的一支签字笔.如果签字笔的单价为小于10元的整数,请通过计算,直接写出签字笔的单价可能为元.2013-2014学年陕西省西安市西工大附中七年级(上)期末数学试卷参考答案与试题解析一、选择题.1.(3分)|﹣2|=()A.2B.﹣2C.D.【解答】解:根据绝对值的性质可知:|﹣2|=2.故选:A.2.(3分)在墙壁上固定一根横放的木条,则至少需要钉子的枚数是()A.1枚B.2枚C.3枚D.任意枚【解答】解:∵两点确定一条直线,∴至少需要2枚钉子.故选:B.3.(3分)下列方程为一元一次方程的是()A.y+3=0B.x+2y=3C.x2=2x D.+y=2【解答】解:A、正确;B、含有2个未知数,不是一元一次方程,选项错误;C、最高次数是2次,不是一元一次方程,选项错误;D、不是整式方程,不是一元一次方程,选项错误.故选:A.4.(3分)下列各组数中,互为相反数的是()A.﹣(﹣1)与1B.(﹣1)2与1C.|﹣1|与1D.﹣12与1【解答】解:A、﹣(﹣1)=1,所以A选项错误;B、(﹣1)2=1,所以B选项错误;C、|﹣1|=1,所以C选项错误;D、﹣12=﹣1,﹣1与1互为相反数,所以D选项正确.故选:D.5.(3分)下列各组单项式中,为同类项的是()A.a3与a2B.a2与2a2C.2xy与2x D.﹣3与a【解答】解:A、相同字母的指数不同不是同类项,故A错误;B、字母相同且相同字母的指数也相同,故B正确;C、字母不同的项不是同类项,故C错误;D、字母不同的项不是同类项,故D错误;故选:B.6.(3分)如图,数轴A、B上两点分别对应实数a、b,则下列结论正确的是()A.a+b>0B.ab=0C.﹣<0D.+>0【解答】解:A、∵b<﹣1<0<a<1,∴|b|>|a|,∴a+b<0,故选项A错误;B、∵b<0<a,∴ab<0,故选项B错误;C、∵b<0<a,∴﹣>0,故选项C错误;D、∵b<﹣1<0<a<1,∴+>0,故选项D正确.故选:D.7.(3分)下列各图中,可以是一个正方体的平面展开图的是()A.B.C.D.【解答】解:A出现了“田”字格,故不能,B折叠后上面两个面无法折起来,而且下边没有面,不能折成正方体,D折叠后,上面的两个面重合,不能折成正方体.故选:C.8.(3分)把两块三角板按如图所示那样拼在一起,则∠ABC等于()A.70°B.90°C.105°D.120°【解答】解:∠ABC=30°+90°=120°.故选:D.9.(3分)在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为()A.69°B.111°C.141°D.159°【解答】解:由题意得:∠1=54°,∠2=15°,∠3=90°﹣54°=36°,∠AOB=36°+90°+15°=141°,故选:C.10.(3分)一件夹克衫先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是()A.(1+50%)x×80%=x﹣28B.(1+50%)x×80%=x+28C.(1+50%x)×80%=x﹣28D.(1+50%x)×80%=x+28【解答】解:标价为:x(1+50%),八折出售的价格为:(1+50%)x×80%;∴可列方程为:(1+50%)x×80%=x+28,故选:B.11.(3分)轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A 港和B港相距x千米.根据题意,可列出的方程是()A.B.C.D.【解答】解:设A港和B港相距x千米,可得方程:.故选:A.12.(3分)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是()A.110B.158C.168D.178【解答】解:根据排列规律,10下面的数是12,10右面的数是14,∵8=2×4﹣0,22=4×6﹣2,44=6×8﹣4,∴m=12×14﹣10=158.故选:B.二、填空题.13.(3分)﹣3的倒数是﹣.【解答】解:﹣3的倒数是﹣.14.(3分)单项式﹣xy2的系数是﹣.【解答】解:单项式﹣xy2的系数是﹣,故答案为:﹣.15.(3分)若x=2是方程8﹣2x=ax的解,则a=2.【解答】解:把x=2代入方程,得:8﹣4=2a,解得:a=2.故答案是:2.16.(3分)计算:15°37′+42°51′=58°28′.【解答】解:∵37+51=88,∴15°37′+42°51′=58°28′.故答案为:58°28′.17.(3分)青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示为 2.5×106.【解答】解:2 500 000=2.5×106,故答案为:2.5×106.18.(3分)已知a﹣b=2,那么2a﹣2b+5=9.【解答】解:∵a﹣b=2,∴原式=2(a﹣b)+5=4+5=9,故答案为:919.(3分)已知y1=x+3,y2=2﹣x,当x=2时,y1比y2大5.【解答】解:根据题意得:(x+3)﹣(2﹣x)=5,去括号得:x+3﹣2+x=5,移项合并得:2x=4,解得:x=2,则当x=2时,y1比y2大5.故答案为:220.(3分)根据图中提供的信息,可知一个杯子的原价是10元.【解答】解:设一个杯子x元,则一个暖瓶(40﹣x)元,根据题意得:3x+2(40﹣x)=90解得:x=10.故答案为:10.三、解答题.21.计算:(﹣1)3﹣×[2﹣(﹣3)2].【解答】解:原式=﹣1﹣×(2﹣9)=﹣1+=.22.一个角的余角比这个角的少30°,请你计算出这个角的大小.【解答】解:设这个角的度数为x,则它的余角为(90°﹣x),由题意得:x﹣(90°﹣x)=30°,解得:x=80°.答:这个角的度数是80°.23.化简求值:(﹣4x2+2x﹣8)﹣(x﹣1),其中x=.【解答】解:原式=﹣x2+x﹣2﹣x+1=﹣x2﹣1,将x=代入得:﹣x2﹣1=﹣.故原式的值为:﹣.24.解方程:﹣=1.【解答】解:去分母得:2×(5x+1)﹣(2x﹣1)=6,去括号得,10x+2﹣2x+1=6移项、合并同类项得,8x=3系数化为1得,x=.25.一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位…(1)写出第一次移动后这个点在数轴上表示的数为3;(2)写出第二次移动结果这个点在数轴上表示的数为4;(3)写出第五次移动后这个点在数轴上表示的数为7;(4)写出第n次移动结果这个点在数轴上表示的数为n+2;(5)如果第m次移动后这个点在数轴上表示的数为56,求m的值.【解答】解:(1)第一次移动后这个点在数轴上表示的数是3;(2)第二次移动后这个点在数轴上表示的数是4;(3)第五次移动后这个点在数轴上表示的数是7;(4)第n次移动后这个点在数轴上表示的数是n+2;(5)m+2=56,解得m=54.故答案为3,4,7,n+2,54.26.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.【解答】解:∵∠AOB=90°,OC平分∠AOB∴∠BOC=∠AOB=45°(3分)∵∠BOD=∠COD﹣∠BOC=90°﹣45°=45°∠BOD=3∠DOE(6分)∴∠DOE=15°(8分)∴∠COE=∠COD﹣∠DOE=90°﹣15°=75°(10分)故答案为75°.27.如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.【解答】解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.∵点E、点F分别为AB、CD的中点,∴AE=AB=1.5xcm,CF=CD=2xcm.∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5xcm.∵EF=10cm,∴2.5x=10,解得:x=4.∴AB=12cm,CD=16cm.28.某中学为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元.(1)求钢笔和毛笔的单价各为多少元?(2)①学校仍需要购买上面的两种笔共105支(每种笔的单价不变).陈老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领2447元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.②陈老师突然想起,所做的预算中还包括校长让他买的一支签字笔.如果签字笔的单价为小于10元的整数,请通过计算,直接写出签字笔的单价可能为2或6元.【解答】解:(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元.由题意得:30x+45(x+4)=1755,解得:x=21,∴毛笔的单价为:x+4=25.答:钢笔的单价为21元,毛笔的单价为25元.(2)①设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105﹣y)支.根据题意,得21y+25(105﹣y)=2447.解之得:y=44.5 (不符合题意).∴陈老师肯定搞错了.②设单价为21元的钢笔为z支,签字笔的单价为a元,则根据题意,得21z+25(105﹣z)=2447﹣a.∴4z=178+a,∵a、z都是整数,∴178+a应被4整除,∴a为偶数,又因为a为小于10元的整数,∴a可能为2、4、6、8.当a=2时,4z=180,z=45,符合题意;当a=4时,4z=182,z=45.5,不符合题意;当a=6时,4z=184,z=46,符合题意;当a=8时,4z=186,z=46.5,不符合题意.所以签字笔的单价可能2元或6元.故答案为:2元或6元.附赠:数学考试技巧一、心理准备细心+认真=成功!1、知己知彼,百战百胜。
陕西省西工大附中2013届高三上学期第一次适应性训练数学理试题含答案

2013年普通高等学校招生全国统一考试西工大附中适应性训练高三数学(理科)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。
考试时间120分钟第Ⅰ卷(选择题 共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{{},2013A y y B x x m ===-<,若A B A =,则m 的取值范围是( )A .[]2012,2013-B .()2012,2013-C .[]2013,2011-D .()2013,2011- 2.若1tan 3,tan θθ+=则sin 2θ=( ) A . 15 B . 13 C . 23 D . 123.已知,a b R ∈,命题“若1a b +=,则2212a b +≥”的否命题是( ) A .若1a b +≠,则2212a b +< B . 若1a b +=,则2212a b +< C .若2212a b +<,则1a b +≠ D . 若2212a b +≥,则1a b += 4.由曲线x x y 22-=与直线0=+y x 所围成的封闭图形的面积为( )A .32 B .65 C .31 D .61 5. 函数()f x = )A .[]1,2B .[]0,2 C.(D.⎡⎣6. 设0.50.50.30.5,0.3,log 0.2a b c ===,则,,a b c 的大小关系是( ) A .a b c >> B . a b c << C . c b a << D .b a c <<7.已知某人每天早晨乘坐的某一班次公共汽车的准时到站的概率为35,则他在3天乘车中,此班次公共汽车至少有2天准时到站的概率为( ) A .36125 B . 54125 C . 81125 D . 271258.已知两个等差数列{}n a 和{}n b 的前n 项和分别为n A 和n B ,且7453n n A n B n +=+,则使得nna b 为整数的正整数n 的个数是( ) A .2 B .3 C .4 D .59.已知函数()ln ,00,0x x f x x ⎧≠⎪=⎨=⎪⎩,则方程()()20f x f x -=的不相等的实根个数为( )A .5B .6C .7D .810.已知21,F F 分别为双曲线12222=-by a x )0,0(>>b a 的左、右焦点,P 为双曲线左支上任意一点,若||||122PF PF 的最小值为a 8,则双曲线离心率e 的取值范围是( )A.),1(+∞B.]3,0(C.]3,1(D.]2,1(第Ⅱ卷(非选择题 共100分)二.填空题:本大题共5小题,每小题5分,共25分.将答案填写在题中的横线上.11.如图,在四棱锥P-ABCD 中,底面ABCD 是边长为m 的正方形, PD ⊥底面ABCD,且若在这个四棱锥内放一个球,则此球的最大半径是 . 12. 已知直线()()1:3410l k x k y -+-+=与()2:23230l k x y --+=平行,则k 的值是 .13. 已知实数,x y 满足121y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩,如果目标函数z x y =-的最小值为-1,则实数m = .14. 已知()13nx +的展开式中,末三项的二项式系数的和等于121,则展开式中系数最大的项为 .15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)A .(不等式选做题)不等式|21|1x x --<的解集是 ;CBB .(几何证明选做题) 如图,过点P 作圆O 的割线PAB 与切线PE ,E 为切点,连接,AE BE ,APE ∠的平分线与,AE BE 分别交于点,CD ,若030AEB ∠=,则PCE ∠= ;C.(极坐标系与参数方程选做题) 若,M N 分别是曲线2cos ρθ=和sin()4πρθ-=上的动点,则,M N 两点间的距离的最小值是 ; 三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知向量()2sin a x x =,()sin ,2sin b x x =,函数()f x a b =⋅ (Ⅰ)求)(x f 的单调递增区间;(Ⅱ)若不等式]2,0[)(π∈≥x m x f 对都成立,求实数m 的最大值.17.(本小题满分12分).一个口袋中装有大小相同的2个红球,3个黑球和4个白球,从口袋中一次摸出一个球,摸出的球不再放回.(Ⅰ)连续摸球2次,求第一次摸出黑球,第二次摸出白球的概率; (Ⅱ)如果摸出红球,则停止摸球,求摸球次数不超过3次的概率. 18.(本小题满分12分).如图所示,等腰△ABC 的底边AB=66,高CD=3,点E 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF ⊥AB.现沿EF 将△BEF 折起到△PEF 的位置,使PE ⊥AE.记BE x =,用()V x 表示四棱锥P-ACFE 的体积. (Ⅰ)求 ()V x 的表达式;(Ⅱ)当x 为何值时,()V x 取得最大值?(Ⅲ)当V(x)取得最大值时,求异面直线AC 与PF 所成角的余弦值 19.(本小题满分12分)设函数2()(0),f x ax bx c a =++≠曲线y =f (x )通过点(0,2a +3),且在点 (-1,f (-1))处的切线垂直于y 轴.(Ⅰ)用a 分别表示b 和c ;(Ⅱ)当bc 取得最小值时,求函数g (x )= ()x f x e --的单调区间. 20.(本小题满分13分)已知直线1y x =-+与椭圆12222=+by a x ()0a b >>相交于A 、B 两点.(1)若椭圆的离心率为33,焦距为2,求线段AB 的长; (2)若向量OA 与向量OB 互相垂直(其中O 为坐标原点),当椭圆的离心率]22,21[∈e 时,求椭圆长轴长的最大值.21.(本小题满分14分)数列{}n a 的各项均为正数,n S 为其前n 项和,对于任意*N n ∈,总有22n n n S a a =+.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ) 设正数数列{}n c 满足())(,*11N n c a n n n ∈=++,求数列{}n c 中的最大项;(Ⅲ) 求证:444412311111110n n T a a a a =++++<.2013年普通高等学校招生全国统一考试西工大附中适应性训练高三数学(理科)参考答案本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。
2013-2014学年陕西省西安市西工大附中高一(上)期中数学试卷(解析版)
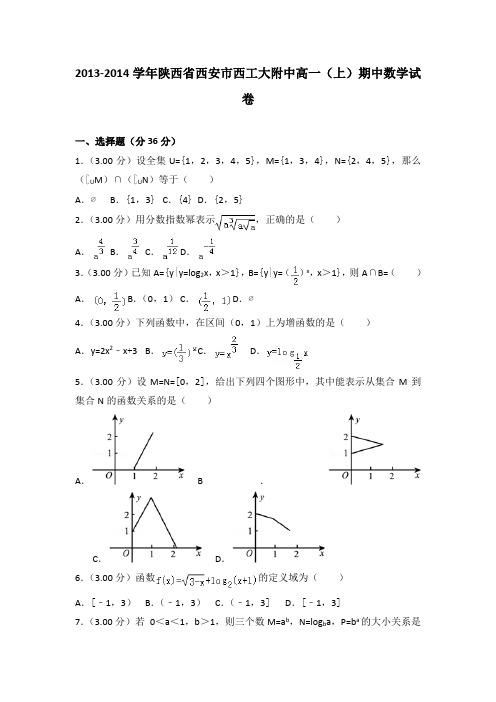
2013-2014学年陕西省西安市西工大附中高一(上)期中数学试卷一、选择题(分36分)1.(3.00分)设全集U={1,2,3,4,5},M={1,3,4},N={2,4,5},那么(∁U M)∩(∁U N)等于()A.∅B.{1,3}C.{4}D.{2,5}2.(3.00分)用分数指数幂表示,正确的是()A.B.C. D.3.(3.00分)已知A={y|y=log2x,x>1},B={y|y=()x,x>1},则A∩B=()A. B.(0,1) C. D.∅4.(3.00分)下列函数中,在区间(0,1)上为增函数的是()A.y=2x2﹣x+3 B.C.D.5.(3.00分)设M=N=[0,2],给出下列四个图形中,其中能表示从集合M到集合N的函数关系的是()A.B.C.D.6.(3.00分)函数的定义域为()A.[﹣1,3)B.(﹣1,3)C.(﹣1,3]D.[﹣1,3]7.(3.00分)若0<a<1,b>1,则三个数M=a b,N=log b a,P=b a的大小关系是()A.M<N<P B.N<M<P C.P<M<N D.P<N<M8.(3.00分)函数y=x2+2(a﹣2)x+5在区间上(4,+∞)是增函数,则实数a 的取值范围是()A.(﹣∞,﹣2]B.[﹣2,+∞)C.(﹣∞,﹣6]D.[﹣6,+∞)9.(3.00分)若f:A→B能构成映射,则下列说法中不正确的是()A.A中的任一元素在B中必须有像且必须是唯一的B.B中的元素可以在A中有多个原像C.B中的元素可以在A中无原像D.集合B就是像的集合10.(3.00分)已知(x,y)在映射f作用下的像是(x+y,x﹣y),则(1,2)关于f的原像是()A.(1,2) B.(3,﹣1)C.D.11.(3.00分)已知定义在R上的偶函数f(x)在(﹣∞,0]上是减少的,且f ()=0,则不等式f(x)>0的解集为()A.(﹣∞,﹣)B.(,+∞)C.(﹣∞,﹣)∪(,+∞)D.(﹣,)12.(3.00分)函数y=﹣2x2的图象是由函数y=﹣2x2+4x+6经过怎样的变换得到的()A.向左平移1个单位,向上平移8个单位B.向右平移1个单位,向上平移8个单位C.向左平移1个单位,向下平移8个单位D.向右平移1个单位,向下平移8个单位二、填空题(分18分)13.(3.00分)已知集合A={x|ax2+(a+1)x+1=0},若集合A中只有一个元素,则实数a=.14.(3.00分)计算(lg2)2+lg2•lg50+lg25=.15.(3.00分)已知函数,则f(5)=.16.(3.00分)函数y=()的单调递增区间为.17.(3.00分)不等式21﹣2x<(0.5)2﹣x的解集为.18.(3.00分)已知函数f(x)=,若f(x)=5,则x=.三、解答题(共46分)19.(8.00分)在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.(Ⅰ)求四边形FDEC的面积函数f(x);(Ⅱ)当x为何值时,f(x)最大?并求出f(x)的最大值.20.(8.00分)已知奇函数f(x)是定义在区间(﹣3,3)上的减函数,若f(m ﹣2)+f(2m﹣1)>f(0),求实数m的取值范围.21.(10.00分)已知偶函数f(x)在区间[3,5]是增加的,用定义证明f(x)在区间[﹣5,﹣3]上是减少的.22.(10.00分)已知函数f(x)=a+是奇函数,(Ⅰ)求实数a的值,并证明你的结论;(Ⅱ)求函数y=f(x)的值域.23.(10.00分)已知函数f(x)=ln(a x﹣b x)(0<b<1<a)(Ⅰ)求函数f(x)的定义域G,并判断f(x)在G上的单调性;(Ⅱ)当a、b满足什么条件时,f(x)在区间[1,+∞)上恒取正值.2013-2014学年陕西省西安市西工大附中高一(上)期中数学试卷参考答案与试题解析一、选择题(分36分)1.(3.00分)设全集U={1,2,3,4,5},M={1,3,4},N={2,4,5},那么(∁U M)∩(∁U N)等于()A.∅B.{1,3}C.{4}D.{2,5}【解答】解:∵∁U M={2,5},∁U N={1,3},∴(∁U M)∩(∁U N)=∅.故选:A.2.(3.00分)用分数指数幂表示,正确的是()A.B.C. D.【解答】解:====.故选:B.3.(3.00分)已知A={y|y=log2x,x>1},B={y|y=()x,x>1},则A∩B=()A. B.(0,1) C. D.∅【解答】解:∵,∴=.故选:A.4.(3.00分)下列函数中,在区间(0,1)上为增函数的是()A.y=2x2﹣x+3 B.C.D.【解答】解:∵y=2x2﹣x+3的对称轴x=,∴在区间(0,1)上不是增函数,故A错;又,故B错;,故D错,在[0,+∞)单调递增,C故正确.故选C.5.(3.00分)设M=N=[0,2],给出下列四个图形中,其中能表示从集合M到集合N的函数关系的是()A.B.C.D.【解答】解:因为一个x只能对应一个y,所以排除B;A项中的x只有[1,2]间的元素有y对应,故不满足M中元素全部对应出去,故排除A;其中C,D都满足函数对应定义中的两条,故CD都是函数,但C的函数的N超出[0,2].故选:D.6.(3.00分)函数的定义域为()A.[﹣1,3)B.(﹣1,3)C.(﹣1,3]D.[﹣1,3]【解答】解:由题意得:,解得﹣1<x≤3.故选:C.7.(3.00分)若0<a<1,b>1,则三个数M=a b,N=log b a,P=b a的大小关系是()A.M<N<P B.N<M<P C.P<M<N D.P<N<M【解答】解:由于0<a<1,b>1,N=log b a<0;P=b a>1;M=a b∈(0,1)所以N<M<P故选:B.8.(3.00分)函数y=x2+2(a﹣2)x+5在区间上(4,+∞)是增函数,则实数a 的取值范围是()A.(﹣∞,﹣2]B.[﹣2,+∞)C.(﹣∞,﹣6]D.[﹣6,+∞)【解答】解:∵函数y=x2+2(a﹣2)x+5,∴函数y=x2+2(a﹣2)x+5图象是抛物线,开口向上,对称轴方程为:x=,∴函数y=x2+2(a﹣2)x+5在区间[2﹣a,+∞)上单调递增.∵函数y=x2+2(a﹣2)x+5在区间上(4,+∞)是增函数,∴2﹣a≤4,∴a≥﹣2.故选:B.9.(3.00分)若f:A→B能构成映射,则下列说法中不正确的是()A.A中的任一元素在B中必须有像且必须是唯一的B.B中的元素可以在A中有多个原像C.B中的元素可以在A中无原像D.集合B就是像的集合【解答】解:根据映射的定义,对于两个集合A,B,对于集合A中的每一个元素,在集合B中都有唯一的元素和它对应,A中的任意一元素在B中都必须有像且唯一;故A正确A中的多个元素可以在B中有相同的像;故B正确像的集合就是集合B的子集,B中的元素可以在A中无原像,故C正确,D错误,故选:D.10.(3.00分)已知(x,y)在映射f作用下的像是(x+y,x﹣y),则(1,2)关于f的原像是()A.(1,2) B.(3,﹣1)C.D.【解答】解:由题意可得x+y=1,x﹣y=2,解得x=,y=﹣,故选:C.11.(3.00分)已知定义在R上的偶函数f(x)在(﹣∞,0]上是减少的,且f ()=0,则不等式f(x)>0的解集为()A.(﹣∞,﹣)B.(,+∞)C.(﹣∞,﹣)∪(,+∞)D.(﹣,)【解答】解:∵函数f(x)是定义在R上的偶函数,∴f(﹣x)=f(x),函数图象关于y轴对称.∵函数f(x)在(﹣∞,0]上是单调递减的,∴函数f(x)在(0,+∞)上单调递增.∵f()=0,∴函数f(x)的图象经过点()和(﹣).∴当x<﹣时,f(x)>0,当﹣<x≤0时,f(x)<0,当0<x<时,f(x)<0,当x>时,f(x)>0,∴不等式f(x)>0的解集为{x|x<﹣或x>},故选:C.12.(3.00分)函数y=﹣2x2的图象是由函数y=﹣2x2+4x+6经过怎样的变换得到的()A.向左平移1个单位,向上平移8个单位B.向右平移1个单位,向上平移8个单位C.向左平移1个单位,向下平移8个单位D.向右平移1个单位,向下平移8个单位【解答】解:∵y=﹣2x2+4x+6=﹣2(x﹣1)2+8,∴y=﹣2x2的图象可看作由函数y=﹣2x2+4x+6经过向左平移1个单位,向下平移8个单位得到,故选:C.二、填空题(分18分)13.(3.00分)已知集合A={x|ax2+(a+1)x+1=0},若集合A中只有一个元素,则实数a=0或1.【解答】因为集合A={x|ax2+(a+1)x+1=0}有且只有一个元素,当a=0时,ax2+(a+1)x+1=0只有一个解x=﹣1,当a≠0时,一元二次方程只有一个元素则方程有重根,即△=(a+1)2﹣4a=0即a=1.所以实数a=0或1.故答案为:0或1.14.(3.00分)计算(lg2)2+lg2•lg50+lg25=2.【解答】解:原式=2 lg5+lg2•(1+lg5)+(lg2)2=2 lg5+lg2(1+lg5+lg2)=2 lg5+2 lg2=2;故答案为2.15.(3.00分)已知函数,则f(5)=.【解答】解:由题意可得,f(5)=f(5﹣3)=f(2)=f(2﹣3)=f(﹣1)=2﹣1=故答案为:16.(3.00分)函数y=()的单调递增区间为[1,+∞).【解答】解:令t=2x﹣x2=﹣(x﹣1)2+1,则y=,故本题即求函数t的减区间.再利用二次函数的性质可得t=2x﹣x2的减区间为[1,+∞),故答案为:[1,+∞).17.(3.00分)不等式21﹣2x<(0.5)2﹣x的解集为(1,+∞).【解答】解:不等式21﹣2x<(0.5)2﹣x等价为21﹣2x<2x﹣2,则1﹣2x<x﹣2,即3x>3,解得x>1,故不等式的解集为(1,+∞),故答案为:(1,+∞)18.(3.00分)已知函数f(x)=,若f(x)=5,则x=1或﹣2.【解答】解:当x>1时,f(x)=﹣x+1,若f(x)=5,则﹣x+1=5,解得x=﹣4,不满足要求;当x=1时,f(x)=5,若f(x)=5,则x=1,满足要求;当x<1时,f(x)=x2+1,若f(x)=5,则x2+1=5,解得x=±2,∴x=﹣2;综上,x的值为1或﹣2,故答案为:1或﹣2三、解答题(共46分)19.(8.00分)在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.(Ⅰ)求四边形FDEC的面积函数f(x);(Ⅱ)当x为何值时,f(x)最大?并求出f(x)的最大值.【解答】解:(1)设设CE=x.则AE=3﹣x,∵=,∴EF=4﹣,0<x<3,∴四边形FDEC的面积函数f(x)=x(4﹣),0<x<3,(2)∵f(x)=x(4﹣)=12××(1﹣)≤12×=3,0<x<3,∴当=时,即x=时,等号成立.∴当x=时,f(x)最大=3.20.(8.00分)已知奇函数f(x)是定义在区间(﹣3,3)上的减函数,若f(m ﹣2)+f(2m﹣1)>f(0),求实数m的取值范围.【解答】解:由题意,∵f(x)是奇函数,∴f(0)=0,∴f(m﹣2)+f(2m﹣1)>f(0)可化为f(m﹣2)+f(2m﹣1)>0,即f(m﹣2)>﹣f(2m﹣1),即f(m﹣2)>f(1﹣2m),又∵f(x)是定义在区间(﹣3,3)上的减函数,∴﹣3<m﹣2<1﹣2m<3,解得,﹣1<m<1.21.(10.00分)已知偶函数f(x)在区间[3,5]是增加的,用定义证明f(x)在区间[﹣5,﹣3]上是减少的.【解答】证明:令﹣5≤m<n≤﹣3,则5≥﹣m>﹣n≥3,由于f(x)在区间[3,5]是增加的,即有f(﹣m)>f(﹣n),由偶函数f(x),得f(﹣m)=f(m),f(﹣n)=f(n),即有f(m)>f(n),则f(x)在区间[﹣5,﹣3]上是减少的.22.(10.00分)已知函数f(x)=a+是奇函数,(Ⅰ)求实数a的值,并证明你的结论;(Ⅱ)求函数y=f(x)的值域.【解答】解:(Ⅰ)∵函数f(x)=a+是奇函数,∴f(﹣x)=﹣f(x),∴a+=﹣(a+),∴∴a=.(Ⅱ)由(Ⅰ)知:函数函数f(x)=+.∵2x>0,∴2x﹣1>﹣1.∴﹣1<2x﹣1<0或2x﹣1>0,∴或,∴+或+.∴函数y=f(x)的值域为:().23.(10.00分)已知函数f(x)=ln(a x﹣b x)(0<b<1<a)(Ⅰ)求函数f(x)的定义域G,并判断f(x)在G上的单调性;(Ⅱ)当a、b满足什么条件时,f(x)在区间[1,+∞)上恒取正值.【解答】解:(Ⅰ)由a x﹣b x>0,得()x>1,由于0<b<1<a,则>1,即有x>0,则定义域为(0,+∞);由于0<b<1<a,则a x递增,b x递减,则a x﹣b x递增,即有f(x)在(0,+∞)上递增;(Ⅱ)由于f(x)在(0,+∞)上递增,则f(x)在区间[1,+∞)上恒取正值,即为f(x)≥f(1)=ln(a﹣b),即有ln(a﹣b)>0,即有a﹣b>1.则有当a、b满足a﹣b>1时,f(x)在区间[1,+∞)上恒取正值.。
陕西省西工大附中2012-2013学年高二上学期期中考试物理试题 含答案

2012—-2013学年度第一学期模块质量检测试卷高二物理(试题卷)试卷说明:(1)考试时间100分钟,试卷满分100分.(2)答案一律答在答题卷相应位置上。
一、选择题(本题共10小题,在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错的得0分)1.关于磁场和磁感线的描述,下列说法中正确的是 A .磁感线总是从磁体的N 极出发,终止于S 极B .磁场的方向就是通电导体在磁场中某点受磁场作用力的方向C .沿磁感线方向,磁感应强度逐渐减弱D .通电导线在磁场强的地方受力可能比在磁场弱的地方受力小 2.电子在匀强磁场中做匀速圆周运动,下列说法中正确的是 A .速率越大,周期就越大 B .速率越小,周期就越大 C .速度方向与磁场方向垂直 D .速度方向与磁场方向平行3.下列四副图关于各物理量方向间的关系中,正确的是4.如图甲所示为一正方形线圈,垂直线圈平面有一随时间呈正弦规律变化的磁场,如图乙所示,规定垂直纸面向里为磁场正方向,则关于感应电流的大小和方F CDAB向说法正确的是A .0~t 1时间内,电流为逆时针方向,t 1时刻电流最大B .t 1~t 2时间内,电流为顺时针方向,t 2时刻电流最大C .t 2~t 3时间内,电流为逆时针方向,t 3时刻电流最大D .t 3~t 4时间内,电流为顺时针方向,t 4时刻电流最大5.如图所示,匀强磁场的边界为直角三角形abc ,一束带正电的粒子以不同的速度v 沿bc 从b 点射入磁场,不计粒子的重力,关于粒子在磁场中的运动情况下列说法中正确的是A .入射速度越大的粒子,其运动时间越长B .入射速度越大的粒子,其运动轨迹越长C .从ab 边出射的粒子的运动时间都相等D .从ac 边出射的粒子的运动时间都相等6.一条长直导线中通有电流,电流方向如图所示,一矩形导线框与长直导线处在同一平面内,则下列说法中不正确的是A .若线框以AB 边为轴转动,线框中一定会产生感应电流 B .若线框以AD 为轴转动,线框中一定会产生感应电流C .若线框以长直导线为轴转动,线框中一定会产生感应电流D .若长直导线以AD 边为轴转动,线框中一定会产生感应电流 7.真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m ,带电量为q 的物体以速度v 在竖直平面内做半径为R 的匀速圆周运动,假设t =0时刻物IABCD体在轨迹最低点且重力势能为零,电势能也为零,那么,下列说法正确的是A .物体带正电且逆时针转动B .物体运动的过程中,机械能守恒,且机械能为221mvE =C .物体运动的过程中,机械能不守恒,且在最高点机械能最大D .物体运动的过程中,机械能不守恒,且在最低点机械能最大8.如图所示,L 1和L 2两盏灯的规格完全相同,线圈L 的直流电阻不计。
西工大附中2013届第十一次模考理综试题

D.弹簧的弹性势能最大时圆环动能最大
18.如图所示,水平面内有一平行金属导轨,导轨光滑且电阻不 计。匀强磁场与导轨垂直。阻值为 R 的导体棒垂直于导轨静止放 置,且与导轨良好接触。t=0 时,将开关 S 由 1 掷到 2。Q、i、v 和 a 分别表示电容器所带的电荷量、棒中的电流、棒的速度和加速度。则下列图象正确的是 ( )
16. 假设有一载人宇宙飞船在距地面高度为 4200km 的赤道上空绕地球匀速圆周运动,地 球半径约为 6400km,地球同步卫星距地面高 36000km,宇宙飞船和一地球同步卫星绕地球 同向运动。每当二者相距最近时,宇宙飞船就向同步卫星发射一信号,然后再由同步卫星将 信号发送到地面接收站。某时刻二者相距最远,从此刻开始,在一昼夜的时间内,接收站共 接收到信号的次数为( ) A.4 次 B.6 次 C.7 次 D.8 次 17.如图所示,倾角α=30°的固定光滑倾斜杆上套有一个质量为 m 的圆环,圆环与竖直放 置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的 A 点,开始弹簧恰好处于原长 h .现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的 重力加速度大小为 g . 则在圆环下滑的整个过程中 ( ) A.圆环与弹簧和地球组成的系统机械能守恒 B.弹簧的弹性势能先增大后减小 C.弹簧的弹性势能增大了 mgh
第Ⅱ卷
本卷包括必考题和选考题两部分。第 22 题~第 32 题 为必考题,每个试题考生都必须做答。第 33 题~第 39 题 为选考题,考生根据要求做答。
(一)必考题(12 题,129 分)
22. (5分)如图所示,质量不同的两个物体A和B,用跨 过定滑轮的细绳相连.开始时B放在水平桌面上,A离地面有一定的高度,从静止开始释放 让它们运动,在运动过程中B始终碰不到滑轮,A着地后不反 B 弹.不计滑轮与轴间摩擦及绳子和滑轮的质量,用此装置可测 出B物体与水平桌面间的动摩擦因数μ. (1)在本实验中需要用到的测量工具是 理量是 (2)动摩擦因数μ的表达式为μ= ;需要测量的物 .
西工大附中2012—2013学年度第一学期期中质量检测试卷语文参考答案

2013年普通高等学校招生全国统一考试西工大附中第二次适应性训练语文参考答案1.B【解析】(B项根据文中“道德标准是成为伟大作家的首要条件”和“‘伟大’不仅取决于文学艺术作品…还取决于作家本人在为人行事方面的崇高和磊落”,可知是故意曲解原意)2.【解析】A(A项“后人”范围太广,文中说宋人因为”陷贼“事件指摘王维,而排斥王维于”大家“之外的是主流诗学)3.C(C项“文学才华介于‘大家’和‘名家’之间有误。
)4. D(A总:统领B假: 临时代理职务C降:下传,下达)5. A(②是卢承业对娄师德的高度评价。
④体现了娄师德的智慧。
)6. C(“怯懦、窝囊”语气过重,“根本原因”在原文中没有依据)(1—6题每题3分,共18分)7.(10分)(1)为人不浮躁宽宏大量,有人冒犯自己,就逊让来避免自己(与别人的矛盾),不露(不满)神色。
(“忤”1分,“逊”1分,“自免”1分,“见”1分,整句1分。
)(2)娄公大德,我被他宽容却不知道,我跟他们相比差远了!(“为所”1分,补出“为”的宾语1分,“乃”1分,“逮”1分,整句1分)8.(5分)“屠”,是杀掉的意思。
“屠得热”,指清风小而无力驱暑,而更主要的是用“清风无力”来衬托暑旱之甚,酷热难当。
(2分)既使“热”人格化了,又有力地表现了诗人恨暑热的情感。
(2分)这首诗抒发了乐以天下、忧以天下的胸襟抱负。
(1分)9.①比拟(或拟人)。
暑旱难耐,清风也无能为力,落日插上翅膀;②对比(衬托)。
“人固已惧江海竭,天岂不惜河汉干”,这里的“天”著上了人的感情色彩,它不痛惜“河汉”(指银河)干涸,这与人害怕江海枯竭的心理形成了强烈对比,字里行间渗透了诗人对老天爷的憎恨之情。
或者首联东风无力与落日酷热形成对比(或以东风无力衬托落日酷热);③虚实结合,诗人由现实中的“暑旱苦热”想到昆仑、蓬莱等现实与传说中的清凉世界,突出了暑旱之苦。
(每点2分)(6分)10.(6分)(1)而莫之夭阏者(2)佩缤纷其繁饰兮(3)既窈窕以寻壑,(4)俨骖騑于上路,访风景于崇阿。
