19c01(教师讲评版分类训练专题)八年级数学下册矩形菱形正方形分类训练专题一
19c13(教师讲评版分类训练专题)八年级数学下册矩形菱形正方形分类训练专题十三

二、中心对称倍长线段法
(3)①结论 AM=AD+MC 仍然成立. 延长 AE、BC 交于点 P,如图 2(1), ∵四边形 ABCD 是矩形, ∴AD∥BC.∴∠DAE=∠EPC. ∵AE 平分∠DAM,∴∠DAE=∠MAE. ∴∠EPC=∠MAE.∴MA=MP.
在△ADE 和△PCE 中,
∴△ADE≌△PCE(AAS).
二、中心对称倍长线段法
∵AM=DE+BM,∴QB=DE. 在△ABQ 和△ADE 中, ∴△ABQ≌△ADE(AAS). ∴AB=AD.与条件“AB≠AD“矛盾,故假设不成立. ∴AM=DE+BM 不成立.
二、中心对称倍长线段法
练习 2.如图,在□ABCD 中,点 M 为边 AD 的中点,过点 C 作 AB 的垂线 交 AB 于点 E,连接 ME. (1)若 AM=2AE=4,∠BCE=30°,求□ABCD 的面积; (2)若 BC=2AB,求证:∠EMD=3∠MEA.
拓展延伸: (3)若四边形 ABCD 是长与宽不相等的矩形,其他条件不变,如图 2, 探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要 证明.
二、中心对称倍长线段法
(1)证明:延长 AE、BC 交于点 N,如图 1(1), ∵四边形 ABCD 是正方形, ∴AD∥BC.∴∠DAE=∠ENC. ∵AE 平分∠DAM,∴∠DAE=∠MAE. ∴∠ENC=∠MAE.∴MA=MN.
在△ADE 和△NCE 中,
∴△ADE≌△NCE(AAS).
∴AD=NC. ∴MA=MN=NC+MC=AD+MC.
一、矩形的性质与判定例题分析
(2)AM=DE+BM 成立. 过点 A 作 AF⊥AE,交 CB 的延长线于点 F,如图 1(2)所示. ∵四边形 ABCD 是正方形, ∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC. ∵AF⊥AE,∴∠FAE=90°. ∴∠FAB=90°﹣∠BAE=∠DAE.
19c06(教师讲评版分类训练专题)八年级数学下册矩形菱形正方形分类训练专题六

.
二、折叠中长度问题
连接 BF 交 AE 于 H,
由折叠可知,AB=AF,∠BAE=∠FAE,
∴AH⊥BF,BH=FH.
∵BC=6,点 E 为 BC 的中点,∴EC=BE=3.
又∵AB=4,∴AE= AB2+BE2=5.∴BH=12,则 BF=24.
5
5
∵FE=BE=EC,∴∠EBF=∠EFB,∠EFC=∠ECF,
二、折叠中长度问题
练习 3.如图,把一张矩形的纸沿对角线 BD 折叠,若
AD=8,CE=3,则 DE=
.
二、折叠中长度问题
5
二、折叠中长度问题
练习 4.如图,在矩形 ABCD 中,AB=4,BC=6,点 E
为 BC 的中点,将△ABE 沿 AE 折叠,使点 B 落在矩形内
点 F 处,连接 CF,则 CF 的长为
折叠,使得点 B 落在线段 CD 上的点 F 处,则线段 BE
的长为
.
二、折叠中长度问题
∵四边形 ABCD 是矩形,∴∠B=∠D=90°. ∵将矩形折叠,使得点 B 落在线段 CD 上的点 F 处, ∴AF=AB=5,AD=BC=4,EF=BF. 在 Rt△ADF 中,由勾股定理,得 DF= AF2-AD2=3. 在矩形 ABCD 中,∵DC=AB=5,∴CF=DC-DF=2. 设 EC=x,则 EF=BE=4-x. 在 Rt△CEF 中,CE2+CF2=EF2,即 x2+22=(4-x)2, 解得 x=1.5.∴BE=4-1.5=2.5.
片展平;(2)再一次折叠纸片,使点 A 落在 EF 上,并
使折痕经过点 B,得到折痕 BM,同时得到线段 BN.观察
探究可以得到∠ABM 的度数是( )
A.25° B.30° C.36°
2020—2021年华东师大版八年级数学下册《矩形、菱形、正方形》单元复习题及答案.docx

(新课标)2017-2018学年华东师大版八年级下册第19章矩形菱形正方形单元复习题一、选择题(4分×12=48分)1、下列图形中,是中心对称但不一定是轴对称图形的是(D)A.等边三角形B.矩形C.菱形D.平行四边形2、下列命题正确的是(D)A.一组对边相等,另一组对边平行的四边形一定是平行四边形B.对角线相等的四边形一定是矩形C.两条对角线互相垂直的四边形一定是正方形D.两条对角线相等且互相垂直平分的四边形一定是正方形3、矩形,菱形,正方形都具有的性质是(C)A.每一条对角线平分一组对角B.对角线相等C.对角线互相平分D.对角线互相垂直4、如图,已知四边形ABCD是平行四边形,下列结论中不正确的是(D)A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形5、如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为(B)A.2cm B.3cm C.4cm D.3cm6、菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为(C)A.3:1 B.4:1 C.5:1 D.6:17、如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为(C)A.3 B.4 C.5 D.68、平行四边形ABCD中,AB≠BC,其四个内角的角平分线所围成的四边形一定是(D)A.有一个角为30°的平行四边形B.有一个角为45°的平行四边形C.有一个角为60°的平行四边形D.矩形9、(2015辽宁省朝阳)如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为(A)A.1或2 B. 2或3 C. 3或4 D. 4或510、如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为(C)A. 28°B.52°C.62°D.72°11、如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有(C)A.1个B.2个C.3个D.4个12、如图,在平面直角坐标系中.矩形OABC的对角线OB,AC 相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为(A)A.B.C.D.二、填空题(4分×6=24分)13、如图,在周长为20cm的▱ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为10 cm.14、在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是对角线相等.(写出一种即可)15、已知矩形ABCD,作CE⊥BD于点E。
【新】八年级下册数学 人教版 矩形、菱形、正方形的知识应用(知识点讲解+练习题)

矩形菱形正方形基本知识教案【知识梳理】一、矩形:1、定义:有一个角是角的平行四边形叫做矩形。
2、性质:⑴矩形的四个角都是;⑵矩形的对角线。
3、判定:⑴用定义判定;⑵有三个角是________的是矩形;⑶对角线的平行四边形是矩形。
特征总结:1、矩形既是又是对称图形,对称轴有条;2、矩形被它的对角线分成四个全等的三角形和两个全等的三角形;3、矩形中常见题目是对角线相交成600或1200角时,利用直角三角形、等边三角形等知识解决问题。
二、菱形:1、定义:有一组邻边的平行四边形叫做菱形。
2、性质:⑴菱形的四条边都;⑵菱形的对角线且每条对角线。
3、判定:⑴用定义判定;⑵对角线互相垂直的是菱形;⑶四条边都相等的是菱形。
特征总结:1、菱形既是对称图形,也是对称图形,它有条对称轴,分别是;2、菱形被对角线分成四个全等的三角形和两对全等的三角形;3、菱形的面积可以用平行四边形面积公式计算,也可以用两条对角线的积来计算;4、菱形常见题目是内角为1200或600时,利用等边三角形或直角三角形知识计算的题目。
【重点考点例析】考点一、矩形的性质与判定【例1】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN ∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE,AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.分析:判定一个四边形是矩形,可以先判定四边形是平行四边形,再找一个内角是直角或说明对角线相等.考点二:和矩形有关的折量问题【例2】如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;(2)若∠DBC=30°,BO=4,求四边形ABED的面积.考点三:和菱形有关的对角线、周长、面积的计算问题【例3】如图,菱形ABCD的周长为20cm,且tan∠A BD=34,则菱形ABCD的面积为cm2.考点四:四边形综合性题目:【例5】如图,正方形ABCD与正三角形A EF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是.考点五:矩形、菱形、正方形的判定例1、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.(1)求∠CAE的度数;(2)取AB边的中点F,连接CF、CE,试证明四边形AFCE是矩形.例2、如图,AB∥CD,∠B = 72°,∠D = 32°,求∠F的度数?变式1、如图,已知∠AEC=∠A+∠C,试说明:AB∥CD.变式2、如图,已知∠1=∠C,∠2=∠3, BE是否平分∠ABC?请说明理由。
八年级数学下册 正方形、矩形、菱形_练习 人教版

BCE F A初二正方形、矩形、菱形 练习一.选择题:1.如图,将边长为 8 ㎝的正方形 ABCD 折叠,使点 D 落在 BC 边的中点 E 处,点 A 落在 F 处,折痕为 MN ,则线段 CN 的长是( )A .3cmB .4cmC .5cmD .6cmADMFBNE C2.在矩形 ABCD 中,AB=1,AD= ,正确的是-------------;,AF 平分∠DAB ,过 C 点作 CE⊥BD 于 E ,延长 AF 、EC 交于点 H ,下列结论中:①AF=FH ;②BO=BF ;③CA=CH④BE=3EDA .②③ C .①②④B .③④ D .②③④3.如图,矩形 ABCD 中,AB=3,BC=5, 过对角线交点 O 作 OE⊥AC 交 AD 于 E, 则 AE 的长是( )A .1.6B .2.5C .3D .3.44.如图 2,将一个长为 10cm ,宽为 8cm 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为---------------- cm ; A .10 B .20 C .40 D .80DAC图 2B5.如图,正方形 ABCD 的边长为 2,将长为 2 的线段 QR 的两端放在正方形的相邻的两边上同时滑动.如果 Q 点从 A 点出发,沿图中所示方向按 A→B→C→D→A 滑动到 A 止,同时点 R 从 B 点 AQD出发,沿图中所示方向按 B→C→D→A→B 滑动到 B 止,在这个过程中,线段 QR 的中点 M 所经过的路线围成的图形的面积为( ). A .2 B .4 -πC .πD .π - 1MR6.如图,在菱形 ABCD 中,∠A =110°, , 分别是边 AB 和 BC 的中点,EP ⊥CD 于点 P ,则∠FPC =------------;.35° B .45° C .50° D .55°DAEPCBF7. 如图,矩形 ABCD 中,E 点在 BC 上,且 AE 平分 ÐBAC 。
2024学年八年级数学经典好题专项(矩形、菱形、正方形)练习(附答案)
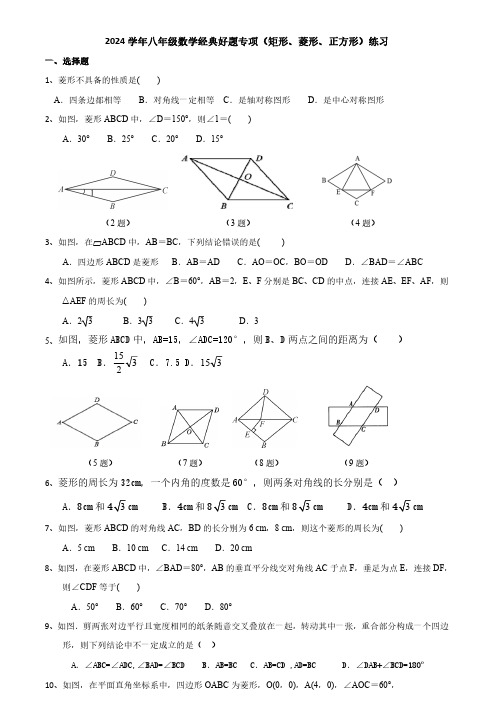
2024学年八年级数学经典好题专项(矩形、菱形、正方形)练习一、选择题1、菱形不具备的性质是( )A .四条边都相等B .对角线一定相等C .是轴对称图形D .是中心对称图形2、如图,菱形ABCD 中,∠D =150°,则∠1=( )A .30°B .25°C .20°D .15°(2题) (3题) (4题)3、如图,在▱ABCD 中,AB =BC ,下列结论错误的是( )A .四边形ABCD 是菱形B .AB =ADC .AO =OC ,BO =OD D .∠BAD =∠ABC4、如图所示,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为( )A .2 3B .3 3C .4 3D .35、如图,菱形ABCD 中,AB=15,∠ADC=120°,则B、D 两点之间的距离为( )A.15 B.3215 C.7.5 D.315(5题) (7题) (8题) (9题)6、菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是( )A.8cm 和cm B.4cm 和cm C.8cm 和cm D.4cm 和cm7、如图,菱形ABCD 的对角线AC ,BD 的长分别为6 cm ,8 cm ,则这个菱形的周长为( )A .5 cmB .10 cmC .14 cmD .20 cm8、如图,在菱形ABCD 中,∠BAD =80°,AB 的垂直平分线交对角线AC 于点F ,垂足为点E ,连接DF ,则∠CDF 等于( )A .50°B .60°C .70°D .80°9、如图.剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BC C.AB=CD ,AD=BC D.∠DAB+∠BCD=180º10、如图,在平面直角坐标系中,四边形OABC 为菱形,O(0,0),A(4,0),∠AOC =60°,则对角线交点E 的坐标为( )A .(2, 3 )B .( 3 ,2)C .( 3 ,3)D .(3, 3 )(10题) (11题) (12题) (13题)二、填空题11、如图,在△ABC 中,点D ,E ,F 分别在边BC ,AB ,CA 上,且DE ∥CA ,DF ∥BA.小聪认为如果AD平分∠BAC ,那么四边形AEDF 是菱形,小聪的说法 .(填“正确”或“不正确”)12、在菱形ABCD 中,对角线AC 、BD 相交于点O ,若∠ABC =140°,则∠BAD =________°,∠ABD =________°,∠BCA =________°;13、如图,菱形ABCD 的边长为2 cm ,E 是BC 的中点,且AE ⊥BC ,则菱形ABCD 的面积为_____.14、如图,P 是菱形ABCD 的对角线AC 上一点,PE ⊥AD 于点E ,且PE =3 cm ,则点P 到AB 的距离为__ __ cm.(14题) (15题) (17题) (20题)15、如图,在菱形ABCD 中,AB =5,AO =3,点E 在BC 的延长线上,∠E =12∠ABC ,DE =16、菱形ABCD 的周长为48cm,∠BAD:∠ABC=1:2,则BD=_____,菱形的面积是______.17、如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,若AC =8 cm ,BD =6 cm ,则该菱形的面积为________cm 2,周长为________cm.18、已知菱形ABCD 的面积为24 cm 2,若对角线AC =6 cm ,则这个菱形的边长为____ cm.19、四边形ABCD 是菱形,∠BAD =60°,AB =6,对角线AC 与BD 相交于点O ,点E 在AC 上,若OE =3,则CE 的长为_________20、如图,点P 是边长为1的菱形ABCD 对角线AC 上的一个动点,点M ,N 分别是AB ,BC 边的中点,则MP +PN 的最小值是______.三、解答题21、已知:如图,在△ABC 中,CD 平分∠ACB 交AB 于点D ,DE ∥AC 交BC 于点E ,DF ∥BC 交AC于点F. 四边形DECF 是菱形吗?为什么?22、如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8 cm,BD=6 cm,DH⊥AB于H.(1)求菱形ABCD的面积;(2)求DH的长.23、如图,在菱形ABCD中,对角线AC与BD相交于点O,BD=12 cm,AC=6 cm.求菱形的周长.24、已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE的面积.25、如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:(1)△ABF≌△DAE;(2)DE=BF+EF.26、已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.参考答案一、选择题1、菱形不具备的性质是( B )A .四条边都相等B .对角线一定相等C .是轴对称图形D .是中心对称图形2、如图,菱形ABCD 中,∠D =150°,则∠1=( D )A .30°B .25°C .20°D .15°3、如图,在▱ABCD 中,AB =BC ,下列结论错误的是( D )A .四边形ABCD 是菱形B .AB =ADC .AO =OC ,BO =OD D .∠BAD =∠ABC4、如图所示,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为( B )A .2 3B .3 3C .4 3D .35、如图,菱形ABCD 中,AB=15,∠ADC=120°,则B、D 两点之间的距离为( A )A.15 B.3215 C.7.5 D.3156、菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是(C )A.8cm 和cm B.4cm 和cm C.8cm 和cm D.4cm 和cm7、如图,菱形ABCD 的对角线AC ,BD 的长分别为6 cm ,8 cm ,则这个菱形的周长为(D )A .5 cmB .10 cmC .14 cmD .20 cm8、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( B )A.50° B.60° C.70° D.80°9、如图.剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BC C.AB=CD ,AD=BC D.∠DAB+∠BCD=180º解析:∵四边形ABCD是用两张等宽的纸条交叉重叠放在一起而组成的图形,∴AB∥CD,AD∥BC, ∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形).过点A分别作BC,CD边上的高为AE,AF,连接AC,则AE=AF(两纸条相同,纸条宽度相同),∴在平行四边形ABCD中.S△ABC=S△ACD,即BC•AE=CD•AF,∴BC=CD,AB=BC.故B中结论成立;∴平行四边形ABCD为菱形(邻边相等的平行四边形是菱形),∴∠ABC=∠ADC,∠BAD=∠BCD(菱形的对角相等),故A中结论成立;AB=CD,AD=BC(平行四边形的对边相等),故C中结论成立:当四边形ABCD是矩形时,有∠DAB+∠BCD=180º.故D中结论不一定成立,故选D.10、如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为( D )A.(2, 3 ) B.( 3 ,2) C.( 3 ,3) D.(3, 3 )二、填空题11、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA.小聪认为如果AD平分∠BAC,那么四边形AEDF是菱形,小聪的说法正确.(填“正确”或“不正确”)12、在菱形ABCD中,对角线AC、BD相交于点O,若∠ABC=140°,则∠BAD=________°,∠ABD=________°,∠BCA=________°;答案:40,70,2013、如图,菱形ABCD的边长为2 cm,E是BC的中点,且AE⊥BC,则菱形ABCD的面积为__2 3 cm2 ____.14、如图,P是菱形ABCD的对角线AC上一点,PE⊥AD于点E,且PE=3 cm,则点P到AB的距离为__3 __ cm.15、如图,在菱形ABCD中,AB=5,AO=3,点E在BC的延长线上,∠E=12∠ABC,DE=816、菱形ABCD的周长为48cm,∠BAD:∠ABC=1:2,则BD=_____,菱形的面积是______.217、如图,在菱形ABCD中,对角线AC、BD相交于点O,若AC=8 cm,BD=6 cm,则该菱形的面积为________cm2,周长为________cm.答案:24,2018、已知菱形ABCD的面积为24 cm2,若对角线AC=6 cm,则这个菱形的边长为__5 __ cm.19、四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=3,则CE的长为___43或23______20、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是__1 ____.三、解答题21、已知:如图,在△ABC中,CD平分∠ACB交AB于点D,DE∥AC交BC于点E,DF∥BC交AC于点F. 四边形DECF是菱形吗?为什么?解:四边形DECF是菱形.理由如下:∵DE∥FC,DF∥EC,∴四边形DECF为平行四边形.由AC∥DE,知∠2=∠3. ∵CD平分∠ACB,∴∠1=∠2,∴∠1=∠3,∴DE=EC,∴平行四边形DECF为菱形.22、如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8 cm,BD=6 cm,DH⊥AB于H.(1)求菱形ABCD的面积;(2)求DH的长.解:(1)∵四边形ABCD 是菱形,AC =8 cm ,BD =6 cm ,∴S 菱形ABCD =12ACꞏBD =12×6×8=24(cm 2).(2)∵四边形ABCD 是菱形,∴AC ⊥BD ,OA =OC =12=4 cm ,OB =OD =3 cm ,∴在直角三角形AOB 中,AB =OB 2+OA 2=32+42=5 cm ,∴DH =S 菱形ABCD AB =4.8 cm.23、如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,BD =12 cm ,AC =6 cm.求菱形的周长.解:∵四边形ABCD 是菱形,∴AC ⊥BD ,AO =12AC ,BO =12 BD.∵AC =6 cm ,BD =12 cm , ∴AO =3 cm ,BO =6 cm.在Rt △ABO 中,由勾股定理,得AB =AO 2+BO 2=32+62=3 5 cm ,∴菱形的周长=4AB=4×3 5 =12 5 cm.24、已知:如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,DE ∥AC ,AE ∥BD.(1)求证:四边形AODE 是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE 的面积.解答:(1)证明:∵DE ∥AC ,AE ∥BD ,∴四边形AODE 是平行四边形,∵在菱形ABCD 中,AC ⊥BD ,∴ AOD=90 , ∴平行四边形AODE 是是矩形;(2)∵∠BCD=120°,AB ∥CD ,∴∠ABC=180°‐120°=60°,∵AB=BC ,∴△ABC 是等边三角形,∴OA=21×6=3, OD=OB=6×23=33,∴四边形AODE 的面积=OA ∙OD=9325、如图,在菱形ABCD 中,点P 是BC 边上一点,连接AP ,点E ,F 是AP 上的两点,连接DE ,BF ,使得∠AED =∠ABC ,∠ABF =∠BPF .求证:(1)△ABF ≌△DAE ;(2)DE =BF +EF .证明:(1)∵四边形ABCD 是菱形,∴AB =AD ,AD ∥BC . ∴∠BP A =∠DAE .∵∠ABC =∠AED ,∴∠BAF =∠ADE .∵∠ABF =∠BPF ,∠BP A =∠DAE ,∴∠ABF =∠DAE .∵AB =DA ,∴△ABF ≌△DAE (ASA).(2)∵△ABF ≌△DAE , ∴BF =AE ,AF =DE .∵AF =AE +EF =BF +EF ,∴DE =BF +EF .26、已知:如图,在菱形ABCD 中,F 为边BC 的中点,DF 与对角线AC 交于点M ,过M 作ME ⊥CD 于点E ,∠1=∠2.(1)若CE =1,求BC 的长;(2)求证:AM =DF +ME.(1)解:∵四边形ABCD 是菱形,∴AB ∥CD ,∴∠1=∠ACD ,∵∠1=∠2,∴∠ACD =∠2,∴MC =MD ,∵ME ⊥CD ,∴CD =2CE , ∵CE =1,∴CD =2,∴BC =CD =2(2)证明:如图,∵F 为边BC 的中点,∴BF =CF =12BC ,∴CF =CE ,在菱形ABCD 中,AC 平分∠BCD ,∴∠ACB =∠ACD ,在△CEM 和△CFM 中,∵⎩⎪⎨⎪⎧CE =CF ,∠ACB =∠ACD ,CM =CM ,∴△CEM ≌△CFM(SAS),∴ME =MF ,延长AB 交DF 的延长线于点G , ∵AB ∥CD ,∴∠G =∠2, ∵∠1=∠2,∴∠1=∠G ,∴AM =MG ,在△CDF 和△BGF 中,∵⎪⎩⎪⎨⎧=∠=∠∠=∠FC FB DFC GFB G 2,∴△CDF ≌△BGF(AAS),∴GF =DF , 由图形可知,GM =GF +MF ,∴AM =DF +ME。
19c07(教师讲评版分类训练专题)八年级数学下册矩形菱形正方形分类训练专题七

二、关于边对称问题
(2)延长 AD 到 G.使 MG=MB.连接 FG,FB, ∵BM=DM+CD,∴DG=DC=BC, ∵∠GDF=∠C=90° , DF=CF , ∴△FDG≌△FCB ( SAS ), ∴∠DFG=∠CFB, ∴B,F,G 共线, ∵E 为 AD 边上的中点,点 F 是 CD 边的中点,AD=CD,∴AE=CF, ∵AB=BC , ∠C=∠BAD=90° , AE=CF , ∴△ABE≌△CBF , ∴∠ABE=∠CBF, ∵AG∥BC,∴∠AGB=∠CBF=∠ABE, ∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE, ∴∠MBC=2∠ABE.
一、关于对角线对称问题
练习 1.如图,在正方形 ABCD 中,边长为 2 的等边三角 形 AEF 的顶点 E、F 分别在 BC 和 CD 上.下列结论: ①CE=CF;②∠AEB=75°; ③BE+DF=EF;④S 正方形 ABCD=2+ . 其中正确的个数为( ) A.1 B.2 C.3 D.4
一、关于对角线对称问题
(1)当点 P 在线段 AO 上时;
∵四边形 ABCD 是正方形,∴AB=AD,∠BAP=∠DAP=45°,
AB AD
在△ABP
和△ADP
中,
BAP DA AP AP
P
,
∴△ABP≌△ADP(SAS),∴BP=DP,
∵PB=PE,∴PE=PD,
一、关于对角线对称问题
过点 P 作 PM⊥CD 于点 M,作 PN⊥BC 于点 N, ∵PB=PE,PN⊥BE,∴BN=NE, ∵BN=DM,∴DM=NE,
三、关于过顶点的直线对称问题
(2)由(1)得:AE=AD,∠EAD=60°, ∴△AED 是等边三角形,ED=6, ∵AQ 垂直平分 DE, ∴EG=3,∠FGE=90°, ∵∠EAD=30°,∠AEB=15°, ∴∠EFG=∠FEG=45°, ∴EG=FG=3.
19c05(教师讲评版分类训练专题)八年级数学下册矩形菱形正方形分类训练专题五

三、特殊四边形的动态探究
一、特殊四边形中的最值问题
练习 1.如图,MN 是正方形 ABCD 的一条对称轴,点 P
是直线 MN 上的一个动点,当 PC+PD 最小时,∠PCD
的度数为( )
A.60° B.90°
C.45°
D.75°
一、特殊四边形中的最值问题
作出 D 点关于 MN 的对称点,正好是 A 点, 此时 PC+PD=PC+PA, 连接 AC,当点 P 为 AC 与 MN 的交点时,PC+PD 的值最小. ∵AC 为正方形对角线, 根据正方形的性质易知∠PCD=45°.故选 C.
(1)FG=CE FG∥CE
三、特殊四边形的动态探究
(2)成立.证明如下: 如图,过点 G 作 GH⊥CB 的延长线于点 H, ∵EG⊥DE,∴∠GEH+∠CED=90°. ∵∠GEH+∠HGE=90°,∴∠CED=∠HGE.
∠GHE=∠ECD, 在△HGE 与△CED 中, ∠HGE=∠CED,∴△HGE≌△CED(AAS),
二、四边形间的综合问题
(4)当△ABC 满足∠BAC=60°时,∠DAF=180°, 此时 D,A,F 三点在同一条直线上, 以 A,D,E,F 为顶点的四边形就不存在.
二、四边形间的综合问题
练习 3.如图,在▱ ABCD 中,已知 AD>AB. (1)实践与操作:作∠BAD 的平分线交 BC 于点 E,在 AD 上截取 AF=AB,连接 EF(要求:尺规作图,保留作图 痕迹,不写作法); (2)猜想并证明:猜想四边形 ABEF 的形状,并给予证 明.
如图,连接 PA.∵在△ABC 中,AB=6,AC=8,BC=10, ∴BC2=AB2+AC2,∴∠BAC=90°. 又∵PE⊥AB 于点 E,PF⊥AC 于点 F, ∴∠AEP=∠AFP=90°,∴四边形 PEAF 是矩形,∴AP=EF, ∴当 PA 最小时,EF 也最小,当 AP⊥CB 时,PA 最小. ∵12AB·AC=12BC·AP,即 AP=AB·BCAC=6×108=4.8, ∴线段 EF 的最小值为 4.8.故选 B.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、正方形中的最短距离
(1)因为四边形 ABCD 是正方形,所以 AC⊥BD, 因为 PF⊥BD,所以 PF∥AC,同理 PE∥BD, 所以四边形 PFOE 为矩形, 故 PE=OF. 又因为∠PBF=45°,所以 PF=BF,PE+PF=OF+FB=OB= 2 a.
2
三、正方形中的最短距离
(2)因为四边形 ABCD 是正方形,所以 AC⊥BD, 因为 PF⊥BD,所以 PF∥AC, 同理 PE∥BD, 所以四边形 PFOE 为矩形,故 PE=OF. 又因为∠PBF=∠OBA=45°,所以 PF=BF. 所以 PE-PF=OF-BF=OB= 2 a.
2
B
二、菱形中的最短距离
2.如图,在周长为 12 的菱形 ABCD 中,AE=1,AF=2,若 P 为对角线 BD 上一动点,则 EP+FP 的最小值为( ) A.1 B.2 C.3 D.4
二、菱形中的最短距离
C
二、菱形中的最短距离
3.如图,点 P 是边长为 1 的菱形 ABCD 对角线 AC 上的一
矩形菱形正方形分类训练专题一
佳文韵赢
一、矩形中的最短距离
1.矩形 OABC 在平面直角坐标系中的位置如图所示,点
B 的坐标为(3,4),D 是 OA 的中点,点 E 在 AB 上,当△CDE
的周长最小时,点 E 的坐标为(
)
A.(3,1)
B.(3,
4 3
)
C.(3,
5 3
)
D.(3,2)
一、矩形中的最短距离
)
A. 12 B.4
C.3
D. 6
三、正方形中的最短距离
B
三、正方形中的最短距离
5.如图,正方形 ABCD 的边长为 2,点 E 为边 BC 的中点,
点 P 在 对 角 线 BD 上 移 动 , 则 PE+PC 的 最 小 值
是
.
三、正方形中的最短距离
5
三、正方形中的最短距离
6.已知正方形 ABCD 的边长为 a,两条对角线 AC,BD 交于 点 O,P 是直线 AB 上任意一点。过 P 点分别作直线 AC、BD 的垂线 PE、PF,垂足为 E,F。 (1)如图 1,当 P 点在线段 AB 上时, 求 PE+PF 的值; (2)如图 2,当 P 点在线段 AB 的延 长线上时,求 PE-PF 的值。
个动点,点 M,N 分别是 AB,BC 边的中点,则 MP+NP 的最
小值是(
)
1Байду номын сангаас
A. 2
B.1
C. 2
D.2
二、菱形中的最短距离
B
三、正方形中的最短距离
4.如图,正方形 ABCD 的面积为 16,△ABE 是等边三角形,
点 E 在正方形 ABCD 内,在对角线 AC 上有一动点 P,则
PD+PE 的最小值为(
