下料问题的解法
【原创】下料方案专题一:合理下料问题

【原创】下料方案专题一:合理下料问题
问题描述: 从给定尺寸的材料中,按需要的尺寸截取给定数量的零件,使用料最少或残余废料总量最小的问题。 原型范例: 用长9米的原料截取3.1米200根,2.5米100根,1.7米300根,如何截取用料最少。 求解过程: 1:求解单根原材料截取零件的全部可行性方案。
方案 3.1米 2.5米 1.ቤተ መጻሕፍቲ ባይዱ米 废料长
123456789 221110000 102103210 010230235 0.3 1.1 0.9 0.0 0.8 1.5 0.6 1.4 0.5
2:建立数学模型 假定方案i(i=0,1,2,...,9)下料根数为xi,则: 目标函数:用料最少 Z=x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 约束方程:3.1米200根 2*x1 + 2*x2 + x3 + x4 + x5 = 200 2.5米100根 x1 + 2*x3 + x4 + 3*x6 + 2*x7 + x8 = 100 1.7米300根 x2 + 2*x4 + 3*x5 + 2*x7 + 3*x8 + 5*x9 = 300 非负约束 xi >= 0 (i=0,1,2,...,9) 整数约束 xi为整数(i=0,1,2,...,9) 3:求解 最优解为:x1=30, x2=35, x4=70, x9=25, x3=x5=x6=x7=x8=0
合理下料问题

0 0 3 5.4 0.6
0 1 2 5.8 0.2
0 2 0 4.4 1.6
1 0 1 4.6 1.4
1 1 0 5.0 1.0
2 0 0 5.6 0.4
(1)为了获得100套钢架,需要混合使用种下料方案。设按六种方案下料的原材料的 根数
合理下料问题
现要做100套钢架,每套由长2.8m,2.2m,1.8m的元钢各一根组成,已知原材料长6.0m, 问应如何下料,可以使原材料最省。 解: 由于要裁成的三种元钢的总长度是2.8m+2.2m+1.8m=6.8m,超过了原材料6m 的长度, 因此, 我们容易实现的裁法是:在原材料上分别裁下2.8m,2.2m的元钢各一根,这样要100根原材料 才能裁到100跟2.8m,2.2m的元钢,再来考虑如何裁得1.8m的元钢,由于一根原材料可以裁得 3根1.8m的元钢,这样要裁得100根1.8m的元钢,就需要原材料34根。采取上述裁法需134根原 材料方可裁得2.8m,2.2m,1.8m的元钢各100根。 但如果改用套裁,则可节约原材料。经过简单分析,我们得到几种可供套裁的方案,如 下表:
min z x1 x2 x3 x4 x5 x6 0 x1 0 x2 0 x3 1x4 1x5 2 x6 100, 0 x1 1x2 2 x3 0 x4 1x5 0 x6 100, 3x1 2 x2 0 x3 1x4 0 x5 0 x6 100, x1 , x2 , x3 , x4 , x5 , x6 0.
(2)利用单纯形法求解以上线性规划模型,通过WinQSB软件Linear and Integer Programming模型运算求解过程如下表所示: 输入数据。以电子表格形式输入变量系数矩阵和右端常数:
下料口堵塞解决方法

下料口堵塞解决方法
下料口堵塞是工厂生产过程中经常会出现的一种现象,会对生产进程产生严重的影响。
因此,有效地解决下料口堵塞问题,是工厂生产稳定性和效率的关键因素之一。
下料口堵塞的主要原因有:材料堵塞、堵塞物沉积、设备故障。
针对上文提到的几种原因,有效解决下料口堵塞的方法有:
首先,加强原料管理,确保原料材质洁净,合适的原料颗粒大小,有效地防止材料堵塞的发生。
其次,定期检查下料口,确保下料口没有堵塞物沉积,以便正常下料。
再者,定期检查设备,确保设备状态良好,防止因设备故障而引发下料口堵塞。
此外,当出现下料口堵塞现象时,要及时采取科学的措施解决,如合理地调整设备参数,改善堵塞部位的热量传递,增强清理空气流动,以及增加旋风式粉团打磨等。
有效解决下料口堵塞的关键在于发现问题的及时性和有效性,采取正确的措施,提高工厂的生产稳定性和效率。
只有经常检查设备,及时发现问题,并采取有效措施,才能有效解决下料口堵塞问题,确保工厂的正常运行。
因此,要想成功解决下料口堵塞问题,有必要采用多种方法,从基础上建立一套合理有效的下料口堵塞解决方案。
在实施方案时,需要建立一个专业的团队,按照发现问题的及时性、有效性、可持续性
的原则进行,并确保措施的有效性,以确保工厂的运行质量、减少不必要的损失。
总之,通过建立专业的团队,加强设备管理,定期检查设备,合理调整参数,积极配合,并有效响应,可以有效地解决下料口堵塞问题,从而为工厂的生产保驾护航。
4.3 下料问题

两种 标准
2.所用原料钢管总根数最少 ������������������ ������2 = ������1 +������2 +������3 + ������4 + ������5 +������6 +������7
一般下料问题的最优解法
模 4米 6米 8米 余 式 根数 根数 根数 料
约束
������������ ≤ ������������������������ + ������������������������ + ������������������������ + ������������������������ ≤ ������������ ������������ ≤ ������������������������ + ������������������������ + ������������������������ + ������������������������ ≤ ������������ ������������ ≤ ������������������������ + ������������������������ + ������������������������ + ������������������������ ≤ ������������
大型下料问题的解法
53种零件的所 有 下料方式共 10307032
种
大型下料问题的解法
方法1:先下料最长的零件,直至下完,再下料次长的零件,尽量 利 用余料。。。
方法2:从零件的所有下料方式中挑选1种下料,完成部分零件的 下 料任务,再从剩余零件的所有下料方式中挑选一种下料。。。
下料问题-2

实用下料问题一.问题的重述“下料问题(cutting stock problem)”是把相同形状的一些原材料分割加工成若干个不同规格大小的零件的问题,此类问题在工程技术和工业生产中有着重要和广泛的应用. 这里的“实用下料问题”则是在某企业的实际条件限制下的单一材料的下料问题。
现考虑单一原材料下料问题. 设这种原材料呈长方形,长度为L ,宽度为W ,现在需要将一批这种长方形原料分割成m 种规格的零件, 所有零件的厚度均与原材料一致,但长度和宽度分别为),(,),,(11m m w l w l ,其中w i <m i W w L l i i ,,1,, . m 种零件的需求量分别为m n n ,,1 .下料时,零件的边必须分别和原材料的边平行。
这类问题在工程上通常简称为二维下料问题。
特别当所有零件的宽度均与原材料相等,即m i W w i ,,1, ,则问题称为一维下料问题。
一个好的下料方案首先应该使原材料的利用率最大,从而减少损失,降低成本,提高经济效益。
其次要求所采用的不同的下料方式尽可能少,即希望用最少的下料方式来完成任务。
因为在生产中转换下料方式需要费用和时间,既提高成本,又降低效率。
此外,每种零件有各自的交货时间,每天下料的数量受到企业生产能力的限制。
因此实用下料问题的目标是在生产能力容许的条件下,以最少数量的原材料,尽可能按时完成需求任务, 同时下料方式数也尽量地小。
现在我们要为某企业考虑下面两个问题。
1.建立一维单一原材料实用下料问题的数学模型, 并用此模型求解下列问题,制定出在生产能力容许的条件下满足需求的下料方案, 同时求出等额完成任务所需的原材料数,所采用的下料方式数和废料总长度. 单一原材料的长度为 3000mm, 需要完成一项有53种不同长度零件的下料任务. 具体数据见表一(略),其中 i l 为需求零件的长度,i n 为需求零件的数量. 此外,在每个切割点处由于锯缝所产生的损耗为5mm. 据估计,该企业每天最大下料能力是100块 ,要求在4天内完成的零件标号(i )为: 5,7,9,12,15,18,20,25, 28,36,48;要求不迟于6天完成的零件标号(i )为:4,11,24,29,32,38,40,46,50。
下料问题

关于一维下料问题的研究摘要:“下料问题”是把相同形状的一些原材料分割加工成若干个不同规格大小的零件的问题.此类问题在工程技术和工业生产中有着重要和广泛的应用.在生产实践中通常要求解决用料最省、浪费最少等问题.下料问题即是其一。
属最优化研究范畴.一维下料问题是生产实践中常见的问题,优化下料要求最大限度地节约原材料,提高原材料的利用率。
本文介绍了两种方法,其一提出分支定界算法优化一维下料问题,并用MATLAB编写程序,通过计算机来完成这一复杂的过程。
另一种方法-lingo,针对单一原材料的一维下料问题, 建立了整数规划模型, 然后将模型转化为求解最优下料方式问题; 利用lingo进行编程, 实现循环调用得到一维下料问题的局部最优解。
实际上本文就是给出了解决适当规模下料问题的求解方法.该方法既可手工演算又可通过计算机求解。
在实践中可以借鉴使用.Abstract: The “℃utting Stock Problem”is a problem of dividing raw materials in the same shape into several parts in different shapes. This kind of problem has important and wide appliance in engineering and industry production.Being living to give birth to in the practice requires use to anticipate to save most usually and Squanders at least and so on ,First of all Immediate future the cutting stock problem is ,The category optimization is researched the category 。
料仓下料口卡堵处置方案

料仓下料口卡堵处置方案1. 背景生产过程中会面临料仓下料口卡堵的问题,这会导致生产中断、生产流程受阻、生产效率降低等问题。
因此,需要及时采取有效措施处理料仓下料口卡堵问题。
2. 卡堵原因分析料仓下料口卡堵的原因有很多,主要包括以下几方面:•料仓存储物料过多导致下料口堵塞;•物料质量问题,如过于潮湿或结块;•料仓下料口构造问题,如设计不合理或下料口位置不当。
3. 处理方案3.1 清理料仓下料口如果发现料仓下料口卡堵,需要立即进行清理。
清理时需要先停止下料机的运转,然后采用专业工具将下料口内的物料清理干净,特别是一些大块物料。
对于潮湿的物料,可以使用干燥剂或加热方式进行处理。
在清理过程中,需要注意安全操作,如戴好防护手套和口罩,避免对工作人员造成伤害。
3.2 调整下料口位置如果是由于下料口位置不当导致的卡堵问题,需要进行调整。
在进行调整时需要根据实际情况采取合适的方式,如加装振动器或改变下料口位置等,以保障物料的正常下料。
3.3 增加物料下料口如果料仓下料口较少,需要增加物料下料口,以扩大下料通道。
在增加物料下料口时,需要考虑物料流动方向,以确保物料能够顺利地下料。
3.4 将堵塞的物料打散在有些情况下,物料不是因为存储过多而导致的卡堵,而是因为物料结块。
这时,可以通过将结块的物料打散并加以加热来解决卡堵问题。
既可以使用机械方式将结块的物料打散,也可以使用气体或水蒸气加热。
4. 预防措施除了及时处理卡堵问题外,还需要采取一些措施以预防料仓下料口卡堵。
主要包括以下几个方面:•定期检查下料设备,确保设备正常运行,减少卡堵问题的发生;•注意物料存储方式,切忌物料存储过多,避免出现下料口卡堵问题;•定期清理料仓内的物料,避免物料沉积在下料口内;•选择合适的物料下料口位置,避免下料口不当导致的卡堵问题。
5. 结论料仓下料口卡堵问题在生产过程中是时常会遇到的问题。
为了避免卡堵问题的发生,需要采取一些预防措施,并对卡堵问题及时采取有效的处理方案。
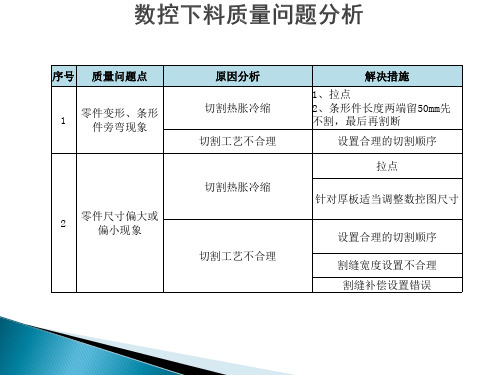
数控下料质量问题分析
序号
质量问题点
原因分析 切割氧压力太高
解决措施 调整合适的氧压力 调整割嘴与板材高度 清理杂物或更换 选择合适的割嘴
7
火焰切割断面凹 凸不平
割嘴与板材高度太高 割嘴有杂物堵塞,风线受干扰 割嘴号太大
切割氧压力太低
切割速度太快或太慢 8 火焰切割后挂渣, 清渣困难 割嘴与工件之间的高度太大 钢板表面有氧化皮锈蚀或不干净 使用的割嘴号太小
序号
质量问题点
原因分析 切割速度太快
解决措施 孔切割速度一般取正常 切割的70%左右
3
调整割嘴与板材高度 火焰切割孔不圆、 割嘴与板材的高度太大(上宽下窄) 切割边斜度大 选择合适的割嘴,设置 割嘴偏大、使氧流量太高(上窄下宽) 合理氧流量 割嘴不垂直或板材不平 调正割嘴及板材平整
等离子自身的弧线弧度导致精细(等离 子进口电源斜度在3-5°,国产的普通 厚板及精度要求高的零 件选择火焰切割 等离子切割孔不 电源斜度在5-15°)例如:t10,斜度 5°则零件单边误差0.9mm 4 圆、切割边斜度 大(呈V型) 调整合适的高度,一般 等离子割嘴离板高度不合理 割嘴离板材4-7mm 割嘴不垂直或板材不平 调正割嘴及板材平整
调整合适的氧压力
设置合理的切割速度 调整割嘴与板材高度 采购合格的钢板 选择合适的割嘴
序号
质量问题点
原因分析 切割速焰
选择合适的割嘴 调整割嘴与板材高度 设置合理的切割速度
5
孔的切入和引出 点存在凹坑
割嘴号太大 割嘴与板材高度太高或太低
6
孔的切入和引出 点存在凸台
切割速度太快 设置过烧长度2mm 割嘴与板材高度太高或太低 调整割嘴与板材高度
序号
质量问题点
原因分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有交货时间限制的大规模实用下料问题朱珠,王辉,志敏指导老师:鲁习文(华东理工大学理学院数学系,200237)摘要:本文讨论了有交货时间限制的大规模单一原材料下料问题。
对于一维下料问题,本文提出一种新的算法:DP 贪婪算法。
在一维的基础上建立了二维的求解模型,运用降维思想结合一维的DP 贪婪算法,给出解决该模型的算法。
数值计算结果表明该算法对大规模下料问题是有效的。
关键词:下料问题,DP ,贪婪算法 1、问题描述单一原材料下料问题. 设这种原材料呈长方形,长度为L ,宽度为W ,现在需要将一批这种长方形原料分割成m 种规格的零件, 所有零件的厚度均与原材料一致,但长度和宽度分别为),(,),,(11m m w l w l ,其中m i W w L l w i i i ,,1,, =<<<。
m 种零件的需求量分别为m n n ,,1 。
下料时,零件的边必须分别和原材料的边平行。
这类问题在工程上通常简称为二维下料问题。
特别当所有零件的宽度均与原材料相等,即m i W w i ,,1, ==,则问题称为一维下料问题。
一个好的下料方案是在生产能力容许的条件下,以最少数量的原材料,尽可能按时完成需求任务, 同时下料方式数也尽量地小.2、一维下料问题2.1 模型假设在充分了解并分析了实际情况后,我们对一维下料问题提出如下假设:(1)每天下料的数量受到企业生产能力的限制,在未完成需求任务前,每天下料的数量等于最大下料能力。
(2)每个切割点处由于锯缝所产生的损耗不可忽略。
(3)增加一种下料方式大致相当于使原材料总损耗增加%08.0。
(4)每种零件有各自的交货时间,若某零件无交货时间,则记该零件交货时间为无穷大。
2.2 一维单一原材料实用下料问题的模型根据公司要求,目标是既要所用材料最少,也要下料方式少。
记m :零件种类总数,i x :第i 种下料方式下料的根数,k :下料方式的种类数,:i δ第i 种下料方式的余料。
借助函数⎩⎨⎧=01)(i x signal 00=>i i x x ,可得所用材料)(1x f 和采用的下料方式)(2x f 分别为:∑==k i i i x x f 11)(δ,()∑==ki i x signal x f 12)(借助模型假设中假设(3):增加一种下料方式大致相当于使原材料总损耗增加%08.0。
故可将双目标转化为单目标:()⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⨯+⨯=∑∑==1%08.01)(min 11k i i ki i i x signal x x f δ由于每天下料的数量受到企业生产能力max 的限制,假设在d 天各种下料方式的下料总根数分别为1y ,2y ,…,k y ,零件j 的需求数量为j n ,第i 种下料方式下料一次产生的零件j 的个数为ij a 。
设F 是要求在d 天完成的零件集合,则必须满足:⎪⎪⎩⎪⎪⎨⎧⋅≤∈=∑∑==max (11d y F j n y a k i i j ki i ij )即d 天需要完成的零件必须在前max ⋅d 根原材料的切割中得到。
根据上述分析,得到有时间限制的一维单一下料问题模型: ()()⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⨯+⨯=∑∑==1%08.01min 11k i i ki i i x signal x x f δs.t.()()()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥<=≤≤∈==⋅≤==∑∑∑===),,1;,,1(0,);,,1(,,1max ,...,1,,,1,1,1m j k i y x d d k i x y y S j n y a m j d y m j n x a j j l j j j d i i j l i d i d i d j k i d i ij j k i d i j k i i ij 且为整数 其中j d i y ,:第i 种下料方式前j d 天下料总根数,j d S :交货时间均等于j d 的零件集合2.3 模型求解对于该问题,因为可能的下料方式将随需要的零件种类数量成指数级增长,所以它是一个NP -Hard 问题。
这样对于大多数问题,一般方法无法得到最优结果或无法及时得到最优结果。
因此对于大规模的一维下料问题,我们给出了结合动态规划和贪婪算法的新算法,称之为DP 贪婪算法。
基本思想是:对模型计算时,不用先得到一定数量的下料方案,而是在选取下料方案时就以数学模型中的目标和约束条件为基础来进行寻找。
为了保证尽量节省材料,应该尽量将比较大的零件先进行处理,并同时辅以长度小的零件,以保证单个原料的利用率尽量大。
因此对每一个零件按照其长度大小依次给定处理顺序的权值。
为了保证时间的要求,有要求的零件应该尽量优先处理,对每一个零件按时间紧迫度t 依次给定一个处理顺序的权值。
两者的结合将作为每一个零件动态规划初始权值。
在决定了处理顺序后,首先利用贪婪思想,选取当前尚没有得到的零件集合中权值最大的一个进行处理。
调用动态规划方法,得到一种下料方式,此方法里含有当前的零件,在得到此下料方式后,先尽可能按照此方式进行处理,以尽量减少下料方式数,然后再应用贪婪思想。
依次类推,直到得到所有的零件。
这样我们将得到一种下料方案。
如果此方案满足约束要求则停止处理,否则对权值进行调整,如果结果不能满足时间紧迫度的限制,则将优先权值步长直接调节到理论上限,随后通过二分查找的方法进行选择,如果材料利用率过低,则参照以上方法进行调节。
而后重复上述过程,直到得到合理结果。
算法描述:1. 局部最优//计算当前单根利用率最大值,并得到一组可行下料方案FOR I = 1 TO 工件总种类数FOR J = 原材料总长度 DOWNTO 0IF 在J 的位置已经有解FOR K = 第I 件工件中未切割的数量 DOWNTO 1当前长度 = J + 第I 件工件的长度*KIF 当前长度位置尚未得到解 THEN保存当前解ELSE 对两个解进行比较选取较优解FOR I = 材料长度 DOWNTO 1IF 当前长度有解存在 THEN返回解2. 全局贪婪对所有需要的零件进行处理FOR I = 1 TO 工件种类总数WHILE 如果当前种类还有剩余(按照权值大小依次处理) DO利用上述局部最优处理选取一种至少含有当前种类一根的最优解累加计算结果更新数据表格3. 反复调整调整权值IF 得到全局的解法不合理IF 不能按时完成零件 按规则加大优先权值ELSE 浪费过于大 按规则加大长度权值调用上述全局贪婪3、二维下料问题二维情况下,假设在矩形原料切割时采用正交切割,切割时的锯缝可以是直的也可以是弯的;不允许零件旋转;而且切割所引起的锯缝损耗忽略不计。
3.1 模型建立假设共有k 种不同下料方式,第i 种下料方式下料的总块数记为()k i x i ,...,1=,并记第i 种下料方式产生零件j 的个数记为ij a (如果某零件j (M j ≤≤1)满足W w L l j j >>或,则0≡ij a (k i ,,1 =)),记第i 种下料方式下料一次产生的余料(即料头)为()k i i ,...,1=δ。
二维单一原材料下料模型的建模思想与一维单一原材料下料模型类似。
得到如下有交货时间限制的二维下料问题的数学模型:()()⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⨯+⨯=∑∑==1%08.01min 11k i i ki i i x signal x x f δs.t. ()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥<=≤≤===⋅≤==+∑∑∑===+),,1;,,1(0,);,,1(),,1(),,1(max ,...,1)(,,,1,1,1,m j k i y x d d k i x y y m j n y a m j d y m j n x a a j j l j j d i i j l i d i d i j k i d i ij j k i d i j ki i ij m j i 且为整数 3.3 模型求解目前,解有交货时间限制的二维下料问题的常用方法是启发式算法,但是这种方法在大规模的下料问题中并不能将问题的规模降到一个合理的围。
对于大规模的二维下料问题,本文给出新的求解方法。
先利用降维思想将二维下料问题化为两个一维下料问题,对每一个一维下料问题,再使用本文一维下料问题的DP 贪婪算法进行计算,再将两者的结果结合起来,得到最终的结果。
本文采用的降维思想为:第一步,先考虑长度(或宽度)这一维(以下采用先考虑宽度为例进行说明),将宽度相同的零件归为一类,对每一类,假设各自存在与该类等宽与原母板等长的母板。
这样,每一类零件宽度与各自的母板宽度相等,这就转化为一维下料问题。
故可借助一维下料模型的算法解出原母板在长度维上的切割方式。
这种方式找到的是长度维上的局部近似最优。
第二步,考虑宽度(或长度)这一维。
由上一步,我们可以得到每一宽度各自所需的母板根数,可将每一类宽度视为一维切割中一个零件的长度,将每一类所需的根数作为零件的下料任务,原母板的宽度作为现在一维切割原料的长,这样又得到一个一维下料问题,同样借助一维下料模型的解法来获得局部近似最优解。
经过上述两步后,二维下料问题就转化为了两个一维下料问题,在借助一维下料问题的求解算法得到两个局部最优解后,可以通过两者的结合得到最终解。
算法的基本思想是:首先比较长的种类和宽的种类,从中选取种类比较少的一个作为第一次降维考虑的基础(在不影响一般性的前提下,以下假设宽度种类较少来进行描述)。
按照宽度对所有零件进行分类,然后假设已经有各种宽度的模板足够多,而模板的长和原材料的长相等。
这样在接下来的切割过程中将不考虑跨度问题,这样将完全变为一维下料问题。
为了得到更优的解应该优先处理宽度最宽的一类,所以依据宽度给定每一类零件一个权值。
同时要考虑到交货时间的要求,交货时间比较短的零件应该优先处理,所以依据交货时间给定每一类零件一个权值,两者的结合作为处理顺序的权值。
在接下来的处理中,应该选取当前未处理集合中权值最大一类宽度的零件借助一维下料算法进行处理,以得到需要此类宽度模板的数量。
为了提高原材料利用率,当一类宽度零件处理完毕后,如果有一些余料,将采用动态规划方法,在利用率高的要求下将其它宽度的零件尽量用这些余料来获得,直到剩下的余料不能再被使用为止。
重复这个过程,可以得到每一类宽度的模板需要多少数目,同时得到一种下料方案。
接下来,将每一种宽度作为一维下料问题中零件的规格,而每一类宽度需要的数目就是一维下料问题中零件的数量要求,而此次一维下料问题的原材料长度是二维下料问题中原材料的宽度,对于这个一维下料问题借助上文的算法对其进行处理,得到一种下料方案。
将第一次得到的一维下料方案和第二次得到的一维下料方案按顺序进行组合,即得到这个问题的下料方案。
