实验1离散时间信号的产生与运算
数字信号处理实验报告

《数字信号处理》实验报告学院:信息科学与工程学院专业班级:通信1303姓名学号:实验一 常见离散时间信号的产生和频谱分析一、 实验目的(1) 熟悉MATLAB 应用环境,常用窗口的功能和使用方法;(2) 加深对常用离散时间信号的理解;(3) 掌握简单的绘图命令;(4) 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对离散信号进行频域分析。
二、 实验原理(1) 常用离散时间信号a )单位抽样序列⎩⎨⎧=01)(n δ00≠=n n 如果)(n δ在时间轴上延迟了k 个单位,得到)(k n -δ即:⎩⎨⎧=-01)(k n δ0≠=n k n b )单位阶跃序列⎩⎨⎧=01)(n u 00<≥n n c )矩形序列 ⎩⎨⎧=01)(n R N 其他10-≤≤N nd )正弦序列)sin()(ϕ+=wn A n xe )实指数序列f )复指数序列()()jw n x n e σ+=(2)离散傅里叶变换:设连续正弦信号()x t 为0()sin()x t A t φ=Ω+这一信号的频率为0f ,角频率为002f πΩ=,信号的周期为00012T f π==Ω。
如果对此连续周期信号()x t 进行抽样,其抽样时间间隔为T ,抽样后信号以()x n 表示,则有0()()sin()t nT x n x t A nT φ===Ω+,如果令w 为数字频率,满足000012s sf w T f f π=Ω=Ω=,其中s f 是抽样重复频率,简称抽样频率。
为了在数字计算机上观察分析各种序列的频域特性,通常对)(jw e X 在[]π2,0上进行M 点采样来观察分析。
对长度为N 的有限长序列x(n), 有∑-=-=10)()(N n n jw jw k k e n x e X其中 1,,1,02-==M k k Mw k ,π 通常M 应取得大一些,以便观察谱的细节变化。
取模|)(|k jw e X 可绘出幅频特性曲线。
数字信号处理实验指导

奇偶合成:
几何级数:
序列相关:
卷积运算:
差分方程:
在Matlab中: 三、实验内容
1.典型序列的实现 单位阶跃序列;实数指数序列;复数指数序列;正余弦序列;随机 序列用rand(1,N)和randn(1,N)来生成;
2.序列的运算 给定序列x1=[1 2 3 4 5 6 7 8 9], ns1=-4; x2=[9 8 7 6 5 4 3 2 1], ns2=4 求:1) x1+x2; 2) y3=x1×x2;
三、实验内容 IIR滤波器 给定IIR滤波器,求其典范型、级连型、并联型结构。 FIR滤波器 给定FIR滤波器,求其级连型、频率抽样型结构。
四、本实验用到的一些函数 求多项式的根:b=roots(a) 构造指定根的多项式:a=poly(b) 部分分式展开:[r1,p1,k]=residuez(b,a) [b,a]=residuez(r1,p1,k) 对复数进行重新排序:p1=cplxpair(p) 变直接形式为级联形式:[b0,B,A]=dir2cas(b,a) 滤波器的级联实现:y=casfiltr(b0,B,A,x) 变级联形式为直接形式:[b,a]=cas2dir(b0,B,A)
五、MATLAB编程和调试技巧 因为 MATLAB 语言是一种解释性语言,所以有时 MATLAB 程序的 执行速度不是很理想。因此尽量避免使用循环,用向量化的运算来代
替循环操作。 注意;的使用。
如果有的同学对MATLAB的使用不熟悉,请在老师处考取语言学习 PPT。 六、实验报告的要求 实验目的; 实验原理; 实验内容:要求有程序,有图形(坐标要标识清楚)。 实验结论。
实验二 离散时间傅立叶变换
一、实验目的 1.复习离散时间傅立叶正反变换 2.复习DTFT的两个重要特性 3.复习DTFT的其它特性 4.离散LTI系统的频率响应 5.采样及重构信号
实验一 离散时间信号的时域分析
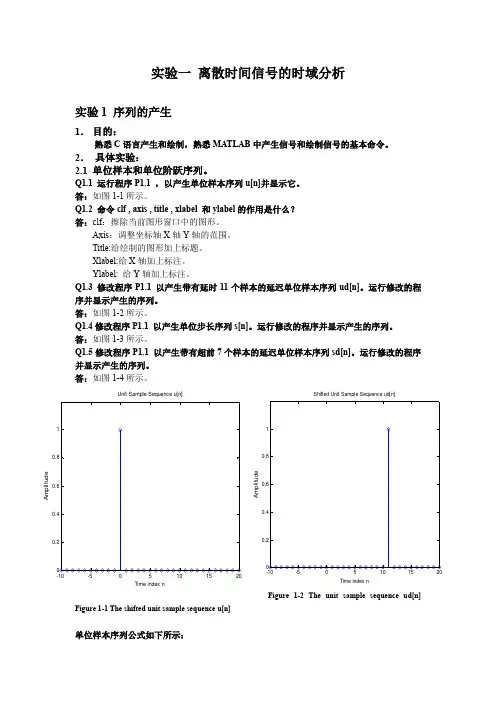
实验一 离散时间信号的时域分析实验1 序列的产生1. 目的:熟悉C 语言产生和绘制,熟悉MATLAB 中产生信号和绘制信号的基本命令。
2. 具体实验:2.1 单位样本和单位阶跃序列。
Q1.1 运行程序P1.1 ,以产生单位样本序列u[n]并显示它。
答:如图1-1所示。
Q1.2 命令clf , axis , title , xlabel 和ylabel 的作用是什么? 答:clf :擦除当前图形窗口中的图形。
Axis :调整坐标轴X 轴Y 轴的范围。
Title:给绘制的图形加上标题。
Xlabel:给X 轴加上标注。
Ylabel: 给Y 轴加上标注。
Q1.3 修改程序P1.1 以产生带有延时11个样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
答:如图1-2所示。
Q1.4修改程序P1.1 以产生单位步长序列s[n]。
运行修改的程序并显示产生的序列。
答:如图1-3所示。
Q1.5修改程序P1.1 以产生带有超前7个样本的延迟单位样本序列sd[n]。
运行修改的程序并显示产生的序列。
答:如图1-4所示。
Figure 1-2 The unit sample sequence ud[n]Figure 1-1 The shifted unit sample sequence u[n]单位样本序列公式如下所示:Time index nA m p l i t u d eUnit Sample Sequence u[n]Time index nA m p l i t u d eShifted Unit Sample Sequence ud[n]1 , n=0 1 , n=k δ[n]= δ[n-k]=0 , 0≠0 0 , 0≠kFigure 1-3 The unit step sequence s[n] Figure 1-4 The shifted unit step sequence sd[n]单位阶跃序列公式如下所示:1 , n ≥0 1 , n ≥k μ[n]= μ[n-k]=0 , n <0 0 , n <k2.2 指数信号Q1.6 运行程序P1.2 ,以产生复数值的指数序列。
实验一 离散信号的时域运算与变换

实验一 离散信号的时域运算与变换1. 熟悉MA TLAB 编程特点将序列x(n)={1,2,3,4,0,7},其中n =0:5的每一个样本都移动3个周期,移位后的序列y(n)=x(n-3)2.序列的奇偶分解将序列x(n)={0,1,2,3,4,3,2,1,0},其中n =-3:5进行奇偶分解用函数stem 显示其奇偶序列3.序列的加法运算设x1(n)={1,0.5,0.3,0.4}其中n=-1:2 ;x2(n)={0.2,0.3,0.4,0.5,0.8,1}其中n=-2:34.实现2中序列的翻转2.对本实验结果做理论计算,解释实验结果3.总结实验体会及实验中存在的问题1. 在matlab 中应如何实现序列的相乘运算2. 在matlab 中应如何实现序列的倒相运算?2)]()([2)]()([)(,)(),()()(n x n x o n x n x e o e n x n x n x n x n x ---+==+=奇序列其中偶序列)()()(21n x n x n x +=x(-n)y(n)=首先,在用MA TLAB 表示离散序列并将其可视化时,我们还应注意以下几点:第一、离散时间序列无法用符号运算来表示,要用矩阵的形式;第二、由于在MA TLAB 中矩阵的元素个数有限,因此,MA TLAB 无法表示无限长的序列;第三、在绘制离散信号波形的函数stem 命令,而不是plot 命令。
下面是MA TLABn0是单位抽样序列的位移量,n1,n2[x,n]=impuls (n0,n1,n2);figure上图为右移了一个单位的单位抽样序列其次,对于离散序列来说,序列相加、相乘是将两序列对应时间序号的值逐项相加或相乘,平移、反折、及倒相变换与连续信号的定义完全相同,但需要注意,与连续信号不同的是,在MA TLAB 中,离散序列的时域运算和变换不能用符号运算来实现,必须用向量表示的方法,即在MA TLAB 中离散序列的相加、相乘需表示成两个向量的相加、相乘,因而参加运算的两序列向量必须具有相同的维数。
时域离散信号的产生与基本运算

实验一 时域离散信号的产生与基本运算一、实验目的1、了解常用的时域离散信号及其特点。
2、掌握MATLAB 产生常用时域离散信号的方法。
3、掌握时域离散信号简单的基本运算方法。
二、实验内容1、自己设定参数,分别表示并绘制单位抽样序列、单位阶跃序列、正弦序列、 实指数序列、随机序列。
2、自己设定参数,分别表示并绘制信号移位、信号相加、信号相乘、信号翻转、 信号和、信号积、信号能量。
3、已知信号(1) 描绘)(n x 序列的波形。
(2) 用延迟的单位脉冲序列及其加权和表示)(n x 序列。
(3) 描绘以下序列的波形:)2()(),2(2)(),2(2)(321n x n x n x n x n x n x -=+=-=三、实现步骤1、自己设定参数,分别表示并绘制单位抽样序列、单位阶跃序列、正弦序列、 实指数序列、随机序列。
(1)单位抽样序列程序:x=zeros(1,10);x(2)=1;stem(x,'filled')axis([0,10,-0.2,1]);title('µ¥Î»³éÑùÐòÁÐ');-0.200.20.40.60.8图1 (2)单位阶跃序列程序:N=10;u=ones(1,N);stem(u,'filled')axis([-10,10,0,1]);title('µ¥Î»½×Ô¾ÐòÁÐ');00.10.20.30.40.50.60.70.80.91单位阶跃序列图2 (3)正弦序列程序:x=-20:1:20;y=sin(0.2*pi.*x+0.5*pi);stem(x,y,'filled');axis([-20,20,-2,2]);title('ÕýÏÒÐòÁÐ');正弦序列-20-15-10-505101520图3 (4)实指数序列a=1/2程序:n=0:10;a1=1/2;y1=a1.^n;stem(n,y1,'filled');axis([0,10,0,1]);title('ʵָÊýÐòÁУ¬a=1/2');实指数序列,a=1/2图4 5实指数序列a=2程序:n=0:10;a2=2;y2=a2.^n;stem(n,y2,'filled');title('ʵָÊýÐòÁÐ,a=2');实指数序列,a=2图5 6 随机序列程序:y=rand(1,20);stem(y,'filled');title('Ëæ»úÐòÁÐ');0246810121416182000.10.20.30.40.50.60.70.80.91随机序列图62、自己设定参数,分别表示并绘制信号移位、信号相加、信号相乘、信号翻转、 信号和、信号积、信号能量。
《数字信号处理》上机实验指导书

《数字信号处理》上机实验指导书实验1 离散时间信号的产生1.实验目的数字信号处理系统中的信号都是以离散时间形态存在,所以对离散时间信号的研究是数字信号处理的基本所在。
而要研究离散时间信号,首先需要产生出各种离散时间信号。
MATLAB 是一套功能强大的工程计算及数据处理软件,广泛应用于工业,电子,医疗和建筑等众多领域。
使用MATLAB软件可以很方便地产生各种常见的离散时间信号,而且它还具有强大的绘图功能,便于用户直观地输出处理结果。
通过本实验,学生将学习如何用MATLAB产生一些常见的离散时间信号,并通过MATLAB中的绘图工具对产生的信号进行观察,加深对常用离散信号的理解。
2.实验要求本实验要求学生运用MATLAB编程产生一些基本的离散时间信号,并通过MATLAB的几种绘图指令画出这些图形,以加深对相关教学内容的理解,同时也通过这些简单的函数练习了MATLAB的使用。
3.实验原理(1)常见的离散时间信号1)单位抽样序列,或称为离散时间冲激,单位冲激:?(n)???1?0n?0 n?0如果?(n)在时间轴上延迟了k个单位,得到?(n?k)即:?1n?k ?(n?k)??0n?0?2)单位阶跃序列n?0?1 u(n)?n?0?0在MATLAB中可以利用ones( )函数实现。
x?ones(1,N);3)正弦序列x(n)?Acos(?0n??)这里,A,?0,和?都是实数,它们分别称为本正弦信号x(n)的振幅,角频率和初始相位。
f0??02?为频率。
x(n)?ej?n4)复正弦序列5)实指数序列x(n)?A?n(2)MATLAB编程介绍MATLAB是一套功能强大,但使用方便的工程计算及数据处理软件。
其编程风格很简洁,没有太多的语法限制,所以使用起来非常方便,尤其对初学者来说,可以避免去阅读大量的指令系统,以便很快上手编程。
值得注意得就是,MATLAB中把所有参与处理的数据都视为矩阵,并且其函数众多,希望同学注意查看帮助,经过一段时间的训练就会慢慢熟练使用本软件了。
时域离散信号实验报告(3篇)
第1篇一、实验目的1. 理解时域离散信号的基本概念和特性。
2. 掌握时域离散信号的表示方法。
3. 熟悉常用时域离散信号的产生方法。
4. 掌握时域离散信号的基本运算方法。
5. 通过MATLAB软件进行时域离散信号的仿真分析。
二、实验原理时域离散信号是指在时间轴上取离散值的一类信号。
这类信号在时间上不连续,但在数值上可以取到任意值。
时域离散信号在数字信号处理领域有着广泛的应用,如通信、图像处理、语音处理等。
时域离散信号的基本表示方法有:1. 序列表示法:用数学符号表示离散信号,如 \( x[n] \) 表示离散时间信号。
2. 图形表示法:用图形表示离散信号,如用折线图表示序列。
3. 时域波形图表示法:用波形图表示离散信号,如用MATLAB软件生成的波形图。
常用时域离散信号的产生方法包括:1. 单位阶跃信号:表示信号在某个时刻发生突变。
2. 单位冲激信号:表示信号在某个时刻发生瞬时脉冲。
3. 正弦信号:表示信号在时间上呈现正弦波形。
4. 矩形脉冲信号:表示信号在时间上呈现矩形波形。
时域离散信号的基本运算方法包括:1. 加法:将两个离散信号相加。
2. 乘法:将两个离散信号相乘。
3. 卷积:将一个离散信号与另一个离散信号的移位序列进行乘法运算。
4. 反褶:将离散信号沿时间轴翻转。
三、实验内容1. 实验一:时域离散信号的表示方法(1)使用序列表示法表示以下信号:- 单位阶跃信号:\( u[n] \)- 单位冲激信号:\( \delta[n] \)- 正弦信号:\( \sin(2\pi f_0 n) \)- 矩形脉冲信号:\( \text{rect}(n) \)(2)使用图形表示法绘制以上信号。
2. 实验二:时域离散信号的产生方法(1)使用MATLAB软件生成以下信号:- 单位阶跃信号- 单位冲激信号- 正弦信号(频率为1Hz)- 矩形脉冲信号(宽度为2)(2)观察并分析信号的波形。
3. 实验三:时域离散信号的基本运算(1)使用MATLAB软件对以下信号进行加法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(2)使用MATLAB软件对以下信号进行乘法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(3)使用MATLAB软件对以下信号进行卷积运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(4)使用MATLAB软件对以下信号进行反褶运算:- \( u[n] \)4. 实验四:时域离散信号的仿真分析(1)使用MATLAB软件对以下系统进行时域分析:- 系统函数:\( H(z) = \frac{1}{1 - 0.5z^{-1}} \)(2)观察并分析系统的单位冲激响应。
数字信号处理实验报告
一、实验目的1. 理解数字信号处理的基本概念和原理。
2. 掌握离散时间信号的基本运算和变换方法。
3. 熟悉数字滤波器的设计和实现。
4. 培养实验操作能力和数据分析能力。
二、实验原理数字信号处理(Digital Signal Processing,DSP)是利用计算机对信号进行采样、量化、处理和分析的一种技术。
本实验主要涉及以下内容:1. 离散时间信号:离散时间信号是指时间上离散的信号,通常用序列表示。
2. 离散时间系统的时域分析:分析离散时间系统的时域特性,如稳定性、因果性、线性等。
3. 离散时间信号的变换:包括离散时间傅里叶变换(DTFT)、离散傅里叶变换(DFT)和快速傅里叶变换(FFT)等。
4. 数字滤波器:设计、实现和分析数字滤波器,如低通、高通、带通、带阻滤波器等。
三、实验内容1. 离散时间信号的时域运算(1)实验目的:掌握离散时间信号的时域运算方法。
(2)实验步骤:a. 使用MATLAB生成两个离散时间信号;b. 进行时域运算,如加、减、乘、除等;c. 绘制运算结果的时域波形图。
2. 离散时间信号的变换(1)实验目的:掌握离散时间信号的变换方法。
(2)实验步骤:a. 使用MATLAB生成一个离散时间信号;b. 进行DTFT、DFT和FFT变换;c. 绘制变换结果的频域波形图。
3. 数字滤波器的设计和实现(1)实验目的:掌握数字滤波器的设计和实现方法。
(2)实验步骤:a. 设计一个低通滤波器,如巴特沃斯滤波器、切比雪夫滤波器等;b. 使用MATLAB实现滤波器;c. 使用MATLAB对滤波器进行时域和频域分析。
4. 数字滤波器的应用(1)实验目的:掌握数字滤波器的应用。
(2)实验步骤:a. 采集一段语音信号;b. 使用数字滤波器对语音信号进行降噪处理;c. 比较降噪前后的语音信号,分析滤波器的效果。
四、实验结果与分析1. 离散时间信号的时域运算实验结果显示,通过MATLAB可以方便地进行离散时间信号的时域运算,并绘制出运算结果的时域波形图。
实验一 离散时间信号的产生
实验一 离散时间信号的产生1. 实验目的数字信号处理系统中的信号都是以离散时间形态存在的,所以对离散时间信号的研究是数字信号处理的基本所在。
而要研究离散时间信号,首先需要产生各种离散时间信号。
使用MATLAB 软件 很方便的产生各种常见的离散时间信号,而且它还有强大的绘图功能,便于用户直接地处理输出结果。
2. 实验原理离散时间信号是指在离散时刻才有定义的信号,简称离散信号,或者序列。
离散序列通常用x(n)来表示,自变量必须是整数,常见的离散时间信号如下:(1) 单位冲激序列⎩⎨⎧=01)(n δ 00≠=n n如果)(n δ在时间轴上延迟了k 个单位,)(k n -δ即:⎩⎨⎧=-01)(k n δ 0≠=n k n长度为N 的单位冲激序列δ(n)可以通过下面的MATLAB 命令获得。
n=-(N-1):N-1x=[zeros(1,N-1) 1 zeros(1,N-1)];setm(n,x)延迟K 个采样点的长度为N 的单位冲激序列δ(N-k )(k<N)可以用下面的命令获得: n=-(N-1):N-1x=[zeros(1,M) 1 zeros(1,N-M-1)];setm(n,y)(2)单位阶跃序列⎩⎨⎧01)(n u 00<≥n n 长度为N 的单位阶跃序列u (n)可以通过下面的MA TLAB 命令获得。
n=-(N-1):N-1x=[zeros(1,N-1) ones(1,N)];setm(n,x)延迟的单位阶跃序可以用类似于单位冲激信号的方法产生。
(3)矩形序列R N =u(n)-u(n-N)(4)正弦序列x (n ) = A cos(ωn +φ).这里A ,ω,φ都是实数分别为正弦信号的振幅,角频率,和初始相位,可以用下面的命令获得:n=0:N-1x=A*cos(2*pi*f*n/Fs+phase)(5) 单边指数序列:n a n x =)(u (n) 长度为N 的单边指数序列可以通过下面的MA TLAB 命令实现n a x N n .^1:0=-=setm(n,x)(6)复指数序列3实验内容(1)绘制程序产生单位冲激序列⎩⎨⎧=01)(n δ00≠=n n 及δ(n-“学号后两位”)并绘出其图形>> n=-10:10;>> x=[zeros(1,10),1,zeros(1,10)];>> stem(n,x)>> title('单位冲激序列'); >> xlabel('n');ylabel('x(n)');>> n=0:50;>> y=[zeros(1,40),1,zeros(1,10)];>>stem(n,y);>> title('单位冲激采样后的序列');>> xlabel('n');ylabel('y(n)');(2)绘制程序产生单位阶跃信号⎩⎨⎧01)(n u 00<≥n n 及u(n-“学号后两位”)及u(n)- u(n-“学号后两位”),并绘出其图形。
离散信号的产生及运算
离散信号的产生及运算实验一离散信号的产生及运算一.实验目的:1.复习和巩固数字信号处理中离散信号的产生和运算2.学习和掌握用MATLAB 产生离散信号的方法3.学习和掌握用MATLAB 对离散信号进行运算二.实验原理1.用MATLAB 函数产生离散信号信号是数字信号处理的最基本内容。
没有信号,数字信号处理就没了工作对象。
MATLAB7.0 内部提供了大量的函数,用来产生常用的信号波形。
例如,三角函数(sin,cos), 指数函数(exp),锯齿波函数(sawtooth), 随机数函数(rand)等。
⑴产生被噪声污染的正弦信号用随机数函数产生污染的正弦信号。
⑵产生单位脉冲序列和单位阶跃序列按定义,单位脉冲序列为0 0 0 1, ( ) 0,n n n n n n单位阶跃序列为。
0 0 0 1, ( ) 0,n n u n n n n⑶矩形脉冲信号:在MATLAB 中用rectpuls 函数来表示,其调用形式为:y=rectpuls(t,width),用以产生一个幅值为1,宽度为width,相对于t=0 点左右对称的矩形波信号,该函数的横坐标范围由向量t 决定,是以t=0 为中心向左右各展开width/2 的范围,width 的默认值为1。
例:以t=2T(即t-2×T=0)为对称中心的矩形脉冲信号的MATLAB 源程序如下:(取T=1)t=0:0.001:4;T=1;ft=rectpuls(t-2*T,2*T);plot(t,ft);grid on; axis([0 4 –0.5 1.5]);⑷周期性矩形波(方波)信号在MATLAB 中用square 函数来表示,其调用形式为:y=square(t,DUTY),用以产生一个周期为2π、幅值为±1 的周期性方波信号,其中的DUTY 参数表示占空比,即在信号的一个周期中正值所占的百分比。
例如频率为30Hz 的周期性方波信号的MATLAB 参考程序如下:t=-0.0625:0.0001:0.0625;y=square(2*pi*30*t,75);plot(t,y);axis([-0.0625 0.0625 –1.5 1.5]);grid on ;2.MATLAB 中信号的运算乘法和加法:离散信号之间的乘法和加法,是指它的同序号的序列值逐项对应相乘和相加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理
实验报告
班级:
学号:
姓名:word文档可自由复制编辑
实验1离散时间信号的产生与运算
一、实验目的
(1)了解离散时间信号的特点。
(2)掌握在计算机中生成及绘制各种常用离散时间信号序列的方法。
(3)掌握序列的加、减、乘、除和平移、反转、尺度变换等基本运算及计算机的
实现方法。
二、实验原理
信号是随时间变化的物理量,而计算机只能处理离散信号。
离散信号是在某些不连续的时间上有信号值,而在其它时间点上没有定义的一类信号。
离散信号一般可以由连续信号通过模数转换得到。
常用的离散信号有单位脉冲序列、单位阶跃序列、复指数序列、正弦信号序列、随机序列等。
离散信号的基本运算包括信号的加、减、乘、除。
离散信号的时域变换包括信号的平移、反转、尺度变换等。
三、实验内容与方法
1、编写程序,生成如下数字信号:sqrt(2*k)u(k错误!未找到引用源。
3),
δ(k+5)。
(1) f(k)=sqrt(2*k)u(k错误!未找到引用源。
3)
代码:
k=(1:10);
n=3;
u=[(k-n)>=0];
a=sqrt(2*k);
stem(k,a.*u);
title('sqrt(2*k)u(k 3)的图像');
xlabel('时间(k)');ylabel('幅值f(k)');
运行图:
word文档可自由复制编辑
(2) f(k)= δ(k+5)
代码:
k1=-10;k2=0;k=k1:k2;
n=-5; %单位脉冲出现的位置
f=[(k-n)==0];
stem(k,f,'filled');title('δ(k+5)序列的图像')
xlabel('时间(k)');ylabel('幅值f(k)');
运行图:
word文档可自由复制编辑
2、f(k)=sin(0.1πk),设计并编写程序,完成信号f(k)到f(2k+2)的转化。
(1) f(k)
代码:
k1=-20;k2=20;
k=k1:k2;
f=sin(0.1*pi*k);
stem(k,f,'filled');
title('正弦序列');xlabel('时间(k)');ylabel('幅值f(k)');
运行图:
(2) f(2k+2)
代码:
k1=-20;k2=20;
k=k1:k2;
d=k+1; %对k平移一个单位
f1=sin(0.2*pi*d); %周期变为原来的一半
stem(k,f1,'filled');
title('正弦序列2');xlabel('时间(k)');ylabel('幅值f(2k+2)');
运行图:
word文档可自由复制编辑
word 文档 可自由复制编辑
四、 思考题
(1) 脉冲序列信号与阶跃序列信号各有什么特性?
答:单位脉冲序列只在n=0 处有一个单位值1,其余点上皆为0; 单位阶跃序列只有在n>=0时,才取非零值1,当n<0时均取零值。
(2) 脉冲序列信号和阶跃序列信号有什么关系?
答:n 个冲激信号(每个冲激信号都是1个U 单位)的集合就是阶跃信号,u(n)和单位采样序列之间的关系如下列公式所示:。
