湖南大学研究生机械振动_习题第一章
机械振动习题集
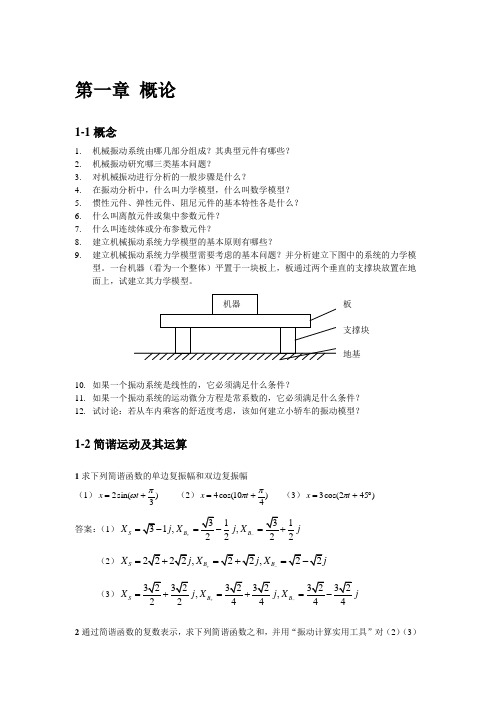
第一章 概论1-1概念1. 机械振动系统由哪几部分组成?其典型元件有哪些?2. 机械振动研究哪三类基本问题?3. 对机械振动进行分析的一般步骤是什么?4. 在振动分析中,什么叫力学模型,什么叫数学模型?5. 惯性元件、弹性元件、阻尼元件的基本特性各是什么?6. 什么叫离散元件或集中参数元件?7. 什么叫连续体或分布参数元件?8. 建立机械振动系统力学模型的基本原则有哪些?9.建立机械振动系统力学模型需要考虑的基本问题?并分析建立下图中的系统的力学模型。
一台机器(看为一个整体)平置于一块板上,板通过两个垂直的支撑块放置在地面上,试建立其力学模型。
10. 如果一个振动系统是线性的,它必须满足什么条件?11. 如果一个振动系统的运动微分方程是常系数的,它必须满足什么条件? 12. 试讨论:若从车内乘客的舒适度考虑,该如何建立小轿车的振动模型?1-2简谐运动及其运算1求下列简谐函数的单边复振幅和双边复振幅 (1))3sin(2πω+=t x (2))410cos(4ππ+=t x (3))452cos(3︒+=t x π答案:(1)111,,2222S B B X j X j X j +-==-=+ (2),,S B B X X X +-== (3),,224444S B B X j X j X j +-=+=+=-2通过简谐函数的复数表示,求下列简谐函数之和,并用“振动计算实用工具”对(2)(3)进行校核(1))3sin(21πω+=t x )32s i n (32πω+=t x (2)t x π10sin 51=)410cos(42ππ+=t x(3))302sin(41︒+=t x π )602sin(52︒+=t x π)452cos(33︒+=t x π)382cos(74︒+=t x π )722cos(25︒+=t x π答案:(1))6.6cos(359.412︒+=t x ω (2))52.4710cos(566.312︒-=t x π (3))22.92cos(776.1412345︒+=t x π3试计算题1中)(t x 的一阶导数和二阶导数对应的复振幅,并给出它们的时间历程4设)(t x 、)(t f 为同频简谐函数,并且满足)(t f cx x b x a =++ 。
湖南大学机械振动习题课

2 n 1 tan 2 1 n
等效激励:旋转部件偏心质量引起的振动
M
me m t u x
M
2
sin t u x
e
2
k c
a
2
k
k
c
b
The rotating unbalance system can be equated to a SDOF system as shown above. 由动量定理(theorem of momentum)
Therefore, solve to get: B = 0 and A = 0.0353. Hence, x 0.0353e
n t
sin d t
For maximum displacement: velocity x
0
dx x 0.0353e nt (n sin d t d cos d t ) 0 dt n sin d t d cos d t 0
振幅: A u (
n
0 u
)
2
n
v0
v0
m k
最大张力: T mg kA mg v0 mk 1000 9.8 0.5 1000 4 105 1.98 104 (N)
此题基本理论:单自由度自由振动 Free vibration of SDOF
( 2 1)n t ( 2 1)n t
k c 0 2m m
2
2
Over-damped ( 1 )
x(t ) a1e
Critically Damped ( 1 )
a2e
机械振动学习题解答(一).PPT24页

16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
机械振动一章习题解答

T = 2π
所以应当选择答案(C)。
m ( k1 + k 2 ) m = 2π k k1 k 2
习题 12—4
一质点作简谐振动,周期为 T,当它由平衡位置向 X 轴正方向运动 ]
时,从二分之一最大位移处到最大位移处这段路程所需要的时间为: [ (A) T/4。 (B) T/12。 (C) T/6。 (D) T/8。
解: 单摆的振动满足角谐振动方程, 这里所给的 θ 是初始角位移,显然是从最大角位移处计时。由 旋转矢量法容易判断该单摆振动的初位相为 “0” , 因此,应当选择答案(C) 。 −θm
题解 12―1 图
习题 12—2
轻弹簧上端固定,下端系一质量为 m1 的物体,稳定后在 m1 下边又
系一质量为 m2 的物体,于是弹簧又伸长了 ∆x ,若将 m2 移去,并令其振动,则 振动周期为: [ (A) T = 2π ]
位相 ϕ = π 2 ,故振动方程为
x = 0.02 cos(1.5t +
π ) 2
(SI)
习题 12─17
两个同方向的简谐振动的振动方程分别为
1 , x 2 = 3 × 10 − 2 cos 2π (t + ) 4
1 x1 = 4 × 10 − 2 cos 2π (t + ) 8
(SI)
求:合振动方程。 解:设合振动方程为
X
习题 12─12
一质点作简谐振动,振动图
线如图所示,根据此图,它的周期
4 O –2
2
t (s)
T=
ϕ=
,用余玄函数描述时的初位相
习题 12―12 图
。 解:根据振动图线可画出旋转矢量图,可得
t=2
∴ ∴
机械振动习题和答案解析

《机械振动噪声学》习题集1-1 阐明下列概念,必要时可用插图。
(a) 振动;(b) 周期振动和周期;(c) 简谐振动。
振幅、频率和相位角。
1-2 一简谐运动,振幅为0.20 cm,周期为0.15 s,求最大的速度和加速度。
1-3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g,求其振动的振幅。
1-4 一简谐振动频率为10 Hz,最大速度为4.57 m/s,求其振幅、周期和最大加速度。
1-5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即:A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' ),并讨论φ=0、π/2 和π三种特例。
1-6 一台面以一定频率作垂直正弦运动,如要求台面上的物体保持与台面接触,则台面的最大振幅可有多大?1-7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。
其中ε << ω。
如发生拍的现象,求其振幅和拍频。
1-8 将下列复数写成指数A e i θ形式:(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i )2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8]2-1 钢结构桌子的周期τ=0.4 s,今在桌子上放W = 30 N 的重物,如图2-1所示。
已知周期的变化∆τ=0.1 s。
求:( a ) 放重物后桌子的周期;( b )桌子的质量和刚度。
2-2 如图2-2所示,长度为L、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住,求杆绕O点微幅振动的微分方程。
2-3 如图2-3所示,质量为m、半径为r的圆柱体,可沿水平面作纯滚动,它的圆心O用刚度为k的弹簧相连,求系统的振动微分方程。
图2-1 图2-2 图2-32-4 如图2-4所示,质量为m、半径为R的圆柱体,可沿水平面作纯滚动,与圆心O 距离为a 处用两根刚度为k的弹簧相连,求系统作微振动的微分方程。
机械振动试题(含答案)(1)

机械振动试题(含答案)(1)一、机械振动 选择题1.如图所示,在一根张紧的水平绳上,悬挂有 a 、b 、c 、d 、e 五个单摆,让a 摆略偏离平衡位置后无初速释放,在垂直纸面的平面内振动;接着其余各摆也开始振动,当振动稳定后,下列说法中正确的有( )A .各摆的振动周期与a 摆相同B .各摆的振动周期不同,c 摆的周期最长C .各摆均做自由振动D .各摆的振幅大小不同,c 摆的振幅最大2.如图所示,质量为m 的物块放置在质量为M 的木板上,木板与弹簧相连,它们一起在光滑水平面上做简谐振动,周期为T ,振动过程中m 、M 之间无相对运动,设弹簧的劲度系数为k 、物块和木板之间滑动摩擦因数为μ,A .若t 时刻和()t t +∆时刻物块受到的摩擦力大小相等,方向相反,则t ∆一定等于2T 的整数倍 B .若2T t ∆=,则在t 时刻和()t t +∆时刻弹簧的长度一定相同 C .研究木板的运动,弹簧弹力充当了木板做简谐运动的回复力 D .当整体离开平衡位置的位移为x 时,物块与木板间的摩擦力大小等于m kx m M+ 3.用图甲所示的装置可以测量物体做匀加速直线运动的加速度,用装有墨水的小漏斗和细线做成单摆,水平纸带中央的虚线在单摆平衡位置的正下方。
物体带动纸带一起向左运动时,让单摆小幅度前后摆动,于是在纸带上留下如图所示的径迹。
图乙为某次实验中获得的纸带的俯视图,径迹与中央虚线的交点分别为A 、B 、C 、D ,用刻度尺测出A 、B 间的距离为x 1;C 、D 间的距离为x 2。
已知单摆的摆长为L ,重力加速度为g ,则此次实验中测得的物体的加速度为( )A .212()x x g L π-B .212()2x x g L π-C .212()4x x g L π-D .212()8x x g Lπ- 4.如图所示,弹簧下面挂一质量为m 的物体,物体在竖直方向上做振幅为A 的简谐运动,当物体振动到最高点时,弹簧正好处于原长,弹簧在弹性限度内,则物体在振动过程中A .弹簧的弹性势能和物体动能总和不变B .物体在最低点时的加速度大小应为2gC .物体在最低点时所受弹簧的弹力大小应为mgD .弹簧的最大弹性势能等于2mgA5.如图所示是扬声器纸盆中心做简谐运动的振动图象,下列判断正确的是A .t =2×10-3s 时刻纸盆中心的速度最大B .t =3×10-3s 时刻纸盆中心的加速度最大C .在0〜l×10-3s 之间纸盆中心的速度方向与加速度方向相同D .纸盆中心做简谐运动的方程为x =1.5×10-4cos50πt (m )6.在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议,可行的是( ) A .适当加长摆线B .质量相同,体积不同的摆球,应选用体积较大的C .单摆偏离平衡位置的角度要适当大一些D .当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆振动的周期7.图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子,图(乙)为这个弹簧振子的振动图象,由图可知下列说法中正确的是( )A.在t=0.2s时,弹簧振子可能运动到B位置B.在t=0.1s与t=0.3s两个时刻,弹簧振子的速度相同C.从t=0到t=0.2s的时间内,弹簧振子的动能持续地增加D.在t=0.2s与t=0.6s两个时刻,弹簧振子的加速度相同8.悬挂在竖直方向上的弹簧振子,周期T=2s,从最低点位置向上运动时刻开始计时,在一个周期内的振动图象如图所示,关于这个图象,下列哪些说法是正确的是()A.t=1.25s时,振子的加速度为正,速度也为正B.t=1.7s时,振子的加速度为负,速度也为负C.t=1.0s时,振子的速度为零,加速度为负的最大值D.t=1.5s时,振子的速度为零,加速度为负的最大值9.如图所示,一端固定于天花板上的一轻弹簧,下端悬挂了质量均为m的A、B两物体,平衡后剪断A、B间细线,此后A将做简谐运动。
机械振动习题集与答案123

《机械振动噪声学》习题集1-1 阐明下列概念,必要时可用插图。
(a) 振动;机械或结构在平衡位置附近的往复运动称为机械振动。
(b) 周期振动和周期;能用时间的周期函数表示系统相应的振动叫做周期振动,周期振动完全重复一次的时间叫做周期(c) 简谐振动。
能用一项时间的正弦,余弦表示系统响应的振动叫做简谐振动振幅:物体离开平衡位置的最大位移频率:每一秒重复相同运动的次数相位角:1-2 一简谐运动,振幅为0.20 cm,周期为0.15 s,求最大的速度和加速度。
最大速度=A*w 最大加速度=A*W*W1-3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g,求其振动的振幅。
a =A*W*W=A*(2*PI*f)*(2*PI*f)------将f=82,a=500代入即可1-4 一简谐振动频率为10 Hz,最大速度为4.57 m/s,求其振幅、周期和最大加速度。
略(方法同上一题)1-5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即:A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' ),并讨论φ=0、π/2 和π三种特例。
将两个简谐运动化成复数形式即可相加1-6 一台面以一定频率作垂直正弦运动,如要求台面上的物体保持与台面接触,则台面的最大振幅可有多大?设台面运动频率为f, 即要求a=A*W*W =A*(2*PI*f)*(2*PI*f)<=g1-7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。
其中ε << ω。
如发生拍的现象,求其振幅和拍频。
1-8 将下列复数写成指数A e i θ形式:(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i ) 2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8 ]2-1 钢结构桌子的周期τ=0.4 s,今在桌子上放W = 30 N 的重物,如图2-1所示。
机械振动学习题解答1

机械振动学习题解答11-4一简谐振动频率为10Hz,最大速度为4.57m/,-求其振幅、周期和最大加速度。
解:简谐振动的位移某(t)=Ain(ωnt+)速度&某(t)=ωnAco(ωnt+)&速度幅值某ma某=ωnA某加速度幅值&&ma某=ωn2A 某加速度&&(t)=ωn2Ain(ωnt+)&由题意,fn=10Hz,某ma某=4.57m/所以,圆频率ωn=2πfn=20π圆频率振幅A=&某ma某ωn=0.072734m周期T=1/fn=0.1最大加速度2&&ma某=ωnA=ωn某ma某=287.14m/2&某1-6一台面以一定频率作垂直正弦运动,如要求台-面上的物体保持与台面接触,则台面的最大振幅可有多大?解:对物体受力分析&&mgN=m 某物体N当N=0时,物体开始脱离台面,此时台面的加速度为最大值。
即&&mg=m某ma某2&&ma某=ωnA某2A=g/ωn台面mg&&某又由于所以1-7计算两简谐运动某1=某coωt和某2=某co(ω+ε)t-之和。
其中ε<<ω。
如发生拍的现象,求其振幅和拍频。
解:某1+某2=2某co(t)co(2ε当ε<<ω时,某1+某2≈2某co(2t)coωt可变振幅ε2ω+εt)210co(2πt)εε拍振的振幅为2某,拍频为f=(不是)2π4π例:当ω=80π,ε=4π,某=5时,某1+某2≈10co(2πt)co(80πt)10振幅为10拍频为2Hz0-1000.510co(2πt)1拍的周期为0.5(不是)(不是1)1.52补充若两简谐运动振幅和频率都不同:=某1coωt+(某2coωt某2coωt)+某2co(ω+ε)t某=某1+某2=某1coωt+某2co(ω+ε)t 可变振幅A(t)=某1某2+2某2coεε≈(某1某2)coωt+2某2cotcoωt=某1某2+2某2cotcoωt22可变振幅ε%2t%%拍振的振幅为Ama某Amin=2某2(假设某2较小),拍频为f=例:当ω=80π,ε=4π,某1=8,某2=5时,13ε2π某1+某2=[3+10co(2πt)]co(80πt)振幅为13-1303+10co(2πt)0.511.52拍频为1Hz2-2如图所示,长度为L、质量为m的均质刚性杆-由两根刚度为k的弹簧系住,求杆绕O点微幅振动的微分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
某一数值附近反复变化。
一、振动工程的重要性
• 1. 大型回转机械动态失稳造成事故 • 2. 桥梁由于共振、风激振动倒塌 • 3. 产品包装 • 4. 汽车舒适性,航天工程 • 5. 机床加工质量 • 6. 夯士、振动检测
国家重点工程:长江三峡水利 枢纽工程,135米蓄水前中孔 闸门振动试验现场(2003年4 月应用锤击模态法)
st
m
d2x dt 2
P
k ( st
x)
mg k st
O x
F
m
d2x dt 2
kx
x
P
表明,物体偏离平衡位置于坐标x处,受到与偏离距离成正 比而与偏离方向相反的合力,称此力为恢复力。
在恢复力作用下维持的振动称为无阻尼自由振动。
重力加在振动系统上只改变其平衡位置,只要将坐标原点取 在平衡位置,可得到如上形式的运动微分方程。
无阻尼自由振动是简谐振动,是一种周期振动,任何瞬时t,其 运动规律x(t)总可以写为: x(t)= x(t+T)
T为常数,称为周期,单位符号为s。 这种振动经过时间T后又重复原来的运动。
考虑无阻尼自由振动微分方程
d2x dt 2
2 n
x
0
解为:
x Asin(nt )
角度周期为2π,则有:
[n (t T ) ] (nt ) 2
武汉大桥局桥科院、北方交通大学进行 的“秦-沈线中华之星高速列车通过桥梁 振动及结构应变试验” 。 中华之星高速 列车设计时速260Km/h,实际测试时速 321.5 Km / h 。大桥为 28 孔双线后张 法 预应力混凝土简支箱梁桥 , 梁顶宽 12.4m,梁高2.2m,梁跨长24.6m。
案例:齿轮箱故障诊断 通过齿轮箱振动信号频谱分 析,确定最大频率分量,然后 根据机床转速和传动链,找出 故障齿轮。
d2x m kx
dt 2
l0
两端除以质量m,并设
பைடு நூலகம்
2 n
k m
移项后得:
d2x dt 2
2 n
x
0
st O
x
无阻尼自由振动微分方程的标准形式
F
是一个二阶齐次线性常系数微分方程。 x
P
设: x ert
代入微分方程,消去ert
得特征方程:
r2
2 n
0
两个根为: r1 i n r2 i n
方程解表示为: x C1 cosnt C2 sin nt
机械振动理论
于德介
绪论
振动是日常生活和工程中普遍存在的现象,有机械振动、 电磁振荡、光的波动等不同的形式。
这里研究机械振动,如钟摆的摆动、汽车的颠簸、混凝 土振动捣实以至地震等。
特点:物体围绕其平衡位置而往复运动。
掌握机械振动的基本规律,可以更好地利用有益的振动而 减少振动的危害。
机械振动
振动有各种不同的形式 电磁振动
三、工程振动问题类型
• 1. 振动分析(已知输入,系统求输出) • 2. 系统识别(已知输入和输出求系统) • 3. 载荷识别(已知系统,输出求输入)
四、振动现象分类
• 1. 按系统分:线性、非线性 • 2. 按响应分:定则、随机 • 3. 按输入分:自由、强迫、自激(由系统反馈引
起)、参数激励、(随机或周期改变系统特性) • 4. 按自由度分、离散、连续 • 离散:常微 • 连续:偏微 • 本课程:线性、时不变系统。
x C1 cosnt C2 sin nt
C1和C2是积分常数,由运动 的起始条件确定。
设: A
C12
C
2 2
tan C1
C2
则解为: x Asin(nt )
表明:无阻尼自由振动是简谐振动。
其运动图线为:
x
A x0
l0
st O
x
x
Ot n
F P
t T
x
2.无阻尼自由振动的特点
(1)固有频率
案例:螺旋浆设计 可以通过频谱分析确定螺旋浆 的固有频率和临界转速,确定 螺旋浆转速工作范围。
二、动态问题特点
• 1. 复杂性:载荷作用的后效性,响应对 载荷的记忆性
• 2. 危险性:共振、自激振动(在无外力 的激励情况下突然振动,振幅上升,如机 床、轧钢机、飞机)、颤振
• 3. 超常性:振动现象难以直观解释,如 共振、调谐消振器
l0
弹簧变形为δs,称为静变形,该位置为平
衡位置。重力和弹簧力。
st
Fst k st
P mg
O
平衡时满足:
mg k st
st
mg k
x
取重物的平衡位置点O为坐标原点,取x轴
的正向铅直向下。受力如图 。
x
Fst
mg
F P
弹簧力F: F k(x st )
l0
由质点运动微分方程可列:
第一章 单自由度系统自由振动
一. 单自由度系统的自由振动
1. 自由振动微分方程 工程中许多振动可简化为一个质量和一个弹簧的弹簧质量系统,系统在
重力作用下沿铅垂方向振动的,具有一个自由度,简化为图示模型。 下面来分析其运动规律,先列出其运动微分方程。
设弹簧原长为l0,刚性系数为k。
在重力P=mg 的作用下
满载车厢的弹簧静变形比空载车厢大,则其振动频率比空载车厢低。
(2)振幅与初位相 谐振振动表达式
x Asin(nt )
A表示相对于振动中心点O的最大位移,称为振幅。 (ωnt+θ)称为相位(或相位角),相位决定了质点在某瞬时t 的位置,它具有角度的量纲,而θ称为初相位,它决定了质点 运动的起始位置。
自由振动中的振幅A和初相位θ是两个待定常数,它们由运动 的初始条件确定。
设在起始t=0时,物块的坐标x=x0,速度v=v0。为求A和θ,
x Asin(nt )
则自由振动的周期为:
T 2 n
可得: 其中
T 2 n
n
2
1 T
2f
f 1 T
称为振动的频率 表示每秒钟的振动次数,其单位符号为1/s或Hz(赫兹)。 因为ωn=2πf 所以ωn表示2π秒内的振动次数,称为圆频率 单位符号为rad/s(弧度/秒)。 由
2 n
k m
n
k m
自由振动的圆频率ωn只与表征系统本身特性的质量m和刚度k有关,而与 运动的初始条件无关;
它是振动系统的固有的特性,所以称ωn为固有圆频率。
固有频率是振动理论中的重要概念,它反映了振动系统的动力学特性, 计算系统的固有频率是研究系统振动问题的重要课题之一。
由
mPg
k
P st
n
k m
n
g
st
上式表明:上述振动系统,知道重力作用下的静变形,就可求得系统的 固有频率。
如:我们可以根据车厢下面弹簧的压缩量来估算车厢上下振动的频率。
