信号与系统习题解答 (1)
信号与系统第一章习题答案

t 0 > 0 函数式的信号的波形如图 1.2(b)所示. 。
3
cos ωt
1 … …
−
5π 2ω
−
3π 2ω
−
π 2ω
-1
π 2ω
(a)
3π 2ω
5π 2ω
t
cos ωtε (t )
1
ε (t )
1
…
π 2ω
3π 2ω
5π 2ω
t
t
(b)
-1 (c ) 图 1.1
cos ωtε (t − t 0 )
1
P = lim
E =∞
1 T → ∞ 2T
1 ∫ [ε (t )] dt = 2
T 2 −T
(2) ε (t ) − ε (t − 1) 是脉冲信号,其为能量信号,能量为:
E = lim
[ε (t ) − ε (t − 1)]2 dt = ∫0 [ε (t ) − ε (t − 1)]2 dt =1 T →∞ ∫−T
T
2
(4) 3 cos (ω 0t + θ ) 是功率信号,其平均功率为:
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
1 2T
2
∫
T
−T
9
cos 2(ω0 t + θ ) + 1 1 9 9 dt = lim ⋅ ⋅ 2T = T → ∞ 2 2T 2 2
T 2
2ω t 1 − cos 0 1 cos ω0 t + 1 9ω 0t ω t 5 dt = lim + sin − sin 0 + ∫ − T T →∞ 2T 2 20 20 2
信号系统(第3版)习题解答

信号系统(第3版)习题解答《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。
信号与线性系统分析习题答案
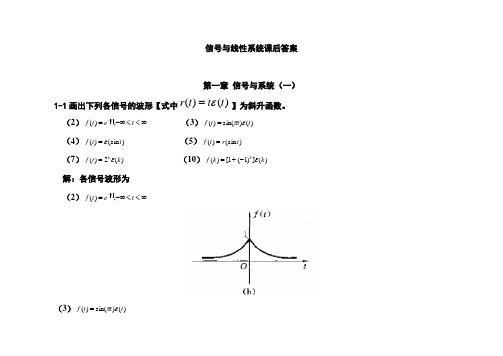
信号与线性系统课后答案第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
信号与系统课后习题答案
f 2 (−1) (t) =
δ (t − 2) − δ (t − 3)
*
t ε e(−t+1) (t + 1)dt
−∞
= [δ (t − 2) − δ (t − 3)]* (1 − e−(t+1) )ε (t + 1)
= (1 − e−(t−2+1) )ε (t − 2 + 1) − (1 − e−(t−3+1) )ε (t − 3 + 1)
) − iL (t) − uC (t) R1
R2
状态方程为:
⎪⎪⎧u&C (t) ⎨
=
f (t) R1C
−
uC (t) R1C
−
iL (t) C
⎪⎪⎩i&L
(t)
=
uC
(t)
− R2iL L
(t)
1.17 写出题图 1.8 系统的输入输出方程。
解: (b)系统框图等价为:
⎧x′′(t) = f (t) − 3x′(t) − 2 y(t)
x2(0-)=1 时,y2(t)=4e-t-2e-3t,t≥0 则 x1(0-)=5,x2(0-)=3 时,系统的零输入响应: yx(t)=y(t)=5y1(t)+3y2(t)=22e-t 十 9e-3t,t≥0
1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
奥本海姆《信号与系统(第二版)》习题参考答案.
[信号与系统作业解答]第一章
1-3、分别求下列各周期信号的周期 T 1) cos(10 t ) cos(30 t) ; 2) e j 10 t ; 4)
(1)n[u(t nT ) u(t nT T )]
n 0
n
(1) [u(t nT ) u(t nT T )]
图(b)表达式为:
f ( t ) u( t ) u( t 1) 2[u( t 1) u( t 2)] 3u( t 2) ; u( t ) u( t 1) u( t 2)
图(c)表达式为: f ( t ) sin
t [u( t ) u( t T )] ; T
C1e1 (t ) C2e2 (t ) sin[C1e1 (t ) C2e2 (t )]u(t ) C1r1 (t ) C2r2 (t )
由于
所以系统是非线性的。
e( t ) r (t ) sin[e( t )]u(t )
而
e(t t0 ) sin[e(t t0 )]u(t ) r (t t0 ) sin[e(t t0 )]u(t t0 )
5)由于 e1 (t ) r1 (t ) e1 (2t ) , e2 (t ) r2 (t ) e2 (2t ) , 而
C1e1 (t ) C2e2 (t ) C1e1 (2t ) C2e2 (2t ) C1r1 (t ) C2r2 (t )
由于
所以系统是线性的。
C1e1 ( t ) C 2e2 ( t ) C1e1 (t ) C 2e2 (t ) C1r1 (t ) C 2r2 (t )
由于
2
所以系统是非线性的。
信号与系统第一章答案
w0 )*m, and m=3. w0 )*m=10
Because
w0 =3 /5, N=(2 /
m/3 ,
it’s not a rational number.
13/37
5 Exercises Answers
1.11 Solution
x[n ] 1 e e
j 4 n 7 j 4 n 7 j 2 n 5
Then,
y[n] 2 x[n 2] 5x[n 3] 2 x[n 4]
16/37
5 Exercises Answers
(b) No. For it’s linearity.
the relationship between
y1 [ n ]
and x 2 [n]
is the same in-out relationship with (a).
2
9/37
5 Exercises Answers
(e) x 2 [n] e
E
j(
) 2n 8 2 j( ) 2n 8
n
e
12
n -
N 1 1 1 P lim E lim 1 lim 2N+1 1 N 2N 1 N 2N 1 N 2N 1 n -N (f) x 2 [n ] cos( 4 n ) n 1 cos 2 E cos2 ( n ) 4 2 n n 1 cos n N 1 1 1 1 2 P lim E lim lim N N 2N 1 N 2N 1 N 2 2N 1 2 n N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章作业参考答案: 1.18求下列积分值: (a )解:26242)2()2(2)()0()2()(2)()()]2(2)([)()]2(2)()[23(44444444442=+=-+=-+=-+=-+++⎰⎰⎰⎰⎰-----dtt x dt t x dtt t x dt t t x dtt t t x dt t t t t δδδδδδδδ(b) 解:6510)2()2()()0()5()5()2()()()()5()()]2()()5([)()]2()()5()[1(4444444444442=++=-+++-=-+++=-+++=-++++⎰⎰⎰⎰⎰⎰------dtt x dt t x dt t x dtt t x dt t t x dt t t x dtt t t t x dt t t t t δδδδδδδδδδδδ(C )解:1)2()cos 1()2()cos 1(2=--=--⎰⎰--ππππππδπδdt t dt t t(d )解:42312121231)(cos )23()(cos )2()(cos )2()(cos )23()(cos )1(200222=++++-+-=++-+-=+⎰⎰⎰⎰⎰-----ππππδπδπδπδπδππππππππdtt x dt t x dt t x dt t x dt t t 1.19解:1.21 判断下列每个信号是否周期的?如果是周期的,是求它的基波周期。
(a )解:32,/23)cos(2)43cos(200ππωϕωπ===+=+T T t t 基波周期为:是周期信号(b)解:e eeT e e et j T t j Tj T j t j T t j )1()1)(()1()1)((12--±±±--±====ππππππ,时,当 是周期信号,基波周期是 T 0=2(c)解:互质与是有理数,且74,742782)2cos()278cos(==Ω+Ω=+ππππn n 所以原式是周期信号,基波周期N 0=7.(d)解:不是有理数,,812412cos 4cos πππ==ΩΩ=nn所以原式不是周期信号(e )解:。
有为整数,其中则令][][4/,)4/(4`,`]}41[`]4[{]}41[]4[{][,]}41[]4[{][:n x N n x N N k k k n k n k N n k N n N n x k n k n n x k k k =+-=----=--+--+=+----=∑∑∑∞-∞=∞-∞=∞-∞=δδδδδδ所以原式是周期信号,基波周期N 0=4.(f )解:,它们的最小公倍数是,则ππωππωπωωϕωϕω22,52,4,10)sin()cos()14sin()110cos(22211212211======+++=--+T T t t t t所以原式的基波周期为 T 0=π(g)解:4,16,8,412,1612,8122,8,4)cos(2)sin()cos(2)2cos(2)8sin()4cos(2321321321321====Ω=Ω=Ω=Ω=Ω=ΩΩ-Ω+Ω=-+N N N n n n nnn即,πππππππππ它们的最小公倍数为16,故基波周期是N 0=16.(h)解:5,5125/22,7,7227/4211221152421=∴==Ω=∴==Ω-+=-+ΩΩN N e e e e nj n j n j n j ππππππππ它们的最小公倍数为35,故基波周期是N 0=35.1.23一个LTI 系统,当输入x 1(t )=u (t )时,输出为y 1 (t )=e -t u (t)+u (-1-t )求该系统对图P1.23所示输入x (t )的响应,并概略地画出其波形.图P1.23 解:由上图x (t)=u (t-1)-u (t-2)= x 1(t-1)+ x 1(t-2)对于本题的LTI 系统,x 1(t)→y 1(t)= e -t u (t )+u (-1-t )就有:x (t)→y (t)=y 1 (t-1)+ y 1 (t -2)= e -t+1u (t-1)+u (-t )+ e -t+2u (t-2)+u (1-t )=[ u (-t )- u (1-t )]+[ e -t+1u (t-1) + e -t+2u (t-2)]1.25(a)解:线性:)()()()()]()([)()()(21212121t y b t y a dt t x d b dt t x d a t x b t x a dt dt y t x b t x a +=+=+=→+ 时不变性:)()()(ˆ)(000t t y t t x dtdt yt t x -=-=→-(b)解:线性:)()()]2()2([)]2()2([)]2()2([)]2()2([)()()(212121212121t y b t y a t x t x b t x t x a t x b t x a t x b t x a t y t x b t x a +=-+-+-+-=-+-+-+-=→+时变:)2()2()()2()2()(ˆ)(000000t t x t t x t t y t t x t t x t yt t x +-+--=-≠--+--=→-(c)解:线性:)()()()3(cos )()3(cos )]()([3cos )()()(21212121t y b t y a t x b t t x a t t x b t x a t t y t x b t x a +=+=+=→+ 时变:)()](3[cos )()()3(cos )(ˆ)(00000t t x t t t t y t t x t t yt t x --=-≠-=→-(d)解:线性:)()()]()()]()([)()()(21222122121t y b t y a d x b d x a d x b x a t y t x b t x a ttt+=+=+=→+⎰⎰⎰∞-∞-∞-τττττττ 时变:ττττd x t t y duu x d t x t yt t x t t t t t⎰⎰⎰-∞--∞-∞-=-≠=-=→-)(20220000)()()()()(ˆ)((e)解:线性:)()()]3()3([)()()(212121t y b t y a t x b t x a t y t x b t x a +=+=→+时变:)3/3/()3/)(()()3/()(ˆ)(00000t t x t t x t t y t t x t yt t x -=-=-≠-=→-(f)解:线性:● 可分解,)()()(3)0(~)(02t y t y t x t x t y x +=+= ● 零输入线性,)()()()0(~)0(~2121t y b t y a t y x b x a +=→+● 零状态线性, )()()]()([3)()()(2121221t y b t y a t x b t x a t t y t x b t x a x +=+=→+时变:)()(3)0(~)()(3)0(~)(ˆ)(0020020t t x t t x t t y t t x t x t y t t x --+=-≠-+=→-1.26 试判断下列每一个离散时间系统是否是线性系统和是不变系统。
(a)解:线性:()())()(])1[][(])1[2][(]1[]1[2][][][][][212211212121t y b t y a n x n x b n x n x a n x b n x a n x b n x a n y n x b n x a +=-+-+=-+--+=→+时不变性:][]1[2][][ˆ][0000n n y n n x n n x n yn n x -=--+-=→-(b)解:线性:()][][][][][][][][][21212121n y b n y a n nx b n x an n x b n x a n n y n x b n x a +=+=+=→+时变:][)(][][][ˆ][00000n n x n n n n y n n nx n yn n x --=-≠-=→-(c)解:非线性:()()][]2[][]2[)()(][][]2[]2[][][][221121212121n x n bx n x n x a t y b t y a n x b n x a n x b n x a n y n x b n x a -+-=+≠+-+-=→+时不变性:][][]2[][ˆ][0000n n y n n x n n x n yn n x -=---=→-(d)解:线性:()][][][][][][][212121n y b n y a n x b n x a n y n x b n x a +=-+-=→+时变:][][][][ˆ][0000n n x n n y n n x n yn n x +-=-≠--=→-(e) 解:线性:()][][]14[]14[][][][212121n y b n y a n x b n x a n y n x b n x a +=+++=→+时变:]44[)](4[][]4[][ˆ][00000n n x n n x n n y n n x n yn n x -=-=-≠-=→-(f) 解:线性:()()][][1,]1[0,01,][]1[0][1,]1[]1[0,01,][][][][][212211212121n y b n y a n n x b n n n x b n x a n x a n n x b n x a n n n x b n x a n y n x b n x a +=⎪⎩⎪⎨⎧-≤+=≥+⎪⎩⎪⎨⎧+=⎪⎩⎪⎨⎧-≤+++=≥+=→+ 时变:⎪⎩⎪⎨⎧+-≤-+=+≥-=-≠⎪⎩⎪⎨⎧-≤-+=≥-=→-nn n n x n n n n n n x n n y n n n x n n n n x n y n n x 0000000001,]1[,01,][][1,]1[0,01,][][ˆ][第一章作业参考答案: 1.18求下列积分值: (a )解:26242)2()2(2)()0()2()(2)()()]2(2)([)()]2(2)()[23(44444444442=+=-+=-+=-+=-+++⎰⎰⎰⎰⎰-----dtt x dt t x dtt t x dt t t x dt t t t x dt t t t t δδδδδδδδ(b) 解:6510)2()2()()0()5()5()2()()()()5()()]2()()5([)()]2()()5()[1(4444444444442=++=-+++-=-+++=-+++=-++++⎰⎰⎰⎰⎰⎰------dtt x dt t x dt t x dtt t x dt t t x dt t t x dtt t t t x dt t t t t δδδδδδδδδδδδ(C )解:1)2()cos 1()2()cos 1(2=--=--⎰⎰--ππππππδπδdt t dt t t(d )解:42312121231)(cos )23()(cos )2()(cos )2()(cos )23()(cos )1(200222=++++-+-=++-+-=+⎰⎰⎰⎰⎰-----ππππδπδπδπδπδππππππππdtt x dt t x dt t x dt t x dt t t 1.19解:1.21 判断下列每个信号是否周期的?如果是周期的,是求它的基波周期。
