STATISTICAL MODELING OF MONETARY POLICY AND ITS effects
nominal rigidities and the dynamic effects of a shock to monetary policy

Nominal Rigidities and the Dynamic Effects of a Shockto Monetary Policy∗Lawrence J.Christiano†Martin Eichenbaum‡Charles L.Evans§August27,2003AbstractWe present a model embodying moderate amounts of nominal rigidities that ac-counts for the observed inertia in inflation and persistence in output.The key featuresof our model are those that prevent a sharp rise in marginal costs after an expansion-ary shock to monetary policy.Of these features,the most important are staggeredwage contracts which have an average duration of three quarters,and variable capitalutilization.JEL:E3,E4,E5∗Thefirst two authors are grateful for thefinancial support of a National Science Foundation grant to the National Bureau of Economic Research.We would like to acknowledge helpful comments from Lars Hansen and Mark Watson.We particularly want to thank Levon Barseghyan for his superb research assistance,as well as his insightful comments on various drafts of the paper.This paper does not necessarily reflect the views of the Federal Reserve Bank of Chicago or the Federal Reserve System.†Northwestern University,National Bureau of Economic Research,and Federal Reserve Banks of Chicago and Cleveland.‡Northwestern University,National Bureau of Economic Research,and Federal Reserve Bank of Chicago.§Federal Reserve Bank of Chicago.1.IntroductionThis paper seeks to understand the observed inertial behavior of inflation and persistence in aggregate quantities.To this end,we formulate and estimate a dynamic,general equilibrium model that incorporates staggered wage and price contracts.We use our model to investigate what mix of frictions can account for the evidence of inertia and persistence.For this exercise to be well defined,we must characterize inertia and persistence precisely.We do so using estimates of the dynamic response of inflation and aggregate variables to a monetary policy shock.With this characterization,the question that we ask reduces to:‘Can models with moderate degrees of nominal rigidities generate inertial inflation and persistent output movements in response to a monetary policy shock?’1Our answer to this question is,‘yes’.The model that we construct has two key features.First,it embeds Calvo style nominal price and wage contracts.Second,the real side of the model incorporates four departures from the standard textbook one sector dynamic stochastic growth model.These depar-tures are motivated by recent research on the determinants of consumption,asset prices, investment and productivity.The specific departures that we include are habit formation in preferences for consumption,adjustment costs in investment and variable capital utilization. In addition,we assume thatfirms must borrow working capital tofinance their wage bill.Our keyfindings are as follows.First,the average duration of price and wage contracts in the estimated model is roughly2and3quarters,respectively.Despite the modest nature of these nominal rigidities,the model does a very good job of accounting quantitatively for the estimated response of the US economy to a policy shock.In addition to reproducing the dynamic response of inflation and output,the model also accounts for the delayed,hump-shaped response in consumption,investment,profits,productivity and the weak response of the real wage.2Second,the critical nominal friction in our model is wage contracts,not price contracts.A version of the model with only nominal wage rigidities does almost as well as the estimated model.In contrast,with only nominal price rigidities,the model performs very poorly.Consistent with existing results in the literature,this version of the model cannot generate persistent movements in output unless we assume price contracts of extremely long duration.The model with only nominal wage rigidities does not have this problem.Third,we document how inference about nominal rigidities varies across different spec-ifications of the real side of our model.3Estimated versions of the model that do not in-1This question that is the focus of a large and growing literature.See,for example,Chari,Kehoe and McGrattan(2000),Mankiw(2001),Rotemberg and Woodford(1999)and the references therein.2In related work,Sbordone(2000)argues that,taking as given aggregate real variables,a model with staggered wages and prices does well at accounting for the time series properties of wages and prices.See also Ambler,Guay and Phaneuf(1999)and Huang and Liu(2002)for interesting work on the role of wage contracts.3For early discussions about the impact of real frictions on the effects of nominal rigidities,see Blanchardcorporate our departures from the standard growth model imply implausibly long price and wage contracts.Fourth,wefind that if one only wants to generate inertia in inflation and persistence in output with moderate wage and price stickiness,then it is crucial to allow for variable capital utilization.To understand why this feature is so important,note that in our modelfirms set prices as a markup over marginal costs.The major components of marginal costs are wages and the rental rate of capital.By allowing the services of capital to increase after a positive monetary policy shock,variable capital utilization helps dampen the large rise in the rental rate of capital that would otherwise occur.This in turn dampens the rise in marginal costs and,hence,prices.The resulting inertia in inflation implies that the rise in nominal spending that occurs after a positive monetary policy shock produces a persistent rise in real output.Similar intuition explains why sticky wages play a critical role in allowing our model to explain inflation inertia and output persistence.It also explains why our assumption about working capital plays a useful role:other things equal,a decline in the interest rate lowers marginal cost.Fifth,although investment adjustment costs and habit formation do not play a central role with respect to inflation inertia and output persistence,they do play a critical role in accounting for the dynamics of other variables.Sixth,the major role played by the working capital channel is to reduce the model’s reliance on sticky prices.Specifically,if we estimate a version of the model that does not allow for this channel,the average duration of price contracts increases dramatically.Finally,wefind that our model embodies strong internal propagation mechanisms.The impact of a monetary policy shock on aggregate activity continues to grow and persist even beyond the time when the typical contract in place at the time of the shock is reoptimized.In addition,the effects persist well beyond the effects of the shock on the interest rate and the growth rate of money.We pursue a particular limited information econometric strategy to estimate and evaluate our model.To implement this strategy wefirst estimate the impulse response of eight key macroeconomic variables to a monetary policy shock using an identified vector autoregres-sion(V AR).We then choose six model parameters to minimize the difference between the estimated impulse response functions and the analogous objects in our model.4 The remainder of this paper is organized as follows.In section2we briefly describe our estimates of how the U.S.economy responds to a monetary policy shock.Section3 displays our economic model.In Section4we discuss our econometric methodology.Our empirical results are reported in Section5and analyzed in Section6.Concluding commentsand Fisher(1989),Ball and Romer(1990)and Romer(1996).For more recent quantitative discussions, see Chari,Kehoe and McGrattan(2000),Edge(2000),Fuhrer(2000),Kiley(1997),McCallum and Nelson (1998)and Sims(1998).4Christiano,Eichenbaum and Evans(1998),Edge(2000)and Rotemberg and Woodford(1997)have also applied this strategy in the context of monetary policy shocks.are contained in Section7.2.The Consequences of a Monetary Policy ShockThis section begins by describing how we estimate a monetary policy shock.We then re-port estimates of how major macroeconomic variables respond to a monetary policy shock. Finally,we report the fraction of the variance in these variables that is accounted for by monetary policy shocks.The starting point of our analysis is the following characterization of monetary policy:R t=f(Ωt)+εt.(2.1)Here,R t is the Federal Funds rate,f is a linear function,Ωt is an information set,andεt is the monetary policy shock.We assume that the Fed allows money growth to be whatever is necessary to guarantee that(2.1)holds.Our basic identifying assumption is thatεt is orthogonal to the elements inΩt.Below,we describe the variables inΩt and elaborate on the interpretation of this orthogonality assumption.We now discuss how we estimate the dynamic response of key macroecomomic variables to a monetary policy shock.Let Y t denote the vector of variables included in the analysis. We partition Y t as follows:Y t=[Y1t,R t,Y2t]0.The vector Y1t is composed of the variables whose time t elements are contained inΩt,and are assumed not to respond contemporaneously to a monetary policy shock.The vector Y2t consists of the time t values of all the other variables inΩt.The variables in Y1t are real GDP, real consumption,the GDP deflator,real investment,the real wage,and labor productivity. The variables in Y2t are real profits and the growth rate of M2.All these variables,except money growth,have been logged.We measure the interest rate,R t,using the Federal Funds rate.The data sources are in an appendix,available from the authors.With one exception(the growth rate of money)all the variables in Y t are include in levels.Altig,Christiano,Eichenbaum and Linde(2003)adopt an alternative specification of Y t,in which cointegrating relationships among the variables are imposed.For example,the growth rate of GDP and the log difference between labor productivity and the real wage are included.The key properties of the impulse responses to a monetary policy shock are insensitive to this alternative specification.The ordering of the variables in Y t embodies two key identifying assumptions.First,the variables in Y1t do not respond contemporaneously to a monetary policy shock.Second,the time t information set of the monetary authority consists of current and lagged values of the variables in Y1t and only past values of the variables in Y2t.Our decision to include all variables,except for the growth rate of M2and real profits in Y1t,reflects a long-standing view that macroeconomic variables do not respond instanta-neously to policy shocks(see Friedman(1968)).We refer the reader to Christiano,Eichen-baum and Evans(1999)for a discussion of sensitivity of inference to alternative assumptions about the variables included in Y1t.While our assumptions are certainly debatable,the anal-ysis is internally consistent in the sense that we make the same assumptions in our economic model.To maintain consistency with the model,we place profits and the growth rate of money in Y2t.The V AR contains4lags of each variable and the sample period is1965Q3-1995Q3.5 Ignoring the constant term,the V AR can be written as follows:Y t=A1Y t−1+...+A4Y t−4+Cηt,(2.2)where C is a9×9lower triangular matrix with diagonal terms equal to unity,andηt is a9−dimensional vector of zero-mean,serially uncorrelated shocks with diagonal variance-covariance matrix.Since there are six variables in Y1t,the monetary policy shock,εt,is the7th element ofηt.A positive shock toεt corresponds to a contractionary monetary policy shock. We estimate the parameters-A i,i=1,...,4,C,and the variances of the elements ofηt-using standard least squares ing these estimates,we compute the dynamic path of Y t following a one-standard-deviation shock inεt,setting initial conditions to zero.This path, which corresponds to the coefficients in the impulse response functions of interest,is invariant to the ordering of the variables within Y1t and within Y2t(see Christiano,Eichenbaum and Evans(1999).)The impulse response functions of all variables in Y t are displayed in Figure1.Lines marked‘+’correspond to the point estimates.The shaded areas indicate95%confidence intervals about the point estimates.6The solid lines pertain to the properties of our structural model,which will be discussed in section3.The results suggest that after an expansionary monetary policy shock there is a:•hump-shaped response of output,consumption and investment,with the peak effect occurring after about1.5years and returning to their pre-shock levels after about three years,•hump-shaped response in inflation,with a peak response after about2years,•fall in the interest rate for roughly one year,•rise in profits,real wages and labor productivity,and5This sample period is the same as in Christiano,Eichenbaum and Evans(1999).6We use the method described in Sims and Zha(1999).•an immediate rise in the growth rate of money.Interestingly,these results are consistent with the claims in Friedman(1968).For example, Friedman argued that an exogenous increase in the money supply leads to a drop in the interest rate that lasts one to two years,and a rise in output and employment that lasts from two tofive years.Finally,the robustness of the qualitative features of ourfindings to alternative identifying assumptions and sample sub-periods,as well as the use of monthly data,is discussed in Christiano,Eichenbaum and Evans(1999).Our strategy for estimating the parameters of our model focuses on only a component of thefluctuations in the data,namely the portion that is due to a monetary policy shock. It is natural to ask how large that component is,since ultimately we are interested in a model that can account for the variation in the data.With this question in mind,the following table reports variance decompositions.In particular,it displays the percent of the variance of the k−step forecast error in the elements of Y t due to monetary policy shocks, for k=4,8and20.Numbers in parentheses are the boundaries of the associated95% confidence interval.7Notice that policy shocks account for only a small fraction of inflation. At the same time,with the exception of real wages,monetary policy shocks account for a non-trivial fraction of the variation in the real variables.This last inference should be treated with caution.The confidence intervals about the point estimates are rather large. Also,while the impulse response functions are robust to the various perturbations discussed in Christiano,Eichenbaum and Evans(1999)and Altig,Christiano,Eichenbaum and Linde (2003),the variance decompositions can be sensitive.For example,the analogous point estimates reported in Altig,Christiano,Eichenbaum and Linde(2003)are substantially smaller than those reported in Table1.3.The Model EconomyIn this section we describe our model economy and display the problems solved byfirms and households.In addition,we describe the behavior offinancial intermediaries and the monetary andfiscal authorities.The only source of uncertainty in the model is a shock to monetary policy.7These confidence intervals are computed based on bootstrap simulations of the estimated VAR.In each artificial data set we computed the variance decompositions corresponding to the ones in Table1.The lower and upper bounds of the confidence intervals correspond to the2.5and97.5percentiles of simulated variance decompositions.3.1.Final Good FirmsAt time t,afinal consumption good,Y t,is produced by a perfectly competitive,representative firm.Thefirm produces thefinal good by combining a continuum of intermediate goods, indexed by j∈[0,1],using the technologyY t=·Z10Y jt1f dj¸λf(3.1) where1≤λf<∞and Y jt denotes the time t input of intermediate good j.Thefirm takes its output price,P t,and its input prices,P jt,as given and beyond its control.Profit maximization implies the Euler equationµP t jt¶λfλf−1=Y jt t.(3.2)Integrating(3.2)and imposing(3.1),we obtain the following relationship between the price of thefinal good and the price of the intermediate good:P t=·Z10P11−λf jt dj¸(1−λf).(3.3) 3.2.Intermediate Good FirmsIntermediate good j∈(0,1)is produced by a monopolist who uses the following technology:Y jt=½kαjt L1−αjt−φif kαjt L1−αjt≥φ0otherwise(3.4) where0<α<1.Here,L jt and k jt denote time t labor and capital services used to produce the j th intermediate good.Also,φ>0denotes thefixed cost of production.We rule out entry and exit into the production of intermediate good j.Intermediatefirms rent capital and labor in perfectly competitive factor markets.Profits are distributed to households at the end of each time period.Let R k t and W t denote the nominal rental rate on capital services and the wage rate,respectively.Workers must be paid in advance of production.As a result,the j thfirm must borrow its wage bill,W t L jt, from thefinancial intermediary at the beginning of the period.Repayment occurs at the end of time period t at the gross interest rate,R t.Thefirm’s real marginal cost iss t=∂S t(Y)∂Y,where S t(Y)=mink,l©r k t k+w t R t l,Y given by(3.4)ª,where r k t=R k t/P t and w t=W t/P t.Given our functional forms,we haves t=µ1¶1−αµ1¶α¡r k t¢α(w t R t)1−α.(3.5)Apart fromfixed costs,thefirm’s time t profits are:·P jt P t−s t¸P t Y jt,where P jt isfirm j’s price.We assume thatfirms set prices according to a variant of the mechanism spelled out in Calvo(1983).This model has been widely used to characterize price-setting frictions.A useful feature of the model is that it can be solved without explicitly tracking the distribution of prices acrossfirms.In each period,afirm faces a constant probability,1−ξp,of being able to reoptimize its nominal price.The ability to reoptimize its price is independent across firms and time.If afirm can reoptimize its price,it does so before the realization of the time t growth rate of money.Firms that cannot reoptimize their price simply index to lagged inflation:P jt=πt−1P j,t−1.(3.6) Here,πt=P t/P t−1.We refer to this price-setting rule as lagged inflation indexation.Let˜P t denote the value of P jt set by afirm that can reoptimize at time t.Our notation does not allow˜P t to depend on j.We do this in anticipation of the well known result that, in models like ours,allfirms who can reoptimize their price at time t choose the same price (see Woodford,1996and Yun,1996).Thefirm chooses˜P t to maximize:∞X l=0¡βξp¢lυt+l h˜P t X tl−s t+l P t+l i Y j,t+l,(3.7)E t−1subject to(3.2),(3.5)and.(3.8)X tl=½πt×πt+1×···×πt+l−1for l≥11l=0In(3.7),υt is the marginal value of a dollar to the household,which is treated as exogenous by thefiter,we show that the value of a dollar,in utility terms,is constant across households.Also,E t−1denotes the expectations operator conditioned on lagged growth rates of money,µt−l,l≥1.This specification of the information set captures our assumption that thefirm chooses˜P t before the realization of the time t growth rate of money.To understand (3.7),note that˜P t influencesfirm j’s profits only as long as it cannot reoptimize its price.The probability that this happens for l periods is¡ξp¢l,in which case P j,t+l=˜P t X tl.The presence of¡ξp¢l in(3.7)has the effect of isolating future realizations of idiosyncratic uncertainty in which˜P t continues to affect thefirm’s profits.3.3.HouseholdsThere is a continuum of households,indexed by j∈(0,1).The j th household makes a sequence of decisions during each period.First,it makes its consumption decision,its capital accumulation decision,and it decides how many units of capital services to supply.Second, it purchases securities whose payoffs are contingent upon whether it can reoptimize its wage decision.Third,it sets its wage rate afterfinding out whether it can reoptimize or not. Fourth,it receives a lump-sum transfer from the monetary authority.Finally,it decides how much of itsfinancial assets to hold in the form of deposits with afinancial intermediary and how much to hold in the form of cash.Since the uncertainty faced by the household over whether it can reoptimize its wage is idiosyncratic in nature,households work different amounts and earn different wage rates.So, in principle,they are also heterogeneous with respect to consumption and asset holdings.A straightforward extension of arguments in Erceg,Henderson and Levin(2000)and Woodford (1996)establish that the existence of state contingent securities ensures that,in equilibrium, households are homogeneous with respect to consumption and asset holdings.Reflecting this result,our notation assumes that households are homogeneous with respect to consumption and asset holdings but heterogeneous with respect to the wage rate that they earn and hours worked.The preferences of the j th household are given by:∞X l=0βl−t[u(c t+l−bc t+l−1)−z(h j,t+l)+v(q t+l)].(3.9)E j t−1Here,E j t−1is the expectation operator,conditional on aggregate and household j idiosyn-cratic information up to,and including,time t−1;c t denotes time t consumption;h jt denotes time t hours worked;q t≡Q t/P t denotes real cash balances;Q t denotes nominal cash balances.When b>0,(3.9)allows for habit formation in consumption preferences.The household’s asset evolution equation is given by:M t+1=R t[M t−Q t+(µt−1)M a t]+A j,t+Q t+W j,t h j,t(3.10)+R k t u t¯k t+D t−P t¡i t+c t+a(u t)¯k t¢.Here,M t is the household’s beginning of period t stock of money and W j,t h j,t is time t labor income.In addition,¯k t,D t and A j,t denote,respectively,the physical stock of capital,firm profits and the net cash inflow from participating in state-contingent securities at time t. The variableµt represents the gross growth rate of the economy-wide per capita stock of money,M a t.The quantity(µt−1)M a t is a lump-sum payment made to households by the monetary authority.The quantity M t−P t q t+(µt−1)M a t,is deposited by the household with afinancial intermediary where it earns the gross nominal rate of interest,R t.The remaining terms in(3.10),aside from P t c t,pertain to the stock of installed capital, which we assume is owned by the household.The household’s stock of physical capital,¯k t, evolves according to:¯k=(1−δ)¯k t+F(i t,i t−1).(3.11)t+1Here,δdenotes the physical rate of depreciation and i t denotes time t purchases of invest-ment goods.The function,F,summarizes the technology that transforms current and past investment into installed capital for use in the following period.We discuss the properties of F below.Capital services,k t,are related to the physical stock of capital byk t=u t¯k t.Here,u t denotes the utilization rate of capital,which we assume is set by the household.8 In(3.10),R k t u t¯k t represents the household’s earnings from supplying capital services.The increasing,convex function a(u t)¯k t denotes the cost,in units of consumption goods,of setting the utilization rate to u t.3.4.The W age DecisionAs in Erceg,Henderson and Levin(2000),we assume that the household is a monopoly sup-plier of a differentiated labor service,h jt.It sells this service to a representative,competitive firm that transforms it into an aggregate labor input,L t,using the following technology:L t=·Z10h1λjt dj¸λw.The demand curve for h jt is given by:h jt=µW t jt¶λwλw−1L t,1≤λw<∞.(3.12) Here,W t is the aggregate wage rate,i.e.,the price of L t.It is straightforward to show that W t is related to W jt via the relationship:W t=·Z10(W jt)11−λw dj¸1−λw.(3.13) The household takes L t and W t as given.8Our assumption that households make the capital accumulation and utilization decisions is a matter of convenience.At the cost of a more complicated notation,we could work with an alternative decentralization scheme in whichfirms make these decisions.Households set their wage rate according to a variant of the mechanism used to model price setting byfirms.In each period,a household faces a constant probability,1−ξw, of being able to reoptimize its nominal wage.The ability to reoptimize is independent across households and time.If a household cannot reoptimize its wage at time t,it sets W jt according to:W j,t=πt−1W j,t−1.(3.14) 3.5.Monetary and Fiscal PolicyWe assume that monetary policy is given by:µt=µ+θ0εt+θ1εt−1+θ2εt−2+...(3.15)Here,µdenotes the mean growth rate of money andθj is the response of E tµt+j to a time t monetary policy shock.We assume that the government has access to lump sum taxes and pursues a Ricardianfiscal policy.Under this type of policy,the details of tax policy have no impact on inflation and other aggregate economic variables.As a result,we need not specify the details offiscal policy.93.6.Loan Market Clearing,Final Goods Clearing and EquilibriumFinancial intermediaries receive M t−Q t from households and a transfer,(µt−1)M t from the monetary authority.Our notation here reflects the equilibrium condition,M a t=M t. Financial intermediaries lend all of their money to intermediate goodfirms,which use the funds to pay for L t.Loan market clearing requiresW t L t=µt M t−Q t.(3.16) The aggregate resource constraint isc t+i t+a(u t)≤Y t.We adopt a standard sequence-of-markets equilibrium concept.In the appendix we discuss our computational strategy for approximating that equilibrium.This strategy involves taking a linear approximation about the non-stochastic steady state of the economy and using the solution method discussed in Christiano(2003).For details,see the previous version of this paper,Christiano,Eichenbaum and Evans(2001).In principle,the non-negativity constraint on intermediate good output in(3.4)is a problem for this approximation.It turns out that the constraint is not binding for the experiments that we consider and so we ignore it.Finally, it is worth noting that since profits are stochastic,the fact that they are zero,on average, 9See Sims(1994)or Woodford(1994)for a further discussion.implies that they are often negative.As a consequence,our assumption thatfirms cannot exit is binding.Allowing forfirm entry and exit dynamics would considerably complicate our analysis.3.7.Functional Form AssumptionsWe assume that the functions characterizing utility are given by:u(·)=log(·)z(·)=ψ0(·)2.(3.17)v(·)=ψq(·)1−σqqIn addition,investment adjustment costs are given by:F(i t,i t−1)=(1−Sµi t i t−1¶)i t.(3.18) We restrict the function S to satisfy the following properties:S(1)=S0(1)=0,andκ≡S00(1)>0.It is easy to verify that the steady state of the model does not depend on the adjustment cost parameter,κ.Of course,the dynamics of the model are influenced byκ. Given our solution procedure,no other features of the S function need to be specified for our analysis.We impose two restrictions on the capital utilization function,a(u t).First,we require that u t=1in steady state.Second,we assume a(1)=0.Under our assumptions,the steady state of the model is independent ofσa=a00(1)/a0(1).The dynamics do depend onσa.Given our solution procedure,we do not need to specify any other features of the function a. 4.Econometric MethodologyIn this section we discuss our methodology for estimating and evaluating our model.We partition the model parameters into three groups.Thefirst group is composed ofβ,φ,α,δ,ψ0,ψq,λw andµ.We setβ=1.03−0.25,which implies a steady state annualized real interest rate of3percent.We setα=0.36,which corresponds to a steady state share of capital income equal to roughly36percent.We setδ=0.025,which implies an annual rate of depreciation on capital equal to10percent.This value ofδis roughly equal to the estimate reported in Christiano and Eichenbaum(1992).The parameter,φ,is set to guarantee that profits are zero in steady state.This value is consistent with Basu and Fernald(1994),Hall (1988),and Rotemberg and Woodford(1995),who argue that economic profits are close to zero on average.Although there are well known problems with the measurement of profits, we think that zero profits is a reasonable benchmark.。
Mathematical Modelling and Numerical Analysis Will be set by the publisher Modelisation Mat

c EDP Sciences, SMAI 1999
2
PAVEL BEL K AND MITCHELL LUSKIN
In general, the analysis of stability is more di cult for transformations with N = 4 such as the tetragonal to monoclinic transformations studied in this paper and N = 6 since the additional wells give the crystal more freedom to deform without the cost of additional energy. In fact, we show here that there are special lattice constants for which the simply laminated microstructure for the tetragonal to monoclinic transformation is not stable. The stability theory can also be used to analyze laminates with varying volume fraction 24 and conforming and nonconforming nite element approximations 25, 27 . We also note that the stability theory was used to analyze the microstructure in ferromagnetic crystals 29 . Related results on the numerical analysis of nonconvex variational problems can be found, for example, in 7 12,14 16,18,19,22,26,30 33 . We give an analysis in this paper of the stability of a laminated microstructure with in nitesimal length scale that oscillates between two compatible variants. We show that for any other deformation satisfying the same boundary conditions as the laminate, we can bound the pertubation of the volume fractions of the variants by the pertubation of the bulk energy. This implies that the volume fractions of the variants for a deformation are close to the volume fractions of the laminate if the bulk energy of the deformation is close to the bulk energy of the laminate. This concept of stability can be applied directly to obtain results on the convergence of nite element approximations and guarantees that any nite element solution with su ciently small bulk energy gives reliable approximations of the stable quantities such as volume fraction. In Section 2, we describe the geometrically nonlinear theory of martensite. We refer the reader to 2,3 and to the introductory article 28 for a more detailed discussion of the geometrically nonlinear theory of martensite. We review the results given in 34, 35 on the transformation strains and possible interfaces for tetragonal to monoclinic transformations corresponding to the shearing of the square and rectangular faces, and we then give the transformation strain and possible interfaces corresponding to the shearing of the plane orthogonal to a diagonal in the square base. In Section 3, we give the main results of this paper which give bounds on the volume fraction of the crystal in which the deformation gradient is in energy wells that are not used in the laminate. These estimates are used in Section 4 to establish a series of error bounds in terms of the elastic energy of deformations for the L2 approximation of the directional derivative of the limiting macroscopic deformation in any direction tangential to the parallel layers of the laminate, for the L2 approximation of the limiting macroscopic deformation, for the approximation of volume fractions of the participating martensitic variants, and for the approximation of nonlinear integrals of deformation gradients. Finally, in Section 5 we give an application of the stability theory to the nite element approximation of the simply laminated microstructure.
计量经济学李子奈第三版STATA答案

[856.20328+2.356*17.39*sqrt(1+4.5389992), 856.20328-2.356*17.39*sqrt(1+4.5389992) ] =[ 759.77809, 952.51758] 均值E(Y0)的置信区间: 856.20328+2.356*17.39*sqrt(4.5389992), 856.20328-2.356*17.39*sqrt(4.5389992) ] =[ 768.58,943.82]
2
yt xt
• 作为数理经济学模型是正确的,作为计量经济学模型则 不是正确的。计量经济学模型中必须包含随机误差项。 (2) y xt
t
t
正确。作为计量经济学模型它是正确的。该模型是经济计量模型的 理论模型,理论模型由被解释变量、解释变量、随机误差项、待估 计的参数和运算符构成。
• 7.下列假设模型是否属于揭示因果关系的计量经济模型?为什 么? • (1)St=112.0+0.12Rt • 其中St为第t年农村居民储蓄增加额(亿元), Rt为第t年城镇居 民可支配收入总额(亿元)。 • (2)St-1=4432.0+0.30Rt • 其中St-1为第t-1年农村居民储蓄增加额(亿元),Rt为第t年农村 居民可支配收入总额(亿元)。 • 解: (1)式不是揭示因果关系的计量经济模型。根据经济学理 论,储蓄额是由收入决定的,农村居民的储蓄额应由农村居民的 纯收入总额决定,而不是由城镇居民可支配收入总额决定。 (2)式中还存在时间动态上的逻辑错误,当年的收入不可能确 定上一年的储蓄,即今日事件确定昨日(已经发生)的事件。 1
. adjust x1=35 x2=20000,ci stdf Dependent variable: y Command: regress Covariates set to value: x1 = 35, x2 = 20000
【国家自然科学基金】_随机前沿方法(sfa)_基金支持热词逐年推荐_【万方软件创新助手】_20140802
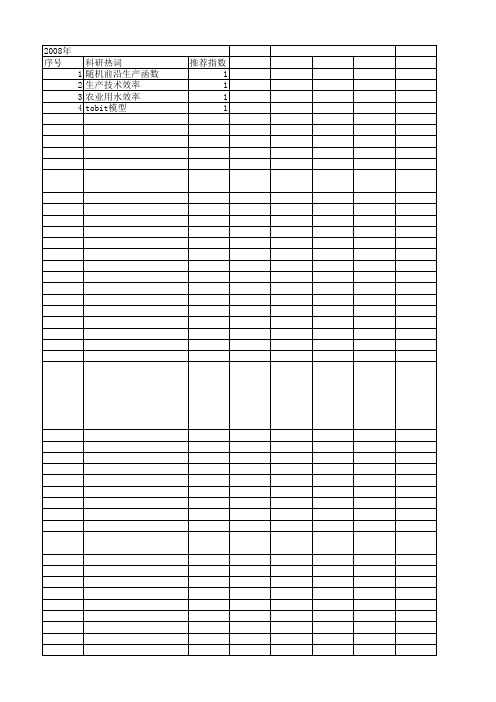
科研热词 随机前沿生产函数 生产技术效率 农业用水效率 tobit模型
推荐指数 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词 随机前沿分析 灌溉用水效率 sfa dea 面板数据 随机前沿生产函数 通径分析 跨国公司r&d投资 绩效 生产效率 玉米优势产区 玉米 溢出效应 投资效率 技术非效率模型 大股东控制 多层次/随机前沿分析 农户 全要素生产率 供应商 人力资源外包 主成分变量 c-d生产函数
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 随机前沿分析 技术效率 物流业 数据包络分析 全要素生产率 随机前沿方法 随机前沿主方程组方法 配置效率 能源消耗 股权结构 综合绩效 经济增长 空间相关性 空间收敛性 研究现状 研发技术效率 独立董事 影响因素 大型综合医院 复合残差项 地区差异 区域增长 全要素生产率变动分解 企业效率 代理成本 主成分分析 sfa
2014年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 高技术产业 随机前沿函数 环境因素 旅游业 医疗服务 医疗卫生服务效率 医疗卫生服务 全要素生产率 专利产业化效率 sfa方法 malmquist指数
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2013年 科研热词 推荐指数 随机前沿方法 4 随机前沿分析 4 技术效率 4 高校校办产业 2 随机前沿分析(sfa) 2 效率 2 投资来源 2 成本函数 2 全要素生产率 2 fdi 2 高校知识创新链 1 高校 1 随机前沿分析方法(sfa) 1 随机前沿 1 绩效评价 1 统计分析 1 科技创新 1 碳排放 1 湖北省 1 数据包络分析 1 政产学研用 1 技术转移效率 1 房地产上市公司 1 战略性新兴产业 1 成本效率 1 成本一效益效率 1 成本-效益效率 1 影响因素 1 当地政府支持 1 外部运营环境 1 国防科技工业 1 商业银行 1 参数法 1 协同 1 医疗卫生 1 区域市场需求规模不确定性 1 创新效率 1 创意经济 1 农地城市流转效率 1 军民融合 1 公交线路 1 企业规模 1 人力资本 1 产权类型 1 产业集聚 1 产业竞争力 1 交通运输系统工程 1 专利转化效率 1 x效率 1 malmquist指数 1
Two Illustrations of the Quantity Theory of Money-Breakdowns and Revivals

American Economic Review 101 (February 2011): 109–128/articles.php?doi =10.1257/aer .101.1.109109Robert E. Lucas Jr. (1980) used near unit slopes of univariate regressions of moving averages of inflation and interest rates on money growth for the United States for the period 1953–1977 to illustrate “two central implications of the quan-tity theory of money: that a given change in the rate of change in the quantity of money induces (i ) an equal change in the rate of price inflation; and (ii ) an equal change in nominal rates of interest.’’ Lucas said that those two quantity-theoretic propositions…possess a combination of theoretical coherence and empirical verification shared by no other propositions in monetary economics. By “theoretical coherence,’’ I mean that each of these laws appears as a characteristic of solutions to explicit theoretical models of idealized economies, models which give some guidance as to why one might expect them to obtain in reality, also as to conditions under which one might expect them to break down (emphasis added ) (1980, p. 1005).This paper extends Lucas’s analysis to a longer US dataset and uses an explicit the-oretical model to identify conditions on monetary policy that cause the unit slopes to “obtain in reality’’ as well as to “break down.” We find that Lucas’s l ow-frequencyTwo Illustrations of the Quantity Theory of Money:Breakdowns and RevivalsBy Thomas J. Sargent and Paolo Surico*By extending his data , we document the instability of low-frequency regression coefficients that Lucas (1980) used to express the quantity theory of money. We impute the differences in these regression coef-ficients to differences in monetary policies across periods. A DSGE model estimated over a subsample like Lucas’s implies values of the regression coefficients that confirm Lucas’s results for his sample period. But perturbing monetary policy rule parameters away from the values estimated over Lucas’s subsample alters the regression coefficients in ways that reproduce their instability over our longer sample. ( JEL C51, E23, E31, E43, E51, E52)* Sargent: Department of Economics, New York University, 19 W. Fourth Street, New York, NY 10012-1119, and Hoover Institution (e-mail: ts43@ ); Surico: Department of Economics, London Business School and CEPR, Department of Economics, London Business School, Regent’s Park, London NW1 4SA (e-mail: psurico@ ). We wish to thank Tim Besley, Efrem Castelnuovo, Martin Ellison, William Fuchs, Lars Peter Hansen, Peter Ireland, Dirk Krueger, Robert E. Lucas Jr., Haroon Mumtaz, Ed Nelson, David Romer, James Stock, Roman Sustek, Harald Uhlig, Francesco Zanetti, and three anonymous referees for very useful suggestions, and seminar participants at the European University Institute, University of Chicago, NBER Monetary Economics Program meeting held in November 2008, University of Cambridge, University of Oxford, London School of Economics, University College London, London Business School, University of Warwick, EIFE, and ESSIM 2009 for com-ments. Sargent thanks the Bank of England for providing research support when he was a Houblon-Norman Fellow. The views expressed in this paper are those of the authors and do not necessarily reflect those of the Bank of England or the Monetary Policy Committee.110THE AMERICAN ECONOMIC REVIEW FEBRuARy 2011 regression slopes are not stable over time, an empirical outcome that we explain in terms of quantitative versions of our theoretical “break down’’ conditions. In our theoretical model, the regression coefficients on moving averages depend on mon-etary policy.1 By freezing all nonmonetary policy structural parameters at values estimated over a sample period approximating Lucas’s, we display variations in two parameters of a monetary policy rule that push the population values of those low frequency slopes over a range that covers the empirical outcomes found in our extended sample. In this way, we construct different monetary policy rules that, in the context of our structural model, can explain the differences over time in the esti-mated low-frequency regression slopes.2Why have we written this paper now? For most of the last 25 years, the quantity theory of money has been sleeping, but during the last year, unprecedented growth in leading central banks’ balance sheets has prompted some of us to worry because the quantity theory has slept before, only to reawaken. Our DSGE model tells us that what puts those quantity-theoretic unit slopes to sleep is a monetary policy rule that responds to inflationary pressure aggressively enough to prevent the emer-gence of persistent movements in money growth, and that what awakens them is a monetary policy rule that accedes to persistent movements in money growth by responding too weakly to inflationary pressure. It seems timely to characterize the features of monetary policy rules needed to arrest the reemergence of the empirical patterns that Lucas takes as tell-tale signs of the quantity theory.To set the stage for our empirical findings, Section I recounts Charles H. Whiteman’s (1984) observation that the slope of Lucas’s scatter plot estimates the sum of coefficients in a long two-sided distributed lag regression, then indicates how the population value of that slope is linked to the parameters of a state space representation for either a vector autoregression or a DSGE model. Section II reports scatter plots and sums of distributed lag coefficients constructed from estimates of both time-invariant and time-varying vector autoregressions. These document substantial instability of Lucas’s two scatter plot slopes. Section III uses Bayesian methods to estimate our DSGE model over a subperiod approxi-mating Lucas’s, verifies that the estimated structural parameters confirm Lucas’s unit slope findings over his sample, and then, by perturbing monetary policy while freezing other model parameters, indicates how variations in the conduct of monetary policy cause outcomes to break down in ways that can account for the1 Lucas interpreted his unit slope findings as measuring “…the extent to which the inflation and interest rate experience of the postwar period can be understood in terms of purely classical, monetary forces’’ (italics added). Lucas’s purpose, including the qualification we have italicized, was precisely to indicate that the unit slope finding depends for its survival on maintenance of the monetary policy in place during the 1953–1977 period.2 Why, among the list of possible structural parameters in our model, do we confine ourselves to the monetary policy rule when searching for the cause of observed instability in the two low-frequency regressions? We have carried out robustness exercises (e.g., perturbed values for nonmonetary policy rule parameters within the structural model presented in the text and even experiments within a calibrated version of a quite different structural model of Lucas 1975), and these have pushed us toward emphasizing the monetary policy rule as the most likely cause of the low-frequency regression coefficient instabilities that we are trying to explain. Furthermore, DSGE models like the one we are using were intentionally designed as devices to use the cross-equation restrictions emerging from rational expectations models in the manner advocated by Lucas (1972) and Sargent (1971), to interpret how regres-sions involving inflation would depend on monetary and fiscal policy rules. We think that we are using our structural model in one of the ways its designers intended.111SARGENT AND SuRICO: ILLuSTRATIONS OF THE QuANTITy THEORy VOL. 101 NO. 1observed range of instability in the slopes of the scatter plots. Section IV offers concluding remarks.I. Lucas’s and Whiteman’s MethodsFor US data over 1955–1975, Lucas (1980) plotted moving averages of inflation and a nominal interest rate on the y axis against the same moving average of money growth on the x axis. In this section, we revisit Whiteman’s (1984) argument that the slope of the regression through the scatter plot of Lucas’s moving averages can be approximated as the sum of distributed lag coefficients, and that this sum can be com-puted using the spectral density implied by a state space representation of the data.A. The Slope of Scatter Plots of Filtered SeriesFor a scalar series x tand β ∈ [0, 1), Lucas (1980) constructed moving averages_ x t (β) = α ∑ k =− nn β |k | x t +k where choosing α according to α = (1 − β ) 2 /(1 − β2 − 2 β n +1 (1 − β)) made the sum of weights equal one.Whiteman (1984) observed that fitting straight lines through scatter plots of mov-ing averages is an informal way of computing sums of coefficients in long two-sideddistributed lag regressions. Let { y t, z t } be a bivariate jointly covariance stationary process with unconditional means of zero and consider the two-sided infinite least-squares projection of y t on past, present, and future z ’s:(1) y t = ∑ j =− ∞∞h j z t−j + ϵ t ,where ϵ t is a random process that satisfies the population orthogonality conditions E ϵ t z t −j = 0 ∀j . Let the spectral densities of y and z be denoted S y(ω) and S z (ω), respectively, and let the cross-spectral density be denoted S y z (ω). Let the Fourier trans-form of { h j } be ˜ h (ω) = ∑ j =− ∞ ∞ h j e − i ωj . Then (2)˜ h (ω) = S yz (ω) _ S z(ω)and the sum of the distributed lag regression coefficients is (3)∑ j =− ∞ ∞h j= ˜ h (0) = S yz (0) _ S z(0) .Whiteman (1984) showed that for β close to 1, the regression coefficient b f of aLucas moving average _ y t (β) on a Lucas moving average _ x t (β) satisfies (4)b f ≈ S yz (0) _ S z(0) = ˜ h (0).112THE AMERICAN ECONOMIC REVIEW FEBRuARy 2011B. Mappings from VAR and DSGE Models to ˜ h (0)Time-invariant versions of our V ARs and of our log-linear DSGE models can bothbe represented in terms of the state space system (5)X t +1 = A X t + B W t +1 ,y t +1 = C X t + D W t +1 ,where X t is an n X × 1 state vector, W t +1 is an n W × 1 Gaussian random vector withmean zero and unit covariance matrix and that is distributed identically and inde-pendently across time, y t is an n y × 1 vector of observables, and A , B , C , D arematrices, with the eigenvalues of A being bounded strictly above by unity (A can be said to be a “stable” matrix ). DSGE models make elements of the matrices A , B , C , D be (nonlinear ) functions of a vector of structural parameters η, some of which describe monetary policy.The spectral density matrix of y is 3(7)S y (ω) = C (I − Ae − i ω ) − 1 BB ′(I − A ′ i ω ) − 1 C ′ + DD ′.The Fourier transform of the population regression coefficients ˜ h (ω) can be com-puted from formula (2) where S y z(ω), the cross spectrum between y and z , and S z (ω), the spectrum of z , are the appropriate elements of S y (ω). In figures 6 and 7 inSection III, we summarize the mapping to ˜ h (0) from the elements of the parametervector η that govern monetary policy.II. Scatter Plots and RegressionsIn this section, we present data and extend Lucas’s scatter plots of moving averages of money growth and inflation as well as money growth and the nominal interest rate. Then we compute regressions on filtered data and sums of distributed lag coefficients by applying “temporary” versions of formulas (2) and (7) to a V AR with drifting coeffi-cients and stochastic volatility. Both the scatter plots and the regressions point to instabil-ity in the two low-frequency relationships that Lucas took to signify the quantity theory.4A. DataWe use quarterly US data. Real and nominal GDP (M2 stock ) are available from the FRED database since 1947:I (1959:I ). Prior to that, we apply backward the3The spectral density matrix is the Fourier transform of the sequence of autocovariance matrices E y t y t −j ′ , j = − ∞, … , − 1, 0, 1, … , + ∞ whose typical element can be recovered from S y (ω) via the inversion formula(6) E y t y t −j ′ = ( 1_ 2 π)∫− π π S y(ω) e i ω jd ω.4Rather than estimating ˜ h (1) by first estimating a V AR as we do, another worthwhile strategy would be to apply the dynamic ordinary least squares or the dynamic generalized least squares estimator of James H. Stock and MarkW. Watson (1993) to estimate ˜ h (1) as the simple regression coefficient of _ y t on _ z t. Procedures of Peter C.B. Phillips (1991) can also be applied to estimate ˜ h (1) viewed as a regression coefficient.113SARGENT AND SuRICO: ILLuSTRATIONS OF THE QuANTITy THEORy VOL. 101 NO. 1growth rates on the real GNP and M2 series constructed by Nathan S. Balke and Robert J. Gordon (1986).5 As for the nominal short-term interest rate, we use the six-month commercial paper rate available from Balke and Gordon (1986) until 1983 and from the FRED database afterwards. Figure 1 displays year-on-year first differences of logs of raw variables. The interest rate is displayed in level. Figure 2 reports moving averages of the raw data using Lucas’s β = 0.95 filter. The shaded regions in these two filters isolate the 1955–1975 period that Lucas focused on.These figures reveal some striking patterns.• Figure 1 reveals that for money growth, inflation, and output growth, but not for the interest rate, volatility decreased markedly after 1950.• The filtered data in Figure 2 indicate that the shaded period studied by Lucas exhibits persistent increases in money growth, inflation, and the interest rate. These features let Lucas’s two quantity-theoretic propositions leap off the page. However,• For the filtered data, the shaded Lucas sample observations are atypical.5As for M2, Balke and Gordon (1986) build upon Milton Friedman and Anna J. Schwartz (1963).Figure 1. M2 Growth, GNP /GDP Deflator Inflation, 6-Month Commercial Paper Rate,and Real GNP /GDP Growth.(Sample : 1900:I–2005:IV )20100−10−2020100−10−20161412108642151050−5−10−15−201900 1920 1940 1960 1980 20001900 1920 1940 1960 1980 20001900 1920 1940 1960 1980 20001900 1920 1940 1960 1980 2000Money growthIn ationInterest rateOutput growthLucas’s original sample:1955–75-------------------------114THE AMERICAN ECONOMIC REVIEW FEBRuARy 2011B. Scatter PlotsFigures 3 and 4 show scatter plots of second quarter observations of each year of filtered series over selected subperiods in the sample 1900–2005. We selected the subsamples to include Lucas’s subperiod, 1955–1975. In addition, we follow John F. Boschen and Christopher M. Otrok’s (1994) comment on Mark E. Fisher and John J. Seater (1993) and split the sample around the Great Depression. To emphasize the link between Lucas’s calculations and monetary policy regimes, we also present results for the periods 1960–1983 and 1984–2005, which are typically the focus of the literature on the great moderation. Altogether, we display six subperiods in different panels in figures 3 and 4. In subsection D, we show that the subsample instabilities presented in this section do not depend on the particular sample selection used here.These graphs reveal the following patterns to us. The scatters of points can be said to align with the two quantity propositions in the 1955–75 and 1960–83 subperiods, and to a lesser extent between 1976 and 2005: the points adhere to lines that at least seem to be parallel to the 45 degree line. But for the other three subperiods there are substan-tial deviations from unit slopes. The inflation on money growth scatter is steeper than 45 degrees during 1900–1928, flatter during 1929–1954, and even negative duringFigure 2. β = 0.95-Filtered Series for M2 Growth, GNP /GDP Deflator Inflation, 6-Month CommercialPaper Rate, and Real GNP /GDP Growth6420−2−41900 1920 1940 1960 1980 2000Money growth: lter β = 0.95 In ation: lter β = 0.95Interest rate: lter β = 0.95 Output growth: lter β = 0.95Lucas’s original sample:1955–75-----6420−2543210543210−1−2−31900 1920 1940 1960 1980 20001900 1920 1940 1960 1980 20001900 1920 1940 1960 1980 2000----------------115SARGENT AND SuRICO: ILLuSTRATIONS OF THE QuANTITy THEORy VOL. 101 NO. 11984–2005; while the interest on money growth scatter is flatter than the 45 degree line during 1900–1928 and negatively sloped during 1929–1954 and 1984–2005.6C. Regressions on Filtered DataTable 1 reports regression coefficients of inflation and the nominal interest rate on money growth for filtered data using different values of β ranging from 0.95 to 0.As in Lucas’s graphs, the entries of Table 1 reveal that the closer is β to one (and therefore the smoother are the series ) the larger are the regression slopes of filtered data. However, with a few exceptions concentrated in the 1955–75 and 1960–1983 periods, most estimates are significantly different from one and they span values between − 0.03 and 1.13 for money growth and inflation at β = 0.95, and − 0.08 and 0.75 for money growth and the nominal interest rate. In the Appendix, we show6We obtain similar results using the band-pass filter proposed by Lawrence Christiano and Terry Fitzgerald (2003), and also employed by Luca Benati (2005), on frequency above eight or 20 years.Figure 3. Scatter Plots of Filtered Inflation and Filtered Money Growth Using Lucas’s Formula Note: Results are reported for the second quarter of each year.−20246−20246Annual rate of money growthA n n u a l r a t e o f i n f l a t i o n1900−1928β = 0.9545 line π on ∆m−4−2246−4−20246Annual rate of money growthA n n u a l r a t e o f i n f l a t i o n1929−1954β = 0.95012345Annual rate of money growthA n n u a l r a t e o f i n f l a t i o n1955−1975012345Annual rate of money growthA n n u a l r a t e o f i n f l a t i o n1976−2005012345Annual rate of money growth A n n u a l r a t e o f i n f l a t i o n1960−1983012345Annual rate of money growthA n n u a l r a t e o f i n f l a t i o n1984−2005116THE AMERICAN ECONOMIC REVIEW FEBRuARy 2011that the message from Table 1 is not altered by using different measures of inflation, money, or short-term interest rate.D. Evidence from a Time-Varying VARIn this section, we use a time-varying V AR with stochastic volatility to construct“temporary” estimates of ˜ h (0) that vary over time.7 There are at least three goodinterconnected reasons to allow for such time variation. First, the dynamics of money growth, inflation, nominal interest rate, and output growth have exhibited substan-tial instabilities over a century that witnessed two world wars, a Great Depression,7The description of the statistical model is presented in Sargent and Surico (2008), who followed Timothy Cogley and Sargent (2005) and Giorgio Primiceri (2005), and therefore it will not be repeated here. The full sample is 1875:1–2007:IV . A training sample of 25 years is used to calibrate the priors. Results are based on 500,000 Gibbs sampling repetitions.Figure 4. Scatter Plots of Filtered Short-Term Interest Rate and Filtered Money GrowthUsing Lucas’s FormulaNote : Results are reported for the second quarter of each year.−20246−20246Annual rate of money growthS h o r t −t e r m i n t e r e s t r a t e1900−1928β = 0.95 45 line R on ∆m−4−20246Annual rate of money growthS h o r t −t e r m i n t e r e s t r a t e1929−1954012345Annual rate of money growthS h o r t −t e r m i n t e r e s t r a t e1955−1975012345Annual rate of money growthS h o r t −t e r m i n t e r e s t r a t e1976−2005012345Annual rate of money growthS h o r t −t e r m i n t e r e s t r a t e1960−1983012345Annual rate of money growthS h o r t −t e r m i n t e r e s t r a t e1984−2005117SARGENT AND SuRICO: ILLuSTRATIONS OF THE QuANTITy THEORy VOL. 101 NO. 1the great inflation, and then a great moderation. Second, our long sample arguably transcends several monetary regimes, starting with a gold standard and ending with the fiat standard supported by a dual mandate to promote high employment and stable prices that succeeded Bretton Woods. Third, the results in the previous sec-tion are based on a subsample selection that, while consistent with Lucas (1980) and Boschen and Otrok (1994), is admittedly arbitrary.In Figure 5, we report as red solid lines the central 68 percent posterior bands of the following object constructed from our time-varying V AR:(8)˜ h y x,t | T (0) = S y x , t | T (0)_S x , t | T(0) ,namely, the temporary cross-spectrum divided by the temporary spectrum at t ,formed from the smoothed estimates of the time-varying V AR conditioned on the dataset 1, … , T . We compute the temporary spectral objects by applying formulas (7) and (3) and to the (t , T ) versions of A , B , C , D .We view equation (8) as a local-to-date t approximation of equation (3). Ideally, when extracting the low-frequency relationships, we should also account for the fact that the parameters drift going forward from date t . But this is computationally chal-lenging because it requires integrating a high-dimensional predictive density across all possible paths of future parameters. Adhering to a practice in the learning litera-ture (referred to as “anticipated-utility” by David Kreps 1998), we instead updatethe elements of θ t , H t , and A t period-by-period and then treat the updated values asif they would remain constant going forward in time.For comparison, we also report as blue dotted (solid ) lines the 68 percent pos-terior bands (median values ) based on the estimates for the full-sample from a fixed-coefficient V AR in money growth, inflation, the nominal interest rate, and output growth, whose details can be found in Sargent and Surico (2008).The medians of the distributions of the ˜ h (0)s display substantial time variation.The posteriors reveal substantial uncertainty about the ˜ h (0)s, however, and in someepisodes like the 1970s, ˜ h (0) values of zero and one are simultaneously inside theposterior bands in both panels. The most recent 20 years as well as the 1940s are char-acterized by the lowest values of the median estimates and the smallest uncertainty. The 1970s, in contrast, are associated with the highest values and the largest uncertainty.Table 1—Coefficients of the Regressions on Filtered Data, 1900–2005Data–m : M2; p : GNP /GDP deflator; R: 6-month commercial paper rateπ on ΔmR on Δm β0.950.80.500.950.80.501900–20050.580.570.560.540.070.050.020.011900–1928 1.13 1.18 1.21 1.150.060.040.00 −0.011929–19540.390.390.370.34 −0.08 −0.07 −0.06 −0.061955–19750.860.690.360.220.620.450.130.001976–20050.480.450.380.320.750.740.660.561960–20050.590.520.360.270.520.450.280.181960–1983 1.010.530.06−0.040.700.26−0.18−0.251984–2005−0.03−0.04−0.05−0.050.060.060.040.00Note: Numbers in bold are not statistically different from one at 10 percent significance level using heteroskedastic-ity and autocorrelation consistent standard errors.118THE AMERICAN ECONOMIC REVIEW FEBRuARy 2011The median estimates of ˜ h π, Δm (0) and ˜h R , Δm (0) based on the fixed coefficient multivariate BV AR for the full sample are 0.55 and 0.25 respectively.As for the unit coefficients associated with the quantity theory of money, the value of one is outside the posterior bands for most of the sample, with exceptions typi-cally concentrated in the 1970s. A comparison over different subperiods between the results based on the time-varying V AR and the straight lines from the fixed-coefficient V AR reveals that the two models can yield very different results.III. Interpreting the Observed Instabilities with a DSGE ModelTo investigate the extent to which changes in monetary policy can account for observed changes in our˜ h (0) statistics between nominal variables, we proceed in three steps. First, we describe a version of what is currently a popular model form onetary policy analysis, a model that under the appropriate monetary policies is Figure 5. Median and 68 Percent Central Posterior Bands for ˜ h π, Δm (0) and ˜ h R , Δm (0)Based on a Fixed-Coefficient V AR over the Full Samples and a V AR with Time-Varying Coefficientand Stochastic V olatility1900192019401960198020000.511.52Inflation and money growth190019201940196019802000−0.500.511.52Interest rate and money growthwell within the class of models capable of illustrating Lucas’s two quantity theory propositions. Second, we estimate the parameters of the model over a post–World War II subsample that, arguably, was characterized by a homogenous policy regime. Third, we lock all except the monetary policy parameters at their estimated values from the post–World War II subsample and then vary the coefficients describing the policy response to inflation and output over a broad range of values.8 Then, for each pair of policy coefficients, we compute the implied ˜h (0) statistics. By proceeding in this way, we aim to assess how well, within our estimated DSGE model, changes in monetary policy alone can account for the changes observed in the low frequency relationships between money growth and inflation, and money growth and the nomi-nal interest rate.9A. A Model for Monetary Policy AnalysisIn this section, we lay out the log-linearized version of a model with sticky price, price indexation, habit formation, and unit root technology shocks derived by Peter Ireland (2004). While our results are not sensitive to this particular choice, it makes sense to frame our analysis within a model that has become popular in some policy and academic circles.10The structure of the economy is:(9)πt= θ (1− απ)E tπt+1+ θ αππt−1+ κ x t− 1_τe t,(10)x t= (1− αx)E t x t+1+ αx x t−1− σ( R t− E tπ t+1)+ σ (1− ξ)(1− ρa)a t,(11)Δ m t= πt+ z t+ 1_σγΔ x t− 1_γΔ R t+ 1_γ(Δ χt− Δ a t),(12)˜y t= x t+ ξ a t, Δ y t= ˜y t− ˜y t−1+ z t,where πt, x t, Δ m t, and R t are inflation, the output gap, nominal money growth, and the short-term interest rate, respectively. The level of detrended output is ˜y t,and Δ y t refers to output growth. The rate of technological progress is z t. Equation (9) is an example of a new Keynesian Phillips curve, while (10) is called the new Keynesian8 Friedman and Schwartz (1963) documented significant changes in the monetary operations of the US gov-ernment and, after 1914, the Fed over the first half of our sample period. More recently, Ibrahim Chowdhury and Andreas Schabert (2008) have shown that the systematic component of a Fed money supply rule shifted significantly during the early 1980s. As for interest rate rules, Richard Clarida, Jordi Galí, and Mark Gertler (2000), Thomas Lubik and Frank Schorfheide (2004), and Jesus Fernandez-Villaverde, Pablo Guerrón, and Juan F. Rubio-Ramirez (2009), among many others, have argued that the new policy regime established by Paul V olcker during the first years of his mandate as Fed chairman represented an unprecedented break in the conduct of US monetary policy.9 Other factors such as financial innovation may have also contributed to the instabilities documented in Section II. Investigating the role of diminishing financial frictions, however, would require a different model relative to the current workhorse, and it is beyond the scope of this paper.10 Sargent and Surico (2008)show that changes in monetary policy induce significant changes in the low-frequency relationships between nominal variables also in a neoclassical model à la Lucas (1975) that was also featured by Whiteman (1984).。
自考商务英语词汇

Lesson 1exacerbated=deteriorated 恶化came into force=took effect 生效objective=purpose 目标buoyant=brisk 上涨的scope=opportunity 机会accelerating=speeding up 加速outcome=result 结果breakdown=analysis record 分类overhang=threat 威协reinforce 加强concessionary 优惠的减让的recognition=realization 认识到surplus=excess 盈余industrialization programme 工业化项目national income 国民收入volume of foreign trade 对外贸易额visible trade account 有形贸易收支invisible trade account 无形贸易收支growth rate 增长率foreign exchange 外汇trade fair 贸易展览会trade surplus 贸易顺差compensation trade 补偿贸易joint venture 合资企业planned economy 计划经济export quota 出口定额growth point 增长点high tech industries 高科技产业most favored nation status/treatment最惠国地位/待遇current account 经常项目stock taking=evaluating 盘点Production goods 生产资料customs duties 关税capital stock 实际资本infrastructure 基础设施foreign trade reserves 外汇储备customer goods 消费品saturation point 饱和点showpiece 优秀样品industrial crops 经济作物special economic zone 经济特区income tax rate 所得税税率technology transformation 技术改造technology transfer 技术转让capital equipments 资本设备preferential tax rate 优惠税率cooperative enterprise 合作企业imports of capital 资本进口services industry 服务业foreign exchange control 外汇管制capital intensive investment 劳动密集型投资Lesson 3farfetched=improbable 不大可能的nose=move slowly 缓慢的bound=heading 满载dynamic=booming 有活力的radiates=spreads 辐射bustling=booming 繁荣的surpass=exceed 超越slight=neglect 轻视bloc=group 集团laggard=backward 落后的per capita 人均preferred status 优先权competitive advantage 竞争优势trade bloc 贸易集团newly raising enterprise 新兴企业container plant 集装箱工厂consortium 国际财团bounce back 反弹free market 自由市场Lesson 4stagnated=stopped 停滞的aggregate=total 总计robust=strong 强健的meun=arrangements 安排adverse=unfavorable 不利的dampened=reduced 减小降低slackened= weakened 变缓慢deflator=index 指数curtailing=cutting off 消减catch up=competition 竞争in a row= in succession 连续的per capita income 人均收入hard currency 硬通货commodities market 商品市场portfolio investment 证券投资nominal terms 名义价constant terms 不变价debt restructuring 债务调整deinflationary policies 反通胀政策anti-inflationary monetary policy 反通胀货币政策industrial and agricultural productiobnuoyed=supported 支撑domestic demands 国内需求工农业生产Lesson 2assembled=formed 形成incentives=inducements 诱因promulgated=announced 发布couple with=together with 结合cope with=deal with 处理,应付uniform=same 统一的waive=exempt 免除afflicting=troubling 困扰的deftly=cleverly 巧妙地passage=pass 通过reaping=harvesting 收获gross national product 国民生产总值economic power 经济强国punitive import tariff 惩罚性进口关税securities and real estate markets 证券和房地产市场conglomerate 跨行业工公司private business 私人企业high tech,high wage econom高y科技高薪经济commercial hub 商业中心transfer component 资本转移部分direct investment 直接投资budget deficit 预算赤字interest rate 利率primary commodity price 初级产品价格high rates of growth 高增长率the group of seven 7 国集团workers remittance 工人侨汇monetary policies 货币政策primary goods 初级产品per capita GDP 人均国内生产总值Lesson 5retaliating=taking revenge 报复sanctions=punishments 制裁misgivings=doubt 疑惑expires=become due 期满underpinnings=evidence 根据,证据divergent=different 有分歧的seething=troubled 困惑的peeved=irritated 恼怒的mollify=relieve 减轻amenable=responsive 有责任的trade sanctios 贸易制裁trade barriers 贸易壁垒trade agreements 贸易协议government procurement 政府采购North America Free Trade Agreement 北美自由贸易协定trade priority 贸易优先权trade partner 贸易伙伴trade in deficit 贸易赤字trade discrimination 贸易歧视trade concession 贸易让步unblock 扫除……障碍stall 拖延turn up 升级live with consequence 承担后果bully 威吓instigate 挑动Lesson 6dour=severe 严厉的soured=worsened 恶化directive=instructions 指令over-nigh=suddenly 突然justifications=reasons 正当的理由wind up=end 结束skidding=reducing suddenly 急剧下降breach=breaking 违反European community 欧共体European union 欧盟the single market 统一大市场free trade zone 自由贸易区plant modernization 工厂现代化European integration 欧洲一体化economic integration 经济一体化political integration 政治一体化barrier-freed market 无壁垒市场economic benefits 经济利益anticipate 预料accomplish 完成实现stake 利害关系merger 兼并Lesson 7die down=disappear 消失foreshadows=predicts 预示capitulating=giving in 屈服geared=adapted 使……适应amplified=strengthened 增强的withstood=resisted 经受misconceived=misunderstood 设想错误的caved in=given in 屈服come up with=put forth 拿出obtain access to a market 获得市场准入机会trade reprisal 贸易报复trade representative 贸易代表import targets 进口指标fiscal packages 财政一揽子计划multilateral rules 多边规则quantifiable results 定量结果managed trade 管理贸易trade balance 贸易差额trade deficit 贸易赤字market share 市场份额white paper 白皮书bilateral surplus 双边顺差be bound to 肯定be opposed to 反对compound 加重Lesson 8poised=ready 作好准备的delve=study 钻研puts=expresses 解释trendy=fashionable 时髦的volatile=changeable 不稳定的clout=influence 影响力shuddered=trembled 战栗edge=advantage 优势eroding=disappearing 消融beset=troubled 困扰bolstered=supported 支撑siphon=draw out 抽取state of the a rt=markedly advanced 目前最先进的sprawl 规模庞大petrochemical complex 石油化工综合企业glistening 闪闪发光的jostle with 贴近eke out 勉强维持routinely 按常规chaebol 大企业集团know how 技术技能leviathan zaibatsu 大财团The lion ’s share 最大的份额antidumping 反倾销annual growth rates 年增长率investment capital 投资资本tax breaks 税额优惠financial system 金融体制embargo 禁运economic liberalization 经济自由化market force 市场力量Lesson 9was outed from=was d riven out 离开soaring=rising 上涨wary=cautious 谨慎的compromise=harm 妥协、危害materialise=realize 实现impressive=great 印象深刻unduly=excessively 过份地seesawed=rised and fell 动荡head off =prevent 阻止capacity expansion 生产能力扩张loss leader 亏本出售的商品carbon tax 双重税CECF 中国出口商品交易会impose import surcharge 征进口附加税re-export 再出口certifications of origin 产地证明书Lesson 10spur=promote 促进squandered=wasted 浪费bedeviled=perplexed 困惑的allowing for=taking … …intoconsideration 考虑到detached=disconnected 分离的pose a threat=form 形成一种威胁sensible=reasonable 合理的awkward=improper 不适宜的countervailing duty 反补贴税intellectual property rights 知识产权trade in service 服务贸易common agriculture polic共y 同农业政策on a conservative estimate据保守估计economic growth 经济增大the Uruguay round talk 乌拉圭回合谈判farm protection 农业保护Lesson 11proceeds=earnings 收入steered=introduced 引导convertible=exchangeable 可变的antiquated=old fashioned 过时tap=choose 选择camouflage=disguised 违装的perpetuate=make everlasting 持续的access=opportunity 机会convertible currency 可兑换货币debt service 偿还贷款counterpurchase 反向购买debtor nations 债务国creditor nations 债权国reformulation 重新配方franchise 特许经销权coupons 优惠券exclusive contract 独家经销合同bottler 经销商test market 试销市场market share 市场份额Lesson 13eightfold=eight times 八倍outlets=markets 市场promote sales 促销商品USDA 美国农业部luck dray 幸运抽奖competitive edge 竞争优势Lesson 14yields=profits 利润elapsed=passed 时间消逝tumble=slump 下降boost=accelerate 促进impeded=hindered 阻碍的offset=balance 分支volatility=fluctuation 价格变化spin-offs 副产品liquid assets 流动资产surplus produce 生产过剩financial futures 期货currency movements 货币流通price index 价格指数soft commodities 软商品UNCTAD 贸发会incentive=stimulus 激励monopolize= dominate 垄断discrimination=prejudice 偏见located=found 建立balance of payment 国际收支closing price 收盘价merge of banks 银行兼并brain trust 智囊团good resistance 良好的性耐性cash crops 经济作物equivalent value 等值short supply 供应短缺the world bank 世界银行productivity 生产力exchange revenue 外汇收入import duty 进口税profit remittance 利润汇款vested interests 既得利益buzzword 专业术语insolvency 破产take title 取得所有权market regulation 市场规则public tender 公开投标market power 市场动力transferor/assignor 转让人entrepreneurship 企业家精神headquarters 总部the new and expanding industry新兴工业trade balance 贸易平衡/差额The international financial institutiop n rice cutting war削价战国际金融机构currency reserves 货币储存currency exchange 货币交换clearing agreements 清算协定compensation agreements 补偿协定leverage 杠杆机构Lesson 12live up to=tally with 符合precipitate=accelerate 促成flagship=no.1 佼佼者poses=offerspony up=pay 付账gauge=judge 衡量take it hands down 轻易接受niches=status 合适的地位soft drink 软饮料retail sales 零售investment funds 投资基金export quota system 出口配额制度Lesson 15aggravated=worsened 恶化prompted=exacerbate 加剧rallied=increase after a fall 渐缓eased=fell 下跌dampened=reduced 挫伤undertone=underlying trendat origin=at the place of origin underpinned=supported 支撑spot market 现货市场futures market 期货市场base metal 贱金属precious metals 贵金属discount rate 贴现率历年。
课程名称中英文对照参考表

外国文学作选读Selected Reading of Foreign Literature现代企业管理概论Introduction to Modern Enterprise Managerment电力电子技术课设计Power Electronics Technology Design计算机动画设计3D Animation Design中国革命史China’s Revolutionary History中国社会主义建设China Socialist Construction集散控制DCS Distributed Control计算机控制实现技术Computer Control Realization Technology计算机网络与通讯Computer Network and CommunicationERP/WEB应用开发Application & Development of ERP/WEB数据仓库与挖掘Data Warehouse and Data Mining物流及供应链管理Substance and Supply Chain Management成功心理与潜能开发Success Psychology & Potential Development信息安全技术Technology of Information Security图像通信Image Communication金属材料及热加工Engineering Materials & Thermo-processing机械原理课程设计Course Design for Principles of Machine机械设计课程设计Course Design for Mechanical Design机电系统课程设计Course Design for Mechanical and Electrical System 创新成果Creative Achievements课外教育Extracurricular education。
计量经济学(重要名词解释)

——名词解释将因变量与一组解释变量和未观测到的扰动联系起来的方程,方程中未知的总体参数决定了各解释变量在其他条件不变下的效应。
与经济分析不同,在进行计量经济分析之前,要明确变量之间的函数形式。
经验分析(Empirical Analysis):在规范的计量分析中,用数据检验理论、估计关系式或评价政策有效性的研究。
确定遗漏变量、测量误差、联立性或其他某种模型误设所导致的可能偏误的过程线性概率模型(LPM)(Linear Probability Model, LPM):响应概率对参数为线性的二值响应模型。
没有一个模型可以通过对参数施加限制条件而被表示成另一个模型的特例的两个(或更多)模型。
有限分布滞后(FDL)模型(Finite Distributed Lag (FDL) Model):允许一个或多个解释变量对因变量有滞后效应的动态模型。
布罗施-戈弗雷检验(Breusch-Godfrey Test):渐近正确的AR(p)序列相关检验,以AR(1)最为流行;该检验考虑到滞后因变量和其他不是严格外生的回归元。
布罗施-帕甘检验(Breusch-Pagan Test)/(BP Test):将OLS 残差的平方对模型中的解释变量做回归的异方差性检验。
若一个模型正确,则另一个非嵌套模型得到的拟合值在该模型是不显著的。
因此,这是相对于非嵌套对立假设而对一个模型的检验。
在模型中包含对立模型的拟合值,并使用对拟合值的t 检验来实现。
回归误差设定检验(RESET)(Regression Specification Error Test, RESET):在多元回归模型中,检验函数形式的一般性方法。
它是对原OLS 估计拟合值的平方、三次方以及可能更高次幂的联合显著性的F 检验。
怀特检验(White Test):异方差的一种检验方法,涉及到做OLS 残差的平方对OLS 拟合值和拟合值的平方的回归。
这种检验方法的最一般的形式是,将OLS 残差的平方对解释变量、解释变量的平方和解释变量之间所有非多余的交互项进行回归。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
STATISTICAL MODELING OF MONETARY POLICY AND ITSEFFECTSCHRISTOPHER A.SIMSA BSTRACT.The science of economics has some constraints and tensions that set it apart from other sciences.One reflection of these constraints and tensions is that,more than in most other scientific disciplines,it is easy tofind economists of high reputation who disagree strongly with one another on issues of wide public interest.This may suggest that economics,un-like most other scientific disciplines,does not really make progress.Its theories and results seem to come and go,always in hot dispute,rather than improving over time so as to build an increasing body of knowledge. There is some truth to this view;there are examples where disputes of ear-lier decades have been not so much resolved as replaced by new disputes. But though economics progresses unevenly,and not even monotonically, there are some examples of real scientific progress in economics.This es-say describes one—the evolution since around1950of our understand-ing of how monetary policy is determined and what its effects are.The story described here is not a simple success story.It describes an ascent to higher ground,but the ground is still shaky.Part of the purpose of the essay is to remind readers of how views strongly held in earlier decades have since been shown to be mistaken.This should encourage continu-ing skepticism of consensus views and motivate critics to sharpen their efforts at looking at new data,or at old data in new ways,and generating improved theories in the light of what they see.We will be tracking two interrelated strands of intellectual effort:the methodology of modeling and inference for economic time series,and the Date:January3,2012.c 2012by Christopher A.Sims.This document is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike3.0Unported License.http:// /licenses/by-nc-sa/3.0/.1STATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS2 theory of policy influences on business cyclefluctuations.Keynes’s anal-ysis of the Great Depression of the1930’s included an attack on the Quan-tity Theory of money.In the30’s,interest rates on safe assets had been at approximately zero over long spans of time,and Keynes explained why, under these circumstances,expansion of the money supply was likely to have little effect.The leading American Keynesian,Alvin Hansen in-cluded in his(1952)book A Guide to Keynes a chapter on money,in which he explained Keynes’s argument for the likely ineffectiveness of mone-tary expansion in a period of depressed output.Hansen concluded the chapter with,“Thus it is that modern countries place primary emphasis onfiscal policy,in whose service monetary policy is relegated to the sub-sidiary role of a useful but necessary handmaiden.”Jan Tinbergen’s(1939)book was probably thefirst multiple-equation, statistically estimated economic time series model.His efforts drew heavy criticism.Keynes(1939),in a famous review of Tinbergen’s book,dis-missed it.Keynes had many reservations about the model and the meth-ods,but most centrally he questioned whether a statistical model like this could ever be a framework for testing a theory.Haavelmo(1943b),though he had important reservations about Tinbergen’s methods,recognized that Keynes’s position,doubting the possibility of any confrontation of theory with data via statistical models,was unsustainable.At about the same time,Haavelmo published his seminal papers explaining the ne-cessity of a probability approach to specifying and estimating empirical economic models(1944)and laying out an internally consistent approach to specifying and estimating macroeconomic time series models(1943a). Keynes’s irritated reaction to the tedium of grappling with the many numbers and equations in Tinbergen’s bookfinds counterparts to this day in the reaction of some economic theorists to careful,large-scale probabil-ity modeling of data.Haavelmo’s ideas constituted a research agenda that to this day attracts many of the best economists to work on improved successors to Tinbergen’s initiative.Haavelmo’s main point was this.Economic models do not make pre-cise numerical predictions.Even if they are used to make a forecast that is a single number,we understand that the forecast will not be exactly correct.Keynes seemed to be saying that once we accept that models’predictions will be incorrect,and thus have“error terms”,we must give up hope of testing them.Haavelmo argued that we can test and compareSTATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS3 models,but that to do so we must insist that they include a characteri-zation of the nature of their errors.That is,they must be in the form of probability distributions for the observed data.Once they are given this form,he pointed out,the machinery of statistical hypothesis testing can be applied to them.In the paper where he initiated simultaneous equations modeling(1943a), he showed how an hypothesized joint distribution for disturbance terms is transformed by the model into a distribution for the observed data,and went on to show how this allowed likelihood-based methods for estimat-ing parameters.1After discussing inference for his model,Haavelmo explained why the parameters of his equation system were useful:One could contemplate intervening in the system by replacing one of the equa-tions with something else,claiming that the remaining equations would continue to hold.This justification of—indeed definition of—structural modeling was made more general and explicit later by Hurwicz(1962). Haavelmo’s ideas and research program contained two weaknesses that persisted for decades thereafter and at least for a while partially discred-ited the simultaneous equations research program.One was that he adopted the frequentist hypothesis-testing framework of Neyman and Pearson. This framework,if interpreted rigorously,requires the analyst not to give probability distributions to parameters.This limits its usefulness in con-tributing to analysis of real-time decision-making under uncertainty,where assessing the likelihood of various parameter values is essential.It also inhibits combination of information from model likelihood functions with information in the beliefs of experts and policy-makers themselves.Both these limitations would have been overcome had the literature recognized the value of a Bayesian perspective on inference.When Haavelmo’s ideas were scaled up to apply to models of the size needed for serious macroe-conomic policy analysis,the attempt to scale up the hypothesis-testing theory of inference simply did not work in practice.1The simultaneous equations literature that emerged from Haavelmo’s insights treated as the standard case a system in which the joint distribution of the disturbances was unrestricted,except for havingfinite covariance matrix and zero mean.It is in-teresting that Haavelmo’s seminal example instead treated structural disturbances as independent,as has been the standard case in the later structural VAR literature.STATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS4 The other major weakness was the failure to confront the conceptual difficulties in modeling policy decisions as themselves part of the eco-nomic model,and therefore having a probability distribution,yet at the same time as something we wish to consider altering,to make projec-tions conditional on changed policy.In hindsight,we can say this should have been obvious.Policy behavior equations should be part of the sys-tem,and,as Haavelmo suggested,analysis of the effects of policy should proceed by considering alterations of the parts of the estimated system corresponding to policy behavior.Haavelmo’s paper showed how to analyze a policy intervention,and did so by dropping one of his three equations from the system while maintaining the other two.But his model contained no policy behavior equation.It was a simple Keynesian model,consisting of a consumption behavior equation,an investment behavior equation,and an accounting identity that defined output as the sum of consumption and investment. It is unclear how policy changes could be considered in this framework. There was no policy behavior equation to be dropped.What Haavelmo did was to drop the national income accounting identity!He postulated that the government,by manipulating“g”,or government expenditure (a variable not present in the original probability model),could set na-tional income to any level it liked,and that consumption and investment would then behave according to the two behavioral equations of the sys-tem.From the perspective of1943a scenario in which government ex-penditure had historically been essentially zero,then became large and positive,may have looked interesting,but by presenting a policy inter-vention while evading the need to present a policy behavior equation, Haavelmo set a bad example with persistent effects.The two weak spots in Haavelmo’s program—frequentist inference and unclear treatment of policy interventions—are related.The frequen-tist framework in principle(though not always in practice)makes a sharp distinction between“random”and“non-random”objects,with the for-mer thought of as repeatedly varying,with physically verifiable prob-ability distributions.From the perspective of a policy maker,her own choices are not“random”,and confronting her with a model in which her past choices are treated as“random”and her available current choices are treated as draws from a probability distribution may confuse or annoy her.Indeed economists who provide policy advice and view probabilitySTATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS5 from a frequentist perspective may themselvesfind this framework puz-zling.2A Bayesian perspective on inference makes no distinction between random and non-random objects.It distinguishes known or already ob-served objects from unknown objects.The latter have probability distri-butions,characterizing our uncertainty about them.There is therefore no paradox in supposing that econometricians and the public may have probability distributions over policy maker behavior,while policy mak-ers themselves do not see their choices as random.The problem of econo-metric modeling for policy advice is to use the historically estimated joint distribution of policy behavior and economic outcomes to construct accu-rate probability distributions for outcomes conditional on contemplated policy actions not yet taken.This problem is not easy to solve,but it has to be properly posed before a solution effort can begin.I.K EYNESIAN ECONOMETRICS VS.MONETARISMIn the1950’s and60’s economists worked to extend the statistical foun-dations of Haavelmo’s approach and to actually estimate Keynesian mod-els.By the mid-1960’s the models were reaching a much bigger scale than Haavelmo’s two-equation example model.Thefirst stage of this large scale modeling was reported in a volume with25contributors(Duesen-berry,Fromm,Klein,and Kuh,1965),776pages,approximately150esti-mated equations,and a50×75cm foldoutflowchart showing how sectors were linked.The introduction discusses the need to include a“param-eter”for every possible type of policy intervention.That is,there was no notion that policy itself was part of the stochastic structure to be es-timated.There were about44quarters of data available,so without re-strictions on the covariance matrix of residuals,the likelihood function would have been unbounded.Also,in order to obtain even well-defined single-equation estimates by standard frequentist methods,in each equa-tion a large fraction of the variables in the model had to be assumed not to enter.There was no analysis of the shape of the likelihood function or of the model’s implications when treated as a joint distribution for all the observed time series.2An example of a sophisticated economist struggling with this issue is Sargent(1984). That paper purports to characterize both Sargent’s views and my own.I think it does characterize Sargent’s views at the time,but it does not correctly characterize my own.STATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS6 The1965volume was just the start of a sustained effort that produced another volume in1969,and then evolved into the MIT-Penn-SSRC(or MPS)model that became the main working model used in the US Federal Reserve’s policy process.Important other work using similar modeling approaches and methods has been pursued in continuing research by Ray Fair described e.g.in his1984book,as well as in several central banks. While this research on large Keynesian models was proceeding,Mil-ton Friedman and Anna Schwartz(1963b,1963a)were launching an al-ternative view of the data.They focused on a shorter list of variables, mainly measures of money stock,high-powered money,broad price in-dexes,and measures of real activity like industrial production or GDP, and they examined the behavior of these variables in detail.They pointed out the high correlation between money growth and both prices and real activity,evident in the data over long spans of time.They pointed out in the1963b paper that money growth tended to lead changes in nom-inal income.Their book(1963a)argued that from the detailed histori-cal record one could see that in many instances money stock had moved first,and income had followed.Friedman and Meiselman(1963)used single-equation regressions to argue that the relation between money and income was more stable than that between what they called“autonomous expenditure”and income.They argued that these observations supported a simpler view of the economy than that put forward by the Keynesians: monetary policy had powerful effects on the economic system,and in-deed that it was the main driving force behind business cycles.If it could be made less erratic,in particular if money supply growth could be kept stable,cyclicalfluctuations would be greatly reduced.The confrontation between the monetarists and the Keynesian large-scale modelers made clear that econometric modeling of macroeconomic data had not delivered on Haavelmo’s research program.He had pro-posed that economic theories should be formulated as probability distri-butions for the observable data,and that they should be tested against each other on the basis of formal assessments of their statisticalfit.This was not happening.The Keynesians argued that the economy was com-plex,requiring hundreds of equations,large teams of researchers,and years of effort to model it.The monetarists argued that only a few vari-ables were important and that a single regression,plus some charts and historical story-telling,made their point.The Keynesians,pushed bySTATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS7 the monetarists to look at how important monetary policy was in their models,found(Duesenberry,Fromm,Klein,and Kuh,1969,Chapter7, by Fromm,e.g.)that monetary policy did indeed have strong effects. They argued,though,that it was one among many policy instruments and sources offluctuations,and therefore that stabilizing money growth was not likely to be a uniquely optimal policy.Furthermore,neither side in this debate recognized the centrality of in-corporating policy behavior itself into the model of the economy.In the exchanges between Albert Ando and Franco Modigliani(1965)on the one hand,and Milton Friedman and David Meiselman on the other,much of the disagreement was over what should be taken as“autonomous”or“exogenous”.Ando and Modigliani did argue that what was“au-tonomous”ought to be a question of what was uncorrelated with model error terms,but both they and their adversaries wrote as if what was con-trolled by the government was exogenous.Tobin(1970)explained that not only the high correlations,but also the timing patterns observed by the monetarists could arise in a model where erratic monetary policy was not a source offluctuations,but he did so in a deterministic model,not in a probability model that could be con-fronted with data.Part of his story was that what the monetarists took as a policy instrument,the money stock,could be moved passively by other variables to create the observed statistical patterns.I contributed to this debate(1972)by pointing out that the assumption that money stock was exogenous,in the sense of being uncorrelated with disturbance terms in the monetarist regressions,was testable.The monetarists regressed in-come on current and past money stock,reflecting their belief that the re-gression described a causal influence of current and past money stock on current income.If the high correlations reflected feedback from income to money,future money stock would help explain income as well.It turned out it did not,confirming the monetarists’statistical specification.The monetarists’views,that erratic monetary policy was a major source offluctuations and that stabilizing money growth would stabilize the economy,were nonetheless essentially incorrect.With the right statistical tools,the Keynesians might have been able to display a model in which not only timing patterns(as in Tobin’s model),but also the statistical exo-geneity of the money stock in a regression,would emerge as predictions despite money stock not being the main source offluctuations.But theySTATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS8 could not do so.Their models were full of unbelievable assumptions3of convenience,making them weak tools in the debate.And because they did not contain models of policy behavior,they could not even be used to frame the question of whether erratic monetary policy behavior ac-counted for much of observed business cycle variation.II.W HAT WAS MISSINGHaavelmo’s idea,that probability models characterize likely and less likely data outcomes,and that this can be used to distinguish better from worse models,fits neatly with a Bayesian view of inference,and less com-fortably with the Neyman-Pearson approach that he adopted.Since stan-dard statistics courses do not usually give a clear explanation of the differ-ence between Bayesian and frequentist inference,it is worth pausing our story briefly to explain the difference.Bayesian inference aims at produc-ing a probability distribution over unknown quantities,like“parameters”or future values of variables.It does not provide any objective method of doing so.It provides objective rules for updating probability distributions on the basis of new information.When the data provide strong informa-tion about the unknown quantities,it may be that the updating leads to nearly the same result over a wide range of possible initial probability distributions,in which case the results are in a sense“objective”.But the updating can be done whether or not the results are sensitive to the initial probability distribution.Frequentist inference estimates unknown parameters,but does not pro-vide probability distributions for them.It provides probability distribu-tions for the behavior of the estimators.These are“pre-sample”probabil-ities,applying to functions of the data before we observe the data.We can illustrate the difference by considering the multiplier-accelerator model that Haavelmo4used to show that probability-based inference on these models should be possible.Though it is much smaller than the Keynesian econometric models that came later,at the time much fewer 3This fact,which everyone in some sense knew,was announced forcefully by Liu (1960),and much later re-emphasized in my1980b paper.4Haavelmo’s model differs from the classic Samuelson(1939)model only in using current rather than lagged income in the consumption function.STATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS9data were available,so that even this simple model could not have been sharply estimated from the short annual time series that were available. The model as Haavelmo laid it out wasC t=β+αY t+εt(1)I t=θ(C t−C t−1)+ηt(2)Y t=C t+I t.(3) He assumedεt∼N(0,σ2c)andηt∼N(0,σ2i)and that they were indepen-dent of each other and across time.He suggested estimating the system by maximum likelihood.He intended the model to be useful for predicting the effect of a change in government spending G t,though G t does not appear in the model.This was confusing,even contradictory.We will expand the model to use data on G t in estimating it.He also had no constant term in the investment equation.We will be using data on gross investment,which must be non-zero even when there is no growth,so we will add a constant term.Our modified version of the model,then,isC t=β+αY t+εt(1 )I t=θ0+θ1(C t−C t−1)+ηt(2 )Y t=C t+I t+G t(3 )G t=γ0+γ1G t−1+νt(4)We will confront it with data on annual real consumption,gross private investment,and government purchases from1929to1940.5The model does not make sense if it implies a negative multiplier—that is if it implies that increasing G within the same year decreases Y.It also does not make sense ifθ1,the“accelerator”coefficient,is negative. Finally,it is hard to interpret ifγ1is much above1,because that implies explosive growth.We therefore restrict the parameter space toθ1>0,γ1< 1.03,1−α(1+θ1)>0.The last of these restrictions requires a positive multiplier.The likelihood maximum over this parameter space is then at5We use the chain indexed data,which did not exist when Haavelmo wrote.We construct Y as C+I+G,since the chain indexed data do not satisfy the accounting identity and we are not using data on other GDP components.STATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS10αβθ0θ1γ0γ10.56616663.00.00010.70.991Note that the maximum likelihood estimator(MLE)forθ1is at the bound-ary of the parameter space.At this value,the investment equation of the model makes little sense.Furthermore,the statistical theory that is used in a frequentist approach to measure reliability of estimators assumes that the true parameter value is not on the boundary of the parameter space and that the sample is large enough so that a random sample of the data would makefinding the MLE on the boundary extremely unlikely.A Bayesian approach to inference provides a natural and reasonable re-sult,though.The probability density over the parameter space after see-ing the data is proportional to the product of the likelihood function with a prior density function.If the prior density function is muchflatter than the likelihood,as is likely if we began by being very uncertain about the parameter values,the likelihood function itself,normalized to integrate to one,characterizes our uncertainty about the parameter values.With mod-ern Markov Chain Monte Carlo methods,it is a straightforward matter to trace out the likelihood and plot density functions for parameters,func-tions of parameters,or pairs of parameters.Under aflat prior,the density function forθ1has the shape shown in Figure1.While the peak is at zero, any value between0and.25is quite possible,and the expected value is .091.The system’s dynamics withθ1=.2would be very different from dynamics withθ1close to zero.So the data leave substantively important uncertainty about the value ofθ1and do not at all rule out economically significant accelerator effects.The within-year multiplier in this model, that is the effect of a unit change in G t on Y t,is1/(1−α(1+θ1)).Its flat-prior posterior density is shown in Figure2.Note that the maximum likelihood estimate of the multiplier,shown as a vertical line in thefigure, is2.30,well to the left of the main mass of the posterior distribution.This occurs because the multiplier increases withθ1,and the MLE at zero is unrepresentative of the likely values ofθ1.In calculating the“multiplier”here,I am looking at the impact of a change in G t,in the context of a model in which G t is part of the data vector for which the model proposes a probability distribution.There are several ways of thinking about what is being done in this calculation. One is to say that we are replacing the“policy behavior equation”(4) by the trivial equation G t=G∗,holding the other equationsfixed,andSTATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS 110.00.10.20.30.42468θ1 probability densityN = 100000 Bandwidth = 0.007981F IGURE 1.considering variations in G ∗.Another,equivalent,way to think of it is that we are considering choosing values of νt ,the disturbance to the policy equation.The latter approach has the advantage that,since we have an estimated distribution for νt ,we will notice when we are asking about the effects of changes in νt that the model considers extremely unlikely.6While there is nothing logically wrong with asking the model to predict the effects of unlikely changes,simplifying assumptions we have made in setting up the model to match data become more and more questionable as we consider more extreme scenarios.Neither of these ways of looking at a multiplier on G is what Haavelmo did in his hypothetical policy experiment with the model.In fact he did not calculate a multiplier at all.He instead suggested that a policy-maker could,by setting G (which,recall,was not in his probability model),achieve any desired level Y ∗of total output.He recognized that this implied the policy-maker could see εt and ηt and choose G t so as to offset their effects.6This is the point made,with more realistic examples,by Leeper and Zha (2003).STATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS 12234560.00.51.01.52.0Probability density of multiplierN = 100000 Bandwidth = 0.03035F IGURE 2.He noted that under these assumptions,the effects of changes in Y ∗on C t and I t could be easily calculated from equations (1)and (2).He said that what he was doing was dropping the accounting identity (3)and replac-ing it with Y t =Y ∗,but one cannot “drop”an accounting identity.What he was actually doing was replacing an implicit policy equation,G t ≡0,with another,G t =Y ∗−C t −I t ,while preserving the identity (3 ).Since policy-makers probably cannot in fact perfectly offset shocks like ηt and εt ,and since they are more likely to have seen themselves as controlling G t than as directly controlling Y t ,this policy experiment is rather artificial.If Haavelmo had tried to fit his model to data,he would have had to confront the need to model the determination of his policy variable,G t .My extension of Haavelmo’s model in (1 )-(4)specifies that lagged val-ues of C t and I t do not enter the G t equation (4)and that the disturbance of that equation is independent of the other two disturbances.This im-plies,if this equation is taken as describing policy behavior,that G t was determined entirely by shifts in policy,with no account being taken ofSTATISTICAL MODELING OF MONETARY POLICY AND ITS EFFECTS13 other variables in the economy.This would justify estimating thefirst two equations in isolation,as Haavelmo suggested.But in fact the data contain strong evidence that lagged C t and I t do help predict G t.7If the model was otherwise correct,this would have implied(quite plausibly) that G t was responding to private sector developments.Even to estimate the model properly would then have required a more complicated ap-proach.This discussion is meant only as an example to illustrate the difference between frequentist and Bayesian inference and to show the importance of explicitly modeling policy.It is not meant to suggest that Haavelmo’s model and analysis could have been much better had he taken a Bayesian approach to inference.The calculations involved in Bayesian analysis of this simple model(and described more fully in the appendix)take sec-onds on a modern desktop computer,but at the time Haavelmo wrote were completely infeasible.And the model is not a good model.The esti-mated residuals from the MLE estimates show easily visible,strong serial correlation,implying that the data have richer dynamics than is allowed for in the model.In large macroeconomic models it is inevitable that some parameters —some aspects of our uncertainty about how the economy works—are not well-determined by the data alone.We may nonetheless have ideas about reasonable ranges of values for these parameters,even though we are uncertain about them.Bayesian inference deals naturally with this situation,as it did with the prior knowledge thatθ1should be positive in the example version of Haavelmo’s model.We can allow the data, via the likelihood function,to shape the distribution where the data are informative,and use pre-data beliefs where the data are weak.When we are considering several possible models for the same data, Bayesian inference can treat“model number”as an unknown parameter and produce post-sample probabilities over the models.When a large model,with many unknown parameters,competes with a smaller model, these posterior probabilities automatically favor simpler models if theyfit as well as more complicated ones.7I checked this by byfitting bothfirst and second order VAR’s.。
