2016黑龙江旅游职业技术学院单招数学模拟试题(附答案)
单招数学试题及答案

单招数学试题及答案一、选择题(每题4分,共40分)1. 若函数f(x) = 2x + 3,则f(1)的值为:A. 5B. 4C. 3D. 2答案:A2. 已知集合A={1,2,3},B={2,3,4},则A∩B的元素个数为:A. 1B. 2C. 3D. 4答案:B3. 计算(3x - 2)(x + 1)的展开式中x²的系数为:A. 1B. 3C. -1D. -3答案:B4. 函数y = x² - 4x + 4的最小值是:A. 0B. 4C. -4D. 1答案:A5. 已知等差数列{an}的首项a1=1,公差d=2,那么a5的值为:A. 9B. 10C. 11D. 12答案:A6. 若sinθ = 3/5,且θ∈(0, π/2),则cosθ的值为:A. 4/5B. -4/5C. 3/5D. -3/5答案:A7. 已知圆心为C(0,0),半径为1的圆的方程是:A. x² + y² = 1B. x² + y² = 2C. x² + y² = 0D. x² + y² = -1答案:A8. 计算极限lim(x→0) (sin x / x)的值为:A. 0B. 1C. -1D. 2答案:B9. 已知函数f(x) = x³ - 3x,求f'(x)的值为:A. 3x² - 3B. x² - 3C. x³ - 3x²D. 3x - 3答案:A10. 计算定积分∫(0 to 1) x² dx的值为:A. 1/3B. 1/2C. 1D. 2答案:B二、填空题(每题4分,共20分)1. 函数f(x) = x³ + 2x² - 5x + 6的导数f'(x)为______。
答案:3x² + 4x - 52. 已知等比数列{bn}的首项b1=2,公比q=3,那么b3的值为______。
2016年黑龙江单招数学模拟试题:集合的基本运算

2016年某某单招数学模拟试题:集合的基本运算【试题内容来自于相关和学校提供】1:A= 与B= 的关系是()A、B、C、D、2:设集合,,则下列结论正确的是()A、B、C、D、3:全集S={0,1,3,5,7,9},C S A={0,5,9},B={3,5,7}则A∩B=" "A、B、C、D、4:已知集合,若,则实数的取值集合为A、B、C、D、5:设全集为R, 函数的定义域为M, 则为A、(-∞,1)B、(1, + ∞)C、D、6:设全集,,,则。
7:设集合,,若Æ。
则实数的取值X围是。
8:已知集合,集合,则 .9:已知全集为R,集合A=,B=,则A∩∁R B等于________。
10:设集合,,则 .11:已知集合M={x|x(x-a-1)<0,x∈R},N={x|x 2-2x-3≤0},若M∪N =N,某某数a的取值X围。
12:(本小题满分12分)已知集合(1)若,求(C ;(2)若,某某数a的取值X围.13:已知A={x|2a≤x≤a+3},B={x|x<-1或x>5},若A∩B= ,求a的取值X围。
14:(本小题满分12分)已知(1)若a=4,求(2)若,求a的取值X围.15:已知集合,,且,某某数的取值X围。
(本题8分)答案部分1、C解:因为A= 表示的为y轴上角的集合与B= 表示的为y轴正半轴上角的集合,因此选C2、C考点:集合的包含关系判断及应用。
分析:根据题意,对于Q,求出x2-x>0的解集,化为区间的形式,进而与P进行比较,即可得答案。
解:对P有,P=(1,+∞),对于Q,有x2-x>0,解可得x>1,或x<0;则Q=(-∞,0)∪(1,+∞);所以,故选择C、3、B略4、A试题分析:因为,所以或由得:,此时,适合题意;由得:或当时,,当时,,均适合题意;综上所述,实数的取值集合为,所以答案应选A. 考点:集合的概念.5、B,,所以选B6、,,又,。
2016年黑龙江单招数学模拟试题:概率的应用

2016年黑龙江单招数学模拟试题:概率的应用【试题内容来自于相关网站和学校提供】1:在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用X表示这10个村庄中交通不方便的村庄数,下列概率中等于的是()A、P(X=2)B、P(X≤2)C、P(X=4)D、P(X≤4)2:从2004名学生中选取50名组成参观团,若采用下面的方法选取先用简单随机抽样法从2004人中剔除4人,再从剩下的2000人中按系统抽样的方法抽取50人,则每人入选的概率()A、不全相等B、均不相等C、都相等且为D、都相等且为3:任意抛掷两枚骰子,所得点数之和为3的概率是()A、B、C、D、4:1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,则从2号箱取出红球的概率是( )A、B、C、D、5:在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是A、B、C、D、6:若甲、乙、丙三人随机地站成一排,则甲、乙两人相邻而站的概率为.7:图(1)中实线围成的部分是长方体(图2)的平面展开图,其中四边形ABCD是边长为1的正方形。
若向图(2)中虚线围成的矩形内任意抛掷一点,它落在长方体的平面展开图内的概率是,则此长方体的体积是。
8:从3台甲型彩电和2台乙型彩电中任取3台,其中两种品牌的彩电齐全的概率是________。
9:。
用0.618法选取试点过程中,如果试验区间为,为第一个试点,且处的结果比处好,则为10:一个人在打靶中连续射击2次,事件“至少有1次中靶”的对立事件是____。
11:某寻呼台共有客户3000人,若寻呼台准备了100份小礼品,邀请客户在指定时间来领取。
假设任一客户去领奖的概率为4%。
问:寻呼台能否向每一位顾客都发出奖邀请?若能使每一位领奖人都得到礼品,寻呼台至少应准备多少礼品?12:甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:甲运动员乙运动员若将频率视为概率,回答下列问题:(1)求甲运动员射击1次击中10环的概率.(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).13:袋中有红、黄、白色球各1个,每次任取1个,有放回地抽取三次,求基本事件总数,并计算下列事件的概率。
2016黑龙江民族职业学院单招数学模拟试题(附答案)

考单招——上高职单招网2016黑龙江民族职业学院单招数学模拟试题(附答案)一、本题共12小题,每小题5分,共50分,在每小题给出的四个选项中只有一个选项是符合题目要求的.1.设a 、b 、c 是任意的非零平面向量,且相互不共线,则( ) ①(a ·b )c -(c ·a )b =0 ②|a |-|b |<|a -b |;③(b ·c )a -(c ·a )b 不与c 垂直; ④(3a +2b )·(3a -2b )=9|a |2-4|b |2. 其中的真命题是( )A .②④B .③④C .②③D .①②2.若直线mx +ny =4和⊙O ∶422=+y x 没有交点,则过(m ,n )的直线与椭圆14922=+y x 的交点个数( ) A .至多一个 B .2个 C .1个 D .0个3.将正方形ABCD 沿对角线BD 折成120°的二面角,C 点到C '处,这时异面直线AD 与C B '所成角的余弦值是( )A .22 B .21 C .43D .434.现用铁丝做一个面积为1平方米、形状为直角三角形的框架,有下列四种长度的铁丝各一根供选择,其中最合理(即够用,浪费最少)的一根是( ). A .4.6米 B .4.8米 C .5.米 D .5.2米 5.在△ABC 中,||AC =5,||BC =3,||AB =6,则AC AB ⋅=( )考单招——上高职单招网A .13B .26C .578D .24 6.一个圆锥和一个半球有公共底面,如果圆锥的体积与半球的体积恰好相等,则圆锥轴截面顶角的余弦值是( ) A .43 B .34 C .53- D .537.已知双曲线12222=-by a x 的离心率2[∈e ,]2.双曲线的两条渐近线构成的角中,以实轴为角平分线的角记为θ,则θ的取值范围是( ).A .6π[,]2πB .3π[,]2π C .2π[,]32π D .32π[,π]8.已知函数)sin(2θω+=x y 为偶函数0(<θ<π),其图像与直线y =2的某两个交点横坐标为1x ,2x ,||12x x -的最小值为π,则( ) A .2=ω,2π=θ B .21=ω,2π=θ C .21=ω,4π=θ D .2=ω,4π=θ9.过抛物线x y 42=的焦点作直线l 交抛物线于A 、B 两点,若线段AB 中点的横坐标为3,则||AB 等于( )A .10B .8C .6D .410.若)10(0log log log 3)1(212<<>==+a x x x a a a,则1x ,2x ,3x 的大小关系是( )A .123x x x <<B .312x x x <<C .132x x x << 1B .231x x x <<考单招——上高职单招网二、填空题:本题共5小题,共20分,把答案填在题中的横线上 11.若不等式23+>ax x 的解集是非空集合=<<a m x x 则},4|{,m=.12.)(x f 是定义在实数有R 上的奇函数,若x ≥0时,)1(log )(3x x f +=,则=-)2(f ________.13.若点P (αcos ,αsin )在直线上x y 2-=上,则=+αα2cos 22sin ________. 14.用一个与正方体的各面都不平行的平面去截正方体,截得的截面是四边形的图形可能是下列选项中的________(把所有符合条件的图形序号填入). ①矩形 ②直角梯形 ③菱形 ④正方形15.某宇宙飞船的运行轨道是以地球中心F 为焦点的椭圆,测得近地点A 距离地面)km (m ,远地点B 距离地面)km (n ,地球半径为)km (R ,关于这个椭圆有以下四种说法:①焦距长为m n -;②短轴长为))((R n R m ++;③离心率Rn m mn e 2++-=;④若以AB 方向为x 轴正方向,F 为坐标原点,则与F 对应的准线方程为)())((m n R n R m x -++2-=,其中正确的序号为________.三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤. 16.(12分)设函数)(cos sin 322cos )(R x x x x x f ∈+=的最大值为M,最小正周期为T.(Ⅰ)求M 、T ;(Ⅱ)10个互不相等的正数i x 满足),10,,2,1(10,)( =<=i x M x f i i π且求++x x 21… +x n 的值.考单招——上高职单招网17.(12分)无穷数列}{n a 的前n 项和)(*N n npa S n n ∈=,并且1a ≠2a . (1)求p 的值;(2)求}{n a 的通项公式;18.(14分)(甲)如图,已知斜三棱柱111C B A ABC -的侧面C A 1⊥底面ABC ,∠ABC =90°,BC =2,AC =32,又1AA ⊥C A 1,1AA =C A 1.(1)求侧棱A A 1与底面ABC 所成的角的大小;(2)求侧面B A 1与底面所成二面角的大小;(3)求点C 到侧面B A 1的距离.(乙)在棱长为a 的正方体C B A O OABC ''''-中,E ,F 分别是棱AB ,BC 上的动点,且AE =BF .考单招——上高职单招网(1)求证:E C F A '⊥';(2)当三棱锥BEF B -'的体积取得最大值时,求二面角B EF B --'的大小(结果用反三角函数表示).19.(14分)在抛物线x y 42=上存在两个不同的点关于直线l ;y =kx +3对称,求k 的取值范围.20.(14分)某地区预计明年从年初开始的前x 个月内,对某种商品的需求总量)(x f (万件)与月份x 的近似关系为:*)(235)(1(1501)(N x x x x x f ∈-+=,且)12≤x . (1)写出明年第x 个月的需求量)(x g (万件)与月x 的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?(2)如果将该商品每月都投放市场p 万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问:p 至少为多少万件?考单招——上高职单招网21.(14分)已知函数22log )(+-=x x x f a的定义域为[α,β],值域为)1([log -βa a ,)]1(log -a a a ,并且)(x f 在α[,]β上为减函数.(1)求a 的取值范围;(2)求证:βα<<<42;参考答案1.A 2.B 3.D 4.C 5.B 6.D 7.C 8.A 9.B 10.C :11. 8112.-1 13.-2 14.①③④ 15.①③④考单招——上高职单招网16. )62sin(22cos 2sin 3)(π+=+=x x x x f ……………………2分(Ⅰ)M=2…………4分 T=ππ=22…………6分 (Ⅱ),2262,2)(πππ+=+∴=k x x f i i )(6Z k k x i ∈+=ππ…………9分又9,,1,0,100 =∴<<k x i π610)921(1021ππ⨯++++=+++∴ x x x =π3140………………12分 17.(1)∵ 111pa S a == ∴ 01≠a ,且p =1,或01=a . 若是01≠a ,且p =1,则由22212pa S a a ==+.∴ 21a a =,矛盾.故不可能是:01≠a ,且p =1.由01=a ,得02≠a . 又22212pa S a a ==+,∴ 21=p . (2)∵ 11)1(21+++=n n a n S ,n n na S 21=, ∴ n n n na a n a 21)1(2111-+=++. n n na a n =-+1)1(. 当k ≥2时,11-=+k ka a k k . ∴ n ≥3时有 223211a a a a a a a a n n n n n ⋅⋅⋅⋅---=22)1(123221a n a n n n n -=----=⋅⋅⋅⋅ . ∴ 对一切*N ∈n 有:2)1(a n a n -=.考单招——上高职单招网18.(甲)(1)∵ 侧面⊥C A 1底面ABC , ∴ A A 1在平面ABC 上的射影是AC .A A 1与底面ABC 所成的角为∠AC A 1.∵ C A A A 11=,C A A A 11⊥, ∴ ∠AC A 1=45°.(2)作O A 1⊥AC 于O ,则O A 1⊥平面ABC ,再作OE ⊥AB 于E ,连结E A 1,则AB E A ⊥1,所以∠EO A 1就是侧面B A 1与底面ABC 所成二面角的平面角.在Rt △EO A 1中,3211==AC O A ,121==BC OE , ∴ 3tan 11==∠OEOA EO A . =∠EO A 160°. (3)设点C 到侧面B A 1的距离为x . ∵ BC A C ABC A V V 11--=, ∴ABC ABC BC A ABC S x S O A S x S O A ∆∆∆∆⋅⋅⋅⋅⋅⋅=⇔=1113131.(*) ∵ 31=O A ,1=OE , ∴ 2131=+=E A .又222)32(22=-=AB ,∴ 22222211==⋅⋅∆AB A S . 又2222221=⨯⨯=∆ABC S . ∴ 由(*)式,得12222==⋅x .∴ 1=x(乙)(1)证明:如图,以O 为原点建立空间直角坐标系.考单招——上高职单招网设AE =BF =x ,则A '(a ,0,a ),F (a -x ,a ,0),C '(0,a ,a ),E (a ,x ,0),∴ ='F A (-x ,a ,-a ), ='E C (a ,x -a ,-a ).∵ 0)(2=+-+-=''⋅a a x a xa E C F A , ∴ E C F A '⊥'.(2)解:记BF =x ,BE =y ,则x +y =a ,则三棱锥BEF B -'的体积为 22241)2(61a y x b a xya V =+≤=. 当且仅当2ay x ==时,等号成立,因此,三棱锥BEF B -'的体积取得最大值时,2a BF BE ==. 过B 作BD ⊥BF 交EF 于D ,连结D B ',则EF D B ⊥'.∴ ∠DB B '是二面角B EF B --'的平面角.在Rt △BEF 中,直角边2a BF BE ==,BD 是斜边上的高, ∴ 42=BD 在Rt △DB B '中,tan ∠22='='BDBB DB B .故二面角B EF B --'的大小为22arctan .19.∵ k =0不符合题意, ∴ k ≠0,作直线l ':考单招——上高职单招网b x ky +-=1,则l l ⊥'. ∴ 满足条件的⎩⎨⎧='⇔EAB l B A 、x y l k 的中点过交于两个不同点与;42由⎪⎩⎪⎨⎧=+-=x y b x ky 412消去x ,得0412=-+b y y k, 041412>+=∆⋅⋅b k .01>+kb .(*) 设1(x A ,)2y 、2(x B 、)2y ,则 k y y 421-=+. 又b xx k y y ++-=+⋅2122121. ∴)2(221b k k x x +=+. 故AB 的中点)2((b k k E +,)2k -. ∵ l 过E , ∴ 3)2(22++=-b k k k ,即 k k k b 2322---=. 代入(*)式,得)1(032032012323333+⇔<++⇔<+⇔>+---k k k k k k k k k 0)3(2<+-k k 01<<-⇔k20.(1)251133211501)1()1(=⨯⨯⨯==f g .当x ≥2时, )1()()(--=x f x f x g考单招——上高职单招网)237()1(1501)235)(1(1501x x x x x x -----=)]23937()23335[(150122x x x x x -+---+=⋅ )672(1501x x -=⋅ )12(251x x -=⋅. ∴ *)(12(251)(N x x x x g ∈-=,且)12≤x . ∵ 2536]2)12([251)(2=-+≤x x x g . ∴ 当x =12-x ,即x =6时,2536)(max =x g (万件).故6月份该商品的需求量最大,最大需求量为2436万件. (2)依题意,对一切∈x {1,2,…,12}有)()()2()1(x f x g g g px =+++≥ . ∴ )235)(1(1501x x p -+≥(x =1,2,…,12). ∵ )23335(1501)(2x x x h -+=]433281369[15012--=x ∴ 14.1)8()(max ==h x h . 故 p ≥1.14.故每个月至少投放1.14万件,可以保证每个月都保证供应.21.(1)按题意,得)1(log )(22log max -==+-αααa x f a a . ∴ ⎪⎩⎪⎨⎧>->+-.,01022ααα 即 2>α.考单招——上高职单招网又)1(log )(22log min -==+-βββa x f a a ∴ 关于x 的方程)1(log 22log -=+-x a x x a a. 在(2,+∞)内有二不等实根x =α、β.⇔关于x 的二次方程x a ax )1(2-+ 0)1(2=-+a 在(2,+∞)内有二异根α、β.9100)1(2)1(242210)1(8)1(102<<⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧>-+-+>-->-+-=∆≠>⇔a a a a aa a a a a a 且. 故 910<<a . (2)令)1(2)1()(2a x a ax x Φ-+-+=,则)218(4)4()2(-=⋅⋅a a ΦΦ)19(8-=a a0<.∴ βα<<<42.。
黑龙江高职对口招生考试数学模拟试题一(含答案)
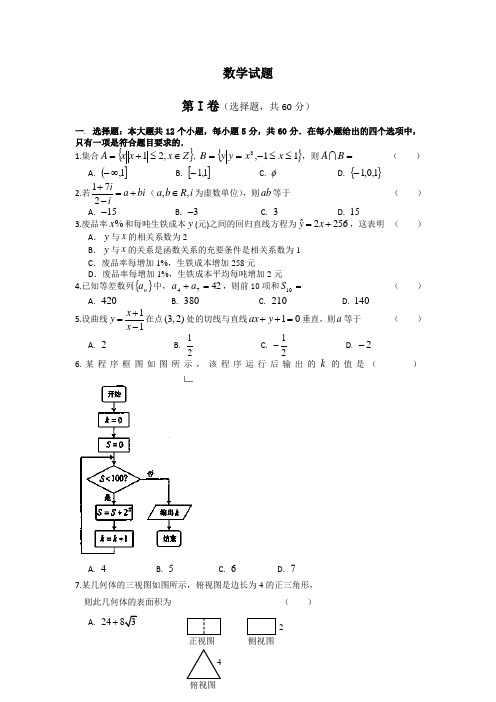
数学试题第I 卷(选择题,共60分)一. 选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}Z x x x A ∈≤+=,21,{}11,3≤≤-==x x y y B ,则=B A ( ) A. (]1,∞-B. []1,1-C. φD. {}1,0,1-2.若172ia bi i+=+-(,,a b R i ∈为虚数单位),则ab 等于 ( ) A. 15- B. 3- C. 3 D. 153.废品率%x 和每吨生铁成本y (元)之间的回归直线方程为ˆ2256y x =+,这表明 ( )A .y 与x 的相关系数为2B .y 与x 的关系是函数关系的充要条件是相关系数为1C .废品率每增加1%,生铁成本增加258元D .废品率每增加1%,生铁成本平均每吨增加2元4.已知等差数列{}n a 中,4274=+a a ,则前10项和=10S ( ) A. 420 B. 380C. 210D. 1405.设曲线11x y x +=-在点(3,2)处的切线与直线10ax y ++=垂直,则a 等于 ( ) A. 2 B. 12 C. 12- D. 2-6.某程序框图如图所示,该程序运行后输出的k 的值是( )A. 4B. 5C. 6D. 7 7.某几何体的三视图如图所示,俯视图是边长为4的正三角形, 则此几何体的表面积为 ( ) A. 2483+ 4正视图侧视图俯视图2B.C. 12+D. 24+8.已知函数()2xf x =的反函数()g x 满足()()4g a g b +=,则11a b+的最小值为 ( ) A. 1 B. 13 C. 12 D. 149.定义运算:12142334a a a a a a a a =-,将函数cos2()sin2xf x x =的图像向左平移m (0m >)个单位,所得图像对应的函数为偶函数,则m 的最小值是 ( )A. 3πB. 32πC. 34πD. 37π10.已知函数2()f x x bx c =++,其中04,04b c ≤≤≤≤,记事件A 为 “函数()f x 满足条件:(2)12(1)1f f ≤⎧⎨-≤⎩”,则事件A 发生的概率为 ( )A. 49B. 13C. 12D. 1911.已知12,F F 分别为双曲线22221x y a b-=(a >0,b >0)的左、右焦点,P 为双曲线左支上的任意一点,若221||||PF PF 的最小值为8a ,则双曲线离心率e 的取值范围是 ( )A. (1,)+∞B. (0,3]C. (1,3]D. (1,2] 12.定义域为R 的偶函数()f x ,对x R ∀∈,有(2)()(1)f x f x f +=+,且当[2,3]x ∈ 时,2()21218f x x x =-+-,若函数()log (1)a y f x x =-+在()0,+∞上至少有三个零点,则a 的取值范围是 ( )A.B.C.D. 第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~(24)题为选考题,考生根据要求做答.二. 填空题:本大题共4小题,每小题5分,共20分.13.已知圆C 与直线04=--y x 及0=-y x 都相切,且圆心在直线0=+y x 上,则圆C 的方程为 .14.某高中在校学生2000人,高一年级与高二年级人数相同并且都比高三年级多1人,为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而其中::2:3:5a b c =,全校参与跳绳的人数占总人数的5,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人. 15.已知向量13(,),,22a OA ab OB a b =-=-=+,若OAB ∆是等边三角形,则OAB ∆的面积为 .16.数列{}n a 满足11a =,且对任意的正整数,m n 都有m n m n a a a mn +=++,则12201220131111a a a a ++++= .三. 解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知向量()sin m x x =,()sin ,cos n x x =,设函数()n m x f ⋅=. (Ⅰ)求函数()f x 的解析式,并求()f x 在区间⎥⎦⎤⎢⎣⎡-6,4ππ上的最小值; (Ⅱ)在ABC ∆中,c b a ,,分别是角C B A ,,的对边,A 为锐角,若()()32f A f A +-=, 7b c +=,ABC ∆的面积为32,求a .18.(本小题满分12分)甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别.(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率; (Ⅱ)将这两个盒子中的球混合在一起,从中任取2个,求取出的2个球中至少有一个黑球的概率. 19.(本小题满分12分) 四棱锥S ABCD -中,底面ABCD 为平行四边形, 侧面SBC ⊥底面ABCD ,E 为SD 的中点,已知452ABC AB BC ∠===,,SB SC == (Ⅰ)求证:SA BC ⊥;(Ⅱ)在BC 上求一点F ,使//EC 平面SAF ; (Ⅲ)求三棱锥D EAC -的体积.20.(本小题满分12分)已知椭圆C 的焦点在x 轴上,离心率2e =,且经过点(2,1)A -. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)斜率为1-的直线l 与椭圆C 相交于,P Q 两点,求证:直线AP 与AQ 的倾斜角互补.21.(本小题满分12分)已知函数()ln f x x a x =-,1(), (R).ag x a x+=-∈(Ⅰ)若1a =,求函数()f x 的极值;(Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间; (Ⅲ)若在区间[]1,e (e 2.718=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.AB C D S E答案一、 选择题:(本大题共12小题,每小题5分,共60分)题号123456789 10 11 12 答案 D B D C D A A C CBCA二、填空题:(本大题共4小题,每小题5分,共20 分) 13. ()()21122=++-y x 14. 36 15.33 16.10072013 三、解答题:(本大题共6小题,共70分。
职高单招数学试题及答案

职高单招数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是不等式2x - 5 > 3的解集?A. x > 4B. x < 4C. x > 1D. x < 12. 函数f(x) = 3x^2 - 2x + 5的顶点坐标是:A. (1, 4)B. (-1, 4)C. (1, 6)D. (-1, 6)3. 已知等差数列的前三项分别为2, 5, 8,求第5项的值:A. 11B. 13C. 15D. 174. 圆的半径为5,求圆的面积:A. 25πB. 50πC. 75πD. 100π5. 已知sinθ = 1/3,求cosθ的值(假设θ为锐角):A. 2√2/3B. √3/3C. √6/3D. -√3/36. 一个长方体的长、宽、高分别是2米、3米、4米,求其体积:A. 24立方米B. 26立方米C. 28立方米D. 30立方米7. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∪B:A. {1, 2, 3}B. {1, 2, 3, 4}C. {2, 3}D. {1, 4}8. 一个直角三角形的两条直角边分别为3和4,求斜边的长度:A. 5B. 6C. 7D. 89. 已知等比数列的首项为2,公比为3,求第5项的值:A. 486B. 243C. 81D. 5410. 函数y = log2(x)的定义域是:A. x > 0B. x < 0C. x ≥ 0D. x ≤ 0二、填空题(每题4分,共20分)11. 将分数3/4化简为最简分数是_________。
12. 已知函数f(x) = x^3 - 2x^2 + x - 2,求f(1)的值是_________。
13. 一个正六边形的内角是_________度。
14. 将弧度制下的角α=π/4转换为角度制,其值为_________度。
15. 已知方程x^2 - 5x + 6 = 0的根是x1和x2,那么x1 * x2的值为_________。
2016黑龙江林业职业技术学院单招数学模拟试题(附答案)

2016黑龙江林业职业技术学院单招数学模拟试题(附答案)一、选择题:本大题共10小题、每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合2{|1(1)}A x x x =-≥-,{1}B x x =≤-,,,则p 是q 的 ( )A .充分条件,但不是必要条件B .必要条件,但不是充要条件C .充分必要条件D .既不是充分条件,也不是必要条件 2.(理) z ∈C ,若|z |-z =2-4i ,则43iz+的值是( ) A .1B .-1C .iD .- i(文) 若a = 100tan ,则用a 表示sin40°的结果为 ( ) A .a1-B .2224(1)(1)a a a -+C .2224(1)(1)a a a -+D .211a+-3.已知直线1l 、2l 及平面α,12l l ⊥,α//1l ,则2l 与α的位置关系为 ( )A .2l 与α相交,不垂直B .α⊂2lC .2l α⊥D .以上三种情况都有可能4.若偶函数y =f (x )(∈x R )满足f (x +2)= f (x ),且x ∈(-1,0)时,()||f x x =,则函数y =f (x )的图象与函数4log ||y x =图象的交点的个数为 ( )A .3B .4C .6D .85.从单词“e xc l a im ”中选取5个不同的字母排成一排,则含“e x ”(“e x ”相连且顺序不变)的概率为( ) A .221 B .181 C .4321 D .7561 6.f ’(x )是f (x )的导函数,f ’(x )的图象如图所示,则f (x )的图象只可能是( )A B C D7.路灯距地平面为8m ,一个身高为1.75m 的人以80m/min 的速率从路灯在地面上的射影点C 处,沿某直线离开路灯,那么人影长度的变化速率为v 为( ) A .28 m/s 75B .s /m 247C .s /m 227D .s /m 2378.已知点P (x ,y )的坐标满足430352510x y x y x -+≤⎧⎪+≤⎨⎪-≥⎩,设A (6,0),则||cos OP AOP∠(O 为坐标原点)的最大值为( ) A .3B .5C .4D .19.过底面边长为1的正三棱锥的一条侧棱和高作截面,如果这个截面的面积为21,那么这个棱锥的侧面与底面所成角的正切值为 ( ) A .1B .2C .4D .21 10.双曲线2221(1)x y a a-=>的一个焦点为F ,点P 在双曲线上,且||||OP OF =(O 为坐标原点),则△OPF 的面积S =( )A .1B .14C .4D .21第Ⅱ卷(非选择题,共90分)二、填空题。
高职数学试题试卷及答案

高职数学试题试卷及答案一、选择题(每题2分,共10分)1. 下列哪个数是自然数?A. -3B. 0C. 1.5D. π2. 函数f(x) = 2x^2 + 3x - 5的图像与x轴的交点个数是:A. 0B. 1C. 2D. 33. 圆的面积公式是:A. A = πrB. A = πr^2C. A = 2πrD. A = 4πr^24. 已知集合A = {1, 2, 3},B = {2, 3, 4},A∩B是:A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3}5. 等差数列的第5项是15,第1项是5,求公差d:A. 2B. 3C. 4D. 5二、填空题(每题2分,共10分)6. 若a + b = 10,a - b = 4,则a = __________。
7. 将分数\(\frac{3}{4}\)化为最简分数是 __________。
8. 一个直角三角形的两条直角边分别为3和4,其斜边长为__________。
9. 函数y = log_2(x)的定义域是 __________。
10. 一个圆的半径为5,其周长为 __________。
三、简答题(每题10分,共20分)11. 证明:若a > b > 0,则a^3 > b^3。
12. 解不等式:2x - 5 > 3x + 1。
四、计算题(每题15分,共30分)13. 计算下列定积分:\(\int_{0}^{1} (2x + 1)dx\)。
14. 求函数f(x) = 3x^2 - 2x + 1的极值。
五、解答题(每题15分,共30分)15. 解方程组:\[\begin{cases}x + y = 4 \\2x - y = 2\end{cases}\]16. 已知数列{an}的通项公式为an = 2n - 1,求前n项和Sn。
六、论述题(每题15分,共15分)17. 论述函数的连续性与可导性之间的关系。
答案:一、选择题1. B2. C3. B4. B5. B二、填空题6. 77. \(\frac{3}{4}\)8. 59. \((0, +\infty)\)10. \(10\pi\)三、简答题11. 证明略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考单招——上高职单招网2016黑龙江旅游职业技术学院单招数学模拟试题(附答案)一、填空题(4′×12)1.函数))((R x x f y ∈=图象恒过定点)1,0(,若)(x f y =存在反函数)(1x fy -=,则1)(1+=-x f y 的图象必过定点 ()1,1 。
2.已知集合{}R x y y A x∈-==,12,集合{}R x x x y y B ∈++-==,322,则集合{}B x A x x ∉∈且=()+∞,2 。
3.若角α终边落在射线)0(043≤=-x y x 上,则=⎥⎦⎤⎢⎣⎡-+)22arccos(tan α71- 。
4.关于x 的方程)(01)2(2R m mi x i x ∈=+++-有一实根为n ,则=+ni m 1i 2121- 。
5.数列{}n a 的首项为21=a ,且))((21211N n a a a a n n ∈+++=+ ,记n S 为数列{}n a 前n 项和,则n S =1232-⎪⎭⎫⎝⎛⋅n 。
6.新教材同学做:若y x ,满足⎪⎪⎩⎪⎪⎨⎧-≥-≤-≥+≤+1315y x y x y x y x ,则目标函数y x s 23-=取最大值时=x 4 。
老教材同学做:若)(13N n x x n∈⎪⎭⎫ ⎝⎛-的展开式中第3项为常数项,则展开式中二项式系数最大的是第 5 项。
7.已知函数)20,0)(2sin()(πϕϕ<<>+=A x A x f ,若对任意R x ∈有)125()(πf x f ≥成立,则方程0)(=x f 在[]π,0上的解为 326ππor 。
8.新教材同学做:考单招——上高职单招网某校高二(8)班四位同学的数学期中、期末和平时成绩可分别用矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=6078929083768588,75809095321,XX X 表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵X 可用321,X ,X X 表示为 3213.04.03.0X X X X ++= 。
老教材同学做:某足球队共有11名主力队员和3名替补队员参加一场足球比赛,其中有2名主力和1名替补队员不慎误服违禁药物,依照比赛规定,比赛后必须随机抽取2名队员的尿样化验,则能查到服用违禁药物的主力队员的概率为9125。
(结果用分数表示) 9.将最小正周期为2π的函数)2,0)(sin()cos()(πϕωϕωϕω<>+++=x x x g 的图象向左平移4π个单位,得到偶函数图象,则满足题意的ϕ的一个可能值为 4π。
10.据某报《自然健康状况》的调查报道,所测血压结果与相应年龄的统计数据如下表,观察表中数据规律,并将最适当的数据填入表中括号内。
年龄(岁) 3035404550556065……收缩压 (水银柱/毫米) 110115120125130135(140)145 ……舒张压 (水银柱/毫米)70737578807385(88)……11.若函数⎭⎬⎫⎩⎨⎧+=x x x f 241log ,log 3min )(,其中{}q p ,min 表示q p ,两者中的较小者,考单招——上高职单招网则2)(<x f 的解为 404<<>x or X 。
12.如图,1P 是一块半径为1的半圆形纸板,在1P 的左下端剪去一个半径为21的半圆得到图形2P ,然后依次剪去一个更小的半圆(其直径是前 一个被剪掉半圆的半径)可得图形 ,,,,43n P P P ,记纸板n P 的面积为n S ,则=∞→n n S lim 3π 。
二、选择题(4′×4)13.已知c b a ,,满足0<<<ac a b c 且,则下列选项中不一定能成立的是 ( C )A 、ac ab >B 、0)(>-a b cC 、22ca cb <D 、0)(<-c a ac 14.下列命题正确的是 ( C )A 、若A a n n =∞→lim ,B b n n =∞→lim ,则)0(lim≠=∞→n nn n b B Ab a 。
B 、函数)11(arccos ≤≤-=x x y 的反函数为R x x y ∈=,cos 。
C 、函数)(12N m x y m m∈=-+为奇函数。
D 、函数21)32(sin )(2+-=xx x f ,当2004>x 时,21)(>x f 恒成立。
15.函数11)(2-+-=x x a x f 为奇函数的充要条件是( B )A 、10<<aB 、10≤<aC 、1>aD 、1≥a 16.不等式)10(2sin log ≠>>a a x x a 且对任意)4,0(π∈x 都成立,则a 的取值范围为( B )考单招——上高职单招网A 、)4,0(πB 、)1,4(πC 、)2,1()1,4(ππ⋃ D 、)1,0(三、解答题:17.(本题满分12分)新教材同学做:在ABC ∆中,角C B A ,,所对边分别为c b a ,,,已知,2,32==c aC sin B sin 00 b c 2- = 0,求ABC ∆的面积S 。
A cos 0 1解:计算行列式的值,得 0sin cos 2sin =-B A c C b ,由正弦定理,得0sin sin cos 2sin sin =-C B A C B 即21cos =A ,∴︒=60A ,再由C c A a sin sin =,得213260sin 2sin =︒=C ,∴︒=30C∴ABC ∆是直角三角形,∴3221==ac S 。
老教材同学做:在ABC ∆中,角C B A ,,所对边分别为c b a ,,,已知,2,32==c a bctgB tgA 21=+,求ABC ∆ 的面积S 。
解:由b c tgB tgA 21=+及正弦定理,得 ()B CBB B A B A sin sin 2cos sin cos cos sin =+,即 21cos =A ,(其余同上)18.(本题满分12分)设复数)0,,(1≠∈+=y R y x yi x z ,复数)(sin cos 2R i z ∈+=ααα,且1121,2z R z z ∈+在复平面上所对应点在直线x y =上,求21z z -的取值范围。
考单招——上高职单招网解:⎩⎨⎧=∈+11121Im Re 2z z R z z ⎩⎨⎧≠=∈-++-⇒022222y x R yi x xyi y x ⎩⎨⎧≠==-⇒0022y x y xy 1==⇒y x i z +=⇒1121z z -()()⎪⎭⎫ ⎝⎛+-=-+-=4sin 223sin 1cos 122πααα ∴21z z -[]12,12+-∈19.(本题满分14分) 已知关于x 的不等式052<--ax ax 的解集为M 。
(1)当4=a 时,求集合M ;(2)若M M ∉∈53且,求实数a 的取值范围。
解:(1)4=a 时,不等式为04542<--x x ,解之,得 ()⎪⎭⎫⎝⎛⋃-∞-=2,452,M (2)25≠a 时,⎩⎨⎧∉∈M M 53⎪⎪⎩⎪⎪⎨⎧≥--<--⇒025550953a a aa ⎪⎩⎪⎨⎧<≤<>251359a ora a ()25,935,1⋃⎪⎭⎫⎢⎣⎡∈⇒a25=a 时,不等式为0255252<--x x , 解之,得 ()⎪⎭⎫⎝⎛⋃-∞-=5,515,M , 则 M M ∉∈53且, ∴25=a 满足条件综上,得 (]25,935,1⋃⎪⎭⎫⎢⎣⎡∈a 。
20.(本题满分14分)如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数n m ,时,输出结果记为),(n m f ,且计算装置运算原理如下: ① 若Ⅰ、Ⅱ分别输入1,则1)1,1(=f ;②若Ⅰ输入固定的正整数, Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,考单招——上高职单招网Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:(1))1,(m f 的表达式)(N m ∈;(2)),(n m f 的表达式),(N n m ∈; (3)若Ⅰ、Ⅱ都输入正整数n ,则输出结果),(n n f 能否为2005?若能,求出相应的n ;若不能,则请说明理由。
解:(1)()()()()11231,131,231,131,--===-=-=m m f m f m f m f (2)()()()()()()133131,232,31,,1-+=-+==⨯+-=+-=-n n m f n m f n m f n m f m(3)()()133,1-+=-n n n f n ,∵()20057471837,76<=+=f ,()200522082138,87>=+=f∴),(n n f 输出结果不可能为2005。
21.(本题满分16分)对数列{}n a ,规定{}n a ∆为数列{}n a 的一阶差分数列,其中。
对自然数,规定{}n k a ∆为{}n a 的阶差分数列,其中)(1111n k n k n k n k a a a a --+-∆∆=∆-∆=∆。
(1)已知数列{}n a 的通项公式),(2N n n n a n ∈+=,试判断{}n a ∆,{}n a 2∆是否为等差或等比数列,为什么?(2)若数列{}n a 首项11=a ,且满足)(212N n a a a n n n n ∈-=+∆-∆+,求数列{}n a 的通项公式。
(3)对(2)中数列{}n a ,是否存在等差数列{}n b ,使得n n n n n n a C b C b C b =+++ 2211对一切自然N n ∈都成立?若存在,求数列{}n b 的通项公式;若不存在,则请说明理由。
解:(1)()()()2211221+=+-+++=-=∆+n n n n n a a a n n n ,∴{}n a ∆是首项为4,公差为2的等差数列。
()()2222122=+-++=∆n n a n)(1N n a a a n n n ∈-=∆+k k考单招——上高职单招网∴{}n a 2∆是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2)n n n n a a a 212-=+∆-∆+,即n n n n n a a a a 211-=+∆-∆-∆++,即n n n a a 2=-∆,∴n n n a a 221+=+∵11=a ,∴12224⨯==a ,232312⨯==a ,342432⨯==a ,猜想:12-⋅=n n n a证明:ⅰ)当1=n 时,01211⨯==a ; ⅱ)假设k n =时,12-⋅=k k k a1+=k n 时,()()111212222-++⋅+=+⋅=+=k k k k k k k k a a 结论也成立∴由ⅰ)、ⅱ)可知,12-⋅=n n n a(3)n n n n n n a C b C b C b =+++ 2211,即 122112-⋅=+++n nn n n n n C b C b C b ∵()1112111013212321------⋅=++++=++++n n n n n n n n n n n n C C C C n nC C C C ∴存在等差数列{}n b ,n b n =,使得n n n n n n a C b C b C b =+++ 2211对一切自然N n ∈都成立。
