湖南师大附中教育集团2019-2020学年九年级上学期第一次联考数学试题(解析版)
2019-2020学年湖南师大附中九年级(上)第一次联考数学试卷(含解析)

2019-2020学年湖南师大附中九年级(上)第一次联考数学试卷一、选择题(本大题共12小题,共36.0分)1.下列运算正确的是()A. a 2 + a 3 = a ,B.仃)2 = q 5D. —2a 2 • a = —2a 2.C. (。
+ 3)2 = / + 9如图,AB//CD,匕£) = 30。
,ZE = 35%则匕B 的度数为()A. 60°B. 65°C. 70°D. 7S°3. 若avb,则下列式子中错误的是()A.a — 3Vb — 3B. a + 3 < b + 3 C •:q V ;3 D. —2a < —2b 4. 某小组7位同学的中考体育测试成绩(满分50分)依次为47, 50. 49. 47, 50. 48. 50.则这组 数据的众数与中位数分别是()A.50, 47B.50, 49C. 49, 50D. 50. 485. 在平面直角坐标系中,若点F (a — 3,a+l )在第二象限.则〃的取值范围为()A. -1 <a< 3B. a > 3C. a < -1D. a > -16. 已知一元二次方程2x 2+mx-7 = 0的一个根为x = l,剧另一根为()A. 1B. 2C. -3.5D. -57. 如图是“北大西洋公约组织”标志的主体部分(平面图).它是由四个完全 相同的四边形OABC 拼成的.测得AB = BC, OA = OC . OA 1 OC , ^ABC = 36。
,则匕。
4B 的度数是()A. 116°B. 117°C. 118°D. 119°8. 如图所示,已知匕1 = 3, AC = AD.增加下列条件:①砧=AE^@BC = ED. @ZLC = ZD.④匕B = 其中能使△ ABC 兰△ AED成立的条件有()A.4个B.3个C.2个D.1个9.如图,半径为3的。
2020-2021学年长沙师大滨江中学九年级上第一次联考数学试题及答案

由(1)得: AB AD ,
8分 2分
∴ DBA BDA 45 ,
∴ ABD 为直角边为 2 的等腰直角三角形,
6分
∴ BD2 2 AB2 ,即 BD 2 2 ,
∴ AD DF FC AC AB 2 ,
∴ BF BD DF 2 2 2 .
8分
22.【解析】(1)设分别购进 A 型、B 型台灯 x 盏、y 盏,根据题意,得
解之,得
65
a
68
.
∵a 为非负整数,∴a 取 66,67.
∴160 a 相应取 94,93.
答:有两种购货方案,方案一:A 型台灯购进 66 盏,B 型台灯购进 94 盏;方案二:A 型台灯购进 67 盏,
B 型台灯购进 93 盏.
8分
其中获利最大的是方案一.
9分
23.【解析】(1)∵四边形 ABCD 是平行四边形,
21.如图,已知 ABC 中,AB AC ,把 ABC 绕 A 点沿顺时针方向旋转得到 ADE ,连接 BD , CE 交于点 F. (1)求证: AEC≌ADB ; (2)若 AB 2 , BAC 45 ,当四边形 ADFC 是菱形时,求 BF 的长.
22.某商店需要购进 A 型、B 型两种节能台灯共 160 盏,其进价和售价如下表所示. (1)若商店计划销售完这批台灯后能获利 1100 元,问 A 型、B 型两种节能台灯应分别购进多少盏(注: 获利=售价-进价)? (2)若商店计划投入资金少于 4300 元,且销售完这批台灯后获利多于 1260 元,请问有哪几种进货方案? 并直接写出其中获利最大的进货方案.
题号 1
2
3
4
5
6
7
8
9
10
湖南师大附中教育集团2019-2020学年九年级上学期第一次联考数学试题(解析版)

湖南师大附中教育集团2019-2020学年度第一次九年级联考数学试题一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的. )A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间 【答案】C【解析】【分析】根据5.766 6.25,1.962 2.25<<<<,即可求出和的取值范围,+,即可得出结论.【详解】解:∵5.766 6.25,1.962 2.25<<<<∴2.4 2.5,1.4 1.5<<<∴2.4 1.4 2.5 1.5+<+<+即3.84<+3和4之间故选C . 【点睛】此题考查的是判断无理数的取值范围,根据被开方数的取值范围,求出算术平方根的取值范围是解决此题的关键.2.下列运算正确的是( )A. 428a a a =•B. 2242a a a +=C. 222()a b a b +=+D. 326(2)4a a -= 【答案】D【解析】【分析】根据同底数幂的乘法、合并同类项法则、完全平方公式、积的乘方和幂的乘方逐一判断即可.【详解】解:A . 44262a a a a +==•,故本选项错误;B . ()2222112a a a a +=+=,故本选项错误; C . 222()2a b a ab b +=++,故本选项错误;D . 322326(2)(2)4a a a ⨯-=-=,故本选项正确.故选D .【点睛】此题考查的是幂的运算性质、合并同类项和完全平方公式,掌握同底数幂的乘法、合并同类项法则、完全平方公式、积的乘方和幂的乘方是解决此题的关键.3.太阳与地球之间的平均距离约为150000000km ,用科学记数法表示这一数据为( )A. 81.510km ⨯B. 71510km ⨯C. 100.1510km ⨯D. 91.510km ⨯【答案】A【解析】【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】解:根据科学记数法的定义:150000000km =81.510km ⨯故选A .【点睛】此题考查的是科学记数法,掌握科学记数法的定义是解决此题的关键.4.2019年全国高中数学联赛,湖南师大附中入选省队人数、签约清北人数、一等奖人数均为全省第一.其中一等奖获奖人数附中及其他三所兄弟学校从高到低依次为:20,17,12,12.这组数据的中位数是( )A. 17B. 12C. 14.5D. 15.5 【答案】C【解析】【分析】根据中位数的定义:一组数据按从小到大(或从大到小)的顺序依次排列,处在中间位置的一个数或最中间两个数据的平均数,即可得出结论.【详解】解:根据中位数的定义,这组数据的中位数是(17+12)÷2=14.5故选C .【点睛】此题考查的是求一组数据的中位数,掌握中位数的定义是解决此题的关键.5.如图,//AB CD ,EF 分别为交AB ,CD 于点E ,F ,150∠=o ,则2∠的度数为( )A. 50oB. 120oC. 130oD. 150o【答案】C【解析】【分析】 根据两直线平行,同位角相等可得∠BEF=∠1=50°,然后根据平角的定义即可求出∠2的度数.【详解】解:∵//AB CD∴∠BEF=∠1=50°∴∠2=180°-∠BEF=130°故选C .【点睛】此题考查的是平行线的性质和平角的定义,掌握两直线平行,同位角相等和平角的定义是解决此题的关键.6.如图,O e 的直径AB 垂直于弦CD ,垂足为E ,22.5A ∠=︒,4OC =,CD 的长为( )A. B. 4 C. 8 D. 【答案】A【解析】【分析】根据圆心角等于同弧所对圆周角的2倍得到∠COE=45︒,由垂径定理得到CD=2CE, 90CEO ∠=︒,,用勾股定理求得CE =CD=2CE= 【详解】∵22.5A ∠=︒,∵∵COE=45︒,∵直径AB 垂直于弦CD ,∵CD=2CE, 90CEO ∠=︒,∵4OC =,∵CE=sin 4542OC ⋅︒=⨯=,∵CD=2CE=故选:A.【点睛】此题考查圆的垂径定理、圆周角定理,利用∠COE=45︒求得CE =CD=2CE=.7.如图,D ,E 分别是ABC ∆中AB ,AC 边上的点,//DE BC ,下列结论错误的( )A. AD AE AB AC =B. AD AE DB EC =C. AB AC DB EC =D. DE AE BC EC= 【答案】D【解析】【分析】根据平行线分线段成比例定理及推论逐一判断即可.【详解】解:∵//DE BC ∴AD AE AB AC=,故A 正确;AD AE DBEC =,故B 正确; AB AC DB EC=,故C 正确; DE AE AE BC AC EC=≠,故D 错误. 故选D .【点睛】此题考查的是平行线分线段成比例定理及推论,掌握根据平行线分线段成比例定理及推论判断比例式是解决此题的关键.8.若1x 、2x 是一元二次方程2750x x -+=的两根,则1211+x x 的值是( ) A. 75 B. 75- C. 57 D. 57- 【答案】A【解析】【详解】这里a=1,b=-7,c=5,由题意知,x 1x 2=5,x 1+x 2=7, 则1211+x x =121275x x x x += 故选A9.如图,菱形ABCD 中,对角线AC 、BD 交于点O ,E 为边AD 中点,菱形ABCD 的周长为28,则OE 的长等于( )A. 3.5B. 4C. 7D. 14【答案】A【解析】【分析】 根据菱形的性质和周长,即可求出AD ,然后根据直角三角形斜边上的中线等于斜边的一半即可得出结论.【详解】解:∵菱形ABCD 的周长为28,∴AD=AB=BC=CD=28÷4=7,∠AOD=90°∵E 为边AD 中点,∴在Rt △AOD 中,OE=1 3.52AD = 故选A .【点睛】此题考查的是菱形的性质和直角三角形的性质,掌握菱形的四边都相等、菱形的对角线互相垂直和直角三角形斜边上的中线等于斜边的一半是解决此题的关键.10.化简22422b a a b b a+--的结果是( ) A. 2a b -+B. 2a b --C. 2a b +D. 2a b -【答案】B【解析】【分析】先将分式化成同分母,再计算分式的减法,最后化简分式即可. 【详解】原式22422b a a b a b=--- 2242b a a b-=- (2)(2)2b a b a a b+-=- 2a b =--故选:B.【点睛】本题考查了分式的加减法运算,根据运算法则将分式转化为同分母是解题关键11.一次函数1y kx b =+与反比例函数2m y x=的图象交于(1,2)A -、(2,1)B -两点,使12y y >成立的自变量x 的取值范围是( )A. 12x -<<B. 10x -<<或2x >C. 1x <-或2x >D. 1x <-或02x << 【答案】D【解析】【分析】在同一直角坐标系中,画出两个函数的图象,根据图象找到一次函数图象在反比例函数图象上方时,x 的取值范围即可.【详解】解:在同一直角坐标系中,根据A 、B 两点坐标画出一次函数1y kx b =+与反比例函数2m y x=的图象,如下图所示由图可知:当12y y >时,1x <-或02x <<故选D .【点睛】此题考查的是一次函数和反比例函数的结合题,掌握一次函数和反比例函数图象的画法、结合图象求自变量的取值范围是解决此题的关键.12.如图,在平行四边形ABCD 中,78ABC ∠=o ,AE BC ⊥于点E ,AE 交BD 于点F ,若2DF AB =,则AFD ∠的大小是( )A. 62oB. 64oC. 66oD. 68o【答案】B【解析】【分析】 取DF 的中点G ,连接AG ,根据平行四边形的性质和平行线的性质可得∠FAD=∠AEB=90°,∠CBD=∠GDA ,然后根据直角三角形斜边上的中线等于斜边的一半可推出AB=AG=FG=DG ,根据等边对等角可得∠ABG=∠AGB ,∠GAD=∠GDA ,然后根据三角形的外角的性质和已知条件即可求出∠GDA ,然后根据直角三角形的两个锐角互余即可得出结论.【详解】解:取DF 的中点G ,连接AG ,如下图所示∵四边形ABCD 是平行四边形,AE BC ⊥∴BC ∥AD ,∠AEB=90°∴∠FAD=∠AEB=90°,∠CBD=∠GDA在Rt △FAD 中,DF=2AG=2FG=2GD∵2DF AB =∴AB=AG=FG=DG∴∠ABG=∠AGB ,∠GAD=∠GDA∴∠ABG=∠AGB=∠GAD +∠GDA=2∠GDA=2∠CBD∴∠ABC=∠ABG +∠CBD=3∠CBD=78°∴∠CBD=26°∴∠GDA=26°在Rt △AFD 中,∠AFD=90°-∠GDA=64°故选B .【点睛】此题考查的是平行四边形的性质、平行线的性质、直角三角形的性质和等腰三角形的性质,掌握平行四边形的性质、平行线的性质、直角三角形斜边上的中线等于斜边的一半和等边对等角是解决此题的关键.二、填空题(本大题共6个小题,每题3分,满分18分,将答案填在答题纸上) 13.因式分解:2818a b b -=__________.【答案】2(23)(23)b a a -+【解析】【分析】先提取公因式,然后利用平方差公式因式分解即可【详解】解:2818a b b -=()2249b a -=2(23)(23)b a a -+故答案为:2(23)(23)b a a -+.【点睛】此题考查的是因式分解,掌握用提公因式法和平方差公式因式分解是解决此题的关键. 14.从大小形状完全相同标有1、2、3数字的三张卡片中随机抽取两张,和为偶数的概率为____. 【答案】13【解析】试题解析:画出树状图得:∵和为偶数的情况有两种,所有可能的情况有6种,∴P (和为偶数)=21=63.15.圆心角为120o 的扇形的半径为3,则这个扇形的面积为__________.【答案】3π【解析】【分析】根据扇形的面积公式:S 扇形=2360n r π计算即可. 【详解】解:这个扇形的面积为212033360ππ••= 故答案为:3π.【点睛】此题考查的是求扇形的面积,掌握扇形的面积公式S 扇形=2360n r π是解决此题的关键. 16.如图,AB 为圆O 的直径,C ,D 是圆O 上两点,若50ABC ∠=o ,则D ∠的度数为__________.【答案】40o【解析】【分析】根据直径所对的圆周角为直角,可得∠ACB=90°,然后根据直角三角形的两个锐角互余即可求出∠CAB ,最后根据同弧所对的圆周角相等即可求出∠D .【详解】解:∵AB 为圆O 的直径,50ABC ∠=o∴∠ACB=90°∴∠CAB=90°-∠ABC=40°∴∠D=∠CAB=40°故答案为:40°.【点睛】此题考查的是圆周角定理的推论和直角三角形的性质,掌握直径所对的圆周角为直角、同弧所对的圆周角相等和直角三角形的两个锐角互余是解决此题的关键.17.计算:22244(4)2x x x x x+--÷+= . 【答案】x -2【解析】试题解析:原式=244(2)(2)(2)x x x x x x x +-+⨯+-=2(2)(2)(2)(2)x x x x x x -+⨯+- =x-2.考点:分式的混合运算.18.已知关于x 的一元二次方程2(1)40ax a x -+-=的两根分别为1x ,2x ,且110x -<<,223x <<,则实数a 的取值范围是__________. 【答案】332a << 【解析】【分析】设2(1)4y ax a x =-+-,根据一元二次方程的解和二次函数图象与x 轴交点的关系,并求出二次函数的图象与y 轴的交点坐标,即可画出二次函数的大致图象,然后根据图象分别找到当x=-1、x=2、x=3时,y 的取值范围代入即可求出a 的取值范围.【详解】解:设2(1)4y ax a x =-+-∵关于x 的一元二次方程2(1)40ax a x -+-=的两根分别为1x ,2x , ∴二次函数2(1)4y ax a x =-+-的图象与x 轴的两个交点的横坐标为1x ,2x ,将x=0代入二次函数解析式中,解得y=-4∴二次函数的图象与y 轴交于(0,-4)∵110x -<<,223x <<,∴该二次函数的图象大致为如下图所示,由图可知:a >0,当x=-1时,y >0,即()()211(1)40y a a =---+->,解得:32a >; 当x=2时,y <0,即222(1)40y a a =-+-<,解得:3a <当x=3时,y >0,即233(1)40y a a =-+->,解得:76a >∴实数a 的取值范围是332a << 故答案为:332a <<. 【点睛】此题考查的是一元二次方程的解和二次函数图象与x 轴交点的关系,掌握把一元二次方程的问题转化成二次函数的问题是解决此题的关键.三、解答题:本大题共8个小题,第19、20题每小题6分,第21、22题每小题8分,第23、24题每小题9分,第25、26题每小题10分,共66分.解答应写出文字说明、证明过程或演算步骤.19.201(()(12-⨯--【答案】-7【解析】【分析】根据二次根式的性质、负指数幂的性质和零指数幂的性质计算即可.【详解】解:原式2(2)41=+-⨯- 281=--7=-【点睛】此题考查的是实数的混合运算,掌握二次根式的性质、负指数幂的性质和零指数幂的性质是解决此题的关键.20.解不等式组2723222334x x x x x --⎧≤⎪⎪⎨--⎪<-+⎪⎩. 【答案】24x <≤【解析】【分析】根据不等式的基本性质分别解出不等式①和②,然后取公共解集即可.【详解】解:2723222334x x x x x --⎧≤⎪⎪⎨--⎪<-+⎪⎩①② 解不等式①,得4x ≤解不等式②,得2x >∴不等式组的解集为24x <≤【点睛】此题考查的是解不等式组,掌握不等式组的解法和公共解集的取法是解决此题的关键. 21.为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A 级:优秀;B 级:良好;C 级:及格;D 级:不及格),并将测试结果绘制成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)本次抽样测试的学生人数是 人;(2)图1中α∠的度数是 ,并把图2条形统计图补充完整;(3)该县九年级有学生4500名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 . (4)老师想从4位同学(分别记为E 、F 、G 、H ,其中E 为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.【答案】(1)40;(2)162o ,图详见解析;(3)450;(4)12. 【解析】【分析】(1)根据B 级的人数和所占抽样总人数的百分率,即可求出抽样总人数;(2)先用抽样总人数减去A 级、B 级、D 级人数即可得到C 级的人数,用C 级人数除以抽样总人数乘360°即可得出α∠的度数,然后补全条形统计图即可.(3)根据D 级的人数和抽样总人数求出不及格率,再乘九年级总人数即可;(4)根据题意画出树形图,然后根据树形图求概率即可.【详解】解:(1)本次抽样测试的学生人数是12÷30%=40人故答案为:40.(2)C 级人数为40-6-12-4=18人∴α∠=1836016240⨯︒=︒ 故答案为:162o条形统计图如下图所示:(3)不及格率为:4÷40×100%=10%∴不及格的人数为4500×10%=450人故答案为:450(4)根据题意画树形图如下:共有12种等可能的结果,其中选中小明的有6种,则P (选中小明)61122==. 【点睛】此题考查的是条形统计图、扇形统计图和求概率问题,掌握结合条形统计图和扇形统计图得出有用信息和画树状图求概率是解决此题的关键.22.如图,AD 是圆O 的弦,AB 经过圆心O ,交圆O 于点C ,30DAB B ∠=∠=o .(1)求证:直线BD 与圆O 相切.(2)连接CD ,若5CD =,求AB 的长.【答案】(1)详见解析;(2)15【解析】【分析】(1)连接OD ,根据等边对等角可得30ODA DAB B ∠=∠=∠=o ,然后根据三角形的内角和定理即可求出∠ODB ,最后根据切线的判定定理即可得;(2)先证出DOC ∆是等边三角形,即可求出OA=OD=CD=5,然后根据30°所对的直角边是斜边的一半即可求出OB ,从而求出AB .【详解】解:(1)连接OD∵OA=OD ,30DAB B ∠=∠=o∴30ODA DAB B ∠=∠=∠=o∴18018030303090ODB ODA DAB B ∠=-∠-∠-∠=---=o o o o o o∴直线BD 与圆O 相切(2)由(1)知,30ODA DAB ∠=∠=o∴60DOB ODA DAB ∠=∠+∠=o又∵OC OD =∴DOC ∆是等边三角形∴5OA OD CD ===又∵30B ∠=o ,90ODB ∠=o∴210OB OD ==∴51015AB OA OB =+=+=【点睛】此题考查的是切线的判定、等腰三角形的性质、等边三角形的判定及性质和直角三角形的性质,掌握切线的判定定理、等边对等角、等边三角形的判定及性质和30°所对的直角边是斜边的一半是解决此题的关键.23.某商店计划购进一批A 、B 两种型号的计算器,若购进A 型计算器10只和B 型计算器8只,共需要资金880元;若购进A 型计算器2只和B 型计算器5只,共需要资金380元.(1)求A 、B 两种型号的计算器每只进价各是多少元?(2)该商店计划购进这两种型号计算器共50只.根据市场行情,销售一只A 型计算器可获利9元,销售一只B 型计算器可获利18元.该商店希望销售完这50只计算器,所获利润不少于购进总成本的25%.则该商店至少要采购B 型计算器多少只?【答案】(1)A 种型号的计算器每只进价40元,B 种型号的计算器每只进价为60元;(2)该经销商至少要采购B 型计算器13只.【解析】【分析】(1)设A 种型号的计算器每只进价x 元,B 种型号的计算器每只进价为y 元,根据题意,列出二元一次方程组,并解方程组即可;(2)设该经销商要采购B 型计算器m 只,根据“所获利润不少于购进总成本的25%”列不等式,并解不的【详解】解:(1)设A 种型号的计算器每只进价x 元,B 种型号的计算器每只进价为y 元,根据题意,得 10888025380x y x y +=⎧⎨+=⎩ 解得:4060x y =⎧⎨=⎩答:A 种型号计算器每只进价40元,B 种型号的计算器每只进价为60元.(2)设该经销商要采购B 型计算器m 只,根据题意,得189(50)[6040(50)]25%m m m m +-≥+-•解之,得12.5m ≥所以,该经销商至少要采购B 型计算器13只答:该经销商至少要采购B 型计算器13只.【点睛】此题考查的是二元一次方程组的应用和一元一次不等式的应用,掌握实际问题中的等量关系和不等关系是解决此题的关键.24.如图,四边形ABCD 中,AB AD =,60BAD ∠=o ,30BCD ∠=o ,将AC 绕着点A 顺时针旋转60o 得AE ,连接BE ,CE .(1)求证:ADC ∆≌ABE ∆;(2)求证:222AC DC BC =+; (3)若2AB =,点Q 在四边形ABCD 内部运动,且满足222AQ BQ DQ =+,求点Q 运动路径的长度.【答案】(1)详见解析;(2)详见解析;(3)23π. 【解析】的(1)根据等式的基本性质可得DAC BAE ∠=∠,然后利用SAS 即可证出ADC ∆≌ABE ∆;(2)根据四边形的内角和和全等三角形的性质可得270ABC ABE ∠+∠=o ,从而求出∠CBE=90°,根据勾股定理可得222CE BE BC =+,根据等边三角形的判定及性质可得CE AE AC ==,从而证出结论; (3)如图,设Q 为满足条件的点,将AQ 绕着点A 顺时针旋转60度得AF ,连接QF ,BF , QB ,DQ ,AF , DB ,先利用SAS 证出ADQ ∆≌ABF ∆,从而得出BF DQ =,∠AQD=∠AFB ,然后证出AFQ ∆为等边三角形,△ADB 为等边三角形,从而得出AQ FQ =, DB=AB=2,然后根据勾股定理的逆定理可得90FBQ ∠=o,根据四点共圆证出点Q 的路径为过B 、D 、C 三点的圆上»BD ,求出圆心角和半径即可求出点Q 运动路径的长度.【详解】证明:(1)∵60CAE DAB ∠=∠=o∴DAB CAB CAE CAB ∠-∠=∠-∠∴DAC BAE ∠=∠在ADC ∆和ABE ∆中AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴ADC ∆≌ABE ∆(2)在四边形ABCD 中360270ADC ABC DAB DCB ∠+∠=-∠-∠=o o∵ADC ∆≌ABE ∆∴ADC ABE ∠=∠,CD BE =∴270ABC ABE ABC ADC ∠+∠=∠+∠=o∴360()90CBE ABE ABC ∠=-∠+∠=o o∴222CE BE BC =+又∵AC AE =,60CAE ∠=o∴△AEC 为等边三角形∴CE AE AC ==∴222AC DC BC =+(3)如图,设Q 为满足条件的点,将AQ 绕着点A 顺时针旋转60度得AF ,连接QF ,BF , QB ,DQ ,AF , DB .∵60QAF DAB ∠=∠=o∴DAB QAB QAF QAB ∠-∠=∠-∠∴DAQ BAF ∠=∠在ADQ ∆和ABF ∆中 AD AB DAQ BAF AQ AF =⎧⎪∠=∠⎨⎪=⎩∴ADQ ∆≌ABF ∆∴BF DQ =,∠AQD=∠AFB ,∵60QAF ∠=o ,AQ=AF ,∠DAB=60°,AD=AB∴AFQ ∆为等边三角形,△ADB 为等边三角形∴AQ FQ =, DB=AB=2∵222AQ BQ DQ =+∴222FQ BQ BF =+∴90FBQ ∠=o∴()360DQB AQD AQB ∠=-∠+∠o()()360360360150AFB AQB QAF FBQ =-∠+∠⎡⎤=--∠+∠⎣⎦=o o o o∵∠BCD=30°∴∠DQB +∠BCD=180°∴点Q 的路径为过B 、D 、C 三点的圆上»BD设圆心为O ,连接OD 、OB则260BOD BCD ∠=∠=o ,∴△OBD 为等边三角形∴2DO DB ==,∴点Q 的运动的路径长为:60221803ππ⨯=. 【点睛】此题考查的是全等三角形的判定及性质、等边三角形的判定及性质、勾股定理及逆定理、四点共圆和求点的运动路径长度,掌握构造全等三角形的方法、全等三角形的判定定理、等边三角形的判定及性质、勾股定理及逆定理、利用四点共圆判定点的运动路径及弧长公式是解决此题的关键.25.四边形的一条对角线将这个四边形分成两个三角形,如果这两个三角形相似(不全等),那么我们将这条对角线叫做这个四边形的相似对角线.(1)如图1,四边形ABCD 中,100DAB ∠=o ,130DCB ∠=o ,对角线AC 平分DAB ∠,求证:AC 是四边形ABCD 的相似对角线;(2)如图2,直线33y x =-+分别与x ,y 轴相交于A ,B 两点,P 为反比例函数k y x=(k 0<)上的点,若AO 是四边形ABOP 的相似对角线,求反比例函数的解析式;(3)如图3,AC 是四边形ABCD 的相似对角线,点C 的坐标为(3,1),//AC x 轴,30BCA DCA ∠=∠=o ,连接BD ,BCD ∆A ,C 两点的抛物线2y ax bx c =++(0a <)与x 轴交于E ,F 两点,记1m AC =+,若直线y mx =与抛物线恰好有3个交点,求实数a 的值.【答案】(1)详见解析;(2)y x =或y x -=y x-=;(3)12a =-或92a =- 【解析】【分析】 (1)设ACD α∠=,则130ACB α∠=-o ,然后根据角平分线的性质可求得∠BAC=∠DAC=50°,根据三角形的内角和定理可得B α∠=,最后根据相似三角形的判定定理可证AC 是四边形ABCD 的相似对角线;(2)根据一次函数即可求出点A 、B 的坐标,再根据锐角三角函数值即可求出30OAB ∠=o ,60OBA ∠=o ,然后根据相似对角线的定义和相似三角形对应角的情况分类讨论,分别利用锐角三角函数求出点P 的坐标,即可求出反比例函数的解析式;(3)根据锐角三角函数和面积公式可得4CD BC •=,然后根据相似对角线的定义即可求出AC ,从而求出两个m 的值和两条直线的解析式3y x =-和3y x =,根据图形可知3y x =-,一定与抛物线有两个交点,故3y x =与抛物线有且仅有一个交点,然后联立方程令一元二次方程的△=0即可求出a 的值.【详解】(1)证明:如图1,设ACD α∠=,则130ACB α∠=-o∵100DAB ∠=o ,AC 平分DAB ∠∴∠BAC=∠DAC=1502DAB ∠=o ∴18018050(130)B BAC ACB αα∠=-∠-∠=---=o o o o在ABC ∆和ACD ∆中∵B ACD ∠=∠,BAC CAD ∠=∠∴ABC ∆∽ACD ∆∴AC 是四边形ABCD 的相似对角线.(2)如图2,可求得直线33y x =-+与两坐标轴交点分别为(4,0)A ,(0,)3B ∴OA=4,在Rt △AOB中,tan OB OAB OA ∠== ∴30OAB ∠=o ,60OBA ∠=o当OA 是四边形OBAP 的相似对角线时,有如下情况:①当∠APO=∠AOB=90°时,过点P 作PQ ⊥x 轴于Q ,如下图所示,此时又分以下两种情况的(i )当60AOP ABO ∠=∠=o ,Rt △OAP 中,OP=OA ·cos ∠AOP=2在Rt △OPQ 中,OQ=OP ·cos ∠AOP=1,PQ= OP ·sin ∠∴此时点(1,P ,将P 点坐标代入k y x=,得k =∴该反比例函数的解析式为y =; (ii )30BAO AOP ∠=∠=o ,在Rt △OAP 中,OP=OA ·cos ∠在Rt △OPQ 中,OQ=OP ·cos ∠AOP=3,PQ= OP ·sin ∠∴此时点(3,P ,将P 点坐标代入k y x=,得k =-∴该反比例函数的解析式为y x-= ②当∠OAP=∠AOB=90°时,此时又分以下两种情况(i )当∠AOP=∠OAB=30°时,如下图所示,∵OA=AO ,∠OAP=∠AOB=90°∴△OAP ≌AOB ,不符合相似对角线的定义,故舍去;(ii )当60AOP ABO ∠=∠=o 时,如下图所示,在Rt △OAP 中,AP=OA ·tan ∠AOP=∴此时点(4,P -,将P 点坐标代入k y x=,得k =-该反比例函数的解析式为y =; ③当∠AOP=∠AOB=90°时,此时点P 在y 轴上,故不存在反比例函数图象,故舍去.综上所述:反比例函数的解析式为y =y =y =. (3)如图3,作BCD ∆的底边CD 边上的高BH ,则30CBH ∠=o , ∴12CH BC =在Rt CHB ∆中,由勾股定理可求得BH BC =,∵12BCD S CD BC ∆=BC •=∴4CD BC •=∵AC 是四边形ABCD 的相似对角线若BCA ∆∽DCA ∆,由CA=CA 可得BCA ∆≌DCA ∆,不符合相似对角线的定义,故舍去,∴BCA ∆∽ACD ∆, ∴BC AC AC DC=, ∴2AC CD BC =•∴24AC =,即2AC =由点C 的坐标为(3,1)可知,点A 的坐标为(1,1),将A ,C 两点的坐标代入抛物线2(0)y ax bx c a =++<,得1931a b c a b c ++=⎧⎨++=⎩解得4b a =-,31c a =+,所以抛物线的解析式可化为2431y ax ax a =-++ 由1m AC =+,得直线y mx =的解析为3y x =,3y x =-,∵直线3y x =-与抛物线2431y ax ax a =-++(0)a <的交点必有两个∴直线3y x =与该抛物线的交点有且只有一个∴方程组23431y x y ax ax a =⎧⎨=-++⎩有且只有一组解 即关于x 的一元二次方程2(43)310ax a x a -+++=有两个相等的实数根.∴2(43)4(31)0a a a ∆=+-+=, 解得12a =-或92a =-【点睛】此题考查的是新定义问题、新定义与反比例函数、新定义与二次函数的综合大题,此题难度较大,涉及知识点较多,掌握相似三角形的性质、利用待定系数法求反比例函数解析式、二次函数与一次函数交点个数与一元二次方程根的判别式的关系和分类讨论的数学思想是解决此题的关键.26.如图,已知二次函数2y ax bx c =++(0a ≠)的图象与x 轴交于点A 和点(2,0)B -,与交y 轴于点(0,4)C ,0()f x 表示当自变量为0x 时的函数值,对于任意实数m ,均有(1)(3)f m f m -=-. (1)求该二次函数的解析式;(2)点Q 是线段AB 上的动点,过点Q 作//QE AC ,交BC 于点E ,连接CQ .当CQE ∆的面积最大时,求点Q 的坐标;(3)若平行于x 轴的动直线l 与该抛物线交于点P ,与直线AC 交于点F ,点D 的坐标为(2,0).是否存在这样的直线l ,使得ODF ∆是等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)2142y x x =-++;(2)(1,0)Q ;(3)存在,点P 的坐标为:(1+或(1-或(1+或(1【解析】【分析】 (1)根据题意即可求出抛物线的对称轴,然后利用抛物线的对称性即可求出点A 的坐标,设二次函数的解析式为(2)(4)y a x x =+-,将点C 的坐标代入即可求出二次函数的解析式,化为一般式即可;(2)设点Q 的坐标为(,0)m ,过点E 作EG x ⊥轴于点G ,根据点A 、B 、C 的坐标即可求出OA 、OB 、OC 、BQ 和AB ,根据相似三角形的判定及性质,即可用含m 的式子表示EG ,然后根据CQE CBQ EBQ S S S ∆∆∆=-即可求出CQE S ∆与m 的二次函数关系式,根据二次函数求最值即可;(3)根据等腰三角形腰的情况分类讨论,分别在每种情况下求出点F 的坐标,然后根据点P 和点F 的纵坐标相等,将点P 的纵坐标代入二次函数解析式中即可求出点P 的横坐标.【详解】解:(1)当1x m =-与3x m =-时函数值相等,可知抛物线的对称轴为1312m m x -+-==, 由点B 的坐标(2,0)-可求得A 点的坐标为(4,0)设二次函数的解析式为(2)(4)y a x x =+-将点(0,4)C 代入,得12a =- 所以,二次函数解析式为2142y x x =-++. (2)设点Q 的坐标为(,0)m ,过点E 作EG x ⊥轴于点G ,如图∵A (4,0),(2,0)B -, (0,4)C ,∴OA=4,OB=2,OC=4, BQ=m+2∴AB=6∵//QE AC ∴BE BQ BC BA = ∵//EG OC ∴BE EG BC CO= ∴EG BQ CO BA =,即246EG m +=, ∴243m EG += ∴CQE CBQ EBQ S S S ∆∆∆=-1122BQ CO BQ EG =•-• ()12BQ CO EG =•- 124(2)(4)23m m +=+- 21(1)33m =--+ 又∵24m -≤≤ 的∴当1m =时,CQE S ∆有最大值3,此时(1,0)Q(3)存在.①若DO DF =,如下图所示则2AD OD DF ===,∴∠DOF=∠DFO ,∠DAF=∠DFA∴∠DOF+∠DAF=∠DFO+∠DFA=∠OFA∴AFO ∆是直角三角形,OF ⊥AC∵OA=OC=4∴点F 为AC 的中点∴根据中点坐标公式:点F 的坐标为4004,(2,2)22++⎛⎫=⎪⎝⎭∵直线l ∥x 轴 ∴点P 的纵坐标=点F 的纵坐标=2,将y=2代入二次函数解析式中,得21422x x -++=,得11x =+21x =此时点P 的坐标为:(12)P +或(12)P -②若FO FD =,过点F 作FM x ⊥轴于点M由等腰三角形的性质得:112OM OD ==, ∴3AM =, 在等腰直角三角形AOC 中,∠OAC=45°∴△AMF 也是等腰直角三角形∴FM=AM=3∴(1,3)F∵直线l ∥x 轴∴点P 的纵坐标=点F 的纵坐标=3,将y=3代入二次函数解析式中,得由21432x x -++=,得11x =,21x =此时,点P 的坐标为:(1P +或(1P③若OD OF =,∵4OA OC ==,且90AOC ∠=o∴AC =∴点O 到AC 的距离为而2OF OD ==<∴AC 上不存在点F 使得2OD OF ==此时,不存在这样的直线l ,使得ODF ∆是等腰三角形综上,存在这样的直线l ,使得ODF ∆是等腰三角形,所求点P 的坐标为:(1+或(1-或(1或(1【点睛】此题考查的是二次函数与几何图形的综合大题,难度系数较大,掌握利用待定系数法求二次函数解析式、把面积最值问题转化为二次函数最值问题和分类讨论的数学思想是解决此题的关键.。
湖南省师大附中2019-2020学年上学期初中九年级第一次联考数学试卷

湖南省师大附中2019-2020学年上学期初中九年级第一次联考数学试卷 注意事项:1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;3.答题时,请考生注意各大题题号后面的答题提示;4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;5.答题卡不得使用涂改液、涂改胶和贴纸;6.本学科试卷共26个小题,考试时量120分钟,满分120分。
一、选择题(本大题共12个小题,每小题3分,共36分。
在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项。
)1A .1和2之间B .2和3之间C .3和4之间D .4和5之间2.下列运算正确的是A .428a a a ⋅=B .2242a a a +=C .()222a b a b +=+D .()23624a a -= 3.太阳与地球之间的平均距离纸业150000000km ,用科学记数法表示这一数据为A .81.510km ⨯B .71510km ⨯C .91.510km ⨯D .100.1510km ⨯4.2019年全国高中数学联赛,湖南师大附中入选省队人数、签约清北人数、一等奖人数均为全省第一,其中一等奖获奖人数附中及其他三所兄弟学校从高到低依次为:20,17,12,12。
这组数据的中位数是A .17B .12C .14.5D .15.55.如图,//AB CD ,EF 分别为交AB ,CD 于点E ,F ,50∠=︒,则2∠的度数为A .50°B .120°C .130°D .150°6.如图,O e 的直径AB 垂直于弦CD ,垂足为E ,22.5,4A OC ∠=︒=的长为A. B .4 C. D .87.如图,D ,E 分别是ABC ∆中AB ,AC 边上的点,//DE BC ,下列结论错误的是A .AD AE AB AC= B .AD AE DB EC =C .AB AC DB EC =D .DE AE BC EC= 8.12,x x 是一元二次方程2750x x -+=的两根,则实数1211x x +的值为 A .75- B .75 C .57- D .579.如图,菱形ABCD 中,对角线AC 、BD 交于点O ,E 为边AD 中点,菱形ABCD 的周长为28,则OE 的长等于A .3.5B .4C .7D .1410.化简22422b a a b b a+--的结果是 A .2a b -- B .2b a - C .2a b - D .2b a +11.一次函数1y kx b =+与反比例函数2m y x=的图象交于()()1,2,2,1A B --两点,使12y y >成立的自变量x 的取值范围是A .12x -<<B .10x -<<或2x >C .1x <-或2x >D .1x <-或02x << 12.如图,在平行四边形ABCD 中,78,ABC AE BC ∠=︒⊥于点E ,AE 交BD 于点F ,若2DF AB =,则AFD ∠的大小是A .62°B .64°C .66°D .68°二、填空题(本大题共6个小题,每小题3分,共18分)13.因式分解:2818a b b -=________。
湖南师大附中教育集团2019-2020学年度上学期九年级第一次联考(期中考试)数学试卷及答案

、 ( $ 9 7 12 9 , 9 3 ,7 36 .Z f 9 A & , / 9 e A ,; Z 8 9 [ & G | 9 e A .)
1.槡6+槡20 1 2 3
A.1 4 2 5 6
ቤተ መጻሕፍቲ ባይዱB.2 4 3 5 6
(1)ð u ¾ ñ Ý Þ 0 * Ú b L > b ; (2)y1W∠α 0L> ,åßy2òëÍyóô³ê; (3)õØÙS- · * Ú 4500 +,x T Û ö ÷ P u W Ï Ð Ñ J Ò Ý Þ,
A.2槡2
B.4
C.4槡2
D.8
7.xy,犇,犈 z{>△犃犅犆 W犃犅,犃犆 0~,犇犈∥犅犆,890
>
A.犃犃犅犇=犃犃犆犈
B.犇犃犅犇=犈犃犆犈
C.犇犃犅犅=犈犃犆犆
D.犅犇犆犈=犈犃犆犈
. 1 6(786)
8.狓1 ,狓2
>
Q
u
狓2
-7狓+5=0
0
,
L1 狓1
+狓12
C.2犪-犫
D.犫+2犪
11.QuL 狔1 =犽狓+犫 7
L
狔2
=
犿 狓
0
y
¡
|
}
犃
(-1,2)、
犅(2,-1)~,¢狔1>狔2 £¤0¥¦§ 狓 0¨©ª>
A.-1<狓<2
B.-1<狓<0 « 狓>2
C.狓< -1 « 狓>2
D.狓< -1 « 0<狓<2
12.x y,3 C ¬ 犃犅犆犇 W,∠犃犅犆 = 78°,
2020-2021长沙市湖南师大附中九年级数学上期末一模试卷含答案

本题主要考查直角三角形的性质以及相似三角形的性质,解题的关键是清楚直角三角形斜边上的中线是斜边的一半以及会运用相似三角形线段成比例求出各边长的长.
12.C
解析:C
【解析】
正五边形绕着它的中心旋转后与它本身重合,最小的旋转角度数是 =72度,
故选C.
二、填空题
13.③④【解析】【分析】①首先根据抛物线开口向上可得a>0;然后根据对称轴为x=﹣>0可得b<0据此判断即可②根据抛物线y=ax2+bx+c的图象可得x=﹣1时y>0即a﹣b+c>0据此判断即可③首先判
【详解】
∵P是CH的中点,PH=PC,∵AH=AH,AG=AD,且AGH与ADH都是直角,∴△AGH≌△ADH,∴∠GHA=∠AHD,又∵GHA=HAP,∴∠AHD=∠HAP,∴△AHP是等腰三角形,∴PH=PA=PC,∴∠HAC是直角,在Rt△ABC中,AC= =10,∵△HAC∽△ADC,∴ = ,∴AH= = =7.5,又∵△HAC∽△HAD, = ,∴DH=4.5,∴HP= =6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.
10.C
解析:C
【解析】
【分析】
连接OD,根据勾股定理求出CD,根据直角三角形的性质求出∠AOD,根据扇形面积公式、三角形面积公式计算,得到答案.
【详解】
解:连接OD,
在Rt△OCD中,OC= OD=2,
∴∠ODC=30°,CD=
∴∠COD=60°,
∴阴影部分的面积= ,
故选:C.
【点睛】
本题考查的是扇形面积计算、勾股定理,掌握扇形面积公式是解题的关键.
【点睛】
本题考查了概率的求法,能根据题意列出树状图或列表是解题关键.
2019-2020学年湖南师大附中博才实验中学九年级(上)第一次月考数学试卷 (含解析)
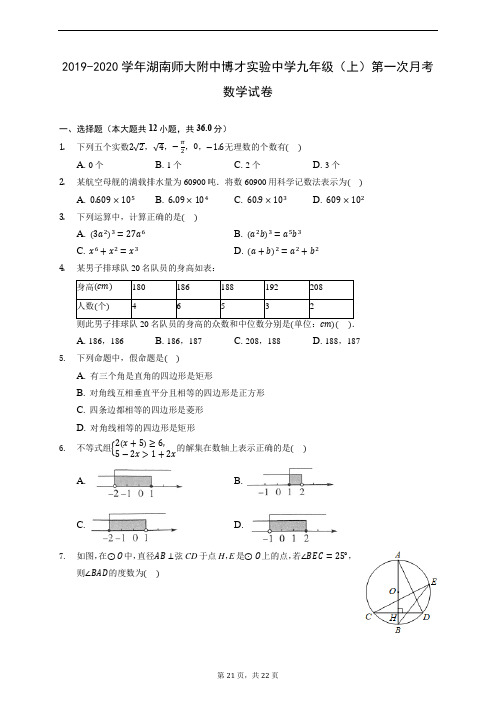
2019-2020学年湖南师大附中博才实验中学九年级(上)第一次月考数学试卷一、选择题(本大题共12小题,共36.0分)1. 下列五个实数2√2,√4,−π2,0,−1.6无理数的个数有( ) A. 0个B. 1个C. 2个D. 3个 2. 某航空母舰的满载排水量为60900吨.将数60900用科学记数法表示为( ) A. 0.609×105B. 6.09×104C. 60.9×103D. 609×102 3. 下列运算中,计算正确的是( ) A. (3a 2)3=27a 6B. (a 2b)3=a 5b 3C. x 6+x 2=x 3D. (a +b)2=a 2+b 24. 某男子排球队20名队员的身高如表: 身高(cm) 180 186188 192 208 人数(个) 46 5 3 2A. 186,186B. 186,187C. 208,188D. 188,1875. 下列命题中,假命题是( )A. 有三个角是直角的四边形是矩形B. 对角线互相垂直平分且相等的四边形是正方形C. 四条边都相等的四边形是菱形D. 对角线相等的四边形是矩形6. 不等式组{2(x +5)≥6,5−2x >1+2x的解集在数轴上表示正确的是( ) A. B.C. D.7. 如图,在⊙O 中,直径AB ⊥弦CD 于点H ,E 是⊙O 上的点,若∠BEC =25°,则∠BAD 的度数为( )A. 65°B. 50°C. 25°D. 12.5°8.如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为ℎ1、ℎ2、ℎ3.若ℎ1=2,ℎ2=1,则正方形ABCD的面积为()A. 9B. 10C. 13D. 259.若实数a,b满足:a+b=0且a<b,则函数y=bx+a的图象可能是()A. B.C. D.10.如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是()A. 50°B. 60°C. 70°D.80°11.某种商品的进价为每件180元,按标价的九折销售时,利润率为20%,这种商品每件的标价为()元.A. 200B. 240C. 245D. 25512.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②4a+2b+c<0;③a−b+c>0;④(a+c)2<b2.其中正确的结论是()A. ①②B. ①③C. ①③④D.①②③④二、填空题(本大题共6小题,共18.0分)13.当x=______时,二次根式√x+3的值为0.14. 若a−b b =34,则ab =______. 15. 如图,DE//AB ,若∠A =50°,则∠ACD = ______ .16. 如图,在⊙O 中,OC ⊥弦AB 于点C ,AB =4,OC =1,则OB 的长是______.17. 若|a +3|+√b −2+(m −7)2=0,则(a +b)m 的值为______ .18. 如图,边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1,边B 1C 1与CD 交于点O ,则四边形AB 1OD 的周长是______ .三、计算题(本大题共1小题,共6.0分)19. (6−π)0+(−15)−1−3√13+|−√3|四、解答题(本大题共7小题,共60.0分)20. 先化简,再求值:(1−1x−1)÷x 2−4x 2−2x+1,其中x =5.21.某校开展“阳光体育”活动,决定开设乒乓球、篮球、跑步、跳绳这四种运动项目,学生只能选择其中一种,为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成两张不完整的统计图,请你结合图中的信息解答下列问题:(1)样本中喜欢篮球项目的人数百分比是______;其所在扇形统计图中的圆心角的度数是______;(2)把条形统计图补画完整并注明人数;(3)已知该校有1000名学生,根据样本估计全校喜欢乒乓球的人数是多少?22.如图,已知在⊙O中,AB,CD两弦互相垂直,E为垂足,AB被分成4cm和10cm两段.(1)求圆心O到CD的距离;(2)若⊙O的半径为8cm,求CD的长.23.我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为x元/件(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.(1)求y与x的函数关系式(不要求写出自变量的取值范围);(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)若每件文具的利润不超过80%,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.24.已知:如图,正方形ABCD,对角线AC、BD相交于O,Q为线段DB上的一点,∠MQN=90°,点M、N分别在直线BC、DC上,(1)如图1,当Q为线段OD的中点时,求证:DN+13BM=12BC;(2)如图2,当Q为线段OB的中点,点N在CD的延长线上时,探索:线段DN、BM、BC的数量关系为_______________________ ;(3)在(2)的条件下,连接MN,交AD、BD于点E、F,若MB:MC=3:1,NQ=9√5,求EF的长.25.对于某一函数给出如下定义:若存在实数m,当其自变量的值为m时,其函数值等于−m,则称−m为这个函数的反向值.在函数存在反向值时,该函数的最大反向值与最小反向值之差n 称为这个函数的反向距离.特别地,当函数只有一个反向值时,其反向距离n为零.例如,图中的函数有4,−1两个反向值,其反向距离n等于5.(1)分别判断函数y=−x+1,y=−1,y=x2有没有反向值?如果有,直接写出其反向距离;x(2)对于函数y=x2−4b2x,①若其反向距离为零,求b的值;②若−1≤b≤3,求其反向距离n的取值范围;26.如图,已知抛物线y=ax2+bx+3经过点A(−1,0)、B(3,0)两点,且交y轴交于点C.(1)求抛物线的解析式;(2)点M是线段BC上的点(不与B、C重合),过M作MN//y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.-------- 答案与解析 --------1.答案:C解析:解:五个实数2√2,√4,−π2,0,−1.6中,无理数的有2√2,−π2这2个.故选:C.无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.答案:B解析:解:将数60900用科学记数法表示为6.09×104.故选:B.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n的值.3.答案:A解析:解:A、(3a2)3=27a6,故A正确;B、(a2b)3=a6b3,故B错误;C、x6与x2不是同类项,不能合并,故C错误;D、(a+b)2=a2+2ab+b2,故D错误;故选:A.根据积的乘方和幂的乘方、合并同类项的法则、完全平方公式进行计算即可.本题考查了积的乘方和幂的乘方,合并同类项,完全平方公式,掌握运算法则是解题的关键.4.答案:B解析:【分析】本题考查了众数与中位数的定义.众数是一组数据中出现次数最多的数据,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.根据众数是一组数据中出现次数最多的数据,找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或最中间两个数的平均数)为中位数可得答案.【解答】解:在这一组数据中身高为186cm的有6人,最多,故众数是186cm;排序后处于中间位置的两个数是186cm、188cm,那么由中位数的定义可知,这组数据的中位数是187cm;故选B.5.答案:D解析:【分析】此题主要考查了矩形、菱形、正方形的判定以及命题的概念等知识,熟练掌握相关定理是解题关键.根据矩形、菱形、正方形的判定、性质得出答案即可.【解答】解:A.有三个角是直角的四边形是矩形,故此命题是真命题,故此选项错误;B.根据对角线互相垂直、互相平分且相等的四边形是正方形,故此命题是真命题,故此选项错误;C.四条边都相等的四边形是菱形,故此命题是真命题,故此选项错误;D.对角线相等的四边形是矩形,也可能是等腰梯形,故此命题是假命题,故此选项正确.故选D.6.答案:C解析:【分析】本题考查了解一元一次不等式组,并在数轴上表示不等式组的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.求不等式组的解集应遵循“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则.先分别求出各不等式的解集,再求其公共解集即可.【解答】解:令{2(x +5)≥6①5−2x >1+2x②, 解不等式①得:x ≥−2,解不等式②得:x <1,则不等式组的解集为:−2≤x <1,在数轴上表示为C 选项,故选C .7.答案:C解析:【分析】本题考查了圆周角定理及垂径定理的知识,解题的关键是构造辅助线得到等弧所对的圆周角相等.连接AC ,根据直径AB ⊥弦CD 于点H ,利用垂径定理得到BC⏜=BD ⏜,从而利用等弧所对的圆周角相等得到∠CAB =∠DAB ,利用圆周角定理得到∠BAD =∠BAC =25°.【解答】解:连接AC ,∵直径AB ⊥弦CD 于点H ,∴BC⏜=BD ⏜, ∴∠CAB =∠DAB ,∵∠BAC =∠BEC =25°,∴∠BAD =∠BAC =25°.故选C .8.答案:C解析:【分析】本题考查正方形的性质,全等三角形的判定与性质,勾股定理等.过点A作AM⊥l3分别交l2、l3于点N、M,过C点作CH⊥l2分别交l2、l 3于点H、G,由正方形ABCD,l1//l2//l3//l4,得AB=CD,∠BAE=∠BCD=90°,再得用AAS证△ABN≌△CDG,得出AN=CG=ℎ1,BN=CH=ℎ1+ℎ2,在Rt△ABE中由勾股定理得AB2=AN2+BN2=22+32,即可得出正方形ABCD的面积.【解答】解:过点A作AM⊥l3分别交l2、l3于点N、M,过C点作CH⊥l2分别交l2、l 3于点H、G,如图,∵正方形ABCD,∴AB=CD,∠ABN+∠HBC=∠ABC=90°,∵CH⊥l2,∴∠BCH+∠HBC=90°,∴∠BCH=∠ABN,同理∠BCH=∠CDG,∴∠ABN=∠CDG,∵∠ANB=∠CGD=90°,∴△ABN≌△CDG(AAS),∴AN=CG,BN=CH=ℎ2+ℎ3,∵l1//l2//l3//l4,∴ℎ3=ℎ1=2,BN=2+1=3,在Rt△ABN中由勾股定理得AB2=AN2+BN2=22+32=13,∴正方形ABCD的面积=AB2=13.故选C.9.答案:C解析:【分析】本题考查了一次函数图象与系数的关系:y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.k>0,b>0⇔y=kx+b的图象在一、二、三象限;k>0,b<0⇔y=kx+b的图象在一、三、四象限;k<0,b>0⇔y=kx+b的图象在一、二、四象限;k<0,b<0⇔y=kx+b的图象在二、三、四象限.先根据有理数的性质得到a<0,b>0,然后根据一次函数图象与系数的关系进行判断.【解答】解:∵a+b=0且a<b,∴a<0,b>0,∴函数y=bx+a的图象经过第一、三、四象限.故选C.10.答案:C解析:解:∵△ADE由△ABC旋转而成,∴AB=AD,∵∠BAD=40°,∴∠ADB=180°−∠BAD2=180°−40°2=70°.故选C.先根据图形旋转的性质得出AB=AD,再根据等腰三角形的性质即可得出∠ADB的度数.本题考查的是图形旋转的性质,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件.11.答案:B解析:【分析】本题考查一元一次方程的应用,关键知道利润=售价−进价,根据此可列方程求解.设这种商品的标价是x元,根据某种商品每件的进价为180元,按标价的九折销售时,利润率为20%可列方程求解.【解答】解:设这种商品的标价是x元,90%x−180=180×20%x=240这种商品的标价是240元.故选:B.12.答案:C>0,则b<0,正确;解析:解:①图象开口向上,对称轴在y轴右侧,能得到:a>0,−b2a②∵对称轴为直线x=1,∴x=2与x=0时的函数值相等,∴当x=2时,y=4a+2b+c>0,错误;③当x=−1时,y=a−b+c>0,正确;④∵a−b+c>0,∴a+c>b;∵当x=1时,y=a+b+c<0,∴a+c<−b;∴b<a+c<−b,∴|a+c|<|b|,∴(a+c)2<b2,正确.所以正确的结论是①③④.故选C.由抛物线的开口方向判断a与0的关系,由对称轴及抛物线与x轴交点情况进行推理,利用图象将x=1,−1,2代入函数解析式判断y的值,进而对所得结论进行判断.本题主要考查二次函数图象与系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,将x=1,−1,2代入函数解析式判断y的值是解题关键,得出b<a+c<−b 是本题的难点.13.答案:−3解析:【分析】根据二次根式的值为零时,被开方数是零解答.主要考查了二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数.【解答】解:依题意得:x+3=0,解得x=−3.故答案是:−3,14.答案:74解析:解:∵a−bb =34,∴4(a−b)=3b,∴4a=7b,∴ab =74.故答案为:74.根据两内项之积等于两外项之积列式整理即可得解.本题考查了比例的性质,熟记两内项之积等于两外项之积是解题的关键.15.答案:50°解析:解:∵DE//AB,∠A=50°,∴∠A=∠ACD=50°,故答案为:50°.根据平行线的性质,两直线平行,内错角相等,可得出结论.本题考查了平行线的性质,关键是根据平行线的性质,两直线平行,内错角相等解答.16.答案:√5解析:【分析】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.先根据垂径定理得到BC=AC=2,然后根据勾股定理可计算出OB.【解答】解:∵OC⊥弦AB于点C,∴BC=AC=12AB=12×4=2,在Rt△OBC中,OC=1,BC=2,∴OB=√OC2+BC2=√5.故答案为√5.17.答案:−1解析:解:∵|a+3|+√b−2+(m−7)2=0,∴a=−3,b=2,m=7∴(a+b)m=(−3+2)7=−1.故答案为:−1.首先根据绝对值、平方与二次根式的非负性,得出a、b、m的值,然后代入多项式(a+b)m中直接计算即可解决问题.此题主要考查了非负数的性质和幂的运算,有一定的综合性.18.答案:2√2解析:解:连接AC1,∵四边形AB1C1D1是正方形,×90°=45°=∠AC1B1,∴∠C1AB1=12∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,∴∠B1AB=45°,∴∠DAB1=90°−45°=45°,∴AC1过D点,即A、D、C1三点共线,∵正方形ABCD的边长是1,∴四边形AB1C1D1的边长是1,在Rt△C1D1A中,由勾股定理得:AC1=√12+12=√2,则DC1=√2−1,∵∠AC1B1=45°,∠C1DO=90°,∴∠C1OD=45°=∠DC1O,∴DC1=OD=√2−1,同理求出A、B1、C三点共线,求出OB1=√2−1,∴四边形AB1OD的周长是AD+OD+OB1+AB1=1+√2−1+√2−1+1=2√2,故答案为2√2.连接AC1,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1=√2,求出DC1=√2−1=OD,同理求出A、B1、C三点共线,求出OB1=√2−1,代入AD+OD+OB1+AB1求出即可.本题考查了正方形性质,勾股定理等知识点,主要考查学生运用性质进行计算的能力,题目比较好,但有一定的难度.19.答案:解:原式=1−5−3×√33+√3=−4.解析:原式利用零指数幂、负整数指数幂法则,二次根式性质,以及绝对值的代数意义化简,计算即可得到结果.此题考查了实数的运算,熟练掌握运算法则是解本题的关键.20.答案:解:原式=x−2x−1⋅(x−1)2 (x+2)(x−2)=x−1x+2,当x=5时,原式=5−15+2=47.解析:本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.21.答案:(1)20%;72°;(2)调查的总人数是:44÷44%=100(人),则喜欢篮球的人数是:100×20%=20(人),;(3)全校喜欢乒乓球的人数是1000×44%=440(人).答:根据样本估计全校喜欢乒乓球的人数是440人.解析:【解答】解:(1)1−44%−8%−28%=20%,所在扇形统计图中的圆心角的度数是:360×20%=72°,故答案为:20%,72°;(2)见答案;(3)见答案.【分析】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.(1)利用1减去其它各组所占的比例即可求得喜欢篮球的人数百分比,利用百分比乘以360度即可求得扇形的圆心角的度数;(2)根据喜欢A乒乓球的有44人,占44%即可求得调查的总人数,乘以对应的百分比即可求得喜欢篮球的人数,补全统计图即可;(3)总人数1000乘以喜欢乒乓球的人数所占的百分比即可求解.22.答案:解:(1)过点O分别作OM⊥AB于点M,ON⊥CD于点N,则∠ONE=∠OME=90°,∵AB⊥CD,∴∠NEM=90°,∴四边形ONEM是矩形,∴ON=EM.∵OM⊥AB,∴AM=12AB=12(4+10)=7cm,∴EM=7−4=3cm,∴ON=3cm,即圆心O到CD的距离为3cm;(2)连接OD,∵ON⊥CD,∴ND=12CD,∵ON=3cm,OD=8cm,∴ND=√82−32=√55cm,∴CD=2√55cm.解析:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.(1)过点O分别作OM⊥AB于点M,ON⊥CD于点N,易知四边形ONEM是矩形,所以ON=EM,再根据垂径定理和已知数据求出EM的长即可得到ON的长,即圆心O到CD的距离;(2)连接OD,先根据勾股定理求出ND的长,再由垂径定理即可得出CD的长.23.答案:解:(1)由题意y=(x−5)(100−x−60.5×5)=−10x2+210x−800故y与x的函数关系式为:y=−10x2+210x−800(2)要使当天利润不低于240元,则y≥240,∴y=−10x2+210x−800=−10(x−10.5)2+302.5=240解得,x1=8,x2=13∵−10<0,抛物线的开口向下,∴当天销售单价所在的范围为8≤x≤13.(3)∵每件文具利润不超过80%∴x−55≤0.8,得x≤9∴文具的销售单价为6≤x≤9,由(1)得y=−10x2+210x−800=−10(x−10.5)2+302.5∵对称轴为x=10.5∴6≤x≤9在对称轴的左侧,且y随着x的增大而增大∴当x=9时,取得最大值,此时y=−10(9−10.5)2+302.5=280即每件文具售价为9元时,最大利润为280元.解析:本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=−b2a时取得.(1)根据总利润=每件利润×销售量,列出函数关系式,(2)由(1)的关系式,即y≥240,结合二次函数的性质即可求x的取值范围(3)由题意可知,利润不超过80%即为利润率=(售价−进价)÷售价,即可求得售价的范围.再结合二次函数的性质,即可求.24.答案:解:(1)如图1,过Q点作QP⊥BD交DC于P,∴∠PQB=90°.∵∠MQN=90°,∴∠NQP=∠MQB,∵四边形ABCD是正方形,∴CD=CB,∠BDC=∠DBC=45°,DO=BO.∴∠DPQ=45°,DQ=PQ.∴∠DPQ=∠DBC,∴△QPN∽△QBM,∴NPMB =PQQB.∵Q是OD的中点,且PQ⊥BD,∴DO=2DQ,DP=12DC,∴BQ=3DQ.DN+NP=12BC,∴BQ=3PQ,∴NPMB =13,∴NP=13BM.∴DN+13BM=12BC;(2)BM−13DN=12BC;(3)∵MB:MC=3:1,设CM=x,∴MB=3x,∴CB=CD=4x,∴HB=2x,∴HM=x.∵HM=13ND,∴ND=3x,∴CN=7x ∵四边形ABCD是正方形,∴ED//BC,∴△NDE∽△NCM,△DEF∽△BMF,∴NDCN =DECM=NENM,DEBM=EFFM,∴3x7x =DEx,NENM=37,∴DE=37x,∴37x3x=EFFM=17,∵NQ=9√5,∴QM=3√5,在Rt△MNQ中,由勾股定理得:MN=√(9√5)2+(3√5)2=15√2.,∴15√2=37,∴NE=45√27,∴EM=60√27,设EF=a,则FM=7a,∴a+7a=60√2 7∴a=15√214.解析:【分析】本题是一道相似的综合试题,考查了正方形的性质的运用,相似三角形的判定于性质的运用,勾股定理的运用及平行线等分线段定理的运用,在解答时利用三角形相似的性质求出线段的比是解答本题的关键.(1)如图1,过Q点作QP⊥BD交DC于P,然后根据正方形的性质证明△QPN∽△QBM,就可以得出结论;(2)如图2,过Q点作QH⊥BD交BC于H,通过证明△QHM∽△QDN,由相似三角形的性质就可以得出结论;(3)由条件设CM=x,MB=3x,就用CB=4x,得出BH=2x,由(2)相似的性质可以求出MQ的值,再根据勾股定理就可以求出MN的值,可以表示出ND,由△NDE∽△NCM就可以求出NE,也可以表示出DE,最后由△DEF∽△BMF而求出结论.【解答】(1)见答案;(2)如图2,过Q点作QH⊥BD交BC于H,∴∠BQH=∠DQH=90°,∴∠BHQ=45°.∵∠OCB=45°,∴QH//OC.∵Q是OB的中点,∴BH=CH=12BC∵∠NQM=90°,∴∠NQD=∠MQH,∵∠QND+∠NQD=45°,∠MQH+∠QMH=45°∴∠QND=∠QMH,∴△QHM∽△QDN,∴HMND =QHDQ=QMNQ=13,∴HM=13ND,∵BM−HM=HB,∴BM−13DN=12BC.故答案为:BM−13DN=12BC;(3)见答案.25.答案:解:(1)由题意可得,当−m=−m+1时,该方程无解,故函数y=−x+1没有反向值,当−m=−1m 时,m=±1,∴n=1−(−1)=2,故y=−1x有反向值,反向距离为2,当−m=m2,得m=0或m=−1,∴n=0−(−1)=1,故y=x2有反向值,反向距离是1;(2)①令−m=m2−4b2m,解得,m=0或m=4b2−1,∵反向距离为零,∴|4b2−1−0|=0,解得,b=±12;②令−m=m2−4b2m,解得,m=0或m=4b2−1,∴n=|4b2−1−0|=|4b2−1|,∵−1≤b≤3,∴0≤n≤35.解析:本题是一道二次函数综合题,解答本题的关键是明确题目中的新定义,找出所求问题需要的条件,利用新定义解答相关问题. (1)根据题目中的新定义可以分别计算出各个函数是否有方向值,有反向值的可以求出相应的反向距离;(2)①根据题意可以求得相应的b 的值;②根据题意和b 的取值范围可以求得相应的n 的取值范围.26.答案:解:(1)∵抛物线y =ax 2+bx +3经过点A(−1,0)、B(3,0)两点,∴{a −b +3=09a +3b +3=0, 解得{a =−1b =2, ∴抛物线的解析式:y =−x 2+2x +3;(2)由抛物线y =ax 2+bx +3可知,C(0,3),设直线BC 的解析式为:y =kx +3,代入B(3,0)得,3k +3=0,解得k =−1故直线BC 的解析式:y =−x +3,已知点M 的横坐标为m ,MN//y ,则M(m,−m +3)、N(m,−m 2+2m +3),∴故MN =−m 2+2m +3−(−m +3)=−m 2+3m(0<m <3);(3)如图;∵S △BNC =S △MNC +S △MNB =12MN(OD +DB)=12MN ⋅OB ,∴S △BNC =12(−m 2+3m)⋅3=−32(m −32)2+278(0<m <3); ∴当m =32时,△BNC 的面积最大,最大值为278.解析:本题考查了二次函数综合题,利用待定系数法求二次函数解析式以及待定系数法求一次函数的解析式,二次函数的性质,利用三角形的面积得出二次函数是解题关键.(1)直接利用待定系数法即可求出抛物线的解析式;(2)先利用待定系数法求出直线BC 的解析式,已知点M 的横坐标,代入直线BC 、抛物线的解析式中,可得到M 、N 点的坐标,N 、M 纵坐标的差的绝对值即为MN 的长;(3)设MN 交x 轴于D ,那么△BNC 的面积可表示为:S △BNC =S △MNC +S △MNB =12MN(OD +DB)=12MN ⋅OB ,MN 的表达式在(2)中已求得,OB =3,由此列出关于S △BNC 关于m 的函数关系式,根据函数的性质即可判断出△BNC 是否具有最大值.。
2019-2020学年湖南师大附中梅溪湖中学九年级(上)第一次月考数学试卷 (含解析)

2019-2020学年湖南师大附中梅溪湖中学九年级(上)第一次月考数学试卷一、选择题(本大题共12小题,共36.0分)1.如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD//AB,则∠BAC的大小为()A. 30°B. 35°C. 40°D. 70°2.在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为()A. 6B. 9C. 12D. 15(x>0)的图象相交于A(3,4),B(6,2)两点,若3.如图,一次函数y1=k1x+b与反比例函数y2=k2xk1x+b<k2,则x的取值范围是()xA. x<3或x>6B. 3<x<6C. 0<x<3或x>6D. x>64.已知⊙O的半径为3cm,点O到直线l的距离为4cm,则l与⊙O的位置关系是()A. 相离B. 相切C. 相交D. 不能确定5.如果一个正多边形的中心角为72∘,那么这个多边形的边数是()A. 4B. 5C. 6D. 76.如图,A、B、C、D是⊙O上的四个点,AB⏜=BC⏜,∠AOB=58°,则∠BDC的度数是()A. 58°B. 42°C. 32°D. 29°7.用一个圆心角为120°,半径为2的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为()A. 43B. 34C. 32D. 238.下列事件中,随机事件是()A. 打开电视,正在播广告B. 没有水分,种子发芽C. 13个人中,至少有2人的出生月份相同D. 明天太阳从西边升起9.已知点A(2,y1)、B(m,y2)是反比例函数y=kx(k>0)的图象上的两点,且y1<y2.满足条件的m 值可以是()A. −6B. −1C. 1D. 310.已知一个三角形的三边长分别为6,8,10.则其内切圆的半径为()A. √3B. 2C. 3√2D. 611.当a≠0时,函数y=ax+1与函数y=ax在同一坐标系中的图象可能是()A. B.C. D.12.如图,在△ABC中,∠BAC=90°,AB=AC=4.将△ABC绕点B逆时针旋转45°,得△A′BC′,则阴影部分的面积为()A. 2B. 2πC. 4D. 4π二、填空题(本大题共6小题,共18.0分)13.如图,四边形ABCD内接于⊙O,外角∠DCE=85°,则∠BAD=______.14.如图,已知点A在反比例函数y=−4x 的图象上,点D在反比例函数y=kx(k≠0)的图象上,AD//x轴,AB⊥x轴于B,DC⊥x轴于C,若OB=13OC,则k的值为______.15.如图,转盘中灰色扇形的圆心角为90°,白色扇形的圆心角为270°,让转盘自由转动一次,指针落在白色区域的概率是_____.16.如图,点P在⊙O外,PA、PB分别切⊙O于点A、点B,若∠P=50°,则∠A=______.17.“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法,即“割圆术”.“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆.刘徽从圆内接正六边形出发,将边数逐次加倍,并逐次得到正多边形的周长和面积.如图,AB是圆内接正六边形的一条边,半径OB=1,OC⊥AB于点D,则圆内接正十二边形的边BC的长是______(结果不取近似值).18. 如图,点P 是函数y =−2x (x <0)图象上的−个动点,PE ⊥x 轴于E ,PF ⊥y 轴于F ,线段PE ,PF 分别与直线AB :y =x +2交于C ,D 两点,则AD ⋅BC 的值为________.三、计算题(本大题共1小题,共6.0分) 19. 计算:π0−(12)−1+√83.四、解答题(本大题共7小题,共60.0分) 20. 解不等式组{5x −12≤2(4x −3),3x−12<1,并把它的解在数轴上表示出来.21.6月5日是“世界环境日”,某校举行了“洁美家园”的演讲比赛,将学生的成绩分成A、B、C、D四个等级,并制成了如下的条形统计图和扇形图(如图1、图2).(1)补全条形统计图.(2)学校决定从本次比赛中获得A和B的学生中各选出一名去参加市中学生环保演讲比赛.已知A等中男生有2名,B等中女生有3名,请你用“列表法”或“树形图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率.22.已知一次函数y1=kx+b与反比例函数y2=6的图像交于A(m,3),B(−3,n)两点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南师大附中教育集团2019-2020学年度第一次九年级联考数学试题一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的. )A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间 【答案】C【解析】【分析】根据5.766 6.25,1.962 2.25<<<<,即可求出和的取值范围,+,即可得出结论.【详解】解:∵5.766 6.25,1.962 2.25<<<<∴2.4 2.5,1.4 1.5<<<∴2.4 1.4 2.5 1.5+<+<+即3.84<+3和4之间故选C . 【点睛】此题考查的是判断无理数的取值范围,根据被开方数的取值范围,求出算术平方根的取值范围是解决此题的关键.2.下列运算正确的是( )A. 428a a a =•B. 2242a a a +=C. 222()a b a b +=+D. 326(2)4a a -= 【答案】D【解析】【分析】根据同底数幂的乘法、合并同类项法则、完全平方公式、积的乘方和幂的乘方逐一判断即可.【详解】解:A . 44262a a a a +==•,故本选项错误;B . ()2222112a a a a +=+=,故本选项错误; C . 222()2a b a ab b +=++,故本选项错误;D . 322326(2)(2)4a a a ⨯-=-=,故本选项正确.故选D .【点睛】此题考查的是幂的运算性质、合并同类项和完全平方公式,掌握同底数幂的乘法、合并同类项法则、完全平方公式、积的乘方和幂的乘方是解决此题的关键.3.太阳与地球之间的平均距离约为150000000km ,用科学记数法表示这一数据为( )A. 81.510km ⨯B. 71510km ⨯C. 100.1510km ⨯D. 91.510km ⨯【答案】A【解析】【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】解:根据科学记数法的定义:150000000km =81.510km ⨯故选A .【点睛】此题考查的是科学记数法,掌握科学记数法的定义是解决此题的关键.4.2019年全国高中数学联赛,湖南师大附中入选省队人数、签约清北人数、一等奖人数均为全省第一.其中一等奖获奖人数附中及其他三所兄弟学校从高到低依次为:20,17,12,12.这组数据的中位数是( )A. 17B. 12C. 14.5D. 15.5 【答案】C【解析】【分析】根据中位数的定义:一组数据按从小到大(或从大到小)的顺序依次排列,处在中间位置的一个数或最中间两个数据的平均数,即可得出结论.【详解】解:根据中位数的定义,这组数据的中位数是(17+12)÷2=14.5故选C .【点睛】此题考查的是求一组数据的中位数,掌握中位数的定义是解决此题的关键.5.如图,//AB CD ,EF 分别为交AB ,CD 于点E ,F ,150∠=o ,则2∠的度数为( )A. 50oB. 120oC. 130oD. 150o【答案】C【解析】【分析】 根据两直线平行,同位角相等可得∠BEF=∠1=50°,然后根据平角的定义即可求出∠2的度数.【详解】解:∵//AB CD∴∠BEF=∠1=50°∴∠2=180°-∠BEF=130°故选C .【点睛】此题考查的是平行线的性质和平角的定义,掌握两直线平行,同位角相等和平角的定义是解决此题的关键.6.如图,O e 的直径AB 垂直于弦CD ,垂足为E ,22.5A ∠=︒,4OC =,CD 的长为( )A. B. 4 C. 8 D. 【答案】A【解析】【分析】根据圆心角等于同弧所对圆周角的2倍得到∠COE=45︒,由垂径定理得到CD=2CE, 90CEO ∠=︒,,用勾股定理求得CE =CD=2CE= 【详解】∵22.5A ∠=︒,∵∵COE=45︒,∵直径AB 垂直于弦CD ,∵CD=2CE, 90CEO ∠=︒,∵4OC =,∵CE=sin 4542OC ⋅︒=⨯=,∵CD=2CE=故选:A.【点睛】此题考查圆的垂径定理、圆周角定理,利用∠COE=45︒求得CE =CD=2CE=.7.如图,D ,E 分别是ABC ∆中AB ,AC 边上的点,//DE BC ,下列结论错误的( )A. AD AE AB AC =B. AD AE DB EC =C. AB AC DB EC =D. DE AE BC EC= 【答案】D【解析】【分析】根据平行线分线段成比例定理及推论逐一判断即可.【详解】解:∵//DE BC ∴AD AE AB AC=,故A 正确;AD AE DBEC =,故B 正确; AB AC DB EC=,故C 正确; DE AE AE BC AC EC=≠,故D 错误. 故选D .【点睛】此题考查的是平行线分线段成比例定理及推论,掌握根据平行线分线段成比例定理及推论判断比例式是解决此题的关键.8.若1x 、2x 是一元二次方程2750x x -+=的两根,则1211+x x 的值是( ) A. 75 B. 75- C. 57 D. 57- 【答案】A【解析】【详解】这里a=1,b=-7,c=5,由题意知,x 1x 2=5,x 1+x 2=7, 则1211+x x =121275x x x x += 故选A9.如图,菱形ABCD 中,对角线AC 、BD 交于点O ,E 为边AD 中点,菱形ABCD 的周长为28,则OE 的长等于( )A. 3.5B. 4C. 7D. 14【答案】A【解析】【分析】 根据菱形的性质和周长,即可求出AD ,然后根据直角三角形斜边上的中线等于斜边的一半即可得出结论.【详解】解:∵菱形ABCD 的周长为28,∴AD=AB=BC=CD=28÷4=7,∠AOD=90°∵E 为边AD 中点,∴在Rt △AOD 中,OE=1 3.52AD = 故选A .【点睛】此题考查的是菱形的性质和直角三角形的性质,掌握菱形的四边都相等、菱形的对角线互相垂直和直角三角形斜边上的中线等于斜边的一半是解决此题的关键.10.化简22422b a a b b a+--的结果是( ) A. 2a b -+B. 2a b --C. 2a b +D. 2a b -【答案】B【解析】【分析】先将分式化成同分母,再计算分式的减法,最后化简分式即可. 【详解】原式22422b a a b a b=--- 2242b a a b-=- (2)(2)2b a b a a b+-=- 2a b =--故选:B.【点睛】本题考查了分式的加减法运算,根据运算法则将分式转化为同分母是解题关键11.一次函数1y kx b =+与反比例函数2m y x=的图象交于(1,2)A -、(2,1)B -两点,使12y y >成立的自变量x 的取值范围是( )A. 12x -<<B. 10x -<<或2x >C. 1x <-或2x >D. 1x <-或02x << 【答案】D【解析】【分析】在同一直角坐标系中,画出两个函数的图象,根据图象找到一次函数图象在反比例函数图象上方时,x 的取值范围即可.【详解】解:在同一直角坐标系中,根据A 、B 两点坐标画出一次函数1y kx b =+与反比例函数2m y x=的图象,如下图所示由图可知:当12y y >时,1x <-或02x <<故选D .【点睛】此题考查的是一次函数和反比例函数的结合题,掌握一次函数和反比例函数图象的画法、结合图象求自变量的取值范围是解决此题的关键.12.如图,在平行四边形ABCD 中,78ABC ∠=o ,AE BC ⊥于点E ,AE 交BD 于点F ,若2DF AB =,则AFD ∠的大小是( )A. 62oB. 64oC. 66oD. 68o【答案】B【解析】【分析】 取DF 的中点G ,连接AG ,根据平行四边形的性质和平行线的性质可得∠FAD=∠AEB=90°,∠CBD=∠GDA ,然后根据直角三角形斜边上的中线等于斜边的一半可推出AB=AG=FG=DG ,根据等边对等角可得∠ABG=∠AGB ,∠GAD=∠GDA ,然后根据三角形的外角的性质和已知条件即可求出∠GDA ,然后根据直角三角形的两个锐角互余即可得出结论.【详解】解:取DF 的中点G ,连接AG ,如下图所示∵四边形ABCD 是平行四边形,AE BC ⊥∴BC ∥AD ,∠AEB=90°∴∠FAD=∠AEB=90°,∠CBD=∠GDA在Rt △FAD 中,DF=2AG=2FG=2GD∵2DF AB =∴AB=AG=FG=DG∴∠ABG=∠AGB ,∠GAD=∠GDA∴∠ABG=∠AGB=∠GAD +∠GDA=2∠GDA=2∠CBD∴∠ABC=∠ABG +∠CBD=3∠CBD=78°∴∠CBD=26°∴∠GDA=26°在Rt △AFD 中,∠AFD=90°-∠GDA=64°故选B .【点睛】此题考查的是平行四边形的性质、平行线的性质、直角三角形的性质和等腰三角形的性质,掌握平行四边形的性质、平行线的性质、直角三角形斜边上的中线等于斜边的一半和等边对等角是解决此题的关键.二、填空题(本大题共6个小题,每题3分,满分18分,将答案填在答题纸上) 13.因式分解:2818a b b -=__________.【答案】2(23)(23)b a a -+【解析】【分析】先提取公因式,然后利用平方差公式因式分解即可【详解】解:2818a b b -=()2249b a -=2(23)(23)b a a -+故答案为:2(23)(23)b a a -+.【点睛】此题考查的是因式分解,掌握用提公因式法和平方差公式因式分解是解决此题的关键. 14.从大小形状完全相同标有1、2、3数字的三张卡片中随机抽取两张,和为偶数的概率为____. 【答案】13【解析】试题解析:画出树状图得:∵和为偶数的情况有两种,所有可能的情况有6种,∴P (和为偶数)=21=63.15.圆心角为120o 的扇形的半径为3,则这个扇形的面积为__________.【答案】3π【解析】【分析】根据扇形的面积公式:S 扇形=2360n r π计算即可. 【详解】解:这个扇形的面积为212033360ππ••= 故答案为:3π.【点睛】此题考查的是求扇形的面积,掌握扇形的面积公式S 扇形=2360n r π是解决此题的关键. 16.如图,AB 为圆O 的直径,C ,D 是圆O 上两点,若50ABC ∠=o ,则D ∠的度数为__________.【答案】40o【解析】【分析】根据直径所对的圆周角为直角,可得∠ACB=90°,然后根据直角三角形的两个锐角互余即可求出∠CAB ,最后根据同弧所对的圆周角相等即可求出∠D .【详解】解:∵AB 为圆O 的直径,50ABC ∠=o∴∠ACB=90°∴∠CAB=90°-∠ABC=40°∴∠D=∠CAB=40°故答案为:40°.【点睛】此题考查的是圆周角定理的推论和直角三角形的性质,掌握直径所对的圆周角为直角、同弧所对的圆周角相等和直角三角形的两个锐角互余是解决此题的关键.17.计算:22244(4)2x x x x x+--÷+= . 【答案】x -2【解析】试题解析:原式=244(2)(2)(2)x x x x x x x +-+⨯+-=2(2)(2)(2)(2)x x x x x x -+⨯+- =x-2.考点:分式的混合运算.18.已知关于x 的一元二次方程2(1)40ax a x -+-=的两根分别为1x ,2x ,且110x -<<,223x <<,则实数a 的取值范围是__________. 【答案】332a << 【解析】【分析】设2(1)4y ax a x =-+-,根据一元二次方程的解和二次函数图象与x 轴交点的关系,并求出二次函数的图象与y 轴的交点坐标,即可画出二次函数的大致图象,然后根据图象分别找到当x=-1、x=2、x=3时,y 的取值范围代入即可求出a 的取值范围.【详解】解:设2(1)4y ax a x =-+-∵关于x 的一元二次方程2(1)40ax a x -+-=的两根分别为1x ,2x , ∴二次函数2(1)4y ax a x =-+-的图象与x 轴的两个交点的横坐标为1x ,2x ,将x=0代入二次函数解析式中,解得y=-4∴二次函数的图象与y 轴交于(0,-4)∵110x -<<,223x <<,∴该二次函数的图象大致为如下图所示,由图可知:a >0,当x=-1时,y >0,即()()211(1)40y a a =---+->,解得:32a >; 当x=2时,y <0,即222(1)40y a a =-+-<,解得:3a <当x=3时,y >0,即233(1)40y a a =-+->,解得:76a >∴实数a 的取值范围是332a << 故答案为:332a <<. 【点睛】此题考查的是一元二次方程的解和二次函数图象与x 轴交点的关系,掌握把一元二次方程的问题转化成二次函数的问题是解决此题的关键.三、解答题:本大题共8个小题,第19、20题每小题6分,第21、22题每小题8分,第23、24题每小题9分,第25、26题每小题10分,共66分.解答应写出文字说明、证明过程或演算步骤.19.201(()(12-⨯--【答案】-7【解析】【分析】根据二次根式的性质、负指数幂的性质和零指数幂的性质计算即可.【详解】解:原式2(2)41=+-⨯- 281=--7=-【点睛】此题考查的是实数的混合运算,掌握二次根式的性质、负指数幂的性质和零指数幂的性质是解决此题的关键.20.解不等式组2723222334x x x x x --⎧≤⎪⎪⎨--⎪<-+⎪⎩. 【答案】24x <≤【解析】【分析】根据不等式的基本性质分别解出不等式①和②,然后取公共解集即可.【详解】解:2723222334x x x x x --⎧≤⎪⎪⎨--⎪<-+⎪⎩①② 解不等式①,得4x ≤解不等式②,得2x >∴不等式组的解集为24x <≤【点睛】此题考查的是解不等式组,掌握不等式组的解法和公共解集的取法是解决此题的关键. 21.为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A 级:优秀;B 级:良好;C 级:及格;D 级:不及格),并将测试结果绘制成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)本次抽样测试的学生人数是 人;(2)图1中α∠的度数是 ,并把图2条形统计图补充完整;(3)该县九年级有学生4500名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 . (4)老师想从4位同学(分别记为E 、F 、G 、H ,其中E 为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.【答案】(1)40;(2)162o ,图详见解析;(3)450;(4)12. 【解析】【分析】(1)根据B 级的人数和所占抽样总人数的百分率,即可求出抽样总人数;(2)先用抽样总人数减去A 级、B 级、D 级人数即可得到C 级的人数,用C 级人数除以抽样总人数乘360°即可得出α∠的度数,然后补全条形统计图即可.(3)根据D 级的人数和抽样总人数求出不及格率,再乘九年级总人数即可;(4)根据题意画出树形图,然后根据树形图求概率即可.【详解】解:(1)本次抽样测试的学生人数是12÷30%=40人故答案为:40.(2)C 级人数为40-6-12-4=18人∴α∠=1836016240⨯︒=︒ 故答案为:162o条形统计图如下图所示:(3)不及格率为:4÷40×100%=10%∴不及格的人数为4500×10%=450人故答案为:450(4)根据题意画树形图如下:共有12种等可能的结果,其中选中小明的有6种,则P (选中小明)61122==. 【点睛】此题考查的是条形统计图、扇形统计图和求概率问题,掌握结合条形统计图和扇形统计图得出有用信息和画树状图求概率是解决此题的关键.22.如图,AD 是圆O 的弦,AB 经过圆心O ,交圆O 于点C ,30DAB B ∠=∠=o .(1)求证:直线BD 与圆O 相切.(2)连接CD ,若5CD =,求AB 的长.【答案】(1)详见解析;(2)15【解析】【分析】(1)连接OD ,根据等边对等角可得30ODA DAB B ∠=∠=∠=o ,然后根据三角形的内角和定理即可求出∠ODB ,最后根据切线的判定定理即可得;(2)先证出DOC ∆是等边三角形,即可求出OA=OD=CD=5,然后根据30°所对的直角边是斜边的一半即可求出OB ,从而求出AB .【详解】解:(1)连接OD∵OA=OD ,30DAB B ∠=∠=o∴30ODA DAB B ∠=∠=∠=o∴18018030303090ODB ODA DAB B ∠=-∠-∠-∠=---=o o o o o o∴直线BD 与圆O 相切(2)由(1)知,30ODA DAB ∠=∠=o∴60DOB ODA DAB ∠=∠+∠=o又∵OC OD =∴DOC ∆是等边三角形∴5OA OD CD ===又∵30B ∠=o ,90ODB ∠=o∴210OB OD ==∴51015AB OA OB =+=+=【点睛】此题考查的是切线的判定、等腰三角形的性质、等边三角形的判定及性质和直角三角形的性质,掌握切线的判定定理、等边对等角、等边三角形的判定及性质和30°所对的直角边是斜边的一半是解决此题的关键.23.某商店计划购进一批A 、B 两种型号的计算器,若购进A 型计算器10只和B 型计算器8只,共需要资金880元;若购进A 型计算器2只和B 型计算器5只,共需要资金380元.(1)求A 、B 两种型号的计算器每只进价各是多少元?(2)该商店计划购进这两种型号计算器共50只.根据市场行情,销售一只A 型计算器可获利9元,销售一只B 型计算器可获利18元.该商店希望销售完这50只计算器,所获利润不少于购进总成本的25%.则该商店至少要采购B 型计算器多少只?【答案】(1)A 种型号的计算器每只进价40元,B 种型号的计算器每只进价为60元;(2)该经销商至少要采购B 型计算器13只.【解析】【分析】(1)设A 种型号的计算器每只进价x 元,B 种型号的计算器每只进价为y 元,根据题意,列出二元一次方程组,并解方程组即可;(2)设该经销商要采购B 型计算器m 只,根据“所获利润不少于购进总成本的25%”列不等式,并解不的【详解】解:(1)设A 种型号的计算器每只进价x 元,B 种型号的计算器每只进价为y 元,根据题意,得 10888025380x y x y +=⎧⎨+=⎩ 解得:4060x y =⎧⎨=⎩答:A 种型号计算器每只进价40元,B 种型号的计算器每只进价为60元.(2)设该经销商要采购B 型计算器m 只,根据题意,得189(50)[6040(50)]25%m m m m +-≥+-•解之,得12.5m ≥所以,该经销商至少要采购B 型计算器13只答:该经销商至少要采购B 型计算器13只.【点睛】此题考查的是二元一次方程组的应用和一元一次不等式的应用,掌握实际问题中的等量关系和不等关系是解决此题的关键.24.如图,四边形ABCD 中,AB AD =,60BAD ∠=o ,30BCD ∠=o ,将AC 绕着点A 顺时针旋转60o 得AE ,连接BE ,CE .(1)求证:ADC ∆≌ABE ∆;(2)求证:222AC DC BC =+; (3)若2AB =,点Q 在四边形ABCD 内部运动,且满足222AQ BQ DQ =+,求点Q 运动路径的长度.【答案】(1)详见解析;(2)详见解析;(3)23π. 【解析】的(1)根据等式的基本性质可得DAC BAE ∠=∠,然后利用SAS 即可证出ADC ∆≌ABE ∆;(2)根据四边形的内角和和全等三角形的性质可得270ABC ABE ∠+∠=o ,从而求出∠CBE=90°,根据勾股定理可得222CE BE BC =+,根据等边三角形的判定及性质可得CE AE AC ==,从而证出结论; (3)如图,设Q 为满足条件的点,将AQ 绕着点A 顺时针旋转60度得AF ,连接QF ,BF , QB ,DQ ,AF , DB ,先利用SAS 证出ADQ ∆≌ABF ∆,从而得出BF DQ =,∠AQD=∠AFB ,然后证出AFQ ∆为等边三角形,△ADB 为等边三角形,从而得出AQ FQ =, DB=AB=2,然后根据勾股定理的逆定理可得90FBQ ∠=o,根据四点共圆证出点Q 的路径为过B 、D 、C 三点的圆上»BD ,求出圆心角和半径即可求出点Q 运动路径的长度.【详解】证明:(1)∵60CAE DAB ∠=∠=o∴DAB CAB CAE CAB ∠-∠=∠-∠∴DAC BAE ∠=∠在ADC ∆和ABE ∆中AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴ADC ∆≌ABE ∆(2)在四边形ABCD 中360270ADC ABC DAB DCB ∠+∠=-∠-∠=o o∵ADC ∆≌ABE ∆∴ADC ABE ∠=∠,CD BE =∴270ABC ABE ABC ADC ∠+∠=∠+∠=o∴360()90CBE ABE ABC ∠=-∠+∠=o o∴222CE BE BC =+又∵AC AE =,60CAE ∠=o∴△AEC 为等边三角形∴CE AE AC ==∴222AC DC BC =+(3)如图,设Q 为满足条件的点,将AQ 绕着点A 顺时针旋转60度得AF ,连接QF ,BF , QB ,DQ ,AF , DB .∵60QAF DAB ∠=∠=o∴DAB QAB QAF QAB ∠-∠=∠-∠∴DAQ BAF ∠=∠在ADQ ∆和ABF ∆中 AD AB DAQ BAF AQ AF =⎧⎪∠=∠⎨⎪=⎩∴ADQ ∆≌ABF ∆∴BF DQ =,∠AQD=∠AFB ,∵60QAF ∠=o ,AQ=AF ,∠DAB=60°,AD=AB∴AFQ ∆为等边三角形,△ADB 为等边三角形∴AQ FQ =, DB=AB=2∵222AQ BQ DQ =+∴222FQ BQ BF =+∴90FBQ ∠=o∴()360DQB AQD AQB ∠=-∠+∠o()()360360360150AFB AQB QAF FBQ =-∠+∠⎡⎤=--∠+∠⎣⎦=o o o o∵∠BCD=30°∴∠DQB +∠BCD=180°∴点Q 的路径为过B 、D 、C 三点的圆上»BD设圆心为O ,连接OD 、OB则260BOD BCD ∠=∠=o ,∴△OBD 为等边三角形∴2DO DB ==,∴点Q 的运动的路径长为:60221803ππ⨯=. 【点睛】此题考查的是全等三角形的判定及性质、等边三角形的判定及性质、勾股定理及逆定理、四点共圆和求点的运动路径长度,掌握构造全等三角形的方法、全等三角形的判定定理、等边三角形的判定及性质、勾股定理及逆定理、利用四点共圆判定点的运动路径及弧长公式是解决此题的关键.25.四边形的一条对角线将这个四边形分成两个三角形,如果这两个三角形相似(不全等),那么我们将这条对角线叫做这个四边形的相似对角线.(1)如图1,四边形ABCD 中,100DAB ∠=o ,130DCB ∠=o ,对角线AC 平分DAB ∠,求证:AC 是四边形ABCD 的相似对角线;(2)如图2,直线33y x =-+分别与x ,y 轴相交于A ,B 两点,P 为反比例函数k y x=(k 0<)上的点,若AO 是四边形ABOP 的相似对角线,求反比例函数的解析式;(3)如图3,AC 是四边形ABCD 的相似对角线,点C 的坐标为(3,1),//AC x 轴,30BCA DCA ∠=∠=o ,连接BD ,BCD ∆A ,C 两点的抛物线2y ax bx c =++(0a <)与x 轴交于E ,F 两点,记1m AC =+,若直线y mx =与抛物线恰好有3个交点,求实数a 的值.【答案】(1)详见解析;(2)y x =或y x -=y x-=;(3)12a =-或92a =- 【解析】【分析】 (1)设ACD α∠=,则130ACB α∠=-o ,然后根据角平分线的性质可求得∠BAC=∠DAC=50°,根据三角形的内角和定理可得B α∠=,最后根据相似三角形的判定定理可证AC 是四边形ABCD 的相似对角线;(2)根据一次函数即可求出点A 、B 的坐标,再根据锐角三角函数值即可求出30OAB ∠=o ,60OBA ∠=o ,然后根据相似对角线的定义和相似三角形对应角的情况分类讨论,分别利用锐角三角函数求出点P 的坐标,即可求出反比例函数的解析式;(3)根据锐角三角函数和面积公式可得4CD BC •=,然后根据相似对角线的定义即可求出AC ,从而求出两个m 的值和两条直线的解析式3y x =-和3y x =,根据图形可知3y x =-,一定与抛物线有两个交点,故3y x =与抛物线有且仅有一个交点,然后联立方程令一元二次方程的△=0即可求出a 的值.【详解】(1)证明:如图1,设ACD α∠=,则130ACB α∠=-o∵100DAB ∠=o ,AC 平分DAB ∠∴∠BAC=∠DAC=1502DAB ∠=o ∴18018050(130)B BAC ACB αα∠=-∠-∠=---=o o o o在ABC ∆和ACD ∆中∵B ACD ∠=∠,BAC CAD ∠=∠∴ABC ∆∽ACD ∆∴AC 是四边形ABCD 的相似对角线.(2)如图2,可求得直线33y x =-+与两坐标轴交点分别为(4,0)A ,(0,)3B ∴OA=4,在Rt △AOB中,tan OB OAB OA ∠== ∴30OAB ∠=o ,60OBA ∠=o当OA 是四边形OBAP 的相似对角线时,有如下情况:①当∠APO=∠AOB=90°时,过点P 作PQ ⊥x 轴于Q ,如下图所示,此时又分以下两种情况的(i )当60AOP ABO ∠=∠=o ,Rt △OAP 中,OP=OA ·cos ∠AOP=2在Rt △OPQ 中,OQ=OP ·cos ∠AOP=1,PQ= OP ·sin ∠∴此时点(1,P ,将P 点坐标代入k y x=,得k =∴该反比例函数的解析式为y =; (ii )30BAO AOP ∠=∠=o ,在Rt △OAP 中,OP=OA ·cos ∠在Rt △OPQ 中,OQ=OP ·cos ∠AOP=3,PQ= OP ·sin ∠∴此时点(3,P ,将P 点坐标代入k y x=,得k =-∴该反比例函数的解析式为y x-= ②当∠OAP=∠AOB=90°时,此时又分以下两种情况(i )当∠AOP=∠OAB=30°时,如下图所示,∵OA=AO ,∠OAP=∠AOB=90°∴△OAP ≌AOB ,不符合相似对角线的定义,故舍去;(ii )当60AOP ABO ∠=∠=o 时,如下图所示,在Rt △OAP 中,AP=OA ·tan ∠AOP=∴此时点(4,P -,将P 点坐标代入k y x=,得k =-该反比例函数的解析式为y =; ③当∠AOP=∠AOB=90°时,此时点P 在y 轴上,故不存在反比例函数图象,故舍去.综上所述:反比例函数的解析式为y =y =y =. (3)如图3,作BCD ∆的底边CD 边上的高BH ,则30CBH ∠=o , ∴12CH BC =在Rt CHB ∆中,由勾股定理可求得BH BC =,∵12BCD S CD BC ∆=BC •=∴4CD BC •=∵AC 是四边形ABCD 的相似对角线若BCA ∆∽DCA ∆,由CA=CA 可得BCA ∆≌DCA ∆,不符合相似对角线的定义,故舍去,∴BCA ∆∽ACD ∆, ∴BC AC AC DC=, ∴2AC CD BC =•∴24AC =,即2AC =由点C 的坐标为(3,1)可知,点A 的坐标为(1,1),将A ,C 两点的坐标代入抛物线2(0)y ax bx c a =++<,得1931a b c a b c ++=⎧⎨++=⎩解得4b a =-,31c a =+,所以抛物线的解析式可化为2431y ax ax a =-++ 由1m AC =+,得直线y mx =的解析为3y x =,3y x =-,∵直线3y x =-与抛物线2431y ax ax a =-++(0)a <的交点必有两个∴直线3y x =与该抛物线的交点有且只有一个∴方程组23431y x y ax ax a =⎧⎨=-++⎩有且只有一组解 即关于x 的一元二次方程2(43)310ax a x a -+++=有两个相等的实数根.∴2(43)4(31)0a a a ∆=+-+=, 解得12a =-或92a =-【点睛】此题考查的是新定义问题、新定义与反比例函数、新定义与二次函数的综合大题,此题难度较大,涉及知识点较多,掌握相似三角形的性质、利用待定系数法求反比例函数解析式、二次函数与一次函数交点个数与一元二次方程根的判别式的关系和分类讨论的数学思想是解决此题的关键.26.如图,已知二次函数2y ax bx c =++(0a ≠)的图象与x 轴交于点A 和点(2,0)B -,与交y 轴于点(0,4)C ,0()f x 表示当自变量为0x 时的函数值,对于任意实数m ,均有(1)(3)f m f m -=-. (1)求该二次函数的解析式;(2)点Q 是线段AB 上的动点,过点Q 作//QE AC ,交BC 于点E ,连接CQ .当CQE ∆的面积最大时,求点Q 的坐标;(3)若平行于x 轴的动直线l 与该抛物线交于点P ,与直线AC 交于点F ,点D 的坐标为(2,0).是否存在这样的直线l ,使得ODF ∆是等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)2142y x x =-++;(2)(1,0)Q ;(3)存在,点P 的坐标为:(1+或(1-或(1+或(1【解析】【分析】 (1)根据题意即可求出抛物线的对称轴,然后利用抛物线的对称性即可求出点A 的坐标,设二次函数的解析式为(2)(4)y a x x =+-,将点C 的坐标代入即可求出二次函数的解析式,化为一般式即可;(2)设点Q 的坐标为(,0)m ,过点E 作EG x ⊥轴于点G ,根据点A 、B 、C 的坐标即可求出OA 、OB 、OC 、BQ 和AB ,根据相似三角形的判定及性质,即可用含m 的式子表示EG ,然后根据CQE CBQ EBQ S S S ∆∆∆=-即可求出CQE S ∆与m 的二次函数关系式,根据二次函数求最值即可;(3)根据等腰三角形腰的情况分类讨论,分别在每种情况下求出点F 的坐标,然后根据点P 和点F 的纵坐标相等,将点P 的纵坐标代入二次函数解析式中即可求出点P 的横坐标.【详解】解:(1)当1x m =-与3x m =-时函数值相等,可知抛物线的对称轴为1312m m x -+-==, 由点B 的坐标(2,0)-可求得A 点的坐标为(4,0)设二次函数的解析式为(2)(4)y a x x =+-将点(0,4)C 代入,得12a =- 所以,二次函数解析式为2142y x x =-++. (2)设点Q 的坐标为(,0)m ,过点E 作EG x ⊥轴于点G ,如图∵A (4,0),(2,0)B -, (0,4)C ,∴OA=4,OB=2,OC=4, BQ=m+2∴AB=6∵//QE AC ∴BE BQ BC BA = ∵//EG OC ∴BE EG BC CO= ∴EG BQ CO BA =,即246EG m +=, ∴243m EG += ∴CQE CBQ EBQ S S S ∆∆∆=-1122BQ CO BQ EG =•-• ()12BQ CO EG =•- 124(2)(4)23m m +=+- 21(1)33m =--+ 又∵24m -≤≤ 的∴当1m =时,CQE S ∆有最大值3,此时(1,0)Q(3)存在.①若DO DF =,如下图所示则2AD OD DF ===,∴∠DOF=∠DFO ,∠DAF=∠DFA∴∠DOF+∠DAF=∠DFO+∠DFA=∠OFA∴AFO ∆是直角三角形,OF ⊥AC∵OA=OC=4∴点F 为AC 的中点∴根据中点坐标公式:点F 的坐标为4004,(2,2)22++⎛⎫=⎪⎝⎭∵直线l ∥x 轴 ∴点P 的纵坐标=点F 的纵坐标=2,将y=2代入二次函数解析式中,得21422x x -++=,得11x =+21x =此时点P 的坐标为:(12)P +或(12)P -②若FO FD =,过点F 作FM x ⊥轴于点M由等腰三角形的性质得:112OM OD ==, ∴3AM =, 在等腰直角三角形AOC 中,∠OAC=45°∴△AMF 也是等腰直角三角形∴FM=AM=3∴(1,3)F∵直线l ∥x 轴∴点P 的纵坐标=点F 的纵坐标=3,将y=3代入二次函数解析式中,得由21432x x -++=,得11x =,21x =此时,点P 的坐标为:(1P +或(1P③若OD OF =,∵4OA OC ==,且90AOC ∠=o∴AC =∴点O 到AC 的距离为而2OF OD ==<∴AC 上不存在点F 使得2OD OF ==此时,不存在这样的直线l ,使得ODF ∆是等腰三角形综上,存在这样的直线l ,使得ODF ∆是等腰三角形,所求点P 的坐标为:(1+或(1-或(1或(1【点睛】此题考查的是二次函数与几何图形的综合大题,难度系数较大,掌握利用待定系数法求二次函数解析式、把面积最值问题转化为二次函数最值问题和分类讨论的数学思想是解决此题的关键.。
