山东滨州2012届高三期中联考试题(数学理)
山东各市2012高三数学(理)下学期模拟考试题分类解析统计(精)
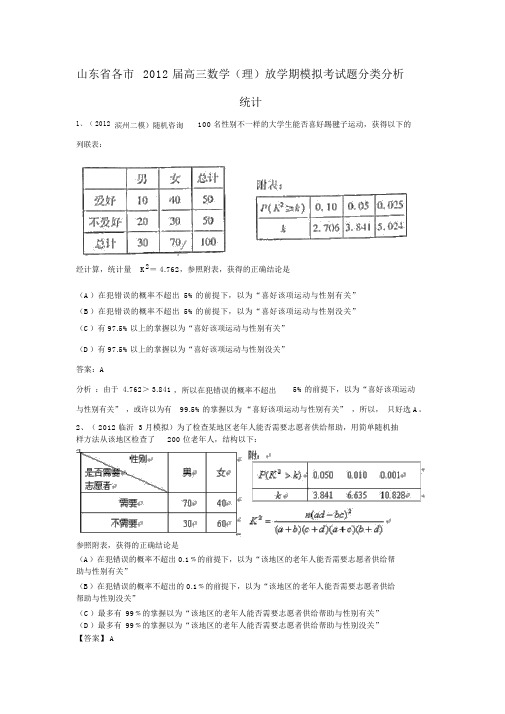
山东省各市2012 届高三数学(理)放学期模拟考试题分类分析统计1、( 2012滨州二模)随机咨询100 名性别不一样的大学生能否喜好踢毽子运动,获得以下的列联表:经计算,统计量K2= 4.762,参照附表,获得的正确结论是(A)在犯错误的概率不超出5%的前提下,以为“喜好该项运动与性别有关”(B)在犯错误的概率不超出5%的前提下,以为“喜好该项运动与性别没关”(C)有 97.5%以上的掌握以为“喜好该项运动与性别有关”(D)有 97.5%以上的掌握以为“喜好该项运动与性别没关”答案:A分析:由于 4.762> 3.841,所以在犯错误的概率不超出5%的前提下,以为“喜好该项运动与性别有关” ,或许以为有99.5%的掌握以为“喜好该项运动与性别有关”,所以,只好选 A。
2、( 2012 临沂 3 月模拟)为了检查某地区老年人能否需要志愿者供给帮助,用简单随机抽样方法从该地区检查了200 位老年人,结构以下:参照附表,获得的正确结论是(A)在犯错误的概率不超出 0.1﹪的前提下,以为“该地区的老年人能否需要志愿者供给帮助与性别有关”(B)在犯错误的概率不超出的 0.1﹪的前提下,以为“该地区的老年人能否需要志愿者供给帮助与性别没关”(C)最多有99﹪的掌握以为“该地区的老年人能否需要志愿者供给帮助与性别有关”(D)最多有99﹪的掌握以为“该地区的老年人能否需要志愿者供给帮助与性别没关”【答案】 A【分析】 由公式可计算K2n(ad bc) 2(a b)(c d )(ac)(b d )200(7060 30 40)2,即 P(K 210.828 ) 0.001,所以在犯错误的概率不100 100 110 90 18.18超出 0.1﹪的前提下, 以为“该地区的老年人能否需要志愿者供给帮助与性别有关” ,答案选A.3、( 2012 临沂二模)为了认识某校今年准备报考翱翔员的学生的体重状况,将所得的数据整理后,画出了频率分布直方图 (如图),已知图中从左到右的前 3 个小组的频率之比为 1:2:3 ,第 2 小组的频数位 12,则抽取的学生人数是 __________ 。
山东省各地市2012年高考数学(理科)最新试题分类大汇编9平面向量

山东省各地市2012年高考数学(理科)最新试题分类大汇编:第9部分:平面向量一、选择题【山东省淄博市第一中学2012届高三第一学期期中理】10、已知在△ABC 中,点D 在BC 边上,且2=,s r +=,则s r +的值为( )A 0B 43C 23D -3【答案】A【山东省青州市2012届高三上学期期中理】4.O 是ABC ∆所在平面内的一点,且满足()(2)0OB OC OB OC OA -⋅+-=,则ABC ∆的形状一定为( ) A .正三角形 B .直角三角形 C .等腰三角形 D .斜三角形 【答案】C【山东省曲阜师大附中2012届高三上学期期中理】11.在ABC ∆中,90C =︒,且CA=CB=3,点M 满足2BM MA =,则CM CB ⋅等于( )A .2B .3C .4D .6 【答案】B【山东省日照市2012届高三上学期期末理】(3)如图所示,已知,,,,2c OC b OB a OA BC AB ====则下列等式中成立的是(A )a b c 2123-=(B )a b c -=2 (C )b a c -=2(D )b a c 2123-=【答案】A 解析:由OB OA OC OC BO (OB AO BC AB 3222+-=+=+=即得,即a b c 2123-=。
【山东省青州市2012届高三2月月考理】11.在△ABC 中,点O 是斜边BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若,AB mAM AC nAN ==,则mn 的最大值为 A . 1 B. 12 C. 14D. 2 【答案】A【山东省临沭一中2012届高三9月调研理】5. 设向量a ,b 均为单位向量,且|a b +|1=,则a 与b 的夹角为( ) A .3π B .2π C .23π D .34π【答案】C【山东省临沭一中2012届高三9月调研理】10.在△ABC 中,2AB =,1AC =,BD =DC ,则AD BD ⋅的值为 ( ) A.-23 B. 23 C.-34 D. 34【答案】C【山东省临沂市2012届高三上学期期中理】10.若等边△ABC 的边长为2,平面内一点M 满足11,32CM CB CA MA MB =+⋅则= ( )A .139B .—139C .89D .—89【答案】D【山东省青岛十九中2012届高三上学期模块检测理】8.设平面向量a =(1,2),b = (-2,y ),若a //b ,则|3a 十b |等于( )A BCD .26【答案】A【山东省莱芜市2012届高三上学期期末检测 理】已知向量m n ⋅的夹角为6π,且|m |3,|n |2,|m n |==-=A.1B.2C.3D.4 【答案】A【山东省济宁一中2012届高三第三次定时检测理】5.已知A ,B ,C 是锐角ABC ∆的三个内角,向量(sin ,1),(1,cos )p A q B =-=,则p q 与的夹角是( ) A .锐角 B .钝角C .直角D .不确定【答案】B【山东省济宁一中2012届高三第三次定时检测理】11.已知||2||0a b =≠且关于x 的函数3211()||32f x x a x a bx =+⋅+⋅在R 上有极值,则a 与b 的夹角范围是( )A .0,6π⎡⎫⎪⎢⎣⎭B .,6ππ⎛⎤⎥⎝⎦C .,3ππ⎛⎤⎥⎝⎦D .2,33ππ⎛⎤⎥⎝⎦【答案】C【山东省济宁一中2012届高三第三次定时检测理】12.已知向量(1,1),(1,1),(2cos )a b c αα==-=,实数m ,n 满足m a n b c +=,则22(3)m n -+的最大值为( ) A .2 B .4C .8D .16【答案】D【山东省鄄城一中2012届高三上学期期中理】3.设向量a b 与的模分别为6和5,夹角为120︒,则||a b +等于 ( )A .23 B .23- C D 【答案】D【山东省实验中学2012届高三第三次诊断理】平面向量a 与b 夹角为32π, a (3,0),|b |2==,则|a 2b |+=( )A.7B.37C.13D.3【答案】C【山东省实验中学2012届高三第三次诊断理】在三角形中,对任意λ都有|A B A C ||A B A λ-≥-,则ABC ∆形状( )A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形 【答案】C【山东省泰安市2012届高三上学期期中理】5.已知平面向量,a b 满足3,3,2,a b b a b ===与的夹角为60°,若(),a mb a -⊥则实数m 的值为 A.1B.32C.2D.3【答案】D【山东省潍坊市寿光现代中学2012届高三12月段考理】平面向量a 与b 的夹角为600,a=(2,0),|b|=1 则|a +2b|=A.3B. 23C.4D.12【答案】B【山东省潍坊市寿光现代中学2012届高三12月段考理】已知a=(-3,2),b=(-1,0),向量λa +b 与a -2b 垂直,则实数λ的值为A.-71 B.71 C. -61 D.61 【答案】A【山东省潍坊市寿光现代中学2012届高三12月段考理】5.已知向量b a d ,R k b a kc b a -=∈+===)(),1,0(),0,1(,如果c ∥d,那么A.k=1且c 与d同向B.k=1且c 与d反向C.k=-1且c 与d同向D.k=-1且c 与d反向【答案】D【山东省潍坊市寿光现代中学2012届高三12月段考理】9.在△ABC 中,M 是BC 的中点,AM=1,点P 在AM 上且满足学PM PA 2=,则)PC PB (PA+·等于 A.94B.34C. 34-D. 94-【答案】D【山东省潍坊市寿光现代中学2012届高三12月段考理】11. 02≠=b a且关于x 的函数x b a x a x x f ··2131)(23++=在R 上有极值,则a 与b 的夹角范围是A. ⎪⎭⎫⎢⎣⎡6,0πB. ⎥⎦⎤⎝⎛ππ,6C. ⎥⎦⎤⎝⎛ππ,3 D. ⎥⎦⎤⎝⎛32,3ππ 【答案】C【山东省潍坊市寿光现代中学2012届高三12月段考理】12. △ABC 的外接圆的圆心为O ,半径为1,若,且2=+=,则向量在向量方向上的射影的数量为( )A.23B.23 C.3D. 23-【答案】A【山东省日照市2012届高三12月月考理】如图所示,已知,,,,2c OC b OB a OA BC AB ====则下列等式中成立的是(A )ab c 2123-=(B )a b c -=2 (C )b a c -=2(D )b a c 2123-=【答案】A 解析:由),(3222+-=+=+=即得,即a b c 2123-=。
2012年山东省滨州市中考数学试卷含答案.docx

2012 年中考真題2012 年山东省滨州市中考数学试卷一.选择题:本大题共12 个小题,在每个小题的四个选项中只有一个是正确的,请把正确的选出来,并将其字母标号填写在答题栏内.每小题选对得 3 分,选错、不选或选出的答案超过一个均记0 分,满分36 分.1.( 2012 滨州)23等于()A .6B. 6C.8D. 8考点:有理数的乘方。
解答:解:238.故选 C.2.( 2012 滨州)以下问题,不适合用全面调查的是()A .了解全班同学每周体育锻炼的时间B .鞋厂检查生产的鞋底能承受的弯折次数C.学校招聘教师,对应聘人员面试D.黄河三角洲中学调查全校753 名学生的身高考点:全面调查与抽样调查。
解答:解: A 、数量不大,应选择全面调查;B、数量较大,具有破坏性的调查,应选择抽样调查;C、事关重大,调查往往选用普查;D、数量较不大应选择全面调查.故选 B .3.( 2012 滨州)借助一副三角尺,你能画出下面哪个度数的角()A .65°B. 75°C. 85° D . 95°考点:角的计算。
解答:解:利用一副三角板可以画出75°角,用45°和 30°的组合即可,故选: B.4.( 2012 滨州)一个三角形三个内角的度数之比为2: 3: 7,这个三角形一定是()A .等腰三角形B.直角三角形C.锐角三角形D.钝角三角形考点:三角形内角和定理。
解答:解:三角形的三个角依次为180°×=30 °, 180°×=45 °, 180°×=105°,所以这个三角形是钝角三角形.故选D.2x1 5.( 2012 滨州)不等式8xA .x 3B .x2考点:解一元一次不等式组。
x1的解集是()4 x1C.2x 3D.空集解答:解:2x1x1①x8 4 x1,②解①得: x 2 ,解②得: x 3 .则不等式组的解集是:x 3 .故选 A .2012 年中考真題6.( 2012 滨州)某几何体的三视图如图所示,则这个几何体是()A .圆柱B .正方体C.球D.圆锥考点:由三视图判断几何体。
山东省各地市2012年高考数学最新联考试题分类大汇编(11)排列组合

一、选择题:
6.(山东省济南市2012年2月高三定时练习理科)三位老师和三位学生站成一排,要求任何两位学生都不相邻,则不同的排法总数为 ( B )
A.720
B. 144
C.36
D.12
10.(山东省烟台市2012年高三诊断性检测理)用0,1,2,3,4排成无重复数字的五位数,要求偶数字相邻,奇数字也相邻,则这样的五位数的个数是( D )
A.36 B.32 C.24 D.20
二、填空题:
15.(山东省潍坊市2012年3月高三一轮模拟理科)某工厂将甲、乙等五名新招聘员工分配到三个不同的车间.每个车间至少分配一名员工,凰甲、乙两名员工必须分到同一个车间,则不同分法的种数为36 。
三、解答题:
- 1 -。
山东省各地市2012年高考数学(理科)最新试题分类大汇编:7:三角函数(2)

山东省各地市2012年高考数学(理科)最新试题分类大汇编:第3部分:三角函数(2)一、选择题【山东省莱州一中2012届高三第一次质检理】3.不解三角形,下列判断正确的是( ) A.30,25,150a b A ===︒,有一解. B.7,14,30a b A ===︒,有两解. C.6,9,45a b A ===︒,有两解.D.9,10,60a b A ===︒,无解.【答案】A【山东省莱州一中2012届高三第一次质检理】5.将函数y f =′()sin x x 的图象向左平移4π个单位,得到函数212sin y x =-的图象,则()f x 是( ) A.2cos xB.cos xC.sin xD.2sin x【答案】D【山东省莱州一中2012届高三第一次质检理】7.已知1,0,tan ,23αβαπ<<π-π<<=-2αβ+=( ) A.34π B.54π D.34π或74π【答案】C【山东省莱州一中2012届高三第一次质检理】9.在地面上某处测得山峰的仰角为θ,对着山峰在地面上前进600m 后,测得仰角为2θ,继续前进后又测得仰角为4θ,则山的高度为( )m . A.200B.300C.400D.500【答案】B【山东省莱州一中2012届高三第一次质检理】11.设函数()sin()(0,0,)22f x A x A ωϕωϕππ=+≠>-<<的图象关于直线23x =π对称,它的周期是π,则下列结论一定..正确的是( ) A.()f x 的图象过点1(0,)2B.()f x 的图象在52,123⎡⎤ππ⎢⎥⎣⎦上是减函数 C.()f x 的最大值为AD.()f x 的一个对称中心是点5(,0)12π 【答案】D【山东省济宁市重点中学2012届高三上学期期中理】11.把函数)(x f y =的图像沿x 轴向右平移2个单位,所得的图像为C ,C 关于x 轴对称的图像为x y 2=的图像,则)(x f y =的函数表达式为 ( )A .22+=x yB .22+-=x yC .22--=x yD .)2(log 2+-=x y【答案】B【山东省济宁市鱼台一中2012届高三第三次月考理】5.给定性质: ①最小正周期为π;②图象关于直线x=3π对称,则下列四个函数中,同时具有性质①、②的是( )A .y = sin(2x +6π)B ..y = sin|x | D .y = sin(2x -6π)【答案】D8.已知sin =+)6(απ31,则 D .31-9.如图为一半径是3米的水轮,水轮4圈,水轮上的点P 到水面的距离y (米)x 2)++ϕωx ,则有 ( )A .3,125==A πω B .2,315A πω==C .5,125==A πω D .2,515A πω== 【答案】B【山东济宁梁山二中2012届高三12月月考理】8. 函数1)cos (sin )(2--=x x x f 是 A.最小正周期为π2的偶函数B.最小正周期为π2的奇函数C.最小正周期为π的偶函数D.最小正周期为π的奇函数【答案】D【山东济宁金乡一中2012届高三12月月考理】6.若函数sin()y A x ωϕ=+(0A >,0ω>,||2πϕ<)在一个周期内的图象如图所示,,M N 分别是这段图象的最高点和最低点,且0OM ON ⋅=,(OA 、6πB 、C 、D 【答案】C【山东济宁金乡一中2012届高三12月月考理】x 的图象,可以将函数y=sin2x 的图象( )A .向右平移π个单位长度 B .向右平移3π个单位长度C π.向左平移π个单位长度sin =+)6(απ31,则cos =-)232(απ( )D.31- 在△ABC 中,已知045,2,2===A b a ,则B 等于A. 30°B. 60°C. 30°或150°D. 60°或120° 【答案】A【山东滨州2012届高三期中联考理10.已知函数()sin (0)f x x x ωωω=>的图象与x 轴的两个相邻交点的距离等于2π,若将函数()y f x =的图象向左平移6π个单位得到函数()y g x =的图象,则()y g x =是减函数的区间为 ( )A. (,0)3π-B. (,)44ππ-C. (0,)3π D. (,)43ππ【答案】D【山东滨州2012届高三期中联考理11.若()2sin()f x x m ωϕ=++,对任意实数t 都有()(),()3888f t f t f πππ+=-=-且,则实数m 的值等于( )A .-1B .5±C .-5或-1D .5或1【答案】C【莱州一中2012高三第三次质量检测理】12.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置(,)P x y .若初始位置为01)2P ,当秒针从0P (注此时0t =)正常开始走时,那么点P 的纵坐标y 与时间关系为A.ππsin()306y t =+B.ππsin()606y t =--C.ππsin()306y t =-+【答案】C【山东济宁汶上一中2012届高三12月月考理】3.若函数)0()32cos(>+=ωπωx y 的图象之间的距离为2π,则=ω.2 D .4 6.已知A ,B ,C 三点的坐标分别是(3,0)A ,3,22ππ⎛⎫⎪⎝⎭,若1AC BC ⋅=- ,则21tan 2sin sin 2ααα++的值为 ( )A .95-B .59-C .2D .3【答案】A【山东济宁汶上一中2012届高三12月月考理】8.如图,圆O 的内接“五角星”与圆O 交与),5,4,3,2,1(=i A i 点,记弧 1i i A A +在圆O 中所对的圆心角为),4,3,2,1(=i a i ,弧51A A 所对的圆心角为5a ,则425312sin 3sin )cos(3cos a a a a a -+=( )A . 23-B .21-C .0D .1【答案】D【山东济宁汶上一中2012届高三12月月考理】12.已知函数R x x A x f ∈+=),sin()(ϕω(其中)22,0,0πϕπω<<->>A ,其部分图象如右图所示,则)(x f 的解析式为 (A )()sin(2)4f x x π=+ (B )()sin(2)4f x x π=- )π()sin()4x x π=+7.函数sin 2y x =的图象经过适当变换可)B .沿x 轴向左平移4π个单位 D .沿x 轴向右平移2π个单位8.下列命题错误的是( ) A .在ABC ∆中,“A B >”是“sin sin A B >”的充要条件;B .点(,0)8π为函数()tan(2)4f x x π=+的一个对称中心;C .若||1,||2a b ==,向量a 与向量b 的夹角为120°,则b 在向量a 上的投影为1;D .“s i n s i n αβ=”的充要条件是“(21)k αβπ+=+或2k αβπ-=(k Z ∈)”. 【答案】C【山东聊城莘县实验高中2012届高三上学期期中】10.在ABC ∆中,若有2cos 22a b Cb +=,则ABC ∆的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .直角三角形或锐角三角形 【答案】B【山东聊城莘县实验高中2012届高三第三次月考理】2.若1sin 34πα⎛⎫-= ⎪⎝⎭,则cos 23πα⎛⎫+ ⎪⎝⎭=( )A .78-B .14-C .14D .7【答案】A二、填空题【山东省莱州一中2012届高三第一次质检理】56π<,则cos θ= .14.ABC ∆中,A B C 、、所对的边长2AB BC ⋅=-,则b = .13. 已知角α的终边经过点P (,6)x -,. 【山东省济宁市鱼台一中2012届高三第三次月考理】16. 在,90Rt ABC C ∆∠=中,且A ∠.B ∠.C ∠所对边分别为,,a b c ,若a b c x +=,则实数x 的取值范围为__________.【答案】(【山东济宁金乡一中2012届高三12月月考理】16.给出下列命题: (1)在△ABC 中,若A <B ,则sinA <sinB ;(2)将函数)32sin(π+=x y 的图象向右平移3π个单位,得到函数y=sin2x 的图象; (3)在△ABC 中, 若AB=2,AC=3,∠ABC=3π,则△ABC 必为锐角三角形; (4)在同一坐标系中,函数sin =y x 的图象和函数2=xy 的图象有三个公共点;其中正确命题的序号是 (写出所有正确命题的序号)。
山东省各地市2012年高考数学(理科)最新试题分类大汇编6数列(3)

山东省各地市2012年高考数学(理科)最新试题分类大汇编:第6部分:数列(3)一、选择题【山东省微山一中2012届高三10月月考理】3.已知n S 为等差数列{}n a 的前n 项的和,254,a a +=,721S =,则7a 的值为 ( )A . 6B .7C .8D .9 答案: D解析: 由条件254,a a +=721S =可转化为1254,a d +=133,a d +=解得:13,2,a d =-=73629,a =-+⨯=这里考查等差数列通项公式与求和公式以及解方程组. 【山东省潍坊市2012届高三上学期期中四县一校联考理】7.在等比数列{}n a 中,5,6,64821=+=⋅<+a a a a a a n n ,则75a a 等于 A.65 B.56 C.32 D.23 【答案】D【山东省潍坊市2012届高三上学期期中四县一校联考理】11.已知等差数列{}n a 的公差为)0(≠d d ,且32131063=+++a a a a ,若8=m a ,则m 为A.12B.10C.8D.4【答案】C【山东省淄博市第一中学2012届高三第一学期期中理】11、等差数列{a n }的公差不为零,首项a 1=1,a 2是a 1和a 5的等比中项,则数列{a n }的前10项之和是 ( )A 90B 100C 145D 190 【答案】B【山东省实验中学2012届高三上学期第一次诊断性考试理】4.已知{〜;}为等差数列,其公差为-2,且O 7是屮与〜的等比中项,为的前n项和,,则的值为( ) (A). -110 (B). -90(C). 90 (D). 110【答案】D【山东省滕州二中2012届高三上学期期中理】6: 设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( )A .63B .45C .36D .27【答案】B【山东省青州市2012届高三上学期期中理】9.已知{}n a 为等差数列,{}n b 为等比数列,其公比1q ≠,且10(1,2,,)b i n >=,若111111,,a b a b ==则( )A .66a b >B .66a b =C.66a b < D .6666a b a b <<或【答案】A【山东省曲阜师大附中2012届高三上学期期中理】4.等差数列{}n a 的前n 项和为n S ,已知57684,2a a a a +=+=-,则当n S 取最大值时n 的值是( ) A .5 B .6C .7D .8【答案】B【山东省曲阜师大附中2012届高三上学期期中理】12.已知正项等比数列{}n a 满足7652a a a =+,若存在两项,m n a a14a =,则14m n+的最小值为( )A .32B .53C .256 D .43【答案】A【山东省青州市2012届高三2月月考理】3.已知n S 为等差数列{}n a 的前n 项的和,254a a +=,721S =,则7a 的值为A .6B .7C .8D .9【答案】D【山东省临沭一中2012届高三9月调研理】4.已知{}n a 为等差数列,若9843=++a a a ,则9S =( )A.24B. 27C. 15D. 54 【答案】B【山东省临沭一中2012届高三9月调研理】9. 已知等比数列{}n a 中,公比1q >,且168a a +=, 3412a a =,则20112006a a =( ) .2A .3B .6C .36D 或 【答案】B【山东省临沂市2012届高三上学期期中理】3.设n S 为等比数列{}n a 的前n 项和,2580a a -=,则42S S = ( ) A .5 B .8C .-8D .15【答案】A【山东省青岛市2012届高三期末检测 理】7.等差数列{}n a 中,已知16a =-,0n a =,公差d ∈N *,则n ()3n ≥的最大值为 A .7B .6C .5D .8【答案】A【山东省济宁一中2012届高三第三次定时检测理】2.在等差数列{}n a 中,若4812120a a a ++=,则112014a a -的值是( ) A .30 B .45C .50D .80【答案】A【山东省济宁一中2012届高三第三次定时检测理】4.设{}n a 是由正数组成的等比数列,nS 为其前n 项和,已知2431,7,S n a a s ⋅==则= ( )A .152B .314C .334D .172【答案】B【山东省济宁一中2012届高三第三次定时检测理】9.各项均为正数的等比数列{}n a 的前n项和为n S ,若32,14,n n S S ==则4n S 等于 ( ) A .80 B .30C .26D .16【答案】B【山东省实验中学2012届高三第三次诊断理】数列{n a }满足22,11==a a ,),2(111N n n a a a a a a nnn n n n ∈≥-=++--,则13a 等于( ) A.26 B.24 C.122×12! D.!13213⨯ 【答案】D【山东省济宁一中2012届高三第三次定时检测理】10.已知函数log (1)3(0,1)a y x a a =-+>≠所过定点的横、纵坐标分别是等差数列{}n a 的第二项与第三项,若11n n n b a a +=⋅,数列{}n b 的前n 项和为n T ,则10T =( )A .911B .1011C .1D .1211【答案】B【山东省实验中学2012届高三第三次诊断理】在等差数列}{n a 中,24)(3)(2119741=++++a a a a a ,则此数列前13项的和=13S ( )A.13B.26C.52D.156 【答案】B【山东省潍坊一中2012届高三阶段测试理】5.已知等比数列{}n a 中,21=a ,且有27644a a a =,则=3aA.1B.2C.41D.21【答案】A【山东省潍坊一中2012届高三阶段测试理】若数列{}n a 中,,,10987,654,32,14321⋯+++=++=+==a a a a 则=10aA.1540B.500C.505D.510【答案】C【山东省泰安市2012届高三上学期期中理】3.已知等差数列{}n a 的n 项和为n S ,且满足32S S 132-=,则数列{}n a 的公差是 A.12B.1C.2D.3【答案】C【山东省莱芜市2012届高三上学期期末检测 理】已知数列{}n a 是首项为2,公差为1的等差数列,{}n b 是首项为1,公比为2的等比数列,则数列{}n b a 前10项的和等于A.511B.512C.1023D.1033 【答案】D二、填空题【山东省临沭一中2012届高三12月理】15. 已知等差数列{}n a 满足:*1(N )n n a a n +>∈,11a =,该数列的前三项分别加上1,1,3后顺次成为等比数列{}n b 的前三项. 求数列{}n b 的通项公式n b =_______________【答案】n 2【山东省淄博市第一中学2012届高三第一学期期中理】15、在递增等比数列{a n }中,a 7·a 11=6,a 4+a 14=5,则a 20a 10等于____________________ 【答案】 32【山东省青州市2012届高三上学期期中理】16.已知数列{}n a 中,11211,241n n a a a n +==+-,则n a = 。
山东省各地市2012年高考数学(理科)最新试题分类大汇编3函数(3)

山东省各地市2012年高考数学(理科)最新试题分类大汇编:第3部分:函数(3)一、选择题【山东省阳信一中2012届高三上学期期末理】13.曲线)0(42≤--=x x y 的长度为 【 】A .32π B .23πC .π2D .π 【答案】D【山东枣庄市2012届高三上学期期中理】6.已知4(7),0,()(2012)log (),0.f x x f x f x x -≥⎧=⎨-<⎩则等于( )A .-1B .0C .1D .2【答案】C【山东枣庄市2012届高三上学期期中理】9.在函数||([1,1])y x x =∈-的图象上有一点(,||)P t t ,此函数图象与x 轴、直线1x x t =-=及围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图象可表示为 ( )【答案】B【山东枣庄市2012届高三上学期期中理】10.对于函数2()c o s ,,,f x a x b x c a b c R =++∈其中,适当地选取,,a b c 的一组值计算(1)(1)f f -和,所得出的正确结果只可能...是 ( ) A .4和6 B .3和-3C .2和4D .1和1【答案】D【山东枣庄市2012届高三上学期期中理】12.对实数a b 和,定义运算“⊗”:,,,.a ab a b b a b ≤⎧⊗=⎨<⎩设函数22()(1)(),.f x x x x x R =-⊗-∈若函数()y f x c =-恰有两个不同的零点,则实数c 的取值范围是( )A .3(,1)(,0)4-∞-⋃- B .3{1,}4--C .3(1,)4--D .3(,1)[,0)4-∞-⋃-【答案】A【山东省枣庄市2012届高三上学期期末理】4.函数x y 24-=的值域是A.[)+∞,0B.[]2,0C.[)2,0D.(0,2)【答案】C【山东省枣庄市2012届高三上学期期末理】10.设,32m ba==且,211 =+ba 则=m A.6B.6C.12D.36【答案】A【烟台市莱州一中2012届高三模块检测理】3.函数x xx f lg 1)(+-=的零点所在的区间是A.(0,1)B.(1,2)C.(2,3)D.(3,10) 【答案】C【烟台市莱州一中2012届高三模块检测理】10.已知⎪⎪⎩⎪⎪⎨⎧>≤⎪⎭⎫⎝⎛=)0()0(21)(21x x x x f x ,若1)(0>x f ,则0x 的取值范围是A.(0,1)B.(-),0()0,+∞⋃∞C.),1()0,(+∞⋃-∞D.(1,+)∞ 【答案】C11.【烟台市莱州一中2012届高三模块检测理】函数221ln )(x x x f -=的大致图像是【答案】B【山东潍坊诸城一中2012届高三10月阶段测试理】3.已知函数⎩⎨⎧≤+>=0,10,2)(x x x x x f ,若0)1f(f(a)=+,则实数a 的值等于A.-3B.-1C.1D.3 【答案】A【山东潍坊诸城一中2012届高三10月阶段测试理】具有性质:)()1(x f xf -=的函数,我们称为满足“倒负”变换的函数,下列函数:①x 1x -=y ;②x1x y +=;③y= )1(1)1(,0)10(,>-=<<x xx x x 中满足“倒负”变换的函数是A.①②B.①③C.②③D.只有①【答案】B【山东潍坊诸城一中2012届高三10月阶段测试理】已知函数lnx x g(x),2x f(x)x +=+=,1x x h(x)--=的零点分别为21x ,x ,3x 则21x ,x ,3x 的大小关系是A.321x x x <<B.312x x x <<C.231x x x <<D.123x x x << 【答案】A【山东潍坊诸城一中2012届高三10月阶段测试理】下列函数中,在其定义域内既是奇函数又是减函数的是A.)0(1≠∈=x R x xy 且 B.)()21(R x y x ∈=C.)(R x x y ∈=D.)(3R x x y ∈-=【答案】D【山东师大附中2012届高三第一次阶段测试理】5.若函数xa x x x f ))(1()(+-=为奇函数,则a 的值为( )A. 2B. 1C. -1D. 0【答案】B【山东师大附中2012届高三第一次阶段测试理】6.已知函数⎪⎩⎪⎨⎧≥<<--≤+=)2(2),22()2(2)(2x x x x x x x f 若8)(=a f ,则a 等于( )A.6B.22±C.4D.-6【答案】C【山东师大附中2012届高三第一次阶段测试理】7. 下列函数)(x f 中,满足“对任意),0(,21+∞∈x x ,当21x x <时,都有)()(21x f x f >”的是( )A.xx f 1)(=B.2)1()(-=x x f C.xe xf =)(D.)1ln()(+=x x f【答案】A【山东师大附中2012届高三第一次阶段测试理】8. 设0>abc ,二次函数c bx ax x f +-=2)(的图象不.可能是( )【答案】D【山东师大附中2012届高三第一次阶段测试理】9.若函)1(-=x f y 的图象与x y ln =的图象关于直线x y =对称,则)(x f 为( ) A.xe xf =)( B. 1)(+=x ex fC. 1)(-=x e x fD.)1ln()(+=x x f【答案】B【山东师大附中2012届高三第一次阶段测试理】10. 已知偶函数)(x f 满足)()2(x f x f -=+,当]2,0[∈x 时,22)(x x f =,则)2011(f 为( )A. 2B.0C.-2D.1【答案】A【山东师大附中2012届高三第一次阶段测试理】11.若方程0232=--k x x 在(-1,1)上有实根,则k 的取值范围为( )A.)21,169[--B.)25,21[-C.)25,169[-D.),169[+∞-【答案】C【山东师大附中2012届高三第一次阶段测试理】12. 已知定义在R 上的奇函数)(x f ,满足)()4(x f x f -=-,且在区间[0,2]上是增函数,若方程)0()(>=m m x f 在区间[-8,8]上有四个不同的根4321,,,x x x x ,则4321x x x x +++=( ) A. 0B. 8C. -8D. -4【答案】C【山东实验中学2012届高三第一次诊断性考试理】7. 函数的一个零点落在下列哪个区;间 (.)(A) (0,1) (B). (1,2) (C). (2,3) (D). (3,4) 【答案】B【解析】根据函数的实根存在定理,要验证函数的零点的位置,只要求出函数在区间的两个端点上的函数值,得到结果。
山东省各市2012届高三数学(理)下学期模拟考试题分类解析--复数

山东省各市2012届高三数学(理)下学期模拟考试题分类解析复数1、(2012滨州二模)设z =1+i (i 是虚数单位),则22z z+= (A )-1-i (B )-1+i(C )1-i (D )1+i答案:D 解析:22z z+=22(1)1i i +++=1-i +2i =1+i ,选D 。
2、(2012德州二模)若复数12a i i--是纯虚数,则实数a 的值为 A .-2 B .12- C .2 D .25- 答案:A解析:12a i i --=()(12)221(12)(12)55a i i a a i i i -++-=+-+,由25a +=0,得a =-2,所选A 。
3、(2012德州一模)若复数211z (x )(x )i =-+-为纯虚数,则实数x 的值为( )A .1-B .0C .1D .1-或1答案:A解析:由纯虚数的概念可得:21010x x ⎧-=⎨-≠⎩,所以,x =-1,选A 。
4、(2012济南3月模拟)复数1+i 4+3i的虚部是 A. 1i 25 B. 125 C. 125- D. 1i 25- 【答案】B 【解析】i i i i i i i i 251251251)34)(34()34)((1(341+=+=-+-+=++,所以虚部为251,选B. 5、(2012济南三模)i 是虚数单位,能使得i i n n ⋅-=+2)1(2成立的成立的最小正整数是 答案:3解析:由i i n n ⋅-=+2)1(2,得i i i n n n n ⋅-=⋅=22)2(,所以i i n -=,即N k k n ∈+=,34,所以最小的正整数为3。
6、(2012临沂3月模拟)复数=+++ii i i 1432 (A )i 2121+ (B )i 2121- (C )i 2121+- (D )i 2121-- 【答案】D 【解析】i i i i i i i i i i i i i i 212121)1)(1()1(11111432--=--=-+--=+-=++--=+++,选D. 7、(2012临沂二模)若纯虚数z 满足(2)4i z bi -=-,(i 是虚数单位,b 是实数),则b =(A )8 (B )8- (C )2 (D )2-【答案】B【解析】因为z 是纯虚数,所以设)0(,≠=a ai z ,则bi i ai -=-4)2(,即bi ai a -=+42,根据复数相等,得82,4==-=a b a ,所以8-=b ,选B.8、(2012青岛二模). 设复数21z i =+(其中i 为虚数单位),则23z z +的虚部为 A .2iB .0C .10-D .2 【答案】D【解析】i iz 2121-=+=,所以i i z 43)21(22--=-=,i z 21+=,所以i i i z z 2)21(34332=++--=+,所以虚部为2,选D.9、(2012青岛3月模拟)已知复数z 满足()21i z i -=+,i 为虚数单位,则复数z = . 答案:1355i + 【解析】()()12113.255i i i i z i ++++===- 10、(2012日照5月模拟)已知i 为虚数单位,复数ii z -+=121,则复数z 的虚部是 (A )i 21- (2)21- (C)i 23 (D )23 答案:D 【解析】i i i i i i i i z 2321231)1)(1()1)(21(121+-=+-=+-++=-+= ,∴复数z 的虚部是23.选D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省滨州市2012届高三期中联考试题数学试题2011.10一、选择题1. 已知全集{}1,2,3,4,5,6,7,8U =,集合{}6,3,2=A 和{}60<<∈=x N x B 的关系 如图所示,则阴影部分所示的集合是: ( ) A .{}N x x x ∈≤<,42 B .{}6,5,4,1C .{}2,3D .{}N x x x ∈≤≤,422.已知命题:,sin 1p x R x ∃∈≤,则( ) A .:,sin 1p x R x ⌝∃∈≥ B .:,sin 1p x R x ⌝∀∈≥C .:,sin 1p x R x ⌝∃∈>D .:,sin 1p x R ⌝∀∈>3. 函数)13lg(13)(2++-=x xx x f 的定义域是( )A .),31(+∞-B . )1,31(- C . ]1(,13-D . )31,(--∞4. 等差数列}{n a 的前n 项和为30,1191=++a a a S n 若,那么13S 值的是( ) A .65 B .70C .130D .2605、已知sin =+)6(απ31,则cos =-)232(απ( ) A.97 B.31 C.97- D.31- 6. 已知偶函数()f x 在区间[0,)+∞单调递增,则满足(21)f x -<1()3f 的x 取值范围是( )A .(13,23) B .(∞-,23) C .(12,23) D .⎪⎭⎫⎝⎛+∞,32 7. 在△ABC 中,已知045,2,2===A b a ,则B 等于 ( )A. 30°B. 60°C. 30°或150°D. 60°或120°8. 设)(x f 是),(+∞-∞上的奇函数,)()2(x f x f -=+,当10≤≤x 时,x x f =)(,则)5.47(f 等于 ( ) A .0.5 B .5.0- C .1.5 D . 5.1- 9. 已知函数⎩⎨⎧>+-≤-=2,3)1(log 2,1)(x x x ax x f a 是定义域上的单调函数,则a 的取值范围是( )A. ()+∞,1B. [)+∞,2C. ()2,1D. (]2,110.已知函数()sin (0)f x x x ωωω=>的图象与x 轴的两个相邻交点的距离等于2π,若将函数()y f x =的图象向左平移6π个单位得到函数()y g x =的图象,则()y g x =是 减函数的区间为 ( ) A. (,0)3π-B. (,)44ππ-C. (0,)3πD. (,)43ππ11.若()2sin()f x x m ωϕ=++,对任意实数t 都有()(),()3888f t f t f πππ+=-=-且,则实数m 的值等于( )A .-1B .5±C .-5或-1D .5或112.函数32()393,f x x x x =--+若函数()()[2,5]g x f x m x =-∈-在上有3个零点,则m的取值范围为 ( )A .(-24,8)B .(-24,1]C .[1,8]D .[1,8)二、填空题13已知21cos sin =-αα,且0,2π⎛⎫α∈ ⎪⎝⎭,则cos 2sin 4πα⎛⎫α- ⎪⎝⎭的值为 14.数列{}n a 对一切正整数n 都有21n n S a =-,其中n S 是{a n }的前n 项和,则3a =15.设函数2()()f x g x x =+,曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+,则曲线()y f x =在点(1,(1))f 处切线的斜率为 16.给出下列命题: ①存在(0,)2x π∈,使1sin cos ;3x x += ②存在区间(a ,b ),使cos y x =为减函数而sin 0;x < ③tan y x =在其定义域内为增函数; ④2cos sin()2y x x π=+-既有最大值和最小值,又是偶函数;⑤sin |2|6y x π=+的最小正周期为.π其中错误..的命题为 。
(把所有符合要求的命题序号都填上) 三、解答题17.已知,1||,2||==b aa与b的夹角为3π,若向量b k a +2与b a +垂直, 求k.18.在△ABC 中,内角A ,B ,C 所对边长分别为,,a b c ,8AB AC ⋅=,BAC θ∠=,4a =.(Ⅰ)求b c ⋅的最大值及θ的取值范围;(Ⅱ)求函数22()()2cos 4f πθθθ=++-.19. 如图,正在海上A 处执行任务的渔政船甲和在B 处执行任务的渔政船乙,同时收到同一片海域上一艘渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km 的C 处,渔政船乙在渔政船甲的南偏西20°方向的B 处,两艘渔政船协调后立即让渔政船甲向渔船丙所在的位置C 处沿直线AC 航行前去救援,渔政船乙仍留在B 处执行任务,渔政船甲航行30km 到达D 处时,收到新的指令另有重要任务必须执行,于是立即通知在B 处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿直线BC 航行前去救援渔船丙),此时B 、D 两处相距42km ,问渔政船乙要航行多少距离才能到达渔船丙所在的位置C 处实施营救.20.已知等差数列{}n a 和正项等比数列{}n b ,111==b a ,1073=+a a , 3b =4a (1)求数列{}n a 、{}n b 的通项公式(2)若n n n b a c ∙=,求数列{}n c 的前n 项和n T21.已知函数()21,(),f x x g x x x R =+=∈,数列{},{}n n a b 满足条件:*111,()(),n n n a a f b g b n N +===∈.(1)求证:数列{1}n b +为等比数列;(2)令12,n n n n n c T a a +=⋅是数列{}n c 的前n 项和,求使20112012n T >成立的最小的n 值.22. 设函数3()3(0)f x x ax b a =-+≠.(Ⅰ)若曲线()y f x =在点(2,())f x 处与直线8y =相切,求,a b 的值; (Ⅱ)求函数()f x 的单调区间与极值点.山东省无棣第一中学2012届高三期中联考模拟试题数学试题一、选择题CDBCC AABDD CD 二、填空题 13.214-14. 4 15. 4 16. ①②③⑤ 三、解答题17.解:3πcos ||||b a b a =⋅=2×1×21=1.∵b k a+2与b a +垂直,∴(b k a+2))(b a+⋅= 0,∴20222=++⋅+b k b a k b a a ⇒ k = - 5. 18.解(Ⅰ)cos 8bc θ⋅= 2222c o s 4b c b cθ+-= 即2232b c += ……………………2分 又222b c bc +≥,所以16bc ≤,即bc 的最大值为16………………4分 即816cos θ≤ 所以 1cos 2θ≥, 又0<θ<π 所以0<θ3π≤ ……6分(Ⅱ)()[1cos(2)]1cos 22cos 212f πθθθθθ=-+++=++2sin(2)16πθ=++ ……………………………………………9分因0<θ3π≤,所以6π<5266ππθ+≤, 1sin(2)126πθ≤+≤ ………10分当5266ππθ+= 即3πθ=时,min 1()2122f θ=⨯+= ……………11分当262ππθ+=即6πθ=时,max ()2113f θ=⨯+= ……………12分19.解:设ABD α∠=,在△ABD 中,AD=30,BD=42,60BAD ︒∠=,由正弦定理得:sin sin AD BDBADα=∠,sin sin AD BAD BD α=∠30sin 6042︒==,又∵AD <BD ∴60α︒︒0<<,11cos 14α==()1cos cos 607BDC α∠=+=-,在△BDC 中,由余弦定理得:()222222cos 40428042cos 603844BC DC BD DC BD BDC α︒=+-⋅∠=+-⨯+=∴()62BC km =答:渔政船乙要航行62km 才能到达渔船丙所在的位置C 处实施营救. 20.)∵ n n n b a c ⋅==12-⋅n n∴ n T =1212232221-⨯++⨯+⨯+⨯n n∴ n T 2 = n n n n 22)1(2322211321⨯+⨯-++⨯+⨯+⨯- 以上两式相减,得-n T =n n n 22222121⨯-++++- ………………………9分=n n n 221)21(1⨯---⨯=12)1(-⨯-n n ∴ n T =12)1(+⨯-nn ………………………………………………………………12分21.解:(1) 证明:由题意得121n n b b ++=,∴ 11222(1)n n n b b b ++=+=+ ···························· 3分又 ∵ 11211a b =+=∴ 110110b b =+=≠, ················································································· 4分 故数列{b n + 1}是以1为首项,2为公比的等比数列 ································· 5分(2) 由 (1) 可知,112n n b -+=,∴ 2121n n n a b =+=- ············································· 7分故1112211(21)(21)2121n n n n n n n n n c a a +++===----- ············································· 9分∴ 12n n T c c c =+++11111111(1)()()1337212121nn n ++=-+-++-=---- ··························· 10分 由20112012n T >,且*n N ∈,解得满足条件的最小值为10 ·································· 12分 22.解:(Ⅰ)()'233fx x a =-,∵曲线()y f x =在点(2,())f x 处与直线8y =相切,∴()()()'203404,24.86828f a a b a b f ⎧=-=⎧=⎧⎪⎪⇒⇒⎨⎨⎨=-+==⎪⎩⎪⎩⎩(Ⅱ)∵()()()'230f x x aa =-≠,当0a <时,()'0f x >,函数()f x 在(),-∞+∞上单调递增, 此时函数()f x 没有极值点.当0a >时,由()'0f x x =⇒=当(,x ∈-∞时,()'0f x >,函数()f x 单调递增,当(x ∈时,()'0f x <,函数()f x 单调递减,当)x ∈+∞时,()'0f x >,函数()f x 单调递增,∴此时x =()f x 的极大值点,x =()f x 的极小值点.。
