概率论习题解答3

合集下载

概率论第三章部分习题解答

ydxdy.
定理1 cov(X ,Y ) E( XY ) E( X )E(Y )
定理2 若X与Y 独立，则：covX ,Y 0. 逆命题不成立。
注设X与Y是任两个随机变量，
10
D( X Y ) D( X ) D(Y ) 2cov(X ,Y )
2、X与Y 的相关系数
定义 R( X ,Y ) cov( X ,Y )
EX
xf
xdx
1
二、二维随机变量的数学期望
（1）设二维离散随机变量(X,Y)的联合概率函数为p(xi , yj)，则
随机变量X及Y 的数学期望分别定义如下：
EX xi p xi , y j , EY y j p xi , y j .
i j
ji
即： EX xi pX xi , EY y j pY y j .
第三章随机变量的数字特征
（一）基本内容一、一维随机变量的数学期望
定义1：设X是一离散型随机变量，其分布列为：
X x1 x2 xi
P p( x1 ) p( x2 )p( xi )
则随机变量X 的数学期望为: EX xi pxi
i
定义2：设X是一连续型随机变量，其分布密度为 f x,
则随机变量X的数学期望为
i
j
假定级数是绝对收敛的.
（2）设二维连续随机变量(X,Y)的联合概率密度为f(x, y)，则
随机变量X及Y 的数学期望分别定义如下：
EX
xf
x,
ydxdy,
EY
yf x, ydxdy.
即：EX
xf X x dx,
EY
yfY y dy.
2
假定积分是绝对收敛的.

概率统计练习题3答案

概率统计练习题3答案《概率论与数理统计》练习题3答案考试时间：120分钟题目部分，一、选择题1、设A,B,C 为随机试验中的三个事件，则A?B?C等于()。

A、A?B?C B、A?B?C C、A?B?C D、A?B?C 答案：B 2、同时抛掷3枚匀称的硬币，则恰好有两枚正面向上的概率为()。

A、B、C、0125.D、答案：D 3、设?是一个连续型变量，其概率密度为?(x)，分布函数为F(x)，则对于任意x 值有()。

A、P(??0)?0 B、F?(x)??(x)C、P(??x)??(x)D、P(??x)?F(x) 答案：A 4、设?,?相互独立，并服从区间[0，1]上的均匀分布则()。

A、?????服从[0，2]上的均匀分布，B、?????服从[??1，1]上的均匀分布，C、??Max{?,?}服从[0，1]上的均匀分布，D、(?,?)服从区域?答案：D5、随机变量?服从[?3, 3]上的均匀分布，则E(?)?()。

A、3 B、2?0?x?1上的均匀分布0?y?1?9 C、9D、18 2答案：A 试卷答案第 1 页6、D??4, D??1, ????，则D(3??2?)?()。

A、40B、34C、D、答案：C7、设?1,?2,???,?100服从同一分布，它们的数学期望和方差均是2，那么n??P?0???i?4n??()。

i?1??A、12n?111B、C、D、2n22nn答案：B8、设T~t(n),则T2~()。

A、t(2n) 答案：D9、设某种零件的寿命Y~N(?,?2)，其中?和?均未知。

现随机抽取4只，测得寿命(单位小时)为1502,1453,1367,1650，则用矩法估计可求得2B、?2(n) C、F(n,1)D、F(1, n) ?2=___________。

?=________ __,??答案：1493,14069 10、设对统计假设H0构造了一种显著性检验方法,则下列结论错误的是()。

概率论练习册答案第三章

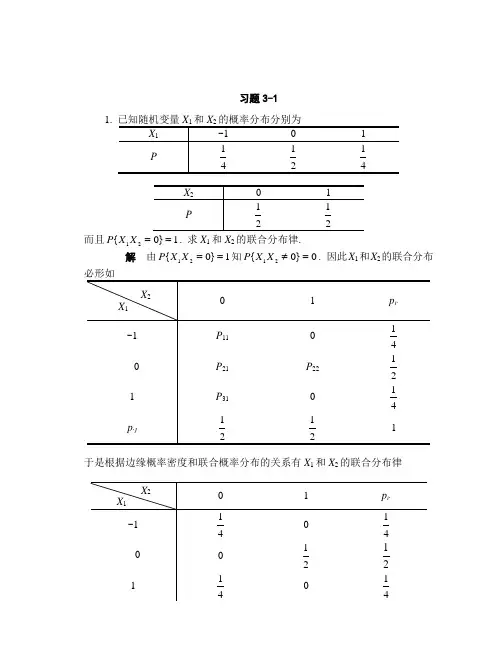
习题3-11.而且12{0}1P X X ==. 求X 1和X 2的联合分布律.解由12{0}1P X X ==知12{0}0P X X ≠=. 因此X 1和X 2的联合分布于是根据边缘概率密度和联合概率分布的关系有X 1和X 2的联合分布律(2) 注意到12{0,0}0P X X ===, 而121{0}{0}04P X P X =⋅==≠, 所以X 1和X 2不独立.2. 一盒子中有3只黑球、2只红球和2只白球, 在其中任取4只球. 以X 表示取到黑球的只数, 以Y 表示取到红球的只数. 求X 和Y 的联合分布律.解从7只球中取4球只有3547=C 种取法. 在4只球中, 黑球有i 只, 红球有j 只(余下为白球4i j --只)的取法为4322i j i j C C C --,0,1,2,3,0,1,2,i j i j ==+≤4.于是有0223221{0,2}3535P X Y C C C ====,1113226{1,1}3535P X Y C C C ====,1213226{1,2}3535P X Y C C C ====,2023223{2,0}3535P X Y C C C ====,21132212{2,1}3535P X Y C C C ====,2203223{2,2}3535P X Y C C C ====,3013222{3,0}3535P X Y C C C ====, 3103222{3,1}3535P X Y C C C ====,{0,0}{0,1}{1,0}{3,2}0P X Y P X Y P X Y P X Y ============.3. (,)(6),02,24,0,.f x y k x y x y =--<<<<⎧⎨⎩其它求: (1) 常数k ; (2) {1,3}P X Y <<; (3) { 1.5}P X <; (4) {4}P X Y +≤.解 (1) 由(,)d d 1f x y x y +∞+∞-∞-∞=⎰⎰, 得2424222204211d (6)d (6)d (10)82y k x y x k y x x y k y y k =--=--=-=⎡⎤⎢⎥⎣⎦⎰⎰⎰, 所以 18k =. (2) 3121,31{1,3}d (6)d 8(,)d d x y P X Y y x y x f x y x y <<<<==--⎰⎰⎰⎰1322011(6)d 82y x x y =--⎡⎤⎢⎥⎣⎦⎰321113()d 828y y =-=⎰. (3) 1.51.5{ 1.5}d (,)d ()d X P X x f x y y f x x +∞-∞-∞-∞<==⎰⎰⎰4 1.521d (6)d 8y x y x --=⎰⎰1.5422011(6)d 82y x x y =--⎡⎤⎢⎥⎣⎦⎰ 421633()d 882y y =-⎰ 2732=. (4) 作直线4x y +=, 并记此直线下方区域与(,)0f x y ≠的矩形区域(0,2)(0,4)⨯的交集为G . 即:02,0G x y <<<≤4x -.见图3-8. 因此{P X Y +≤4}{(,)}P X Y G =∈(,)d d Gf x y x y =⎰⎰44201d (6)d 8x y x y x -=--⎰⎰ 4422011(6)d 82xy x x y -=--⎡⎤⎢⎥⎣⎦⎰ 42211[(6)(4)(4)]d 82y y y y =----⎰ 42211[2(4)(4)]d 82y y y =-+-⎰423211(4)(4)86y y =----⎡⎤⎢⎥⎣⎦23=. 图3-8 第4题积分区域4. 二维随机变量(,)X Y 的概率密度为2(,),1,01,0,f x y kxy x y x =⎧⎨⎩≤≤≤≤其它. 试确定k , 并求2{(,)},:,01P X Y G G x y x x ∈≤≤≤≤.解由21114001(,)d d d (1)d 26x k kf x y xdy x kxy y x x x +∞+∞-∞-∞====-⎰⎰⎰⎰⎰,解得6=k .因而 2112401{(,)}d 6d 3()d 4x xP X Y G x xy y x x x x ∈==-=⎰⎰⎰. 5. 设二维随机变量(X , Y )概率密度为4.8(2),01,0,(,)0,.y x x y x f x y -=⎧⎨⎩≤≤≤≤其它求关于X 和Y 边缘概率密度.解 (,)X Y 的概率密度(,)f x y 在区域:0G ≤x ≤1,0≤y ≤x 外取零值.因而, 有24.8(2)d ,01,()(,)d 0,2.4(2),01,0,x X y x y x f x f x y y x x x +∞-∞-<<==-<<=⎧⎪⎨⎪⎩⎧⎨⎩⎰⎰其它.其它.124.8(2)d ,01,()(,)d 0,2.4(34),01,0,yY y x x y f y f x y x y y y y +∞-∞-<<==-+<<=⎧⎪⎨⎪⎩⎧⎨⎩⎰⎰其它.其它. 6. 假设随机变量U 在区间[-2, 2]上服从均匀分布, 随机变量 1,1,1,1,U X U --=>-⎧⎨⎩若≤若 1,1,1, 1.U Y U -=>⎧⎨⎩若≤若试求：(1) X 和Y 的联合概率分布；(2){P X Y +≤1}.解(2){P X Y +≤1}1{1}P X Y =-+>1{1,1}P X Y =-==12133=-=. 习题3-21. 设(X , Y )的分布律为求: (1) 在条件X =2下Y 的条件分布律;(2){22}P X Y ≥≤.解 (1) 由于6.02.01.003.0}2{=+++==X P ,所以在条件X =2下Y 的条件分布律为216.03.0}2{}1,2{}2|1{========X P Y X P X Y P ,06.00}2{}2,2{}2|2{========X P Y X P X Y P ,616.01.0}2{}3,2{}2|3{========X P Y X P X Y P ,316.02.0}2{}4,2{}2|4{========X P Y X P X Y P ,{P Y ≤2}{1}{2}P Y P Y ==+==0.10.3000.20.6++++=. 而{2,2}{2,1}{2,2}{3,1}{3,2}P X Y P X Y P X Y P X Y P X Y ===+==+==+==≥≤0.3000.20.5=+++=.因此{2,2}{22}{2}P X Y P X Y P Y =≥≤≤≥≤0.550.66==. 2. 设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成, 二维随机变量(X , Y )在区域D 上服从均匀分布, 求(X , Y )关于X 的边缘概率密度在x =2处的值.解由题设知D 的面积为22e e111d ln 2D S x x x ===⎰. 因此, (X ,Y )的密度为 1,(,),(,)20x y D f x y ∈=⎧⎪⎨⎪⎩，其它.由此可得关于X 的边缘概率密度 ()(,)d X f x f x y y +∞-∞=⎰.显然, 当x ≤1或x ≥e 2时,()0X f x =; 当21e x <<时,111()d 22x X f x y x==⎰.故(2)14X f =. 3. 设二维随机变量(X , Y )的概率密度为(,)1,01,02,0,.f x y x y x =<<<<⎧⎨⎩其它求：(1) (X , Y )的边缘概率密度(),()X Y f x f y ；(2)11{}.22P Y X ≤≤ 解 (1) 当01x <<时,20()(,)d d 2xX f x f x y y y x +∞-∞===⎰⎰;当x ≤0时或x ≥1时, ()0X f x =. 故 2,01,()0,其它.X x x f x <<=⎧⎨⎩当0<y <2时,12()(,)d d 12y Y y f y f x y x x +∞-∞===-⎰⎰;当y ≤0时或y ≥2时, ()0Y f y =.故 1,02,()20,.Y yy f y -<<=⎧⎪⎨⎪⎩其它(2) 当z ≤0时,()0Z F z =; 当z ≥2时,1)(=z F Z ;当0<z <2时, (){2Z F z P X Y =-≤2}(,)d d x y zz f x y x y -=⎰⎰≤2x12202-2d 1d d 1d zxz x zx y x y =⋅+⋅⎰⎰⎰⎰24z z =-.故 1,02,()20,.()其它Z z zz f z F z -<<'==⎧⎪⎨⎪⎩(3) {}{}11311322161122442≤，≤≤≤≤P X Y P Y X P X ===⎧⎫⎨⎬⎩⎭. 4. 设G 是由直线y =x , y =3,x =1所围成的三角形区域, 二维随机变量(,)X Y 在G 上服从二维均匀分布.求:(1) (X , Y )的联合概率密度；(2) {1}P Y X -≤；(3) 关于X 的边缘概率密度. 解 (1)由于三角形区域G 的面积等于2, 所以(,)X Y 的概率密度为⎪⎩⎪⎨⎧∉∈=.),(,0,),(,21),(G y x G y x y x f (2)记区域x y y x D -=|),{(≤}1与G 的交集为0G ,则{1}P Y X -≤0011113d d (2)22224G G x y S ===-=⎰⎰.其中0G S 为G 0的面积.(3) X 的边缘概率密度()(,)d X f x f x y y +∞-∞=⎰. 所以,当]3,1[∈x 时, 311()d (3)22X xf x y x ==-⎰. 当1<x 或3>x 时, 0)(=x f X .因此 ⎪⎩⎪⎨⎧∈-=.,0],3,1[),1(21)(其它x x x f X习题3-31. 设X 与Y 相互独立, 且分布律分别为下表:求二维随机变量(,)X Y 的分布律.解由于X 与Y 相互独立, 所以有}{}{},{j i j i y Y P x X P y Y x X P =⋅====,6,5,2,0;0,21,1=--=j i .因此可得二维随机变量(,)X Y 的联合分布律2. 设(X , Y )的分布律如下表:问,αβ为何值时X 与Y 相互独立? 解由于边缘分布满足23111,1i j i j p p ⋅⋅====∑∑, 又X , Y 相互独立的等价条件为 p ij = p i . p .j (i =1,2; j =1,2,3).故可得方程组 21,3111().939αβα++==⋅+⎧⎪⎪⎨⎪⎪⎩解得29α=,19β=.经检验, 当29α=,19β=时, 对于所有的i =1,2; j =1,2,3均有p ij = p i . p .j 成立.因此当29α=,19β=时, X 与Y 相互独立..3. 设随机变量X 与Y 的概率密度为()e (,)0,.,01,0,x y b f x y x y -+=⎧<<>⎨⎩其它(1) 试确定常数b .(2) 求边缘概率密度()X f x , ()Y f y . (3) 问X 与Y 是否相互独立？解 (1) 由11()101(,)d d e d d e d e d (1e )x y y x f x y x y b y x b y x b +∞+∞+∞+∞-+----∞-∞====-⎰⎰⎰⎰⎰⎰,得 111eb -=-.(2) ()(,)d X f x f x y y ∞-∞=⎰1e ,01,1e 0,xx --<<=-⎧⎪⎨⎪⎩其它.()(,)d Y f y f x y x ∞-∞=⎰e ,0,0,y y ->=⎧⎨⎩其它.(3) 由于(,)()()X Y f x y f x f y =⋅，所以X 与Y 相互独立.4. 设X 和Y 是两个相互独立的随机变量, X 在(0, 1)上服从均匀分布, Y 的概率密度为21e ,0,()2Y yy f y y ->=⎧⎪⎨⎪⎩，≤0.(1) 求X 和Y 的联合概率密度.(2) 设关于a 的二次方程为220a Xa Y ++=, 试求a 有实根的概率.解 (1) 由题设知X 和Y 的概率密度分别为1,01,()0,X x f x <<=⎧⎨⎩其它， 21e ,0,()20,.yY y f y ->=⎧⎪⎨⎪⎩其它因X 和Y 相互独立, 故(X , Y )的联合概率密度为21e ,01,0(,)()()20,.yX Y x y f x y f x f y -<<>==⎧⎪⎨⎪⎩其它 (2) 方程有实根的充要条件是判别式大于等于零. 即244X Y ∆=-≥20X ⇔≥Y .因此事件{方程有实根}2{X =≥}Y .下面计算2{P X ≥}Y (参见图3-3).2{P X ≥}Y 2211221(,)d d e d (1e)d 2yxx Df x y xdy x y x --===-⎰⎰⎰⎰⎰2121ed 12[(1)(0)]0.1445xx πΦΦ-=-=--≈⎰.图3-3 第6题积分区域习题3-41. 设二维随机变量(X ,Y )的概率分布为YX0 1若随机事件{X =0}与{X +Y =1}相互独立, 求常数a , b .解首先, 由题设知0.40.11a b +++=. 由此得0.5a b +=. 此外,{0}0.4P X a ==+,{1}{0,1}{1,0}0.5P X Y P X Y P X Y a b +====+===+=, {0,1}{0,1}P X X Y P X Y a =+=====. 根据题意有{0,1}{0}{1}P X X Y P X P X Y =+===+=,即(0.4)0.5a a =+⨯. 解得0.4,0.1a b ==.2. 设两个相互独立的随机变量X ,Y 的分布律分别为求随机变量Z = X + Y 的分布律. 解随机变量Z = X + Y 的可能取值为7,5,3.Z 的分布律为18.06.0.03}2,1{}3{=⨯=====Y X P Z P , {5}{1,4}{3,2}0.30.4070.60.54P Z P X Y P X Y ====+===⨯+⨯=,28.04.07.0}4,3{}7{=⨯=====Y X P Z P ,或写为3. 随机变量X 与Y 相互独立, 且均服从区间[0,3]上的均匀分布, 求{}max{,}1P X Y ≤.解由题意知, X 与Y 的概率密度均为1,03,()30x f x =⎧⎪⎨⎪⎩≤≤，其它.又由独立性, 有P {max{X +Y }≤1}=P {X ≤1,Y ≤1}= P {X ≤1} P {Y ≤1}.而 P {X ≤1}= P {Y ≤1}11011()d d 33f x x x -∞===⎰⎰, 故 P {max{X +Y }≤1}=111339⨯=.4. 设X 和Y 是两个相互独立的随机变量, 且X 服从正态分布N (μ, σ2), Y 服从均匀分布U (-a , a )( a >0), 试求随机变量和Z =X +Y 的概率密度.解已知X 和Y 的概率密度分别为22()2()e2x X f x μσπσ--=, ),(+∞-∞∈x ; ⎪⎩⎪⎨⎧-∉-∈=).,(,0),,(,21)(a a y a a y ay f Y .由于X 和Y 相互独立, 所以22()21()()()d e d 22z y aZ X Y a f z f z y f y y y a μσπσ---+∞-∞-=-=⎰⎰=1[()()]2z μa z μa ΦΦa σσ-+---. 10. 设随机变量X 和Y 的联合分布是正方形G={(x,y )|1≤x ≤3, 1≤y ≤3}上的均匀分布, 试求随机变量U=|X -Y|的概率密度f (u ).解由题设知, X 和Y 的联合概率密度为111,3,3,(,)40,.x y f x y =⎧⎪⎨⎪⎩≤≤≤≤其它记()F u 为U 的分布函数, 参见图3-7, 则有当u ≤0时,(){||F u P X Y =-≤u }=0; 当u ≥2时,()1F u =;当0< u <2时, 图3-7 第8题积分区域||(){}(,)d d x y uF u P U u f x y x y -==⎰⎰≤≤21[42(2)]412u =-⨯- 211(2)4u =--.故随机变量||U X Y =-的概率密度为1(2),02,()20,u u p u -<<=⎧⎪⎨⎪⎩其它..总习题三1. 设随机变量(X , Y )的概率密度为⎪⎩⎪⎨⎧<<<=.,0,10,||,1),(其它x x y y x f 求条件概率密度)|()|(||y x f x y f Y X X Y 和.解首先2,01,()0,.(,)其它X x x f x f x y dy +∞-∞<<==⎧⎨⎩⎰1,01,()1,10,0,(,)≤其它.Y y y f y y y f x y dx +∞-∞-<<==+-<⎧⎪⎨⎪⎩⎰图3-9第1题积分区域当01y <<时, |1,1,1(|)0,X Y y x y f x y x <<-=⎧⎪⎨⎪⎩取其它值.当1y -<≤0时, |1,1,1(|)0,X Y y x y f x y x -<<+=⎧⎪⎨⎪⎩取其它值.当10<<x 时, |1,||,(|)20,Y X y x f y x x y <=⎧⎪⎨⎪⎩取其它值.2. 设随机变量X 与Y 相互独立, 下表列出二维随机变量(,)X Y 的分布律及关于X 和关于Y 的边缘分布律中部分数值, 试将其余数值填入表中空白处 .解首先, 由于11121{}{,}{,}P Y y P X x Y y P X x Y y ====+==, 所以有11121111{,}{}{,}6824P X x Y y P Y y P X x Y y ====-===-=.在此基础上利用X 和Y 的独立性, 有11111{,}124{}1{}46P X x Y y P X x P Y y =======.于是 2113{}1{}144P X x P X x ==-==-=.再次, 利用X 和Y 的独立性, 有12211{,}18{}1{}24P X x Y y P Y y P X x =======.于是 312111{}1{}{}1623P Y y P Y y P Y y ==-=-==--=.最后, 利用X 和Y 的独立性, 有2222313{,}{}{}428P X x Y y P X x P Y y ======⨯=; 2323311{,}{}{}434P X x Y y P X x P Y y ======⨯=;1313111{,}{}{}4312P X x Y y P X x P Y y ======⨯=.因此得到下表3. (34)e (,)0,.,0,0,x y k f x y x y -+=⎧>>⎨⎩其它 (1) 求常数k ；(2) 求(X ,Y )的分布函数；(3) 计算{01,02}P X Y <<≤≤; (4) 计算(),x f x ()y f y ；(5) 问随机变量X 与Y 是否相互独立? 解 (1)由3401(,)d d e d e d 12xy kf x y x y k x y +∞+∞+∞+∞---∞-∞===⎰⎰⎰⎰,可得12=k .(2) (X ,Y )的分布函数(,)(,)d d x y F x y f u v x y -∞-∞=⎰⎰.当x <0或y <0时,有 0),(=y x F ; 当0,0x y ≥≥时, 34340(,)12e d e d (1e )(1e )x yuv x y F x y u v ----==--⎰⎰.即 34(1e )(1e ),0,0,(,)0,.x y x y F x y --⎧--≥≥=⎨⎩其它(3) {01,02}P X Y <<≤≤38(1,2)(0,0)(1e )(1e )F F --=-=--. (4) (34)012ed ,0,()(,)d 0,其它.x y X y x f x f x y y +∞-++∞-∞⎧>⎪==⎨⎪⎩⎰⎰所以 33e ,0,()0,其它.x X x f x -⎧>=⎨⎩类似地, 有44e ,0,()0,其它.y Y y f y -⎧>=⎨⎩显然2),(),()(),(R y x y f x f y x f Y X ∈∀⋅=, 故X 与Y 相互独立. 4.解已知的分布律为注意到41260}1{}1{=++====Y P X P , 而0}1,1{===Y X P ,可见P {X =1, Y =1}≠P {X =1}P {Y =1}. 因此X 与Y 不相互独立.(2) Z X Y =+的可能取值为3, 4, 5, 6, 且316161}1,2{}2,1{}3{=+===+====Y X P Y X P Z P , }1,3{}2,2{}3,1{}4{==+==+====Y X P Y X P Y X P Z P3112161121=++=, 316161}2,3{}3,2{}5{=+===+====Y X P Y X P Z P . 即Z X Y =+(3) V =21}2,2{}1,2{}2,1{}2{===+==+====Y X P Y X P Y X P V P , 21}2{1}3{==-==V P V P . 即max(,)V X Y =的分布律为(4) min{U =}3,1{}2,1{}1{==+====Y X P Y X P U P}1,2{}1,3{==+==+Y X P Y X P 21=, 21}1{1}2{==-==U P U P . 即min{,}U X Y =的分布律为(5) W U V =+31}1,2{}2,1{}2,1{}3{===+=======Y X P Y X P V U P W P ,}2,2{}3,1{}4{==+====V U P V U P W P31}2,2{}1,3{}3,1{===+==+===y X P Y X P Y X P ,31}2,3{}3,2{}3,2{}5{===+=======Y X P Y X P V U P W P .5. 2,01,01,(,)0,x y x y f x y --<<<<⎧=⎨⎩其它. (1) 求P {X >2Y }; (2) 求Z = X +Y 的概率密度f Z (z ).解 (1) 1120227{2}(,)d d d (2)d 24yx yP X Y f x y x y y x y x >>==--=⎰⎰⎰⎰. (2) 方法一: 先求Z 的分布函数:()()(,)d d Z x y zF z P X Y Z f x y x y +=+=⎰⎰≤≤.当z <0时, F Z (z )<0; 当0≤z <1时, 1()(,)d d d (2)d zz yZ D F z f x y x y y x y x -==--⎰⎰⎰⎰= z 2-13z 3; 当1≤z <2时, 2111()1(,)d d 1d (2)d Z z z yD F z f x y x y y x y x --=-=---⎰⎰⎰⎰= 1-13(2-z )3; 当z ≥2时, F Z (z ) = 1.故Z = X +Y 的概率密度为222,01,()()(2),12,0,Z Z z z z f z F z z z ⎧-<<⎪'==-<⎨⎪⎩≤其它.方法二: 利用公式()(,)d :Z f z f x z x x +∞-∞=-⎰2(),01,01,(,)0,x z x x z x f x z x ---<<<-<⎧-=⎨⎩其它 2,01,1,0,.z x x z x -<<<<+⎧=⎨⎩其它当z ≤0或z ≥2时, f Z (z ) = 0; 当0<z <1时, 0()(2)d (2);zZ f z z x z z =-=-⎰当1≤z <2时, 121()(2)d (2).Zz f z z x z -=-=-⎰故Z = X +Y 的概率密度为222,01,()(2),12,0,.Z z z z f z z z ⎧-<<⎪=-<⎨⎪⎩≤其它.6. 设随机变量(X , Y )得密度为21,01,02,(,)30,.其它x xy x y x y ϕ⎧+⎪=⎨⎪⎩≤≤≤≤试求: (1) (X , Y )的分布函数; (2) (X , Y )的两个边缘分布密度; (3) (X , Y )的两个条件密度; (4) 概率P {X +Y >1}, P {Y >X }及P {Y <12|X <12}.解 (1) 当x<0或y <0时, φ(x , y ) = 0, 所以 F (x , y ) = 0.当0≤x <1, 0≤y <2时, φ(x , y ) = x 2+13xy ,所以 201(,)(,)d d [()d ]d 3x yx yF x y u v u v u uv v u -∞-∞==+⎰⎰⎰⎰ϕ32211312x y x y =+. 当0≤x <1, 2≤y 时,2(,)(,)d d [(,)d ]d [(,)d ]d xyx y x F x y u v u v u v v u u v v u -∞-∞===⎰⎰⎰⎰⎰⎰ϕϕϕ22001[()d ]d 3xu uv v u =+⎰⎰21(21)3x x =+. 当1≤x , 0≤y <2时,1(,)(,)d d [(,)d ]d xyyF x y u v u v u v v u -∞-∞==⎰⎰⎰⎰ϕϕ12001[()d ]d 3yu uv v u =+⎰⎰1(4)12y y =+. 当1≤x , 2≤y 时,122001(,)[()d ]d 13F x y u uv v u =+=⎰⎰.综上所述, 分布函数为220,00,1(),01,02,341(,)(21),01,2,31(4),1,02,121,1, 2.x y y x y x x y F x y x x x y y y x y x y <<⎧⎪⎪+<<⎪⎪⎪=+≥⎨⎪⎪+≥⎪⎪≥≥⎪⎩或≤≤≤≤≤< (2) 当0≤x ≤1时,22202()(,)d ()d 2,33X xy x x y y x y x x ϕϕ+∞-∞==+=+⎰⎰故 222,01,()30,.其它≤≤X x x x x ϕ⎧+⎪=⎨⎪⎩当0≤y ≤2时,12011()(,)d ()d ,336Y xy y x y x x x y ϕϕ+∞-∞==+=+⎰⎰ 故 11,02,()360,.其它≤≤Y y y y ϕ⎧+⎪=⎨⎪⎩(3) 当0≤y ≤2时, X 关于Y = y 的条件概率密度为2(,)62(|).()2Y x y x xy x y y yϕϕϕ+==+当0≤x ≤1时, Y 关于X = x 的条件概率密度为(,)3(|).()62X x y x yy x y x ϕϕϕ+==+(4) 参见图3-10.图3-10 第9题积分区域图3-11 第9题积分区域1{1}(,)d d x y P X Y x y x y ϕ+>+>=⎰⎰12201165d ()d .372xx x xy y -=+=⎰⎰ 同理, 参见图3-11.{}(,)d d y xP Y X x y x y ϕ>>=⎰⎰122117d ()d .324xx x xy y =+=⎰⎰ 1111{,}(,)112222{|}1122{}()22X P X Y F P Y X P X F <<<<==<211(,)221201()534.32()d |X y x y x x xϕ+==⎰。

概率论第一章习题解答

（1）若至少有一次及格，他就能够获得某种资格，求他获得资格的概率。
（2）若知道他第二次已经及格，求他第一次及格的概率。解设＝“第次及格”，（）。
B＝“获得资格” （1）已知，，
，显然，，故
。（2）（贝叶斯公式）。 23 将两信息分别编码为A和B传送出去，接收站收到时，A误作B的概率为0.02， B误作为A的概率为0.01。信息A与B传送的频繁程度为 2：1。若接收站收到的信息为A，原发信息为A的概率是多少？解设＝“发出的信息为A”，＝“发出的信息为B”，
而；；。（注意到从第二个盒子中取球时，它里面装有11只球。）
（此时第三个盒子中有7只白球。）（此时第二个盒子中有6只白球，5只红球。）（此时第二个盒子中有5只白球,6只红球。）于是。 20 某种产品的商标为“MAXAM”，其中有2个字母脱落，有人捡起随意放回，求放回后仍为“MAXAM”的概率。解设B＝“放回的结果正确”，字母脱落的五种情况记为：＝“M，X”，＝“A，X”，＝“M，A”，＝“ A，A”，＝“M，M”，则，样本空间所包含的基本事件数即脱落的总数：事件所包含的基本事件数：，（2个M，1个X）事件所包含的基本事件数：，（2个A，1个X）事件所包含的基本事件数：，（2个M，2个A）事件所包含的基本事件数：事件所包含的基本事件数：于是；；。，（），，（）根据全概率公式，有。 21 已知男子有5%是色盲患者，女子有0.25%是色盲患者，今从男女人数相等的人群中随机地选1人，恰好是色盲，此人是男性的概率是多少？解设A＝“色盲患者”，B＝“男性” 则事件“随机地选1人，恰好是色盲，此人是男性”＝于是所求概率为：由贝叶斯公式已知（从男女人数相等的人群中随机选取1人。），于是。 22 一学生接连参加同一课程的两次考试，每一次及格的概率为p，若第一次及格第二次也及格的概率为p。若第一次不及格第二次及格的概率为p/2。

大学概率论习题三详解

大学概率论习题三详解（A ）1、某推销人与工厂约定，用船把一箱货物按期无损的运到目的地可得佣金10元，若不按期但无损则扣2元，若货物按期有损则扣5元，若既不按期又有损坏不仅得不到佣金还需要赔偿对方6元。

推销人按他的经验认为，一箱货物按期无损的运到目的地有60％把握，不按期但无损到达占20％，货物按期有损占10％，不按期又有损的占10％。

问推销人在用船运货物时，每箱期望得到多少？解设X 表示该推销人用船运货物时每箱可得钱数，则按题意，X 的分布为：)(X E =()5.71.061.052.086.010=⨯-+⨯+⨯+⨯元2、某工厂每天用水量保持正常的概率为7/5，求7天内用水量保持正常的平均天数。

解 7天内用水量保持正常的天数为X ，则)75,7(~B X5==np EX3、设一机器在一天内发生故障的概率为2.0,机器发生故障时全天停止工作,若一周5个工作日里无故障,可获利润10万元，发生1次故障仍可获利润5万元，发生2次故障获利0万元，发生3次以上故障亏损2万元，求一周5个工作日内期望利润。

解令X 表示一周发生的故障数，依题意)2.0,5(~B X 令Y 表示一周内利润：328.08.0)0()10(5=====X P Y P 410.08.08.02.0)1()5(4415==⨯====C X P Y P205.08.04.08.02.0)2()0(33225=⨯=⨯====C X P Y P057.08.04.08.08.01)3()2(345=⨯---=≥=-=X P Y P Y756.5057.02410.05382.010=⨯-⨯+⨯=EY4、把四个球随机地放入4个盒子中，设X 表示空盒子的个数，求EX 。

解首先求X 的概率分布 323444)0(4444====！P X P 1694)1(422241314=⋅⋅⋅==P C C C X P64214)()2(414122424=⋅+⋅==C C C C X P 6414)3(434===C X P648164136421216913230)(=⨯+⨯+⨯+⨯=X E5、某射手每次击中目标的概率是p ，现携带10发子弹对目标连续射击（每次一发）一旦击中或子弹打完立即转移地方，求他转移前平均射击次数。

《概率论与数理统计》习题三答案解析

《概率论与数理统计》习题及答案习题二1.将一硬币抛掷三次，以X表示在三次中出现正面的次数，以丫表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X和丫的联合分布律.【解】X和丫的联合分布律如表：2.盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球，以X表示取到黑球的只数，以丫表示取到红球的只数.求X和丫的联合分布律.3.设二维随机变量（X, Y）的联合分布函数为F（x, y）Jsinxsiny,。

沁兰才gy 写L0, 其他.求二维随机变量（X, Y）在长方形域｛o<x< -,n y<内的概率.I 4 6 3., n n n【解】如图P{0 cx < - —c Y<—}公式（3.2）4 6 3F（n，n）-F（n n-F（o, n+F（o, n4 3 4 6 3 6n n n — n厂n厂n=sin — 0n — —sin — sin — -sin0sin — + sin 比sin — 4 3 4" 6 3 6出(屁1). 4[k(6 - X - y),0 c X c 2, 2 c y c 4, (x ，y )=( 0,其他.确定常数求 P{X <1 , Y v 3}; 求 P{X<1.5}; 求 P{X+Y W 4}. 【解】(1)由性质有说明：也可先求出密度函数, 4.设随机变量求：(1)(2) (3) 【解】(1)(X , 丫)的分布密度f (X , y )=0,,XA0,yA0,其他.常数A ;随机变量(X , 丫)的分布函数； P{0 <X<1 , 0<丫<2}.-be -be -be -be由 L LcfXyMxdy^ .0 Ae严d y)dxdy=4=112 得(2) A=12由定义，有y XF (x, y) = LcL f (u,v)dudv」「［任4和dudv 10,"(1-e 」X )(1-e"4y )y A 0,XA 0,0,其他⑶ P{0 <X <1,0 < 丫 <2}= P{0 cX <1,0cY <2}1「0[12e 5.设随机变量(仲枷)dxdy =(1-e 冷(1-e*“ 0.9499.Y ) 的概率密度为(1)(2) (3) (4) k ;-be -be2 4f f f(x,y)dxdy = r r k(6-x-y)dydx=8k=1,・0・21 R = -81 3-UU f (x ,y)d y d x1 313=0 L8k (6_x-y )dydx=8⑶ P{X v 1.5} = JJ f (x, y)dxdy 如图 a JJ f (x, y)dxdyx £5D 11.541 27=f dx f -(6 — x- y)dy =——. 0 28、 ” y 32⑷ P{X + Y <4} = ff f (x,y)dxdy 如图b JJ f (x, y)dxdyX -Y <D224_x12 =[dx f -(6 - X - y)dy =-. 0」2 8 3y,1.5 2 fa)求：（1） X 与丫的联合分布密度；（2） P{Y^X}.题6图【解】（1）因X 在（0, 0.2 ）上服从均匀分布，所以X 的密度函数为I 1I ——,0ex <0.2, fx (X )= \ 0.2 0,其他.(2) P{X <1,Yc3} 6.设X 和丫是两个相互独立的随机变量,0.2）上服从均匀分布，丫的密度函数为 yf Y ( y )=y>o,其他.题5图X 在（0，y=yf(x,y X Y 独立f x xCf Y y()(2) P(Y <X) = ff f (x,y)dxdy 如图仃25e'y dxdyy < D0.2 x50.2 5=f 0 dx 0 25e ydy = J o (-5e +5)dx-1=e 止 0.3679.7.设二维随机变量(X ，Y )的联合分布函数为「(1—e"x )(1 —e 'y ), XA 0, y 》。

概率论第三章习题解答

第三章习题解1 在一箱子中装有12只开关，其中2 只是次品，在其中任取两次，每次任取一只，考虑两种实验：（1）放回抽样；（2）不放回抽样。

概念随机变量X ，Y 如下：0,1X ⎧=⎨⎩若第一次取出的是正品，，若第一次取出的是次品。

0,Y 1⎧=⎨⎩若第二次取出的是正品，，若第二次取出的是次品。

试别离就（1），（2）两种情形写出X ，Y 的联合散布律。

解（1）放回抽样由于每次抽取时都是12只开关，第一次取到正品有10种可能，即第一次取到正品的概率为 105{0}126P X ===，第一次掏出的是次品的概率为 21{1}126P X === 同理，第二次取到正品的概率105{0}126P Y === 第二次取到次品的概率为21{1}126P Y === 由乘法公式得X ，Y 的联合散布率为{,}{|}{}{}{}P X i Y j P Y j X i P X i P X i P Y j =========，0,1i =，0,1j =。

具体地有5525{0,0}6636P X Y ===⨯=，515{0,1}6636P X Y ===⨯=，155{1,0}6636P X Y ===⨯=，111{1,1}6636P X Y ===⨯=用表格的形式表示为（2）不放回抽样5{0}6P X ==，1{1}6P X == 因为第二次抽取时，箱子里只有11只开关，当第一次抽取的是正品，那么箱子中有9只正品）。

因此9{0|0}11P Y X ===， 2{1|0}11P Y X === 10{0|1}11P Y X ===， 1{1|1}11P Y X ===则5945{0,0}61166P X Y ===⨯= 5210{0,1}61166P X Y ===⨯=， 11010{1,0}61166P X Y ===⨯=，111{1,1}61166P X Y ===⨯= 用表格表示为2 （1）盒子里装有3只黑球，2只红球，2只白球，在其中任取4只球，以X 表示取到黑球的只数，以Y 表示取到红球的只数，求X 和Y 的联合散布律。

概率论与数理统计浙大四版习题答案第三章

第三章多维随机变量及其分布1.[一] 在一箱子里装有12只开关，其中2只是次品，在其中随机地取两次，每次取一只。

考虑两种试验：（1）放回抽样，（2）不放回抽样。

我们定义随机变量X ，Y 如下：⎪⎩⎪⎨⎧= 若第一次取出的是次品若第一次取出的是正品,1,,0X ⎪⎩⎪⎨⎧=若第二次取出的是次品若第二次取出的是正品,1,,0Y试分别就（1）（2）两种情况，写出X 和Y 的联合分布律。

解：（1）放回抽样情况由于每次取物是独立的。

由独立性定义知。

P (X=i , Y=j )=P (X=i )P (Y=j ) P (X=0, Y=0 )=362512101210=⋅ P (X=0, Y=1 )=3651221210=⋅ P (X=1, Y=0 )=3651210122=⋅ P (X=1, Y=1 )=361122122=⋅ 或写成（2）不放回抽样的情况P {X=0, Y=0 }=66451191210=⋅ P {X=0, Y=1 }=66101121210=⋅P {X=1, Y=0 }=66101110122=⋅ P {X=1, Y=1 }=661111122=⋅ 或写成3.[二] 盒子里装有3只黑球，2只红球，2只白球，在其中任取4只球，以X 表示Y 的联合分布律。

解：（X ，Y ）的可能取值为(i , j )，i =0，1，2，3， j =0，12，i + j ≥2，联合分布律为P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C CP {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=05.[三] 设随机变量（X ，Y ）概率密度为⎪⎩⎪⎨⎧<<<<--=其它,042,20),6(),(y x y x k y x f（1）确定常数k 。

概率论课后习题答案第三章

概率论课后习题答案第三章第三章概率论课后习题答案概率论是一门研究随机现象的数学学科，它在现代科学和工程领域中有着广泛的应用。

而习题则是巩固和加深对概率论知识的理解和应用的重要手段。

在第三章的习题中，我们将探讨一些与随机变量和概率分布相关的问题，并给出相应的答案和解析。

1. 设随机变量X服从参数为λ的指数分布，即X～Exp(λ)，其概率密度函数为f(x) = λe^(-λx)，x≥0。

求以下概率：(a) P(X > 2)(b) P(X ≤ 1)(c) P(1 ≤ X ≤ 3)答案：(a) P(X > 2) = ∫[2,∞] λe^(-λx) dx = e^(-2λ)(b) P(X ≤ 1) = ∫[0,1] λe^(-λx) dx = 1 - e^(-λ)(c) P(1 ≤ X ≤ 3) = ∫[1,3] λe^(-λx) dx = e^(-λ) - e^(-3λ)解析：根据指数分布的性质，我们可以利用概率密度函数求解概率。

对于(a)，我们计算X大于2的概率，即求解X在区间[2,∞]上的概率密度函数的积分。

对于(b)，我们计算X小于等于1的概率，即求解X在区间[0,1]上的概率密度函数的积分。

对于(c)，我们计算X在1到3之间的概率，即求解X在区间[1,3]上的概率密度函数的积分。

2. 设随机变量X服从参数为μ和σ^2的正态分布，即X～N(μ,σ^2)，其概率密度函数为f(x) = (1/(σ√(2π))) * e^(-(x-μ)^2/(2σ^2))，-∞<x<∞。

求以下概率：(a) P(X > μ)(b) P(X ≤ μ)(c) P(μ-σ ≤ X ≤ μ+σ)答案：(a) P(X > μ) = 1 - P(X ≤μ) = 1 - 0.5 = 0.5(b) P(X ≤ μ) = 0.5(c) P(μ-σ ≤ X ≤ μ+σ) = P(X ≤ μ+σ) - P(X ≤ μ-σ) = 0.6827 - 0.3173 =0.3654解析：对于正态分布，我们可以利用概率密度函数求解概率。

概率论与数理统计习题解答(第3章)

习题三（A ）三、解答题1. 设口袋中有3个球，它们上面依次标有数字1，1，2，现从口袋中无放回地连续摸出两个球，以X ，Y 分别表示第一次与第二次摸出的球上标有的数字，求(X ，Y )的分布律．解：(X ，Y )取到的所有可能值为(1，1)，(1，2)，(2，1)由乘法公式： P {X =1，Y =1}=P {X =1}P {Y =1|X =1}=2/3⨯1/2=/3， P {X =1，Y =2}= P {X =1}P {Y =2|X =1}=2/3⨯1/2=1/3， P {X =2，Y =1}= P {X =2}P {Y =1|X =2}=1/3⨯2/2=1/3. (X ，Y )的分布律用表格表示如下：2．设盒中装有8支圆珠笔芯，其中3支是蓝的，3支是绿的，2支是红的，现从中随机抽取2支，以X ，Y 分别表示抽取的蓝色与红色笔芯数，试求： (1) X 和Y 的联合分布律；(2) P {X ，Y } ∈ A }，其中A = {(x ，y )| x + y ≤ 1}．解：X ，Y 所有可能取到的值是0， 1， 2(1) P {X =i ， Y =j }=P {X =i }P {Y =j |X =i }=282223C C C C j i j i --， i ， j =0，1，2， i +j ≤2 或者用表格表示如下：(2)P{(X ，Y )∈A }=P {X +Y ≤1}=P {X =0， Y =0}+P {X =1，Y =0}+P {X =0，Y =1}=3/28+9/28+6/28=9/14.3．设事件B A 、满足,21)|(,21)|(,41)(===A B P B A P A P 记X ，Y 分别为一次试验中A ，B 发生的次数，即⎩⎨⎧=不发生，发生A A X 0,1，⎩⎨⎧=不发生，发生，B B Y 0 1，求：二维随机变量(X ，Y )的分布律．解：因为P (A )=1/4，,21)|(=A B P 由P (B |A )=2/14/1)()()(==AB P A P AB P 得P (AB )=1/8，由P (A |B )=2/1)()(=B P AB P 得P(B)=1/4.(X ，Y )取到的所有可能数对为(0，0)，(1，0)，(0，1)，(1，1)，则 P {X =0，Y =0}=)(1)()(B A P B A P B A P -===1-P (A )-P (B )+P (AB )=5/8, P {X =0，Y =1}=)(B A P =P (B -A )=P (B )-P (AB )=1/8, P {X =1，Y =0}=)(B A P =P (A -B )=P (A )-P (AB )=1/8, P {X =1，Y =1}=P (AB )=1/8.4．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧<<<<=.,0,10,10 ,),(其它y x Axy y x f 试求： (1) 常数A (2) P {X = Y } (3) P {X < Y }(4) (X ，Y )的分布函数．解：(1)由归一性知：1=，故A=4(2) P {X =Y }=0, (3) P {X <Y }=.(4)F (x ，y )=即F (x ，y )=5．设二维随机变量),(Y X 的联合概率密度为⎪⎩⎪⎨⎧<<<<+=其它0,20,10 ,3),(2y x xyx y x f求P {X + Y ≥ 1}．解：P{X+Y ≥1}=7265)3(),(102121=+=⎰⎰⎰⎰-≥+dydx xy x dxdy y x f xy x 6．将一枚硬币掷3次，以X 表示前2次中出现正面的次数，以Y 表示3次中出现正面的次数，求X ，Y 的联合分布律及(X ，Y )的边缘分布律．解：X 的所有可能取值为0，1，2，Y 的所有可能取值为0，1，2，3. P {X =0，Y =0}=0.53=0.125; P {X =0，Y =1}=0.53=0.125P {X =1，Y =1}=25.05.05.0212=⨯C ， P {X =1，Y =2}=25.05.05.0212=⨯C P {X =2，Y =2}=0.53=0.125， P {X =2，Y =3}==0.53=0.125 X ，Y 的分布律及边缘分布律可用表格表示如下：Y X 0 1 2 3 P i . 0 0.125 0.125 0 0 0.25 1 0 0.25 0.250.52 00.125 0.125 0.25P .j0.125 0.375 0.375 0.125 1解法2：,21)21()21(}|{}{},{22⨯=======-iiiC i X j Y P i X P j Y i X P.1,0,3,2,1,0,2,1,0=-==i j j i7．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧<<=-其它,00,),(yx e y x f y 求边缘概率密度f X (x )，f Y (y )．解：⎩⎨⎧<<=-其它,00,),(yx e y x f y⎩⎨⎧<≥=⎪⎩⎪⎨⎧<≥==-+∞-∞+∞-⎰⎰0,00,0,00,),()(x x e x x dy e dy y x f x f xxy X ⎩⎨⎧<≥=⎪⎩⎪⎨⎧<≥==--∞+∞-⎰⎰0,00,0,00,),()(0y y ye y y dx e dx y x f y f y y yY 8．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧≤≤=其它,01,),(22y x y cx y x f 求：(1) 确定常数c(2) 边缘概率密度f X (x )，f Y (y )．解：⎩⎨⎧<≤≤=0,01,),(22x y x y cx y x f(1)214212),(1104211122cdx x x c ydydx cx dxdy y x f x =-===⎰⎰⎰⎰⎰-∞+∞-∞+∞-所以 c=21/4(2) ⎪⎩⎪⎨⎧<-=⎪⎩⎪⎨⎧<==⎰⎰∞+∞-其它其它，,01||,8)1(2101||,421),()(42122x x x x ydy x dy y x f x f x X⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==⎰⎰-∞+∞-其它其它，,010********),()(252y y y ydx x dx y x f y f y yY 9．设平面区域D 由曲线xy 1=及直线y = 0，x = 1，x = e 2围成，二维随机变量(X ，Y )在区域D 上服从均匀分布，求边缘概率密度f X (x )，f Y (y )．解：2|ln 12211===⎰e e D x dx xS (X ，Y )在区域D 上服从均匀分布，故f (x ，y )的概率密度为⎪⎩⎪⎨⎧∈=其它，0),(,21),(Dy x y x f ⎪⎩⎪⎨⎧≤≤==⎰⎰∞+∞-其它（,01,21),()210X e x dy dy y x f x f x⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤≤≤-=-===--∞+∞-⎰⎰⎰其它（10,0),11(2121,2121),()221112X 2y e e y y dx e dx dx y x f x f y e 10．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧<<<<=其它,00,10,3),(xy x x y x f 试求条件概率密度f (y | x )．解：⎩⎨⎧<<<<=其它,00,10,3),(xy x x y x f)0)(( )(),()|(|>=x f x f y x f x y f X X X Y ⎪⎩⎪⎨⎧≤<===⎰⎰∞+∞-其它,010,233),()(20x x xdy dy y x f x f x X当0<x ≤1时，⎪⎩⎪⎨⎧<<==其它,00,233)(),()|(2|xy x x x f y x f x y f X X Y即，⎪⎩⎪⎨⎧≤<<=其它,010,2)|(|x y x x y f X Y11．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧<<<=其它,0,10,1),(xy x y x f 求条件概率密度f (x | y )．解：⎩⎨⎧<<<=其它,0||,10,1),(xy x y x f⎪⎩⎪⎨⎧>-=≤+===⎰⎰⎰-∞+∞-0,10,1),()(11y y dx y y dx dx y x f y f y y Y当y ≤0时，⎪⎩⎪⎨⎧<<-<<+==其它,0,10,11)(),()|(|x y x x y x f y x f y x f Y Y X当y >0时，⎪⎩⎪⎨⎧<<-<<-==其它,0,10,11)(),()|(|x y x x y x f y x f y x f Y Y X所以，⎪⎩⎪⎨⎧<<<-==其它,01||0,||11)(),()|(|x y y x f y x f y x f Y Y X12．已知随机变量Y 的概率密度为⎩⎨⎧<<=其它,010,5)(4y y y f Y 在给定Y = y 条件下，随机变量X 的条件概率密度为⎪⎩⎪⎨⎧<<<=其它,010,3)(32y x y x y x f 求概率P {X > 0.5}．解：由)(),()|(|x f y x f y x f Y Y X =得 ⎩⎨⎧<<<<==其它,00,10,15)()|(),(2|yx y yx y f y x f y x f Y Y X644715),(}5.0{15.0125.0===>⎰⎰⎰⎰+∞+∞∞-xdydx yx dydx y x f X P 13．设二维随机变量(X ，Y )的分布律为试分别求),max(Y X Z =和),min(Y X W =的分布律．解：Z =max(X ，Y )，W =min(X ，Y )的所有可能取值如下表Z =max(X ，Y )，W =min(X ，Y )的分布律为14．设X 和Y 是相互独立的随机变量，且)(~),(~θθE Y E X ，如果定义随机变量Z 如下：⎩⎨⎧>≤=Y X YX Z ,0,1 求Z 的分布律．解：⎪⎩⎪⎨⎧≤>=-0,00,1)(x x e x f x X θθ ⎪⎩⎪⎨⎧≤>=-0,00,1)(y y e y f yY θθ 由独立性得X ，Y 的联合概率密度为⎪⎩⎪⎨⎧>>=+-其它,00,0,1),(2y x e y x f yx θθ 则P {Z =1}=P {X ≤Y }=211),(002==⎰⎰⎰⎰∞++-≤xyx yx dydx edxdy y x f θθ P {Z =0}=1-P {Z =1}=0.5故Z 的分布律为15．设二维随机变量(X ，Y )的概率密度为⎪⎩⎪⎨⎧≤+=其它,01,1),(22y x y x f π求边缘概率密度f X (x )，f Y (y )；并问X 与Y 是否独立？解：⎪⎩⎪⎨⎧≤+=其它,01,1),(22y x y x f π⎪⎩⎪⎨⎧<-===⎰⎰---∞+∞-其它，01||,121),()(222112x x dy dy y x f x f x x X ππ 同理，⎪⎩⎪⎨⎧<-=其它，01||,12)(2y y y f Y π显然，)()(),(y f x f y x f Y X ≠，所以X 与Y 不相互独立16．设随机变量X 和Y 相互独立，试在以下情况下求Y X Z +=的概率密度， (1) )1,0(~),1,0(~U Y U X ； (2) )1(~),1,0(~Exp Y U X ．解：(1)⎩⎨⎧<<=其它,010,1)(x x f X ⎩⎨⎧<<=其它,010,1)(Y y y f利用卷积公式：⎰+∞∞--=dx x z f x f z f Y X Z )()()(求f Z (z ))()(x z f x f Y X -=⎩⎨⎧+<<<<其它,01,10,1x z x x⎪⎪⎩⎪⎪⎨⎧<≤<≤-===-=⎰⎰⎰-∞+∞-其它2110,02,)()()(110z z z dx z dx dx x z f x f z f z z Y X Z(2) ⎩⎨⎧<<=其它,010,1)(x x f X ⎩⎨⎧≤>=-0,00,)(Y y y e y f y 利用卷积公式：⎰+∞∞--=dy y f y z f z f Y X Z )()()(⎩⎨⎧+<<>=--其它,01,0,)()(y z y y e y f y z f y Y X⎰+∞∞--=dy y f y z f z f Y X Z )()()(⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≥<≤--=≥<≤=-----⎰⎰其它其它110,0,)1(,1110,0,,10z z e e e z z dy e dy e z zzz y z y17．设)1,1(~),1,0(~N Y N X ，且X 与Y 独立，求}1{≤+Y X P ．解：由定理3.1（P75）知，X +Y ~N (1，2)，故5.0)0(}21121{}1{=Φ=-≤-+=≤+Y X P Y X P 18．设随机变量(X ，Y )的概率密度为⎪⎩⎪⎨⎧>>+=+-. ,0;0,0,)(21),()(其它y x e y x y x f y x(1) 问X 和Y 是否相互独立？ (2) 求Y X Z +=的概率密度．解：(1) )1(21)(21),()0)(X +=+==-+∞+-+∞∞-⎰⎰x e dy e y x dx y x f x f x y x （(x>0) 同理，)1(21)(+=-y e y f yY y>0 显然，)()x (),(y f f y x f Y X =，所以X 与Y 不相互独立 (2).利用公式⎰+∞∞--=dx x z x f z f Z )()(，被积函数⎪⎩⎪⎨⎧>>=⎪⎩⎪⎨⎧>->-+=---+-其它其它,0,0,21,00,0,)(21),()(xz x ze x z x e x z x x z x f z x z x所以⎰+∞∞--=dx x z x f z f Z )()(，⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧≤>=≤>=--⎰0,00,210,00,2120z z e z z z dx ze z z z19. 设某系统L 由两个相互独立的系统L 1，L 2联合而成，各连接方式如图所示．已知L 1，L 2的使用寿命X 与Y 分别服从参数为α，β 的指数分布，求以下各系统L 使用寿命Z 的分布函数及概率密度．解：并联时，系统L 的使用寿命Z=max{X ，Y} 因X ~Exp (α)，Y ~Exp (β)，故⎪⎩⎪⎨⎧≤>=-0,00,1)(x x e x f x X αα， ⎪⎩⎪⎨⎧≤>=-0,00,1)(y y e y f y Y ββ ⎪⎩⎪⎨⎧≤>-=-0,00,1)(x x e x F xX α， ⎪⎩⎪⎨⎧≤>-=-0,00,1)(y y e y F y Y β ⎪⎩⎪⎨⎧≤>--==--0,00),1)(1()()()(z z e e z F z F z F z z Y X Z βα⎪⎩⎪⎨⎧≤>+-+=⎪⎪⎭⎫⎝⎛+---0,00,)11(11)(11z z e e e z f z z z Z βαβαβαβα 串联时，系统L 的使用寿命Z =min{X ，Y }⎪⎩⎪⎨⎧≤>-=---=⎪⎪⎭⎫⎝⎛+-0,00,1)](1)][(1[1)(11z z e z F z F z F z Y X Z βα ⎪⎩⎪⎨⎧≤>⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫⎝⎛+-0,00,11)(11z z e z f zZ βαβα （B ）1．设二维随机变量(X ，Y )的分布律为已知随机事件{X = 0}与{X + Y = 1}相互独立，求a ，b 的值．解：P {X =0}=a +0.4，P {X +Y =1}=P {X =1，Y =0}+P {X =0，Y =1}=a +b. P {X =0，X +Y =1}=P {X =0，Y =1}=a 由于{X =0}与{X +Y =1}相互独立，所以 P {X =0， X +Y =1}=P {X =0} P {X +Y =1}即 a =(a +0.4)(a +b ) (1) 再由归一性知：0.4+a +b +0.1=1 (2) 解(1)，(2)得 a =0.4， b =0.1 2．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧<<<<--=其它 ,010,10 ,2),(y x y x y x f (1) 求P {X > 2Y }(2) 求Z = X + Y 的概率密度f Z (z )．解: (1) 247)2(),(}2{10202=--==>⎰⎰⎰⎰>xyx dydx y x dxdy y x f Y X P (2) 利用公式dx x z x f z f Z ⎰+∞∞--=),()(计算⎩⎨⎧<-<<<-=-其它,010,10,2),(x z x z x z x f ⎪⎩⎪⎨⎧≥<≤-<<-=⎪⎪⎩⎪⎪⎨⎧≥<≤-<<-=-=⎰⎰⎰-∞+∞-2,021,)2(10),22,021,)2(10,)2(),()(2110z z z z z z z dx z z dx z dx x z x f z f z z Z （3．设随机变量X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-=其它,020,4101,21)(x x x f X令2X Y =，),(y x F 为二维随机变量(X ，Y )的分布函数，求 (1) Y 的概率密度)(y f Y ；(2) )4,21(-F ．解：(1) F Y (y )=P {Y ≤y }=P {X 2≤y } 当y <0时，f Y (y )=0当y ≥0时，)()(}{)(y F y F y X y P y F X X Y --=<<-=从而，⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧>≤<≤<=⎪⎩⎪⎨⎧-+=4041,8110,83)]()([21)(y y y y y y f y f yy f X X Y ，(2) F (-1/2，4)=P {X ≤-1/2，Y ≤4}= P {X ≤-1/2，X 2≤4} =P {-2≤X ≤-1/2}=4121)(211212==⎰⎰----dx dx x f X 4．设(X ，Y )为二维离散型随机变量，X 和Y 的边缘分布律分别如下：如果1}0{==XY P ，试求 (1) (X ，Y )的分布律； (2) 问X 与Y 是否独立．解：P {XY ≠0}=1-P {XY =0}=0 即 P {X =-1，Y =1}+P {X =1，Y =1}=0由概率的非负性知，P {X =-1，Y =1}=0，P {X =1，Y =1}=0由边缘分布律的定义，P {X =-1}= P {X =-1，Y =0}+ P {X =-1，Y =1}=1/4 得P {X =-1，Y =0}=1/4再由P {X =1}= P {X =1，Y =0}+ P {X =1，Y =1}=1/4 得P {X =1，Y =0}=1/4再由P {Y =1}=P {X =-1，Y =1}+ P {X =0，Y =1}+ P {X =1，Y =1}= P {X =0，Y =1} 知P {X =0，Y =1}=1/2最后由归一性得：P {X =0，Y =0}=0(X ，Y )的分布律用表格表示如下：(2) 显然，X 和Y 不相互独立，因为P {X =-1，Y =0}≠ P {X =-1}P {Y =0}5．设随机变量X 与Y 相互独立，且),(~),,(~2ππσμ-U Y N X ，求Z = X + Y 的概率密度（计算结果用标准正态分布分布函数)(x Φ表示）．解：X 与Y 相互独立，利用卷积公式dx x z f x fz f Y XZ ⎰+∞∞--=)()()(计算,21)(222)(σμσπ--=x X ex f ⎪⎩⎪⎨⎧-∈=其它,0),(,21)(πππy y f Y ⎪⎩⎪⎨⎧<-<-=---其它,0,221)()(222)(ππππσσμx z e x z f x f x Y X⎰⎰⎰+---+---+∞∞-==-=ππσμπππσμπσππσz z x z z x Y X Z dx edx edx x z f x f z f 22222)(212)(21221)()()()]()([21}{21ππππππ--+=+<<-=z F z F z X z P ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-+Φσμπσμππz z 21 6．设二维随机变量(X ，Y )在矩形}10,20),{(≤≤≤≤=y x y x G 上服从均匀分布，试求边长为X 和Y 的矩形面积S 的概率密度)(s f S ．解：(X ，Y )～Ｕ(G )⎪⎩⎪⎨⎧∈=其它,0),(,21),(Gy x y x f设F (x )和f (s )分别表示S =XY 的分布函数和密度函数 F (s )=P {XY <s} s<0时，F S (s)=0s ≥0时，⎪⎩⎪⎨⎧+≥=⎰⎰⎰⎰s s xs S dydxdydx s F 010*******,1, 所以，⎪⎪⎩⎪⎪⎨⎧≥≥+<=2,12,2ln 220,0s s s s s s F S于是，S =ＸY 概率密度为⎪⎩⎪⎨⎧<<=其它,020,2ln 21)(s ss f S 7．设随机变量X 与Y 相互独立，其中X 的分布律为而Y 的概率密度为f (y )，求随机变量Y X U +=的概率密度)(u g ．解：由全概率公式： F U (u )=P {U ≤u }={X +Y ≤u }=P {X =1}P {X +Y ≤u |X =1}+ P {X =2}P {X +Y ≤u |X =2} = P {X =1}P {1+Y ≤u }+ P {X =2}P {2+Y ≤u } =0.3⨯F Y (u -1)+0.7⨯F Y (u -2)所以，f U (u ) =0.3⨯f Y (u -1)+0.7⨯f Y (u -2)8．设二维随机变量(X ，Y )的概率密度为⎩⎨⎧<<<<=其它，，,020,10 ,1),(x y x y x f 求：(1) (X ，Y )的边缘概率密度f X (x )，f Y (y )； (2) Y X Z -=2的概率密度)(z f Z ；解：(1) ⎩⎨⎧<<<<=其它,00,10,1),(x y x y x f⎩⎨⎧<<=⎪⎩⎪⎨⎧<<==⎰⎰∞+∞-其它其它,010,2,010,1),()(20x x x dy dy y x f x f x X ⎪⎩⎪⎨⎧<<-=⎪⎩⎪⎨⎧<<==⎰⎰∞+∞-其它其它,020,21,020,1),()(12y yy dx dx y x f y f y Y (2) ⎰⎰≤-=≤-=≤=zy x Z dxdy y x f z Y X P z Z P z F 2),(}2{}{)(如图所示，当z<0时，F Z (z)=0; 当z ≥2时，F Z (z)=1 当0≤z<2时:411)(212222020z z dydx dydx z F z xz x zx Z -=+=⎰⎰⎰⎰- 综上所述，⎪⎪⎩⎪⎪⎨⎧≥<≤-<=2,120,40.0)(2z z z z z z F Z 所以Z 的概率密度为：⎪⎩⎪⎨⎧<≤-=20,21,0)(z zz f Z 其它 9．设随机变量X 在区间(0，1)上服从均匀分布，在X = x （0 < x < 1）的条件下，随机变量Y 在区间),0(x 上服从均匀分布，求： (1) 随机变量X 和Y 的联合概率密度； (2) Y 的概率密度； (3) 概率P {X + Y > 1}．解：(1) ⎩⎨⎧<<=其它,010,1)(x x f X⎪⎩⎪⎨⎧<<<<=其它,010,0,1)|(|x x y xx y f X Y ⎪⎩⎪⎨⎧<<<==其它（,010,1)()|),(|x y xx f x y f y x f X X Y(2) ⎩⎨⎧<<-=⎪⎩⎪⎨⎧<<==⎰⎰∞+∞-其它其它,010,ln ,010,1),()(1y y y dx x dx y x f y f y Y (3) 2ln 11),(}1{P 15.011-===≥+⎰⎰⎰⎰-≥+xx y x dydx xdxdy y x f Y X10. 设随机变量X 与Y 相互独立，X 的分布律为31}{==i X P ，（i = – 1，0，1），Y 的概率密度为⎩⎨⎧<≤=其它,010,1)(y y f Y ，记Y X Z +=，求：(1) 求}021{=≤X Z P (2) 求Z 的概率密度)(z f Z ．解：(1) P {Z ≤1/2|X =0}=P {X +Y ≤1/2|X =0}=P {Y ≤1/2}=1/2 (2) 由全概率公式：F Z (z )=P {Z ≤z }=P {X +Y ≤z }=P {X =1}P {X +Y ≤z |X =1} +P {X =0}P {X +Y ≤z |X =0}=P {X =-1}P {X +Y ≤z|X =-1} = P {X =1}P {1+Y ≤z }+P {X =0}P {Y ≤z }=P {X =-1}P {-1+Y ≤z } =1/3⨯[F Y (z -1)+ F Y (z )+ F Y (z +1)]从而，f Z (z ) =1/3⨯[f Y (z -1)+ f Y (z )+ f Y (z +1)]=⎪⎩⎪⎨⎧<<-其它,021,31z11．设X 与Y 的联合概率密度为⎩⎨⎧<<<<=.,0;0,10 ,3),(其它x y x x y x f 试求Y X Z -=的概率密度．解：⎩⎨⎧<<<<=其它,00,10,3).(xy x x y x f⎰⎰-≥=-≥=≤-=≤=zx y Z dxdy y x f Z X Y P z Y X P z Z P z F ),(}{}{}{)(如图，当z<0时，F Z (z)=0; 当z ≥1时，F Z (z )=1当0≤z<1时:22333)(3100z z xdydx xdydx z F z xz x zxZ -=+=⎰⎰⎰⎰-综上得：⎪⎪⎩⎪⎪⎨⎧≥<≤-<=1,010,2230,0)(3z z z z z z F Z 12Z 的概率密度为⎪⎩⎪⎨⎧<≤-=其它,010),1(23)(2z z z f Z12．设X 与Y 独立同分布，且都服从标准正态分布N (0，1)，试求22Y X Z +=的分布．解：,21)(22x X ex f -=π,21)(22y Y ey f -=π22221)()(),(y x Y X e y f x f y x f +-==π}{}{)(22z y x P z Z P z F Z ≤+=≤=当z<0时，F Z (z)=0; 当z ≥0时，220222222222121),(}{)(z zr z y x Z erdrd edxdy y x f z Y X P z F --≤+-===≤+=⎰⎰⎰⎰πθπ所以，Z 的概率密度为⎪⎩⎪⎨⎧≥=-其它,00,)(22z ze z f z Z。

概率论课后习题解答

一、习题详解：1.1 写出下列随机试验的样本空间：(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;解：连续5 次都命中，至少要投5次以上，故}{ ,7,6,51=Ω；(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;解：}{12,11,4,3,22 =Ω；(3) 观察某医院一天内前来就诊的人数;解：医院一天内前来就诊的人数理论上可以从0到无穷，所以}{,2,1,03=Ω； (4) 从编号为1，2，3，4，5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解：属于不放回抽样，故两件产品不会相同，编号必是一大一小，故：()}{;51,4≤≤=Ωj i j i(5) 检查两件产品是否合格;解：用0 表示合格, 1 表示不合格，则()()()()}{1,1,0,1,1,0,0,05=Ω；(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2); 解：用x 表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间，故： ()}{216,T y x T y x ≤≤=Ω ；(7) 在单位圆内任取两点, 观察这两点的距离;解：}{207 x x =Ω；(8) 在长为l 的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.解：()}{l y x y x y x =+=Ω,0,0,8 ；1.2 设A ，B ，C 为三事件, 用A;B;C 的运算关系表示下列各事件：(1) A 与B 都发生, 但C 不发生; C AB ；(2) A 发生, 且B 与C 至少有一个发生;)(C B A ⋃；(3) A,B,C 中至少有一个发生; C B A ⋃⋃；(4) A,B,C 中恰有一个发生;C B A C B A C B A ⋃⋃；(5) A,B,C 中至少有两个发生; BC AC AB ⋃⋃；(6) A,B,C 中至多有一个发生;C B C A B A ⋃⋃； (7) A;B;C 中至多有两个发生;ABC ；(8) A,B,C 中恰有两个发生.C AB C B A BC A ⋃⋃ ；注意：此类题目答案一般不唯一，有不同的表示方式。

(完整版)概率论高等数学习题解答

1(A )三、解答题1•一颗骰子抛两次，以 X表示两次中所得的最小点数(1) 试求X 的分布律； (2)写出X 的分布函数.解：(1)分析：这里的概率均为古典概型下的概率，所有可能性结果共 36种，如果X=1，则表明两次中至少有一点数为1,其余一个1至6点均可，共有C 2 6-1 (这里C 2指任选某次点数为1, 6为另一次有6种结果均可取，减1即减去两次均为1的情形，因为C ； 6多1 1算了一次)或C 2 5 1种，故P X 1 C 26-1C25 1耳，其他结果类似36 3636可得•0, X1P{X 1} ,1X 2P{X 1} P{X 2} ,2X3F(x)P{X 1} P{X 2} P{X 3}， 3 x 4P{X 1} P{X 2} P{X3}P{X 4}, 4 x 5 P{X1} P{X2} P{X 3} P{X4} P{X5}, 5 x 61 ,x 622 •某种抽奖活动规则是这样的：袋中放红色球及白色球各 5只，抽奖者交纳一元钱后得到一次抽奖的机会，然后从袋中一次取出 5只球，若5只球同色，则获奖100元，否则无奖,以X 表示某抽奖者在一次抽取中净赢钱数，求X 的分布律.解:注意，这里 X 指的是赢钱数，X 取0-1或100-1，显然P X 99k3.设随机变量 X 的分布律为P{X k} a ,k 0,1,2, k!k解：因为 a ae 1，所以a e k 0 k!4.设随机变量X 的分布律为X -1 2 3 p1/41/21/4(1)求X 的分布函数;1 3 512627，3 翌,4 3635,5 36x 2 x 3x 4 x 5x 6 62 1 C ；0 1260为常数，试求常数 a .3⑵求P{X 丄}，P{- X 5}，P{2 x 3}.2 2 2解:40, x -1布，而与时间间隔的起点无关(时间以小时计)(1) 求某一天中午12时至下午3时没有收到紧急呼救的概率. (2) 求某一天中午12时至下午5时至少收到一次紧急呼救的概率. 解：(1) X ~ P 0.5t P 1.5 P X 0 e 1.5. (2) 0.5t2.50, x -1P{X 1}， 1 x2(1) F (x)P{X 1} P{X 2}1, x 3⑵P 1XX1 124P 2 X 3 P X 2X 3 5.设随机变量X 的分布律为 P{X k}(1) P{X =偶数｝(2) P{ X 5}(3) P{ X=3的倍数｝2 x 33 ， ,2x341, x 33 51 P — X P X2 —222P X2 3 P X 3.4扌,k 1,2, 求：解：(1) P X 偶数丄1丄 22 221 lim i1(2) P X 51 P X 4115 1 16 16⑶P X 3的倍数23236.某公安局在长度为i123ilim123t 的时间间隔内收到的紧急呼救的次数X 服从参数为0.5t 的泊松分2.5丄，1x2 45 7.某人进行射击，每次射击的命中率为0.02，独立射击400次，试求至少击中2次的概6解：设射击的次数为 X ，由题意知X ~ B 400,0.2i k k 400 kP X 2 1 P X 11 C 4000.02 0.98k 0查表泊松分布函数表得:P{X 2} 1 0.28 0.99728.设事件A 在每一次试验中发生的概率为 0.3,当A 发生不少于3次时，指示灯发出信(1)系数a ;(2) X 落在区间(0,[)内的概率.号•现进行5次独立试验，试求指示灯发出信号的概率.解：设X 为事件A 在5次独立重复实验中出现的次数,则指示灯发出信号的概率 X ~ B 5,0.3 p P X 3 1 P X 3 1 (C 00.3°0.75 C 50.310.74 C ；0.320.73) 1 0.8369 0.1631. 9.设顾客在某银行窗口等待服务的时间 X (以分钟计) 在窗口等待服务，若超过务而离开窗口的次数.写出服从参数为 5 10分钟，他就离开.他一个月要到银行 5次，以 Y 的分布律，并求P{Y 1}.指数分布•某顾客 Y 表示他未等到服 x 解：因为X 服从参数为5的指数分布，则F(x) 1 e T , P X 10 Y~ B5, e 2 , 1 F(10) e 2 ,则 P{Y k} C5 (e 2)k (1 e 2)5k,k 0,1, 5 P{Y 1} 1- P{Y 0} 1 (1 e 2)5 0.5167 a cosx. 10.设随机变量 X 的概率密度为 f(x)0,|x|~2，试求:|x |2解：(1)由归一性知：1 f (x)dx2a cosxdx 2a ，所以 a2由于上面二项分布的概率计算比较麻烦, 所以而且X 近似服P{X 2}18k ek 0k!7⑵-11.2.P{0 X —} ； cosxdx sin x |(424 .0,x011 . 设连续随机变量X的分布函数为F(x)Ax,0x 11,x1⑶X的概率密度.试求:(1) 解系数(1)A；由⑵X落在区间(0.3, 0.7)内的概率；的连续性可得lim F(x)F(x )在x=1 lim F(x) F(1)，即A=1.x 1(2) 0.3 X 0.7 F(0.7) F(0.3) 0.4.(3) X的概率密度 f (x) F (x)2x,00,12.设随机变量X服从(0, 5)上的均匀分布，求的概率.x的方程4x2 4Xx X 0有实根解：因为X服从(0, 5)上的均匀分布，所以1f(x) 50x5其他2 2方程4x 4Xx X(x 2)( X2(4X) 16X1，所以有实根的概率为0有实根，则32 51dx2510dxX〜N(3, 4)13.设求P{2 X 5}, P{(1) X 10}, P{ X 2}, P{X解: 确定c使得P{X c}设d满足P{X d} 0.9，问d至多为多少？(1)因为X ~ N(3,4)所以P{X c};2 3P{2 X 5} P{〒穿}P{1}(1) (0.5) (1) (0.5) 1 0.8413 0.6915 0.5328P 4 X 108F(2)(2.5)经查表得1 (0)，即2专)故斗214.设随机变量1.29，解：P XF(所以(k)15.设随机变量如何变化的？(3.5)2 0.999810 3 4 3(^)2 2(3.5) 2 (3.5)1 0.99962) 1(0.5)0.1，解：X ~ N(,(0.5)0.3023F(3)，则P X2X2(2.5)0.6977(0)得c 3 ；由概率密度关于即(-d 3)20.42.X服从正态分布2 2 (k)0.95 , p XN(0,1 0.5 0.5.c 3 1F(c)(〒)-，x=3对称也容易看出。

概率论何书元编著答案习题三解答

解（1）先求值
1 f ( x, y)dxdy R2
y1 y x2
11dxx12 x2 ydy
2
11( x2
x6 )dx
4
21
21 4
（2）求边缘分布
fX ( x) f ( x, y)dy
y1 y x2
1
x2
21 4
x2
ydy
21 8
x 2 (1
x4 ),
x 1
fY
(
y)
f
(
x,
y)dx
min{X ,Y },max{X ,Y }, X Y 的概率密度。解不适合次序统计量的公式（不同分布），
所以只能重新推导设 X ,Y 的分布函数分别为G( x), H( y), 密度分别为 g( x),h( y) （1）令 Z min{X ,Y }
FZ (z) P(min{ X ,Y } z)（次序统计量的一般推导方法） 1 P(min{ X ,Y } z) 1 P( X z,Y z) 1 [1 G(z)][1 H (z)] 1 ezez I(z0) 1 e()z I(z0)
（2） P( X
1,Y
3)
01dx2318 (6
x
y)dy
3 8
（3） P( X 1.5) P( X 1.5, Y )
01.5
dx
24
1 8
(6
x
y)dy
27 32
（4）P( X Y 4)
x
y4
1 8
(6
x
y)dxdy
02dx24 x
1 (6 8
x
y)dy
2 3
4
3
2
x y4

华农概率论习题三解答

习题三解答1：设二维随变量（X，Y）只能取下列数组中的值：（0，0），（-1，1），（-1，1/3），（2，0），且取这几组值的概率依次为1/6，1/3，1/12，5/12。

求此二维随机变量（X，Y）的分布列。

解：此二维随机变量（X，Y）的分布列是：―――――――――――――――――――――――――――――――――――――――2．一袋中有四个球，它们依次标有数字1，2，2，3。

从这袋中任取一球后，不放回袋中，再从袋中任取球，设每次取球时，袋中每个球被取到的可能性相同。

以X，Y分别记第一、二次取得的球上标有的数字，求（X，Y）的概率分布。

解：由题意得：（X，Y）的可能取值为：（1，2），（1，3），（2，1），（2，2），（2，3），（3，1），（3，2）。

则由概率的乘法公式得：P{X=1,Y=2}=(1/4)×(2/3)=1/6P{X=1,Y=3}=(1/4)×(1/3)=1/12P{X=2,Y=1}=(2/4)×(1/3)=1/6P{X=2,Y=2}=(2/4)×(1/3)=1/6P{X=2,Y=3}=(2/4)×(1/3)=1/6P{X=3,Y=1}=(1/4×(1/3)=1/12P{X=3,Y=2}=(1/4)×(2/3)=1/6而事件(1,1),(3,3)为不可能事件，所以P{X=1,Y=1}=0，P{X=3,Y=3}=0。

则（X ，Y ）的联合分布列为：―――――――――――――――――――――――――――――――――――――――3在一个箱子里装有12只开关，其中2只是次品，在其中随机地取两次，每次取一只，考虑两种试验，（1）有放回抽样，（2）无放回抽样，我们定义随机变量X ，Y 如下⎩⎨⎧=品表示第一次取出的是次品表示第一次取出的是正1X⎩⎨⎧=品表示第二次取出的是次品表示第二次取出的是正1Y解：（1）所求联合概率分布为：（2）所求联合概率分布为：―――――――――――――――――――――――――――――――――――――――4.设二维随机变量（X ，Y ）的概率密度为),(y x f =⎩⎨⎧>>+-其他,00,0,)43(y x ke y x（1）确定常数k ；（2）求（X ，Y ）的分布函数；（3）求P{0＜X ≤1，0＜Y ≤2}。

概率论与数理统计习题及答案----第3章习题详解

概率论与数理统计习题及答案----第3章习题详解习题三1.将一硬币抛掷三次，以X表示在三次中出现正面的次数，以Y表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X和Y的联合分布律.【解】X和Y的联合分布律如表：2.盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球，以X表示取到黑球的只数，以Y表示取到红球的只数.求X和Y的联合分布律.【解】X和Y的联合分布律如表：f （x ，y ）=⎩⎨⎧>>+-.,0,0,0,)43(其他y x A y x e求：（1）常数A ；（2）随机变量（X ，Y ）的分布函数；（3） P {0≤X <1，0≤Y <2}.【解】（1）由-(34)0(,)d d e d d 112x y Af x y x y A x y +∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得 A =12（2）由定义，有(,)(,)d d yx F x y f u v u v -∞-∞=⎰⎰(34)340012ed d (1e )(1e )0,0,0,0,y yu v x y u v y x -+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3){01,02}P X Y ≤<≤<12(34)3800{01,02}12ed d (1e )(1e)0.9499.x y P X Y x y -+--=<≤<≤==--≈⎰⎰ 5.设随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧<<<<--.,0,42,20),6(其他y x y x k（1）确定常数k ；（2）求P {X ＜1，Y ＜3}；（3）求P {X <1.5}；（4）求P {X +Y ≤4}.【解】（1）由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故18R =（2） 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰ (3)11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y<<=⎰⎰⎰⎰如图 1.542127d (6)d .832x x y y =--=⎰⎰(4)24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y+≤+≤=⎰⎰⎰⎰如图b 240212d (6)d .83xx x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量，X 在（0，0.2）上服从均匀分布，Y 的密度函数为f Y （y ）=⎩⎨⎧>-.,0,0,55其他y y e求：（1） X 与Y 的联合分布密度；（2） P {Y ≤X }.题6图【解】（1）因X 在（0，0.2）上服从均匀分布，所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其他所以(,),()()XY f x y X Y f x f y g 独立5515e25e ,00.20,0.20,0,yy x y --⎧⎧⨯<<>⎪==⎨⎨⎩⎪⎩且其他.(2)5()(,)d d 25e d d y y xDP Y X f x y x y x y-≤≤=⎰⎰⎰⎰如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.xyx x y x-==-+≈⎰⎰⎰7.设二维随机变量（X ，Y ）的联合分布函数为F （x ，y ）=⎩⎨⎧>>----.,0,0,0),1)(1(24其他y x y x e e求（X ，Y ）的联合分布密度.【解】(42)28e,0,0,(,)(,)0,x y x yF x yf x yx y-+⎧>>∂==⎨∂∂⎩其他.8.设二维随机变量（X，Y）的概率密度为f（x，y）= 4.8(2),01,0,0,.y x x y x-≤≤≤≤⎧⎨⎩其他求边缘概率密度.【解】()(,)dXf x f x y y+∞-∞=⎰x24.8(2)d 2.4(2),01,=0,.0,y x y x x x⎧⎧--≤≤⎪=⎨⎨⎩⎪⎩⎰其他()(,)dYf y f x y x+∞-∞=⎰12y4.8(2)d 2.4(34),01,=0,.0,y x x y y y y⎧-⎧-+≤≤⎪=⎨⎨⎩⎪⎩⎰其他题8图题9图9.设二维随机变量（X，Y）的概率密度为f（x，y）=⎩⎨⎧<<-.,0,,其他e yxy求边缘概率密度.【解】()(,)dXf x f x y y+∞-∞=⎰e d e,0,=0,.0,y xxy x+∞--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他()(,)dYf y f x y x+∞-∞=⎰e d e,0,=0,.0,y yxx y y--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他题10图10.设二维随机变量（X，Y）的概率密度为f（x，y）=⎩⎨⎧≤≤.,0,1,22其他yxycx（1）试确定常数c；（2）求边缘概率密度.【解】（1）(,)d d(,)d dDf x y x y f x y x y+∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c==⎰⎰得214c=.(2) ()(,)dXf x f x y y+∞-∞=⎰212422121(1),11,d840,0,.xx x xx y y⎧⎧--≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他()(,)dYf y f x y x+∞-∞=⎰5227d,01,420,0,.yyx y x y y-⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩其他11.设随机变量（X，Y）的概率密度为f（x，y）=⎩⎨⎧<<<.,0,10,,1其他xxy求条件概率密度f Y｜X（y｜x），f X｜Y（x｜y）.题11图【解】()(,)dXf x f x y y+∞-∞=⎰1d2,01,0,.xxy x x-⎧=<<⎪=⎨⎪⎩⎰其他111d1,10,()(,)d1d1,01,0,.yY yx y yf y f x y x x y y-+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他所以|1,||1,(,)(|)2()0,.Y XXy xf x yf y x xf x⎧<<⎪==⎨⎪⎩其他|1,1,1(,)1(|),1,()10,.X YYy xyf x yf x y y xf y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他12.袋中有五个号码1，2，3，4，5，从中任取三个，记这三个号码中最小的号码为X，最大的号码为Y.（1）求X与Y的联合概率分布；（2） X 与Y 是否相互独立？【解】（1） X 与Y 的联合分布律如下表 345 {}i P X x =1 3511C 10=3522C 10= 3533C 10= 610 2 0 3511C 10=3522C 10= 310 30 02511C 10=110{}i P Y y =110310610(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠===g 故X 与Y 不独立13.设二维随机变量（X ，Y ）的联合分布律为2 5 80.4 0.80.15 0.30 0.35 0.05 0.12 0.03 （1）求关于X 和关于Y 的边缘分布；（2） X 与Y 是否相互独立？【解】（1）X 和Y 的边缘分布如下表2 5 8P {Y=y i }YX XYX Y0.4 0.15 0.30 0.350.8 0.80.05 0.12 0.03 0.2{}i P X x =0.20.420.38(2) 因{2}{0.4}0.20.8P X P Y ===⨯g 0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.14.设X 和Y 是两个相互独立的随机变量，X 在（0，1）上服从均匀分布，Y 的概率密度为f Y （y ）=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e（1）求X 和Y 的联合概率密度；（2）设含有a 的二次方程为a 2+2Xa +Y =0，试求a 有实根的概率. 【解】（1）因1,01,()0,X x f x <<⎧==⎨⎩其他;21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩g 独立其他题14图(2) 方程220aXa Y ++=有实根的条件是 2(2)40X Y ∆=-≥故X 2≥Y ，从而方程有实根的概率为：22{}(,)d d x yP X Y f x y x y ≥≥=⎰⎰21/2001d e d 212[(1)(0)]0.1445.x y x yπ-==Φ-Φ=⎰⎰15.设X 和Y 分别表示两个不同电子器件的寿命（以小时计），并设X 和Y 相互独立，且服从同一分布，其概率密度为f （x ）=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}ZXF z P Z z P z Y =≤=≤(1) 当z ≤0时，()0ZF z =（2）当0<z <1时，（这时当x =1000时,y =1000z）(如图a) 3366102222101010()d d d d yz Z zxy zF z x y y x x y x y +∞≥==⎰⎰⎰⎰33610231010=d 2z zy yzy +∞⎛⎫-=⎪⎝⎭⎰题15图(3) 当z ≥1时，（这时当y =103时，x =103z ）（如图b ）3366222210101010()d d d d zy Z xy zF z x y y xx y x y +∞≥==⎰⎰⎰⎰336231010101=d 12y yzy z +∞⎛⎫-=- ⎪⎝⎭⎰即11,1,2(),01,20,.Z z z zf z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他故21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他16.设某种型号的电子管的寿命（以小时计）近似地服从N （160，202）分布.随机地选取4 只，求其中没有一只寿命小于180的概率.【解】设这四只寿命为X i (i =1,2,3,4)，则X i ~N （160，202），从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥g 之间独立34{180}{180}P X P X ≥≥g1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<g g g44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ==17.设X ，Y 是相互独立的随机变量，其分布律分别为P {X =k }=p （k ），k =0，1，2，…， P {Y =r }=q （r ），r =0，1，2，…. 证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(，i =0，1，2，….【证明】因X 和Y 所有可能值都是非负整数，所以{}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==U UL U于是{}{,},i k P Z i P X k Y i k X Y =====-∑相互独立0{}{}ik P X k P Y i k ===-∑g()()ik p k q i k ==-∑18.设X ，Y 是相互独立的随机变量，它们都服从参数为n ，p 的二项分布.证明Z =X +Y 服从参数为2n ，p 的二项分布.【证明】方法一：X +Y 可能取值为0，1，2，…，2n .0{}{,}ki P X Y k P X i Y k i =+====-∑00202(){}2ki k i n i k i n k ii kk n ki k n k P X i P Y k i n n p q p q i k i n n p q i k i n p q k =---+=-=-===-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭∑∑∑g方法二：设μ1,μ2,…,μn ;μ1′,μ2′,…，μn ′均服从两点分布（参数为p ），则X =μ1+μ2+…+μn，Y =μ1′+μ2′+…+μn ′,X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以，X +Y 服从参数为（2n ,p )的二项分布.19.设随机变量（X ，Y ）的分布律为0 1 2 3 4 50 1 2 30 0.01 0.03 0.05 0.07 0.090.01 0.02 0.04 0.05 0.06 0.080.01 0.03 0.05 0.05 0.05 0.060.01 0.02 0.04 0.06 0.06 0.05 (1) 求P {X =2｜Y =2}，P {Y =3｜X =0}；（2）求V =max （X ，Y ）的分布律；（3）求U =min （X ，Y ）的分布律；（4）求W =X +Y 的分布律.【解】（1）{2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑X Y{3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑（2）{}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i ====<+≤= 1{,}{,},i ik k P X i Y k P X k Y i -=====+==∑∑0,1,2,3,4,5i =所以V 的分布律为V =max(X ,Y ) 0 12345P 0 0.04 0.16 0.28 0.24 0.28(3){}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k i k i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑0,1,2,3,i =于是 U =min(X ,Y ) 0 1 2 3 P0.28 0.30 0.25 0.17 (4)类似上述过程，有W =X +Y 0 1 2345678P0 0.00.00.10.10.20.10.10.02 63 94 9 25 20.雷达的圆形屏幕半径为R，设目标出现点（X，Y）在屏幕上服从均匀分布.（1）求P{Y＞0｜Y＞X}；（2）设M=max{X，Y}，求P{M＞0}.题20图【解】因（X，Y）的联合概率密度为22221,,(,)π0,.x y Rf x y R⎧+≤⎪=⎨⎪⎩其他（1）{0,}{0|}{}P Y Y XP Y Y XP Y X>>>>=>(,)d(,)dyy xy xf x yf x yσσ>>>=⎰⎰⎰⎰π2π/405π42π/401d dπ1d dπRRr rRr rRθθ=⎰⎰⎰⎰3/83;1/24==(2) {0}{max(,)0}1{max(,)0}P M P X Y P X Y>=>=-≤131{0,0}1(,)d1.44xyP X Y f x yσ≤≤=-≤≤=-=-=⎰⎰21.设平面区域D由曲线y=1/x及直线y=0，x=1,x=e2所围成，二维随机变量（X，Y）在区域D上服从均匀分布，求（X，Y）关于X 的边缘概率密度在x=2处的值为多少？题21图【解】区域D的面积为22e e0111d ln 2.S x xx===⎰（X,Y）的联合密度函数为211,1e,0,(,)20,.x yf x y x⎧≤≤<≤⎪=⎨⎪⎩其他（X，Y）关于X的边缘密度函数为1/211d,1e,()220,.xXy xf x x⎧=≤≤⎪=⎨⎪⎩⎰其他所以1(2).4Xf=22.设随机变量X和Y相互独立，下表列出了二维随机变量（X，Y）联合分布律及关于X 和Y的边缘分布律中的部分数值.试将其余数值填入表中的空白处.y 1 y 2 y 3 P {X =x i }=p i x 1 x 21/8 1/8P {Y =y j }=p j 1/6 1【解】因21{}{,}jjiji P Y y P P X x Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+==从而11111{,}.6824P X x Y y ===-= 而X 与Y 独立，故{}{}{,}ijiiP X x P Y y P X x Y y =====g ,从而11111{}{,}.624P X x P X x Y y =⨯==== 即：1111{}/.2464P X x === 又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+==即1,3111{},4248P X x Y y =++== 从而131{,}.12P X x Y y === 同理21{},2P Y y == 223{,}8P X x Y y ===YX又31{}1jj P Y y ===∑,故3111{}1623P Y y ==--=. 同理23{}.4P X x == 从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====-===-=故1y 2y 3y {}i iP X x P ==1x 124 18 112 14 2x18 38 14 34{}j jP Y y p ==161213123.设某班车起点站上客人数X 服从参数为λ(λ>0)的泊松分布，每位乘客在中途下车的概率为p （0<p <1），且中途下车与否相互独立，以Y 表示在中途下车的人数，求：（1）在发车时有n 个乘客的条件下，中途有m 人下车的概率；（2）二维随机变量（X ，Y ）的概率分布.YX【解】(1){|}C (1),0,0,1,2,m m n mn P Y m X n p p m n n -===-≤≤=L .(2){,}{}{|}P X n Y m P X n P Y m X n ======ge C (1),,0,1,2,.!mmn mnnp p n m n n n λλ--=-≤≤=g L24.设随机变量X 和Y 独立，其中X 的概率分布为X ~⎪⎪⎭⎫⎝⎛7.03.021，而Y 的概率密度为f (y )，求随机变量U =X +Y 的概率密度g (u ).【解】设F （y ）是Y 的分布函数，则由全概率公式，知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|2}P Y u X P Y u X =≤-=+≤-=由于X 和Y 独立，可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(2).F u F u =-+-由此，得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u '''==-+-0.3(1)0.7(2).f u f u =-+-25. 25. 设随机变量X 与Y 相互独立，且均服从区间[0,3]上的均匀分布，求P {max{X ,Y }≤1}.解：因为随即变量服从[0，3]上的均匀分布，于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩因为X ，Y 相互独立，所以1, 03,03,(,)90, 0,0,3, 3.x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩推得1{max{,}1}9P X Y ≤=.26. 设二维随机变量（X ，Y ）的概率分布为-1 01-1 0 1a 00.20.1 b0.20 0.1c其中a ,b ,c 为常数，且X 的数学期望E (X )= -0.2,P {Y ≤0|X ≤0}=0.5，记Z =X +Y .求：（1） a ,b ,c 的值；XY（2） Z 的概率分布；（3） P {X =Z }.解 (1) 由概率分布的性质知，a+b+c +0.6=1 即 a+b+c = 0.4.由()0.2E X =-，可得0.1a c -+=-.再由{0,0}0.1{00}0.5{0}0.5P X Y a b P Y X P X a b ≤≤++≤≤===≤++,得0.3a b +=.解以上关于a ，b ，c 的三个方程得0.2,0.1,0.1a b c ===. (2) Z 的可能取值为-2，-1，0，1，2，{2}{1,1}0.2P Z P X Y =-==-=-=，{1}{1,0}{0,1}0.1P Z P X Y P X Y =-==-=+==-=，{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y ===-=+==+==-=，{1}{1,0}{0,1}0.3P Z P X Y P X Y ====+===，{2}{1,1}0.1P Z P X Y =====，即Z 的概率分布为Z -2 -1 01 2P 0.2 0.1 0.30.3 0.1(3)====++=++=. {}{0}0.10.20.10.10.20.4 P X Z P Y b。

概率论与数理统计习题三参考答案

概率论与数理统计习题三参考答案1．某产品的次品率为0.1，检验员每天检验4次，每次随机地取10件进行检验，如果发现其中的次品多于1，就去调整设备。

以X 表示一天中调整设备的次数，求。

（设诸产品是否为次品是相互独立的。

） )(X E 解：解法一用Y 表示10件中次品的个数，则)1.0,10(~B Y 而X 表示一天中调整设备的次数，，),4(~p B X {}2≥=Y p p {}{}{}1012=−=−=≥Y P Y P Y p Q()()9110100101.011.01.011−⋅−−−=C C 264.0= 056.14)(==∴p X E解法二设为发现次品数i X 4,3,2,1 111,0=⎩⎨⎧=i X i ，，次品数大于发现次品数小于等于则4321X X X X X +++=)()()()()(4321X E X E X E X E X E +++={}{}{}100次品数等于次品数等于P P X P i +==∴()()9110100101.011.01.01−⋅+−=C C 743.0= {}{}264.0011==−==∴i i X P X P 056.1264.04)(=×=∴X E2．将3只球随机地逐个放入4只编号分别为1，2，3，4 的盒子中，以X 表示至少有一只球的盒子的最小号码，是求。

)(X E 解：解法一 X 可取1、2、3、4{}6437433133323213=++==∴C C C X P {}6419422233323213=++==C C C X P{}6474133332313=++⋅==C C C X P {}6414143===X P 162564146473649264371)(=×+×+×+×=∴X E 解法二 1625162316521691)(=×+×+×=∴X E 3．若随机变量X 的分布律为()=⎭⎫⎩⎨⎧−=+i x P ii 21121i ，i =1,2 ,……., 是否存在。

《概率论与数理统计》韩旭里谢永钦版习题三及答案

习题三1.将一硬币抛掷三次，以X 表示在三次中出现正面的次数，以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表：2.盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球，以X 表示取到黑球的只数，以Y 表示取到红球的只数.求X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表：3.设二维随机变量（X ，Y ）的联合分布函数为F （x ，y ）=⎪⎩⎪⎨⎧≤≤≤≤.,020,20,sin sin 其他ππy x y x求二维随机变量（X ，Y ）在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,40πππy x 内的概率. 【解】如图πππ{0,}(3.2)463P X Y <≤<≤公式 ππππππ(,)(,)(0,)(0,434636F F F F −−+ππππππsin sin sin sin sin 0sin sin 0sin4346361).4=−−+=i i i i题3图说明：也可先求出密度函数，再求概率。

4.设随机变量（X ，Y ）的分布密度f （x ，y ）=⎩⎨⎧>>+−.,0,0,0,)43(其他y x A y x e 求：（1）常数A ；（2）随机变量（X ，Y ）的分布函数；（3） P {0≤X <1，0≤Y <2}. 【解】（1）由-(34)0(,)d d e d d 112x y Af x y x y A x y +∞+∞+∞+∞+−∞−∞===∫∫∫∫得 A =12 （2）由定义，有 (,)(,)d d y xF x y f u v u v −∞−∞=∫∫(34)340012ed d (1e )(1e )0,0,0,0,y yu v x y u v y x −+−−⎧⎧−−>>⎪==⎨⎨⎩⎪⎩∫∫其他（3） {01,02}P X Y ≤<≤<12(34)3800{01,02}12ed d (1e )(1e )0.9499.x y P X Y x y −+−−=<≤<≤==−−≈∫∫5.设随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧<<<<−−.,0,42,20),6(其他y x y x k（1）确定常数k ；（2）求P {X ＜1，Y ＜3}；（3）求P {X <1.5}；（4）求P {X +Y ≤4}.【解】（1）由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞−∞−∞=−−==∫∫∫∫故 18R = （2） 13{1,3}(,)d d P X Y f x y y x −∞−∞<<=∫∫130213(6)d d 88k x y y x =−−=∫∫ （3） 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=∫∫∫∫如图1.542127d (6)d .832x x y y =−−=∫∫（4） 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=∫∫∫∫如图b240212d (6)d .83xx x y y −=−−=∫∫题5图6.设X 和Y 是两个相互独立的随机变量，X 在（0，0.2）上服从均匀分布，Y 的密度函数为f Y （y ）=⎩⎨⎧>−.,0,0,55其他y y e求：（1） X 与Y 的联合分布密度；（2） P {Y ≤X }.题6图【解】（1）因X 在（0，0.2）上服从均匀分布，所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他而55e ,0,()0,.y Y y f y −⎧>=⎨⎩其他所以(,),()()X Y f x y X Y f x f y i 独立5515e 25e ,00.20,0.20,0,y y x y −−⎧⎧×<<>⎪==⎨⎨⎩⎪⎩且其他. （2） 5()(,)d d 25ed d yy xDP Y X f x y x y x y −≤≤=∫∫∫∫如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.xy x x y x−==−+≈∫∫∫7.设二维随机变量（X ，Y ）的联合分布函数为F （x ，y ）=⎩⎨⎧>>−−−−.,0,0,0),1)(1(24其他y x y x e e求（X ，Y ）的联合分布密度.【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y −+⎧>>∂==⎨∂∂⎩其他. 8.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）= 4.8(2),01,0,0,.y x x y x −≤≤≤≤⎧⎨⎩其他求边缘概率密度. 【解】()(,)d X f x f x y y +∞−∞=∫x204.8(2)d 2.4(2),01,=0,.0,y x y x x x ⎧⎧−−≤≤⎪=⎨⎨⎩⎪⎩∫其他 ()(,)d Y f y f x y x +∞−∞=∫12y4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ⎧−⎧−+≤≤⎪=⎨⎨⎩⎪⎩∫其他题8图题9图9.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧<<−.,0,0,其他e y x y 求边缘概率密度. 【解】()(,)d X f x f x y y +∞−∞=∫e d e ,0,=0,.0,y x x y x +∞−−⎧⎧>⎪=⎨⎨⎩⎪⎩∫其他 ()(,)d Y f y f x y x +∞−∞=∫0e d e ,0,=0,.0,yy x x y y −−⎧⎧>⎪=⎨⎨⎩⎪⎩∫其他题10图10.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧≤≤.,0,1,22其他y x y cx（1）试确定常数c ；（2）求边缘概率密度. 【解】（1）(,)d d (,)d d Df x y x y f x y x y +∞+∞−∞−∞∫∫∫∫如图2112-14=d d 1.21xx cx y y c ==∫∫得　214c =. （2） ()(,)d X f x f x y y +∞−∞=∫212422121(1),11,d 840,0,.x x x x x y y ⎧⎧−−≤≤⎪⎪==⎨⎨⎪⎪⎩⎩∫其他 ()(,)d Y f y f x y x +∞−∞=∫5227d ,01,20,0, .x y x y y ⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩其他 11.设随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧<<<.,0,10,,1其他x x y 求条件概率密度f Y ｜X （y ｜x ），f X ｜Y（x ｜y ）.题11图【解】()(,)d X f x f x y y +∞−∞=∫1d 2,01,0,.xxy x x −⎧=<<⎪=⎨⎪⎩∫其他 111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y −+∞−∞⎧=+−<<⎪⎪⎪===−≤<⎨⎪⎪⎪⎩∫∫∫其他所以|1,||1,(,)(|)2()0,.Y X X y x f x y f y x xf x ⎧<<⎪==⎨⎪⎩其他|1,1,1(,)1(|),1,()10,.X Y Y y x y f x y f x y y x f y y⎧<<⎪−⎪⎪==−<<⎨+⎪⎪⎪⎩其他12.袋中有五个号码1，2，3，4，5，从中任取三个，记这三个号码中最小的号码为X ，最大的号码为Y .（1）求X 与Y 的联合概率分布；（2） X 与Y 是否相互独立？【解】（1） X 与Y 的联合分布律如下表（2）因6161{1}{3}{1,3},101010010P X P Y P X Y ===×=≠===i 故X 与Y 不独立　（1）求关于X 和关于Y 的边缘分布；（2） X 与Y 是否相互独立？（2）因{2}{0.4}0.20.8P X P Y ===×i 0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.　14.设X 和Y 是两个相互独立的随机变量，X 在（0，1）上服从均匀分布，Y 的概率密度为f Y （y ）=⎪⎩⎪⎨⎧>−.,0,0,212/其他y y e（1）求X 和Y 的联合概率密度；（2）设含有a 的二次方程为a 2+2Xa +Y =0，试求a 有实根的概率.【解】（1）因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y −⎧>⎪==⎨⎪⎩其他. 故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y −⎧<<>⎪=⎨⎪⎩i 独立其他题14图（2）方程220a Xa Y ++=有实根的条件是2(2)40X Y Δ=−≥故 X 2≥Y ，从而方程有实根的概率为：22{}(,)d d x yP X Y f x y x y ≥≥=∫∫21/2001d e d 21(1)(0)]0.1445.x y x y−==Φ−Φ=∫∫15.设X 和Y 分别表示两个不同电子器件的寿命（以小时计），并设X 和Y 相互独立，且服从同一分布，其概率密度为f （x ）=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}Z XF z P Z z P z Y=≤=≤ （1）当z ≤0时，()0Z F z =（2）当0<z <1时，（这时当x =1000时,y =1000z）（如图a ） 3366102222101010()d d d d yz Z zx y zF z x y y x x y x y +∞≥==∫∫∫∫ 33610231010=d 2z zy yzy +∞⎛⎞−=⎜⎟⎝⎠∫题15图（3）当z ≥1时，（这时当y =103时，x =103z ）（如图b ） 3366222210101010()d d d d zy Z xy zF z x y y x x y x y +∞≥==∫∫∫∫336231010101=d 12y y zy z +∞⎛⎞−=−⎜⎟⎝⎠∫即 11,1,2(),01,20,.Z z z zf z z ⎧−≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他16.设某种型号的电子管的寿命（以小时计）近似地服从N （160，202）分布.随机地选取4 只，求其中没有一只寿命小于180的概率.【解】设这四只寿命为X i （i =1,2,3,4），则X i ~N （160，202），从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥i 之间独立34{180}{180}P X P X ≥≥i 1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =−<−<−<−<i i i44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡−⎤⎛⎞=−<=−Φ⎜⎟⎢⎥⎝⎠⎣⎦=−Φ== 17.设X ，Y 是相互独立的随机变量，其分布律分别为P {X =k }=p （k ），k =0，1，2，…， P {Y =r }=q （r ），r =0，1，2，….证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=−ik k i q k p 0)()(，i =0，1，2，….【证明】因X 和Y 所有可能值都是非负整数，所以 {}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====−==∪∪ ∪ 于是0{}{,},ik P Z i P X k Y i k X Y =====−∑相互独立{}{}ik P X k P Y i k ===−∑i()()ik p k q i k ==−∑18.设X ，Y 是相互独立的随机变量，它们都服从参数为n ，p 的二项分布.证明Z =X +Y 服从参数为2n ，p 的二项分布.【证明】方法一：X +Y 可能取值为0，1，2，…，2n .0{}{,}ki P X Y k P X i Y k i =+====−∑00202(){}2ki ki n i k i n k ii kk n ki k n k P X i P Y k i n n p q p qi k i n n p qi k i n p q k =−−−+=−=−===−⎛⎞⎛⎞=⎜⎟⎜⎟−⎝⎠⎝⎠⎛⎞⎛⎞=⎜⎟⎜⎟−⎝⎠⎝⎠⎛⎞=⎜⎟⎝⎠∑∑∑i方法二：设μ1,μ2,…,μn ;μ1′,μ2′,…，μn ′均服从两点分布（参数为p ），则 X =μ1+μ2+…+μn ，Y =μ1′+μ2′+…+μn ′, X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以，X +Y 服从参数为（2n ,p ）的二项分布.（2）求V =max （X ，Y ）的分布律；（3）求U =min （X ，Y ）的分布律；（4）求W =X +Y 的分布律. 【解】（1）{2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑ {3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑ （2）{}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i ====<+≤=10{,}{,},i ik k P X i Y k P X k Y i −=====+==∑∑ 0,1,2,3,4,5i =所以V 的分布律为V =max （X ,Y ） 0 1 2 3 4 5 P 00.04 0.16 0.28 0.24 0.28（3） {}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k ik i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑ 0,1,2,3,i =于是U =min （X ,Y ） 0 1 2 3 P0.28 0.30 0.25 0.17（4）类似上述过程，有W =X +Y 0 1 2 3 4 5 6 7 8 P0.02 0.06 0.13 0.19 0.24 0.19 0.12 0.0520.雷达的圆形屏幕半径为R ，设目标出现点（X ，Y ）在屏幕上服从均匀分布. （1）求P {Y ＞0｜Y＞X }；（2）设M =max{X ，Y }，求P {M ＞0}.题20图【解】因（X ，Y ）的联合概率密度为22221,,(,)π0,.x y R f x y R⎧+≤⎪=⎨⎪⎩其他（1）{0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=>0(,)d (,)d y y xy xf x y f x y σσ>>>=∫∫∫∫π2π/405π42π/401d d π1d d πRR r rR r r R θθ=∫∫∫∫3/83;1/24==（2） {0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=−≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=−≤≤=−=−=∫∫21.设平面区域D 由曲线y =1/x 及直线y =0，x =1,x=e 2所围成，二维随机变量（X ，Y ）在区域D 上服从均匀分布，求（X ，Y ）关于X 的边缘概率密度在x =2处的值为多少？题21图【解】区域D 的面积为 22e e 0111d ln 2.S x x x===∫（X ,Y ）的联合密度函数为211,1e ,0,(,)20,.x y f x y x ⎧≤≤<≤⎪=⎨⎪⎩其他（X ，Y ）关于X 的边缘密度函数为1/2011d 1e ,()220,.x X y x f x x⎧=≤≤⎪=⎨⎪⎩∫其他所以1(2).4X f =22.设随机变量X 和Y 相互独立，下表列出了二维随机变量（X ，Y ）联合分布律及关于X 和x 2 1/8P {Y =y j }=p j 1/6 1【解】因21{}{,}j j iji P Y y P P X x Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+== 从而11111{,}.6824P X x Y y ===−= 而X 与Y 独立，故{}{}{,}i j i i P X x P Y y P X x Y y =====i ,从而11111{}{,}.624P X x P X x Y y =×==== 即：1111{}/.2464P X x ===又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+==即1,3111{},4248P X x Y y =++== 从而131{,}.12P X x Y y ===同理21{},2P Y y == 223{,}8P X x Y y ===又31{}1jj P Y y ===∑,故3111{}1623P Y y ==−−=. 同理23{}.4P X x == 从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====−===−=故23.设某班车起点站上客人数X 服从参数为λ（λ>0）的泊松分布，每位乘客在中途下车的概率为p （0<p <1），且中途下车与否相互独立，以Y 表示在中途下车的人数，求：（1）在发车时有n 个乘客的条件下，中途有m 人下车的概率；（2）二维随机变量（X ，Y ）的概率分布.【解】（1） {|}C (1),0,0,1,2,mmn mn P Y m X n p p m n n −===−≤≤= .（2） {,}{}{|}P X n Y m P X n P Y m X n ======ie C (1),,0,1,2,.!mm n mnnp p n m n n n λλ−−=−≤≤=i 24.设随机变量X 和Y 独立，其中X 的概率分布为X ~⎟⎟⎠⎞⎜⎜⎝⎛7.03.021，而Y 的概率密度为f （y ），求随机变量U =X +Y 的概率密度g （u ）.【解】设F （y ）是Y 的分布函数，则由全概率公式，知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|2}P Y u X P Y u X =≤−=+≤−=由于X 和Y 独立，可见()0.3{1}0.7{2}G u P Y u P Y u =≤−+≤−0.3(1)0.7(2).F u F u =−+−由此，得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u ′′′==−+−0.3(1)0.7(2).f u f u =−+−25. 设随机变量X 与Y 相互独立，且均服从区间[0,3]上的均匀分布，求P {max{X ,Y }≤1}.解：因为随即变量服从[0，3]上的均匀分布，于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩ 1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩因为X ，Y 相互独立，所以1, 03,03,(,)90, 0,0,3, 3.x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩推得 1{max{,}1}9P X Y ≤=. 26. 设二维随机变量（X ，Y ）的概率分布为其中a ,b ,c 为常数，且X 的数学期望E （X ）= −0.2,P {Y ≤0|X ≤0}=0.5，记Z =X +Y .求：（1） a ,b ,c 的值；（2） Z 的概率分布；（3） P {X =Z }.解（1）由概率分布的性质知，a+b+c +0.6=1 即 a+b+c = 0.4. 由()0.2E X =−，可得0.1a c −+=−.再由 {0,0}0.1{00}0.5{0}0.5P X Y a b P Y X P X a b ≤≤++≤≤===≤++,得 0.3a b +=.解以上关于a ，b ，c 的三个方程得0.2,0.1,0.1a b c ===.（2） Z 的可能取值为−2，−1，0，1，2，{2}{1,1}0.2P Z P X Y =−==−=−=，{1}{1,0}{0,1}0.1P Z P X Y P X Y =−==−=+==−=，{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y ===−=+==+==−=，{1}{1,0}{0,1}0.3P Z P X Y P X Y ====+===，{2}{1,1}0.1P Z P X Y =====，即Z 的概率分布为Z −2 −1 0 1 2 P0.2 0.1 0.3 0.3 0.1（3） {}{0}0.10.20.10.10.20.4P X Z P Y b ====++=++=.。

《概率论》数学3章课后习题详解

概率论第三章习题参考解答1. 如果ξ服从0-1分布, 又知ξ取1的概率为它取0的概率的两倍, 求ξ的期望值解：由习题二第2题算出ξ的分布率为ξ0 1 P1/32/3因此有E ξ=0×P (ξ=0)+1×P (ξ=1)=2/3+2η, ξ与η的分布律如下表所示:: 求周长的期望值, 用两种方法计算, 一种是利用矩形长与宽的期望计算, 另一种是利用周长的分布计算.解: 由长和宽的分布率可以算得E ξ=29×P (ξ=29)+30×P (ξ=30)+31×P (ξ=31) =29×0.3+30×0.5+31×E η=19×P (η=19)+20×P (η=20)+21×P (η=21) =19×0.3+20×0.4+21×0.3=20 由期望的性质可得 E ζ=2(E ξ+E η)=2×而如果按ζ的分布律计算它的期望值, 也可以得 E ζ=96×0.09+98×0.27+100×0.35+102×0.23+104× 验证了期望的性质.4. 连续型随机变量ξ的概率密度为⎩⎨⎧><<=其它)0,(10)(a k x kx x aϕ又知Eξ=0.75, 求k 和a 的值。

解: 由性质⎰+∞∞-=1)(dx x ϕ得111)(|10110=+=+==++∞∞-⎰⎰a kx a k dx kx dx x a aϕ即k =a +1(1)又知75.022)(|10211=+=+===+++∞∞-⎰⎰a kx a k dx kx dx x x E a a ϕξ得ka +1.5(2)由(1)与(2)解得a =0.5, 即a =2, k =36. 下表是某公共汽车公司的188辆汽车行驶到发生一次引擎故障的里程数的分布数列.若表中各以组中值为代表. 从188辆汽车中, 任意抽选15辆, 得出下列数字: 90, 50, 150, 110, 90, 90, 110, 90, 50, 110, 90, 70, 50, 70, 150. (1)求这15个数字的平均数; (2) 计算表3-9中的期望并与(1)相比较.解: (1) 15个数的平均数为(2) 按上表计算期望值为(10×5+30×11+50×16+70×25+90×34+110×46+130×33+150×16+170×2)/1887. 两种种子各播种300公顷地, 调查其收获量, 如下表所示, 分别求出它们产量的平均值解: 假设种子甲的每公顷产量数为, 种子乙的每公顷产量数为, 则 E ξ=(4500×12+4800×38+5100×40+5400×10)/100=4944 E η=(4500×23+4800×24+5100×30+5400×23)/100=49598. 一个螺丝钉的重量是随机变量, 期望值为10g , 标准差为1g . 100个一盒的同型号螺丝钉重量的期望值和标准差各为多少?(假设各个螺丝钉的重量相互之间独立) 解: 假设这100个螺丝钉的重量分别为ξ1, ξ2,…, ξ100, 因此有E ξi =10, Dξi =102=12=1, (i =1,2,…,100), 设ξ为这100个螺丝钉的总重量，因此∑==1001i i ξξ，则ξ的数学期望和标准差为gD D D kgg E E E i ii i i i i i 1011001)(1000101001001100110011001=⨯==⎪⎭⎫⎝⎛====⨯==⎪⎭⎫ ⎝⎛=∑∑∑∑====ξξξσξξξξ9. 已知100个产品中有10个次品，求任意取出的5个产品中次品数的期望值.解: 假设ξ为取出5个产品中的次品数, 又假设ξi 为第i 次取出的次品数, 即, 如果第i 次取到的是次品, 则ξi =1否则ξi =0, i =1,2,3,4,5, ξi 服从0-1分布,而且有 P {ξi =0}=90/100, P {ξi =1}=10/100, i =1,2,3,4,5因此, E ξi =10/100=1/10, 因为∑==51i iξξ因此有5.010155151=⨯==⎪⎭⎫ ⎝⎛=∑∑==i i i i E E E ξξξ10. 一批零件中有9个合格品和3个废品, 在安装机器时, 从这批零件中任取一个, 如果取出的是废品就不再放回去. 求取得第一个合格品之前, 已经取出的废品数的数学期望和方差. 解: 假设在取到第一个合格品之前已取出的废品数为ξ, 则可算出0045.02201101112123}3{041.02209109112123}2{2045.0119123}1{75.0129}0{==⋅⋅====⋅⋅===⋅=====ξξξξP P P P因此有319.009.0409.0)(409.090045.04041.02045.03.030045.02041.02045.0222===-==⨯+⨯+==⨯+⨯+=ξξξξξE E D E E11. 假定每人生日在各个月份的机会是同样的, 求3个人中生日在第一个季度的平均人数. 解: 设三个随机变量ξi ,(i =1,2,3), 如果3个人中的第i 个人在第一季度出生, 则ξi =1, 否则ξi =0, 则ξi 服从0-1分布, 且有 P (ξi =1)=1/4, 因此E ξi =1/4, (i =1,2,3)设ξ为3个人在第一季度出生的人数, 则ξ=ξ1+ξ2+ξ3, 因此Eξ=E (ξ1+ξ2+ξ3)=3Eξi12. ξ有分布函数⎩⎨⎧>-=-其它1)(x e x F xλ, 求E ξ及D ξ. 解: 因ξ的概率密度为⎩⎨⎧>='=-其它)()(x e x F x xλλϕ, 因此 ()λλλϕξλλλλλ11)(0=-=+-=-===∞+-∞+-∞+-+∞-+∞-+∞∞-⎰⎰⎰⎰xx xxxe dx e xe e xd dx ex dx x x E()22020222222)(|λξλλϕξλλλλ==+-=-===⎰⎰⎰⎰∞+-∞+-+∞-+∞-+∞∞-E dx xe e x e d x dx ex dx x x E x x x x22222112)(λλλξξξ=-=-=E E D13. ⎪⎩⎪⎨⎧<-=其它1||11)(~2x x x πϕξ, 求E ξ和D ξ.解: 因φ(x )是偶函数, 因此Eξ=0,则D ξ=Eξ2-(Eξ)2=Eξ2 因此有⎰⎰-===+∞∞-1222212)(dx xx dx x x E D πϕξξ令θθθd dx x cos ,sin ==则上式=2112sin 21212cos 2sin 12||20202022=+=+=⎰⎰ππππθπθπθθπθθπd d 即D ξ16. 如果ξ与η独立, 不求出ξη的分布直接从ξ的分布和η的分布能否计算出D (ξη), 怎样计算?解: 因ξ与η独立, 因此ξ2与η2也独立, 则有[]()()222222)()()(ηξηξξηξηξηE E E E E E D -=-=17. 随机变量η是另一个随机变量ξ的函数, 并且η=e λξ(λ>0), 若E η存在, 求证对于任何实数a 都有λξλξEe ea P a⋅≤≥-}{.证: 分别就离散型和连续型两种情况证. 在ξ为离散型的情况: 假设P (ξ=x i )=p i , 则λξλξλλλξEe e e E p e p ep a P a a i i a x ax i a x ax i i i i i --∞=-≥-≥==≤≤=≥∑∑∑][){)(1)()(在ξ为连续型的情况假设ξ的概率密度为φ(x ), 则λξλξλλλϕϕϕξEe e Ee dx x e dx x edx x a P a a a x aa x a--+∞∞--+∞-+∞==≤≤=≥⎰⎰⎰)()()()()()(}{证毕.18. 证明事件在一次试验中发生次数的方差不超过1/4.证: 设ξ为一次试验中事件A 发生的次数, 当然最多只能发生1次, 最少为0次, 即ξ服从0-1分布, P {ξ=1}=P (A )=p , P {ξ=0}=1-p =q ,则4121412124141)1(222≤⎪⎭⎫ ⎝⎛--=-⋅+-=-=-=p p p p p p p D ξ19. 证明对于任何常数c , 随机变量ξ有 D ξ=E (ξ-c )2-(Eξ-c )2证: 由方差的性质可知D (ξ-c )=Dξ, 而2222)()()]([)()(c E c E c E c E c D ---=---=-ξξξξξ证毕.20. (ξ,η)的联合概率密度φ(x ,y )=e -(x +y )(x ,y >0), 计算它们的协方差cov (ξ,η). 解: 由φ(x ,y )=e -(x +y )(x ,y >0)可知ξ与η相互独立, 因此必有cov (ξ,η)=0.21. 袋中装有标上号码1,2,2的3个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求ξ与η的协方差.,P {ξ=2}=P {η=2}=2/3, P {ξ=1}=P {η=1}=1/3, E ξ=E η=35322311=⨯+⨯38314312312},{)(2121=⨯+⨯+⨯====∑∑==i j j i ijP E ηξξη则913538)(),cov(22-=-=⋅-=ηξξηηξE E E22. (ξ , η)只取下列数组中的值：)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12. 求ξ与η的相关系数ρ, 并判断ξ与η是否独立? 解: ξ与的联合分布表及各边缘分布计算表如下表所示: 因此1212260121=⨯+⨯+⨯-=ξE 1225125412512=⨯+⨯=ξE144275144251225)(22=-=-=ξξξE E D3613311121311270=⨯+⨯+⨯=ηE1083731121912=+⨯=ηE129627512961691237129616910837)(22=-⨯=-=-=ηηηE E D36133112131)(-=-⨯-=ξηE则4322211236171336131253613)(),cov(-=⨯⨯-=⋅--=⋅-=ηξξηηξE E E 相关系数804.027522127543236122211296275144275432221),cov(-=-=⨯⨯⨯-=⨯-==ηξηξρD D, 计算ξ与η的相关系数ρ, 并判断ξ与η是否独立? 解: 由上表的数据的对称性可知与η的边缘分布一样, 算出为 P (ξ=-1)=P (η=-1)=3/8 P (ξ=0)=P (η=-0)=2/8P (ξ=1)=P (η=1)=3/8 由对称性可知Eξ=Eη=0831831=⨯+⨯-. 081818181)(=+--=ξηE 因此cov (ξ,η)=E (ξη)-E (ξ)E (η)=0 则ρ=0而P (ξ=0,η=0)=0≠P {ξ=0}P {η=0}=1/16因此ξ与η不独立. 这是一个随机变量间不相关也不独立的例子.24. 两个随机变量ξ与η, 已知Dξ=25, Dη=36, ρξη=0.4, 计算D (ξ+η)与D (ξ-η). 解:374.065236252),cov(2)]()[()]([)(854.065236252),cov(2)]()[()]([)(2222=⨯⨯⨯-+=-+=-+=---==---=-=⨯⨯⨯++=++=++=-+-==+-+=+ξηξηρηξηξηξηξηηξξηξηξηξρηξηξηξηξηηξξηξηξηξD D D D D D E E E E E D D D D D D D E E E E E D《概率论》期中测试题参考解答1、（10分）设A B C 、、表示三个随机事件，试用事件A B C 、、的运算分别表示下列各事件：(1)A 不发生而B C 、都发生；表示为：ABC(2)A B C 、、三个事件至少有一个发生；表示为：AB C ；或表示为：ABC ABC ABC ABC ABC ABC ABC(3)A B C 、、三个事件至多有一个发生；表示为：ABCABC ABC ABC(4)A B C 、、恰有两个不发生；表示为：ABCCAB BAC ；(5)A B C 、、都不发生；表示为：ABC(6)A B C 、、三个事件不少于两个发生；表示为：ABBC AC ；或表示为：ABC ABC ABC ABC(7)A B C 、、同时发生；表示为：ABC(8)A B C 、、三个事件不多于两个发生；表示为：AB C ；或表示为：ABC 或表示为：ABCABC ABC ABC ABC ABC ABC(9)A B C 、、不全发生；表示为：AB C ；或表示为：ABC 或表示为：ABCABC ABC ABC ABC ABC ABC(10)A B C 、、恰有一个发生.或表示为：ABC ABC ABC2、（14分）已知()0.6,()0.3,()0.6,P A P AB P B ===求：(1)()P AB ；(2)()P A B -；(3)()P AB ；(4)()P AB ；(5)()P A B ；(6)()P B A ；(7)()P A B A .解：（1）因为0.3()()()()P AB P A B P A P AB ==-=-，所以有()()0.3[1()]0.30.40.30.1P AB P A P A =-=--=-=；（2）()()()[1()]()(10.6)0.10.3P A B P A P AB P A P AB -=-=--=--= （3）()()()()0.40.60.10.9P AB P A P B P AB =+-=+-=；（4）()()1()10.90.1P AB P A B P A B ==-=-=；（5）()0.11()()0.66P AB P A B P B ===；（6）()()0.33()()1()0.44P AB P A B P B A P A P A -====-；（7）[()]()()()()()()P A B A P AB AA P A B A P B A P B P A P BA ==+- ()()()[()()]P AB P B P A P B P AB =+--()0.11()()0.60.17P AB P A P AB ===++3、（8分）一个盒子中有10个球，其中4个黑球6个红球，求下列事件的概率：(1)A =“从盒子中任取一球，这个球是黑球”；(2)B =“从盒子中任取两球，刚好一黑一红”；(3)C =“从盒子中任取两球，都是红球”；(4)D =“从盒子中任取五球，恰好有两个黑球”.解：（1）141102()5C P A C ==；（2）11462108()15C C P B C ==；（3）262101()3C P C C ==；（4）234651010()21C C P C C ==4、（3分）设甲、乙、丙三人同时独立地向同一目标各射击一次，命中率分别为112,,323，求目标被命中的概率.解：设1A =“甲命中目标”；2A =“乙命中目标”；3A =“丙命中目标”；A =“目标被击中”。

概率论何书元编著答案

n

j 1
j! ( n j )!
j 1

n j 2

k k n k Cn 1 2 j j n j C n 1 2 n
j 0
k k n k Cn 1 2 1 k 2 n k k ) ( ) n Cn ( ( 1 2 ) 1 2 1 2
ds( x ) ( x )dx s( x0) P ( X 0) 1
ln s( x )
x 0
( t )dt
x 0
ln s( x ) ( t )dt
x 0
s( x ) e
0 ( t ) dt
1 P (0) P (1) P (2) P (3)
1 1 1 1 1 1 1 1 8 1 e e e e 1 0.0189 0! 1! 2! 3! 3e
所以方案（2）优于方案（1）
11.收藏家在拍卖会上将参加对5件艺术品的竞买，各拍品是否竞买成功是相互独立的，如果他成功购买每件艺术品的概率是0.1，计算（1）成功竞买2件的概率（2）至少成功竞买3件的概率（3）至少成功竞买1件的概率
（3）当 m 2, M 4 时，点数只能为2，3，4，共 3 n 种，但应减除全为2和全为4的，共 2 2 n种，所以
3 2 1 1 n 1 n 1 n p ( ) 2( ) ( ) n 6 2 3 6
n
n 1
7.设 T 是表示寿命的非负随机变量，有连续的概率密度 f ( x ), 引入 T 的生存函数 s( x ) P ( X x ),
解
令 X 为成功竞买的件数
2 （1 ） P ( X 2 ) C 5 (0.1)2 (0.9)3 0.0729