概率论第三章题库

合集下载

概率论与数理统计第三章习题及答案

概率论与数理统计习题第三章多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球.以X 表示取到黑球的只数，以Y 表示取到红球的只数，求X 和Y 的联合分布律.（X ，Y ）的可能取值为(i , j )，i =0，1，2，3， j =0，12，i + j ≥2，联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f（1）确定常数k ；（2）求{}3,1<<Y X P （3）求{}5.1<X P ；（4）求{}4≤+Y X P . 分析：利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分，其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解：（1）∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ，∴81=k （2）83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P （3）3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P （4）32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次，以X 表示前2次出现H 的次数，以Y 表示3次中出现H 的次数，求Y X ,的联合分布律以及),(Y X 的边缘分布律。

概率论练习册答案第三章

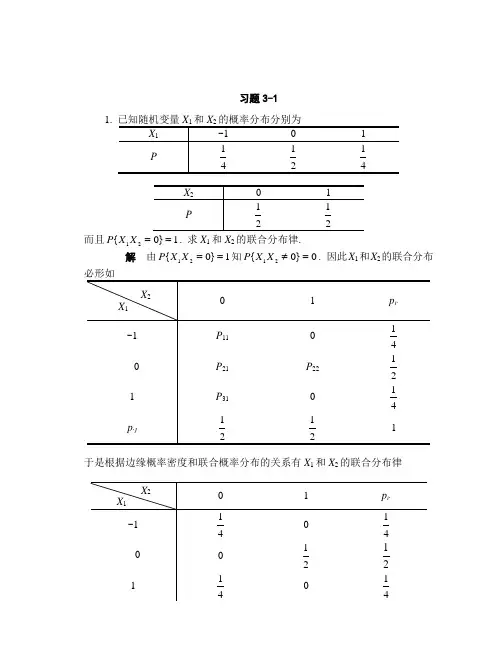
习题3-11.而且12{0}1P X X ==. 求X 1和X 2的联合分布律.解由12{0}1P X X ==知12{0}0P X X ≠=. 因此X 1和X 2的联合分布于是根据边缘概率密度和联合概率分布的关系有X 1和X 2的联合分布律(2) 注意到12{0,0}0P X X ===, 而121{0}{0}04P X P X =⋅==≠, 所以X 1和X 2不独立.2. 一盒子中有3只黑球、2只红球和2只白球, 在其中任取4只球. 以X 表示取到黑球的只数, 以Y 表示取到红球的只数. 求X 和Y 的联合分布律.解从7只球中取4球只有3547=C 种取法. 在4只球中, 黑球有i 只, 红球有j 只(余下为白球4i j --只)的取法为4322i j i j C C C --,0,1,2,3,0,1,2,i j i j ==+≤4.于是有0223221{0,2}3535P X Y C C C ====,1113226{1,1}3535P X Y C C C ====,1213226{1,2}3535P X Y C C C ====,2023223{2,0}3535P X Y C C C ====,21132212{2,1}3535P X Y C C C ====,2203223{2,2}3535P X Y C C C ====,3013222{3,0}3535P X Y C C C ====, 3103222{3,1}3535P X Y C C C ====,{0,0}{0,1}{1,0}{3,2}0P X Y P X Y P X Y P X Y ============.3. (,)(6),02,24,0,.f x y k x y x y =--<<<<⎧⎨⎩其它求: (1) 常数k ; (2) {1,3}P X Y <<; (3) { 1.5}P X <; (4) {4}P X Y +≤.解 (1) 由(,)d d 1f x y x y +∞+∞-∞-∞=⎰⎰, 得2424222204211d (6)d (6)d (10)82y k x y x k y x x y k y y k =--=--=-=⎡⎤⎢⎥⎣⎦⎰⎰⎰, 所以 18k =. (2) 3121,31{1,3}d (6)d 8(,)d d x y P X Y y x y x f x y x y <<<<==--⎰⎰⎰⎰1322011(6)d 82y x x y =--⎡⎤⎢⎥⎣⎦⎰321113()d 828y y =-=⎰. (3) 1.51.5{ 1.5}d (,)d ()d X P X x f x y y f x x +∞-∞-∞-∞<==⎰⎰⎰4 1.521d (6)d 8y x y x --=⎰⎰1.5422011(6)d 82y x x y =--⎡⎤⎢⎥⎣⎦⎰ 421633()d 882y y =-⎰ 2732=. (4) 作直线4x y +=, 并记此直线下方区域与(,)0f x y ≠的矩形区域(0,2)(0,4)⨯的交集为G . 即:02,0G x y <<<≤4x -.见图3-8. 因此{P X Y +≤4}{(,)}P X Y G =∈(,)d d Gf x y x y =⎰⎰44201d (6)d 8x y x y x -=--⎰⎰ 4422011(6)d 82xy x x y -=--⎡⎤⎢⎥⎣⎦⎰ 42211[(6)(4)(4)]d 82y y y y =----⎰ 42211[2(4)(4)]d 82y y y =-+-⎰423211(4)(4)86y y =----⎡⎤⎢⎥⎣⎦23=. 图3-8 第4题积分区域4. 二维随机变量(,)X Y 的概率密度为2(,),1,01,0,f x y kxy x y x =⎧⎨⎩≤≤≤≤其它. 试确定k , 并求2{(,)},:,01P X Y G G x y x x ∈≤≤≤≤.解由21114001(,)d d d (1)d 26x k kf x y xdy x kxy y x x x +∞+∞-∞-∞====-⎰⎰⎰⎰⎰,解得6=k .因而 2112401{(,)}d 6d 3()d 4x xP X Y G x xy y x x x x ∈==-=⎰⎰⎰. 5. 设二维随机变量(X , Y )概率密度为4.8(2),01,0,(,)0,.y x x y x f x y -=⎧⎨⎩≤≤≤≤其它求关于X 和Y 边缘概率密度.解 (,)X Y 的概率密度(,)f x y 在区域:0G ≤x ≤1,0≤y ≤x 外取零值.因而, 有24.8(2)d ,01,()(,)d 0,2.4(2),01,0,x X y x y x f x f x y y x x x +∞-∞-<<==-<<=⎧⎪⎨⎪⎩⎧⎨⎩⎰⎰其它.其它.124.8(2)d ,01,()(,)d 0,2.4(34),01,0,yY y x x y f y f x y x y y y y +∞-∞-<<==-+<<=⎧⎪⎨⎪⎩⎧⎨⎩⎰⎰其它.其它. 6. 假设随机变量U 在区间[-2, 2]上服从均匀分布, 随机变量 1,1,1,1,U X U --=>-⎧⎨⎩若≤若 1,1,1, 1.U Y U -=>⎧⎨⎩若≤若试求：(1) X 和Y 的联合概率分布；(2){P X Y +≤1}.解(2){P X Y +≤1}1{1}P X Y =-+>1{1,1}P X Y =-==12133=-=. 习题3-21. 设(X , Y )的分布律为求: (1) 在条件X =2下Y 的条件分布律;(2){22}P X Y ≥≤.解 (1) 由于6.02.01.003.0}2{=+++==X P ,所以在条件X =2下Y 的条件分布律为216.03.0}2{}1,2{}2|1{========X P Y X P X Y P ,06.00}2{}2,2{}2|2{========X P Y X P X Y P ,616.01.0}2{}3,2{}2|3{========X P Y X P X Y P ,316.02.0}2{}4,2{}2|4{========X P Y X P X Y P ,{P Y ≤2}{1}{2}P Y P Y ==+==0.10.3000.20.6++++=. 而{2,2}{2,1}{2,2}{3,1}{3,2}P X Y P X Y P X Y P X Y P X Y ===+==+==+==≥≤0.3000.20.5=+++=.因此{2,2}{22}{2}P X Y P X Y P Y =≥≤≤≥≤0.550.66==. 2. 设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成, 二维随机变量(X , Y )在区域D 上服从均匀分布, 求(X , Y )关于X 的边缘概率密度在x =2处的值.解由题设知D 的面积为22e e111d ln 2D S x x x ===⎰. 因此, (X ,Y )的密度为 1,(,),(,)20x y D f x y ∈=⎧⎪⎨⎪⎩，其它.由此可得关于X 的边缘概率密度 ()(,)d X f x f x y y +∞-∞=⎰.显然, 当x ≤1或x ≥e 2时,()0X f x =; 当21e x <<时,111()d 22x X f x y x==⎰.故(2)14X f =. 3. 设二维随机变量(X , Y )的概率密度为(,)1,01,02,0,.f x y x y x =<<<<⎧⎨⎩其它求：(1) (X , Y )的边缘概率密度(),()X Y f x f y ；(2)11{}.22P Y X ≤≤ 解 (1) 当01x <<时,20()(,)d d 2xX f x f x y y y x +∞-∞===⎰⎰;当x ≤0时或x ≥1时, ()0X f x =. 故 2,01,()0,其它.X x x f x <<=⎧⎨⎩当0<y <2时,12()(,)d d 12y Y y f y f x y x x +∞-∞===-⎰⎰;当y ≤0时或y ≥2时, ()0Y f y =.故 1,02,()20,.Y yy f y -<<=⎧⎪⎨⎪⎩其它(2) 当z ≤0时,()0Z F z =; 当z ≥2时,1)(=z F Z ;当0<z <2时, (){2Z F z P X Y =-≤2}(,)d d x y zz f x y x y -=⎰⎰≤2x12202-2d 1d d 1d zxz x zx y x y =⋅+⋅⎰⎰⎰⎰24z z =-.故 1,02,()20,.()其它Z z zz f z F z -<<'==⎧⎪⎨⎪⎩(3) {}{}11311322161122442≤，≤≤≤≤P X Y P Y X P X ===⎧⎫⎨⎬⎩⎭. 4. 设G 是由直线y =x , y =3,x =1所围成的三角形区域, 二维随机变量(,)X Y 在G 上服从二维均匀分布.求:(1) (X , Y )的联合概率密度；(2) {1}P Y X -≤；(3) 关于X 的边缘概率密度. 解 (1)由于三角形区域G 的面积等于2, 所以(,)X Y 的概率密度为⎪⎩⎪⎨⎧∉∈=.),(,0,),(,21),(G y x G y x y x f (2)记区域x y y x D -=|),{(≤}1与G 的交集为0G ,则{1}P Y X -≤0011113d d (2)22224G G x y S ===-=⎰⎰.其中0G S 为G 0的面积.(3) X 的边缘概率密度()(,)d X f x f x y y +∞-∞=⎰. 所以,当]3,1[∈x 时, 311()d (3)22X xf x y x ==-⎰. 当1<x 或3>x 时, 0)(=x f X .因此 ⎪⎩⎪⎨⎧∈-=.,0],3,1[),1(21)(其它x x x f X习题3-31. 设X 与Y 相互独立, 且分布律分别为下表:求二维随机变量(,)X Y 的分布律.解由于X 与Y 相互独立, 所以有}{}{},{j i j i y Y P x X P y Y x X P =⋅====,6,5,2,0;0,21,1=--=j i .因此可得二维随机变量(,)X Y 的联合分布律2. 设(X , Y )的分布律如下表:问,αβ为何值时X 与Y 相互独立? 解由于边缘分布满足23111,1i j i j p p ⋅⋅====∑∑, 又X , Y 相互独立的等价条件为 p ij = p i . p .j (i =1,2; j =1,2,3).故可得方程组 21,3111().939αβα++==⋅+⎧⎪⎪⎨⎪⎪⎩解得29α=,19β=.经检验, 当29α=,19β=时, 对于所有的i =1,2; j =1,2,3均有p ij = p i . p .j 成立.因此当29α=,19β=时, X 与Y 相互独立..3. 设随机变量X 与Y 的概率密度为()e (,)0,.,01,0,x y b f x y x y -+=⎧<<>⎨⎩其它(1) 试确定常数b .(2) 求边缘概率密度()X f x , ()Y f y . (3) 问X 与Y 是否相互独立？解 (1) 由11()101(,)d d e d d e d e d (1e )x y y x f x y x y b y x b y x b +∞+∞+∞+∞-+----∞-∞====-⎰⎰⎰⎰⎰⎰,得 111eb -=-.(2) ()(,)d X f x f x y y ∞-∞=⎰1e ,01,1e 0,xx --<<=-⎧⎪⎨⎪⎩其它.()(,)d Y f y f x y x ∞-∞=⎰e ,0,0,y y ->=⎧⎨⎩其它.(3) 由于(,)()()X Y f x y f x f y =⋅，所以X 与Y 相互独立.4. 设X 和Y 是两个相互独立的随机变量, X 在(0, 1)上服从均匀分布, Y 的概率密度为21e ,0,()2Y yy f y y ->=⎧⎪⎨⎪⎩，≤0.(1) 求X 和Y 的联合概率密度.(2) 设关于a 的二次方程为220a Xa Y ++=, 试求a 有实根的概率.解 (1) 由题设知X 和Y 的概率密度分别为1,01,()0,X x f x <<=⎧⎨⎩其它， 21e ,0,()20,.yY y f y ->=⎧⎪⎨⎪⎩其它因X 和Y 相互独立, 故(X , Y )的联合概率密度为21e ,01,0(,)()()20,.yX Y x y f x y f x f y -<<>==⎧⎪⎨⎪⎩其它 (2) 方程有实根的充要条件是判别式大于等于零. 即244X Y ∆=-≥20X ⇔≥Y .因此事件{方程有实根}2{X =≥}Y .下面计算2{P X ≥}Y (参见图3-3).2{P X ≥}Y 2211221(,)d d e d (1e)d 2yxx Df x y xdy x y x --===-⎰⎰⎰⎰⎰2121ed 12[(1)(0)]0.1445xx πΦΦ-=-=--≈⎰.图3-3 第6题积分区域习题3-41. 设二维随机变量(X ,Y )的概率分布为YX0 1若随机事件{X =0}与{X +Y =1}相互独立, 求常数a , b .解首先, 由题设知0.40.11a b +++=. 由此得0.5a b +=. 此外,{0}0.4P X a ==+,{1}{0,1}{1,0}0.5P X Y P X Y P X Y a b +====+===+=, {0,1}{0,1}P X X Y P X Y a =+=====. 根据题意有{0,1}{0}{1}P X X Y P X P X Y =+===+=,即(0.4)0.5a a =+⨯. 解得0.4,0.1a b ==.2. 设两个相互独立的随机变量X ,Y 的分布律分别为求随机变量Z = X + Y 的分布律. 解随机变量Z = X + Y 的可能取值为7,5,3.Z 的分布律为18.06.0.03}2,1{}3{=⨯=====Y X P Z P , {5}{1,4}{3,2}0.30.4070.60.54P Z P X Y P X Y ====+===⨯+⨯=,28.04.07.0}4,3{}7{=⨯=====Y X P Z P ,或写为3. 随机变量X 与Y 相互独立, 且均服从区间[0,3]上的均匀分布, 求{}max{,}1P X Y ≤.解由题意知, X 与Y 的概率密度均为1,03,()30x f x =⎧⎪⎨⎪⎩≤≤，其它.又由独立性, 有P {max{X +Y }≤1}=P {X ≤1,Y ≤1}= P {X ≤1} P {Y ≤1}.而 P {X ≤1}= P {Y ≤1}11011()d d 33f x x x -∞===⎰⎰, 故 P {max{X +Y }≤1}=111339⨯=.4. 设X 和Y 是两个相互独立的随机变量, 且X 服从正态分布N (μ, σ2), Y 服从均匀分布U (-a , a )( a >0), 试求随机变量和Z =X +Y 的概率密度.解已知X 和Y 的概率密度分别为22()2()e2x X f x μσπσ--=, ),(+∞-∞∈x ; ⎪⎩⎪⎨⎧-∉-∈=).,(,0),,(,21)(a a y a a y ay f Y .由于X 和Y 相互独立, 所以22()21()()()d e d 22z y aZ X Y a f z f z y f y y y a μσπσ---+∞-∞-=-=⎰⎰=1[()()]2z μa z μa ΦΦa σσ-+---. 10. 设随机变量X 和Y 的联合分布是正方形G={(x,y )|1≤x ≤3, 1≤y ≤3}上的均匀分布, 试求随机变量U=|X -Y|的概率密度f (u ).解由题设知, X 和Y 的联合概率密度为111,3,3,(,)40,.x y f x y =⎧⎪⎨⎪⎩≤≤≤≤其它记()F u 为U 的分布函数, 参见图3-7, 则有当u ≤0时,(){||F u P X Y =-≤u }=0; 当u ≥2时,()1F u =;当0< u <2时, 图3-7 第8题积分区域||(){}(,)d d x y uF u P U u f x y x y -==⎰⎰≤≤21[42(2)]412u =-⨯- 211(2)4u =--.故随机变量||U X Y =-的概率密度为1(2),02,()20,u u p u -<<=⎧⎪⎨⎪⎩其它..总习题三1. 设随机变量(X , Y )的概率密度为⎪⎩⎪⎨⎧<<<=.,0,10,||,1),(其它x x y y x f 求条件概率密度)|()|(||y x f x y f Y X X Y 和.解首先2,01,()0,.(,)其它X x x f x f x y dy +∞-∞<<==⎧⎨⎩⎰1,01,()1,10,0,(,)≤其它.Y y y f y y y f x y dx +∞-∞-<<==+-<⎧⎪⎨⎪⎩⎰图3-9第1题积分区域当01y <<时, |1,1,1(|)0,X Y y x y f x y x <<-=⎧⎪⎨⎪⎩取其它值.当1y -<≤0时, |1,1,1(|)0,X Y y x y f x y x -<<+=⎧⎪⎨⎪⎩取其它值.当10<<x 时, |1,||,(|)20,Y X y x f y x x y <=⎧⎪⎨⎪⎩取其它值.2. 设随机变量X 与Y 相互独立, 下表列出二维随机变量(,)X Y 的分布律及关于X 和关于Y 的边缘分布律中部分数值, 试将其余数值填入表中空白处 .解首先, 由于11121{}{,}{,}P Y y P X x Y y P X x Y y ====+==, 所以有11121111{,}{}{,}6824P X x Y y P Y y P X x Y y ====-===-=.在此基础上利用X 和Y 的独立性, 有11111{,}124{}1{}46P X x Y y P X x P Y y =======.于是 2113{}1{}144P X x P X x ==-==-=.再次, 利用X 和Y 的独立性, 有12211{,}18{}1{}24P X x Y y P Y y P X x =======.于是 312111{}1{}{}1623P Y y P Y y P Y y ==-=-==--=.最后, 利用X 和Y 的独立性, 有2222313{,}{}{}428P X x Y y P X x P Y y ======⨯=; 2323311{,}{}{}434P X x Y y P X x P Y y ======⨯=;1313111{,}{}{}4312P X x Y y P X x P Y y ======⨯=.因此得到下表3. (34)e (,)0,.,0,0,x y k f x y x y -+=⎧>>⎨⎩其它 (1) 求常数k ；(2) 求(X ,Y )的分布函数；(3) 计算{01,02}P X Y <<≤≤; (4) 计算(),x f x ()y f y ；(5) 问随机变量X 与Y 是否相互独立? 解 (1)由3401(,)d d e d e d 12xy kf x y x y k x y +∞+∞+∞+∞---∞-∞===⎰⎰⎰⎰,可得12=k .(2) (X ,Y )的分布函数(,)(,)d d x y F x y f u v x y -∞-∞=⎰⎰.当x <0或y <0时,有 0),(=y x F ; 当0,0x y ≥≥时, 34340(,)12e d e d (1e )(1e )x yuv x y F x y u v ----==--⎰⎰.即 34(1e )(1e ),0,0,(,)0,.x y x y F x y --⎧--≥≥=⎨⎩其它(3) {01,02}P X Y <<≤≤38(1,2)(0,0)(1e )(1e )F F --=-=--. (4) (34)012ed ,0,()(,)d 0,其它.x y X y x f x f x y y +∞-++∞-∞⎧>⎪==⎨⎪⎩⎰⎰所以 33e ,0,()0,其它.x X x f x -⎧>=⎨⎩类似地, 有44e ,0,()0,其它.y Y y f y -⎧>=⎨⎩显然2),(),()(),(R y x y f x f y x f Y X ∈∀⋅=, 故X 与Y 相互独立. 4.解已知的分布律为注意到41260}1{}1{=++====Y P X P , 而0}1,1{===Y X P ,可见P {X =1, Y =1}≠P {X =1}P {Y =1}. 因此X 与Y 不相互独立.(2) Z X Y =+的可能取值为3, 4, 5, 6, 且316161}1,2{}2,1{}3{=+===+====Y X P Y X P Z P , }1,3{}2,2{}3,1{}4{==+==+====Y X P Y X P Y X P Z P3112161121=++=, 316161}2,3{}3,2{}5{=+===+====Y X P Y X P Z P . 即Z X Y =+(3) V =21}2,2{}1,2{}2,1{}2{===+==+====Y X P Y X P Y X P V P , 21}2{1}3{==-==V P V P . 即max(,)V X Y =的分布律为(4) min{U =}3,1{}2,1{}1{==+====Y X P Y X P U P}1,2{}1,3{==+==+Y X P Y X P 21=, 21}1{1}2{==-==U P U P . 即min{,}U X Y =的分布律为(5) W U V =+31}1,2{}2,1{}2,1{}3{===+=======Y X P Y X P V U P W P ,}2,2{}3,1{}4{==+====V U P V U P W P31}2,2{}1,3{}3,1{===+==+===y X P Y X P Y X P ,31}2,3{}3,2{}3,2{}5{===+=======Y X P Y X P V U P W P .5. 2,01,01,(,)0,x y x y f x y --<<<<⎧=⎨⎩其它. (1) 求P {X >2Y }; (2) 求Z = X +Y 的概率密度f Z (z ).解 (1) 1120227{2}(,)d d d (2)d 24yx yP X Y f x y x y y x y x >>==--=⎰⎰⎰⎰. (2) 方法一: 先求Z 的分布函数:()()(,)d d Z x y zF z P X Y Z f x y x y +=+=⎰⎰≤≤.当z <0时, F Z (z )<0; 当0≤z <1时, 1()(,)d d d (2)d zz yZ D F z f x y x y y x y x -==--⎰⎰⎰⎰= z 2-13z 3; 当1≤z <2时, 2111()1(,)d d 1d (2)d Z z z yD F z f x y x y y x y x --=-=---⎰⎰⎰⎰= 1-13(2-z )3; 当z ≥2时, F Z (z ) = 1.故Z = X +Y 的概率密度为222,01,()()(2),12,0,Z Z z z z f z F z z z ⎧-<<⎪'==-<⎨⎪⎩≤其它.方法二: 利用公式()(,)d :Z f z f x z x x +∞-∞=-⎰2(),01,01,(,)0,x z x x z x f x z x ---<<<-<⎧-=⎨⎩其它 2,01,1,0,.z x x z x -<<<<+⎧=⎨⎩其它当z ≤0或z ≥2时, f Z (z ) = 0; 当0<z <1时, 0()(2)d (2);zZ f z z x z z =-=-⎰当1≤z <2时, 121()(2)d (2).Zz f z z x z -=-=-⎰故Z = X +Y 的概率密度为222,01,()(2),12,0,.Z z z z f z z z ⎧-<<⎪=-<⎨⎪⎩≤其它.6. 设随机变量(X , Y )得密度为21,01,02,(,)30,.其它x xy x y x y ϕ⎧+⎪=⎨⎪⎩≤≤≤≤试求: (1) (X , Y )的分布函数; (2) (X , Y )的两个边缘分布密度; (3) (X , Y )的两个条件密度; (4) 概率P {X +Y >1}, P {Y >X }及P {Y <12|X <12}.解 (1) 当x<0或y <0时, φ(x , y ) = 0, 所以 F (x , y ) = 0.当0≤x <1, 0≤y <2时, φ(x , y ) = x 2+13xy ,所以 201(,)(,)d d [()d ]d 3x yx yF x y u v u v u uv v u -∞-∞==+⎰⎰⎰⎰ϕ32211312x y x y =+. 当0≤x <1, 2≤y 时,2(,)(,)d d [(,)d ]d [(,)d ]d xyx y x F x y u v u v u v v u u v v u -∞-∞===⎰⎰⎰⎰⎰⎰ϕϕϕ22001[()d ]d 3xu uv v u =+⎰⎰21(21)3x x =+. 当1≤x , 0≤y <2时,1(,)(,)d d [(,)d ]d xyyF x y u v u v u v v u -∞-∞==⎰⎰⎰⎰ϕϕ12001[()d ]d 3yu uv v u =+⎰⎰1(4)12y y =+. 当1≤x , 2≤y 时,122001(,)[()d ]d 13F x y u uv v u =+=⎰⎰.综上所述, 分布函数为220,00,1(),01,02,341(,)(21),01,2,31(4),1,02,121,1, 2.x y y x y x x y F x y x x x y y y x y x y <<⎧⎪⎪+<<⎪⎪⎪=+≥⎨⎪⎪+≥⎪⎪≥≥⎪⎩或≤≤≤≤≤< (2) 当0≤x ≤1时,22202()(,)d ()d 2,33X xy x x y y x y x x ϕϕ+∞-∞==+=+⎰⎰故 222,01,()30,.其它≤≤X x x x x ϕ⎧+⎪=⎨⎪⎩当0≤y ≤2时,12011()(,)d ()d ,336Y xy y x y x x x y ϕϕ+∞-∞==+=+⎰⎰ 故 11,02,()360,.其它≤≤Y y y y ϕ⎧+⎪=⎨⎪⎩(3) 当0≤y ≤2时, X 关于Y = y 的条件概率密度为2(,)62(|).()2Y x y x xy x y y yϕϕϕ+==+当0≤x ≤1时, Y 关于X = x 的条件概率密度为(,)3(|).()62X x y x yy x y x ϕϕϕ+==+(4) 参见图3-10.图3-10 第9题积分区域图3-11 第9题积分区域1{1}(,)d d x y P X Y x y x y ϕ+>+>=⎰⎰12201165d ()d .372xx x xy y -=+=⎰⎰ 同理, 参见图3-11.{}(,)d d y xP Y X x y x y ϕ>>=⎰⎰122117d ()d .324xx x xy y =+=⎰⎰ 1111{,}(,)112222{|}1122{}()22X P X Y F P Y X P X F <<<<==<211(,)221201()534.32()d |X y x y x x xϕ+==⎰。

概率论第三章测试题

第三章测试题1、已知随机变量,ξη的分布列分别为求(),()E D ξξ2、设随机变量(,)ξη的分布列为求(),(),(),(|1),(|1),(),(),(,),E E E E E D D Cov ξηξηξηξηηξξηξηρ=-=。

3、设随机变量ξ的概率密度函数为1|1|,02()0,x x f x --<<⎧=⎨⎩其它，求(),()E D ξξ。

4、设随机变量ξ的概率密度函数为2,01()0,ax bx c x f x ⎧++<<=⎨⎩其它，且已知()0.5,()0.15E D ξξ==，求系数,,a b c 。

5、某机场的送客车一次载有20名旅客自机场开出，沿途有10个停车点，若到达停车点无人下车则车不停下，设每名旅客在各个停车点下车是等可能的，求送客车停车次数的数学期望。

6、设()4,()9,0.6D D ξηξηρ===，求(32)D ξη-。

7、设随机变量ξ的方差()D ξ存在且有限，已知(0,,a b a a b ηξ=+≠常数），求ξηρ。

8、设随机变量(,)ξη在以点(0,1),(1,0),(1,1)为顶点的三角形区域上服从均匀分布，求()D ξη+。

9、设随机变量ξ的概率密度函数为,0()0,x e x f x x -⎧>=⎨≤⎩， 2Y eξξ-=+，21Z ξ=-，求(),()E Y E Z 。

10、设随机变量(,)ξη的协方差矩阵为4339-⎛⎫⎪-⎝⎭，求ξηρ。

11、设随机变量(,)ξη的概率密度函数为212,01(,)0,y y x f x y ⎧≤≤≤=⎨⎩其它，求(),(),(),(),(,),E E D D Cov ξηξηξηξηρ。

12、设随机变量(,)ξη的概率密度函数为,01,0(,)0,cxy x y x f x y <<<<⎧=⎨⎩其它，求（1）常数c ；（2）(),(),(),()E E D D ξηξη；（3）边缘密度函数(),()f x f y ξη，并判断,ξη是否相互独立；（4）条件概率密度函数(|)f y x ，1(|)4f y ，(|)f x y ，1(|)2f x ，（5）条件数学期望1(|)4E η，1(|)2E ξ。

期末考试题概率第三章习题(附答案提示)

概率第三章习题（附答案提示）一、填空题1、设随机变量X服从［0，2]上均匀分布，则 .2、设随机变量服从参数为的泊松（Poisson）分布，且已知＝1,则___ ____。

3、已知随机向量(X，Y）的联合密度函数,则E（X)= 。

4、随机变量X的数学期望，方差，k、b为常数，则有= ；= 。

5、设随机变量X服从参数为2的泊松分布,且Y =3X -2，则E(Y）= 。

6、设随机变量X服从［0,2］上的均匀分布,Y=2X+1，则D（X）= ，D(Y）= 。

7、设（X，Y）为二维随机向量，D（X)、D（Y）均不为零。

若有常数a〉0与b使，则X与Y的相关系数。

8、随机变量，则。

9、设随机变量X~B(100，0.8),由中心极限定理可知，P｛74〈X≤86｝≈__________。

((1。

5）=0.9332）二、选择题1、设为标准正态分布函数,且，相互独立。

令，则由中心极限定理知的分布函数近似于（）。

A. B． C． D．2、设离散型随机变量的概率分布为，，则＝（ )。

A. 1。

8B. 2 C。

2。

2 D. 2。

43、若，则（）。

A。

和相互独立 B。

与不相关C. D。

4、若随机向量（)服从二维正态分布，则①一定相互独立；②若，则一定相互独立;③和都服从一维正态分布;④若相互独立，则Cov (X，Y ） =0.几种说法中正确的是（）.A. ①②③④B. ②③④C. ①③④D. ①②④5、已知随机变量和相互独立，且它们分别在区间［－1,3]和［2，4］上服从均匀分布，则（）。

A. 3B. 6C. 10D. 126、两个独立随机变量，则下列不成立的是（ C ）.A。

B. C. D。

7、是二维随机向量，与不等价的是（）A. B。

C. D。

和相互独立8．设随机变量X～B（10，），Y~N(2，10），又E（XY）=14，则X与Y的相关系数=（）A．-0。

8 B．—0。

16C．0.1 D．0.8三、计算题1、2、设随机变量(X，Y)的联合分布为求：（1)E(X），E(Y)，D(X)；（2）Cov(X,Y)．3、一盒同型号螺丝钉共有100个, 已知该型号的螺丝钉的重量是一个随机变量, 期望值是100g，标准差是10g, 求一盒螺丝钉的重量超过10.2kg的概率。

概率论与数理统计习题库,第三章

长沙理工大学二手货QQ 交易群146 808 417#00001已知随机变量X 与Y 独立，其分布律分别为，与*00001解:作下表，表中第一行是自变量(X,Y)的全部可能取值点；第二行是第一行各取值相应的概从上表可以确定Z 的取值域为{0,1},W 的取值域为{-1,0,1,函数变量取某值的概率等于该值在表中相应概率之和。

例如 P{Z=0}=0.12+0.18=0.3于是，Z 、W 的分布律分别为：#00002袋中有两只红球，三只白球，现不放回摸球二次，令⎩⎨⎧=⎩⎨⎧=第二次摸到白球第二次摸到红球第一次摸到白球第一次摸到红球0101Y X(1)求(X,Y)的分布律。

(2)求X 与Y 的相关系数 *00002 解：（1）显然X 、Y 的全部可能取值为X=1，0；Y=1，0而P{X=1，Y=1}=P{两次均摸到红球}=2522C C ，同理计长沙理工大学二手货QQ 交易群146 808417ij （2）256)(256)(52)(52)(====Y D X D Y E X E503254101),(101)(-=-==Y X COV XY E41256256503-=-=∴XY ρ#00003设(X,Y)具有概率密度⎩⎨⎧<<<=其它01||0},{y x c y x f ，1)求常数c ；2)求P{Y>2X} ； 3)求F(0.5,0.5)*00003解：1) 如图所示区域D 为(X,Y)的非0定义域由归一性图⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰====>∴>=⇒=⇒=--GG GGyDyyG S Sdxdy dx dy dxdy X Y P GX Y c cdx dy Cdxdy y 的面积是其中或见如图区域14311}2{}2){21111123)由F(x,y)的几何意义，可将F(0.5,0.5)理*00004解为(X,Y)落在{X ≤0.5,Y ≤0.5}区域（见如图G 1）上的概率。

概率论第三章习题及答案

02
题目8
一个盒子里有100个球，其中红球有30个，蓝球有40个，黄球有20个，
绿球有10个。随机抽取一个球并记录其颜色，然后放回盒子中。连续抽
取三次，求三次抽取中抽到红球的次数的期望值。
03
题目9
一个袋子中有5个红球和5个蓝球，从中随机抽取3个球，求抽取到红球
的个数X的分布律。
02 答案部分
基础题目答案
在处理复杂事件时，应先分解为简单事件，再根据概率的加
法原则进行计算。
注意区分必然事件和不可能事件，它们在概率论中具有特殊
地位。
知识点回顾与巩固
知识点回顾概率的基本性质：概率具有非负性、规范性、有限可加性。
事件的独立性及其性质。
知识点回顾与巩固
条件概率的定义及其性质。贝叶斯公式的应用场景和推导方法。
挑战题目解题思路与技巧
总结词
综合运用知识
详细描述
对于挑战题目，需要综合运用概率论中的知识，如随机变量的分布、随机过程的性质等。要能够准确理解题目的背景和要求，构建合适的概率模型，并运用适当的数学方法进行求解。
示例
题目问的是“一个袋子中有3个红球和2个白球，每次从中随机取出1个球并放回，连续取 5次。求取出的5个球中至少有3个红球的概率。”解题时，应先计算取出的5个球中都是白球的概率，再用1减去这个概率，得出至少有3个红球的概率。
未来学习计划与展望
• 学习随机过程的基本概念和性质，了解常见的随机过程如泊松过程、马尔可夫链等。
未来学习计划与展望
展望
学习概率论与其他数学分支的交叉知识，如统计学、线性代数等。
将概率论的知识应用于实际问题和科学研究，加深对理论知识的理解和掌握。

概率论与数理统计第三章自测题与答案

第三章多维随机变量及其分布自测题(90分钟)一、单项选择题（每题3分，共15分）1．设),1,0(~,21N X X 则21X X Y += （）（A ）)2,0(~N Y （B ）)1,0(~N Y （C ）)2,0(~N Y （D ）Y 不一定服从正态分布 2．设Y X ,相互独立，都服从区间[0,1]上的均匀分布，则服从区间或区域上的均匀分布的是（）（A ）()Y X , （B ）Y X + （C ）2X （D ）Y X -3．设随机变量X 和Y , 已知,73}0{}0{,71}0,0{=≤=≤=≤≤Y P X P Y X P =≤}0),{min(Y X P 则（）（A ）73 （B ）72 （C ）75 （D ）49164．设Y X ,相互独立，且都服从标准正态分布，则（）（A ）41}0{=≥+Y X P （B ）41}0{=≥-Y X P （C ）41}0),{max(=≥Y X P （D ）41}0),{min(=≥Y X P5．设两个随机变量Y X ,相互独立，且5.0}1{}1{}1{}1{=====-==-=Y P X P Y P X P ，则下列各式中正确的是（）（A ）1}{==Y X P （B ）5.0}{==Y X P （C ）25.0}0{==+Y X P （D ）25.0}0{==XY P 二、填空题（每空3分，共24分）1．设()Y X ,的联合分布律如下，且事件{X=0}与{X+Y=1}相互独立，则a= , b= .2．设Y X ,相互独立，表中列出()Y X ,的联合分布律和关于X 和Y 的边缘分布律的部分数值，3．设Y X ,相互独立，且均服从区间[0,3]上的均匀分布，则=≤}1),{max(Y X P 。

4．设随机变量X 和Y 相互独立都服从b (2,p )，且95}1{=≥X P ，则}1{=+Y X P ＝。

5．已知()Y X ,的概率密度为⎩⎨⎧<<=-其他,00,),(yx e y x f y ，则=≤+}1{Y X P ，}21{≤Y X P ＝。

概率论与数理统计习题库-第三章

长沙理工大学二手货QQ 交易群146 808 417#00001，与*00001解:作下表，表中第一行是自变量(X,Y)的全部可能取值点；第二行是第一行各取值相应的概率；第三、第四行分别是第一行各取值点相应的Z 、W 的取值。

从上表可以确定Z 的取值域为{0,1},W 的取值域为{-1,0,1,函数变量取某值的概率等于该值在表中相应概率之和。

例如P{Z=0}=0.12+0.18=0.3于是，Z 、W 的分布律分别为：#00002袋中有两只红球，三只白球，现不放回摸球二次，令(1)求(X,Y)的分布律。

(2)求X 与Y 的相关系数 *00002 解：（1）显然X 、Y 的全部可能取值为X=1，0；Y=1，0而P{X=1，Y=1}=P{两次均摸到红球}=2522C C ，同理计长沙理工大学二手货QQ 交易群146 808 417ij（2）256)(256)(52)(52)(====Y D X D Y E X E#00003设(X,Y)具有概率密度⎩⎨⎧<<<=其它01||0},{y x c y x f ，1)求常数c ；2)求P{Y>2X} ； 3)求F(0.5,0.5)*00003解：1) 如图所示区域D 为(X,Y)的非0定义域由归一性图3)由F(x,y)的几何意义，可将F(0.5,0.5)理*00004解为(X,Y)落在{X ≤0.5,Y ≤0.5}区域（见如图G 1）上的概率。

故有 #00004已知(X,Y)的分布函数为⎪⎩⎪⎨⎧≤≤--≤≤--=----其它00101),(x y ye e yx xe e y x F yy y x （1）求X 与Y 的边缘概率密度。

（2）问X 与Y 是否相互独立？ *00004解：（1）⎩⎨⎧<≥-=∞=-0x 00x e 1)F(x,(x)F xX（2）不独立与Y X y x F y F x F Y X ∴≠),()()(#00005(X,Y)的分布函数为⎪⎩⎪⎨⎧≤≤--≤≤--=----其它00101),(x y ye e yx xe e y x F yy y x .（1）求X 与Y 的联合概率密度及边缘概率密度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章多维随机变量及其分布一、选择题1、（易）设任意二维随机变量（X ，Y ）的两个边缘概率密度函数分别为f X (x )和f Y (y )，则以下结论正确的是（） A.⎰+∞∞-=1)(dx x f XB.⎰+∞∞-=21)(dx y f Y C.⎰+∞∞-=0)(dx x f X D.⎰+∞∞-=0)(dx y f Y2、（易）设二维随机变量221212(,)~(,,,,)X Y N μμσσρ,则X ~（） A. 211(,)N μσB. 221(,)N μσC. 212(,)N μσ D. 222(,)N μσ 3、（易）设二维随机变量(X ，Y )服从区域D ：x 2+y 2≤1上的均匀分布，则(X ，Y )的概率密度为（） A. f(x ，y)=1B. 1(,)0,x y D f x y ∈⎧=⎨⎩，（,）,其他C. f(x ，y)=1πD. 1(,)0,x y D f x y π⎧∈⎪=⎨⎪⎩，（,）,其他4、（中等）下列函数可以作为二维分布函数的是（）.A .1,0.8,(,)0,.x y F x y +>⎧=⎨⎩其他 B .⎪⎩⎪⎨⎧>>⎰⎰=--.,0,0,0,),(00其他y x dsdt ey x F y x t s C . ⎰⎰=∞-∞---y x ts dsdt e y x F ),( D .⎪⎩⎪⎨⎧>>=--.,0,0,0,),(其他y x e y x F yx5、（易）设二维随机变量(X ，Y )的概率密度为f (x ，y )=⎪⎩⎪⎨⎧<<<<,,0;20,20,41其他y x则P{0<X <1，0<Y <1}=（） A ．41 B ．21C ．43D ．16、（中等）设随机变量X ，Y 相互独立，其联合分布为则有（）A ．92,91==βαB ．91,92==βαC ．32,31==βαD ．31,32==βα7、（中等）设二维随机变量(X ,Y )的联合分布函数为F(,x y ). 其联合概率分布律为YX 01 2 -1 0 0 0 2则F （0,1）=（） A.B. C. D.8、（难）设随机变量X 和Y 相互独立，且X ~N (3,4)，Y ~N (2,9)，则Z=3X -Y ~（） A. N (7，21) B. N (7，27) C. N (7，45) D. N (11，45)9、（难）设随机变量X ，Y 相互独立，且X ~N （2，1），Y ~N （1，1），则（） {X -Y ≤1}=21B. P{X -Y ≤0}=21C. P{X +Y ≤1}=21 D. P{X +Y ≤0}=21 10、（易）设二维随机变量),(Y X 的分布函数为),(y x F ，则=∞+),(x F （） A ．0 B ．)(x F X C ．)(y F Y D ．1二、填空题11、（易）设随机变量X ，Y 相互独立，且P{X ≤1}=21，P{Y≤1}=31，则P{X ≤1,Y ≤1}=___. 12、（易）设二维随机变量),(Y X 的分布函数为),(y x F ，则(,)F -∞-∞=______.13、（中等）设二维随机变量(X ,Y )的分布函数为⎩⎨⎧>>--=--,,0,0,0),e 1)(e 1(),(其他y x y x F y x ，则当x >0时, X 的边缘分布函数F X (x )=__________.14、（易）已知当0<x <1,0< y <1时，二维随机变量(X,Y ）的分布函数F(x ,y ) =22x y ，记（x ,y ）的概率密度为f (x ,y ) ，则f (1148，）=__________.15、（中等）设二维随机变量（X ，Y ）的分布律为则{}=≤<2,1Y X P ______.16、（易）设二维随机变量(X ，Y )的概率密度 f (x ,y )=⎩⎨⎧≤≤≤≤，y x ，其他,0,10,101则P {X +Y ≤1}=____.17、（中等）设随机变量XY =X 2，记随机变量Y 的分布函数为F Y （y ），则F Y （3）=__________. 18、（易）设随机变量X 和Y 相互独立，它们的分布律分别为，则{}==+1Y X P ___________.19、（易）设二维随机变量(X,Y)的分布律为则P{XY=0}=__________.三、计算题20、（中等）.袋中有五个号码1，2，3，4，5，从中任取三个，记这三个号码中最小的号码为X ，最大的号码为Y .（1）求X 与Y 的联合概率分布；（2）求关于X 和关于Y 的边缘分布；（3） X 与Y 是否相互独立【解】（1） X 与Y 的联合分布律如下表3 4 5{}i P X x =13511C 10= 3522C 10= 3533C 10= 610 23511C 10= 3522C 10= 310 3 02511C 10= 110{}i P Y y =110 310 610(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠=== 故X 与Y 不独立21、（中等）某高校学生会有8名委员，其中来自理科的2名，来自工科和文科的各3名，现从8名委员中随机指定3名担任学生会主席，设X ，Y 分别为主席来自理科、工科的人数，求：（1）（X,Y ）的联合分布律；（2）X,Y 的边缘分布.231 41 YXP(X=0,Y=0)=C(3,3)/C(8,3)=1/56 P(X=0,Y=1)=C(3,1)*C(3,2)/C(8,3)=9/56 P(X=0,Y=2)=C(3,1)*C(3,2)/C(8,3)=9/56 P(X=0,Y=3)=C(3,3)/C(8,3)=1/56 P(X=1,Y=0)=C(2,1)*C(3,2)/C(8,3)=6/56 P(X=1,Y=1)=C(2,1)*C(3,1)*C(3,1)/C(8,3)=18/56 P(X=1,Y=2)=C(2,1)*C(3,1)/C(8,3)=6/56 P(X=2,Y=0)=C(2,2)*C(3,1)/C(8,3)=3/56 P(X=2,Y=1)=C(2,1)*C(3,1)/C(8,3)=3/56 X 边缘分布 Y Y Y Y P(X=i) 0 1 2 3X 0 1/56 9/56 9/56 1/56 5/14 X 1 3/28 9/28 3/28 0 15/28 X 2 3/56 3/56 0 0 3/28Y 边缘分布 P(Y=j) 5/28 15/28 15/56 1/56 122、（中等）设二维随机变量（X ，Y ）的概率密度为求：（1）常数c ;∫f(x,y)dxdy=∫cxydxdy=c ∫xdx ∫ydy =c(1/2*x^2|从0到2)(1/2*y^2|从0到1) =c(1/2*2^2-0)(1/2*1^2-0) =c*2*1/2=c 并且∫f(x,y)dxdy=1⎩⎨⎧≤≤≤≤=.,0;20,20,),(其他y x cxy y x f所以c=1（2）求（X ，Y ）分别关于X ，Y 的边缘密度);(),(y f x f Y X （3）判定X 与Y 的独立性，并说明理由；（4）求P {}1,1>>Y X .23、（较难）设随机变量(,)X Y 的分布函数为(,)(arctan )(arctan )23xy F x y A B C =++，试求：（1）常数A 、B 、C （2）试问X 与Y 是否独立（3）求X 与Y 的联合概率密度函数 F(x,y)=A(B+arctanx/2)(C+arctany/3) F(-∞,-∞)=A(B-π/2)(C-π/2)=0 F(-∞,+∞)=A(B-π/2)(C+π/2)=0 F(+∞,-∞)=A(B+π/2)(C-π/2)=0 F(+∞,+∞)=A(B+π/2)(C+π/2)=1 解得：A=1/π^2,B=π/2,C=π/2 F(+∞,y)=1/2+1/π*arctan （y/3) F(x,+∞)=1/2+1/π*arctan （x/2) F(x,y)=F(+∞,y)×F(x,+∞) X 和Y 相互独立. (X,Y)的联合概率密度：6/(11π)(π/2+arctan x/2)(π/2+arctan Y/3)24、（中等）设二维随机变量(,)X Y 的概率密度为()()602,24,0k x y x y f x y ⎧--<<<<=⎨⎩求：（1）常数k ；（2）(,)X Y 关于X ,Y 的边缘概率密度(),()X Y f x f y ；（3）{}4P X Y +<. 【解】（1）由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故18R =(3)24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y+≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83xx x y y -=--=⎰⎰题5图25、(中等）设二维随机变量(,)X Y 的概率密度为其他()()2360,0,0x y ex y f x y -+⎧>>⎪=⎨⎪⎩求：（1）(,)X Y 关于X ,Y 的边缘概率密度(),()X Y f x f y ；（2）判断随机变量X 与Y 是否独立26、（中等）设X 和Y 是两个相互独立的随机变量，X 在[0，4]上服从均匀分布，Y 的概率密度为f Y （y ）=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e 求X 和Y 的联合概率密度(,)f x y .【解】（1）因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他. 其他故/21e01,0, (,),()()20,.yX Yx yf x y X Y f x f y-⎧<<>⎪=⎨⎪⎩独立其他题14图。