初三数学阅读理解题集
初三数学《阅读理解》专题训练

2011中考数学专题复习(三):阅读理解班级:___________ 姓名:___________ 学号:____________1. 阅读下列证明过程:已知,如图1四边形ABCD中,AB=DC,AC=BD,AD≠BC,求证:四边形ABCD是等腰梯形.读后完成下列各小题.(1)证明过程是否有错误?如有,错在第几步上,答:_________.(2)作DE∥AB的目的是:__________.(3)有人认为第9步是多余的,你的看法呢?为什么?答:________.(4)判断四边形ABED为平行四边形的依据是:_________.(5)判断四边形ABCD是等腰梯形的依据是__________.(6)若题设中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?为什么?答______.2、阅读以下短文,然后解决下列问题:如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”. 如图8①所示,矩形ABEF即为△ABC的“友好矩形”.显然,当△ABC是钝角三角形时,其“友好矩形”只有一个 .(1) 仿照以上叙述,说明什么是一个三角形的“友好平行四边形”;(2) 如图8②,若△ABC为直角三角形,且∠C=90°,在图8②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;(3) 若△ABC是锐角三角形,且BC>AC>AB,在图8③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.3、阅读材料:某校研究性学习小组在研究相似图形时,发现相似三角形的定义、判定及其性质,可以拓展到扇形的相似中去。
例如,可以定义:“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”;相似扇形有性质:弧长比等于半径比、面积比等于半径比的平方…。
请你协助他们探索这个问题。
(1) 写出判定扇形相似的一种方法:若_____________________________,则两个扇形相似;(2) 有两个圆心角相等的扇形,其中一个半径为a 、弧长为m ,另一个半径为2a ,则它的弧长为_________________;(3) 如图1是一完全打开的纸扇,外侧两竹条AB 和AC 的夹角为120°,AB 为30cm ,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心角和半径。
初中数学题阅读理解类练习
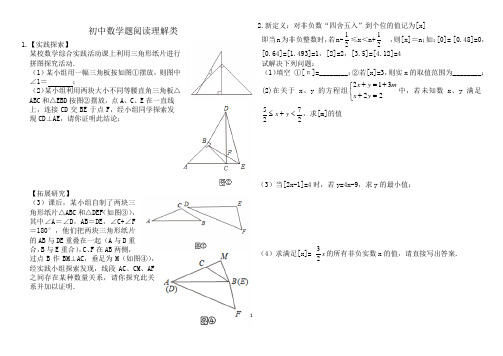
初中数学题阅读理解类1.【实践探索】某校数学综合实践活动课上利用三角形纸片进行拼图探究活动.(1)某小组用一幅三角板按如图①摆放,则图中∠1=;(2)某小组利用两块大小不同等腰直角三角板△ABC和△EBD按图②摆放,点A、C、E在一直线上,连接CD交BE于点F,经小组同学探索发现CD⊥AE,请你证明此结论;【拓展研究】(3)课后,某小组自制了两块三角形纸片△ABC和△DEF(如图③),其中∠A=∠D,AB=DE,∠C+∠F=180°,他们把两块三角形纸片的AB与DE重叠在一起(A与D重合,B与E重合),C、F在AB两侧,过点B作BM⊥AC,垂足为M(如图④),经实践小组探索发现,线段AC、CM、AF之间存在某种数量关系,请你探究此关系并加以证明.2.新定义:对非负数“四舍五入”到个位的值记为[x]即当n为非负整数时,若n-21≤x<n+21,则[x]=n;如:[0]= [0.48]=0,[0.64]=[1.493]=1,[2]=2,[3.5]=[4.12]=4试解决下列问题:(1)填空①[π]=________;②若[x]=3,则实x的取值范围为________;(2)在关于x、y的方程组⎩⎨⎧=++=+22312yxmyx中,若未知数x、y满足2725<+≤yx,求[m]的值(3)当[2x-1]=4时,若y=4x-9,求y的最小值;(4)求满足[x]= x23的所有非负实数x的值,请直接写出答案.13.(2019•天水)如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC ⊥BD.试证明:AB2+CD2=AD2+BC2;(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.4.(2015•黔西南州)求不等式0)3)(12(>+-xx的解集.解:根据“同号两数相乘,积为正”可得:①⎩⎨⎧>+>-312xx或②⎩⎨⎧<+<-312xx.解①得21>x ;解②得3-<x.∴不等式的解集为21>x或3-<x.请你仿照上述方法解决下列问题:(1)求不等式0)1)(32(<+-xx的解集.(2)求不等式02131≥+-xx的解集.25.请阅读下列材料问题:如图1,在等边三角形ABC内有一点P,且PA=2, PB=,PC=1.求∠BPC 度数的大小和等边三角形ABC 的边长.李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连接PP′,可得△P′P B是等边三角形,而△PP′A 又是直角三角形(由勾股定理的逆定理可证).所以∠AP′B=1500,而∠BPC=∠AP′B=150°.进而求出等边△ABC的边长为.问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=,BP=,PC=1.求∠BPC度数的大小和正方形ABCD的边长.6.(10分)(2020•天水)性质探究如图(1),在等腰三角形ABC中,∠ACB=120°,则底边AB与腰AC 的长度之比为.理解运用(1)若顶角为120°的等腰三角形的周长为4+2,则它的面积为;(2)如图(2),在四边形EFGH中,EF=EG=EH,在边FG,GH上分别取中点M,N,连接MN.若∠FGH=120°,EF=20,求线段MN的长.类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为.(用含α的式子表示)375237.(2020•湘潭)阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.(1)特例感知:如图(一),已知边长为2的等边△ABC的重心为点O,求△OBC与△ABC的面积.(2)性质探究:如图(二),已知△ABC的重心为点O,请判断、是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.(3)性质应用:如图(三),在正方形ABCD中,点E是CD的中点,连接BE交对角线AC于点M.①若正方形ABCD的边长为4,求EM的长度;②若S△CME =1,求正方形ABCD的面积.8.(2020•北京)小云在学习过程中遇到一个函数y=|x|(x2﹣x+1)(x≥﹣2).下面是小云对其探究的过程,请补充完整:(1)当﹣2≤x<0时,对于函数y1=|x|,即y1=﹣x,当﹣2≤x<0时,y1随x的增大而,且y1>0;对于函数y2=x2﹣x+1,当﹣2≤x<0时,y2随x的增大而,且y2>0;结合上述分析,进一步探究发现,对于函数y,当﹣2≤x<0时,y随x的增大而.(2)当x≥0时,对于函数y,当x≥0时,y与x的几组对应值如下表:x 0 1 2 3 …y 0 1 …结合上表,进一步探究发现,当x≥0时,y随x的增大而增大.在平面直角坐标系xOy中,画出当x≥0时的函数y的图象.(3)过点(0,m)(m>0)作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数y=|x|(x2﹣x+1)(x≥﹣2)的图象有两个交点,则m的最大值是.49.(2020•深圳)背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点E、A、D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了下列三个问题,请你帮助解答:(1)将正方形AEFG绕点A按逆时针方向旋转(如图1),还能得到BE=DG吗?若能,请给出证明;若不能,请说明理由;(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A 按顺时针方向旋转(如图2),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)把背景中的正方形分别改写成矩形AEFG和矩形ABCD,且,AE =4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.5610.【教材呈现】下面是某数学教材中的部分内容例4:如图,在△ABC 中,D 是BC 的中点,过点C 画直线CE , 使CE ∥AB,交AD 的延长线于点E,求证:AD=ED. 证明:∵CE ∥AB (已知)∴∠ABD=∠ECD, ∠BAD=∠CED(两直线平行,内错角相等)在△ABD 和△ECD 中,⎪⎩⎪⎨⎧=∠=∠∠=∠BD BD CED BAD ECD ABD∴△ABD ≌△ECD(AAS)∴AD=ED(全等三角形的对应边相等)【方法运用】在△ABC 中,AB=4,AC=2,点D 在边BC 上. (1)(2分)如图①,当点D 是BC 的中点时,AD 的取值范围是 ;(2) (6分)如图②,若BD:DC=1:2,求AD 的取值范围.【拓展提升】(4分)如图③,在△ABC 中,点D ,F 分别在边BC ,AB 上,线段AD ,CF 相交于点E ,且BD:DC=1:2,AE:ED=3:5,若△ACF 的面积为2,则△ABC 的面积为11.(2020•怀化)定义:对角线互相垂直且相等的四边形叫做垂等四边形.(1)下面四边形是垂等四边形的是 ;(填序号) ①平行四边形; ②矩形; ③菱形; ④正方形(2)图形判定:如图1,在四边形ABCD 中,AD ∥BC ,AC ⊥BD ,过点D 作BD 垂线交BC 的延长线于点E ,且∠DBC =45°,证明:四边形ABCD 是垂等四边形.(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形ABCD 内接于⊙O 中,∠BCD =60°.求⊙O 的半径.12.(2020•齐齐哈尔)综合与实践在线上教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动﹣﹣折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.实践发现:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM,把纸片展平,连接AN,如图①.(1)折痕BM (填“是”或“不是”)线段AN的垂直平分线;请判断图中△ABN是什么特殊三角形?答:;进一步计算出∠MNE=°;(2)继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,则∠GBN=°;拓展延伸:(3)如图③,折叠矩形纸片ABCD,使点A落在BC边上的点A'处,并且折痕交BC边于点T,交AD边于点S,把纸片展平,连接AA'交ST 于点O,连接AT.求证:四边形SATA'是菱形.解决问题:(4)如图④,矩形纸片ABCD中,AB=10,AD=26,折叠纸片,使点A落在BC边上的点A'处,并且折痕交AB边于点T,交AD边于点S,把纸片展平.同学们小组讨论后,得出线段AT的长度有4,5,7,9.请写出以上4个数值中你认为正确的数值.713.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.(1)观察猜想.图1中,线段NM、NP的数量关系是,∠MNP的大小为.(2)探究证明把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP、BD、CE,判断△MNP的形状,并说明理由;(3)拓展延伸把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请求出△MNP 面积的最大值.14.已知,在△ABC中,∠BAC=900,∠ABC=900,D为直线BC上一动点(不与点B、C重合),以AD为边作正方形ADEF,连接CF.(1)如图①,当点D在线段BC上时, BC,CD,CF三条线段之间的数量关系为;(2)如图②,当点D在线段BC的延长线上时,其他条件不变,请写出CF,BC,CD三条线段之间的关系,并证明;(3)如图③,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;求CF,BC,CD三条线段之间的关系.8参考答案1.2.93. 【解答】解:(1)四边形ABCD是垂美四边形.证明:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;(2)猜想结论:垂美四边形的两组对边的平方和相等.如图2,已知四边形ABCD中,AC⊥BD,垂足为E,求证:AD2+BC2=AB2+CD2证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;故答案为:AD2+BC2=AB2+CD2.(3)连接CG、BE,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,∴GE2=CG2+BE2﹣CB2=73,∴GE=.10114.(1)根据“异号两数相乘,积为负”可得 ①⎩⎨⎧<+>-01032x x 或 ② ⎩⎨⎧>+<-01032x x ……………………………(3分)解不等式组①得无解,解不等式组②得231<<-x ………………………………(4分) ∴原不等式的解集为231<<-x ……………………………………………(6分) (2)依题意可得①⎪⎩⎪⎨⎧>+≥-020131x x 或 ②⎪⎩⎪⎨⎧<+≤-020131x x ……………………………(3分)解①得x ≥3,解②得x<-2……………………………………………………(4分)∴原不等式的解集为x ≥3或x<-2…………………………………………(6分)5. 如图,将△BPC 绕点B 逆时针旋转90°, 得△BP ′A ,则△BPC ≌△BP ′A . ∴AP ′=PC =1,BP =BP ′=. 连结PP ′,在Rt △BP ′P 中, ∵ BP =BP ′=,∠PBP ′=90°, ∴ PP ′=2,∠BP ′P =45°. 在△AP ′P 中, AP ′=PC =1,PP ′=2,AP =,∵ 12 +22 =(5) 2 ,即AP ′2 +PP ′2 =AP 2 .∴ △AP ′P 是直角三角形,即∠AP ′P =90°. ∴∠AP ′B =∠AP ′P +∠BP ′P =135°. ∴ ∠BPC =∠AP ′B =135°.过点B 作BE ⊥AP ′交AP ′的延长线于点E . 则∠EP ′B =45°,∴ EP ′=BE =BP ′=1,∴AE =2.6.【分析】性质探究:如图1中,过点C 作CD ⊥AB 于D .解直角三角形求出AB (用AC 表示)即可解决问题.理解运用:①利用性质探究中的结论,设CA =CB =m ,则AB =m ,构建方程求出m 即可解决问题.②如图2中,连接FH .求出FH ,利用三角形中位线定理解决问题即可. 类比拓展:利用等腰三角形的性质求出AB 与AC 的关系即可. 【解答】解:性质探究:如图1中,过点C 作CD ⊥AB 于D . ∵CA =CB ,∠ACB =120°,CD ⊥AB , ∴∠A =∠B =30°,AD =BD , ∴AB =2AD =2AC •cos30°=AC ,∴AB :AC =:1. 故答案为:1.理解运用:(1)设CA =CB =m ,则AB =m ,由题意2m +m =4+2,∴m =2,∴AC =CB =2,AB =2,∴AD =DB =,CD =AC •sin30°=1,∴S △ABC =•AB •CD =.故答案为.(2)如图2中,连接FH . ∵∠FGH =120°,EF =EG =EH , ∴∠EFG =∠EGF ,∠EHG =∠EGH ,∴∠EFG+∠EHG=∠EGF+∠EGH=∠FGH=120°,∵∠FEH+∠EFG+∠EHG+∠FGH=360°,∴∠FEH=360°﹣120°﹣120°=120°,∵EF=EH,∴△EFH是顶角为120°的等腰三角形,∴FH=EF=20,∵FM=MG.GN=GH,∴MN=FH=10.类比拓展:如图1中,过点C作CD⊥AB于D.∵CA=CB,∠ACB=2α,CD⊥AB,∴∠A=∠B=30°,AD=BD,∠ACD=∠BCD=α∴AB=2AD=2AC•sinα∴AB:AC=2sinα:1.故答案为2sinα:1.【点评】本题属于三角形综合题,考查了等腰三角形的性质,解直角三角形,三角形的中位线定理等知识,解题的关键是学会利用等腰三角形的三线合一的性质解决问题,学会构造三角形的中位线解决问题,属于中考常考题型.7.【分析】(1)连接DE,利用相似三角形证明,运用勾股定理求出AD 的长,运用三角形面积公式求解即可;(2)根据(1)的证明可求解;(3)①证明△CME∽△ABM,得,再运用勾股定理求出BE的长即可解决问题;②分别求出S△BMC和S△ABM即可求得正方形ABCD的面积.【解答】解:(1)连接DE,如图,∵点O是△ABC的重心,∴AD,BE是BC,AC边上的中线,∴D,E为BC,AC边上的中点,∴DE为△ABC的中位线,∴DE∥AB,DE=AB,∴△ODE∽△OAB,∴=,∵AB=2,BD=1,∠ADB=90°,∴AD=,OD=,∴,=;(2)由(1)可知,,是定值;点O到BC的距离和点A到BC的距离之比为1:3,则△OBC和△ABC的面积之比等于点O到BC的距离和点A到BC的距离之比,故=,是定值;(3)①∵四边形ABCD是正方形,∴CD∥AB,AB=BC=CD=4,∴△CME~△AMB,∴,12∵E为CD的中点,∴,∴,∴,∴,即;②∴S△CME=1,且,∴S△BMC=2,∵,∴,∴S△AMB=4,∴S△ABC=S△BMC+S△ABM=2+4=6,又S△ADC=S△ABC,∴S△ADC=6,∴正方形ABCD的面积为:6+6=12.【点评】本题是一道相似形综合题目,主要考查的是三角形重心的性质、全等三角形的判定与性质、勾股定理及相似三角形的判定与性质,解答此题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.8.【分析】(1)利用一次函数或二次函数的性质解决问题即可.(2)利用描点法画出函数图象即可.(3)观察图象可知,x=﹣2时,m的值最大.【解答】解:(1)当﹣2≤x<0时,对于函数y1=|x|,即y1=﹣x,当﹣2≤x<0时,y1随x的增大而减小,且y1>0;对于函数y2=x2﹣x+1,当﹣2≤x<0时,y2随x的增大而减小,且y2>0;结合上述分析,进一步探究发现,对于函数y,当﹣2≤x<0时,y随x的增大而减小.故答案为:减小,减小,减小.(2)函数图象如图所示:(3)∵直线l与函数y=|x|(x2﹣x+1)(x≥﹣2)的图象有两个交点,观察图象可知,x=﹣2时,m的值最大,最大值m=×2×(4+2+1)=,故答案为【点评】本题考查二次函数与不等式,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.9【分析】(1)由正方形的性质得出AE=AF,∠EAG=90°,AB=AD,∠BAD =90°,得出∠EAB=∠GAD,证明△AEB≌△AGD(SAS),则可得出结论;(2)由菱形的性质得出AE=AG,AB=AD,证明△AEB≌△AGD(SAS),由全等三角形的性质可得出结论;(3)方法一:过点E作EM⊥DA,交DA的延长线于点M,过点G作GN⊥AB 交AB于点N,求出AG=6,AD=12,证明△AME∽△ANG,设EM=2a,AM =2b,则GN=3a,AN=3b,则BN=8﹣3b,可得出答案;方法二:证明△EAB∽△GAD,得出∠BEA=∠AGD,则A,E,G,Q四点共圆,得出∠GQP=∠P AE=90°,连接EG,BD,由勾股定理可求出答案.【解答】(1)证明:∵四边形AEFG为正方形,∴AE=AF,∠EAG=90°,又∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠EAB=∠GAD,∴△AEB≌△AGD(SAS),∴BE=DG;(2)当∠EAG=∠BAD时,BE=DG,13理由如下:∵∠EAG=∠BAD,∴∠EAB=∠GAD,又∵四边形AEFG和四边形ABCD为菱形,∴AE=AG,AB=AD,∴△AEB≌△AGD(SAS),∴BE=DG;(3)解:方法一:过点E作EM⊥DA,交DA的延长线于点M,过点G作GN⊥AB交AB于点N,由题意知,AE=4,AB=8,∵=,∴AG=6,AD=12,∵∠EMA=∠ANG,∠MAE=∠GAN,∴△AME∽△ANG,设EM=2a,AM=2b,则GN=3a,AN=3b,则BN=8﹣3b,∴ED2=(2a)2+(12+2b)2=4a2+144+48b+4b2,GB2=(3a)2+(8﹣3b)2=9a2+64﹣48b+9b2,∴ED2+GB2=13(a2+b2)+208=13×4+208=260.方法二:如图2,设BE与DG交于Q,∵,AE=4,AB=8∴AG=6,AD=12.∵四边形AEFG和四边形ABCD为矩形,∴∠EAG=∠BAD,∴∠EAB=∠GAD,∵,∴△EAB∽△GAD,∴∠BEA=∠AGD,∴A,E,G,Q四点共圆,∴∠GQP=∠P AE=90°,∴GD⊥EB,连接EG,BD,∴ED2+GB2=EQ2+QD2+GQ2+QB2=EG2+BD2,∴EG2+BD2=42+62+82+122=260.【点评】本题是相似形综合题,考查了正方形的性质,菱形的性质,矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,熟练掌握特殊平行四边形的性质是解题的关键.10. (1)1<AD<3;(2) 2<AD<310;(3)711.【解答】解:(1)①平行四边形的对角线互相平分但不垂直和相等,故不是垂等四边形;②矩形对角线相等但不垂直,故不是垂等四边形;③菱形的对角线互相垂直但不相等,故不是垂等四边形;④正方形的对角线互相垂直且相等,故正方形是垂等四边形;故选:④;(2)∵AC⊥BD,ED⊥BD,∴AC∥DE,又∵AD∥BC,∴四边形ADEC是平行四边形,∴AC=DE,又∵∠DBC=45°,∴△BDE是等腰直角三角形,∴BD=DE,∴BD=AC,又∵BD⊥AC,∴四边形ABCD是垂等四边形;14(3)如图,过点O作OE⊥BD,∵四边形ABCD是垂等四边形,∴AC=BD,又∵垂等四边形的面积是24,∴AC•BD=24,解得,AC=BD=4,又∵∠BCD=60°,∴∠DOE=60°,设半径为r,根据垂径定理可得:在△ODE中,OD=r,DE=,∴r===4,∴⊙O的半径为4.【点评】本题是一道圆的综合题,主要考查了平行四边形的性质、菱形的性质、矩形的性质、正方形的性质、新定义、圆周角定理、垂径定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用新定义解答问题.12.【分析】(1)由折叠的性质可得AN=BN,AE=BE,∠NEA=90°,BM 垂直平分AN,∠BAM=∠BNM=90°,可证△ABN是等边三角形,由等边三角形的性质和直角三角形的性质可求解;(2)由折叠的性质可得∠ABG=∠HBG=45°,可求解;(3)由折叠的性质可得AO=A'O,AA'⊥ST,由“AAS”可证△ASO≌△A'TO,可得SO=TO,由菱形的判定可证四边形SATA'是菱形;(4)先求出AT的范围,即可求解.【解答】解:(1)如图①∵对折矩形纸片ABCD,使AD与BC重合,∴EF垂直平分AB,∴AN=BN,AE=BE,∠NEA=90°,∵再一次折叠纸片,使点A落在EF上的点N处,∴BM垂直平分AN,∠BAM=∠BNM=90°,∴AB=BN,∴AB=AN=BN,∴△ABN是等边三角形,∴∠EBN=60°,∴∠ENB=30°,∴∠MNE=60°,故答案为:是,等边三角形,60;(2)∵折叠纸片,使点A落在BC边上的点H处,∴∠ABG=∠HBG=45°,∴∠GBN=∠ABN﹣∠ABG=15°,故答案为:15°;(3)∵折叠矩形纸片ABCD,使点A落在BC边上的点A'处,∴ST垂直平分AA',∴AO=A'O,AA'⊥ST,∵AD∥BC,∴∠SAO=∠TA'O,∠ASO=∠A'TO,∴△ASO≌△A'TO(AAS)∴SO=TO,∴四边形ASA'T是平行四边形,又∵AA'⊥ST,∴边形SATA'是菱形;(4)∵折叠纸片,使点A落在BC边上的点A'处,∴AT=A'T,在Rt△A'TB中,A'T>BT,∴AT>10﹣AT,∴AT>5,∵点T在AB上,∴当点T与点B重合时,AT有最大值为10,∴5<AT≤10,∴正确的数值为7,9,故答案为:7,9.【点评】本题是四边形综合题,考查了矩形的性质,菱形的判定,全等三角形的判定和性质,旋转的性质,等边三角形的判定和性质等知识,灵活运用这些性质进行推理是本题的关键.1513.【分析】(1)先证明由AB=AC,AD=AE,得BD=CE,再由三角形的中位线定理得NM与NP的数量关系,由平行线性质得∠MNP的大小;(2)先证明△ABD≌△ACE得BD=CE,再由三角形的中位线定理得NM=NP,由平行线性质得∠MNP=60°,再根据等边三角形的判定定理得结论;(3)由BD≤AB+AD,得MN≤2,再由等边三角形的面积公式得△MNP的面积关于MN的函数关系式,再由函数性质求得最大值便可.【解答】解:(1)∵AB=AC,AD=AE,∴BD=CE,∵点M、N、P分别为DE、BE、BC的中点,∴MN=BD,PN=CE,MN∥AB,PN∥AC,∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,∴∠MNE+∠ENP=∠ABE+∠AEB,∵∠ABE+∠AEB=180°﹣∠BAE=60°,∴∠MNP=60°,故答案为:NM=NP;60°;(2)△MNP是等边三角形.理由如下:由旋转可得,∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵点M、N、P分别为DE、BE、BC的中点.∴MN=BD,PN=CE,MN∥BD,PN∥CE,∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB,∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC+∠ECB=180°﹣∠BAC=60°,∴△MNP是等边三角形;(3)根据题意得,BD≤AB+AD,即BD≤4,∴MN≤2,∴△MNP的面积==,∴△MNP的面积的最大值为.14.(1)证明:如图1,∵在△ABC中,∠BAC=90°,∠ABC=45°,∴∠ACB=45°,∴∠ACB=∠ABC,∴AB=AC.∵四边形ADEF为正方形,∴AD=DE=EF=AF,∠FAD=90°,∴∠BAC=∠FAD,∴∠BAC-∠DAC=∠FAD-∠DAC,∴∠BAD=∠CAF....(1)由等腰直角三角形和正方形的性质可以得出△ABD ≌△ACF ,就可以得出BD=CF,就可以得出结论;(2)如图2,通过证明△ABD≌△ACF,就可以得出BD=CF,就可以得出CF=BC+CD;(3)如图3,通过证明△ABD≌△ACF,就可以得出BD=CF,就可以得出CD=BC+CF.16。
初三数字阅读题库及答案

初三数字阅读题库及答案数字阅读是提高学生数学素养和解决问题能力的重要方式。
以下是一份初三数字阅读题库及答案,供同学们练习和参考。
题目一:某工厂计划生产一批零件,原计划每天生产200个,实际每天生产了220个。
如果原计划生产周期为10天,实际生产周期为多少天?答案:原计划总共生产零件数量为200个/天× 10天 = 2000个。
实际每天生产220个零件,所以实际生产周期为2000个÷ 220个/天≈ 9.09天。
题目二:一个班级有48名学生,其中1/3是男生,剩下的是女生。
如果班级组织一次郊游,需要每4名学生组成一个小组,那么可以组成多少个小组?答案:班级中男生人数为48 × 1/3 = 16人。
女生人数为48 - 16 = 32人。
班级总人数为16 + 32 = 48人。
每组4人,所以可以组成48 ÷ 4 = 12个小组。
题目三:小明计划在暑假期间读一本300页的书。
如果他每天读30页,那么他需要多少天才能读完这本书?答案:小明每天读30页,要读完300页,需要的天数为300页÷ 30页/天= 10天。
题目四:一家超市在促销活动中,原价为100元的商品现在打8折出售。
如果顾客使用优惠券再减去20元,那么顾客实际需要支付多少钱?答案:商品打8折后的价格为100元× 0.8 = 80元。
使用优惠券后的价格为80元 - 20元 = 60元。
顾客实际需要支付60元。
题目五:某公司在第一季度的销售额为500万元,第二季度的销售额比第一季度增长了20%。
如果第三季度的销售额比第二季度减少了15%,那么第三季度的销售额是多少?答案:第二季度销售额为500万元× (1 + 20%) = 500万元× 1.2 = 600万元。
第三季度销售额为600万元× (1 - 15%) = 600万元× 0.85 = 510万元。
中考数学专题复习新定义阅读理解题(一)

(2)在所有的四位数中,最大的“本位数”是,最小的“本位数”是.
(3)在所有三位数中,“本位数”一共有多少个?
4.阅读下列材料解决问题:
材料一:完全平方数是指可以写成某个整数的平方的数,即其平方根为整数的数.例如, 是一个完全平方数.
材料二:对一个四位数,我们可以记为 ,即 ,若一个四位数的千位数字与百位数字相同,十位与个位数字相同,记为 ,我们称之为和谐四位数.
4.(1)3;(2)证明见解析;(3)7744
【解析】
【分析】
(1)对12进行分解,即可得到n为3时,12n成为完全平方数的最小正整数;
(2)将 用整式表示出来,再对整式进行因式分解即可;
(3)由题意易知100x+y要被11整除,且 ,可得x+y=11,再对x、y逐一进行检验即可.
【详解】
解:(1)∵n是使12n成为完全平方数的最小正整数,
2.(1)0;25,(2)证明见详解;(3)满足条件s的最大值 .
【解析】
【分析】
(1)根据定义即可求出;
(2)对任意一个四位数n= ,m= 根据定义求 ,由 均为整数, 也为整数,可得对任意一个四位数n, 均为整数;
(3)由定义可得 = ,由 是一个完全平方数,满足条件s的最大值只要 最大即可,可求 最大=9,可得9b-11为平方数,9b-11=25,解方程即可.
12=2×2×3,
∴n=3.
(2)∵ ,
∴任意一个和谐四位数都是 的倍数.
(3)∵四位数 是一个完全平方数, 是一个完全平方数,
能被 整除,
.
能被 整除,而 ,
只有 ,经检验 ,
故这个四位数为 .
初中数学中考专题-阅读理解、判断说理型专题训练及答案

阅读理解、判断说理型专题训练B总分120分,时间90分钟一、细心填一填(每题3分,共21分)1.(绵阳)我们常用的数是十进制的数,而计算机程序处理中使用的是只有数码0和1的二进制数.这两者可以相互换算,如将二进制1101换算成十进制数应为1×23+1×22+0×21+ 1×20= 13,按此方式,则将十进制数25换算成二进制数应为__________.2.(内江市)对于正数x ,规定f (x )= x 1x +,例如f (3)=33134=+,f (13)=1131413=+,计算f (12006)+ f (12005)+ f (12004)+ …f (13)+ f (12x )+ f (1)+ f (1)+ f (2)+ f (3)+ … + f ()+ f ()+ f ()= .3.(扬州)放假了,小明和小丽去蔬菜加工厂社会实践,两人同时工作了一段时间后,休息时小明对小丽说:“我已加工了28千克,你呢?” 小丽思考了一会儿说:“我来考考你.图⑴、图⑵分别表示你和我的工作量与工作时间的关系,你能算出我加工了多少千克吗?” 小明思考后回答:“你难不倒我,你现在加工了 千克.”图1 图24.(深圳)人民公园的侧门口有9级台阶,小聪一步只能上1级台阶或2级台阶,小聪发现当台阶数分别为1级、2级、3级、4级、5级、6级、7级……逐渐增加时,上台阶的不同方法的种数依次为1、2、3、5、8、13、21、……这就是著名的斐波那契数列.那么小聪上这9级台阶共有________________种不同方法.5.(嘉兴)定义一种对正整数n 的“F ”运算:①当n 为奇数时,结果为3n +5;②当n 为时间()18工作量(kg )时间()7040工作量(kg )偶数时,结果为kn2(其中k 是使kn2为奇数的正整数),并且运算重复进行.例如,取n =26,则:若n =449,则第449次“F 运算”的结果是_____.6.(内江)阅读材料,大数学家高斯在上学读书时曾经研究过这样一个问题:1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+()121+=n n n ,其中n是正整数。
数学阅读理解型问题(专题4)

阅读理解型问题(专题4)——合情推理【考点透视】阅读理解型问题在近年的全国各地的中考试题中频频出现,特别引人注目,这些试题不再囿于教材的内容及其方法,以新颖别致的取材、富有层次和创造力的设问独树一帜.这些试题中还常常出现新的概念和方法,不仅要求学生理解这些新的概念和方法,而且要灵活运用这些新的概念和方法去分析、解决一些简单的问题.在阅读理解型问题中,除了考查学生的分析分析、综合、抽象、概括等演绎推理能力,即逻辑推理能力外,还经常考查学生的观察、猜想、不完全归纳、类比、联想等合情推理能力,考查学生的直觉思维.因此,这类问题需要学生通过对阅读材料的阅读理解,然后进行合情推理,就其本质进行归纳加工、猜想、类比和联想,作出合情判断和推理, 【典型例题】例1.已知正数a 和b ,有下列命题:(1)a +b =2,ab ≤1; (2)a +b =3,ab ≤23; (3)a +b =6,ab ≤3.根据以上三个命题所提供的规律猜想:若a +b =9,ab ≤ .(2000年北京市东城区中考试题)分析:观察(1)、(2)、(3)中的数字规律:不等号右边的数都是等号右边的数的21,由此可以作出猜想.解:ab ≤29. 说明:本题要求直接通过不完全归纳,总结规律,猜想结论. 例2.例2.(1)判断下列各式是否成立,你认为成立的请在括号内打“√”,不成立的打“×”.①322322=+( );②833833=+( ); ③15441544=+( ); ④24552455=+( ). (2)你判断完以上各题之后,发现了什么规律?请用含有n 的式子将规律表示出来,并注明n 的取值范围: .图4—1AD nB CD 1 D 2D 3E 1 E 2 E 3 E n 图4—2(3)请用数学知识说明你所写式子的正确性.(2000年江苏省常州市中考试题)分析:判断式子①、②、③、④内在的规律时可以发现:①中3=2 2-1;②中8=3 2-1;③中15=4 2-1;④中24=5 2-1.这样就可以统一用含n 的式子表示出来.解:(1)①√;②√;③√;④√.(2)12-+n n n =n 12-n n.其中n 为大于1的自然数. (3)12-+n n n =123-n n =122-⋅n n n =n 12-n n . 说明:本题虽然需要说明所写式子的正确性,但本题主要考查学生的合情推理能力,即用含有n 的式子将规律表示出来.例3.下列每个图是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n (n >1)盆花,每个图案花盆的总数是S .按此规律推断,S 和n 的关系式是 .(2000年山西省中考试题)分析:由正三角形每条边的花盆数n 与花盆的总数S 之间的关系,可以看出S 总是比n 的3倍少3. 解:S =3n -3.说明:本题的答案不唯一,其它形式也可以. 例4. 如图4—2所示,在△ABC 中,BC =a ,若D 1、E 1分别是AB 、AC 的中点,则D 1E 1=a 21; 若D 2、E 2分别是D 1B 、E 1C 的中点,则D 2E 2=a a a 43)2(21=+; 若D 3、E 3分别是D 2B 、E 2C 的中点,则D 3E 3=a a a 87)43(21=+;…………若D n 、E n 分别是D 1-n B 、E 1-n C 的中点,则D n E n = (n ≥1,且n 为整数).(2001年山东省济南市中考试题)分析:因为12121=;2221243-=;3321287-=;……,所以D n E n 也可以用含数字2的式子来表示.解:D n E n =11212---n n (n ≥1,且n 为整数).说明:寻找数字规律,应把已给的数写成有规律的一组数.n =2,S =3 n =3,S =6 n =4,S =9例5.问题:你能很快算出19952吗?为了解决这个问题,我们考察个位上的数为5的自然数的平方.任意一个个位数为5的自然数可写成10•n+5,即求(10•n+5)2的值(n为自然数).你试分析n=1,n=2,n=3,…,这些简单情况,从中探索规律,并归纳、猜想出结论(在下面空格内填上你的探索结果).(1)通过计算,探索规律:152=225可写成100×1(1+1)+25,252=625可写成100×2(2+1)+25,352=1225可写成100×3(3+1)+25,452=2025可写成100×4(4+1)+25,……752=5625可写成,852=7225可写成,……(2)从第(1)的结果,归纳、猜想得:(10n+5)2=.(3)根据上面的归纳、猜想,请算出:19952=.(1999年福建省三明市中考试题)分析:在对这些式子进行规律探索的时候,要找出哪些数是不变的,哪些数是随式子的序号变化而逐步变化的.然后就可以用n来表示这些逐步变化的数.解:(1)100×7(7+1)+25;100×8(8+1)+25.(2)100n2+100n+25100n(n+1)+25.(3) 100×199(199+1)+25=3980025.说明:本题不仅要求归纳猜想和探索规律,而且要运用归纳猜想得出的结论解决问题.例6.如图4—3,在平面上,给定了半径为r的圆O,对于任意点P,在射线OP上取一点P',使得OP·OP'=r 2 ,这种把点P变为点P'的变换叫做反演变换,点P与点P'叫做互为反演点.图4—3 图4—4(1) 如图4—4,⊙O 内外各一点A 和B ,它们的反演点分别为A '和B '.求证:∠A '=∠B ; (2) 如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.①选择:如果不经过点O 的直线l 与⊙O 相交,那么它关于⊙O 的反演图形是( ). (A)一个圆 (B)一条直线 (C)一条线段 (D)两条射线 ②填空:如果直线l 与⊙O 相切,那么它关于⊙O 的反演图形是 ,该图形与圆O 的位置关系是 .(2001年江苏省南京市中考试题)分析:求解本题首先要理解“反演变换”的意义,并理解圆内的点的反演点在圆外,圆上的点的反演点在圆上,圆外的点的反演点在圆内;其次,第(2)题的第①小题,由于直线与圆的交点的反演点是它本身,因此只要在该直线的圆内、圆外部分各取几点,画出反演点,便可推测该直线的反演图形.另外,第(2)题的第②小题,由于直线与圆的切点的反演点是它本身,因此只要在该直线上取几点,画出反演点,便可推测该直线的反演图形.(1)证明:∵A 、B 的反演点分别是A’、B’,∴OA ·OA’=r 2,OB ·OB’=r 2. ∴OA ·OA’=OB ·OB’,即''OA OBOB OA . ∵∠O =∠O ,∴△ABO ∽△B’A’O . ∴∠A’=∠B .. (2)解:①A .②圆;内切.说明:本题主要考查学生通过观察、分析,从特殊的点的研究归纳、推测图形形状的合情推理能力.另外,还可以研究下列问题:如果直线⊙O’与⊙O 相切,那么它关于⊙O 的反演图形是什么?该图形与圆O 的位置关系是是什么?例7.阅读下面材料:对于平面图形A ,如果存在一个圆,使图形A 上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A 被这个圆所覆盖.对于平面图形A ,如果存在两个或两个以上的圆,使图形A 上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A 被这些圆所覆盖.例如:图4—5中的三角形被一个圆所覆盖,图4—6中的四边形被两个圆所覆盖.回答下列问题:(1)边长为1cm 的正方形被一个半径为r 的圆所覆盖,r 的最小值是 cm ; (2)边长为1cm 的等边三角形被一个半径为r 的圆所覆盖,r 的最小值是 cm ; (3)长为2cm ,宽为1cm 的矩形被两个半径为r 的圆所覆盖,r 的最小值是 cm , 这两个圆的圆心距是 cm.(2003年江苏省南京市中考试题)图4—5图4—6分析:本题首先要理解图形被圆所覆盖的定义,其次,可以推测正方形、等边三角形被一个半径为r 的圆所覆盖,r 取最小值时,显然这个圆就是正方形、等边三角形的外接圆.而第(3)题可把长为2cm ,宽为1cm 的矩形分割成两个边长为1 cm 的正方形,根据第(1)题,不难得到结论.解:(1)22; (2)33; (3)22,1. 说明:本题的合情推理是建立在空间想象的基础上,并把问题转化为多边形的外接圆问题.另外,还可以研究下列问题:1.如果边长为1cm ,有一个锐角是60°的菱形被一个半径为r 的圆所覆盖,那么r 的最小值是多少?2.如果上低和腰长都是1cm ,下低长是2cm 的梯形被一个半径为r 的圆所覆盖,那么r 的最小值是多少?【习题4】1.观察下列各式,你会发现什么规律?3×5=15,而15=42-1; 5×7=35,而35=62-1;11×13=143,而143=122-1; ……请你猜想到的规律用只含一个字母的式子表示出来: .(2000年山东省济南市中考试题)2.观察下列顺序排列的等式:9×0+1=1, 9×1+2=11, 9×2+3=21, 9×3+4=31, 9×4+5=41, ……猜想:第n 个等式(n 为正整数)应为 .(2003年北京市中考试题)3.观察下列各式: 1×3=12+2×1, 2×4=22+2×2, 3×5=32+2×3,……请你将猜想到的规律用自然数n (n ≥1)表示出来: .(2003年福建省福州市中考试题)4.观察以下等式:1×2=31×1×2×3;1×2+2×3=31×2×3×4;1×2+2×3+3×4=31×3×4×5;1×2+2×3+3×4+4×5=31×4×5×6;……根据以上规律,请你猜测:1×2+2×3+3×4+4×5+…+n ×(n +1)= .(2001年山东省威海市中考试题)5.将正偶数按下表排成5列:第1列 第2列 第3列 第4列 第5列第1行 2 4 6 8 第2行 16 14 12 10 第3行 18 20 22 24 …… …… 28 26根据上面的排列规律,则2000应在( ).A .第125行,第1列B .第125行,第2列C .第250行,第1列D .第250行,第2列(2001年湖北省荆州市中考试题)6.细心观察图形4—7,认真分析各式,然后解答问题. 21,21)1(12==+S ; 22,31)2(22==+S ; 23,41)3(32==+S ; ……(1)请用含有n (n 是正整数)的等式表示上述变化规律; (2)推算出OA 10的长;(3)求出S 1 2+S 2 2+S 3 2+…+S 10 2的值.(2003年山东省烟台市中考试题)7.(1)阅读下面材料:点A 、B 在数轴上分别表示实数a 、b ,A 、B 两点之间的距离表示为|AB |.当A 、B 两点中有一点在原点时,不妨设点A 在原点, 如图4—8,|AB |=|OB |=|b |=|a -b |; 当A 、B 两点都不在原点时,①如图4—9,当点A 、B 都在原点右边时,则 |AB |=|OB |-|OA |=|b |-|a |=b -a =|a -b |; ②如图4—10,当点A 、B 都在原点左边时,则O (A ) B图4—8O B A图4—9O A B 图4—10O A 2 A 4A 1 …1 A 5S 3 S 5 S 2S 1 S 41 1 1A 6 A 3…图4—7|AB |=|OB |-|OA |=|b |-|a |=-b -(-a )=|a -b |;③如图4—11,当点A 、B 在原点的两边时,则 |AB |=|OA |+|OB |=|a |+|b |=a +(-b )=|a -b |. 综上,数轴上A 、B 两点之间的距离|AB |=|a -b |.(2)回答相应问题:①数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 . ②数轴上表示x 和-1的两点A 和B 之间的距离是 ,如果|AB |=2,那么x 为 . ③当代数式|x +1|+|x -2|取最小值时,x 相应的取值范围是 .(2002年江苏省南京市中考试题)8.如图4—12,在正方形ABCD 中,E 是AD 的中点,F 是 BA 延长线上一点, AF =21AB . (1)求证:△ABE ≌△ADF . (2)阅读下面材料:如图4—13,把△ABC 沿直线BC 平行移动线段BC 的长度,可以变到△ECD 的位置; 如图4—14,以BC 为轴把△ABC 翻折180°,可以变到△DBC 的位置; 如图4—15,以点A 为中心,把△ABC 旋转180°,可以变到△AED 的位置.象这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换. (3)回答下列问题:①在图4—12中,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE 变到 △ADF 的位置?答: . ②指出图4—12中线段BE 与DF 之间的关系.答: .(2000年江苏省南京市中考试题)9.在△ABC 中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交AD 于点O .某学生研究这一问题时,发现了如下事实.EDCBADCBAEDCA图4—13 图4—14 图4—15FABC D E图4—12OA B a 图4—11图4—16E A B C O D图4—17 B C A D EOB C A 图4—18 D E O C A 图4—19 D F EO①当11121+==AC AE 时,有21232+==AD AO (如图4-16); ②当21131+==AC AE 时,有22242+==AD AO (如图4-17); ③当31141+==AC AE 时,有32252+==AD AO (如图4-18). 在图4-19中,当n AC AE +=11时,参照上述研究结论,请你猜想用n 表示ADAO的一般结论,并给出证明(其中n 是正整数).(2001年河北省中考试题)10.某厂要制造能装250毫升(1毫升=1厘米3 )饮料的铝制圆柱形易拉罐,易拉罐的侧壁厚度和底部的厚度都是0.02厘米,顶部厚度是底部厚度的3倍,这是为了防止“呯”的一声打开易拉罐时把整个顶盖撕下来.设一个底面半径是x 厘米的易拉罐的用铝量是y 厘米3. (1)利用用铝量=底圆面积×底部厚度+顶圆面积×顶部厚度+侧面积×侧壁厚度)求y 与x 之间的函数关系式;(2②根据上表推测:要使用铝量y (厘米)的值尽可能小,底面半径x (厘米)的值所在范围是( ).A .1.6≤x ≤2.4B .2.4<x <3.2C .3.2≤x ≤4(2002年江苏省南京市中考试题)11.如图20,正方形ABCD 和正方形EFGH 对角线BD 、FH 都在直线l 上.O 1、O 2 分别是正方形的中心,O 1D =2,O 2F =1,线段O 1O 2的长叫做两个正方形的中心距....当中心O 2在直线l 上平移时,正方形EFGH 也随之平移,在平移时正方形EFGH 的形状、大小没有改变.(1)当中心O 2在直线l 上平移到两个正方形只有一个公共点时,中心距O 1O 2 = . (2)随着中心O 2在直线l 上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程 ).(2003年江苏省徐州市中考试题)图4—20【习题4】1.解:(2n -1)(2n +1)=(2n )2-1. 2.解:9(n -1)+n =10(n -1)+1. 3.解: n (n +2)=n 2 +2n .4.解:1×2+2×3+3×4+4×5+…+n ×(n +1)=31×n ×(n +1)×(n +2).5.解:选C .6.解:(1)2,11)(2nS n n n =+=+. (2)∵OA 1=1,OA 2=2,OA 3=3,…, ∴OA 10=10.(3)S 1 2+S 2 2+S 3 2+…+S 10 2=2)21(+2)22(+2)23(+…+2)210(=41(1+2+3+…+10) =455. 7.解:(1)3,3,4;(2)∣x +1∣,-3或1; (3)-1≤x ≤2. 8.解:(1)证明:在正方形ABCD 中, ∵ AB=AD ,AD ⊥AB , ∴∠BAE =∠DAF =90°.∵AE =21AD ,AF =21AB , ∴AE =AF .∴△ABE ≌△ADF .(3)①答:△ABE 绕点A 逆时针旋转90度到△ADF 的位置. ②答:BE =DF ,且BE ⊥DF .9.解:根据题意,可以猜想:当n AC AE +=11时,有n AD AO +=22成立. 证明:过D 作DF ∥BE 交AC 于点F .∵D 是BC 的中点, ∴F 是EC 的中点. ∵n AC AE +=11, ∴n EC AE 1=. ∴nEF AE 2=.∴nAF AE +=22. ∵DF ∥BE , ∴nAF AE AD AO +==22. 10.解:(1)解:222250202.0302.0xx x x y ππππ⋅+⋅⋅+⋅=·0.02 =xx 102522+π. (2)B .11.解:.(1)2,1. (2)3.(3)①当1<O 1O 2<3时,两个正方形有2个公共点;②当O 1O 2=1时,两个正方形有无数个公共点;③当O 1O 2 <1,或O 1O 2>3时,两个正方形没有公共点.。
中考数学阅读理解材料

1.阅读下面材料: 小伟遇到这样一个问题:如图1,在正方形ABCD 中,点E 、F 分别为DC 、BC 边上的点,∠EAF =45°,连结EF ,求证:DE +BF =EF .小伟是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.他的方法是将△ADE 到△ABG (如图2),此时GF 即是DE +BF .请回答:在图2中,∠GAF 的度数是 .参考小伟得到的结论和思考问题的方法,解决下列问题:(1)如图3,在直角梯形ABCD 中,AD ∥BC (AD >BC ),∠D =90°,AD =CD =10,E 是CD 上一点,若∠BAE =45°,DE =4,则BE = .(2)如图4,在平面直角坐标系xOy 中,点B 是x 轴上一动点,且点A (3-,2),连结AB 和AO ,并以3. 阅读下面材料:小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形,∠AOB=∠COD=90°.若△BOC 的面积为1,试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E ,使得OE=CO ,连接BE ,可证△OBE ≌△OAD ,从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2).请你回答:图2中△BCE 的面积等于请你尝试用平移、旋转、翻折的方法,解决下列问题:如图3,已知△ABC ,分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI ,连接EG 、FH 、ID .(1)在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形(保留画图痕迹);(2)若△ABC 的面积为1,则以EG 、FH 、ID 的长度为三边长的三角形的面积等于4.课题学习问题背景??甲、乙、丙三名同学探索课本上一道题:如图1,E 是边长为a 的正方形ABCD 中CD 边上任意一点,以点A 为中心,把△ADE 顺时针旋转90°,画出旋转后的图形任务要求:(1)请你在图1中画出旋转后的图形甲、乙、丙三名同学又继续探索:在正方形ABCD 中,∠EAF=45°,点F 为BC 上一点,点E 为DC 上一点,∠EAF 的两边AE 、AF 分别与直线BD 交于点M 、N .连接EFF E D AB C B E D A G F E D A B C C 图1图2图3C D AO B xy图4甲发现:线段BF ,EF ,DE 之间存在着关系式EF=BF+DE ;乙发现:△CEF 的周长是一个恒定不变的值;丙发现:线段BN ,MN ,DM 之间存在着关系式BN 2+DM 2=MN 2(2)现请也参与三位同学的研究工作中来,你认为三名同学中哪个的发现是正确的,并说明你的理由.5. 小曼和他的同学组成了“爱琢磨”学习小组,有一次,他们碰到这样一道题:“已知正方形ABCD ,点E 、F 、G 、H 分别在边AB 、BC 、CD 、DA 上,若EG ⊥FH ,则EG=FH .”为了解决这个问题,经过思考,大家给出了以下两个方案:方案一:过点A 作AM ∥HF 交BC 于点M ,过点B 作BN ∥EG 交CD 于点N ;方案二:过点A 作AM ∥HF 交BC 于点M ,过点A 作AN ∥EG 交CD 于点N .…(1)对小曼遇到的问题,请在甲、乙两个方案中任选一个加以证明(如图(1)).(2)如果把条件中的“正方形”改为“长方形”,并设AB=2,BC=3(如图(2)),是探究EG 、FH 之间有怎样的数量关系,并证明你的结论.(3)如果把条件中的“EG ⊥FH ”改为“EG 与FH 的夹角为45°”,并假设正方形ABCD 的边长为1,FH 的长为25(如图(3)),试求EG 的长度.6. 如图1,已知正方形ABCD ,将一个45度角∝的顶点放在D 点并绕D 点旋转,角的两边分别交AB 边和BC 边于点E 和F ,连接EF .求证:EF=AE+CF(1)小明是这样思考的:延长BC 到G ,使得CG=AE ,连接DG ,先证△DAE ≌△DCG ,再证△DEF ≌△DGF ,请你借助图2,按照小明的思路,写出完整的证明思路.(2)刘老师看到这条题目后,问了小明两个小问题:①如果正方形的边长和△BEF 的面积都等于6,求EF 的长②将角∝绕D 点继续旋转,使得角∝的两边分别和AB 边延长线、BC 边的延长线交于E 和F ,如图3所示,猜想EF 、AE 、CF 三线段之间的数量关系并给予证明.请你帮忙解决.7. 请阅读下列材料:问题:如图,在正方形ABCD 和平行四边形BEFG 中,点A ,B ,E 在同一条直线上,P 是线段DF 的中点,连接PG ,PC .探究:当PG 与PC 的夹角为多少度时,平行四边形BEFG 是正方形?小聪同学的思路是:首先可以说明四边形BEFG 是矩形;然后延长GP 交DC 于点H ,构造全等三角形,经过推理可以探索出问题的答案.请你参考小聪同学的思路,探究并解决这个问题.(1)求证:四边形BEFG 是矩形;(2)PG 与PC 的夹角为 度时,四边形BEFG 是正方形.理由:8.阅读下面材料:小阳遇到这样一个问题:如图(1),O 为等边△ABC 内部一点,且OA :OB :OC=1:2:3,求∠AOB 的度数.小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△ACO 绕点A 逆时针旋转60°,使点C 与点B 重合,得到△ABO ′,连接OO ′.则△AOO ′是等边三角形,故OO ′=OA ,至此,通过旋转将线段OA 、OB 、OC 转移到同一个三角形OO ′B 中.(1)请你回答:∠AOB= °.(2)参考小阳思考问题的方法,解决下列问题:已知:如图(3),四边形ABCD 中,AB=AD ,∠DAB=60°,∠DCB=30°,AC=5,CD=4.求四边形ABCD 的面积.9. 问题背景(1)如图1,△ABC 中,DE ∥BC 分别交AB ,AC 于D ,E 两点,过点E 作EF ∥AB 交BC 于点F .请按图示数据填空:四边形DBFE 的面积S = ,△EFC 的面积1S = ,△ADE 的面积2S = . 探究发现(2)在(1)中,若BF a =,FC b =,DE 与BC 间的距离为h .请证明2124S S S =. 拓展迁移(3)如图2,□DEFG 的四个顶点在△ABC 的三边上,若△ADG 、△DBE 、△GFC 的面积分别为2、5、3,试利用..(2.)中的结论....求△ABC10. 正方形ABCD 中,点O 是对角线DB 的中点,点P 是DB BC 于E ,PF ⊥DC 于F. (1)当点P 与点O 重合时(如图①),猜测AP 与EF (2)当点P 在线段DB 上 (不与点D 、O 、B 重合)时(如图②)过程;若不成立,请说明理由;(3)当点P 在DB 的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论. B C D G F E 图2 A 图1。
初中数学专题:阅读理解题

专题训练二:阅读理解题一、填空题(1、2每小题5分,3小题7分,4小题3分,5小题6分,6小题4分,共30分)1.(龙岩市)阅读下面材料并完成填空.你能比较两个数20012002和20022001的大小吗?为了解决这个问题,先把问题一般化,即比较n n +1和(n +1)n 的大小(n ≥1的整数).然后,从分析n =1,n =2,n =3,……,这些简单情形入手,从中发现规律,经过归纳,猜想出结论.(1)通过计算,比较下列①~③各组两个数的大小(在横线上填“>”“<”或“=”) ①12______21; ②23______32; ③34______43; ④45>54; ⑤56>65; ⑥67>76; ⑦78>87;…(2)从第(1)小题的结果经过归纳,可以猜想出n n +1和(n +1)n 的大小关系是:_________. (3)根据上面归纳猜想得到的一般结论,可以得到20012002______20022001(填“>”“<”或“=”).2.阅读下列课文中某一例题及解答过程的摘录:“已知方程x 2-2x -1=0,求一个一元二次方程,使它的根是原方程的各根的立方.” 解:设方程x 2-2x -1=0的两根是x 1、x 2,那么所求的方程的两根是x 13、x 23.x 13²x 23=(x 1x 2)3=(-1)3=-1. 请你回答:(1)得到“第一步”式子的根据是______.(2)得到“第二步”式子所使用的具体公式是______.(3)得到“第三步”的中括号内的式子所使用的具体方法是______. (4)作“第三步”变形的具体目的是______. (5)原题最后求得的方程是______.3.先阅读下列(1)题然后解答(2)、(3)题: (1)用分组分解法分解多项式:mx +nx +my +ny =(mx +nx )+(my +ny ),组内公因式分别为x 、y ,组间公因式为m +n ,最后分解结果为:(m +n )(x +y ) (2)也可以这样分解:mx +nx +my +ny =(______)+(______),组内公因式分别为______,组间公因式为______,最后分解结果为:______.(3)上述两种分组的目的都是______,分组分解的另一个目的是分组后能运用公式法分解.请你设计一个关于字母x 、y 的二次四项式因式分解,要求要用到分组分解法和完全平方公式:_________.4.阅读下面一题的解题过程,请判断是否正确,若不正确,请写出正确的解答. 已知a 为实数,化简aaa 13---. 解:a a a aa -=---13-a ²a a-1=(a -1)²a - 答:____________5.阅读下列证明过程:已知,如图1四边形ABCD 中,AB =DC ,AC =BD ,AD ≠BC ,求证:四边形ABCD 是等腰梯形.图1读后完成下列各小题.(1)证明过程是否有错误?如有,错在第几步上,答:_________. (2)作DE ∥AB 的目的是:__________.(3)有人认为第9步是多余的,你的看法呢?为什么?答:________. (4)判断四边形ABED 为平行四边形的依据是:_________. (5)判断四边形ABCD 是等腰梯形的依据是__________.(6)若题设中没有AD ≠BC ,那么四边形ABCD 一定是等腰梯形吗?为什么?答______.6.(2002年鄂州市)从A 、B 、C 3人中选取2人当代表有A 和B 、A 和C 、B 和C 3种不同的选法,抽象成数学模型是:从3个元素中选取2个元素的组合,记作1223C 23⨯⨯==3.一般地,从m 个元素中选取n 个元素的组合,记作12)2)(1()1()2)(1(C ⋅--+---=n n n n m m m m nm .根据以上分析,从6人中选取4人当代表的不同选法有______种.二、选择题(每小题5分,共10分) 7.(2002年扬州市)计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(1101)2表示二进制数,将它转换成十进制形式是1³23+1³22+0³21+1³20=13,那么将二进制(1111)2转换成十进制形式是数( ) A .8 B .15 C .20 D .308.(威海市)如果一个图形绕一个定点旋转一个角α (0°<α ≤180°),能够与原来的图形重合,那么这个图形就叫做旋转对称图形.例如,正三角形绕着它的中心旋转120°(如图2),能够与原来的正三角形重合,因而正三角形是旋转对称图形.图3是一个五叶风车的示意图,它也是旋转对称图形(α =72°).图2图3显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.下面四个图形中,是旋转对称图形的有()A.①②③B.②③④C.①③④D.①②③④三、解答题(每小题10分,共60分)9.请先阅读下列文字,然后解答:初中数学课本有这样一段叙述:“要比较a与b的大小,可先求a与b的差,再看这个差是正数、负数还是零.”由此可见,要判断两个代数式值的大小,只要考虑它们的差就可以.问题:甲乙两人两次同时在同一粮店购买粮食(假设两次购买粮食的单价不相同),甲每次购买粮食100千克,乙每次购买粮用去100元.(1)假设x、y分别表示两次购粮的单价(单位:元/千克).试用含x、y的代数式表示:甲两次购买粮食共需付款______元;乙两次共购买______千克的粮食.若甲两次购粮的平均单价为每千克θ 1元,乙两次购粮的平均单价为每千克θ 2元,则θ 1=______,θ 2=______.(2)若规定:谁两次购粮的平均单价低,谁的购粮方式就更合算,请你判断甲、乙两人的购粮方式哪一个更合算些,并说明理由.10.阅读下面的短文,并解答下列问题:我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.如图4,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比(a∶b).图4设S 甲、S 乙分别表示这两个正方体的表面积,则222)(66b a b a S S ==乙甲 又设V 甲、V 乙分别表示这两个正方体的体积,则333)(bab a V V ==乙甲 (1)下列几何体中,一定属于相似体的是( )A .两个球体B .两个锥体C .两个圆柱体D .两个长方体(2)请归纳出相似体的三条主要性质:①相似体的一切对应线段(或弧)长的比等于______;②相似体表面积的比等于______;③相似体体积比等于______.(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了初三时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)11.(大连市)阅读材料,解答问题. 阅读材料:当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y =x 2-2mx +m 2+2m -1,① 有y =(x -m )2+2m -1,②∴ 抛物线的顶点坐标为(m ,2m -1).当m 的值变化时,x 、y 的值也随之变化.因而y 值也随x 值的变化而变化. 将③代入④,得y =2x -1.⑤可见,不论m 取任何实数,抛物线顶点的纵坐标y 和横坐标x 都满足关系式:y =2x -1. (1)在上述过程中,由①到②所用的数学方法是______,其中运用了______公式.由③、④得到⑤所用的数学方法是______;(2)根据阅读材料提供的方法,确定抛物线y =x 2-2mx +2m 2-3m +1顶点的纵坐标y 与横坐标x 之间的关系式.12.(威海市)某村实行合作医疗制度,村委会规定: (一)每位村民年初缴纳合作医疗基金a 元;设一位村民当年治病花费的医疗费为x 元,他个人实际承担的医疗费用(包括医疗费中个人承担的部分和缴纳的合作医疗基金)为y 元.(1)当0≤x ≤b 时,y =a ;当b <x ≤5000时,y =______(用含有a 、b 、c 、x 的式子表示). (2)下表是该村4位村民2001年治病花费的医疗费和个人实际承担的费用.根据表格中的数据,求a 、b 、c ,并且求当b <x ≤5000时,函数y 的解析式.(3)村民个人一年最多承担医疗费用多少元?13.(昆明市)已知矩形ABCD 的面积为36,以此矩形的对称轴为坐标轴建立平面直角坐标系,设点A 的坐标为(x ,y ),其中x >0,y >0.(1)求出y 与x 之间的函数关系式,求出自变量x 的取值范围;(2)用x 、y 表示矩形ABCD 的外接圆的面积S ,并用下列方法,解答后面的问题:方法:∵ a 2+222)(a k a a k -=+2k (k 为常数且k >0,a ≠0),(a -ak )2≥0,∴ a 2+22a k ≥2k . ∴ 当a -ak =0,即a =±k 时,a 2+22a k 取得最小值2k .问题:当点A 在何位置时,矩形ABCD 的外接圆面积S 最小?并求出S 的最小值;(3)如果直线y =mx +2(m <0)与x 轴交于点P ,与y 轴交于点Q ,那么是否存在这样的实数m ,使得点P 、Q 与(2)中求出的点A 构成△P AQ 的面积是矩形ABCD 面积的61?若存在,请求出m 的值;若不存在,请说明理由.14. A 、B 两点被池塘隔开,在AB 外选一点C ,连结AC 和BC ,并分别找出AC 和BC 的中点M 、N ,如果测得MN =20 m ,那么AB =2³20 m =40 m .图5 图6 图7(1)也可由图6所求,用相似三角形知识来解,请根据题意填空:延长AC 到D ,使CD=21AC ,延长BC 到E ,使CE =______,则由相似三角形得,AB =______. (2)还可由三角形全等的知识来设计测量方案,求出AB 的长,请用上面类似的步骤,在图7中画出图形并叙述你的测量方案.15.(深圳市)阅读材料,解答问题.命题:如图8在锐角△DBC 中,BC =a ,CA =b ,AB =c ,△ABC 的外接圆半径为R .则CcB b A a si n si n si n ===2R .图8证明:连结CO 并延长交⊙O 于点D ,连结DB ,则∠D =∠A . ∵ CD 为⊙O 的直径,∴ ∠DBC =90°. 在Rt △DBC 中,∵ sin D =R a DC BC 2=,∴ sin A =R a 2,即A asin =2R . 同理B b sin =2R ,C csin =2R .∴ R CcB b A a 2sin sin sin ===.请你阅读前面所给的命题及其证明后,完成下面的(1)、(2)两小题. (1)前面的阅读材料中略去了“B b sin =2R 和C c sin =2R ”的证明过程,请你把“Bbsin =2R ”的证明过程补写出来.(2)直接用前面阅读材料中命题的结论解题.已知:如图10,在锐角△ABC中,BC=3,CA=2,∠A=60°,求△ABC的外接圆半径R及∠C.图9 图1016.(咸宁市)已知下面各图形被一条直线将其面积平分:略解由图11可知经过圆的圆心的直线或经过平行四边形的中心的直线平分其面积,据其在图12中作连接其中心的直线即可.(图略)图11观察以上图形,用所得的结论或启示对下面每个图形作一条直线将其阴影部分的面积平分.(不写画法,不证明,保留作图痕迹).图12专题训练二:参考答案 一、1.(1)< < > (2)n n +1<(n +1)n (n ≤2) n n +1>(n +1)n (n ≥3) (3)>2.(1)一元二次方程根与系数的关系; (2)立方和公式; (3)配方法; (4)使用“第一步”所得的结果; (5)y 2-14y -1=03.(2)mx +my nx +ny m 、n (x +y ) (x +y )(m +n );(3)提取公因式;如1-x 2+2xy -y 2=1-(x 2-2xy +y 2)=1-(x -y )2=(1+x -y )(1-x +y ) 4.∵ a <0, ∴a a a aa --=---13+a ²a1²a a a a a a --=-+--=-)1(. 5.(1)没有错误; (2)为了证明AD ∥BC ; (3)并不多余; (4)一组对边平行且相等的四边形是平行四边形; (5)梯形及等腰梯形的定义; (6)不一定,因为当AD =BC 时,四边形ABCD 是矩形. 6.15二、7.B 8.C 三、9.(1)100x +100y ;y x 100100+;θ 1=2yx +,θ 2=y x xy +2; (2)∵ θ 1-θ 2=)(2)(222y x y x y x xy y x +-=+-+,∵ x >0,y >0,且x ≠y , ∴ θ 1-θ 2>0.∴ θ 1>θ 2. ∴ 甲的购粮方式更合算. 10.(1)A ;(2)①相似比,②相似比的平方,③相似比的立方;(3)设他的体重为x 千克,根据题意得3)1.165.1(18=x 解得x =60.75(千克) 答:他的体重是60.75千克.11.(1)配方法、完全平方法、消元法(2)y =x 2-2mx +2m 2-3m +1=x 2-2mx +m 2+m 2-3m +1=(x -m )2+m 2-3m +1∴ 该抛物线顶点坐标为(m ,m 2-3m +1)⎩⎨⎧+-==132m m y m x 即将①代入②,得y =x 2-3x +1.∴ 所给抛物线顶点的纵坐标y 与横坐标x 的关系式为y =x 2-3x +1. 12.(1)y =(x -b )c %+a(2)甲、乙两人花费的医疗费不同,但实际承担的费用相同(都是30元),说明他们两人花费的医疗费都不超过b 元,因此,他们实际承担的费用就是缴纳的合作医疗基金,即a =30.丙、丁两人实际承担的医疗费用超过了30元,说明他们一年的医疗费超过了b 元,但不足5000元.所以⎩⎨⎧=+-=+-8030%)150(5030%)90(c b c b ,解这个方程组,得b =50,c =50,∴ 当b<x ≤5000时,y =(x -50)²50%+30.即y =21x +5. (3)将x =5000代入y 的解析式,得y =5000³0.5+5=2505. ∴ 村民个人一年最多承担医疗费2505元.13.建立平面直角坐标系,(1)根据题意可知:xy =9,∴ y 与x 之间的函数关系式是y=x9,自变量x 的取值范围是x >0. (2)S =π(x 2+y 2),∵ x 2+y 2=x 2+(x 9)2≥18,当且仅当x -x9=0,即x =3时,S 最小=18π.此时,y =x9=3,所以当点A 的坐标为(3,3)时,矩形的外接圆面积S 最小,S 的最小值为18π. (3)存在,如图,设AB 与y 轴相交于点E ,由已知得:A (3,3),Q (0,2),P (-m2,0),∴ S △P AQ =S 梯形APOE -S △AEQ -S △OPQ =21[(-m 2+3)³3-1³3-2³(-m 2)]=3-m1.∴ 3-m 1=61³36.解得:m =-31.14.(1)21BC 2ED(2)延长AC 至D ,使AC =CD ,延长BC 至E ,使BC =EC ,则△ABC ≌△DCE , ∴ AB =DE ,量出DE 即得AB .(图略)15.(1)连结AO 并延长交⊙O 于点E ,连结EC ,则∠E =∠B .∵ AE 为⊙O 直径,∴ ∠ECA =90°,在Rt △ECA 中,sin E =RbAE AC 2=, ∴ sin B =R b 2,∴ Bbsin =2R .(2)由命题结果得:︒=60sin 3sin A a =2R .∴ R =1,又∵ BB b sin 2sin ==2. ∴ sin B =22,∴ ∠B =45°, ∴ ∠C =180°-60°-45°=75°. 16.本题答案不唯一,下面给出一种作法:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学阅读理解题集
1、请你阅读下列计算,再回答所提出的问题:
()()()()()()()()()()()
()2331133111
313111133126
x x x
x A x x x x x B x x x x x x C x -----=-+----=-+-+-=---=--
(1)上面计算过程中,从哪一步开始出现错误?
(2)从B 到C 是否正确;(3)请你正确解答此题。
2、如图,AB 是⊙O 的直径,把AB 分成几条相等的线段,以每条线段为直径分别画小圆,设AB =a ,那么⊙O 的周长l a π=。
A ·
B A · B A · B
计算:(1)把AB 分成两条相等的线段,每个小圆的周长2l = 。
(2)把AB 分成三条相等的线段,每个小圆的周长3l = 。
(3)把AB 分成四条相等的线段,每个小圆的周长4l = 。
(4)把AB 分成n 条相等的线段,每个小圆的周长n l = 。
结论:把大圆的直径分成n 条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的 。
找出规律、计算推导出每个小圆面积与大圆面积的关系。
O O O
4、阅读材料,回答问题:
为解方程()()22215140x x ---+=,我们可以将2
1x -视为一个整体,然后设21x y -=,则()2
221x y -=,原方程化为 2540y y -+= (1) 解得 121,4y y ==
(1)当1y =
时,2211,2x x x -=∴=∴= (2)当4y =
时,2214,5x x x -=∴=∴=
∴原方程的解为
1234,2,5,5
x x x x =-解答问题:
(1)填空:在由原方程得到方程(1)的过程中,利用 法达到了降次的目的,体现了 的数学思想。
(2)解方程 4260x x --=
5、阅读下面材料:
在计算3+5+7+9+11+13+15+17+19+21时,我们发现,从第一个数开始,以后
的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的列数,除了直接相加外,我们还可以用公式()d n n na s 2
1-+=来计算它们的和,(公式中的n 表示数的个数,a 表示第一个数的值,d 表示这个相差的定值) 那么3+5+7+9+11+13+15+17+19+21=10×3+
()2211010⨯-=120。
用上面的知识解决下列问题:
为保护长江,减少水土流失,我市某县决定对原有的坡荒地进行退耕还林,从1995年
起在坡荒地上植树造林,以后每年又以比上一年多植相同面积的树木改造荒地,由于每年因自然灾害、树木成活率、人为因素的影响,都有相同数量的新坡荒地产生,下表为1995、1996、1997三年的坡荒地面积的植树的面积统计数据,假设坡荒地全部种上树后,不再为水土流失形成新的坡荒地,问到哪一年,可以将全县所有的坡荒地全部种上树木。
(2001年重庆市中考题)
5、①以下是一道题目及其解答过程:
已知:如图,从菱形ABCD 对角线的交点O 分别向各边引垂线,垂足分别是E 、F 、G 、H
求证:四边形EFGH 是矩形
证明:∵四边形ABCD 是菱形,∴AO =CO
又∵DO =DO ∴△AOD ≌△COD (1)
∵OH 、OG 分别是Rt △AOD 和Rt △COD 斜边上的高
∴OH =OG (2)
同理 OH =OE ,OE =OF ,则
OH =OE =OF =OG (3)
∴EG 与HF 相等且互相平分……………………………………(4) ∴四边形EFGH 是矩形
以上证明过程中
A 、(1)到(2)有错误
B 、(2)到(3)有错误
C 、(3)到(4)有错误
D 、没有错误
A H D
E
G
B F C
②阅读下题和分析过程,并按照要求进行证明
已知,四边形ABCD 中,AB =DC ,AC =BD ,AD ≠BC
求证:四边形ABCD 是等腰梯形
6、阅读下面的短文,并解答下列问题
我们把相似形的概念推广到空间,如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体。
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比():a b
假设:S 甲,S 乙分别表示 两个正方体的表面积 b ,则2
2266S a a S b b ⎛⎫== ⎪⎝⎭
甲乙 又设,V V 乙甲分别表示这两个正方体的体积,则 3
33V a a V b b ⎛⎫== ⎪⎝⎭
甲乙 (1)下列几何体中,一定属于相似体的是……………………………………( )
A 、两个球体
B 、两个圆锥体
C 、两个长方体
D 、两个圆柱体
(2)请你归纳出相似体的三条主要性质:
① 相似体的一切对应线段(或弧)长的比等于
② 相似体表面积的比等于
③ 相似体体积的比等于 。
O
(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到初三时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)
7、已知抛物线()222410y x m x m =-++-与x 轴交于A 、B 两点,C 是抛物线的顶点。
(1)用配方法求顶点C 的坐标(用含m 的代数式表示)
(2)若AB 的长为,求抛物线的解析式解法的部分步骤如下,补全解题过程,并简述步骤①的解题依据,步骤②的解题方法。
解:由(1)知,对称轴与x 轴交于点D ( ,0)
∵抛物线的对称性及AB =
∴AD =DB =A D x x -= ∵点A (),0A x 在抛物线()2y x h k =-+上
∴()20A x h k =-+……………………………………………………①
∵,C D h x x =-得A D x x -=
m 的方程
()20___;=+ …………………………………………………②
(3)将(2)中的条件“AB 的长为”改为“△ABC 为等边三角形”,用类似的方法求出此抛物线的解析式。
