平行四边形的面积_《平行四边形的面积》典型例题4
北师大版五年级数学上册典型例题系列之第四单元:平行四边形面积的实际应用专项练习(解析版)

五年级数学上册典型例题系列之第四单元:平行四边形面积的实际应用专项练习(解析版)1.一个平行四边形停车场,底是63m,对应的高是25m。
如果每个车位占地15m2,这个停车场一共可以停多少辆车?【答案】105辆【分析】根据平行四边形的面积=底×高,求出面积,再除以15平方米即可。
【详解】63×25÷15=1575÷15=105(辆)答:这个停车场一共可以停105辆车。
【点睛】熟练掌握平行四边形的面积公式,是解答此题的关键。
2.一块平行四边形的玫瑰园,底长32米,高长9米,每3平方米栽一棵玫瑰,可以栽多少棵玫瑰?【答案】96棵【分析】根据平行四边形的面积=底×高,求出面积,再除以3即可。
【详解】32×9÷3=288÷3=96(棵)答:可以栽96棵玫瑰。
【点睛】熟练掌握平行四边形的面积公式,是解答此题的关键。
3.一块街头广告牌的形状是平行四边形,底是12.5m,高是6.5m。
如果要给这块广告牌的一面刷上油漆,每平方米用油漆0.6kg,需要多少千克油漆?【分析】先根据平行四边形的面积=底×高,求出这个平行四边形的面积,再乘每平方米需要油漆的重量即可。
【详解】12.5×6.5×0.6=81.25×0.6=48.75(千克)答:需要48.75千克油漆。
【点睛】本题考查平行四边形面积公式的应用,关键是熟记公式。
4.一块广告牌的形状是平行四边形,底是12.5米,高是6.4米。
如果要涂饰这块广告牌(涂一面),每平方米用油漆0.6千克,共需要多少千克油漆?【答案】48千克【分析】先根据平行四边形的面积=底×高,求出这个平行四边形的面积,再乘每平方米需要油漆的质量即可。
【详解】12.5×6.4×0.6=80×0.6=48(千克)答:共需要48千克油漆。
【点睛】熟练掌握平行四边形的面积公式,属于基础知识,需牢牢记住。
平行四边形的面积_《平行四边形的面积》典型例题
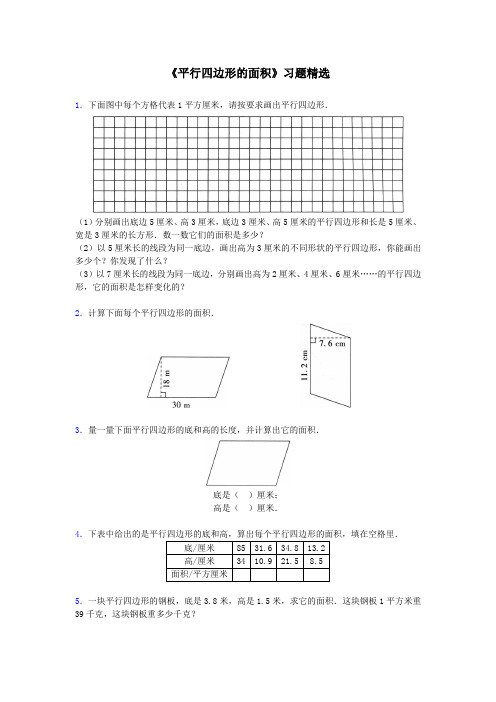
《平行四边形的面积》习题精选1.下面图中每个方格代表1平方厘米,请按要求画出平行四边形.(1)分别画出底边5厘米、高3厘米,底边3厘米、高5厘米的平行四边形和长是5厘米、宽是3厘米的长方形.数一数它们的面积是多少?(2)以5厘米长的线段为同一底边,画出高为3厘米的不同形状的平行四边形,你能画出多少个?你发现了什么?(3)以7厘米长的线段为同一底边,分别画出高为2厘米、4厘米、6厘米……的平行四边形,它的面积是怎样变化的?2.计算下面每个平行四边形的面积.3.量一量下面平行四边形的底和高的长度,并计算出它的面积.底是()厘米;高是()厘米.4.底/厘米85 31.6 34.8 13.2高/厘米34 10.9 21.5 8.5面积/平方厘米5.一块平行四边形的钢板,底是3.8米,高是1.5米,求它的面积.这块钢板1平方米重39千克,这块钢板重多少千克?6.一块平行四边形菜地,底是18.4米,高是9.2米.在这块地种茄子,每棵苗占地0.18平方米,这块地可种茄子多少棵?(得数保留整数)7.一块六边形水泥砖(如图),由三个面积相同的平行四边形组成.要铺300平方米地面大约需要多少块这样的水泥砖?参考答案1.(1)15平方厘米 15平方厘米 15平方厘米(2)无数个它们面积都相等(3)14平方厘米 28平方厘米 42平方厘米2.540m2 85.12cm23.略4.2890 344.44 748.2 112.25.5.7平方米 222.3千克6.169.28 ≈940棵7.≈2858块《平行四边形的面积》习题精选一、填空.1.4.5平方米=()平方分米 2400平方厘米=()平方分米2.一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米.3.一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米.4.一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重()千克.二、判断题.1.平行四边形的面积等于长方形面积.()2.一个平行四边形的底是5分米,高是20厘米,面积是100平方分米.()3.一个平行四边形面积是42平方米,高是6米,底是7米.()三、选择题.1.下面的长方形和平行四边形面积()a.相等b.不相等2.用木条钉成的长方形拉成一个平行四边形,它的高和面积()a.都比原来大b.都比原来小c.都与原来相等3.平行四边形的底扩大3倍,高缩小3倍,面积()a.扩大3倍b.缩小3倍c.不变d.不好判断四、评议.下面是四个平行四边形,小红认为它们的面积都是6平方厘米,你认为对吗?(单位:厘米)23323232五、已知下图中正方形的周长为36厘米,求平行四边形的面积.参考答案一、填空1.450 24 2.162 3.13 4.42.3二、判断题.1.(×) 2.(×) 3.(√)三、选择题.1.a 2.b 3.c四、评议.2332(√)(×)3232(√)(×)五、已知下图中正方形的周长为36厘米,求平行四边形的面积.36÷4=9(厘米) 9×9=81(平方厘米)《平行四边形的面积》典型例题例.求下面平行四边形的面积.分析:图中给出的两个已知条件并不是一组相对应的底和高,要根据平行四边形“对边相等”的特性可以得出和高(6厘米)相对应的底也是4厘米,利用平行四边形的面积公式可以求出它的面积.解:2464=⨯(平方厘米)答:这个平行四边形的面积是24平方厘米.《平行四边形的面积》典型例题例.在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?乙甲CB EFDA分析:平行四边形ABCD 和BCEF 是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等.这两个平行四边形都是以BC 为底,所以说这两个平行四边形的底也相等的.4厘米6厘米底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的.解答:一样大.《平行四边形的面积》典型例题例.如图,正方形BDEC 周长是24厘米,平行四边形ADEB 面积是多少平方厘米?分析:从图上可以看出,平行四边形的底和高,都与正方形的边长相等.而正方形的边长是 (24÷4)厘米,所以平行四边形ADEB 的面积就是(24÷4)×(24÷4)=6×6=36(平方厘米)答:平行四边形ADEB 面积是36平方厘米.《平行四边形的面积》典型例题例.求下面平行四边形的周长(单位:分米)1267分析:已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是84712=⨯(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用14684=÷(分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长.解:5221412=⨯+)((分米)答:这个平行四边形的周长是52分米.《平行四边形的面积》典型例题例.一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?分析:要求原平行四边形的面积,必须知道原平行四边形的底和高.根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高.根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底.解:12)14()26(=÷⨯÷(平方厘米)答:原平行四边形的面积是12平方厘米.《平行四边形的面积》典型例题例.在一块长80米,宽35米的长方形地上,修了两条宽分别为3米和2米的通道,其余的地方铺上草皮(如图).问:应铺多少平方米的草皮?分析:很显然,铺草皮的面积等于长方形的面积减去两条通道的面积,问题的关键是这两条 通道是什么图形?因为两条通道都是四边形,且两组对边分别平行,所以两条通道都是平行四边形.要求出这两个平行四边形的面积,底边分别是3米和2米,高是多少呢?这恐怕是个难点,你发现了吗?它们的高就是长方形的宽35米,问题得解.解:80×35-(3×35+2×35) =2800-175=2625(平方米)答:应铺2625平方米的草皮.《平行四边形的面积》典型例题例.如图,平行四边形的面积是150平方米,它的阴影部分的面积是多少平方米?分析:平行四边形的面积为已知,底边长已知,所以平行四边形的高可求出,由观察知阴影部分是一个直角梯形,这个直角梯形的上底为15米,下底为15-4=11(米),高就是平行四边形的高,问题得解.解:[15+(15-4)]×(150÷15)÷2=26×10÷2=130(平方米)答:阴影部分的面积是130平方米.。
平行四边形面积的计算练习题及答案

平行四边形面积的计算练习题及答案五水产养殖场--多边形的面积第1课时平行四边形面积的计算不夯实基础,难建成高楼。
1、下面图形是平行四边形的是( )。
2. 画出下面每个平行四边形底边上的高。
3. 填一填。
⑴两组对边分别( )的四边形叫做( )。
⑵我们用( )的方法把平行四边形转化成长方形,长方形的面积和原来平行四边形的面积( )。
⑶平行四边形的面积=( ),用字母表示是 ( )。
4. 判一判。
⑴两组对边分别平行的四边形一定是平行四边形。
( )⑵平行四边形只有一条高。
( )⑶等底等高的两个平行四边形的面积相等。
( )5. 一块平行四边形花圃的底是26米,高是14米,这块花圃的面积是多少平方米重点难点,一网打尽。
6. 测量下面平行四边形的底和相对应的高,并计算它们的面积。
7. 油漆如下图所示的广告牌,如果每平方米的成本是5元,那么一共需要多少钱2m3.5m8. 一个面积是384平方米的平行四边形苗圃,底是24米,高是多少米9. 一个平行四边形的停车场,底是63米,高是25米。
平均每辆车占地15平方米,这个停车场可停车多少辆举一反三,应用创新,方能一显身手!10. 在下面的方格纸上画两个不同形状的平行四边形,使它们的面积与图中平行四边形的面积相等。
五水产养殖场--多边形的面积第1课时1. ①③④2. 略3. ⑴平行平行四边形⑵转化相等⑶底×高S=ah4. ⑴√⑵×⑶√5. 26×14=364(平方米)6. 略7. 5××2)=35(元) 8. 384÷24=16(米)9. 63×25÷15=105(辆) 10. 略。
《平行四边形的面积》教案(优秀6篇)

《平行四边形的面积》教案(优秀6篇)数学《平行四边形的面积》教案篇一教学目标:1.使学生在理解的基础上掌握平行四边形面积的计算公式,并会运用公式正确地计算平行四边形的面积.2.通过操作、观察、比较,发展学生的空间观念,培养学生运用转化的思考方法解决问题的能力和逻辑思维能力.3.对学生进行辩诈唯物主义观点的启蒙教育.教学重点:理解公式并正确计算平行四边形的面积.教学难点:理解平行四边形面积公式的推导过程.学具准备:每个学生准备一个平行四边形。
教学过程:1、什么是面积?2、请同学翻书到80页,请观察这两个花坛,哪一个大呢?假如这块长方形花坛的长是3米,宽是2米,怎样计算它的面积呢?二、导入新课根据长方形的面积=长某宽(板书),得出长方形花坛的面积是6平方米,平行四边形面积我们还没有学过,所以不能计算出平行四边形花坛的面积,这节课我们就学习平行四边形面积计算。
三、讲授新课(一)、数方格法用展示台出示方格图1、这是什么图形?(长方形)如果每个小方格代表1平方厘米,这个长方形的面积是多少?(18平方厘米)2、这是什么图形?(平行四边形)每一个方格表示1平方厘米,自己数一数是多少平方厘米?请同学认真观察一下,平行四边形在方格纸上出现了不满一格的,怎么数呢?可以都按半格计算。
然后指名说出数得的结果,并说一说是怎样数的。
2、请同学看方格图填80页最下方的表,填完后请学生回答发现了什么?:如果长方形的长和宽分别等于平行四边形的底和高,则它们的面积相等。
(二)引入割补法以后我们遇到平行四边形的地、平行四边形的零件等等平行四边形的东西,都像这样数方格的方法来计算平行四边形的面积方不方便?那么我们就要找到一种方便、又有规律的计算平行四边形面积的方法。
(三)割补法1、这是一个平行四边形,请同学们把自己准备的平行四边形沿着所作的高剪下来,自己拼一下,看可以拼成我们以前学过的什么图形?2、然后指名到前边演示。
3、教师示范平行四边形转化成长方形的过程。
小学五年级数学平行四边形面积的计算典型例题

平行四边形面积的计算典型例题五年级数学教案典型例题一1.求下面平行四边形的面积。
6厘米4厘米分析:图中给出的两个已知条件并不是一组相对应的底和高,要根据平行四边形“对边相等”的特性可以得出和高(6厘米)相对应的底也是4厘米,利用平行四边形的面积公式可以求出它的面积。
解答: <!--[endif]-->(平方厘米)答:这个平行四边形的面积是24平方厘米。
2.求下面平行四边形的周长(单位:分米)分析:已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用 9分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长。
解答:(分米)。
答:这个平行四边形的周长是52分米。
3、在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?分析与解答:平行四边形abcd和bcef是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等。
这两个平行四边形都是以bc为底,所以说这两个平行四边形的底也相等的,底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的。
4、一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?分析:要求原平行四边形的面积,必须知道原平行四边形的底和高。
根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高。
根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底。
平行四边形的面积练习题
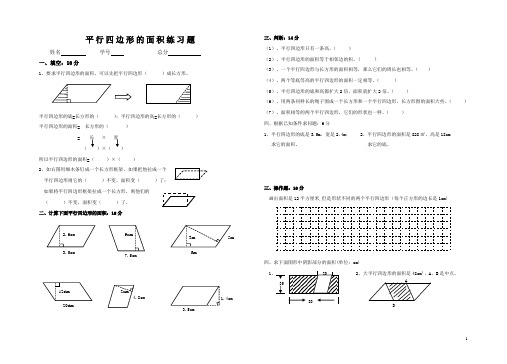
平行四边形的面积练习题姓名 学号 总分 一、填空:10分1、要求平行四边形的面积,可以先把平行四边形( )成长方形。
平行四边形的底=长方形的( );平行四边形的高=长方形的( ) 平行四边形的面积= 长方形的( ) =长 ×宽( )×( ) 所以平行四边形的面积=( )×( )2、如右图用细木条钉成一个长方形框架,如果把他拉成一个 平行四边形则它的( )不变,面积变( )了; 如果将平行四边形框架拉成一个长方形,则他们的 ( )不变,面积变( )了。
二、计算下面平行四边形的面积:18分1.4cm三、判断:14分(1)、平行四边形只有一条高。
( )(2)、平行四边形的面积等于相邻边的积。
( )(3)、一个平行四边形与长方形的面积相等,那么它们的周长也相等。
( ) (4)、两个等底等高的平行四边形的面积一定相等。
( ) (5)、平行四边形的底和高都扩大2倍,面积就扩大2倍。
( )(6)、用两条同样长的绳子围成一个长方形和一个平行四边形,长方形围的面积大些。
( ) (7)、面积相等的两个平行四边形,它们的形状也一样。
( ) 四、根据已知条件求问题:6分1、平行四边形的底是3.5m ,宽是2.4m ;2、平行四边形的面积是828㎡,高是18cm 求它的面积。
求它的底。
三、操作题:10分画出面积是12平方厘米,但是形状不同的两个平行四边形(每个正方形的边长是1cm)四、求下面图形中阴影部分的面积(单位:cm)1802、大平行四边形的面积是48cm ²,A 、B 是中点。
A2cm20dm4.8cm 12dm 3m 2.6cm 9cm 5m3.5cm 7.5cm 6m 3.5cmB四、解决问题:40分1、一块平行四边形的花圃,如下图,如果每平方米的花可以买9.5元。
这块花圃的花能卖多少元?2、一块平行四边形的菜地,底是4.8m ,高是15m 。
如果每平米收蔬菜23kg ,这块地一共 可以收蔬菜多少千克?3、在下图中,A 是BC 的中点,阴影部分的面积是5.6㎡。
完整的两课时平行四边形的面积及练习教案

学习必备欢迎下载《平行四边形的面积》教学设计教学目标:1、通过观察、探索,使学生理解并掌握平行四边形的面积计算公式,会利用公式解决有关的简单生活问题。
2、使学生亲身经历和体会平行四边形面积公式的推导过程,并学会运用观察、比较、割补、验证、感知以及转化、迁移、变换的数学思想方法,从而进一步发展学生的空间观念。
3、在猜测、探索面积计算公式的过程中,体验数学的应用价值以及数学与生活的紧密联系。
4、熟练运用平行四边形的面积公式计算平行四边形的面积,解决相关的实际问题。
5、能根据底、高、面积三个量中间的任意两个量,用算数方法或方程计算第三个量。
6、通过猜测、验证、比较,发现平行四边形的面积跟底和高的直接关系。
7、体会数学的应用价值以及数学与生活的紧密联系。
教学重点:1、学生亲身经历和感受平行四边形面积计算公式的推导过程,理解并掌握平行四边形的面积计算公式。
2、运用所学知识解决有关平行四边形面积的应用题。
教学难点:1、观察拼出来的长方形和原来的平行四边形的面积之间的区别与联系。
2、理解平行四边形面积面积计算公式中底和高的对应关系。
3、逆用平行四边形面积的计算公式。
教学时数:2课时教学准备:多媒体课件、学生学具、答题纸、方格纸、剪刀、板尺、平行四边形、长方形。
《平行四边形的面积》第一课时教学设计教学目标:1、通过观察、探索,使学生理解并掌握平行四边形的面积计算公式,会利用公式解决有关的简单生活问题。
2、使学生亲身经历和体会平行四边形面积公式的推导过程,并学会运用观察、学习必备欢迎下载比较、割补、验证、感知以及转化、迁移、变换的数学思想方法,从而进一步发展学生的空间观念。
3、在猜测、探索面积计算公式的过程中,体验数学的应用价值以及数学与生活的紧密联系。
教学重点:学生亲身经历和感受平行四边形面积计算公式的推导过程,理解并掌握平行四边形的面积计算公式。
教学难点:1、观察拼出来的长方形和原来的平行四边形的面积之间的区别与联系。
《平行四边形的面积》练习题

《平行四边形的面积》练习题一、填空。
1.()的四边形叫做平行四边形。
2.平行四边形有()条边,()个角,它有()的特性,在实践中有广泛的应用。
3.长方形和正方形的两组对边也都分别(),它们是特殊的()。
4.平行四边形一组对边之间能作()条高。
5.我们可以用()的方法,把平行四边形转化成()来计算它的面积。
6.一个平行四边形的底长15厘米,高8厘米,它的面积是()平方厘米。
7.一块平行四边形菜地的面积是54平方米,它的高是6米,底边长()米。
二、判断题。
1.长方体和正方体都有6个面,12条棱,8个顶点。
()2.长方体的6个面不可能有正方形。
()3.长方体的12条棱中,长、宽、高各有4条。
()4.正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
()5.长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
()6.一个长方体长12厘米,宽8厘米,高7厘米,把它切成一个尽可能大的正方体,这个正方体的棱长是8厘米。
()三、选择题。
1.下列物体中,形状不是长方体的是()。
①火柴盒②红砖③茶杯④木箱2.长方体的12条棱中,高有()条。
①4 ②6 ③8 ④123.下列三个图形中,能拼成正方体的是()。
①②4.把棱长3分米的正方体切成两个相等的长方体,增加的两个面的总面积是()平方分米。
①18 ②9 ③36 ④以上答案都不对四、应用题。
1.一块平行四边形菜地,底长63.4米,高31.5米,这块地的面积是多少平方米?2.有一平行四边形瓜地,底长43米,高28米,如果每平方米栽瓜秧9棵,这块地可栽瓜秧多少棵?3.有一块平行四边形钢板,底长5米,高3.6米,如果这种钢板1平方米重39千克,这块钢板重多少千克?4.一块平行四边形玉米地,底长30米,高24米,共收玉米756千克,平均每平方米收玉米多少千克?5.已知一个平行四边形的面积是227.5平方分米,它的底长18.2分米,它的高比底少多少分米?6. 如图,平行四边形的面积是150平方米,它的阴影部分的面积是多少平方米?参考答案。
