武汉科技大学机械原理习题参考答案
机械原理习题及答案
第1章平面机构的结构分析1.1解释下列概念1.运动副；2.机构自由度；3.机构运动简图；4.机构结构分析；5.高副低代。
1.2验算下列机构能否运动，如果能运动，看运动是否具有确定性，并给出具有确定运动的修改办法。
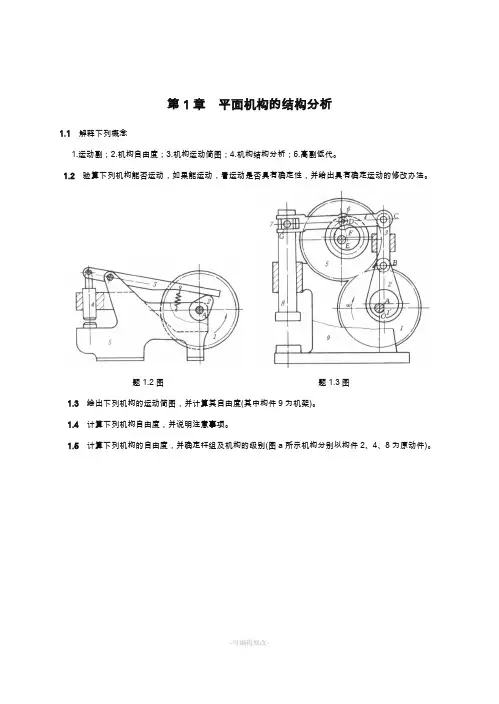
题1.2图题1.3图1.3 绘出下列机构的运动简图，并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度，并说明注意事项。
1.5计算下列机构的自由度，并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中，已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE =120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中，已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度（用相对运动图解法）。
题2.2图题2.3图2.4 在图示机构中，已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ，角加速度α1=0，试求机构在该位置时构件5的速度和加速度，以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
（1）在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
（2）以给出的速度和加速度矢量为已知条件，用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
(完整word版)机械原理习题 (附答案)(word文档良心出品)
第二章一、单项选择题：1．两构件组成运动副的必备条件是。
A．直接接触且具有相对运动；B．直接接触但无相对运动；C．不接触但有相对运动；D．不接触也无相对运动。
2．当机构的原动件数目小于或大于其自由度数时，该机构将确定的运动。
A．有；B．没有；C．不一定3．在机构中，某些不影响机构运动传递的重复部分所带入的约束为。
A．虚约束；B．局部自由度；C．复合铰链4．用一个平面低副联二个做平面运动的构件所形成的运动链共有个自由度。
A．3；B．4；C．5；D．65．杆组是自由度等于的运动链。
A．0；B．1；C．原动件数6．平面运动副所提供的约束为A．1；B．2；C．3；D．1或27．某机构为Ⅲ级机构，那么该机构应满足的必要充分条件是。
A．含有一个原动件组；B．至少含有一个基本杆组；C．至少含有一个Ⅱ级杆组；D．至少含有一个Ⅲ级杆组。
8．机构中只有一个。
A．闭式运动链；B．原动件；C．从动件；D．机架。
9．要使机构具有确定的相对运动，其条件是。
A．机构的自由度等于1；B．机构的自由度数比原动件数多1；C．机构的自由度数等于原动件数二、填空题：1．平面运动副的最大约束数为_____，最小约束数为______。
2．平面机构中若引入一个高副将带入_______个约束，而引入一个低副将带入_____个约束。
3．两个做平面平行运动的构件之间为_______接触的运动副称为低副，它有_______个约束；而为_______接触的运动副为高副，它有_______个约束。
4．在平面机构中，具有两个约束的运动副是_______副或_______副；具有一个约束的运动副是_______副。
5．组成机构的要素是________和________；构件是机构中的_____单元体。
6．在平面机构中，一个运动副引入的约束数的变化范围是_______。
7．机构具有确定运动的条件是____________________________________________。
(完整版)机械原理课后全部习题答案
机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征？机器通常由哪三部分组成？各部分的功能是什么？2）、机器与机构有什么异同点？3）、什么叫构件？什么叫零件？什么叫通用零件和专用零件？试各举二个实例。
4）、设计机器时应满足哪些基本要求？试选取一台机器，分析设计时应满足的基本要求。
2、填空题1)、机器或机构，都是由组合而成的。
2）、机器或机构的之间，具有确定的相对运动。
3）、机器可以用来人的劳动，完成有用的。
4）、组成机构、并且相互间能作的物体，叫做构件。
5）、从运动的角度看，机构的主要功用在于运动或运动的形式。
6）、构件是机器的单元。
零件是机器的单元。
7）、机器的工作部分须完成机器的动作，且处于整个传动的。
8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。
3、判断题1)、构件都是可动的。
（）2）、机器的传动部分都是机构。
（）3）、互相之间能作相对运动的物件是构件。
（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。
（）5）、机构的作用，只是传递或转换运动的形式。
（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。
（）7）、机构中的主动件和被动件，都是构件。
（）2 填空题答案1）、构件2）、构件3）、代替机械功4）、相对运动5）、传递转换6）、运动制造7）、预定终端8）、中间环节9）、确定有用构件3判断题答案1）、√2）、√3）、√4）、√5）、×6）、√7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
机械原理课后习题答案
机械原理课后习题答案1. 两个质量分别为m1和m2的物体，它们分别靠在光滑水平面上的两个弹簧上，两个弹簧的弹性系数分别为k1和k2。
求当两个物体分别受到的外力分别为F1和F2时，两个物体的加速度分别是多少？答，根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。
根据这个公式，可以得出两个物体的加速度分别为a1=F1/m1，a2=F2/m2。
2. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。
求当物体受到外力F时，物体的加速度是多少？答，同样根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。
根据这个公式，可以得出物体的加速度为a=F/m。
3. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。
求当物体受到外力F时，弹簧的位移是多少？答，根据胡克定律，弹簧的位移与受到的外力成正比，即F=kx，其中x为弹簧的位移。
解出x=F/k，即弹簧的位移与外力成反比。
4. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。
求当物体受到外力F时，弹簧的振动周期是多少？答，根据弹簧的振动周期公式T=2π√(m/k)，可以得出弹簧的振动周期与物体的质量和弹簧的弹性系数有关，与受到的外力无关。
5. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。
求当物体受到外力F时，弹簧的振幅是多少？答，根据弹簧振动的公式x=Acos(ωt+φ)，可以得出弹簧的振幅与受到的外力无关，只与弹簧的弹性系数和物体的质量有关。
求当物体受到外力F时，弹簧的振动频率是多少？答，根据弹簧振动的公式f=1/2π√(k/m)，可以得出弹簧的振动频率与受到的外力无关，只与弹簧的弹性系数和物体的质量有关。
7. 一个半径为r的圆盘，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。
求当圆盘受到外力F时，圆盘的加速度是多少？答，根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。
机械原理课后习题答案
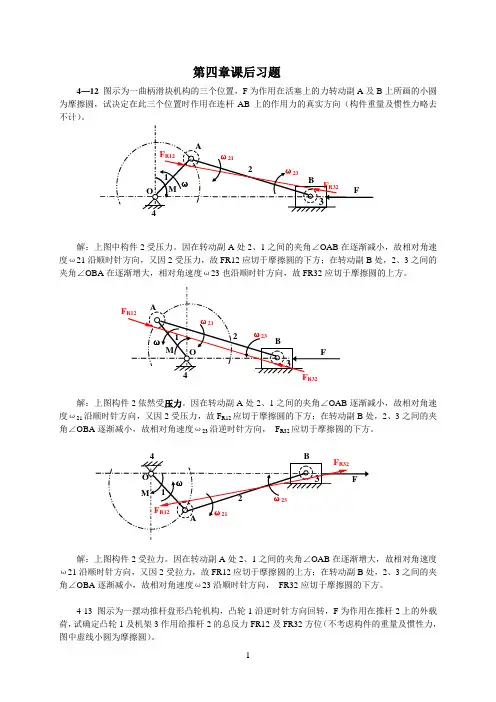
第四章课后习题4—12图示为一曲柄滑块机构的三个位置，F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆，试决定在此三个位置时作用在连杆AB上的作用力的真实方向（构件重量及惯性力略去不计）。
解：上图中构件2受压力。
因在转动副A处2、1之间的夹角∠OAB在逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故FR12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA在逐渐增大，相对角速度ω23也沿顺时针方向，故FR32应切于摩擦圆的上方。
R32解：上图构件2依然受压力。
因在转动副A处2、1之间的夹角∠OAB逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故F R12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿逆时针方向，F R32应切于摩擦圆的下方。
解：上图构件2受拉力。
因在转动副A处2、1之间的夹角∠OAB在逐渐增大，故相对角速度ω21沿顺时针方向，又因2受拉力，故FR12应切于摩擦圆的上方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿顺时针方向，FR32应切于摩擦圆的下方。
4-13 图示为一摆动推杆盘形凸轮机构，凸轮1沿逆时针方向回转，F为作用在推杆2上的外载荷，试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位（不考虑构件的重量及惯性力，解：经受力分析，FR12的方向如上图所示。
在FR12的作用下，2相对于3顺时针转动，故FR32应切于摩擦圆的左侧。
补充题1 如图所示，楔块机构中，已知γ＝β＝60°，Q ＝1000N 格接触面摩擦系数f ＝0.15，如Q 为有效阻力，试求所需的驱动力F 。
解:对机构进行受力分析,并作出力三角形如图。
对楔块1，R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=））o o ① 对楔块2，同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=））o o ②sin(602sin(602F Q ϕϕ+=⋅-））o o且有2112R R F F = ，8.53arctgf ϕ＝＝o ③联立以上三式，求解得F ＝1430.65N2 如图示斜面机构，已知：f （滑块1、2与导槽3相互之间摩擦系数）、λ（滑块1的倾斜角）、Q （工作阻力，沿水平方向），设不计两滑块质量，试确定该机构等速运动时所需的铅重方向的驱动力F 。
武汉科技大学819机械原理-2019(B卷)参考答案
姓名： 报考专业： 准考证号码：密封线内不要写题2019年全国硕士研究生招生考试初试自命题试题科目名称：机械原理（□A 卷 ■B 卷）科目代码：819 （参考答案）考试时间： 3小时 满分150分可使用的常用工具：□无 √计算器 √直尺 √圆规（请在使用工具前打√）注意：所有答题内容必须写在答题纸上，写在试题或草稿纸上的一律无效；考完后试题随答题纸交回。
一、单项选择题（本大题10小题，每题2分，共20分，错选、多选均无分）1. 以下关于机构的说法错误的是 D 。
A ．一个机构中有且仅有一个机架B ．平面机构中，移动副引入了2个约束，齿轮副引入了1个约束C ．任何机构都可以看成是由若干个基本杆组依次联接于原动件和机架上而构成的D ．机构具有确定运动时所必须给定的运动参数的数目，称为机构的自由度 2．以下关于速度瞬心的说法错误的是： A 。
A ．一个平面机构有6个构件，则共有12个瞬心B ．机构中某个构件和机架构成的瞬心一定是绝对瞬心C ．两个互相啮合传动的齿轮的瞬心在过接触点的齿廓公法线上D ．一个平面四杆机构中，绝对瞬心和相对瞬心的数目是一样的 3．铰链四杆机构的最小传动角出现在 A 的两个位置之一。
A ．曲柄和机架共线B ．曲柄和连杆共线C ．曲柄和摇杆共线D ．曲柄与机架垂直 4. 对心曲柄滑块机构有曲柄的条件是 B 。
A ．曲柄大于连杆长度B ．曲柄小于连杆长度C ．曲柄等于连杆长度D ．曲柄等于连杆长度的二分之一 5．在凸轮机构中，当从动件采用等加速等减速运动规律时， B 。
A ． 存在速度突变点而不存在加速度突变点 B ． 存在加速度突变点而不存在速度突变点C ． 不存在速度突变点也不存在加速度突变点D ． 不会产生柔性冲击也不会产生刚性冲击6．一对互相啮合的齿轮由于装配误差，使得实际中心距相比标准中心距略有增大，则此时该对齿轮的 A 。
A ．传动比不变，啮合角变大B ．传动比不变，啮合角不变C ．传动比增大，啮合角变大D ．传动比增大，啮合角不变7．与标准齿轮相比，正变位齿轮的齿顶高 B 标准值。
华科机械原理课后答案
华科机械原理课后答案1. 什么是机械原理？机械原理是研究机械运动规律和机械结构性能的科学。
它是机械工程的基础学科，也是机械设计、制造和运用的理论基础。
机械原理的研究对象是机械系统，包括机械零部件、机械传动、机械结构等。
2. 机械原理的基本内容有哪些？机械原理的基本内容包括静力学、动力学、运动学、材料力学等。
静力学是研究物体静止状态下受力和受力平衡条件的学科，动力学是研究物体运动状态下受力和受力平衡条件的学科，运动学是研究物体运动规律和运动参数的学科，材料力学是研究物体材料的力学性能和力学行为的学科。
3. 机械原理的应用领域有哪些？机械原理的应用领域非常广泛，包括机械工程、汽车工程、航空航天工程、船舶工程、建筑工程、电子工程等。
在这些领域中，机械原理被广泛应用于机械设计、机械制造、机械运动控制、机械结构分析等方面。
4. 机械原理的学习方法和技巧有哪些？学习机械原理需要掌握一定的学习方法和技巧。
首先，要扎实基础知识，包括数学、物理、材料力学等方面的知识。
其次，要多做题，通过做题来加深对机械原理的理解。
另外，要注重实践，通过实验和实践来验证和应用机械原理的知识。
5. 机械原理的未来发展趋势是什么？随着科学技术的不断发展，机械原理将会在机械工程、自动化、智能制造等领域发挥越来越重要的作用。
未来，机械原理将会更加注重与其他学科的交叉融合，形成更加综合和实用的理论体系，为人类社会的发展做出更大的贡献。
以上就是对华科机械原理课后答案的一些简要介绍，希望对大家有所帮助。
如果还有其他问题，欢迎大家继续交流讨论。
武汉科技大学《机械原理》2019年期末试卷及参考答案
武汉科技大学考试卷（A卷）课程：机械原理（闭卷）（2019/06）专业班级姓名学号一、是非题(用“Y”表示正确，“N”表示错误填在题末的括号中)。
(本大题共10小题，每小题1分，总计10分)1．构件是机构或机器中独立运动的单元体，也是机械原理研究的对象。
( y ) 2．机构具有确定相对运动的条件为：其的自由度F 0。
( n ) 3．在摆动导杆机构中，若取曲柄为原动件时，机构的最小传动角γmin=0º；而取导杆为原动件时，则机构的最小传动角γmin=90º。
( n ) 4．机构当出现死点时，对运动传递是不利的，因此应设法避免；而在夹具设计时，却需要利用机构的死点性质。
( y ) 5．当其它条件不变时，凸轮的基圆半径越大，则凸轮机构的压力角就越小，机构传力效果越好。
( y ) 6．在蜗杆传动中，蜗杆的升角等于蜗轮的螺旋角，且蜗杆与蜗轮的螺旋线旋向相同。
( y ) 7．渐开线直齿圆锥齿轮的标准参数取在大端上。
( y ) 8．为了减小飞轮的尺寸，在机器的低速轴上安装飞轮后，可以较好地降低机器的速度波动。
( n ) 9．机器等效动力学模型中的等效质量(或转动惯量)是一个假想质量(或转动惯量)，它不是原机器中各运动构件的质量(或转动惯量)之和，而是根据动能相等的原则转化后计算得出的。
( y ) 10．不论刚性回转体上有多少个不平衡质量，也不论它们如何分布，只需要在任意选定两个平面内，分别适当地加平衡质量即可达到动平衡。
( y ) 二、填空题(将正确的答案填在题中横线上方空格处)。
(本大题共5小题，每空2分，总计10分)1．速度影像的相似原理只能应用于同一构件上的各点，而不能应用于机构的不同构件上的各点。
2．机械中三角带(即Ｖ带)传动比平型带传动用得更为广泛,从摩擦角度来看，其主要原因是：三角带属槽面摩擦性质，当量摩擦系数较平面摩擦系数大，故传力大。
3．在四杆机构中AB BC CD AD AD ====40406060,,,,为机架，该机构是:曲柄摇杆机构 。
机械原理课后全部习题解答
机械原理课后全部习题解答文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征机器通常由哪三部分组成各部分的功能是什么2）、机器与机构有什么异同点3）、什么叫构件什么叫零件什么叫通用零件和专用零件试各举二个实例。
4）、设计机器时应满足哪些基本要求试选取一台机器，分析设计时应满足的基本要求。
2、填空题1)、机器或机构，都是由组合而成的。
2）、机器或机构的之间，具有确定的相对运动。
3）、机器可以用来人的劳动，完成有用的。
4）、组成机构、并且相互间能作的物体，叫做构件。
5）、从运动的角度看，机构的主要功用在于运动或运动的形式。
6）、构件是机器的单元。
零件是机器的单元。
7）、机器的工作部分须完成机器的动作，且处于整个传动的。
8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。
3、判断题1)、构件都是可动的。
（）2）、机器的传动部分都是机构。
（）3）、互相之间能作相对运动的物件是构件。
（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。
（）5）、机构的作用，只是传递或转换运动的形式。
（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。
（）7）、机构中的主动件和被动件，都是构件。
（）2 填空题答案1）、构件 2）、构件 3）、代替机械功 4）、相对运动 5）、传递转换6）、运动制造 7）、预定终端 8）、中间环节 9）、确定有用构件3判断题答案1）、√ 2）、√ 3）、√ 4）、√ 5）、× 6）、√ 7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
武汉科技大学2022年《机械原理》考研真题与答案解析
武汉科技大学2022年《机械原理》考研真题与答案解析一、单项选择题1.以下关于机构的说法错误的是D。
A．一个机构中有且仅有一个机架B．平面机构中，移动副引入了2个约束，齿轮副引入了1个约束C．任何机构都可以看成是由若干个基本杆组依次联接于原动件和机架上而构成的D．机构具有确定运动时所必须给定的运动参数的数目，称为机构的自由度2．以下关于速度瞬心的说法错误的是：A。
A．一个平面机构有6个构件，则共有12个瞬心B．机构中某个构件和机架构成的瞬心一定是绝对瞬心C．两个互相啮合传动的齿轮的瞬心在过接触点的齿廓公法线上D．一个平面四杆机构中，绝对瞬心和相对瞬心的数目是一样的3．铰链四杆机构的最小传动角出现在A的两个位置之一。
A．曲柄和机架共线B．曲柄和连杆共线C．曲柄和摇杆共线D．曲柄与机架垂直4.对心曲柄滑块机构有曲柄的条件是B。
A．曲柄大于连杆长度B．曲柄小于连杆长度C．曲柄等于连杆长度D．曲柄等于连杆长度的二分之一5．在凸轮机构中，当从动件采用等加速等减速运动规律时，B。
A．存在速度突变点而不存在加速度突变点B．存在加速度突变点而不存在速度突变点C．不存在速度突变点也不存在加速度突变点D．不会产生柔性冲击也不会产生刚性冲击6．一对互相啮合的齿轮由于装配误差，使得实际中心距相比标准中心距略有增大，则此时该对齿轮的A。
A．传动比不变，啮合角变大B．传动比不变，啮合角不变C．传动比增大，啮合角变大D．传动比增大，啮合角不变7．与标准齿轮相比，正变位齿轮的齿顶高B标准值。
分度圆齿槽宽标准值。
A．大于；大于B．大于；小于C．小于；大于D．小于；小于8．在设计蜗杆蜗轮机构时，若已经确定了蜗杆的模数m和齿数z1，蜗杆直径系数q，蜗轮的齿数z2，则其中心距为A。
A．m(q+z2)/2B．m(z1+z2)/2C．m(z1+z2)/2qD．m(qz1+z2)/29．在机械装置设计时飞轮一般应安装在B轴上，安装飞轮后机器的运转不均匀系数会。
武汉科技大学机械原理习题参考答案
3-12 如图 3-30 所示，曲柄摆动导杆机构中各杆长，已知 a 400mm, d 500 mm, lBD 250mm ，构件 1 以等角速度 1 20 rad s 绕 A 顺时针方向转动，求此时 vD 及 角速度比 1 3 。
（2）求 C、D 两点的加速度
2 2 a 1 sin 1 a1 cos 1 aC b 2 sin 2 b 2 cos 2 2 2 a 1 cos 1 a1 sin 1 b 2 cos 2 b 2 sin 2
由d21 dt ＝ 2 1 0，得 2 1
机 械 原 理
课后习题参考答案
机械原理课程组编
武汉科技大学机械自动化学院
习题参考答案
第二章 机构的结构分析
2-2 图 2-38 所示为一简易冲床的初拟设计方案。设计者的思路是：动力由齿轮 1 输入，使轴 A 连续回转；而固装在轴 A 上的凸轮 2 与杠杆 3 组成的凸 轮机构将使冲头 4 上下运动以达到冲压的目的。试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。
xD l AD cos 1 求导得速度方程式 vDx l AD1 sin 1 ① 对 D 点列出位置方程式 yD l AD sin 1 vDy l AD1cos1
a Dx l AD 1 sin 1 l AD cos 1 ，则 a a 2 a 2 再求导得加速度方程式 D Dx Dy
b) n=7; Pl=10; Ph=0，F=37-2 10 = 1
由 3 个Ⅱ级杆组构成的Ⅱ级机构。
E B C D A
机械原理习题及课后答案(图文并茂)
2
1 5
解答：原机构自由度 F=33- 2 4-1 = 0，不合理 ， 改为以下几种结构均可：
2-3 图 2-39 所示为一小型压力机，其中，1 为滚子；2 为摆杆；3 为滑块；4 为滑杆；5 为齿轮及凸轮；6 为连杆；7 为齿轮及偏心轮；8 为机架；9 为压头。试绘制 其机构运动简图，并计算其自由度。
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决，机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料1荷试试下卷卷高问总中题体资2配2料，置试而时卷且，调可需控保要试障在验各最；类大对管限设路度备习内进题来行到确调位保整。机使在组其管高在路中正敷资常设料工过试况程卷下中安与，全过要，度加并工强且作看尽下护可都关能可于地以管缩正路小常高故工中障作资高；料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高，核中或对资者定料对值试某，卷些审弯异核扁常与度高校固中对定资图盒料纸位试，置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置，线高尤弯中其曲资要半料避径试免标卷错高调误等试高，方中要案资求，料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高，技料课中并术3试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术，、以术来管及避架系免等统不多启必项动要方方高式案中，；资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资，中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置，作调合并试理且技利进术用行，管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵：导活在。。分对对线于于盒调差处试动，过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调，问试应题技采，术用作是金为指属调发隔试电板人机进员一行，变隔需压开要器处在组理事在；前发同掌生一握内线图部槽纸故内资障，料时强、，电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料，试试线卷卷缆试切敷验除设报从完告而毕与采，相用要关高进技中行术资检资料查料试和，卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
机械原理习题册答案
参考答案 第一章 绪论一，填空题1.1 能量，物料，信息1.2运动，动力 1.3制造，运动，装配 二、选择题2.1 D 2.2 B 三，简答题第二章 机械的结构分析二、综合题1．n = 7 ，p l = 9 ，p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件，而由于原动件数与机构的自由度数相等，故该机构具有确定的运动。
2． （a ）D 、E 处分别为复合铰链（2个铰链的复合）；B 处滚子的运动为局部自由度；构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ，p l = 11 ，p h = 1111128323=-⨯-⨯=--=h l P P n F3． （c ）n = 6 ，p l = 7 ，p h = 313726323=-⨯-⨯=--=h l P P n F（e ）n = 7 ，p l = 10 ，p h = 0101027323=-⨯-⨯=--=h l P P n F 4． （a ）n = 5 ，p l = 7 ，p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的，所以为Ⅱ级机构。
（c ）n = 5 ，p l = 7 ，p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的，所以为Ⅲ级机构。
5． n = 7 ，p l =10 ，p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时，该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时，该机构为Ⅱ级机构。
可见同一机构，若所取的原动件不同，则有可能成为不同级别的机构。
6． （a ）n = 3 ，p l = 4 ，p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0，说明它根本不能运动。
机械原理课后习题答案(部分)
第二章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答：参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况?答：参考教材12~13页。
2-5 在计算平面机构的自由度时，应注意哪些事项?答：参考教材15~17页。
2-6 在图2-22所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗?为什么?答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答：参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答：参考教材20~21页。
2-11 如图所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的。
试绘出其机构运动简图，分析其是否能实现设计意图？并提出修改方案。
解：1）取比例尺绘制机构运动简图。
2）分析其是否可实现设计意图。
F=3n-( 2P l +P h –p’)-F’=3×3-(2×4+1-0)-0=0此简易冲床不能运动,无法实现设计意图。
3）修改方案。
为了使此机构运动，应增加一个自由度。
办法是：增加一个活动构件，一个低副。
修改方案很多，现提供两种。
※2-13图示为一新型偏心轮滑阎式真空泵。
其偏心轮1绕固定轴心A转动，与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动。
当偏心轮按图示方向连续回转时可将设备中的空气吸入，并将空气从阀5中排出，从而形成真空。
华科机械原理课后答案
华科机械原理课后答案1. 机械原理概述。
机械原理是机械工程专业的重要基础课程，它主要研究物体在外力作用下的静力学和动力学性质，以及机械结构的运动规律和力学性能。
学习机械原理对于理解和掌握机械结构的设计、分析和运动控制具有重要意义。
在学习机械原理的过程中，课后习题是巩固知识、提高能力的重要途径。
下面是对华科机械原理课后习题的答案解析。
2. 课后答案解析。
（1）静力学部分。
静力学是机械原理课程的重点内容之一。
在学习静力学时，需要掌握平衡条件、力的合成与分解、力矩的计算等基本原理。
在解答静力学题目时，首先要明确物体的平衡条件，然后根据受力分析和力矩平衡条件进行计算。
例如，对于悬臂梁的平衡问题，可以通过受力分析和力矩平衡方程求解支持力的大小和方向。
（2）动力学部分。
动力学是机械原理课程的另一个重要内容。
在学习动力学时，需要了解牛顿定律、动量定理、功和能量等基本概念。
在解答动力学题目时，可以通过应用牛顿定律和动量定理，结合受力分析和运动规律方程进行计算。
例如，对于物体的运动问题，可以通过受力分析和牛顿定律求解物体的加速度和运动轨迹。
（3）机械结构部分。
机械结构是机械原理课程的核心内容之一。
在学习机械结构时，需要了解各种机械连接件的原理和应用，以及机构的运动规律和性能。
在解答机械结构题目时，可以通过受力分析和运动规律方程，结合机构的特点和运动要求进行计算。
例如，对于齿轮传动系统的设计问题，可以通过齿轮的模数和齿数计算传动比，进而确定齿轮的参数和传动性能。
3. 总结。
通过对机械原理课后习题的答案解析，可以加深对机械原理知识的理解和掌握，提高解题能力和应用能力。
在学习机械原理的过程中，需要注重理论与实践的结合，注重基础知识的打牢和应用技能的培养，从而为将来的工程实践和科学研究打下坚实的基础。
希望同学们在学习机械原理的过程中，能够认真对待课后习题，不断提高自己的综合素质和创新能力。
武汉科技大学819机械原理2012016真题含答案解析
2014年攻读硕士学位研究生入学考试试题科目名称：机械原理（・A卷DB卷）科目代码：819考试时间：3小时满分150分可使用的席用工具：□无叼计算器尺日圆规（请在使用工具对打丿）注意：所有答题内容必须写在答题纸上，写在试题或草稿纸上的一律无效；考完后试题随答题纸交回。
一、单项选择题（本大题10小题，每题2分，共20分，错选、多选均无分）1.对于机构，下而说法错误的是______ OA.由一系列人为的运动单元组成B.各单元之间有确定的相对运动C.是由构件组成的系统D.可以完成机械功或机械能转换2.平而连杆机构中，同一位置的传动角与压力角的关系为 _______ 。
A.互余B.互补C.相等D.没关系3.一对齿轮啮合过程中，下面关于节圆的说法错误的是 _________ 。
A.始终相切B.始终通过节点C.始终和分度圆重合D.随中心距增大而增大4.生产工艺要求某机构将输入的匀速单向运动，转变为按照正玄规律变化的移动输岀，一种可供选择的机构是 ______________________________ ，A.齿轮齿条机构B.直动滚子从动件盘形凸轮机构C.偏置曲柄滑块机构D.摆动导杆机构5.图1示转动副在驱动力矩Md的作用下等速转动，Q为径向载荷，p为摩擦圆图16.渐开线直齿圆柱齿轮中，齿距卩，法向齿距几，基圆齿距內三者之间的关系为:7. 一对平行轴斜齿轮传动，其传动比爲等于 __________ 。
A. Z v2/Z viB. co 2/co xC. r a2/r a}D. r fl /r f}8. 在蜗杆传动中，引入特性系数q 的目的是 _______ 。
A.便于蜗杆尺寸参数的讣算B.容易实现蜗杆传动中心距的标准化C.提高蜗杆传动的 标准化9. 平衡的目的在于确左10. _______________________________________________ 在机器稳迫运转的一个运动循环中，应有 _________________________________________A.惯性力和重力所作的功均为零B.惯性力所做之功为零，重力所做之功不为零 C.惯性力和重力所做之功均不为零D.惯性力所做之功不为零，重力所做之 功为零二、 判断题（本大题10小题，每题2分，共20分。
华科机械原理课后答案
华科机械原理课后答案1. 机械原理概述。
机械原理是机械工程中的基础课程，它主要研究物体在受力作用下的运动规律和力的传递方式。
在学习机械原理的过程中，我们需要掌握静力学、动力学、运动学等方面的知识，这些知识对于理解机械结构的工作原理和设计具有重要意义。
2. 课后练习答案。
（1）静力学。
静力学是研究物体在静止状态下受力平衡的学科。
在学习静力学时，我们需要掌握平衡条件、力的合成与分解、杆件的受力分析等内容。
在解决静力学问题时，可以利用平衡方程和受力分析的方法，通过绘制自由体图和力的分解，找到物体受力平衡的条件。
（2）动力学。
动力学是研究物体在受力作用下的运动规律的学科。
在学习动力学时，我们需要了解牛顿运动定律、动量定理、动能定理等内容。
在解决动力学问题时，可以利用牛顿定律和动能定理，通过分析物体受力情况和速度变化，找到物体的运动规律。
（3）运动学。
运动学是研究物体运动状态和运动轨迹的学科。
在学习运动学时，我们需要了解位移、速度、加速度等概念，以及匀速直线运动、变速直线运动、曲线运动等内容。
在解决运动学问题时，可以利用位移、速度、加速度的关系，通过分析物体的运动状态和运动轨迹，找到物体的运动规律。
3. 学习建议。
在学习机械原理的过程中，我们需要注重理论与实践的结合，通过大量的练习来加深对知识点的理解和掌握。
同时，可以通过查阅相关的参考书籍和资料，扩展对机械原理的认识，提高解决问题的能力。
另外，可以参加一些与机械原理相关的实践活动和竞赛，锻炼动手能力和团队合作能力，提升综合素质。
4. 结语。
机械原理是机械工程中非常重要的一门课程，它对于我们理解机械结构的工作原理和设计具有重要意义。
通过认真学习和练习，我们可以掌握机械原理的基本知识和方法，为将来的学习和工作打下坚实的基础。
希望大家能够在学习机械原理的过程中取得好的成绩，为自己的未来发展打下坚实的基础。
机械原理考试题含答案
机械原理考试题含答案一、单选题（共50题，每题1分，共50分）1、金属切削机床的主轴、拖板属于机器的（）部分。
A、传动B、动力C、执行正确答案：C2、直齿圆锥齿轮应用于两轴（）的传动。
A、相交B、相错C、平行正确答案：A3、导向平键主要采用（）键连接。
A、紧B、较松C、较紧正确答案：B4、定轴轮系传动比大小与轮系中惰轮的齿数（）。
A、无关B、有关，成正比C、有关，成反比正确答案：A5、渐开线齿轮的模数m和齿距p的关系为（）。
A、p=πmB、m=πpC、pm=π正确答案：A6、三星轮换向机构是利用（）来实现从动轴回转方向的改变。
A、首轮B、末轮C、惰轮正确答案：C7、８．V带安装后，要检查带的松紧程度是否合适，一般以拇指按下（）ｍｍ为宜。
A、20B、5C、15正确答案：C8、铰链四杆机构中，各构件之间均以（）相连接。
A、螺旋副B、转动副C、移动副正确答案：B9、采用（）普通平键时，轴上键槽的切制用指状铣刀加工。
A、A型B、B型C、A型和B型正确答案：A10、当曲柄摇杆机构出现死点位置时，可在从动曲柄上（）使其顺利通过死点位置。
A、加设飞轮B、减少阻力C、加大主动力正确答案：A11、铰链四机构中，最短杆件与最长杆件长度之和小于或等于其余两杆件的长度之和时，机构中一定有（）。
A、摇杆B、曲柄C、连杆正确答案：B12、卧式车床走刀系统采用的是（）换向机构。
A、离合器锥齿轮B、滑移齿轮C、三星轮正确答案：C13、蜗轮轮齿的常用材料是（）。
A、铸造锡青铜B、20Cr钢C、45钢正确答案：A14、齿条的齿廓是（）。
A、直线B、圆弧C、渐开线正确答案：A15、两被连接件上均为通孔且有足够装配空间的场合应采用（）。
A、螺栓连接B、螺钉连接C、螺柱连接正确答案：A16、在曲柄滑块机构应用中，往往用一个偏心轮代替（）。
A、机架B、滑块C、曲柄正确答案：C17、根据（）的不同，平键可分为A型、B型、C型三种。
A、截面形状B、尺寸大小C、端部形状正确答案：C18、台虎钳的夹紧机构是采用（）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
机械原理习题参考答案第二章 机构的结构分析2-2 图2-38所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头443512解答：原机构自由度F=3⨯3- 2⨯4-1 = 0，不合理 ， 改为以下几种结构均可：2-3 图2-3936为连杆；7为齿轮及偏心轮；8为机架；9为压头。
试绘制其机构运动简图，并计算其自由度。
O齿轮及偏心轮ωA齿轮及凸轮BEFDC压头机架连杆滑杆滑块摆杆滚子解答：n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 = 12-6 试计算图2-42所示凸轮—连杆组合机构的自由度。
解答：a) n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 =1 L 处存在局部自由度，D 处存在虚约束b) n=5; P l =6; P h =2，F=3⨯5-2 ⨯6-2 =1 E 、B 处存在局部自由度，F 、C 处存在虚约束b)a)A EMDFELKJIFBCCDBA2-7 试计算图2-43所示齿轮—连杆组合机构的自由度。
BDCA(a)CDBA(b )解答：a) n=4; P l =5; P h =1，F=3⨯4-2 ⨯5-1=1 A 处存在复合铰链b) n=6; P l =7; P h =3，F=3⨯6-2 ⨯7-3=1 B 、C 、D 处存在复合铰链2-8 试计算图2-44所示刹车机构的自由度。
并就刹车过程说明此机构自由度的变化情况。
解答：① 当未刹车时，F=3⨯6-2 ⨯8=2② 在刹车瞬时，F=3⨯5-2⨯7=1，此时构件EFG 和车轮接触成为一体，位置保持不变，可看作为机架。
③ 完全刹死以后，F=3⨯4-2⨯6=0，此时构件EFG 、HIJ 和车轮接触成为一体，位置保持不变，可看作为机架。
2-9 先计算图2-45～图2-50所示平面机构的自由度。
再将其中的高副化为低副，确定机构所含杆组的数目和级别，以及机构的级别。
机构中的原动件用圆弧箭头表示。
ABCDE解答：a) n=7; P l =10; P h =0，F=3⨯7-2 ⨯10 = 1 C 、E 处存在复合铰链 由3个Ⅱ级杆组构成。
I F E H J OG C A B Db) n=7; P l =10; P h =0，F=3⨯7-2 ⨯10 = 1 由3个Ⅱ级杆组构成的Ⅱ级机构。
BDECAc) n=3; P l =3; P h =2，F=3⨯3 -2 ⨯3-2 = 1 D 处存在局部自由度，由2个Ⅱ级杆组构成Ⅱ级机构。
d) n=4; P l =5; P h =1，F=3⨯4 -2 ⨯5-1 = 1 由1个Ⅲ级杆组构成的Ⅲ级机构。
AB C D EF G G'H ABD CEF GHIJe) n=6; P l =8; P h =1，F=3⨯6 -2 ⨯8-1 = 1 B 处存在局部自由度，G 、G'处存在虚约束, 由1个Ⅱ级杆组加上1个Ⅲ级杆组构成的Ⅲ级机构。
f) n=9; P l =12; P h =2，F=3⨯9 -2 ⨯12-2 = 1 C 处存在局部自由度，I 处存在复合铰链, 由5个Ⅱ级杆构成的Ⅱ级机构。
杆组拆分如下图所示。
＋＋ ＋ ＋第三章 平面机构的运动分析3-1 如图3-20所示曲柄滑块机构中若已知a ，b ，e ，当ϕ1给定后，试导出滑块位移s 和连杆转角ϕ2的表达式。
ωx解：⎩⎨⎧=+=+eb a s b a 2121sin sin cos cos ϕϕϕϕ 由12s i n s i n ϕϕa e b -= 得到⎪⎪⎩⎪⎪⎨⎧-+=-=))sin (cos(arcsin cos )sin arcsin(1112b a e b a s b a e ϕϕϕϕ 或写成⎪⎩⎪⎨⎧--+=-=212112)sin (cos )sin arcsin(ϕϕϕϕa e b a s ba e3-2 如图3-20，若已知a b e ===-==2014010601011mm mm rad s mm ,,,,ωϕ ，设经计算得到：ϕ22997=-. ，s=149.81mm ，请导出v c 和ω2的表达式，并求出其数值。
解：⎩⎨⎧=+=--0cos cos sin sin 22112211ϕωϕωϕωϕωb a v b a c ， 得：s rad b a /7153.0)997.2cos(140)60cos()10(20cos cos 2112=︒-⨯︒⨯-⨯-=-=ϕϕωω s m v c /1784.0)997.2s i n (7153.014.0)60sin()10(02.0=︒-⨯⨯-︒⨯-⨯-= 3-12 如图3-30所示，曲柄摆动导杆机构中各杆长，已知a d l BD ===400500250m m m m m m ,,，构件1以等角速度ω120=rad 绕A 顺时针方向转动，求此时v D 及角速度比ω13。
解：⎩⎨⎧=+=33ϕϕϕϕsin sin cos cos 11BC BC l d a l a ，其中2式除以1式可得 0207.2cos sin tan11=+=ϕϕϕa d a 3 故得：781.0251mm )6705.63cos()30cos(400 ,6705.63=︒︒⨯=︒=BCl 3ϕ ︒求导得⎪⎩⎪⎨⎧+=-=-3333ϕωϕϕωϕωϕϕωc o s s i n c o s s i n c o s s i n 311311BC BC BC BC l l a l l a 上式中对2式用旋转坐标系法，按逆时针方向旋转3ϕ角得：311)cos(ωϕϕωBC l a =-3所以，s rad /5244.8 ,3462.2/331-==ωωω又⎩⎨⎧︒++=︒++=)240sin(sin )240cos(cos 1133ϕϕϕϕBD D BD D l a y l a x 求导得⎩⎨⎧︒++=︒+--=)240cos(cos )240sin(sin 31131133ϕωϕωϕωϕωBD Dy BD Dx l a v l a v 或写成如下等价形式：⎩⎨⎧︒-+=︒-+=)120sin(sin )120cos(cos 1133ϕϕϕϕBD D BD D l a y l a x 求导得⎩⎨⎧︒-+=︒---=)120cos(cos )120sin(sin 31131133ϕωϕωϕωϕωBD Dy BD Dx l a v l a v 解得：V Dx =-0.4*(-20)*sin(60*pi/180)-0.25*(-8.5244)*sin((63.6705-120)*pi/180)= 2.2264m/s V Dy =0.4*(-20)*cos(60*pi/180)+0.25*(-8.5244)*cos((63.6705-120)*pi/180)= - 8.1097 m/s 合成可得：V D =sqrt(2.2264^2+8.1097^2)＝8.4098 m/s ， β VD ＝-74.6485° 3-12题解法二（瞬心法）：mm CAB ad d a l BC 025.781cos 222=∠-+=由余弦定理：8322.0cos =∠ABC ，得︒=∠6746.33ABC mm ABC l B P BC 5064.938cos /24=∠= 由1324ωω⋅=⋅a B P ，得：3461.231=ωω s rad /5247.83=ω ︒=︒+∠=∠6476.9360ABC ABD mm D P 5945.98624= s m D P V D /4104.8243=⋅=ω3-15 如图3-33所示为采煤康拜因的钻探机构。
已知b a l ===2808401300m m m m m m AD ,,,ϕ115= ,构件2绕构D 两点的速度及加速度。
件1上的B 点以等角速度rad/s 121=ω逆时针方向转动， 求C 、解：（1）求C 、D 两点的速度⎩⎨⎧=+=2121sin sin cos cos ϕϕϕϕb a b l a AC︒=︒⨯=9373.50 ,280)15sin(840sin 22ϕϕ︒⎩⎨⎧=-=-22112211c o s c o s s i n s i n ϕωϕωϕωϕωb a b v a C s r a d b a b a /278.01)1cos cos (1 ,cos cos 112112211212==-=-⋅=ωωϕϕωωωωϕϕω，得，得＝又根据题目已知条件 /4.361278.01300 ,/4079.217sin sin 1122s mm v s mm a b v D C =⨯==-=ϕωϕω（2）求C 、D 两点的加速度⎪⎩⎪⎨⎧-=---=--22222121112222212111sin cos sin cos cos sin cos sin ϕωϕεϕωϕεϕωϕεϕωϕεb b a a b b a a a C 1212210εεεεω==-，得＝由dt d 由上面2式可得：840*ε1*cos(15*pi/180)-840*(0.278^2)*sin(15*pi/180)=280*ε2*cos(50.93*pi/180)-280*(1.278^2)*sin(50.93*pi/180) 811.3777ε1 - 16.8022＝176.4754ε1 -355.0521 得ε1＝ε2＝-0.5328rad/s 2求D 点加速度的方法有两种：第一种按书上的方法列出运动方程式，按步骤求解；第二种方法求出法向加速度和切向加速度的合成。
① 对D 点列出位置方程式⎩⎨⎧==11sin cos ϕϕAD D AD D l y l x 求导得速度方程式⎩⎨⎧=-=1111sin ϕωϕωos l v l v AD Dy AD Dx c 再求导得加速度方程式⎪⎩⎪⎨⎧-=--=1211112111sin cos sin ϕωϕεϕωϕεAD AD Dy AD AD Dx l os l a l l a c ，则22Dy Dx D a a a += a Dx = -1300*(-0.5328)*sin(15*pi/180)-1300*(0.278^2)*cos(15*pi/180)＝82.2226 mm/s 2a Dy = 1300*(-0.5328)*cos(15*pi/180)-1300*(0.278^2)*sin(15*pi/180)＝-695.0422 mm/s 2故D 点的加速度为：a D = sqrt(a Dx ^2+ a Dy ^2) = 699.8887 mm/s 2 ， β aD ＝-83.2533°②22212122/s 699.8887mm )()(=+=+=ωεAD AD Dn Dt D l l a a aC 点的加速度为：1211122222cos sin cos sin ϕωϕεϕωϕεa a b b a C ++--=a C =-280*(-0.5328)*sin(50.9373*pi/180)-280*(1.278^2)*cos(50.9373*pi/180)+840*(-0.5328)*sin(15*pi/180)+840*(0.278^2)*cos(15*pi/180)＝-225.4828 mm/s 23-17 在图3-35所示e R AB m m m m ===2050,,ω110=rad /s ，指出速度瞬心P 12，并用瞬心法求ϕ1045= ,及90 时构件2速度瞬心P 12如图所示，从s mm v /200 ,021=︒=ϕ；s mm v /4214.141 ,4521=︒=ϕ； s mm v /0 ,9021=︒=ϕ3-18 如图3-36=10013P ，并用瞬心法求构件1的角速度ω1。