19-2 圆孔衍射 光学仪器的分辨本领
圆孔的夫朗和费衍射
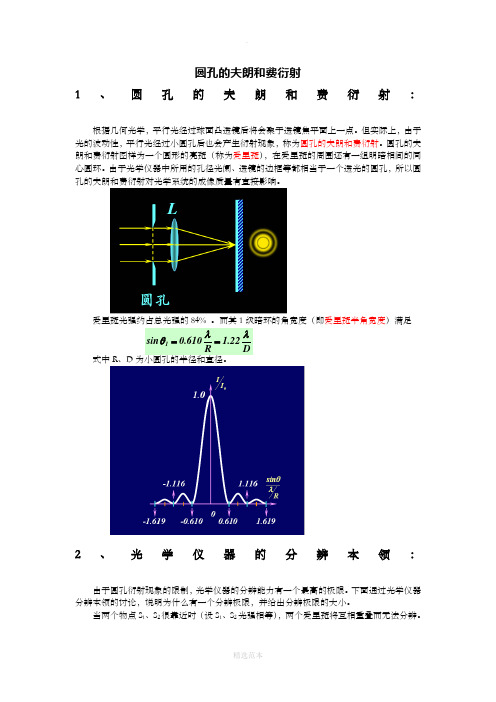
圆孔的夫朗和费衍射1、圆孔的夫朗和费衍射:根据几何光学,平行光经过球面凸透镜后将会聚于透镜焦平面上一点。
但实际上,由于光的波动性,平行光经过小圆孔后也会产生衍射现象,称为圆孔的夫朗和费衍射。
圆孔的夫朗和费衍射图样为一个圆形的亮斑(称为爱里斑),在爱里斑的周围还有一组明暗相间的同心圆环。
由于光学仪器中所用的孔径光阑、透镜的边框等都相当于一个透光的圆孔,所以圆孔的夫朗和费衍射对光学系统的成像质量有直接影响。
爱里斑光强约占总光强的84% 。
而其1级暗环的角宽度(即爱里斑半角宽度)满足D 22.1R610.0sin 1λλθ==式中R 、D 为小圆孔的半径和直径。
2、光学仪器的分辨本领:由于圆孔衍射现象的限制,光学仪器的分辨能力有一个最高的极限。
下面通过光学仪器分辨本领的讨论,说明为什么有一个分辨极限,并给出分辨极限的大小。
当两个物点S 1、S 2很靠近时(设S 1、S 2光强相等),两个爱里斑将互相重叠而无法分辨。
对一个光学仪器来说,若一个点光源产生的爱里斑的中央刚好与另一个点光源产生的爱里斑瑞的1级暗环相重合,这时两个爱里斑重合部分的光强约为单个爱里斑中央光强的80%左右,一般人眼刚好能分辨出这是两个光点的像。
因此,满足上述条件的两个点光源恰好能被该光学仪器所分辨。
这一条件称为瑞利分辨判据。
(见下图)恰能分辨时两光源发出的光线对透镜光心的夹角Δθ 称为最小分辨角,用δθ表示。
由上讨论可知,最小分辨角δθ等于爱里斑的半角宽度θ1:)D 22.1arcsin(1λθδθ==尤其当θ1 ~ 0D 22.1λδθ≈(或称分辨率),用R 表示:λδθ22.1D 1R ==讨论:⑴ 增大透镜的直径D 可提高镜头的分辨率。
光学天文望远镜的镜头孔径可达数米! ⑵ 设r 、d 为爱里斑的半径和直径,则:f 2d f r D 22.1===λδθ即:D f44.2d λ=f D称为镜头的相对孔径(越大越好)。
如照相机镜头上所标示的502:1字样,即表示镜头的焦距mm 50f =,而镜头的孔径mm 25D =。
中国人民公安大学安全防范技术与工程考研 招生人数 参考书 报录比 复试分数线 考研真题 考研经验 招生简章

爱考机构考研-保研-考博高端辅导第一品牌公安技术安全防范技术与工程方向招生目录培养系部、专业及研究方向代码及名称拟招生人数初试科目代码及名称复试科目代码及名称0838公安技术*(按一级学科招生)8201刑事科学技术①(101)思想政治理论②(201)英语一③(302)数学二④(822)公安技术综合刑事科学技术02网络安全执法技术信息安全概论03交通安全执法技术交通安全执法技术综合04安全防范技术与工程信号与线性系统中国人民公安大学2013年硕士研究生各专业招生计划表中国人民公安大学2013年硕士研究生招生计划表专业招生总计划已接收推免生本次复试拟录取人数普通计划骨干计划法学603543公安学1951714434公安技术557471法律(非法学)183141法律(法学)120111警务(刑侦)600600警务(治安)380380警务(网安)220220安全工程5230公共管理5050总计4703239840注:女生招生比例不超过30%(计算基数不包含定向、委培考生)中国人民公安大学2013年硕士研究生各专业复试分数线学科门类(专业)培养部门总分线单科线男女满分=100分满分>100分学术型学位类法学法学院315 335 42 63公安学各院系部340 350 42 63公安技术各院系部295 295 40 60专业学位类法律(非法学)法学院315 315 42 63法律(法学)法学院315 315 42 63警务(刑事侦查)侦查学院333 42 63警务(治安管理)治安学院325 42 63警务(网络安全)网络安全保卫学院315 42 63安全工程警务信息工程学院280 280 37 56公共管理公安管理学院155 155 41 82关于公安技术专业各研究方向考试科目的解释公告报考2013年公安技术专业各研究方向考生:我校2013年公安技术一级学科下设刑事科学技术、网络安全执法技术、交通安全执法技术、安全防范技术与工程等4个研究方向。
光学成像系统的衍射和分辨本领
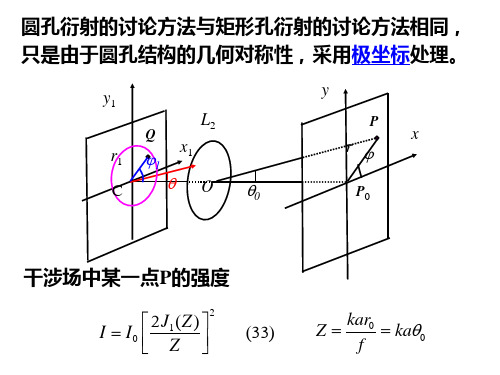
Z 0 1.220 = 3.832 1.635 = 5.136 2.233 = 7.016 2.679 = 8.417 3.238 = 10.174 3.699 = 11.620
[2J1(Z)/Z]2 1 0
0.0175 0
0.00415 0
0.0016
光能分布 83.78% 0 7.22% 0 2.77% 0 1.46%
0
1.22
D
(52)
R
>0
能 分 辨
0
1.22
D
=0
恰
1.0
能
0.81
分
辨
θ0
<0
不 能 分 辨
人眼的最小分辨角约为 1,教室中最后一排(距黑板 15m )的学生对黑板上的两条黄线(5893Å)的最小分辨距 离为多少?并估计瞳孔直径大小。
*S1
dmin
*S2
L
I
解:当两黄线恰可分辨时,两爱里斑中心到人眼张角 为最小分辨角
➢瑞利判据:两个波长的亮条纹只有当它们的合强度曲线 中央极小值低于两边极大值的81%时,才算被分开
IM
0.81IM
G F
设有Sl 和S2 两个非相干点光源,间距为,它们到直
径为D 的圆孔距离为 R,则S1和S2对圆孔的张角 为
R
L
S1
S2
D
R
S1 和 S2 将分别在观察屏上形成各自的弗朗和费衍射
图样。假设其爱里斑中心关于圆孔的张角为0
dmin L
0
1
两条线的最小距离分辨角
1 1 π
dmin
0L
60 180
15 0.00436(m)
由于 因此
0
圆孔衍射

S1 S2
可分辨 此时两爱 里斑重叠 部分的光 强为一个 光斑中心 最大值的 80%。 %。
S1 S2
恰可分辨
两爱里斑中心距d 恰好等于爱里斑半径。 两爱里斑中心距 0恰好等于爱里斑半径。
S1 S2
不可分辨
7
2.光学仪器分辨率 光学仪器分辨率 满足瑞利判据的两物点间的距离, 满足瑞利判据的两物点间的距离,就是光学仪器 所能分辨的最小距离。 所能分辨的最小距离。此时两个物点对透镜中心所张 的角δϕ称为最小分辨角。 δϕ称为最小分辨角 的角δϕ称为最小分辨角。 d0为光学仪器可分辨的最小距离,即为两物点可 为光学仪器可分辨的最小距离, 分辨的最小距离, 为圆孔到两物点的垂直距离, 分辨的最小距离,L为圆孔到两物点的垂直距离,若为 光学仪器, 即为焦距f 为圆孔直径。 光学仪器,则L即为焦距f。D为圆孔直径。 光学仪器中将最小分辨角的倒数称为仪器的分辨率 光学仪器中将最小分辨角的倒数称为仪器的分辨率。
4
二、光学仪器的分辨本领
一般光学仪器成像, 一般光学仪器成像,光学仪器对点物成象是一个 有一定大小的爱里斑。 有一定大小的爱里斑。 所以由于衍射现象 会使图像边缘变得模糊不清, 由于衍射现象, 所以由于衍射现象,会使图像边缘变得模糊不清, 使图像分辨率下降。 使图像分辨率下降。 点物S 象S’ 一个透镜成象的光路 可用两个透镜的作用来 L 等效,如图所示: 等效,如图所示: L1 L2 象 点物就相当于在透 点物 物方焦点处, 镜L1物方焦点处,经通 f1 f2 光孔径A, 光孔径 ,进行夫琅和 费衍射,在透镜L 费衍射,在透镜 2的象 A 方焦点处形成的中央零 仅当通光孔径足够大时, 仅当通光孔径足够大时, 级明斑中心。 级明斑中心。 爱里斑才可能很小。 a >> λ 爱里斑才可能很小。 5
光学仪器的分辨本领

光学仪器的分辨本领第四章光学仪器的基本原理●学习⽬的通过本章的学习,使得学⽣熟悉光学仪器的基本原理,掌握如何使⽤这些光学仪器,了解基本光学仪器的构造和原理以及正确的使⽤⽅法。
●内容提要1、掌握光学仪器的基本⼯作原理;2、了解⼏何光学仪器的构造、使⽤⽅法;3、了解助视仪器的分辨率;4、光度学基础。
●重点1、光学仪器的基本⼯作原理;2、⼏何光学仪器的构造、使⽤⽅法;3、助视仪器的分辨率。
●难点1、光学仪器的基本⼯作原理;2、助视仪器的分辨率。
●计划学时计划授课时间6学时●教学⽅式及教学⼿段课堂集中式授课,采⽤多媒体教学。
●参考书⽬1、《光学教程》第三版姚启钧著,⾼等教育出版社,第四章2、《光学》第⼆版章志鸣等编著,⾼等教育出版社,第三章3、《光学原理》上册,玻恩,科学出版社,第三、四、五、六章§4.1 ⼏何光学仪器⼀、⼈的眼睛1. 眼球壁主要分为外、中、内三层外层由⾓膜、巩膜组成。
前1/6为透明的⾓膜,其余5/6为⽩⾊的巩膜,俗称“眼⽩”。
眼球外层起维持眼球形状和保护眼内组织的作⽤。
⾓膜是接受信息的最前哨⼊⼝。
⾓膜是眼球前部的透明部分,光线经此射⼊眼球。
⾓膜稍呈椭圆形,略向前突。
横径为11.5—12mm ,垂直径约10.5—11mm 。
周边厚约1mm ,中央为0.6mm 。
⾓膜前的⼀层泪液膜有防⽌⾓膜⼲燥、保持⾓膜平滑和光学特性的作⽤。
⾓膜含丰富的神经,感觉敏锐。
因此⾓膜除了是光线进⼊眼内和折射成像的主要结构外,也起保护作⽤,并是测定⼈体知觉的重要部位。
巩膜为致密的胶原纤维结构,不透明,呈乳⽩⾊,质地坚韧。
中层⼜称葡萄膜,⾊素膜,具有丰富的⾊素和⾎管,包括虹膜、睫状体和脉络膜三部分。
虹膜:呈环圆形,在葡萄膜的最前部分,位于晶体前,有辐射状皱褶称纹理,表⾯含不平的隐窝。
不同种族⼈的虹膜颜⾊不同。
中央有⼀2.5-4mm 的圆孔,称瞳孔。
睫状体:前接虹膜根部,后接脉络膜,外侧为巩膜,内侧则通过悬韧带与晶体⾚道部相连。
衍射2

设紫光的波长为=400nm,红光的波长为´=760nm 解:
光栅方程
(a b) sin k
k k 1
要产生完整光谱
(a b) sin k k (a b) sin k 1 (k 1)
k (k 1)
7.6 10 k 4 10 (k 1)
X射线管
-
K
A
+
X射线
伦琴
劳厄(Laue)实验(1912) 证实了X射线的波动性
将X射线通过红宝石晶体(a)和硅单晶体 (b)所拍摄的劳厄斑照片
二. X射线在晶体上的衍射
晶面
d
B dsin d
D C
A
1 2
பைடு நூலகம்
解: 人眼视觉最敏感的黄绿光 最小分辨角
550nm
R 1.22
d
9
550 10 1.22 rad 3 3.0 10
2.2 10 rad
4
设人离开纱窗的距离为s,纱窗上相邻两根细丝的 间距为l
l 张角 s
恰能分辨
3
R
2.0 10 s 9.1m 4 R 2.2 10 l
d
: 掠射角 d : 晶面间距 (晶格常数)
1. 衍射中心 每个原子都是散射子波的子波源
2 .面间散射光的干涉
BC CD 2d sin
散射光干涉加强条件:
2d sin k ( k 1,2,)
—乌利夫—布喇格公式
三. 应用
• 已知、 可测d —晶体结构分析。 • 已知、d可测 — 光谱分析。
大学物理(11.7.2)--圆孔衍射光学仪器的分辨本领

出解两:盏人亮眼灯的?最 小 可 分 辨 角
1.22l
D
L 1.2
L 8200 m
1.2m
Δ
L?
例题:在通常亮度下,人眼的瞳孔直径为 3mm ,问: 人眼最小分辨角为多大? (l=550nm) 如果窗纱上两根 细丝之间的距离为 2.0mm ,问:人在多远恰能分辨。
解 : s
照相机镜头的孔径至少应为 :
D
1.22ldS来自1.22
5.0
107 0.05
1.6
105
1.952 m
光学仪器的分辨率 D λ 提高分辨本领有两个途径 : 1. 增大孔径
( 天文望远镜 , 极限约 5m)
光学仪器的分辨率 D λ 我国造的电子显微镜
JEM-2000EXII
2. 减小波长。
电子的德布罗意波长很短 ,从而可以使电子显微镜的 分辨率比光学显微镜大大提 高 , 可达十多万倍。用电子 显微镜 可分辨 1Å 的两个 点λ。可在0.1 ~ 0.01A
分辨率可达 1.44 A 。 (放大 80万倍)
θ
1.22 λ D
300m radiotelescope in Arecibo, USA
GHz 的毫米波,计算其波束的角宽度; (2) 将此结果与
普通船用雷达发射的波束的角宽度进行比较,设船用雷
达波长为 解
1.57 l1
cmc,圆232形01天01线80m9直H/径sz
为
2.33
1.36
m。
103
m
( 1)
(
2)1 22.424.4Dl411Dl22
0.00603 0.016
rad 4 rad
《大学物理AII》作业No.06光的衍射参考答案

《大学物理AII》作业No.06光的衍射参考答案《大学物理AII 》作业No.06光的衍射班级________学号________姓名_________成绩_______-------------------------------------------------------------------------------------------------------****************************本章教学要求****************************1、理解惠更斯-菲涅耳原理以及如何用该原理解释光的衍射现象。
2、理解夫琅禾费衍射和菲涅耳衍射的区别,掌握用半波带法分析夫琅禾费单缝衍射条纹的产生,能计算明暗纹位置、能大致画出单缝衍射条纹的光强分布曲线;能分析衍射条纹角宽度的影响因素。
3、理解用振幅矢量叠加法求单缝衍射光强分布的原理。
4、掌握圆孔夫琅禾费衍射光强分布特征,理解瑞利判据以及光的衍射对光学仪器分辨率的影响。
5、理解光栅衍射形成明纹的条件,掌握用光栅方程计算主极大位置;理解光栅衍射条纹缺级条件,了解光栅光谱的形成以及光栅分辨本领的影响因素。
6、理解X 射线衍射的原理以及布拉格公式的意义,会用它计算晶体的晶格常数或X 射线的波长。
-------------------------------------------------------------------------------------------------------一、填空题1、当光通过尺寸可与(波长)相比拟的碍障物(缝或孔)时,其传播方向偏离直线进入障碍物阴影区,并且光强在空间呈现(非均匀分布)的现象称为衍射。
形成衍射的原因可用惠更斯-菲涅耳原理解释,即波阵面上各点都可以看成是(子波的波源),其后波场中各点波的强度由各子波在该点的(相干叠加)决定。
2、光源和接收屏距离障碍物有限远的衍射称为(菲涅尔衍射或近场衍射);光源和接收屏距离障碍物无限远的衍射称为(夫琅禾费衍射)或者远场衍射。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
衍射限制了透镜的分辨能力的示意图
2012-12-25
5
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
瑞利判据
对两个像斑的分辨采用瑞利判据
对于两个相等光强的非相干物点 ,如果其一个象 斑的中心恰好落在另一象斑的边缘(第一暗纹处), 则 此两物点被认为是刚刚可以分辨。
刚可分辨 不可分辨
非相干叠加
1.0
0.8
2012-12-25
6
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
光学仪器分辨本领
q
1
最小分辨角 1 1 .2 2
d
定义:光学仪器的分辨本领
R
2012-12-25
1
1
d 1.22
提高仪器分辨本 领的两种方法:增 大孔径,减小波长
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
2012-12-25
1
19-119-2 圆孔衍射 光学爱里斑 Airy disk
θ
84%
d sin 1 1.22
7.2%
(对比单缝 , 有 b sin 1 )
2.8%
2012-12-25 10
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
用电子显微镜观察一种 小蜘蛛的头部
2012-12-25
11
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
用电子显微镜
观察红血球 (假彩色)
2012-12-25
12
直径305m,能探测 射到整个地球表面 仅10-12W的功率, 也可探测引力波。
2012-12-25
9
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
显微镜:
R 1
1
d 1 .2 2
d不会很大,可 R
(紫光显微镜)
(电子显微镜) 电子的波长很小:0.1 Å~ 1Å, ∴分辨本领 R 很大。
7
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
望远镜:
R 1
1
d 1 .2 2
波长不可选择 但可增大d
(射电望远镜 的大天线)
8
2012-12-25
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
世界上最大的射电望远镜 建在美国波多黎各 岛的 Arecibo
由于衍射的存在,一个物点的像不再是一个 点,而是一个衍射斑(主要是爱里斑)。
爱里斑的大小由衍射的规律决定:
设爱里斑的半角宽为1
sin 1 1.22 d
两个物点的像就是这两个衍射斑的非相干叠加。 如果两个衍射斑之间的距离过近,这两个物 点的两个象斑就不能分辨,象也就不清晰了。
2012-12-25 4
2012-12-25 2
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
二 光学仪器的分辨本领 几何光学 : 物点 经透镜(相当一圆孔) 像点 物(物点集合) 像(像点集合) 波动光学 : 物点 ( 经透镜 ) 像斑
物(物点集合) 像(像斑集合)
2012-12-25 3
19-119-2 圆孔衍射 光学仪器的分辨本领 光的衍射现象
