4.2平面直角坐标系(2)
4.2平面直角坐标系(2)-公开课

1.已知点 P( a,b), Q(3,6)且 PQ ∥ x轴, 则 b的值为( )
4
2
o 24 6 8
x
1、点(-1,2)在( B )
A、第一象限;B、第二象限;C、第三象限;D、第四象限
2、若点(X,Y)在第四象限内,则( C )
A、X,Y同是正数
B、X,Y同是负数
C、X是正数,Y是负数
D、X是负数,Y是正数
3、横坐标是正数,纵坐标的绝对值是正数的点在( D )
A、第一、三象限
2. (1,3), (2,2), (4,2), (5,3);
3. (1,4), (2,4), (2,5), (1,5), (1,4);
4. (4,4), (5,4), (5,5), (4,5), (4,4); 5. (3,3).
y
观察所得
的图形,你觉
得它像什么?
8
解:答案不唯一,
可以说“像猫
6
脸”等
• 3.点(-5,7)关于x轴的对称点坐标为 ___(-5_,-_7_) _.
• 4.点(-4,-6)关于x轴的对称点坐标为 __(_-4_,6_) __.
• 1.点(2,5)关于y轴的对称点坐标为 _(_-_2_,5_)__.
• 2.点(3,-4)关于y轴的对称点坐标为 __(_-_3,_-4_)_.
B、第二、四象限
C、第二、三象限
D、第一、四象限
4、若点P(a,b)在第二象限,则点Q(-a,b+1)在(
A、A第一象限;
B、第二象限;
C、第三象限;
D、第四象限
5.点A(4,x-2)在平面直角坐标 系的横轴上,那么x=__2____.
6.已知点P(a+1,2-a)在Y轴上,则
浙教版数学八年级上册《4.2 平面直角坐标系》教案

浙教版数学八年级上册《4.2 平面直角坐标系》教案一. 教材分析《4.2 平面直角坐标系》是浙教版数学八年级上册的一个重要内容。
本节内容主要让学生了解平面直角坐标系的定义、各象限内点的坐标特征及坐标轴上的点的坐标特征。
通过学习,学生能熟练运用平面直角坐标系解决一些实际问题。
二. 学情分析八年级的学生已经掌握了实数、一次函数和二次函数等基础知识,对数学图形有一定的认识。
但部分学生在坐标与图形的对应关系方面可能还存在一定的困难。
因此,在教学过程中,需要关注这部分学生的学习需求,通过直观的教学手段,帮助他们更好地理解平面直角坐标系。
三. 教学目标1.知识与技能:让学生掌握平面直角坐标系的定义,了解各象限内点的坐标特征及坐标轴上的点的坐标特征。
2.过程与方法:通过观察、实践,培养学生运用坐标系解决实际问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的合作意识,使学生在解决实际问题中体会数学的重要性。
四. 教学重难点1.重点:平面直角坐标系的定义,各象限内点的坐标特征及坐标轴上的点的坐标特征。
2.难点:坐标与图形之间的对应关系,以及运用坐标系解决实际问题。
五. 教学方法1.情境教学法:通过生活中的实例,让学生感受坐标系的存在和作用。
2.直观演示法:利用教具和多媒体手段,直观展示坐标系的特点和规律。
3.合作学习法:引导学生分组讨论,共同探究坐标系的性质,提高学生的合作能力。
六. 教学准备1.教具:平面直角坐标系模型、多媒体设备。
2.学具:练习本、笔。
七. 教学过程1.导入(5分钟)利用生活中熟悉的场景,如商场购物、电影院等,引导学生思考如何用数学工具表示这些场景中的位置。
通过分析,引入平面直角坐标系的概念。
2.呈现(10分钟)展示平面直角坐标系模型,让学生直观地了解坐标系的组成。
同时,讲解坐标轴上的点的坐标特征,如原点、正方向等。
3.操练(10分钟)让学生在练习本上绘制一个简单的平面直角坐标系,并标注出各象限内的点。
初中数学八年级 上册 4.2 平面直角坐标系 (2)课件

12 音乐喷泉
蝴蝶园
x 绣湖
观现察在我这们些来坐回标顾系一的下作刚才法建后立,的你坐有标什系么想法?
总结一下:
坐标系该如何建立才最方便? 建立坐标系原则:
1、一般取水平线段所在的直线为横轴,竖直 线段所在的直线为纵轴。
2、考虑坐标轴尽可能多经过些点。 3、使更多的点容易表示。
例3 一个直四棱柱的俯视图如图所示.请建立适当的坐 标系,在直角坐标系中作出俯视图,并标出各顶点的坐标.
2
(一) 平面直角坐标系的概念:
画成水平的轴叫x轴或横轴,取向右的方向为正方向;
画成铅垂的轴叫y轴或纵轴,取向上的方向为正方向。
在平面内有公共原点而且互相垂直的两条数轴,就构成 了平面直角坐标系.简称坐标系 y
5
4
第二象限
3
第一象限
2
1
6 5 4 3 2 1O 1 2 3 4 56 7
x
1
2
第三象限
如图 ,在长方形ABCD中,AB=1cm,BC=2cm,请建
立适当的坐标系,在坐标系中画出长方形并标出各
个顶点的坐(0,0标) 。
(2,0)
(0,1)
(2,1)
A(0,-1)
(2,-1)
(0,0)
D
(2,0)
(-2,1)
B
(-2,0)
(0,1) (0,0)
(-2,0)
(-C2,-1)
(0,0) (0,-1)
y(cm)
D 3
2
1
A
-1 o
1
-1
单位:mm
D
200
解:建立直角坐标系如图,
选择比例为1:10,取C 点E为
C
4.2 平面直角坐标系八年级上册数学浙教版

2.平面上的点与有序实数对的关系:建立了平面直角坐标系后,对于坐标平面内任何一点,我们可以确定它的坐标.反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点.
坐标平面内的点与有序实数对是一一对应的关系
(4)以某个已知点为原点,使其坐标为 .
典例4 如图所示,网格中每个小正方形的边长都是1.
(1) 任选一点作为原点,建立平面直角坐标系;
(2) 写出 , , , , 各点的坐标.
解:(1)以点 所在的竖网格线为 轴,使边 在 轴上,建立平面直角坐标系,如图所示:
(2) , , , , .(本题答案不唯一)
考点2 坐标平面内点的坐标特征
典例6 (金华中考)点 在第二象限内,则 的值可以是(写出一个即可)____________________.
(答案不唯一)
解析: ∵点 在第二象限内,∴ ,则 的值可以是 (答案不唯一).
链接教材 本题取材于教材第121页作业题第3题,考查了坐标平面内点的坐标特征.教材习题是正面考查由点的位置确定点所在的象限,而中考真题是逆向考查,由点所在的象限确定字母的值.
(2)一般情况下,两条数轴的单位长度一致.
2.坐标平面:坐标系所在的平面就叫做坐标平面,两坐标轴的公共原点 叫做直角坐标系的原点.
笛卡尔是法国17世纪的哲学家、数学家,是近代科学方法论的创造人,也是解析几何的创立者.1637年,笛卡尔发表了《几何学》,创立了直角坐标系
典例1 下列关于平面直角坐标系的画法正确的是( )
(2)如图所示.
(2) 描出点,<
例题点拨
利用交点法描点
浙教版八年级上册4.2 平面直角坐标系(2) 课件(共20张PPT)
拓展
2.如图,点A的坐标是(2,2),若 点P在x轴上,且△APO是等腰 三角形,求点P的坐标.
y
2
A
1
-1 0
x
P
1 2 34
达标
3.若点P在第三象限且到x轴的距 离为2, 到y轴的距离为1.5,则点 P的坐标是____(_-1_._5,__-2_)______. 4.若点(a,b-1)在第二象限,则a的
点如的何坐选标择分y轴别?为(2)根据所 根据上述坐标在直角坐标系中 标注(的-1尺,寸0,)如,何(选2择,0坐)标 作点A,B,C,D,并用线段依次连 (轴2的.单5位,1长.度5?),(0,3.5)结各点,
如图中的四边形ABCD就是所求作的图形
若以A为坐标原点, 建立适当的坐标系,你能
D
写出ABCD各点的y坐标吗?
3.在点A(-2,-4)、B(-2,4)、C(3,-4)、D(3,4) 中,属第一象限的点是 点D ,属第二象限的点是 点B , 属第三象限的点是 点A , 属第四象限的点是 点C .
纵轴 y
4
第二象限 3
(-,+) 2
1
-4 -3 -2 -1 o
原点
-1
第三象限 -2
(-,-) -3
-4
第一象限
解:A点在第二象限;B点在第四象限;
C点在第三象限;D点在第一象限;
E点在x轴上;F点在y轴上
3、已知点P(0,a)在y轴的负半轴,则Q(-a2-2,-a+2)在( B ) (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4.如xy>0,且x+y<0,那么P(x,y)在( C ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
《平面直角坐标系》PPT课件 (公开课获奖)2022年浙教版 (3)

5.(5分)如图是益阳市行政区域图,图中益阳市区所在地用 坐标表示为(1,0),安化县城所在地用坐标表示为(-3,- 1),那么南县县城所在地用坐标表示为 (2,4) .
第4题图
第5题图
6.(5分)正方形ABCD的边长为4,请你建立适当的 平面直角坐标系,写出各个顶点的坐标.
A
D
E
F
B
C
1、在一个四边形中,∠A:∠B:∠C:∠D=9: 5:3:7,求这个四边形各内角的度数?
2、四边形ABCD中,AD//BC,那么∠A:∠B:∠C:
∠D的值可能是( D )
A、9:5:3:7 B、2:3:4:5 C、3:5:2:4 D、2:5:4:3
3 、一个多边形,除了一个内角外,其余内角和为1205度, 则这个内角是多少度,这是个几边形?
8.(5分)已知等腰三角形ABC的底边BC=6,腰AB=AC =5,若点C与坐标原点重合,点B在x轴的负半轴上,点A 在x轴的上方,则点A的坐标是 (-3,4) ,点B的坐标是
(-6,0) .
9.(10分)如图所示,AB=DE=GH=MN=2,其余各短边 长为1,且图中的角都是直角,请建立适当的直角坐标系, 并写出各个顶点的坐标.
三角形的重心有一个重要的几何性质:
三角形的重心分每一条中线的比为
1∶2(重心到每边的中点距离∶重心
解:(这是开放题,答案不唯一)以AB所在的直线为 x轴,AD所在的直线为y轴,并以点A为坐标原点,建 立平面直角坐标系,如图所示,则点A,B,C,D的 坐标分别是 (0,0),(4,0),(4,4),(0,4) .
7.(5分)在方格纸上有两点A,B,若以点B为原点建立直 角坐标系,则点A的坐标为(4,3),若以点A为原点建立直 角坐标系,则点B的坐标为 (-4,-3) .
数学八年级上 4.2 平面直角坐标系 课件

(4,2)
(2, -2.5 )
(0,-3)(+ , -)
知识应用2
例2 在平面直角坐标系 内画出点: A(2, 3), B(5, 2), C(-3.5, 0),D(-3.5, -2), E(0, -3), F(-2, 1 ) , P(1, -2 ).
拓展提升
我来设计问题.
已知点P坐标为(2a+1,a-3),
知识拾掇2
有序数对 (-2,3) 就叫做点A在直角 5
y 点A的纵坐标
坐标系中的坐标. 4
A
3
点A的横坐标
2y
M (x,y) 有序数对(x,y) 就叫做点M在直角
1
x 坐标系中的坐标.
-4 -3 -2 -1 O 1 2 3 4 5 x -1
-2
记一记:
-3
横前纵后加括号,
中间不忘加逗号.
-4
知识应用1
拓展提升 说说点P在哪里?
点P(x,y)为平面直角坐标系中的点;
(1)若x=2,y=-3,点P在第几象限? 第四象限 (2)若x>0,y<0,点P在第几象限? 第四象限 (3)若xy>0,点P在哪里? 第一象限或第三象限
(4)若x是任意实数,y=0,点P在哪里? x轴上 (5)若xy=0,点P在哪里? 坐标轴上
例1 如图所示, 指出平面直角坐 标系内点A、B、 C、D、E、F、P 各在什么象限内 或坐标轴上?并 写出各点的坐标.
议一议:
1、每个象限内 点的坐标的符号 各有什么特点?
2、坐标轴上的 点的坐标有什么 特点?
(- , +)
(-2,2) (-3,0)
(-3,-2 )
(- , -)
平面直角坐标系(2)
(3)若点 C(x,y)满足x+y<0, xy>0 ,则点C位于第
____象限.
【解析】(1)点A(a,b)在第三象限,则a<0,b<0.所以
-a+1>0, b-5<0,所以Q(-a+1,b-5)位于第四
象限.
(2)点B(m+4,m-1)在x轴上,则m-1=0,m=1. (3)由xy>0得x,y同号,因为x+y<0,则x<0, y<0,所 以点 C(x,y)位于第三象限. 答案:(1)四 (2)1 (3)三
【解析】选A.第一象限的点横、纵坐标都为正数.
2.(成都·中考)在平面直角坐标系中,点A(2,
﹣3)位于第
象限.
【解析】由象限内的点的坐标的符号规律可得,点A
在第四象限内.
答案:四
3.(1)若点A(a,b)在第三象限,则点Q(-a+1,b-5)
位于第_____象限.
(2)若点B(m+4,m-1)在x轴上,则m=_________.
1、由点 2、由坐标
求
找
坐标 点
y 5 4 3 2
B(-4,1)
A点在x轴上的坐标为4 A点在y轴上的坐标为2 A点的坐标记作:A(4,2)
A
B
·
-3 -2 -1
·
4 5
x轴上的坐标 写在前面
x
1 O -1 1 2 3
-4
3、点坐标几何意义
-2
-3 -4
点P(x,y) 到x轴的距离是〡y〡 到y轴的距离〡x〡
只要持续地努力,不懈地奋斗,就没有征服不
了的东西.
——塞内加
1、四个象限内点的坐标(横坐标,纵坐标)特点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点B , 点C .
例2 对于正方形ABCD,建立如图直角坐标 系。写出A、B、C、D各顶点的坐标。如果把 x轴往下平移2个单位, 那么A、B、C、D各 顶点的坐标在新的坐标系中将怎样变化?
注意: 平面直角坐标系建立得适当,可以容易确定 图形上的点,建立不同的平面直角坐标系, 同一个点就会有不同的坐标
B(3,0)
的图形
对于边长为2的正ΔABC,建立适当的直角坐标 系,写出各个顶点的坐标.
y 6 5 4 3 2 1 -3 -2 y 6 5 4 3 2 1 y 6 5 4 3 2 1 3 x x
A
B -2 -3 o -1 -2 -3
-2 3 1 -3o 2 1 o 2C 31 x 2 -1 -1 -2 -2 -3 -3
课堂小结:
(1)怎样选择建立合适的直角坐标系
(2)不同的直角坐标系,同一个点 的坐标是不同的
如图是传说中的一张藏宝 岛图,藏宝人生前通过建 立直角坐标系画出这幅藏 宝图,现在我们只知道图 上两块大石头的坐标为A (1,2),B(8,9),而藏 宝地的坐标为(5,7),试 设法在地图上找到宝藏, 并表示出来。 解:根据A、B两点的坐标, 可确定原来的坐标系如图 图中的点C即藏宝地.
已知长方形ABCD的长为2,宽为1.以 AB所在直线为x轴,Ab的中点为原点, 建立直角坐标系,求长方形各个顶点的 坐标。
y D A -1 1 C
0
B 1
x
例3、一个直四边形如图所示,请建立适当的坐标系,在直角坐 标系中作出这个四边形,并标出各顶点的坐标: Y(cm) D 单位:mm 分析:为了使这个四边形的各个 200 顶点坐标容易确定,可以把点E C 作为坐标的原点,线段AB画在x 4 D(0,3.5) 150 轴上,那么DE就落在 y轴上,选 • E 择适当的比例,求出A、B、C、 3 B 100 200 50 D、各点的坐标,再描点、用线 A 2 C(2.5,1.5) 段连结起来,就得到所求图形。 • 思考:( 1)为了较方便地 解:建立直角坐标系如右图,选 1 确定点 A ,点 B 在坐标系中的 A (-1,0) 择比例为1:10,取点E为直角 B(2,0) • 0 1 • X(cm) 坐标,可怎样选择 x轴?为 2 3 -1 坐标系的原点,使线段AB在X 较方便地确定点 D的坐标, 轴上,则可得A、B、C、D各 如何选择 y轴?(2)根据所 根据上述坐标在直角坐标系中 点的坐标分别为 标注的尺寸,如何选择坐标 作点A,B,C,D,并用线段依次连 (-1,0),(2,0) 轴的单位长度? (2 .5,1.5),(0,3.5)结各点,
10Leabharlann y8 C(5,7) • 6 4 2 •A(1,2) 0 2 4 6 8 10
•B(8,9)
x
如图中的四边形ABCD就是所求作的图形
若以A为坐标原点, 建立适当的坐标系,作出 图形并写出ABCD各点的坐标。 D 200 C 150 200
y
4 3 2 1 • A
• D(1,3.5)
C(3.5,1.5)
A
100
E
B 50
•
解:建立直角坐标系如右图, (0,0) 3 4 1 2 • x 选择比例为1:10,取点A 为直角坐标系的原点,线段 AB在X轴上,则可得A、 B、C、D各点的坐标分别 用线段依次连结各点 为: 如上图中的四边形ABCD就是所求作
4.2平面直角坐标系(2)
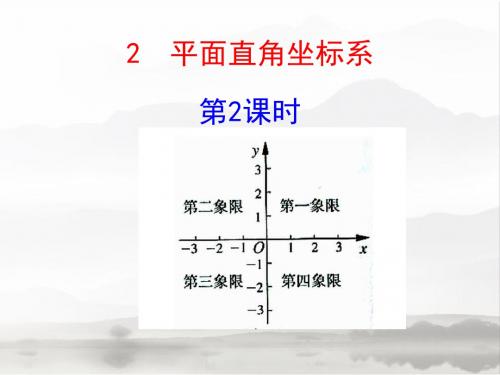
复习回顾
1.在平面上画两条 公共原点
成了平面直角坐标系. 实数 有序数对 互相垂直 、
的数轴,就组
2.数轴上的点和 标系中的点和
是一一对应的.而平面直角坐 也是一一对应的.
3.在点A(-2,-4)、B(-2,4)、C(3,-4)、D(3,4)
中,属第一象限的点是 点D ,属第二象限的点是
