木材的力学性质
木材的力学性质PPT课件

2021/4/14
4
)
表9-1 几种材料的弹性常数(E和G的单位:N/mm2)
树种
阔叶树材 轻木
核桃木
白蜡木 山毛榉 针叶树材 云杉 松木 花旗松
密度 含水率 (kg/m3) (%)
EL
ER
ET
VRT
VLR
VLT
GLT
GTR
GTR
200
9
6271 296 103 0.66 0.23 0.49 200 310 33
2021/4/14
图9-3 木材的应力松弛曲线
8
9.4 木材的各种力学强度
❖ 抗压强度 ❖ 抗拉强度 ❖ 抗剪强度 ❖ 抗弯强度和抗弯模量 ❖ 冲击韧性 ❖ 硬度 ❖ 抗劈力
2021/4/14
9
9.5 影响木材力学性质的主要因素
图9-4 温度和含水率对松木极限强度的影响 A—顺纹抗拉 B—顺纹抗压
2021/4/14
10
纹理方向的影响
❖ 木材强度受纤维倾斜影响显著。拉伸和压 缩强度均为顺纹最大,横纹最小。当载荷 与纤维方向间的夹角由小至大变化时,木 材将有规律地降低。
2021/4/14
11
图9-5木材密度对强度的影响
2021/4/14
12
图9-6 载荷时间的影响
2021/4/14
13
问题解答?
590
11 11239 1172 621 0.72 0.49 0.63 690 896 228
670
9
15790 1516 827 0.71 0.46 0.51 896 1310 269
750
11 13700 2240 1140 0.75 0.45 0.51 1060 1610 460
木材的物理力学性质

影响木材强度的主要因素
✓ 2.环境温度的影响:木材受热时,木纤维中的胶体渐渐软化, 产生强度下降,因此长期在50度的建筑部位,不宜采用木材。
✓ 3 .外力作用时间的影响: 木材在外力的长期作用下,其持久强度是短时间极限强度的 50%~60%; ✓ 4.缺陷的影响: 木材的缺陷,如木节、裂纹,腐朽和虫害,对木材的力学性质 影响也是很明显的。
1.2 湿胀干缩
木地板拼缝不严
某住宅4月份铺地板,完工后尚满意。但半年 后发现部分木地板拼缝不严,请分析原因。
当木板材质较差,而当时其含水率较高,至秋季木块 干缩,而其干缩程度随方向有明显差别,故会出现部分木 板拼缝不严。此外,若芯材向下,裂缝就更明显了。
1.3 木材的强度
• 木材的强度表现为各向异性,顺纹抗拉强度 为最大,抗弯、抗压、抗剪强度,递减。
建筑材料与检测
1.1 木材的含水率
• பைடு நூலகம்材中的水分
木材中的水分
存在部位
蒸发顺序
自由水
存在于细胞腔和细胞间隙中
首先蒸发
吸附水
存在于细胞壁中
在自由水蒸 发后,蒸发
化合水
以化学结合水的形式存在
• 平衡含水率
当木材的含水率与周围空气相对湿度达到平衡时的含水率
• 纤维饱和点含水率
➢ 当木材中细胞壁内被吸附水充满,而细胞腔间隙中没有 水时,此时的含水率称为纤维饱和点。
建筑材料与检测
7木材力学性质

弹性模量 E = σ / ε
弹性模量的意义:在弹性范围内, 物体抵抗外力使其改变形状或体 积的能力。是材料刚性的指标。
木材的拉伸、压缩、静曲弹性 模量大致相等。但压缩弹性极限 远小于拉伸弹性极限.
拉伸 压缩
图8-1 应力-应变曲线
分子表示横向应变,分母表示轴向应变。
2 木材的正交对称性与正交异向弹性
(1) 正交异向弹性 木材为正交异性体。弹性的正交异性为正交异向弹性。
(2) 木材的正交对称性
木材具有圆柱对称性,使它成为近 似呈柱面对称的正交对称性物体。符合 正交对称性的材料,可以用虎克定律来 描述它的弹性。
木材正交对称性
方程中有3个弹性模量、3个剪切弹性模量和3个泊松比。 可以用9个独立的弹性常数来反映木材的正交异向性. 不同 树种间的这9个常数值是存在差异。
木材是高度各向异 性材料,木材三个 主方向的弹性模量 即EL>>ER >ET。
木材正交异向性表现在P190
几种木材的弹性常数
材料
密度 含水
EL
g/cm3 率% MPa
ER MPa
ET MPa
GLT MPa
GLR MPa
GTR MPa
μRT
μLR
μLT
针叶树材
云杉
0.390 12 11583 896 496 690 758 39 0.43 0.37 0.47
Softening temperature of the wood components
Components of wood
cellulose
Softening temperature( ℃ )
木材的力学性质

木材的应力与应变的关系属于既有弹性又有塑 性的材料——黏弹性材料。在较小应力和较短时间 的条件下,木材的性能十分接近于弹性材料;反之, 则近似于黏弹性材料。
8.2 弹性与木材的正交异向弹性
8.2.1 弹性与弹性常数
8.2.1.1 弹性 弹性:应力解除后即产生应变完全回复的性质。 8.2.1.2 弹性常数 (1) 弹性模量和柔量
8.4.4.3 顺纹拉伸
木材顺纹拉伸破坏主要是纵向撕裂和微纤丝之间的剪 切。微纤丝纵向结合非常牢固,所以顺纹拉伸时的变形不 大,通常应变值小于1%~3%,强度值却很高。即使在这 种情况下,微纤丝本身的拉伸强度也未能充分发挥,因为 木材的纤维会在微纤丝之间撕开。木材顺纹剪切强度特别 低,通常只有顺纹抗拉强度的6%~10%。顺纹拉伸时, 微纤丝之间产生滑移使微纤丝撕裂破坏,其破坏断面通常 呈锯齿状、细裂片状或针状撕裂。其断面形状的不规则程 度,取决于木材顺拉强度和顺剪强度之比值。一般健全材 该比值较大,破坏常在强度较弱的部位剪切开,破坏断面 不平整,呈锯齿状木茬。
韧性是指材料在不致破坏的情况下所能抵御 的瞬时最大冲击能量值。
韧性材料往往是强度大的材料,但也有不符 合这个关系的。
8.4.3 木材的破坏
8.4.3.1 破坏 木材结构破坏是指其组织结构在外力或外部
环境作用下发生断裂、扭曲、错位,而使木材宏 观整体完全丧失或部分丧失原有物理力学性能的 现象。
8.4.3.2 木材破坏的原因
8.4.4.4 横纹拉伸
木材横纹拉伸分径向拉伸和弦向拉伸。
木材的横纹拉伸强度很低,只有顺纹拉伸强度的 1/35~1/65。由此可知,木材在径向和弦向拉伸时的强 度差,取决于木材密度及射线的数量与结构。
木材的力学性质

木材的力学性质主要介绍了木材力学性质的基本概念、木材的应力—应变关系;木材的正交异向弹性、木材的黏弹性、木材的塑性;木材的强度与破坏、单轴应力下木材的变形与破坏特点;基本的木材力学性能指标;影响木材力学性质的主要因素等。
木材力学是涉及木材在外力作用下的机械性质或力学性质的科学,它是木材学的一个重要组成部分。
木材力学性质是度量木材抵抗外力的能力,研究木材应力与变形有关的性质及影响因素。
木材作为一种非均质的、各向异性的天然高分子材料,许多性质都有别于其它材料,而其力学性质和更是与其它均质材料有着明显的差异。
例如,木材所有力学性质指标参数因其含水率(纤维饱和点以下)的变化而产生很大程度的改变;木材会表现出介于弹性体和非弹性体之间的黏弹性,会发生蠕变现象,并且其力学性质还会受荷载时间和环境条件的影响。
总的来说,木材的力学性质涉及面广,影响因素多,学习时需结合力学、木材构造、木材化学性质的有关知识。
木材力学性质包括应力与应变、弹性、黏弹性(塑性、蠕变)、强度(抗拉强度、抗压强度、抗弯强度、抗剪强度、扭曲强度、冲击韧性等)、硬度、抗劈力以及耐磨耗性等。
8.1 应力与应变8.1.1 应力与应变的概念8.1.1.1 应力 物体在受到外力时具有形变的趋势,其内部会产生相应的抵抗外力所致变形作用的力,成为内力,当物体处于平衡状态时,内力与外力大小相等,方向相反。
应力就是指物体在外力作用下单位面积上的内力。
当外力均匀地作用于顺纹方向的短柱状木材端面上,柱材全长的各个断面上都将受到应力,此时,单位断面面积上的木材就会产生顺纹理方向的正应力(图8-1a )。
把短柱材受压或受拉状态下产生的正应力分别称为压缩应力和拉伸应力。
当作用于物体的一对力或作用力与反作用力不在同一条作用线上,而使物体产生平行于应力作用面方向被剪切的应力,这种应力被称为剪应力(图8-1b )。
应力单位曾一度使用dyn/cm 2、kgf/cm 2等,近年来开始采用国际单位中的N/mm 2(=MPa )。
木材属性介绍

木材的力学性质木材的力学性质1. 抗压强度木材受到外界压力时,抵抗压缩变形破坏的能力,称为抗压强度。
其单位为Pa。
通常分为顺纹与横纹两种抗压强度。
(1)顺纹抗压强度,外部机械力与木材纤维方向平行时的抗压强度,称为顺纹抗压强度。
由于顺纹抗压强度变化小,容易测定,所以常以顺纹抗压强度来表示木材的力学性质。
一般木材顺纹可承受(30〜79) *106Pa的压力。
其计算公式如下:Dw=P/ab式中D -一含水率为W制,木材的顺纹抗压强度(Pa),P 式样最大载荷(N),a,b 试样的厚度和宽度(M)(2)横纹抗压强度:外部机械力与木材纤维方向互相垂直时的抗压强度,称为横纹抗压强度。
由于木材主要是由许多管状细胞组成,当木材横纹受压时,这些管状细胞很容易被压扁。
所以木材的横纹抗压极限强度比顺纹抗压极限强度低。
但是,横纹受压的面积往往较大,所以破坏时的载荷也相应大些,其公式如下:dw=P/ab式中D -一含水率为W制,木材的横纹抗压强度(Pa),P 式样最大载荷(N),a,b 试样的厚度和宽度(M)由于横纹压力测试较困难,所以我们常以顺纹抗压强度的白分比来估计横纹抗压强度。
但树种不同,比例也不同。
一般针叶树材横纹抗压极限强度为顺纹的10%阔叶树材的横纹抗压极限强度为顺纹的15〜20%2抗拉强度木材受外加拉力时,抵抗拉伸变形破坏的能力,称为抗拉强度。
它分为顺纹和横纹两种抗拉强度。
(1)顺纹抗拉强度;即外部机械拉力与木材纤维方向相互平行时的抗拉强度。
木材的顺纹抗拉强度是所有强度中最大的,各种树种平均为117.6*106Pa(2)横纹抗拉强度:即外部机械拉力与木材纤维方向相互垂直时的抗拉强度。
木材的顺纹抗拉强度。
木材横纹抗拉极限强度远较顺纹抗拉极限强度低,一般只有顺纹抗拉强度的1/10〜1/40。
这是因为木材纤维这间横向联系脆弱,容易被拉开。
因此,家具结构上应避免产生横纹拉力3抗剪强度使木材的相邻两部分产生相对位移的外力,称为剪力。
第六章 木材力学性质

第六章木材力学性质木材力学性质基本慨念与特点、主要力学性质种类及其测定方法和木材允许应力的确定原理。
6.1 木材力学性质有关的基本概念6.2 木材主要力学性质测定原理与方法6.3 影响木材力学性质的因子6.4 木材容许应力及其确定方法木材力学性质是指木材抵抗使之改变其大小和形状外力的能力,也即木材适应外力作用的能力。
现实生活中使用木材大都是利用木材力学性质,例如枕木承受横纹抗压,日用家具中桌、椅、板凳等用品的腿承受顺纹压缩荷载,建筑物上洐架、家具横梁承受弯曲载荷;枪托用材要求重量适中,弹性大,缓冲性能好。
农业机具要求耐磨,硬度大等。
木材的力学性质主要分为弹性、塑性、蠕变、松弛、抗拉强度、抗压强度、抗弯强度、抗剪强度、冲击韧性、抗劈力、抗扭强度、硬度和耐磨性等,其中以抗弯强度和抗弯弹性模量、抗压强度、抗剪强度及硬度等较为重要。
木材力学性质的测定要破坏试样的完整性下,多数性状测定其达到破坏状态时所能承受的最大外力;而处于使用状态下的木材,其所受外力要比其破坏状态时所能承受的最大外力小得多。
木材是生物材料,其构造导致木材的各向异性,因此木材的力学性质也是各向异性的,这与各向同性的金属材料和人工合成材料有很大的不同。
例如木材强度视外力作用于木材纹理的方向,有顺纹强度与横纹强度之分;而横纹强度视外力作用于年轮的方向,又有弦向强度与径向强度之别。
因此学习木材力学性质,掌握其材料的特性,对合理使用木材有着重要意义。
补充阅读资料:材料力学木材是生物质高分子材料,其力学性质主要取决于细胞壁结构特点和木材主要化学成份纤维素、木素和半纤维素的化学键结合特点与排列方式以及外力作用于木材的方式等。
前面木材解剖和木材化学性质知识的掌握对于本章的学习有很大的帮助。
有关物体承受拉、压、弯、剪切等受力分析是木材力学的基础,可参阅有关《材料力学》教材基础部分。
另外,由于木材属于高分子有机材料,木材力学性质带有高分子材料学的特点,因此学完本章后,有兴趣的同学可进一步阅读高分子材料方面的教材。
木材的力学性能
1.化学性质化学组成--纤维素、木质素和半纤维素是构成细胞壁的主要成分,此外还有脂肪、树脂、蛋白质、挥发油以及无机化合物等。
木材对酸碱有―定的抵抗力,对氧化性能强的酸,则抵抗力差;对强碱,会产生变色、膨胀、软化而导致强度下降。
―般液体的浸透对木材的影响较小.2.物理性质1)含水量木材中的含水量以含水率表示,指所含水的质量占干燥木材质量的百分比。
木材内部所含水分,可分为以下三种。
(1)自由水。
存在于细胞腔和细胞间隙中的水分。
自由水的得失影响木材的表观密度、保存性、燃烧性、抗腐蚀性、干燥性、渗透性.(2)吸附水.被吸附在细胞壁内细纤维间的水分。
吸附水的得失影响木材的强度和胀缩。
(3)化合水。
木材化学成分中的结合水。
对木材性能无大影响.纤维饱和点——指当木材中无自由水,仅细胞壁内充满了吸附水时的木材含水率。
树种不同,纤维饱和点随之不同,―般介于25%~35%,平均值约为30%。
纤维饱和点是木材物理力学性质发生变化的转折点.平衡含水率--木材长期处于―定温、湿度的空气中,达到相对稳定(即水分的蒸发和吸收趋于平衡)的含水率。
平衡含水率是随大气的温度和相对湿度的变化而变化的。
木材的含水率:新伐木材常在35%以上;风干木材在15%~25%;室内干燥木材在8%~15%.2)湿胀、干缩的特点当木材从潮湿状态干燥至纤维饱和点时,自由水蒸发,其尺寸不变,继续干燥时吸附水蒸发,则发生体积收缩。
反之,干燥木材吸湿时,发生体积膨胀,直至含水量达纤维饱和点为止。
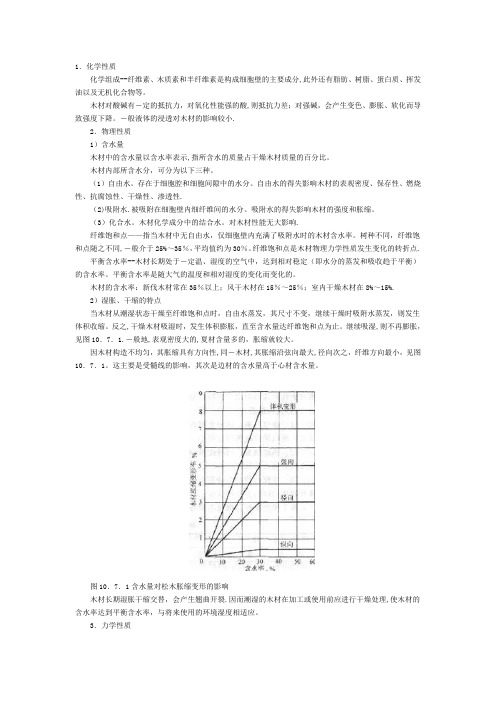
继续吸湿,则不再膨胀,见图10.7.1.―般地,表观密度大的,夏材含量多的,胀缩就较大。
因木材构造不均匀,其胀缩具有方向性,同―木材,其胀缩沿弦向最大,径向次之,纤维方向最小,见图10.7.1。
这主要是受髓线的影响,其次是边材的含水量高于心材含水量。
图10.7.1含水量对松木胀缩变形的影响木材长期湿胀干缩交替,会产生翘曲开裂.因而潮湿的木材在加工或使用前应进行干燥处理,使木材的含水率达到平衡含水率,与将来使用的环境湿度相适应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
木材的力学性质主要介绍了木材力学性质的基本概念、木材的应力—应变关系;木材的正交异向弹性、木材的黏弹性、木材的塑性;木材的强度与破坏、单轴应力下木材的变形与破坏特点;基本的木材力学性能指标;影响木材力学性质的主要因素等。
木材力学是涉及木材在外力作用下的机械性质或力学性质的科学,它是木材学的一个重要组成部分。
木材力学性质是度量木材抵抗外力的能力,研究木材应力与变形有关的性质及影响因素。
木材作为一种非均质的、各向异性的天然高分子材料,许多性质都有别于其它材料,而其力学性质和更是与其它均质材料有着明显的差异。
例如,木材所有力学性质指标参数因其含水率(纤维饱和点以下)的变化而产生很大程度的改变;木材会表现出介于弹性体和非弹性体之间的黏弹性,会发生蠕变现象,并且其力学性质还会受荷载时间和环境条件的影响。
总的来说,木材的力学性质涉及面广,影响因素多,学习时需结合力学、木材构造、木材化学性质的有关知识。
木材力学性质包括应力与应变、弹性、黏弹性(塑性、蠕变)、强度(抗拉强度、抗压强度、抗弯强度、抗剪强度、扭曲强度、冲击韧性等)、硬度、抗劈力以及耐磨耗性等。
8.1 应力与应变8.1.1 应力与应变的概念8.1.1.1 应力 物体在受到外力时具有形变的趋势,其内部会产生相应的抵抗外力所致变形作用的力,成为内力,当物体处于平衡状态时,内力与外力大小相等,方向相反。
应力就是指物体在外力作用下单位面积上的内力。
当外力均匀地作用于顺纹方向的短柱状木材端面上,柱材全长的各个断面上都将受到应力,此时,单位断面面积上的木材就会产生顺纹理方向的正应力(图8-1a )。
把短柱材受压或受拉状态下产生的正应力分别称为压缩应力和拉伸应力。
当作用于物体的一对力或作用力与反作用力不在同一条作用线上,而使物体产生平行于应力作用面方向被剪切的应力,这种应力被称为剪应力(图8-1b )。
应力单位曾一度使用dyn/cm 2、kgf/cm 2等,近年来开始采用国际单位中的N/mm 2(=MPa )。
8.1.1.2 应变 外力作用下,物体单位长度上的尺寸或形状的变化称为应变,或称相对变形。
应变也分为正应变或剪(角)应变γ。
正应变在>0时被称为拉伸变形,在<0时被称为压缩应变。
正应变、剪应变用无量纲表示,也用其百分值(%)表示。
εεε第8章图8-1 顺纹理加压与顺纹理剪切8.1.2 应力与应变的关系8.1.2.1 应力—应变曲线 物体在外力(载荷)作用下产生的变形与外力的大小有关,通常用荷载—变形图来表示它们的关系。
载荷—变形图是以纵轴表示物体受到的载荷,以横轴表示物体的变形量,坐标轴空间中根据载荷数值和变形大小做出的曲线被叫做载荷—变形曲线;同理,把表示应力与应变的关系图定义为应力—应变图,曲线为应力—应变曲线。
应力—应变曲线与材料或物质固有的性质有关,能概括性地描述物体从受外力开始直到破坏时的力学行为,是研究物体力学性质非常有用的工具。
图8-2a 模式地表示了应力—应变曲线的特征。
即:应力—应变曲线由从原点O 开始的直线部分OP 和连续的曲线部分PEDM 组成。
曲线的终点M 表示物体的破坏点。
8.1.2.2 比例极限与永久变形 直线部分的上端点P 对应的应力叫比例极限应力,对应的应变叫比例极限应变;从比例限度P 点到其上方的E 点间对应的应力叫弹性极限。
应力在弹性极限以下时,一旦除去应力,物体的应变就会完全回复,这样的应变称作弹性应变。
应力一旦超过弹性限度,应力—应变曲线的斜率减少,应变显著增大,这时如果除去应力,应变不会完全回复,其中一部分会永久残留,这样的应变称作塑性应变或永久应变。
8.1.2.3 破坏应力与破坏应变 随着应力进一步增加,应力在M 点达到最大值,物体产生破坏。
M 点对应的最大应力称作物体的破坏应力、极限强度等。
与破坏应力对应的应变叫破坏应变。
8.1.2.4 屈服应力 有时,当应力值超过弹性限度值并保持一定或基本上一定,而应变急剧增大,这种现象叫屈服,而应变突然转为急剧增大的转变点处的应力叫屈服应力。
图8-2 b 表示了弹性变形呈直线屈服时的情况,其中表示屈服应力。
8.1.2.5 木材应力与应变的关系 木材的应力与应变的关系比较复杂,因为它的性能既不像真正的弹性材料,又不像真正的塑性材料,而属于既有弹性又有塑性的材料——黏弹性材料。
在较小的应力和较短的时间里,木材的性能十分接近于弹性材料;反之,则近似于黏弹性材料。
所以,要必要先学习一下木材的弹性以及黏弹性的知识。
8.2 弹性与木材的正交异向弹性8.2.1 弹性与弹性常数8.2.1.1 弹性 应力在弹性极限以下时,一旦除去应力,物体的应变就完全消失。
这P σP εM σM εY σa b图8-2 应力-应变曲线(模式图)种应力解除后即产生应变完全回复的性质叫作弹性,而仅表现弹性的物体叫弹性体。
对弹性体的弹性可以用弹性常数来表示。
8.2.1.2 弹性常数(1) 弹性模量和柔量除大理石和橡皮以外,所有建筑材料的直线应力与相应应变的关系在比例限度以下符合虎克定律:(8-1)这里,比例常数E 叫做弹性模量或杨氏模量。
因为是无量纲比例系数,所以E 与的量纲相同,为MPa 。
弹性模量是物体产生单位应变所需要的应力,它表征材料抵抗变形能力的大小,是表示材料力学性质的重要常数。
一般来说,物体的弹性模量值愈大,在外力作用下愈不易变形,材料的强度也愈大。
弹性模量的倒数称为柔量,柔量的物理意义是单位应力的变形,表征材料产生变形的难易程度。
(2) 剪切弹性模量剪切应力τ与剪切应变γ之间,在小的范围内成比例关系,符合虎克定律:τ=G γ 或 γ=τ/G (8-2)这里,比例常数G 为剪切弹性模量,或刚性模量。
(3) 泊松比物体的弹性应变在产生应力主轴方向收缩(拉伸)的同时还往往伴随有垂直于主轴方向的横向应变,将横向应变与轴向应变之比称为泊松比,用表示。
(8-3)式中,表示横向应变,表示轴向应变,为泊松比。
右边的负号表示和的正负方向相反造成的。
泊松比和弹性模量一样,是物质固有的常数。
(4) 弹性常数弹性模量E 、剪切弹性模量G 、泊松比通常统称为弹性常数。
弹性常数用应力—应变曲线的直线区域来确定,但在实用上也可以用对应的曲线区域来确定。
这时,在应力—应变曲线上任意一点,引出切线或者割线,过切点的这条直线的斜率叫做该点或该曲线部分的弹性常数。
8.2.2 木材的正交对称性与正交异向弹性8.2.2.1 正交异向弹性 若物体相互正交的3个方向表现异性,则称物体的这种性质为正交异性,这样的物体称为正交异性体。
同理,弹性的正交异性为正交异向弹性。
8.2.2.2 木材的正交对称性 木材由于组织构造的因素决定了木材的各向异性,但由于木材的绝大多数细胞和组织平行于树干沿轴向排列,而纤维、射线组织是垂直于树干成径向同心环状排列的,这样就赋予了木材的圆柱对称性,使它成为近似呈柱面对称的正交对称性物体。
符合正交对称性的材料,可以用虎克定律来描述它的弹性。
εσE =εσμεεμ'-='εεμμ'εεμ下面,利用正交对称性来讨论木材。
如图8-3所示,假使从树干上距离髓心一定距离,切取一个相切于年轮的正交六面体小试样。
这个试样便具有3个对称轴,将平行于纵向的定义作L 轴,平行于径向的作R 轴,平行于弦向的作T 轴;它们彼此垂直,三轴中的每二轴又可构成一平面,因而又有RT 、LR 和LT 三个面,分别对应横切面、径切面和弦切面。
如果将这三个轴视为弹性对称的轴,则该试样可视为置于一个正交坐标系中,于是可以应用正交对称原理讨论木材的正交异向弹性。
8.2.2.3 木材的正交异向弹性常数 Hearmon (1953)提出用广义虎克定律分述正交对称的木材的三个主轴的应变方程,它们为:(8-4)(8-5)(8-6)(8-7)(8-8) (8-9)式中,、和分别表示轴向、弦向和径向之应变;、和分别表示3个方向之弹性模量;、和分别表示3个方向之应力。
等表示泊松比(又称横向变形系数),下角注的第一个字母表示应力方向、第二个字母表示横向应变。
即为在轴向应力作用下的径向泊松比,数值上等于径向应变与轴向应变之比。
各方向的泊松比均为小于1的数,以压应力和拉应变为正,反之为负。
表示T 和R 轴构成的面(即木材的横切面)的剪切应变。
表示径切面的剪切应力,表示弦切面的剪切模量,以此类推。
可通过上述六个方程式中存在的9个独立的弹性常数来反映木材的正交异向性,这9个常数是:3个弹性模量、3个剪切弹性模量和3个泊松比。
不同树种间的这9个常数值是存在差异的,见表8-1。
表8-1 几种木材的弹性常数 材料密度 g/cm 3 含水率 % E L MPa E R MPa E T MPa G LT MPa G LR MPa G TR MPa μRT μLR μLT 针叶树材云杉0.390 12 11583 896 496 690 758 39 0.43 0.37 0.47 松木0.550 10 16272 1103 573 676 1172 66 0.68 0.42 0.51 花旗松0.590 9 16400 1300 900 910 1180 79 0.63 0.43 0.37 阔叶树材轻木0.200 9 6274 296 103 200 310 33 0.66 0.23 0.49 核桃木0.590 11 11239 1172 621 690 896 228 0.72 0.49 0.63 白蜡木0.670 9 15790 1516 827 896 1310 269 0.71 0.46 0.51 山毛榉 0.750 11 13700 2240 1140 1060 1610 460 0.75 0.45 0.51注:E 代表弹性模量,G 代表剪切弹性模量,μ代表泊松比。
E L —顺纹(L )弹性模量;E R —水平径向(R )弹性模量;E T —水平弦向(T )弹性模量。
G LT —顺纹-弦面剪切弹性模量;G LR —顺纹-径面剪切弹性模量;G TR —水平面剪切弹性模量。
μRT —T 向压力应变/R 向延展应变;μLR —R 向压力应变/L 向延展应变;μLT —T 向压力应变/L 向延展应变。
从表8-1中数据可以看出,木材是高度各向异性材料,纵、横向的差异程度可能是所有)(1T LT R LR L L L E σμσμσζ---=-)(1T R TR L TL T T E σσμσμζ+---=-)(1T RT R L RL R R E σμσσμζ-+--=-TR TRTR G τγ-=RL RL RL G τγ-=LT LTLT G τγ-=L ζT ζR ζL E T E R E L σT σR σLR μL R LR ζζμ/=TR γRL τTL G 图8-3 木材正交对称性示意图建筑材料中的最高者。
