化工仪表及其自动化 第二章过程特性和数学模型
合集下载
化工仪表及自动化第2章
参量模型：用数学方程式表示的系统输入与输出量之间
的关系。
6
第一节 化工过程的特点及其描述方法
8.对象动态特性的研究方法
理论分析
根据系统工艺实际过程的数量关系，分析计算输入 量与输出量之间的关系。 实验研究 有些系统的输入与输出之间的关系是比较难以通过计
算来获得的。需要在实际系统或实验系统中，通过一
消去Q12、Q2、h1
dh1 1 Q1 Q12 dt A dh2 1 Q12 Q2 dt A
整理得
d 2 h2 dh T1T2 T1 T2 2 h2 KQ1 dt 2 dt
式中 T1 AR1 为第一只贮槽的时间常数； T2 AR2 为第 二只贮槽的时间常数；K R2 为整个对象的放大系数。
优点
不能适用。
24
第二节 对象数学模型的建立 一阶对象：
系统输入、输出关系（动态特性）可以用一 阶微分方程来表示的控制对象。
积分对象 系统动态特性可以用一阶积分方程来表示的 控制对象。
二阶对象：
系统动态特性可以用二阶微分方程来表示的 控制对象。
25
第二节 对象数学模型的建立
举例
1.一阶对象
3. 有自衡的振荡过程
在阶跃信号的作用下，被控变量C(t)会上下振荡，且振 荡的幅值逐渐减小，最终能趋近新的稳态值。有自衡的振
荡过程的响应曲线如图所示。在控制过程中，这类过程不
多见，它们的控制也比第一类过程困难一些。
C(t)
t
有自衡的振荡过程
14
第一节 化工过程的特点及其描述方法
4. 具有反向特性的过程 在阶跃信号的作用下，被控变量C (t)先升后降或先 降后升，即阶跃响应在初始情况与最终情况方向相反。
化工仪表及自动化第五版第二章 过程特性及其数学模型.ppt
RC电路
ei
RC
e0 根据基尔霍夫定律 ei iR e0
i C de0 dt
RC
de0 dt
e0
ei
T RC
T
de0 dt
e0
ei
一阶对象： 典型的微分方程
dh T dt h K qi
典型的阶跃响应函数
t
h(t) Ka(1 e T )
·二阶线性对象
控制变量
控制通道
道输出之和
在研究对象特性时，应预先指明对象 的输入量和输出量因为对于同一个对 象，不同通道的特性可能是不同的。
对象的数学模型可分为静态数学模型和动 态数学模型。
静态数学模型描述的是对象在静态时的输 入量与输出量之间的关系。
动态模型描述的时对象在输入量改变以后 输出量的变化情况。
静态数学模型是对象在达到平衡状态时的 动态数学模型的一个特例。
用以控制的数学模型一般是在工艺流程和 设备尺寸等都已经确定的情况下，研究的 是对象的输入变量时如何影响输出变量的， 目的是为了使所设计的控制系统达到更好 的控制效果。
用于工艺设计的数学模型是在产品规格和 产量已经确定的情况下，通过模型的计算 来确定设备的结构、尺寸、工艺流程和某 些工艺条件，以期达到最好的经济效益
一侧。
容量滞后是多容量过程的固有特性，是由于物料或能 量的传递需要通过一定的阻力而引起的。
1
F1
c(t)
h1 2
f(t)
F2
h2
3
c(0)
t
2T
1
纯滞后
容量滞后
（1）纯滞后对控制通道的影响
希望τo小。纯滞后τ对系统控制过程的影响， 是以其与时间常数的比值τ/T来衡量的。
化工仪表及自动化课后习题答案第四版
化⼯仪表及⾃动化课后习题答案第四版第⼀章,⾃动控制系统1、化⼯⾃动化主要包括哪些内容、⾃动检测,⾃动保护,⾃动操纵与⾃动控制等。
2、闭环控制系统与开环控制系统得区别。
闭环控制系统有负反馈,开环系统中被控变量就是不反馈到输⼊端得。
３、⾃动控制系统主要有哪些环节组成。
⾃动化装置及被控对象。
4、什么就是负反馈,负反馈在⾃动控制系统中得意义。
这种把系统得输出信号直接或经过⼀些环节重新返回到输⼊端得做法叫做反馈,当反馈信号取负值时叫负反馈、5、⾃动控制系统分类。
定值控制系统,随动控制系统,程序控制系统６、⾃动控制系统衰减振荡过渡过程得品质指标有及影响因素。
最⼤偏差,衰减⽐,余差,过渡时间,振荡周期对象得性质,主要包括换热器得负荷⼤⼩,换热器得结构、尺⼨、材质等,换热器内得换热情况、散热情况及结垢程度等。
７、什么就是静态与动态。
当进⼊被控对象得量与流出对象得量相等时处于静态、从⼲扰发⽣开始,经过控制,直到系统重新建⽴平衡,在这⼀段时间中,整个系统得各个环节与信号都处于变动状态之中,所以这种状态叫做动态。
第⼆章,过程特性及其数学模型1、什么就是对象特征,为什么要研究它、对象输⼊量与输出量之间得关系系统得控制质量与组成系统得每⼀个环节得特性都有密切得关系。
特别就是被控对象得特性对控制质量得影响很⼤。
2、建⽴对象得数学模型有哪两类机理建模:根据对象或⽣产过程得内部机理,列写出各种有关得平衡⽅程,从⽽获取对象得数学模型。
实验建模:⽤实验得⽅法来研究对象得特性,对实验得到得数据或曲线再加以必要得数据处理,使之转化为描述对象特性得数学模型。
混合建模:将机理建模与实验建模结合起来得,先由机理分析得⽅法提供数学模型得结构形式,然后对其中某些未知得或不确定得参数利⽤实测得⽅法给予确定。
3、反映对象特性得参数有哪些。
各有什么物理意义。
它们对⾃动控制系统有什么影响。
放⼤系数K:对象重新稳定后得输出变化量与输⼊变化量之⽐。
对象得放⼤系数K越⼤,就表⽰对象得输⼊量有⼀定变化时对输出量得影响越⼤、时间常数T:对象受到⼲扰作⽤后,被控变量到达新得稳定值所需得时间。
化工仪表及其自动化 第二章过程特性和数学模型
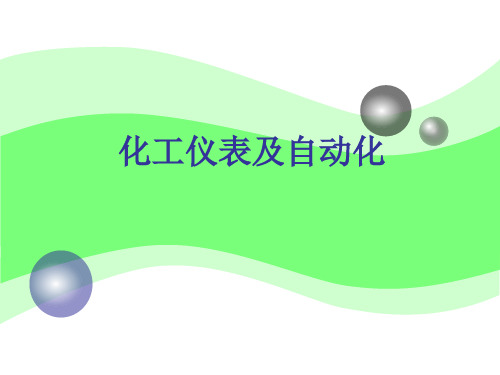
ARs
dh dt
h
RsQ1
令 T ARs , K Rs 则 T称为时间常数，K称为放大系数。
T
dh dt
h
KQ1
13
（2）RC电路
ei若取为输入参数， eo为输出参数，根据基尔霍夫定理
ei iR e0
由于 消去i
i C de0 dt
RC
de0 dt
e0
ei
图2-3 RC电路
或
T
de0 dt
27
hs KQ1 或
K hs 1 Q1 A
图2-6 水槽液位的变化曲线
K在数值上等于对象重新稳定后的输 出变化量与输入变化量之比。K越大， 就表示对象的输入量有一定变化时， 对输出量的影响越大，即被控变量对 这个量的变化越灵敏。
28
举例
以合成氨的转换炉为例，说明各个量的变化对被 控变量K的影响
T1T2
d 2h2 dt 2
T1
T2
dh2 dt
h2
KQ1
式中 T1 AR1 为第一只贮槽的时间常数； T2 AR2 为第二 只贮槽的时间常数；K R2 为整个对象的放大系数。
17
（2）RC串联电路
RC串联电路
根据基尔霍夫定律
1
ei i1R1 C1
i1 i2 dt
1
C1
i1 i2 dt i2R2 e0
传递滞后
滞 分类 后
性 质
又叫纯滞后或时滞，一般用τ0表示。τ0的
产生一般是由于介质的输送需要一段时 间而引起的。
容量滞后
对象在受到阶跃输入作用x后，被控变量y 开始变化很慢，后来才逐渐加快，最后又 变慢直至逐渐接近稳定值。
39
化工过程控制及仪表 第二章 对象数学模型.
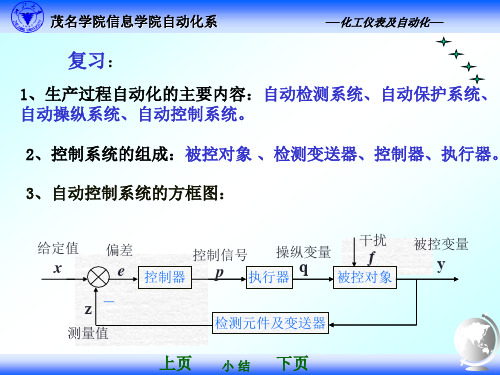
K
(T1s 1)(T2s 1)
b、时间函数（曲线）描述
A1 R1
阀1 A2
h2
R2
Q2
阀2
图2-1 液位对象
条件： 必须有特定输入。（一般常用阶跃输入）
上页 小 结 下页
茂名学院信息学院自动化系
在阶跃输入下，得到输出响应曲线
—化工仪表及自动化—
h(t)
一阶对象的传递函数一般形式: h(∞)
G
p(s)
茂名学院信息学院自动化系
—化工仪表及自动化—
② 积分对象
Q1
Q２为常数
1
Q1→h： dh= A Q1dt
1
h= A Q1 dt
h
Q２
dh T dt KQ1
K1 TA
K
h T Q1 (t t0) （无自衡特性）
上页 小 结 下页
茂名学院信息学院自动化系
—化工仪表及自动化—
使干扰作用对系统影响减小，对系统有利。
上页 小 结 下页
茂名学院信息学院自动化系
—化工仪表及自动化—
流量/（t/h）
K= (150 120 ) / 200
(28 25) / 40
=2
T=4
τ=2
微分方程：
28
25 温度/℃
150
4 dT(t2)
dt
+T(t+2)=2Q(t)
上页
120 2
小 结 下页
控制通道：起控制调整作用(q→y) 干扰通道：起干扰破坏作用(ƒ→y)
意义：是控制方案确定的依据！
上页 小 结 下页
茂名学院信息学院自动化系
—化工仪表及自动化—
一、对象特性的描述方法
第二章 过程特性及其数学模型
A—水槽截面积 将dV代入
0 h h2
t1
t
(Q1 Q2 )dt Adh
h1
t1
t
h Q2 Rs
Rs—阀的阻力
h )dt Adh 代入上式 (Q1 Rs
整理得
dh ARs h Rs Q1 dt
K=Rs
一阶常系数微分 方程
令：T=ARs 所以
dh T h KQ1 dt
t dh T h KQ1 解微分方程得 h KQ (1 e T ) 1 dt
当对象受到阶跃变化Q1=A 输出h是如何变化的。如图
Q1
A
0
h KA(1 e )
当t →∞时， h(∞)=KA 或 K=h(∞)/A
t T
t
h
h(∞) 0
t1
t
放大系数，是对象的静态参数
储槽的阶跃响应曲线
三、对象动态特性的研究方法 1.理论分析 根据系统工艺实际过程的数质量关系，分析计算 输入量与输出量之间的关系。
2.实验研究 需要在实际系统或实验系统中，通过一组输入 ,来 考察输出的跟随变化规律—反映输入与输出关系 的经验曲线和经验函数关系。
第二节 对象数学模型的建立
一、 机理建模法 机理法建摸就是根据生产过程的内在机理，写出各 种有关平衡方程式。如物料平衡方程式、能量平衡 1 方程式等。 1、一阶对象（单容对象） 举例 如图所示为一液体储槽对象 其静态方程
11．已知一个对象特性是具有纯滞后的一阶特性， 其时间常数为5，放大系数为10，纯滞后时间为2 ，试写出描述该对象特性的一阶微分方程式。
无滞后 有滞后 一阶微分方程式：
dy(t 2) 5 y(t 2) 10 x(t ) dt
0 h h2
t1
t
(Q1 Q2 )dt Adh
h1
t1
t
h Q2 Rs
Rs—阀的阻力
h )dt Adh 代入上式 (Q1 Rs
整理得
dh ARs h Rs Q1 dt
K=Rs
一阶常系数微分 方程
令：T=ARs 所以
dh T h KQ1 dt
t dh T h KQ1 解微分方程得 h KQ (1 e T ) 1 dt
当对象受到阶跃变化Q1=A 输出h是如何变化的。如图
Q1
A
0
h KA(1 e )
当t →∞时， h(∞)=KA 或 K=h(∞)/A
t T
t
h
h(∞) 0
t1
t
放大系数，是对象的静态参数
储槽的阶跃响应曲线
三、对象动态特性的研究方法 1.理论分析 根据系统工艺实际过程的数质量关系，分析计算 输入量与输出量之间的关系。
2.实验研究 需要在实际系统或实验系统中，通过一组输入 ,来 考察输出的跟随变化规律—反映输入与输出关系 的经验曲线和经验函数关系。
第二节 对象数学模型的建立
一、 机理建模法 机理法建摸就是根据生产过程的内在机理，写出各 种有关平衡方程式。如物料平衡方程式、能量平衡 1 方程式等。 1、一阶对象（单容对象） 举例 如图所示为一液体储槽对象 其静态方程
11．已知一个对象特性是具有纯滞后的一阶特性， 其时间常数为5，放大系数为10，纯滞后时间为2 ，试写出描述该对象特性的一阶微分方程式。
无滞后 有滞后 一阶微分方程式：
dy(t 2) 5 y(t 2) 10 x(t ) dt
化工仪表及自动化第五版第二章 过程特性及其数学模型.ppt
对象机理数学模型的建立
问题：处于平衡状态的对象加入干扰以后，不经控制系统能否自行达到新的平衡状态？
qi
qi
q0
q0
左图：假设初始为平衡状态qi=qo，水箱水位保持不变。 当发生变化时(qi＞qo)，此时水箱的水位开始升高
根据流体力学原理，水箱出口流量与H是存在一定的对应关系的：q0 H / R
y(t)表示输出量，x(t)表示输入量，通常输出量的阶次不低与输入量的阶次(n≥m) 通常n=1，称该对象为一阶对象模型；n=2，称二阶对象模型。
非参量模型：采用曲线、表格等形式表示。 特点：形象、清晰，缺乏数学方程的解析性质（必要时须进行数学处 理获得参量模型）。
第二节 对象数学模型的建立
建模的目的（略）
因此，qi H qo，直至qi=qo可见该系统受到干扰以后，即使不加控制，最 终自身是会回到新的平衡状态，这种特性称为“自衡特性”。
右图：如果水箱出口由泵打出，其不同之处在于：qi当发生变化时，qo不发生变化。如 果qi＞qo ，水位H将不断上升，直至溢出，可见该系统是无自衡能力。
绝大多数对象都有自衡能力，一般而言有自衡能力的系统比无自衡能力的系统容易控制。
d 2h2 dt 2
(R1 A1
R2
A2
)
dh2 dt
h2
R2
qi
T1T2
d 2h2 dt 2
(T1
T2
)
dh2 dt
h2
K
qi
(T1 A1R1 T2 A2R2
K R2 )
·二阶线性对象（总结）
典型的微分方程
T1T2
d 2h2 dt 2
(T1
化工自动化及仪表教学
⑵ 放大系数K对系统的影响
控制通道 放大系数越大，操纵变量的变化对被控变量的影响就越大，控制作用对扰
动的补偿能力强，有利于克服扰动的影响，余差就越小；反之，放大系数小， 控制作用的影响不显著，被控变量变化缓慢。但放大系数过大，会使控制作用 对被控变量的影响过强，使系统稳定性下降。
扰动通道
当扰动频繁出现且幅度较大时，放大系数大，被控变量的波动就
第三页，编辑于星期一：十五点 三十六分。
过程特性的类型
1.自衡的非振荡过程
在阶跃信号的作用下，被控变量C (t)不经振荡，逐渐向新的稳态值C(∞) 靠拢。
C(t) C(∞)
t
自衡的非振荡过程
第四页，编辑于星期一：十五点 三十六分。
过程特性的类型
例如
如图所示的通过阀门阻力排液的液位系统
Q1
Q1
h
t h
描述过程特性的参数
⑵ 时间常数T对系统的影响
控制通道
在相同的控制作用下，时间常数大，被控变量的变化比较缓 慢，此时过程比较平稳，容易进行控制，但过渡过程时间较 长；若时间常数小，则被控变量的变化速度快，控制过程比 较灵敏，不易控制。时间常数太大或太小，对控制上都不利。 扰动通道 控制通道，对于扰动通道，时间常数大，扰动作用比较平缓， 被控变量的变化比较平稳，过程较易控制。
E
+
-
Ti
⑵ 建立原始微分方程
T0
根据能量守恒定律： 单位时间传入的热量—单位时间传出的热量 =单位时间热量的变化量
热电偶的原始微分方程式为
Qi
Q0
C
dT0 dt
式中 Qi为被测介质以对流方式传给热端的热量；
Qo为热端通过热电极传导出的热量；
控制通道 放大系数越大，操纵变量的变化对被控变量的影响就越大，控制作用对扰
动的补偿能力强，有利于克服扰动的影响，余差就越小；反之，放大系数小， 控制作用的影响不显著，被控变量变化缓慢。但放大系数过大，会使控制作用 对被控变量的影响过强，使系统稳定性下降。
扰动通道
当扰动频繁出现且幅度较大时，放大系数大，被控变量的波动就
第三页，编辑于星期一：十五点 三十六分。
过程特性的类型
1.自衡的非振荡过程
在阶跃信号的作用下，被控变量C (t)不经振荡，逐渐向新的稳态值C(∞) 靠拢。
C(t) C(∞)
t
自衡的非振荡过程
第四页，编辑于星期一：十五点 三十六分。
过程特性的类型
例如
如图所示的通过阀门阻力排液的液位系统
Q1
Q1
h
t h
描述过程特性的参数
⑵ 时间常数T对系统的影响
控制通道
在相同的控制作用下，时间常数大，被控变量的变化比较缓 慢，此时过程比较平稳，容易进行控制，但过渡过程时间较 长；若时间常数小，则被控变量的变化速度快，控制过程比 较灵敏，不易控制。时间常数太大或太小，对控制上都不利。 扰动通道 控制通道，对于扰动通道，时间常数大，扰动作用比较平缓， 被控变量的变化比较平稳，过程较易控制。
E
+
-
Ti
⑵ 建立原始微分方程
T0
根据能量守恒定律： 单位时间传入的热量—单位时间传出的热量 =单位时间热量的变化量
热电偶的原始微分方程式为
Qi
Q0
C
dT0 dt
式中 Qi为被测介质以对流方式传给热端的热量；
Qo为热端通过热电极传导出的热量；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
化工仪表及自动化
上节课主要内容
自动控制系统的组成 自动控制系统的方块图
自动控制系统方块图 反馈 自动控制系统的分类
过渡过程和品质指标
控制系统的静态与动态 控制系统的过渡过程 控制系统的控制指标
1
第二章 过程特性和数学模型
化工过程的特点及描述方法
被控对象数学模型 数学模型的主要形式
或
T RC K=1
14
2、积分对象
当对象的输出参数与输入参数对时间的积分成比例关系时， 称为积分对象。
Q2为常数，变化量为0
1 dh Q1dt A
其中，A为贮槽横截面积
1 h Q1dt A
图2-4 积分对象 说明，所示贮槽具有积分特性。
（2-2）
15
3.二阶对象
（1）串联水槽对象
数学模型的建立
一阶对象 积分对象 二阶对象
描述对象特性的参数
放大系数Κ 时间常数Τ 滞后时间τ
2
第一节 化工过程的特点及描述方法
一、被控对象数学模型
自动控制系统是由被控对象、测量变送装置、控
制器和执行器组成。 研究对象的特性，就是用数学的方法来描述出对象输 入量与输出量之间的关系。这种对象特性的数学描述就称 为对象的数学模型。干扰作用和控制作用都是引起被控变 量变化的因素，如下图所示。 几个概念 通道 调节通道 干扰通道
机理建模 实验建模 混合模型
9
机理模型——从机理出发,即从对象内在的物理和
化学规律出发, 建立描述对象输入输出特性的数学 模型。 优点：具有非常明确的物理意义，所得的模型具有 很大的适应性，便于对模型参数进行调整。 缺点：对象特性比较复杂，有些难于用适当的数 学式表示。
10
经验模型——对于已经投产的生产过程,我们可以
根据基尔霍夫定律
1 ei i1 R1 i1 i2 dt C1 1 i1 i2 dt i2 R2 e0 C1
RC串联电路
1 e0 i2 dt C2
整理得
d 2e0 de0 R1C1R2C2 R1C1 R2C2 R1C2 e0 ei dt2 dt
18
二、实验建模
定义 实验方法 研究对象特性
通过实验来测取对象的输入输出数据并对数据进行必 要处理得到的数学模型。 几个概念 系统辨识 参数估计
测试信号的不同 阶跃反应曲线
矩形脉冲特性曲线 频率特性
19
图2-5 对象特性连接图 特点： 把被研究的对象视为一个黑匣子，完全从外部 特性上来测试和描述它的动态特性，不需要深入了解 其内部机理 。
20
1、阶跃反应曲线法
对象在阶跃输入作用下，输出
量随时间的变化。
不需特殊的仪器或设备，简单
易行；但其精度较差。
阶跃反应曲线
21
2、矩形脉冲法
在对象突然加上一阶跃干扰，
一段时间后突然除去该阶跃干扰，
输出量随时间的变化。 精度较高，对正常生产的影响 较小。
令
T ARs , K Rs
则
T
dh h KQ1 dt
T称为时间常数，K称为放大系输入参数， eo为输出参数，根据基尔霍夫定理
ei iR e0
de0 iC dt
由于
消去i 图2-3 RC电路
de0 RC e0 ei dt
de0 T e0 ei dt
假定输入、输出量变化很小的情况下， 贮槽的液位与输出流量具有线性关系。
h1 Q12 R2
串联水槽对象
h2 Q2 R2
假定每只贮槽的截面积都为A，则
Q1 Q12 dt Adh1
16
Q12 Q2 dt Adh2
转到26页
消去Q12、Q2、h1
dh1 1 Q1 Q12 dt A
动态数学模型的形式主要有微分方程、传递函数、 差分方程及状态方程等
7
第二节 对象数学模型的建立 建模目的
设计控制系统的基础 控制系统的调试和控制器参数确定的基础 制定工业过程操作优化方案 新型控制方案及控制算法的确定 计算机仿真与过程培训系统
设计工业过程的故障检测与诊断系统
8
分类 数学模型建立的途径不同
图2-1 对象的输入、输出量
3
？
对象的数学模型分为静态数学模型和动态数学模型
基础
静态数学模型
特例
动态数学模型
4
用于控制的数学模型与用于工艺设计与分析的数 学模型不完全相同。
一般是在工艺 流程和设备尺 寸等都确定的 情况，研究对 象的输入变量 是如何影响输 出变量的。 研究的 的是为 使所设 的控制 统达到 好的控 效果。 目 了 计 系 更 制 在产品规格和产量 已确定的情况下， 通过模型计算，确 定设备的结构、尺 寸、工艺流程和某 些工艺条件。 工艺设计与分析
整理得
dh2 1 Q12 Q2 dt A
d 2 h2 dh2 T1T2 T1 T2 h2 KQ1 2 dt dt
式中 T1 AR1 为第一只贮槽的时间常数； T2 AR2 为第二 只贮槽的时间常数； K R2 为整个对象的放大系数。
17
（2）RC串联电路
通过实验测试或依据积累的操作数据,对系统的输 入输出数据,通过数学回归方法进行处理。 经验模型更符合对象的特性，可用于机理模型的验 证或修改。
混合模型——通过机理分析,得出模型的结构或函
数形式，而对其中的部分参数通过实测得到。
11
一、机理建模
1、一阶对象
对象特性可用一阶微分方 程描述的对象
（1）水槽对象
依据
对象物料蓄存量的变化率 ＝单位时间流入对象的物料－单位时间流出对象的物料
12
Q1 Q2 dt Adh
h Q2 Rs
（2-1）
若变化量很微小，可以近似认为Q2与h 成正比， 与出水阀的阻力系数Rs成反比
将上式代入（2-1）式，移项
图2-2 水槽对象
dh ARs h Rs Q1 dt
控制
5
二、数学模型的主要形式
非参量模型
当数学模型是采用曲线或数据表格等来表示时，称 为非参量模型。 特点 缺点 表达形式 形象、清晰，比较容易看出其定性的特征 直接利用它们来进行系统的分析和设计往往 比较困难 对象在一定形式输入作用下的输出曲线或数据来表示
6
参量模型
当数学模型是采用数学方程式来描述时，称为参 量模型。 静态数学模型比较简单,一般可用代数方程式表示。
上节课主要内容
自动控制系统的组成 自动控制系统的方块图
自动控制系统方块图 反馈 自动控制系统的分类
过渡过程和品质指标
控制系统的静态与动态 控制系统的过渡过程 控制系统的控制指标
1
第二章 过程特性和数学模型
化工过程的特点及描述方法
被控对象数学模型 数学模型的主要形式
或
T RC K=1
14
2、积分对象
当对象的输出参数与输入参数对时间的积分成比例关系时， 称为积分对象。
Q2为常数，变化量为0
1 dh Q1dt A
其中，A为贮槽横截面积
1 h Q1dt A
图2-4 积分对象 说明，所示贮槽具有积分特性。
（2-2）
15
3.二阶对象
（1）串联水槽对象
数学模型的建立
一阶对象 积分对象 二阶对象
描述对象特性的参数
放大系数Κ 时间常数Τ 滞后时间τ
2
第一节 化工过程的特点及描述方法
一、被控对象数学模型
自动控制系统是由被控对象、测量变送装置、控
制器和执行器组成。 研究对象的特性，就是用数学的方法来描述出对象输 入量与输出量之间的关系。这种对象特性的数学描述就称 为对象的数学模型。干扰作用和控制作用都是引起被控变 量变化的因素，如下图所示。 几个概念 通道 调节通道 干扰通道
机理建模 实验建模 混合模型
9
机理模型——从机理出发,即从对象内在的物理和
化学规律出发, 建立描述对象输入输出特性的数学 模型。 优点：具有非常明确的物理意义，所得的模型具有 很大的适应性，便于对模型参数进行调整。 缺点：对象特性比较复杂，有些难于用适当的数 学式表示。
10
经验模型——对于已经投产的生产过程,我们可以
根据基尔霍夫定律
1 ei i1 R1 i1 i2 dt C1 1 i1 i2 dt i2 R2 e0 C1
RC串联电路
1 e0 i2 dt C2
整理得
d 2e0 de0 R1C1R2C2 R1C1 R2C2 R1C2 e0 ei dt2 dt
18
二、实验建模
定义 实验方法 研究对象特性
通过实验来测取对象的输入输出数据并对数据进行必 要处理得到的数学模型。 几个概念 系统辨识 参数估计
测试信号的不同 阶跃反应曲线
矩形脉冲特性曲线 频率特性
19
图2-5 对象特性连接图 特点： 把被研究的对象视为一个黑匣子，完全从外部 特性上来测试和描述它的动态特性，不需要深入了解 其内部机理 。
20
1、阶跃反应曲线法
对象在阶跃输入作用下，输出
量随时间的变化。
不需特殊的仪器或设备，简单
易行；但其精度较差。
阶跃反应曲线
21
2、矩形脉冲法
在对象突然加上一阶跃干扰，
一段时间后突然除去该阶跃干扰，
输出量随时间的变化。 精度较高，对正常生产的影响 较小。
令
T ARs , K Rs
则
T
dh h KQ1 dt
T称为时间常数，K称为放大系输入参数， eo为输出参数，根据基尔霍夫定理
ei iR e0
de0 iC dt
由于
消去i 图2-3 RC电路
de0 RC e0 ei dt
de0 T e0 ei dt
假定输入、输出量变化很小的情况下， 贮槽的液位与输出流量具有线性关系。
h1 Q12 R2
串联水槽对象
h2 Q2 R2
假定每只贮槽的截面积都为A，则
Q1 Q12 dt Adh1
16
Q12 Q2 dt Adh2
转到26页
消去Q12、Q2、h1
dh1 1 Q1 Q12 dt A
动态数学模型的形式主要有微分方程、传递函数、 差分方程及状态方程等
7
第二节 对象数学模型的建立 建模目的
设计控制系统的基础 控制系统的调试和控制器参数确定的基础 制定工业过程操作优化方案 新型控制方案及控制算法的确定 计算机仿真与过程培训系统
设计工业过程的故障检测与诊断系统
8
分类 数学模型建立的途径不同
图2-1 对象的输入、输出量
3
？
对象的数学模型分为静态数学模型和动态数学模型
基础
静态数学模型
特例
动态数学模型
4
用于控制的数学模型与用于工艺设计与分析的数 学模型不完全相同。
一般是在工艺 流程和设备尺 寸等都确定的 情况，研究对 象的输入变量 是如何影响输 出变量的。 研究的 的是为 使所设 的控制 统达到 好的控 效果。 目 了 计 系 更 制 在产品规格和产量 已确定的情况下， 通过模型计算，确 定设备的结构、尺 寸、工艺流程和某 些工艺条件。 工艺设计与分析
整理得
dh2 1 Q12 Q2 dt A
d 2 h2 dh2 T1T2 T1 T2 h2 KQ1 2 dt dt
式中 T1 AR1 为第一只贮槽的时间常数； T2 AR2 为第二 只贮槽的时间常数； K R2 为整个对象的放大系数。
17
（2）RC串联电路
通过实验测试或依据积累的操作数据,对系统的输 入输出数据,通过数学回归方法进行处理。 经验模型更符合对象的特性，可用于机理模型的验 证或修改。
混合模型——通过机理分析,得出模型的结构或函
数形式，而对其中的部分参数通过实测得到。
11
一、机理建模
1、一阶对象
对象特性可用一阶微分方 程描述的对象
（1）水槽对象
依据
对象物料蓄存量的变化率 ＝单位时间流入对象的物料－单位时间流出对象的物料
12
Q1 Q2 dt Adh
h Q2 Rs
（2-1）
若变化量很微小，可以近似认为Q2与h 成正比， 与出水阀的阻力系数Rs成反比
将上式代入（2-1）式，移项
图2-2 水槽对象
dh ARs h Rs Q1 dt
控制
5
二、数学模型的主要形式
非参量模型
当数学模型是采用曲线或数据表格等来表示时，称 为非参量模型。 特点 缺点 表达形式 形象、清晰，比较容易看出其定性的特征 直接利用它们来进行系统的分析和设计往往 比较困难 对象在一定形式输入作用下的输出曲线或数据来表示
6
参量模型
当数学模型是采用数学方程式来描述时，称为参 量模型。 静态数学模型比较简单,一般可用代数方程式表示。