binarytree1
BinaryTree表示法---阵列
#include <stdlib.h> struct tree /*樹的結構宣告*/ { int data; /*節點資料*/ int left; /*指向左子樹的位置*/ int right; /*指向右子樹的位置 */ }; typedef struct tree treenode; /*樹的結構新型 態*/ treenode btree[15]; /*宣告樹的結構陣列*/ void createbtree(int *data,int len) { int level; /*樹的階層*/ int pos; /* -1是右樹,1是左樹 */ int i; btree[0].data = data[0]; /* 建立樹根節點*/
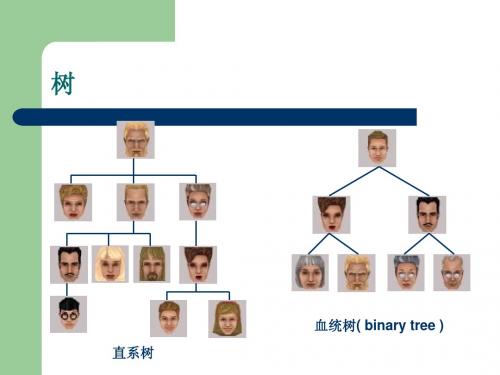
將下列資料依序輸入一個二元樹,則建立的二 元樹如下圖: 15,6,4,8,23,77,1,19
(2) (4) 4 6 (5) 8 (6) 19 15 (1) (3) 23 (7) 77
(8) 1
Binary Tree陣列表示法---程式碼
#include<stdio.h> #include<stdlib.h> void createbtree(int *btree,int *data,int len) { int level; /*樹的階層*/ int i; btree[1] = data[0]; /*建立根節點*/ for ( i = 2; i <= len; i++ ) /*用迴路建立其 它節點*/ { level = 1; /*從階層1開始*/ while ( btree[level] != 0 ) /*是否有子樹*/ { if ( data[i-1] > btree[level] ) /*是左或右 子 樹*/ level = level * 2 + 1; /*右子樹*/ else level = level * 2; /*左子樹*/ } btree[level] = data[i-1]; /*存入節點資料*/ } }
BinaryTree-距离它们最近的共同祖先

BinaryTree-距离它们最近的共同祖先已知在二叉树中,*root为根结点,*p和*q为二叉树中两个结点,试编写求距离它们最近的共同祖先的算法#include <stdio.h> #include <malloc.h>typedef struct BiTNode { //定义二叉树结点char data;struct BiTNode *lChild, *rChild;} BiTNode, *BiTree;void createBiTree(BiTree &T) { //创建二叉树char c = getchar();if(c == '*') T = NULL;else {T = (BiTree)malloc(sizeof(BiTNode));T->data = c;createBiTree(T->lChild);createBiTree(T->rChild);}}bool findPath(BiTree T, BiTree p, BiTree path[], int &n) { //找到共同路径if(T && p) {if(p == T) return true;if(findPath(T->lChild, p, path, n) || findPath(T->rChild, p, path, n)) {path[n] = T;n ++;return true;} else return false;} else return false;}BiTree findCloseAncient(BiTree T, BiTree p, BiTree q) {//在二叉树T中找到p和q的最近祖先int i, j;int x = 0, y = 0;//x表示p的祖先的个数,y表示q的祖先的个数BiTree pathP[255], pathQ[255]; //设立两个辅助数组暂存从根到p,q的路径findPath(T, p, pathP, x);//求从根到p,q的路径放在pathp和pathq中findPath(T, q, pathQ, y);printf("x = %d, y = %d\n", x, y);i = x - 1;//从第x-1到第0个存放p的祖先j = y - 1;//从第y-1到第0个存放q的祖先if(i >= 0 && j >= 0) {//当它们之中的任何一个结点至少存在一个祖先while(pathP[i] == pathQ[j] && i > 0 && j > 0) {i --; j --;}return pathP[i];} else//当它们之中的任何一个结点都不存在祖先,则返回NULLreturn NULL;}//根据c值找到树的一个结点,该结点的值与c相等。
二进制trie树算法

二进制trie树算法二进制Trie树算法概述二进制Trie树算法是一种用于高效存储和查询二进制数据的数据结构。
它通过将二进制数据的每一位作为树的节点来构建树结构,从而实现了对二进制数据的快速检索和插入操作。
本文将介绍二进制Trie树的原理、构建过程、插入和查询操作以及相关的应用场景。
一、原理二进制Trie树是一种前缀树的变种,它的每个节点都有两个子节点,分别对应二进制的0和1。
对于一个二进制数据,根节点表示最高位,每向下一层则表示二进制的下一位。
当插入或查询数据时,从根节点开始,根据数据每一位的值选择相应的子节点,直到达到数据的最后一位或者遇到空节点。
二、构建过程构建二进制Trie树的过程是逐位插入二进制数据的过程。
从根节点开始,根据数据的每一位选择相应的子节点,如果子节点不存在,则新建一个子节点。
如果数据的所有位都插入完成,将最后一个节点标记为叶节点,表示该节点代表一个完整的二进制数据。
三、插入操作插入一个二进制数据的过程就是将该数据的每一位逐个插入到Trie树中的过程。
从根节点开始,根据数据的每一位选择相应的子节点,如果子节点不存在,则新建一个子节点。
如果数据的所有位都插入完成,将最后一个节点标记为叶节点。
四、查询操作查询一个二进制数据的过程是根据数据的每一位在Trie树中查找对应的子节点。
从根节点开始,根据数据的每一位选择相应的子节点,如果子节点不存在,则表示该二进制数据不存在于Trie树中。
如果遍历到了数据的最后一位,并且最后一个节点被标记为叶节点,表示该二进制数据存在于Trie树中。
五、应用场景二进制Trie树广泛应用于网络路由表、IP地址查找、字符串匹配等领域。
在网络路由表中,每个节点表示一个路由前缀,节点的子节点表示该前缀的下一跳路由。
通过二进制Trie树可以快速找到匹配的路由前缀,从而实现高效的数据包转发。
在IP地址查找中,可以将每个IP地址转换为二进制表示,然后通过二进制Trie树进行快速查找。
数据结构之二叉树(BinaryTree)

数据结构之⼆叉树(BinaryTree)⽬录导读 ⼆叉树是⼀种很常见的数据结构,但要注意的是,⼆叉树并不是树的特殊情况,⼆叉树与树是两种不⼀样的数据结构。
⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质(6个) 六、⼆叉树的存储结构(2种) 七、⼆叉树的遍历算法(4种) ⼋、⼆叉树的基本应⽤:⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义(有限个结点组成的具有层次关系的集合),那么就很好理解⼆叉树了。
定义:⼆叉树是n(n≥0)个结点的有限集,⼆叉树是每个结点最多有两个⼦树的树结构,它由⼀个根结点及左⼦树和右⼦树组成。
(这⾥的左⼦树和右⼦树也是⼆叉树)。
值得注意的是,⼆叉树和“度⾄多为2的有序树”⼏乎⼀样,但,⼆叉树不是树的特殊情形。
具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分,不能颠倒。
⽆序树的⼦树⽆左右之分。
2、⼆叉树与有序树也不同(关键) 当有序树有两个⼦树时,确实可以看做⼀颗⼆叉树,但当只有⼀个⼦树时,就没有了左右之分,如图所⽰:三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树;⽽国际定义为,不存在度为1的结点,即结点的度要么为2要么为0,这样的⼆叉树就称为满⼆叉树。
这两种概念完全不同,既然在国内,我们就默认第⼀种定义就好)。
完全⼆叉树:如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号,如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应,那么这就是⼀颗完全⼆叉树。
如图所⽰:五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的,这些性质不必死记,使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。
性质1:⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。
证明:设⼆叉树的叶⼦结点数为X,单分⽀结点数为Y,双分⽀结点数为Z。
BinaryTree哈夫曼树的定...

第6章树和二叉树Tree and Binary Tree(3)树的带权路径长度WPL:树中所有叶子带权路径长度之和∑=×=ni liwi WPL 1n—树叶个数哈夫曼树:由权值为{ w1,w2,...,wn)的n 片叶子构成的所有二叉树中,WPL 值最小的二叉树。
哈夫曼树又被称为最优二叉树结点的带权路径长度:结点的权值乘结点到根的路径长度w i ×l i6.6.2 哈夫曼树的构造1952年,Huffman提出了一个构造最优二叉树的一个精巧算法,被人们称为Huffman算法。
6.6.3 哈夫曼编码和解码编码发送:电文ÖÖÖ0,1 序列(比特流)接收:0, 1序列ÖÖÖ电文解码例如:电文=“abcdedacafcfadcacfdaef”字符集={ a, b, c, d, e, f }字符出现次数={6, 1, 5, 4, 2, 4 }显然,如果ci 是权,比特流长度就是二叉树的WPL 。
哈夫曼树的WPL 是最小的,故用哈夫曼树产生前缀码是最优前缀码,又称为哈夫曼编码。
∑=×=ni lii 1c 比特流长n —字符个数ci-字符在电文中重复出现次数li-串长,根到叶子的路径长度由于哈夫曼树中没有度为1的结点(这类树又称严格的(或正则的)二叉树),则一棵有n个叶子结点的哈夫曼树共有2n-1个结点,可以存储在大小为2n-1的一维数组中。
在哈夫曼树中,为求编码需从叶子结点出发走一条从叶子到根的路径,而为译码需从根出发走一条从根到叶子的路径。
则对每个结点而言,即需知双亲的信息,又需知孩子结点的信息,由此,存储结构定义如下:typedef struct{unsigned int weight;unsigned int parent, lchild, rchild;}HTNode, *HuffmanTree;typedef char **HuffmanCode;HT7cd8求哈夫曼编码的算法描述如下:void HuffmanCoding( HuffmanTree&HT, HuffmanCode&HC, int*w, int n){ //w存放n个字符的权值(均>0),构造哈夫曼树HT,并求出n个字符的哈夫曼编码HCif(n<=1) exit(0) ;m = 2*n-1;HT = (HuffmanTree)malloc((m+1)*sizeof(HTNode));for(p= HT, i=1; i<=n; ++i, ++p, ++w) *p = {*w, 0, 0, 0};for( ; i<=m; ++i, ++p) *p = { 0, 0, 0, 0 };for(i= n+1; i<=m; ++i) { //建立哈夫曼树//在HT[1..i-1]选择parent为0且weight最小的两个结点,其序号分别为S1和S2 Select( HT, i-1, S1, S2 );HT[s1].parent = i; HT[s2].parent = i;HT[i].lchild= S1; HT[i].rchild= S2;HT[i].weight= HT[s1].weight + HT[s2].weight;}//---------从叶子到根逆向求每个字符的哈夫曼编码-----------HC = (HuffmanCode)malloc((n+1)*sizeof(char*));cd= (char*)malloc(n*sizeof(char)); //分配求编码的工作空间cd[n-1] = ‘\0’;for(i= 1; i<n; ++i) //逐个字符求哈夫曼编码{ start = n-1; //编码结束符位置for( c=i, f=HT[i].parent; f!=0; c=f, f=HT[f].parent)if( HT[f].lchild== c) cd[--start] = ‘0’;else cd[--start] = ‘1’;HC[i] = (char*)malloc(n-start)*sizeof(char));strcpy(HC[i], &cd[start]); //从cd复制编码(串)到HC }free(cd); //释放工作空间}//HuffmanCodingHuffman解码:将比特流还原成电文也是在哈夫曼树上实现的:从左至右扫描比特流;自树根开始,逢0沿左链向下,逢1沿右链向下,直到遇到到叶子;还原叶子字符;再回到树根;重复上述过程,直至比特流被扫描完。
Binary Index Tree (1)

算法分享
树状数组逻辑
• 我们考察这两种操作下标变化的规律:
首先看修改操作已知下标i,求其父节点的下标
算法分享
树状数组逻辑
• 对树从逻辑上转化
我们将子树向右对称翻折,虚拟出一些空白结点(图中白色),将原树转化 成完全二叉树。 由图可知,对于节点i,其父节点的 下标与翻折出的空白节点下标相同。
算法分享
/tc?module=Static&d1=tutorials&d2 =binaryIndexedTrees
The End Thank you!
算法分享
树状数组逻辑
• 把树状数组最后一位非0位+1 C[1112]+12=C[10002] C[1102]+102=C[10002] C[1002]+1002=C[10002]
算法分享
树状数组实现
• add()函数 void add(int idx,int delta) { while(idx<=N) { C[idx]+=delta; idx+=lowBit(idx); } }
树状数组逻辑
• 对树从逻辑上转化
因而父节点下标 p=i+2^k (2^k是i用2的幂方和展开式中的最小幂,即i为根节点 子树的规模) 即 p = i + i&(i^(i-1)) 。
算法分享
参考资料
/wifecooky/archive/2010/05/31/116809.a spx
算法分享
树状数组逻辑
• 求和操作 i=710=1112 S[7]=C[1112]+C[1102]+C[1002]+c[0002] =C[7]+C[6]+C[4]+C[0]
软件技术基础第二章(5)
满二叉树和完全二叉树
完全二叉树:深度为k的, 有n个结点的二叉树,当 且仅当其每一个结点都 与深度为k的满二叉树中 编号从1至n的结点一一 对应时,称为完全二叉树. 换句话说:除最后一层外, 每一层上的结点数都达 到最大值,在最后一层上 只缺少右边的若干结点 由此可得:满二叉树也是完全二叉树,而完全二叉树一般不 是满二叉树
path from n1 to nk (从n1到nk的路径)::= 一条 单一 (unique) 的结点序列 n1, n2, …, nk 在序 列中 ni 是 ni+1 (1 i < k).的父结点
A
B E K L F C G H M D I J
Level 1 2 3 4
length of path(路径长度) ::= 路径的结点 数. depth of ni (ni的深度)::= 从根结点到ni的路 径长度Depth(root) = 0.
由于子结点的顺序不同所以表达方式不唯一确定表示为一棵二叉树rotateleftchildrightsiblingtreeclockwise45leftchildrightchilddataleftchildrightchilditsrightchildalwaysemptybinarytree同样我们从根结点和子树的角度来定义二叉树1非空二叉树只有一个根结点
Homework
P107 2.20 2.22
height ( 高度,也有做深度depth的解释 ) ::= 最大级数目(max { levels }.)
例:用树表示表达式
计算机中用树来表示算术表达式,原则如下:
(1)表达式中的每一个运算符在树中对应一个 结点,称为运算符结点。 (2)运算符的每一个运算对象在树中为该运算 符结点的子树(在树中的顺序为从左到右)。 (3) 运 算 对 象 中 的 单 变 量 均 为 叶 子 结 点 。 a*(b+c/d)+e*h-g*f(s,t,x+y)
平衡二叉树详解

动态查找树之平衡二叉树(Balanced Binary Tree,AVL树一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树。
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:(1)左右子树深度之差的绝对值不超过1;(2)左右子树仍然为平衡二叉树.平衡因子BF=左子树深度-右子树深度.平衡二叉树每个结点的平衡因子只能是1,0,-1。
若其绝对值超过1,则该二叉排序树就是不平衡的。
如图所示为平衡树和非平衡树示意图:二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
(1)LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A 作为根结点,A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
(2)RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A 作为根结点,A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
(3)LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Motivation
• List: either search or insert can be efficient, but not both • Tree: efficient access and update • Binary tree: efficient for
A
B D E C F
H
I
Different binary trees
Full and Complete B Nhomakorabeanary Trees
Full binary tree: Each node is either a leaf or
internal node with exactly two non-empty children.
Complete binary tree: If the height of the tree is d,
then all leaves except possibly level d-1 are completely full. The bottom level has all nodes to the left side.
have two leaf nodes.
Induction Hypothesis: Assume any full binary tree T
containing n-1 internal nodes has n leaves.
Full Binary Tree Theorem (2)
Induction Step: Given tree T with n internal
Full Binary Tree Theorem (1)
Theorem: The number of leaves in a non-empty full binary tree is one more than the number of internal nodes.
Full Binary Tree Theorem (1)
Binary Tree Node ADT (1)
// Binary tree node abstract class template <typename E> class BinNode{ public: virtual ̃ BinNode() {} // Base destructor // Return the node’s value virtual E& element() = 0; // Set the node’s value virtual void setElement(const E&) = 0; // Return the node’s left child virtual BinNode* left() const = 0;
F
I
Binary Tree Example
Depth of a node: the length of the path from the root to the node Height of a tree: one more than the depth of the deepest node in the tree
Traversals (3)
• Preorder enumeration • Inorder enumeration • Postorder enumeration
• Level-order enumeration
Traversals (3)
• Preorder enumeration ABDCEGFHI • Inorder enumeration BDAGECHFI • Postorder enumeration DBGEHIFCA • Level-order enumeration ABCDEFGHI
Traversals (1)
Any process for visiting the nodes in some order is called a traversal. Any traversal that lists every node in the tree exactly once is called an enumeration of the tree’s nodes.
Traversals (5)
// Bad implementation template <typename E> void preorder2(BinNode<E>* subroot) { visit(subroot); // Perform some action if (subroot->left() != NULL) preorder2(subroot->left()); if (subroot->right() != NULL) preorder2(subroot->right()); }
Traversals (2)
• Preorder traversal: Visit each node before visiting its children. • Postorder traversal: Visit each node after visiting its children. • Inorder traversal: Visit the left subtree, then the node, then the right subtree. • Level-order traversal: Visit every node on a level before going to a lower level.
A
C D E F
H
I
Binary Tree Example
Path: if n1,n2,….nk is a A sequence of nodes in the tree such that ni is the B C parent of ni+1, then the sequence is called a path. E D The length of the path is k-1 H If there is a path from node R to node M, then R is an ancestor of M and M is a descendant of R
nodes, pick internal node I with two leaf children. Remove I’s children, call resulting tree T’.
By induction hypothesis, T’ is a full binary tree with n leaves. Restore I’s two children. The number of internal nodes has now gone up by 1 to reach n. The number of leaves has also gone up by 1.
A
B D E C F
H
I
Binary Tree Example
Parent: immediate predecessor of a node Children: immediate successor B of a node Edge: from a node to its children Node B and C are children of node A while node A is parents of node B and C
Traversals (4)
// Good implementation template <typename E> void preorder(BinNode<E>* subroot) { if (subroot == NULL) return; // Empty visit(subroot); // Perform some action preorder(subroot->left()); preorder(subroot->right()); }
Full Binary Tree Corollary
Theorem: The number of empty subtrees in a non-empty tree is one more than the number of nodes in the tree.
Proof: Replace each empty subtree with a leaf node. This is a full binary tree.
A
B D E C F
H
I
Binary Tree Example
Level: all node of depth d are at level d in the tree Leaf node: Any node has two empty children Internal node: Any node has at elast one nonempty children
Binary Tree Example
Node: A~H
Root: node that has no predecessor– Node A
Subtree: Left subtree consists of Node B and D Right subtree consists of Node C,E,F,H and I
– searching – describing math expressions – organizing information to drive compression algorithms –…
Binary Trees
