【拿高分,选好题第二波】(新课程)高中数学二轮复习精选考前小题狂练3 新人教版

合集下载

【拿高分,选好题第二波】(新课程)高中数学二轮复习精选第一部分25个必考问题专项突破专题训练16算法

答案 12 9．解析由 (1 － 2i)i ＝i － 2i 2＝ 2＋i ＝ a＋ bi ，根据复数相等的条件可得
＝2.
a＝ 2，b＝1，∴ ab
答案 2 10．解析逐步运行程序框图即可．开始时
n＝ 8，i ＝ 2， k＝1， s＝ 1.
因 i ＝ 2＜ 8，故 s＝1×1×2＝ 2， i ＝ 2＋ 2＝ 4， k＝ 1＋ 1＝ 2； 1
所以 b＝ 0，所以 z∈ R，①正确；
若 z＝ 0，则 z 不是纯虚数，②错；若 a2＋ b2＝－ b＋ai ，则 a＝ 0， b＝0 或 b＝－ 1，
所以 z＝ 0 或 z＝－ i ，③错；若| z1＋ z2| ＝ | z1－ z2| ，设 z1＝a＋ bi( a，b∈ R) ，
z2＝c＋ di( c，d∈ R) ．则( a＋ c) 2＋ ( b＋ d) 2＝ ( a－ c) 2＋ ( b－ d) 2，
整理得： ac＋ bd＝ 0，所以 z1z2＝ ( a＋bi)( c＋ di) ＝ ac－bd＋ ( ad＋bc)i ≠0，④错．
答案 1
4
训练 16 算法与复数 ( 备用 )
( 参考时间： 80 分钟 )
1．(2011 ·南京模拟 ) 已知复数 z＝ 3＋ 4i(i 为虚数单位 ) ，则复数 z ＋ 5i 等于 ________．
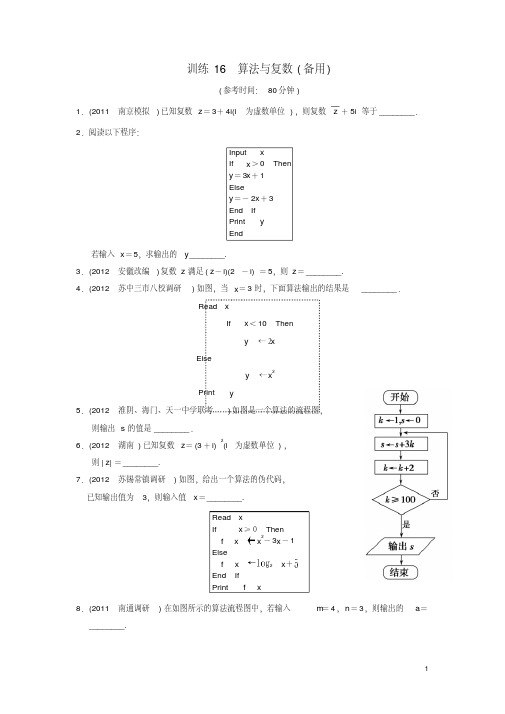
2．阅读以下程序：
Input x If x＞ 0 Then y＝ 3x＋ 1 Else y＝－ 2x＋ 3 End If Print y End
1 a－ 2
i ∈R，所以
1
1
a－ 2＝ 0，a＝ 2.
1 答案
2
z1 a＋2i
a＋
12．解析
z

高中新课程数学(苏教)二轮复习精选考前小题狂练

小题狂练(四)1．已知集合M ＝{1,2,3}，N ＝{2,3,4}，则M ∩N ＝________.2．已知复数z 满足(z －2)i ＝1＋i(i 为虚数单位)，则z 的模为________．3．为了分析某篮球运动员在比赛中发挥的稳定程度，统计了该运动员在6场比赛中的得分，用茎叶图表示如图所示，则该组数据的方差为________．4．在△ABC 中，a ＝8，B ＝60°，C ＝45°，则b ＝________.5．若过正三角形ABC 的顶点A 任作一条直线l ，则l 与线段BC 相交的概率为________．6．已知函数y ＝a n x 2(a n ≠0，n ∈N *)的图象在x ＝1处的切线斜率为2a n －1＋1(n ≥2)，且当n ＝1时其图象过点(2,8)，则a 7的值为________．7．已知函数y ＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，0＜φ≤π2的部分图象如图，则φ的值为________．8．在平面直角坐标系xOy 中，直线3x ＋4y －5＝0与圆x 2＋y 2＝4相交于A ，B 两点，则弦AB 的长等于________．9．如图是一个算法的流程图，则最后输出的S ＝________.10．设l是一条直线，α，β，γ是不同的平面，则在下列命题中，假命题是________．①如果α⊥β，那么α内一定存在直线平行于β②如果α不垂直于β，那么α内一定不存在直线垂直于β③如果α⊥γ，β⊥γ，α∩β＝l，那么l⊥γ④如果α⊥β，l与α，β都相交，那么l与α，β所成的角互余11．已知函数f(x)＝x33＋ax22＋2bx＋c在区间(0,1)内取极大值，在区间(1,2)内取极小值，则z＝(a＋3)2＋b2的取值范围为________．12．平面向量a，b满足|a＋2b|＝5，且a＋2b平行于直线y＝2x＋1，若b＝(2，－1)，则a＝________.13．(2012·南师大附中阶段测试)已知函数f(x)＝|x2＋2x－1|，若a＜b＜－1，且f(a)＝f(b)，则ab＋a＋b的取值范围是________．14．定义在实数集上的偶函数f(x)满足f(x＋2)＝f(x)，且f(x)在[－3，－2]上单调递减，又α，β是锐角三角形的两内角，则f(sin α)与f(cos β)的大小关系是________．参考答案小题狂练(四)1．解析M∩N＝{1,2,3}∩{2,3,4}＝{2,3}．答案M∩N＝{2,3}2．解析由(z－2)i＝1＋i，得z＝1＋ii＋2＝3－i，所以|z|＝10.答案 103．解析平均数x ＝14＋17＋18＋18＋20＋216＝18，故方差s 2＝16(42＋12＋02＋02＋22＋32)＝5.答案 54．解析由正弦定理得b sin B ＝c sin C ，∴b ＝8sin 60°sin 45°＝4 6.答案 4 65．解析 ∠BAC ＝60°，故所求的概率60°360°＝16.答案 166．解析因为y ＝a n x 2在x ＝1处的切线斜率为2a n ，所以2a n ＝2a n －1＋1(n ≥2)，即a n ＝a n －1＋12(n ≥2)，又8＝4a 1⇒a 1＝2，所以a 7＝a 1＋6×12＝5.答案 57．解析由三角函数图象可得周期T ＝2⎝ ⎛⎭⎪⎫5π6－π3＝π＝2πω，解得ω＝2.由函数图象过点⎝ ⎛⎭⎪⎫π3，0，所以sin ⎝ ⎛⎭⎪⎫2×π3＋φ＝0⇒φ＝π3＋2k π，k ∈Z ，且0＜φ≤π2，所以φ＝π3.答案 π38．解析圆x 2＋y 2＝4的圆心O (0,0)到直线3x ＋4y －5＝0的距离d ＝|－5|5＝1，弦AB 的长|AB |＝2r 2－d 2＝2 3.答案 2 3 9．解析这是一个典型的当型循环结构，当n ＝1,3,5,7,9,11时满足条件，执行下面的语句，S ＝1＋3＋5＋7＋9＋11＝36，当n ＝13时不满足条件，退出循环，执行输出S ＝36.答案 3610．解析如果α⊥β，那么α内一定存在直线平行于β，即命题①正确；如果α不垂直于β，那么α内一定不存在直线垂直于β，即命题②正确；如果α⊥γ，β⊥γ，α∩β＝l ，那么l ⊥γ，即命题③正确；如果α⊥β，l 与α，β都相交，那么l 与α，β所成的角不一定互余，即命题④不正确．答案 ④11．解析因为函数f (x )在区间(0,1)内取极大值，在区间(1,2)内取极小值，所以⎩⎪⎨⎪⎧ f ′(0)＞0，f ′(1)＜0，f ′(2)＞0，即⎩⎪⎨⎪⎧ b ＜0，1＋a ＋2b ＜0，a ＋b ＋2＞0，对应可行域如图，目标函数z ＝(a ＋3)2＋b 2的几何意义是可行域上的点(a ，b )到定点P (－3,0)的距离的平方，点P 到边界a ＋b ＋2＝0的距离的平方为⎝ ⎛⎭⎪⎫122＝12，到点(－1,0)的距离的平方为4，因为可行域不含边界，所以z 的取值范围是⎝ ⎛⎭⎪⎫12，4. 答案 ⎝ ⎛⎭⎪⎫12，4 12．解析因为a ＋2b 平行于直线y ＝2x ＋1，所以可设a ＋2b ＝(m,2m )，所以|a＋2b |2＝5 m 2＝5，解得m ＝1或－1，a ＋2b ＝(1,2)或(－1，－2)，所以a ＝(1,2)－(4－2)＝(－3,4)或(－1，－2)－(4，－2)＝(－5，0)．答案 (－3,4)或(－5,0)13．解析作出函数图象可知若a ＜b ＜－1，且f (a )＝f (b )，即为a 2＋2a －1＝－(b 2＋2b －1)，整理得(a ＋1)2＋(b ＋1)2＝4，设⎩⎪⎨⎪⎧ a ＝－1＋2cos θ，b ＝－1＋2sin θ，θ∈⎝ ⎛⎭⎪⎫π，5π4∪⎝ ⎛⎭⎪⎫5π4，3π2，所以ab ＋a ＋b ＝－1＋2sin 2θ∈(－1,1)．答案 (－1,1)14．解析因为f (x ＋2)＝f (x )⇒f (x )的周期为2，所以f (x )，x ∈[－1,0]的单调性与[－3，－2]一致，单调递减，又f (x )是偶函数，所以在[0,1]上单调递增．又α，β是锐角三角形的两个内角，所以π2＜α＋β＜π⇒0＜π2－β＜α＜π2⇒1＞sin α＞sin ⎝ ⎛⎭⎪⎫π2－β＝cos β＞0⇒f (sin α)＞f (cos β)．答案 f (sin α)＞f (cos β)。

【拿高分,选好题第二波】(新课程)高中学数二轮复习精选第二部分洞察高考热点39题《专题三 4

【突破训】在极坐标系中，点
O(0,0)，B2
π 2， . 4
(1)求以 OB 为直径的圆 C 的直角坐标方程； (2)若直线 l 的极坐标方程为 ρcos θ＋ρsin θ＝4，判断直线 l 与圆 C 的位置关系．
解 (1)设 P(ρ，θ)是所求圆上的任意一点，因为 OB 为直径，所以∠OPB＝90° ，则
解圆方程为(x＋1)2＋y2＝4，圆心(－1,0)，直线方程为 x＋y－ 7＝0，(5 分) |－1－7| 圆心到直线的距离 d＝＝4 2，所以(AB)min＝4 2－2.(10 2 分)
评分细则 (1)正确将极坐标方程化为直角坐标方程各得2分. (2)求出圆心到直线的距离得2分. (3)正确得到结果再得3分.
π OP＝OBcosθ－4，即
ρ＝2
π 2cosθ－4，(3
分)
即 x2＋y2－2x－2y＝0，故所求的圆 C 的直角坐标方程为 x2＋y2－2x－2y＝0.(5 分) (2)圆 C 的圆心的坐标为(1,1)，半径为 2，直线 l 的直角坐标方程为 x＋y＝4，(7 分) |1＋1－4| 因为圆心到直线 l 的距离 d＝ 2 2 ＝ 2， 1 ＋1 所以直线 l 与圆 C 相切．(10 分)
专题三 40分附加题大突破
与抢分秘诀
坐标系与参数方程【示例】► (2012·如皋质量检测 )在极坐标系中，A为曲线ρ2＋ 2ρcos θ－3＝0上的动点，B为直线ρcos θ＋ρsin θ－7＝0上的
动点，求AB的最小值．
解题突破曲线 ρ2 ＋ 2ρcos θ － 3 ＝ 0 的直角坐标方程为 (x ＋ 1)2＋y2＝4，直线ρcos θ＋ρsin θ－7＝0先化为直角坐标方程 x ＋ y － 7 ＝0 ，问题变为求圆上的点到直线上点的距离的最小值．

(新课程)高中数学二轮复习精选考前小题狂练3理新人教版.doc

小题，）（限姉分钟一、羅（本大题共12小题，每小题5分，共60分）1.已知全集 U=R,集合 A={1,2,3,4,5}，B= [2 ,十①）则图中阴影部分所表示的集合为3— 2x+1*0A. ? XeR, XB. 不存在XeR, X3— 2x+ 1= 0C. ? XeR, x3.设i 是虚数单位，则A. {0,1,2} 2.命题？ XeR ，xB • {0,1}3 — 2x+1=0”的否定是• {1,2}• {1}3—2x+1*0D. ? XeR, X3—2x-n^rrA. B. 1 +C.D. 1-)•4.在等比数列{a n}中，广况=8，，或二洗洗，贝1J a7=A. B. D.165.要得到函数y sin 2x-只需将函数y=sin 2 x的图象3的图象向左平移TT_个单位12向右平移TT_个单位12向左平移11个单位6向右平移11个单位6.设随机擻（服从正态分咏0,1），F\X>1）=p，则P（X>-1） =8.某同学设计右面的程序框图屏偉2+ 22+ 32+…+202的值，则在阙1 框中应填闫).A. p C.1-2p7.在△ ABC 中，090'且CA= CB= 3，点IVU—> —> —>茜，=2MA，则CM，CB等于A. 2巳.3 C • 4 D .6B. 1-p D.2p开始1=1A. i < 19B. i > 19C. i < 20D. i < 2119. 已知函数 f ( x) =sin x — 2x(xe[0，TT])B. 1：(*)在6，TT 上是减函TTC. ?xe[o ，TT]，f(x)>f/_1( )•T T+是增函数D. ? Xe[0 , TT]，f (X )<T T 3 A―小/sin10.函数y = e—TT < x< TT )的大致图象( )•那么下列结论正确的是/. 1L.JV J八-TT 0IT X 0X -TT 0 IT^Xir rxn2 + y2=5相交于M N两点，则线酸N 的齿_的直线I 与圆4渐近线程#2x ，则双曲线的焦距等于B.D. 2 3二、填空题（本大题共4小题，每小题4分，共16分）13. 在区陶，9]上随机取一实数 X,贝噱数x 满足不等贱log 2x< 2的概率为 14. 一个棱锥的三视图如图新则这个棱锥的耦为 .正（主）视图側（左）视图2 — y2=1的一条渐11.过点（一2,0〉且倾斜 A. C. 2'2 2、B. 3 D. 612.已知抛物线 y 2=4x 的准线过双曲线f 71（ a>0, b>0）的左顶点，且此双曲线的一条A. C. 315.己知双曲线kx（o ）〉0）和 g （x ）=2cos （2 x +（p ） + 1 的图象的对馳近线与直线2x + y+1 = 0垂直，那么双曲线的离心率为16.已知函数 f ( x) 3 sin-| o)x—gI 一ITT ，则f（X）的取值范鼠全相同.若xe 0,参考答案. .【小题练三）】X J1 2x 了 te，，胁符合要求.] 豆的te趣1D1正确.]1 D [鵬部側兵素—2 D丨根据含有量词的命.i i - 11 6=1[由题意知，a4=1,所以q=—,故a?二aq — •] 2 810. D ［取x=_TT ，0, TT 这三个值，可得 y 总是1，故排除A 、C;当=1, .•.双曲线的渐近线方程为13.解析由1S log 2xs 2得：2S xs 4，故所求概率4•巳5. D [要得到函数y = sin 2x-—/ /、需将函 3H-、 ( IL)]sin 2 lx — J= sin |2x — 6 36. B [vP(X<-1) = P(X>1),阀X>-1) = 1 — p.]y=sin 2X 中的X 减去蚤即得到y7. B CB| 2 | D |\/I[CM- CB=(CB+BM)- CB 二 |8. C ［由计算式可知程序到i9. D ［注意到 f'（x ）=cos x _ ( CB^ 9 + 3x2 2x C os 135° 20终止，g(、此判断A 中縝i < 20.] f'(x)<0,因此函数 f(x)在0TT ，当 xe 0， 2 3 K上是增函数，在3TTTT3 ，TT 时， f (x)在[0，TT ］内的最大值是TT3，即？ Xe ［0，TT ］，都有 f （x ）< ，因此D 正 d 确.］函数， y= e- *也是增函数，故选］sin =2.pMN|=22 2=2 3.] 2=4x 的淮线x = -1过双曲线x y12. B [•••抛物线y1（a>0，b>0）的左顶点，.•. a•••b=2, ;.c2+b2=5x —± bx. •.•双曲线的一条渐近线方程为，双曲线的焦距为 2 5.1y=2x,1‘也‘11. C ［直线丨的方程为：x-y+2=0,圆（G ，0）到直线丨的距离d=x(3x4)x3= 12y 1= 1的渐近线方程为 y=± kx,答14.解析锥的赖等答案［15.解析双曲线kx直线2x + y+1 = 0的斜率为一 2，1一）••• kx(-2)1，即 k 二:.e答案16.解析由对称轴完全相同知两函数周期相同，TT...0) = 2，f ( X)=3 sin 2x —由Xe 0,TT< 2 x— < 6n, 32< f (x)< 3.。

【拿高分，选好题第二波】（新课程）高中数学二轮复习精选第二部分洞察高考热点39题《专题三 40分

专题三 40分附加题大突破与抢分秘诀【专题定位】高考中主要考查曲线在矩阵变换下的曲线方程，求二阶矩阵的逆矩阵及二阶矩阵的特征值和特征向量等．如：考查常见的平面变换及二阶矩阵与平面向量的乘法、矩阵的乘法，并且理解连续两次变换所对应二阶矩阵相乘的顺序．熟记几种常见变换，对应点间坐标关系；考查利用二阶矩阵与平面向量乘法的知识求二阶矩阵的方法；考查求一条曲线经过二阶矩阵变换后的曲线方程的方法；考查矩阵的特征值与特征向量的应用等．附加题部分由解答题组成，共6题．其中，必做题2题，考查选修系列2(不含选修系列1)中的内容；选做题共4题，依次考查选修系列4中4－1、4－2、4－4、4－5这4个专题的内容，考生从中选2题作答．附加题部分由容易题、中等题和难题组成．容易题、中等题和难题在试卷中所占分值的比例大致为5∶4∶1.【应对策略】根据《考试说明》提出的要求，控制问题的难度，在本单元的复习中，应该注意突出以下几个方面：1．回归课本，抓好基础知识的落实，高考题“源于课本”，在复习中必须重视对课本中的基础知识、基本方法和基本数学思想的复习，关注课本中的一些重点内容．2．加强训练，提高推理和运算能力，在复习过程中一定要注意加强训练，重视推理论证和运算能力的培养，学会主动地寻求合理、简捷的运算途径，努力提高解题的正确性和有效性．几何证明选讲【示例】► 如图，AT 为单位圆O 的切线，过切点T 引OA 的垂线TH ，H 为垂足．求证：AO ·OH 为定值．解题突破由AT 为单位圆O 的切线，得∠ATH ＝∠TOH ，由TH ⊥OA ，得∠OTH ＝∠OAT ，从而△ATO ∽△THO ，因此得到OH OT ＝OTOA所以AO ·OH 为定值．证明因为AT 为圆O 的切线，TH 为OA 的垂线，所以∠ATH ＝∠TOH ，∠ATO ＝∠THO ，(3分) 故直角三角形ATO 相似于直角三角形THO ，(6分)则OH OT ＝OT OA，即AO ·OH ＝OT 2＝1，即证．(10分) 评分细则1得到∠ATH ＝∠TOH 给3分，如果错误则本题基本不得分，2没有OH OT ＝OT OA，扣3分.【突破训练】如图，直线AB 经过⊙O 上的点C ，并且OA ＝OB ，CA ＝CB ，⊙O 交直线OB 于E ，D ，连接EC ，CD ，若tan ∠CED ＝12，⊙O 的半径为3，求OA 的长．解如图，连接OC ，因为OA ＝OB ，CA ＝CB ，所以OC ⊥AB . 因为OC 是圆的半径，所以AB 是圆的切线．(2分)因为ED 是直径，所以∠ECD ＝90°，所以∠E ＋∠EDC ＝90°，又∠BCD ＋∠OCD ＝90°，∠OCD ＝∠ODC ，所以∠BCD ＝∠E ，又因为∠CBD ＝∠EBC ，所以△BCD ∽△BEC ，所以BC BE ＝BD BC⇒BC 2＝BD ·BE ，(5分) 因为tan ∠CED ＝CD EC ＝12，△BCD ∽△BEC ，所以BD BC ＝CD EC ＝12.(7分)设BD ＝x ，则BC ＝2x ，因为BC 2＝BD ·BE ，所以(2x )2＝x (x ＋6)，所以BD ＝2.(9分) 所以OA ＝OB ＝BD ＋OD ＝2＋3＝5.(10分) 【抢分秘诀】(1)平面几何解题时要重视数学语言表达、数学解题格式的规范性． (2)由图形或定理能推到的一些结论要尽可能的表达出来．矩阵与变换【示例】► 设M ＝⎣⎢⎡⎦⎥⎤1002，N ＝⎣⎢⎢⎡⎦⎥⎥⎤12 0 01，试求曲线y ＝sin x 在矩阵MN 变换下的曲线方程．解题突破可先求出MN ，再求曲线在MN 变换下的曲线方程．解 MN ＝⎣⎢⎡⎦⎥⎤1002⎣⎢⎢⎡⎦⎥⎥⎤12 0 0 1＝⎣⎢⎢⎡⎦⎥⎥⎤12 0 02，(3分) 设(x ，y )是曲线y ＝sin x 上的任意一点，在MN 变换下对应的点为(x ′，y ′)．则⎣⎢⎢⎡⎦⎥⎥⎤120 2⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ′y ′(5分) 所以⎩⎪⎨⎪⎧x ′＝12x ，y ′＝2y ，即⎩⎪⎨⎪⎧x ＝2x ′，y ＝12y ′，(8分)代入y ＝sin x 得：12y ′＝sin 2x ′，即y ′＝2sin 2x ′.即曲线y ＝sin x 在矩阵MN变换下的曲线方程为y ＝2 sin 2x .(10分)评分细则1正确求出MN 得3分.如果不正确本题不给分.2正确表示⎩⎪⎨⎪⎧x ＝2x ′，y ＝12y ′，得8分.3没有正确表示y ＝2sin 2x ，扣1分.【突破训练】已知二阶矩阵A 将点(1,0)变换为(2,3)，且属于特征值3的一个特征向量是⎣⎢⎡⎦⎥⎤11，求矩阵A .解设A ＝⎣⎢⎡⎦⎥⎤ab cd ，由⎣⎢⎡⎦⎥⎤ab c d ⎣⎢⎡⎦⎥⎤10＝⎣⎢⎡⎦⎥⎤23，得⎩⎪⎨⎪⎧ a ＝2，c ＝3.(5分)再由⎣⎢⎡⎦⎥⎤a b cd ⎣⎢⎡⎦⎥⎤11＝3⎣⎢⎡⎦⎥⎤11＝⎣⎢⎡⎦⎥⎤33，得⎩⎪⎨⎪⎧a ＋b ＝3，c ＋d ＝3，∴⎩⎪⎨⎪⎧b ＝1，d ＝0，∴A ＝⎣⎢⎡⎦⎥⎤2130.(10分)【抢分秘诀】(1)正确进行矩阵变换，注意变换的先后顺序． (2)记住求逆矩阵的过程．(3)在求矩阵变换的特征值与特征向量时，可用定义建立关系．坐标系与参数方程【示例】► (2012·如皋质量检测)在极坐标系中，A 为曲线ρ2＋2ρcos θ－3＝0上的动点，B 为直线ρcos θ＋ρsin θ－7＝0上的动点，求AB 的最小值．解题突破曲线ρ2＋2ρcos θ－3＝0的直角坐标方程为(x ＋1)2＋y 2＝4，直线ρcosθ＋ρsin θ－7＝0先化为直角坐标方程x ＋y －7＝0，问题变为求圆上的点到直线上点的距离的最小值．解圆方程为(x ＋1)2＋y 2＝4，圆心(－1,0)，直线方程为x ＋y －7＝0，(5分) 圆心到直线的距离d ＝|－1－7|2＝42，所以(AB )min ＝42－2.(10分)评分细则 1正确将极坐标方程化为直角坐标方程各得2分.2求出圆心到直线的距离得2分.3正确得到结果再得3分. 【突破训练】在极坐标系中，点O (0,0)，B ⎝ ⎛⎭⎪⎫22，π4. (1)求以OB 为直径的圆C 的直角坐标方程；(2)若直线l 的极坐标方程为ρcos θ＋ρsin θ＝4，判断直线l 与圆C 的位置关系．解 (1)设P (ρ，θ)是所求圆上的任意一点，因为OB 为直径，所以∠OPB ＝90°，则OP ＝OB cos ⎝ ⎛⎭⎪⎫θ－π4，即ρ＝22cos ⎝ ⎛⎭⎪⎫θ－π4，(3分)即x 2＋y 2－2x －2y ＝0，故所求的圆C 的直角坐标方程为x 2＋y 2－2x －2y ＝0.(5分) (2)圆C 的圆心的坐标为(1,1)，半径为2，直线l 的直角坐标方程为x ＋y ＝4，(7分) 因为圆心到直线l 的距离d ＝|1＋1－4|12＋12＝2，所以直线l 与圆C 相切．(10分) 【抢分秘诀】(1)把极坐标方程转化为直角坐标方程，把参数方程化为普通方程，可得相应的分数． (2)求解过程要干净利落，条理分明，计算准确．不等式选讲【示例】► 设a 1，a 2，a 3均为正数，且a 1＋a 2＋a 3＝1，求证：1a 1＋1a 2＋1a 3≥9.解题突破利用基本不等式证明．证明因为a 1，a 2，a 3均为正数，且a 1＋a 2＋a 3＝1＞0，所以1a 1＋1a 2＋1a 3＝(a 1＋a 2＋a 3)⎝ ⎛⎭⎪⎫1a 1＋1a 2＋1a 3≥3(a 1a 2a 3)13·3⎝ ⎛⎭⎪⎫1a 11a 21a 313＝9，(8分) 当且仅当a 1＝a 2＝a 3＝13时等号成立，所以1a 1＋1a 2＋1a 3≥9.(10分)评分细则 1正确使用基本不等式得8分.2不说明等号成立条件的扣1分.【突破训练】已知a ＋b ＋c ＝1，m ＝a 2＋b 2＋c 2，求m 的最小值．解 ∵(12＋12＋12)(a 2＋b 2＋c 2)≥(1·a ＋1·b ＋1·c )＝a ＋b ＋c ＝1.(5分) ∴a 2＋b 2＋c 2≥13，当且仅当a ＝b ＝c ＝13时，等号成立．m min ＝13.(10分)【抢分秘诀】(1)利用平均值不等式、柯西定理时要找准“对应点”，使其符合特征，使问题的解决清晰明了，可得一定的分数．(2)注意对而不全，应用绝对值不等式的性质求函数的最值时，注意等号成立的条件． (3)在证明不等式时，要注意推理的逻辑性．空间向量解决立体几何问题【示例】► 如图△BCD 与△MCD 都是边长为2的正三角形，平面MCD ⊥平面BCD ，AB ⊥平面BCD ，AB ＝23，(1)求点A 到平面MBC 的距离；(2)求平面ACM 与平面BCD 所成二面角的正弦值．解题突破 (1)先求出平面MBC 的法向量，再利用公式求距离．(2)通过求平面ACM 与平面BCD 的法向量所成的角，求平面ACM 与平面BCD 所成二面角的正弦值．解取CD 中点O ，连OB ，OM ，由于△BCD 与△MCD 都是正三角形，则OB ⊥CD ，OM ⊥CD ，又平面MCD ⊥平面BCD ，则MO ⊥平面BCD .以O 为原点，直线OC 、BO 、OM 所在的直线为x 轴，y 轴，z 轴，建立空间直角坐标系如图．OB ＝OM ＝3，则各点坐标分别为O (0,0,0)，C (1,0,0)，M (0,0，3)，B (0，－3，0)，A (0，－3，23)，(2分)(1)设n ＝(x ，y ，z )是平面MBC 的法向量，则BC →＝(1, 3，0)， BM →＝(0，3，3)，由n ⊥BC →得x ＋3y ＝0；由n ⊥BM →得3y ＋3z ＝0；取n ＝(3，－1,1)，BA →＝(0,0,23)，(3分) 则距离d ＝|BA →·n ||n |＝2155.(5分)(2)CM →＝(－1,0，3)，CA →＝(－1，－3，23)．设平面ACM 的法向量为n 1＝(x ，y ，z )，由⎩⎪⎨⎪⎧n 1⊥CM →，n 1⊥CA →得⎩⎨⎧－x ＋3z ＝0，－x －3y ＋23z ＝0，解得x ＝3z ，y ＝z ，取n 1＝(3，1,1)．(7分) 又平面BCD 的法向量为n ＝(0,0,1)，(8分) 则cos 〈n 1，n 〉＝n 1·n |n 1|·|n|＝15，设所求二面角为θ，则sin θ＝1－⎝⎛⎭⎪⎫152＝255.(10分) 评分细则 1建立空间坐标系，得到相关点的坐标，得2分；2求出平面MBC 的法向量得1分，求出距离得2分；3 求出平面ACM 的法向量得2分，说出平面BCD 的法向量得1分；4正确求出平面ACM 与平面BCD 所成二面角的正弦值得2分.【突破训练】 (2012·苏北四市联考)在棱长为2的正方体ABCD A 1B 1C 1D 1中，E 为棱AB 的中点，点P 在平面A 1B 1C 1D 1上，D 1P ⊥平面PCE .试求：(1)线段D 1P 的长；(2)直线DE 与平面PCE 所成角的正弦值．解 (1)建立如图所示的空间直角坐标系，则D 1(0,0,2)，E (2,1,0)，C (0，2,0)．设P (x ，y,2)，则D 1P →＝(x ，y,0)，EP →＝(x －2，y －1,2)，EC →＝(－2,1,0)．(2分)因为D 1P ⊥平面PCE ，所以D 1P ⊥EP ，D 1P ⊥EC ，所以D 1P →·EP →＝0，D 1P →·EC →＝0，故⎩⎪⎨⎪⎧x x －2＋y y －1＝0，－2x ＋y ＝0.解得⎩⎪⎨⎪⎧x ＝0，y ＝0.(舍去)或⎩⎪⎨⎪⎧x ＝45，y ＝85.(4分)即P ⎝ ⎛⎭⎪⎫45，85，2，所以D 1P →＝⎝ ⎛⎭⎪⎫45，85，0，所以D 1P ＝1625＋6425＝455.(6分) (2)由(1)知，DE →＝(2,1,0)，D 1P →＝⎝ ⎛⎭⎪⎫45，85，0，D 1P →⊥平面PEC ，设DE 与平面PEC 所成角为θ，D 1P →与DE →所成角为α，则sin θ＝|cos α|＝⎪⎪⎪⎪⎪⎪⎪⎪D 1P →·DE →|D1P →||DE →|＝1655·8025＝45，所以直线DE 与平面PEC 所成角的正弦值为45.(10分)【抢分秘诀】(1)建立空间坐标系，得到相关点的坐标． (2)用坐标正确表示相关向量．(3)尽可能的找出或求出相关平面的法向量．(4)借助符号语言，保证过程条理分明，正确计算求结果．概率、随机变量及其分布列【示例】► 在十字路口的路边，有人在促销木糖醇口香糖，只听喇叭里喊道：木糖醇口香糖，10元钱三瓶，有8种口味供你选择(其中有一种为草莓口味)，小明一看，只见一大堆瓶装口香糖堆在一起(假设各种口味的口香糖均超过3瓶，且每瓶价值均相同)．(1)小明花10元钱买三瓶，请问小明共有多少种选择的可能性？(2)小明花10元钱买三瓶，售货员随便拿三瓶给小明，请列出有小明喜欢的草莓味口香糖瓶数X 的分布列，并计算其数学期望．解题突破 (1)分三类情况讨论：①8种口味均不一样；②两瓶口味一样；③三瓶口味一样．(2)确定X 的取值为0,1,2,3.分别计算各种取值的概率，写出分布列并计算其数学期望．解 (1)若8种口味均不一样，有C 38＝56种；若其中两瓶口味一样，有C 18C 17＝56种；若三瓶口味一样，有8种，所以小明共有56＋56＋8＝120种选择，(4分)(2)X 的取值为0,1,2,3.P (X ＝0)＝C 37＋C 17·6＋7120＝84120＝710；P (X ＝1)＝C 27＋7120＝28120＝730；P (X ＝2)＝7120；P (X ＝3)＝1120.(8分) 所以X 的分布列为X 0 1 2 3 P71073071201120其数学期望EX ＝0×710＋1×730＋2×7120＋3×1120＝38.(10分)评分细则 1三类情况，每对一个1分，结果1分.2求X ＝0，1，2，3.的情形的概率，每对一个1分；3数学期望计算正确2分.【突破训练】某汽车驾驶学校在学员结业前对其驾驶技术进行4次考核，规定：按顺序考核，一旦考核合格就不必参加以后的考核，否则还需要参加下次考核．若小李参加每次考核合格的概率依次组成一个公差为18的等差数列，他参加第一次考核合格的概率超过12，且他直到参加第二次考核才合格的概率为932.(1)求小李第一次参加考核就合格的概率p 1；(2)求小李参加考核的次数X 的分布列和数学期望E (X ) 解 (1)由题意得(1－p 1)·⎝ ⎛⎭⎪⎫p 1＋18＝932， ∴p 1＝14或58.∵p 1＞12，∴p 1＝58.(4分)(2)由(1)知小李4次考核每次合格的概率依次为58，34，78，1，所以P (X ＝1)＝58，P (X ＝2)＝932，P (X ＝3)＝⎝ ⎛⎭⎪⎫1－58⎝ ⎛⎭⎪⎫1－34×78＝21256，P (X ＝4)＝⎝⎛⎭⎪⎫1－58⎝⎛⎭⎪⎫1－34⎝⎛⎭⎪⎫1－78×1＝3256，(6分) 所以X 的分布列为∴E (X )＝1×58＋2×932＋3×21256＋4×3256＝379256.(10分)【抢分秘诀】(1)要明确X 的可能取值情况．(2)利用概率的有关知识，正确计算X 的各个取值的概率． (3)求概率时要充分利用随机变量的概率、古典概型等知识． (4)写分布列时要按规范，注意用分布列的性质验证．排列组合、二项式定理及数学归纳法的综合考查【例1】► (2012·高邮模拟)在各项均为正数的数列{a n }中，数列的前n 项和为S n 满足S n ＝12⎝⎛⎭⎪⎫a n ＋1an.(1)求a 1，a 2，a 3的值；(2)由(1)猜想出数列{a n }的通项公式，并用数学归纳法证明你的猜想．解题突破 (1)由S 1＝a 1＝12⎝ ⎛⎭⎪⎫a 1＋1a 1可求a 1＝1；同理可求a 2，a 3；(2)由a 1，a 2，a 3的特征猜想数列{a n }的通项公式，再用数学归纳法证明．解 (1)由S 1＝12⎝ ⎛⎭⎪⎫a 1＋1a 1得，a 21＝1，而a n ＞0，所以a 1＝1.由S 2＝12⎝ ⎛⎭⎪⎫a 2＋1a 2得，a 22＋2a 2－1＝0，所以a 2＝2－1.又由S 3＝12⎝ ⎛⎭⎪⎫a 3＋1a 3得，a 23＋22a 3－1＝0，所以a 3＝3－ 2.(3分)(2)猜想a n ＝n －n －1(n ∈N *)．(4分) ①当n ＝1时，a 1＝1＝1－1－1，猜想成立； ②假设n ＝k (k ≥1)时猜想成立，即a k ＝k －k －1，则当n ＝k ＋1时，a k ＋1＝S k ＋1－S k ＝12⎝ ⎛⎭⎪⎫a k ＋1＋1a k ＋1－12⎝ ⎛⎭⎪⎫a k ＋1a k . 即a k ＋1＝12⎝ ⎛⎭⎪⎫a k ＋1＋1a k ＋1－12⎝ ⎛⎭⎪⎫k －k －1＋1k －k －1 ＝12⎝ ⎛⎭⎪⎫a k ＋1＋1a k ＋1－k ，(6分)化简得a 2k ＋1＋2k a k ＋1－1＝0，解得a k ＋1＝k ＋1－k ＝k ＋1－k ＋1－1，即n ＝k ＋1时猜想成立，(9分)综上，由①、②知a n ＝n －n －1(n ∈N *)．(10分)评分细则 1a 1，a 2，a 3对一个1分.2正确猜想1分.3根据归纳假设正确变形得2分.4根据归纳假设正确推理得到n ＝k ＋1时猜想成立，得3分；结论1分.【突破训练1】在正项数列{a n }中，对于一切的n ∈N *均有a 2n ≤a n －a n ＋1成立， (1)证明：数列{a n }中的任意一项都小于1； (2)探究a n 与1n的大小，并证明你的结论．(1)证明由a 2n ≤a n －a n ＋1得a n ＋1≤a n －a 2n∵在数列{a n }中a n ＞0，∴a n ＋1＞0，∴a n －a 2n ＞0，∴0＜a n ＜1 故数列{a n }中的任意一项都小于1.(4分)(2)解由(1)知0＜a n ＜1＝11，那么a 2≤a 1－a 21＝－⎝⎛⎭⎪⎫a 1－122＋14≤14＜12，由此猜想：a n ＜1n (n ≥2)．(6分) 下面用数学归纳法证明：①当n ＝2时，显然成立； ②当n ＝k 时(k ≥2，k ∈N *)时，假设猜想正确，即a k ＜1k ≤12，那么a k ＋1≤a k －a 2k ＝－⎝ ⎛⎭⎪⎫a k －122＋14＜－⎝ ⎛⎭⎪⎫1k －122＋14＝1k －1k2＝k －1k 2＜k －1k 2－1＝1k ＋1， ∴当n ＝k ＋1时，猜想也正确综上所述，对于一切n ∈N *，都有a n ＜1n.(10分) 【例2】► (江苏省2012届高三全真模拟一22)已知⎝ ⎛⎭⎪⎫x ＋12x n 的展开式中前三项的系数成等差数列．(1)求n 的值；(2)求展开式中系数最大的项．解题突破 (1)由展开式中前三项的系数成等差数列，建立方程求n 的值．(2)展开式中系数最大的项的系数应满足大于前一项的系数，还大于后一项的系数，由此建立关系式，确定r 的值．解 (1)由题设，得C 0n ＋14×C 2n ＝2×12×C 1n ，即n 2－9n ＋8＝0，解得n ＝8，或n ＝1(舍去)．(3分)(2)设第r ＋1的系数最大，则⎩⎪⎨⎪⎧ 12r C r 8≥12r ＋1Cr ＋18，12r C r8≥12r －1C r －18.(5分)即⎩⎪⎨⎪⎧ 18－r ≥12r ＋1，12r ≥19－1.解得r ＝2或r ＝3.(8分)所以系数最大的项为T 3＝7x 5，T 4＝7x 92.(10分) 【突破训练2】设数列{a n }满足：a 1＝－5，a n ＋1＝2a n ＋3n ＋1，已知存在常数p ，q 使数列{a n ＋pn ＋q }为等比数列．解方程a n ＝0.解由条件令a n ＋1＋p (n ＋1)＋q ＝k (a n ＋pn ＋q )，则a n ＋1＝ka n ＋(kp －p )n ＋kq －q －p ，故⎩⎪⎨⎪⎧ k ＝2，kp －p ＝3，kq －q －p ＝1⇒⎩⎪⎨⎪⎧ k ＝2，p ＝3，q ＝4.又a 1＋p ＋q ＝2， ∴a n ＋3n ＋4＝2·2n －1，∴a n ＝2n－3n －4.(5分) 计算知a 1＝－5，a 2＝－6，a 3＝－5，a 4＝0，a 5＝13. 故猜测n ≥5时，a n ＞0，即2n＞3n ＋4，下证： ①当n ＝5成立； ②假设n ＝k (k ≥5)时成立，即2k ＞3k ＋4，那么当n ＝k ＋1时，2k ＋1＞2·(3k ＋4)＝6k ＋8＞3k ＋7＝3(k ＋1)＋4，故当n ＝k ＋1时成立，由①②可知，命题成立．故方程a n ＝0的解为n ＝4.(10分)【抢分秘诀】1．关于二项式定理(1)二项式定理主要题目类型：①证明某些整除问题或求余数．②证明有关不等式．(2)解题方法归纳：①利用二项式定理可以证明整除问题或求余数问题，在证明整除问题或求余数问题时要进行合理的变形，使被除式(数)展开后的每一项都含有除式的因式，要注意变形的技巧．②由于(a ＋b )n的展开式共有(n ＋1)项，故可通过对某些项的取舍来放缩，从而达到证明不等式的目的．而对于整除问题，关键是拆成两项后，利用二项式定理展开，然后说明各项是否能被整除．2．关于数学归纳法(1)要验证初始值成立．(2)要运用归纳假设，根据归纳假设进行适当的变形．(3)用数学归纳法的两个步骤缺一不可．。

【拿高分,选好题第二波】(新课程)高中数学二轮复习精选考前小题狂练1 新人教版

小题狂练(一)(限时40分钟)一、选择题(本题共12小题，每小题5分，共60分) 1．已知集合A ＝{x |1<x <3}，B ＝{x |1<log 2x <2}，则A ∩B 等于( )．A ．{x |0<x <3}B ．{x |2<x <3}C ．{x |1<x <3}D ．{x |1<x <4}2．复数z ＝x ＋3i1－i(x ∈R ，i 是虚数单位)是实数，则x 的值为( )．A ．3B ．－3C ．0 D. 3 3．“k ＝1”是“直线x －y ＋k ＝0与圆x 2＋y 2＝1相交”的( )．A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件4．已知函数f (x )＝⎩⎪⎨⎪⎧e x，x <0，ln x ，x >0，则f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫1e ＝( )．A.1e B ．e C ．－1eD ．－e 5．若圆C 的半径为1，圆心在第一象限，且与直线4x －3y ＝0和x 轴相切，则该圆的标准方程是( )．A ．(x －3)2＋⎝ ⎛⎭⎪⎫y －732＝1B ．(x －2)2＋(y －1)2＝1C ．(x －1)2＋(y －3)2＝1D.⎝ ⎛⎭⎪⎫x －322＋(y －1)2＝1 6．已知某几何体的三视图如右图，其中正 (主)视图为半径为1，则该几何体体积为( )．A ．24－32πB ．24－π3C ．24－πD ．24－π27．已知函数f (x )＝2cos ⎝⎛⎭⎪⎫2x ＋π6，下面四个结论中正确的是 ( )．A ．函数f (x )的最小正周期为2πB ．函数f (x )的图象关于直线x ＝π6对称C ．函数f (x )的图象是由y ＝2cos 2x 的图象向左平移π6个单位得到 D ．函数f ⎝⎛⎭⎪⎫x ＋π6是奇函数8．若执行如图所示的程序框图，则输出的n 为( )．A ．3B ．4C ．5D ．69．实数x ，y 满足⎩⎪⎨⎪⎧x ≥1，y ≤a a，x －y ≤0，若目标函数z ＝x ＋y 取得最大值4，则实数a 的值为( )．A ．4B ．3C ．2 D.3210．已知数列{a n }，{b n }满足a 1＝1，且a n ，a n ＋1是函数f (x )＝x 2－b n x ＋2n的两个零点，则b 10等于( )．A ．24B ．32C ．48D ．6411．已知函数f (x )＝ax －1＋3(a >0且a ≠1)的图象过一个定点P ，且点P 在直线mx ＋ny －1＝0(m >0，且n >0)上，则1m ＋4n的最小值是( )．A ．12B ．16C ．25D ．2412．已知点F 1，F 2分别是双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点，过F 1且垂直于x 轴的直线与双曲线交于A ，B 两点，若△ABF 2是锐角三角形，则该双曲线离心率的取值范围是( )．A ．(1，3)B ．(3，22)C ．(1＋2，＋∞)D ．(1,1＋2)二、填空题(本大题共4小题，每小题4分，共16分) 13．抛物线y ＝2x 2的准线方程是________________．14．如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人比赛得分的中位数之和是________．15．某商场举行抽奖活动，从装有编号0,1,2,3四个小球的抽奖箱中，每次取出一个小球后放回，连续取两次，取出的两个小球号码相加之和等于5中一等奖，等于4中二等奖，等于3中三等奖，则中奖的概率为________． 16．已知2＋23＝223， 3＋38＝338， 4＋415＝4415，…，若 6＋a t ＝6a t，(a ，t 均为正实数)，类比以上等式可推测a ，t 的值，则a ＋t ＝________.参考答案【小题狂练(一)】1．B [B ＝{x |1<log 2x <2}＝{x |2<x <4}，A ∩B ＝{x |2<x <3}．] 2．B [因为z ＝x ＋3i1－i＝x ＋＋2＝x －＋x ＋2，且是实数，所以x ＝－3，选B.]3．A [若直线x －y ＋k ＝0与圆x 2＋y 2＝1相交，则有圆心(0,0)到直线x －y ＋k ＝0的距离为|k |2<1，解得－2<k <2，故选A.]4．A [因为f ⎝ ⎛⎭⎪⎫1e ＝ln 1e ＝－1，所以f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫1e ＝f (－1)＝1e .] 5．B [设圆心坐标为(a ，b )，则|b |＝1且|4a －3b |5＝1.又b >0，故b ＝1，由|4a －3|＝5得a ＝－12(圆心在第一象限、舍去)或a ＝2，故所求圆的标准方程是(x －2)2＋(y －1)2＝1.]6．A [由三视图可知，几何体是一个长、宽、高分别为4、3、2的长方体挖去了一个半径为1的半圆柱，故V ＝4×2×3－12×3×π×12＝24－32π.]7．D [令g (x )＝f ⎝ ⎛⎭⎪⎫x ＋π6＝2cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π6＋π6＝2cos ⎝ ⎛⎭⎪⎫2x ＋π2＝－2sin x ．] 8．B [执行程序框图可知：n ＝1，s ＝0，p ＝30，s <p 成立；s ＝3，n ＝2，s <p 成立；s ＝3＋9，n ＝3，s <p 成立；s ＝3＋9＋27，n ＝4，s <p 不成立，因此输出的n 的值为4.] 9．C [画出可行域得直线y ＝－x ＋z 过(a ，a )点时取得最大值，即2a ＝4，a ＝2.] 10．D [由题意知：a n ·a n ＋1＝2n，所以a n ＋1·a n ＋2＝2n ＋1，故a n ＋2a n＝2，所以a 1，a 3，a 5，…成等比数列，a 2，a 4，a 6，…也成等比数列，所以a 10＝2·24＝32，a 11＝32，故b 10＝64，选D.]11．C [由题意知，点P (1,4)，所以m ＋4n －1＝0，故1m ＋4n ＝m ＋4nm＋m ＋4nn＝17＋4n m ＋4mn≥25，所以所求最小值为25.]12．D [A ⎝ ⎛⎭⎪⎫－c ，b 2a ，B ⎝ ⎛⎭⎪⎫－c ，－b 2a ，F 2A →＝⎝ ⎛⎭⎪⎫－2c ，b 2a ，F 2B →＝⎝⎛⎭⎪⎫－2c ，－b 2a .F 2A →·F 2B →＝4c2－⎝ ⎛⎭⎪⎫b 2a 2>0，e 2－2e －1<0,1<e <1＋ 2.] 13．解析由题意知：抛物线的开口方向向上，且2p ＝12，所以准线方程为y ＝－18.答案 y ＝－1814．解析由茎叶图可知甲与乙两人比赛得分的中位数分别为28,36，其和为28＋36＝64. 答案 6415．解析从四个小球中连续抽取两次小球，取后放回，共有16种抽法，其中中一等奖的为23,32两种抽取方法；中二等奖的为13,31,22三种抽取方法；中三等奖的为12,21,30,03四种抽取方法，则中奖的概率为P ＝2＋3＋416＝916.答案91616．解析由推理可得a ＝6，t ＝62－1，故a ＋t ＝41. 答案 41。

【拿高分,选好题】高中新课程数学(苏教)二轮复习精选第二部分洞察高考热点32题《专题一 70分

【突破训练1】在数列{an}中，a1＝1，an－an－1＝n，n∈N*，
则a8的值为________．
解析根据累加法求 a8. 由题意可得 a2 － a1 ＝ 2 ， a3 － a2 ＝
7×10 3，…，a8－a7＝8，累加得 a8－a1＝2＋3＋4＋…＋8＝ 2 ＝35，所6 －3 8 ＝ 1 ＋ 5 6 －1 ＝，故 Sn ＝ 5
3 ，n＝2k，k∈N* 56 －1 8×6 －3 * ， n ＝ 2 k － 1. k ∈ N 5
答案
18
36 －1 * ， n ＝ 2 k ， k ∈ N 5 －3 * 8×6 ， n ＝ 2 k － 1. k ∈ N 5
解题方法技巧：类比法的应用一般数列的通项与求和方法是类比等差数列、等比数列的通项
公式、求和公式的推导，如等差数列通项公式的推导方法是累
加法，类比到an＋1－an＝f(n)，都可以用累加法，其它如累乘法、数列的错位相减法、裂项相消法等，也是由课本中一些基本的知识、方法类比得到，所以理解课本决不能流于形式，这个过程真的很重要.
1 a2)＝1＋4×4＝2.
在 Sn＝a1＋4a2＋42a3＋…＋an 1an，①，两边同时乘以 4 得
－
4Sn＝4a1＋42a2＋43a3＋…＋4n 1an－1＋4nan，②，①＋②得
－
5Sn＝a1＋4(a1＋a2)＋42(a2＋a3)＋…＋4n 1(an－1＋an)＋4nan＝1＋
－
n－1＋4nan，故 5Sn－4nan＝n. 答案 2 n
【突破训练 2】定义：F(x，y)＝yx(x＞0，y＞0)，设数列{an} F(n，1) 满足 an＝，设 Sn 为数列 anan＋1 的前 n 项和，则 F(2，n) Sn________1(填“＞”、“＝”、“＜”)．解析 1 1 1 由题意可得 an ＝ n2 ，所以 anan＋1 ＝＝n－ n(n＋1)

【拿高分,选好题第二波】(新课程)高中学数二轮复习精选第二部分洞察高考热点39题《专题三 40分

(1)设 n＝(x，y，z)是平面 MBC 的法向量，则B→C＝(1, 3，0)，
B→M＝(0， 3， 3)，由 n⊥B→C得 x＋ 3y＝0；
由 n⊥B→M得 3y＋ 3z＝0；取 n＝( 3，－1,1)，B→A＝(0,0,2 3)，
(3 分)
→
则距离
d＝|B|An·|n|＝2
15 5 .(5
分)
设 DE 与平面 PEC 所成角为 θ，D→1P与D→E所成角为 α，则 sin θ
＝|cos
α|＝
→→ D1P·DE →→
＝
|D1P||DE|
16 5 80＝45， 5· 25
所以直线 DE 与平面 PEC 所成角的正弦值为45.(10 分)
【抢分秘诀】 (1)建立空间坐标系，得到相关点的坐标． (2)用坐标正确表示相关向量． (3)尽可能的找出或求出相关平面的法向量． (4)借助符号语言，保证过程条理分明，正确计算求结果．
专题三 40分附加题大突破与抢分秘诀
空间向量解决立体几何问题【示例】► 如图△BCD 与△MCD 都是边长为 2 的正三角形，
平面 MCD⊥平面 BCD，AB⊥ 平面 BCD，AB＝2 3， (1)求点 A 到平面 MBC 的距离； (2)求平面 ACM 与平面 BCD 所成二面角的正弦值．解题突破 (1)先求出平面 MBC 的法向量，再利用公式求距离． (2)通过求平面 ACM 与平面 BCD 的法向量所成的角，求平面 ACM 与平面 BCD 所成二面角的正弦值．
故x－(x2－x＋2)y＋＝y0(y. －1)＝0，解得xy＝＝00， . (舍去)或yx＝＝4585， .
(4
分) 即 P45，85，2，所以D→1P＝45，85，0，所以 D1P＝

(新课程)高中数学二轮复习精选考前小题狂练4 理版

小题狂练(四)(限时40分钟)一、选择题(本大题共12小题，每小题5分，共60分)1．已知集合A ＝{y |x 2＋y 2＝1}和集合B ＝{y |y ＝x 2}，则A ∩B 等于( )．A ．(0,1)B ．[0,1]C ．(0，＋∞)D ．{(0,1)，(1,0)}2．复数(3＋4i)i(其中i 为虚数单位)在复平面上对应的点位于( )．A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．“α＝2k π－π4(k ∈Z )”是“tan α＝－1”的( )．A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．将参加夏令营的500名学生编号为：001,002，…，500，采用系统抽样的方法抽取一个容量为50的样本，且随机抽得的号码为003，这500名学生分住在三个营区，从001到200在第一营区，从201到355在第二营区，从356到500在第三营区，三个营区被抽中的人数为( )．A ．20,15,15B ．20,16,14C ．12,14,16D ．21,15,14 5．沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的侧(左)视图为( )．6．如图是一个算法的流程图，若输出的结果是31，则判断框中的整数M 的值为( )．A ．3B ．4C ．5D ．67．设F 1，F 2是双曲线x 2－y 224＝1的两个焦点，P 是双曲线上的一点，且3|PF 1|＝4|PF 2|，则|PF 1|＝( )．A ．8B ．6C ．4D ．28．若 ⎝ ⎛⎭⎪⎫2x ＋1x d x ＝3＋ln 2(a >1)，则a 的值是( )．A ．2B ．3C ．4D ．69．函数f(x)＝e 1－x 2的部分图象大致是( )．10．已知向量a ＝(4,3)，b ＝(－2,1)，如果向量a ＋λb 与b 垂直，则|2a －λb |的值为( )．A ．1 B. 5 C ．5 D ．5 511．在下列的表格中，如果每格填上一个数后，每一横行成等差数列，每一纵列成等比数列，那么x ＋y ＋z 的值为( ).A.1 B．2 C．3 D．412．已知函数f(x)的定义域为[－1,5]，部分对应值如下表.f(x)的导函数下列关于函数f(x)的命题：①函数y＝f(x)是周期函数；②函数f(x)在[0,2]是减函数；③如果当x∈[－1，t]时，f(x)的最大值是2，那么t的最大值为4；④当1<a<2时，函数y＝f(x)－a有4个零点．其中真命题的个数是( )．A．4 B．3 C．2 D．1二、填空题(本大题共4小题，每小题4分，共16分)13．已知圆C过点(1,0)，且圆心在x轴的正半轴上，直线l：y＝x－1被该圆所截得的弦长为22，则圆C的标准方程为________________．14．在△ABC中，角A，B，C所对应的边分别为a，b，c且c＝3，a＝2，a＝2b sin A，则△ABC的面积为________．15．观察下列等式：1＝12＋3＋4＝93＋4＋5＋6＋7＝254＋5＋6＋7＋8＋9＋10＝49……照此规律，第n 个等式为________． 16. 下面四个命题：①已知函数f (x )＝sin x ，在区间[0，π]上任取一点x 0，则使得f (x 0)>12的概率为23；②函数y ＝sin 2x 的图象向左平移π3个单位得到函数y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象； ③命题“∀x ∈R ，x 2－x ＋1≥34”的否定是“∃x 0∈R ，x 20－x 0＋1<34”；④若函数f (x )是定义在R 上的奇函数，且f (x ＋4)＝f (x )，则f (2 012)＝0. 其中所有正确命题的序号是________．参考答案【小题狂练(四)】1．B2．B [因为(3＋4i)·i＝－4＋3i ，所以在复平面上对应的点位于第二象限，选B.]3．A [由α＝2k π－π4(k ∈Z)可得tan α＝－1；而由tan α＝－1得α＝k π－π4(k∈Z)，故选A.]4．B [根据系统抽样特点，被抽到号码l ＝10k ＋3，k ∈N.第353号被抽到，因此第二营区应有16人，所以三个营区被抽中的人数为20,16,14.] 5．B6．B [当A ＝1，S ＝1时，执行S ＝S ＋2A，A ＝A ＋1后，S 的值为3，A 的值为2，……依次类推，当A ＝4时，执行S ＝S ＋2A，A ＝A ＋1后，S 的值为31，A 的值为5，所以M 的值为4.]7．A [由题意可知a ＝1，且点P 在右支上，∴|PF 1|－|PF 2|＝2，又3|PF 1|＝4|PF 2|，∴|PF 1|＝8.]8．A [由题意知，a 2＋ln a －1＝3＋ln 2，解得a ＝2，故选A.] 9．C [容易得出函数f (x )是偶函数，且f (x )>0恒成立，故选C.] 10．D [a ＋λb ＝(4,3)＋λ(－2,1)＝(4－2λ，3＋λ)， ∵(a ＋λb )⊥b ，∴(4－2λ，3＋λ)·(－2,1)＝0，解得λ＝1,2a －λb ＝(8,6)－(－2,1)＝(10,5)，|2a －λb |＝102＋52＝5 5.]11．A [先算出三角函数值，然后根据每一横行成等差数列，每一纵列成等比数列，填表可得，所以选12．D [①显然错误；③容易造成错觉，t max ＝5；④错误，f (2)的不确定影响了正确性；②正确，可有f ′(x )<0得到．] 13．解析待定系数法求圆的方程．答案 (x －3)2＋y 2＝414．解析由题意知，b sin A ＝1，又由正弦定理得：b sin A ＝2sin B ，故解得sin B ＝12，所以△ABC 的面积为12ac sin B ＝32.答案 3215．解析等式左边第一个数为对应行数，每行的整数个数为奇数个，等式右边为对应奇数个的平方，所以通项公式为n ＋(n ＋1)＋(n ＋2)＋…＋(3n －2)＝(2n －1)2.答案 n ＋(n ＋1)＋(n ＋2)＋…＋(3n －2)＝(2n －1)216．解析 ②错误，应该向左平移π6；①使得f (x 0)>12的概率为p ＝56π－16ππ＝23；④f (2 012)＝f (0)＝0. 答案 ①③④。

【拿高分,选好题第二波】(新课程)高中数学二轮复习精选大题冲关解答题规范训练1 新人教版

解答题规X 练(一)1．已知向量m ＝(sin x,1)，n ＝⎝⎛⎭⎪⎫3cos x ，12，函数f (x )＝(m ＋n )·m . (1)求函数f (x )的最小正周期T 及单调递增区间；(2)已知a ，b ，c 分别为△ABC 内角A ，B ，C 的对边，A 为锐角，a ＝23，c ＝4，且f (A )是函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值，求△ABC 的面积S . 2．某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)，…，[140,150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：(1)求分数在[120,130)内的频率；(2)若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为100＋1102＝105)作为这组数据的平均分，据此，估计本次考试的平均分；(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率．3.在数列{a n }中，a 1＝1,2a n ＋1＝⎝ ⎛⎭⎪⎫1＋1n 2·a n (n ∈N *)． (1)证明：数列⎩⎨⎧⎭⎬⎫a n n 2是等比数列，并求数列{a n }的通项公式； (2)令b n ＝a n ＋1－12a n ，求数列{b n }的前n 项和S n . 4．如图，已知AB ⊥平面ACD ，DE ⊥平面ACD ，AC ＝AD ，DE ＝2AB ，F 为CD 的中点．(1)求证：AF ∥平面BCE ；(2)求证：平面BCE ⊥平面CDE .5．已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右顶点的坐标分别为A (－2,0)、B (2,0)，离心率e ＝12. (1)求椭圆C 的方程；(2)设椭圆的两焦点分别为F 1，F 2，点P 是其上的动点．①当△PF 1F 2内切圆的面积最大时，求内切圆圆心的坐标；②若直线l ：y ＝k (x －1)(k ≠0)与椭圆交于M 、N 两点，证明直线AM 与直线BN 的交点在直线x ＝4上．6．已知函数f (x )＝ax 3＋bx 2－3x 在x ＝±1处取得极值．(1)求函数f (x )的解析式；(2)求证：对于区间[－1,1]上任意两个自变量的值x 1，x 2，都有|f (x 1)－f (x 2)|≤4；(3)若过点A (1，m )(m ≠－2)可作曲线y ＝f (x )的三条切线，某某数m 的取值X 围．参考答案【解答题规X 练(一)】1．(1)f (x )＝(m ＋n )·m ＝sin 2x ＋1＋3sin x cos x ＋12＝1－cos 2x 2＋1＋32sin 2x ＋12＝32sin 2x －12cos 2x ＋2＝sin ⎝ ⎛⎭⎪⎫2x －π6＋2. 因为ω＝2，所以T ＝2π2＝π. 由2k π－π2≤2x －π6≤2k π＋π2(k ∈Z )得k π－π6≤x ≤k π＋π3(k ∈Z )，故所求单调递增区间为⎣⎢⎡⎦⎥⎤k π－π6，k π＋π3(k ∈Z )． (2)由(1)知，f (A )＝sin ⎝⎛⎭⎪⎫2A －π6＋2，又A ∈⎝⎛⎭⎪⎫0，π2，∴－π6<2A －π6<5π6. 由正弦函数图象可知，当2A －π6＝π2，即A ＝π3时，f (x )取得最大值3，由余弦这理，a 2＝b 2＋c 2－2bc cos A .可得12＝b 2＋16－2×4b ×12，∴b ＝2. 从而S ＝12bc sin A ＝12×2×4×sin π3＝2 3. 2．解 (1)分数在[120,130)内的频率为1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3.(2)估计平均分为 x ＝95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121.(3)依题意，[110,120)分数段的人数为60×0.15＝9(人)．[120,130)分数段的人数为60×0.3＝18(人)．∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本， ∴需在[110,120)分数段内抽取2人，并分别记为m ，n ；在[120,130)分数段内抽取4人，并分别记为a ，b ，c ，d ；设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A ，则基本事件共有(m ，n )，(m ，a )，…，(m ，d )，(n ，a )，…，(n ，d )，(a ，b )，…，(c ，d )共15种．则事件A 包含的基本事件有(m ，n )，(m ，a )，(m ，b )，(m ，c )，(m ，d )，(n ，a )，(n ，b )，(n ，c )，(n ，d )共9种．∴P (A )＝915＝35. 3．(1)证明由条件得a n ＋1n ＋12＝12·a n n 2，又n ＝1时，a n n2＝1，故数列⎩⎨⎧⎭⎬⎫a n n 2构成首项为1，公比为12的等比数列．从而a n n 2＝12n －1，即a n ＝n 22n －1. (2)解由b n ＝n ＋122n －n 22n ＝2n ＋12n 得 S n ＝32＋522＋…＋2n ＋12n ⇒12S n ＝322＋523＋…＋2n －12n ＋2n ＋12n ＋1，两式相减得12S n ＝32＋2⎝ ⎛⎭⎪⎫122＋123＋…＋12n －2n ＋12n ＋1，所以S n ＝5－2n ＋52n . 4．证明 (1)因为AB ⊥平面ACD ，DE ⊥平面ACD ，所以AB ∥DE .取CE 的中点G ，连接BG ，GF ，因为F 为CD 的中点，所以GF ∥ED ∥BA ，GF ＝12ED ＝BA ，从而ABGF 是平行四边形，于是AF ∥BG .因为AF ⊄平面BCE ，BG ⊂平面BCE ，所以AF ∥平面BCE . (2)因为AB ⊥平面ACD ，AF ⊂平面ACD ，所以AB ⊥AF ，即ABGF 是矩形，所以AF ⊥GF . 又AC ＝AD ，所以AF ⊥CD .而CD ∩GF ＝F ，所以AF ⊥平面GCD ，即AF ⊥平面CDE .因为AF ∥BG ，所以BG ⊥平面CDE .因为BG ⊂平面BCE ，所以平面BCE ⊥平面CDE .5．(1)解由题意知a ＝2，e ＝c a ＝12，所以c ＝1，b ＝ 3. 故椭圆E 的方程为x 24＋y 23＝1. (2)①解 |F 1F 2|＝2，设F 1F 2边上的高为h ，则S △PF 1F 2＝12×2×h ＝h .设△PF 1F 2的内切圆的半径为R ，因为△PF 1F 2的周长为定值6，所以12R ×6＝3R ＝S △PF 1F 2，当P 在椭圆短轴顶点时，h 最大为3，故S △PF 1F 2的最大值为3，于是R 的最大值为33，此时内切圆圆心的坐标为⎝ ⎛⎭⎪⎫0，±33. ②证明将直线l ：y ＝k (x －1)代入椭圆E 的方程x 24＋y 23＝1，并整理得(3＋4k 2)x 2－8k 2x ＋4(k 2－3)＝0.设直线l 与椭圆E 的交点为M (x 1，y 1)，N (x 2，y 2)，由根与系数的关系，得x 1＋x 2＝8k 23＋4k 2，x 1x 2＝4k 2－33＋4k 2.直线AM 的方程为：y ＝y 1x 1＋2(x ＋2)，它与直线x ＝4的交点坐标为P ⎝ ⎛⎭⎪⎫4，6y 1x 1＋2，同理可求得直线BN 与直线x ＝4的交点坐标为Q ⎝ ⎛⎭⎪⎫4，2y 2x 2－2. 下面说明P 、Q 两点重合，即证明P 、Q 两点的纵坐标相等．因为y 1＝k (x 1－1)，y 2＝k (x 2－1)，所以6y 1x 1＋2－2y 2x 2－2＝ 6k x 1－1x 2－2－2k x 2－1x 1＋2x 1＋2x 2－2＝2k [2x 1x 2－5x 1＋x 2＋8]x 1＋2x 2－2＝2k ⎣⎢⎡⎦⎥⎤8k 2－33＋4k 2－40k 23＋4k 2＋8x 1＋2x 2－2＝0.因此结论成立．综上可知，直线AM 与直线BN 的交点在直线x ＝4上．6．解 (1)f ′(x )＝3ax 2＋2bx －3，依题意，f ′(1)＝f ′(－1)＝0，即⎩⎪⎨⎪⎧ 3a ＋2b －3＝0，3a －2b －3＝0，解得a ＝1，b ＝0.∴f (x )＝x 3－3x .(2)∵f (x )＝x 3－3x ，∴f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，当－1<x <1时，f ′(x )<0，故f (x )在区间[－1,1]上为减函数，f (x )max ＝f (－1)＝2，f (x )min ＝f (1)＝－2.∵对于区间[－1,1]上任意两个自变量的值x 1，x 2，都有|f (x 1)－f (x 2)|≤|f (x )max －f (x )min |＝2－(－2)＝4.(3)f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，∵曲线方程为y ＝x 3－3x ，∴点A (1，m )(m ≠－2)不在曲线上．设切点为M (x 0，y 0)，则点M 的坐标满足y 0＝x 30－3x 0. 因f ′(x 0)＝3(x 20－1)，故切线的斜率为3(x 20－1)＝x 30－3x 0－m x 0－1，整理得2x 30－3x 20＋m ＋3＝0.∵过点A (1，m )可作曲线的三条切线，∴关于x 0的方程2x 30－3x 20＋m ＋3＝0有三个实根．设g (x 0)＝2x 30－3x 20＋m ＋3，则g ′(x 0)＝6x 20－6x 0，由g ′(x 0)＝0，得x 0＝0或x 0＝1.∴g (x 0)在(－∞，0)和(1，＋∞)上单调递增，在(0,1)上单调递减． ∴函数g (x 0)＝2x 30－3x 20＋m ＋3的极值点为x 0＝0，x 0＝1.∴关于x 0的方程2x 30－3x 20＋m ＋3＝0有三个实根的充要条件是⎩⎪⎨⎪⎧ g 0>0，g 1<0，解得－3<m <－2.故所求的实数m 的取值X 围是(－3，－2)．。

2021-2022年(新课程)高中数学二轮复习精选考前小题狂练6 理新人教版

2021-2022年（新课程）高中数学二轮复习精选考前小题狂练6 理新人教版一、选择题(本大题共12小题，每小题5分，共60分) 1．复数⎝⎛⎭⎪⎫3－i 1＋i 2＝ ( )．A ．－3－4iB ．－3＋4iC ．3－4iD ．3＋4i2．命题p ：若a ·b <0，则a 与b 的夹角为钝角．命题q ：定义域为R 的函数y ＝f (x )在(－∞，0)及(0，＋∞)上都是增函数，则f (x )在(－∞，＋∞)上是增函数．下列说法正确的是( )．A ．“p 或q ”是真命题B ．“p 且q ”是假命题C ．“綈p ”为假命题D ．“綈q ”为假命题3．函数f (x )＝2x 3－6x 2＋7在(0,2)内零点的个数为( )．A ．0B ．1C ．2D ．4 4．已知向量a ＝(x ＋1,2)，b ＝(－1，x )．若a 与b 垂直，则|b |＝( )．A ．1 B. 2 C ．2 D ．4 5．若3sin α＋cos α＝0，则1cos 2α＋sin 2α的值为 ( )．A.103 B.53 C.23D ．－2 6．由曲线y ＝x 2，y ＝x 3围成的封闭图形面积为( )．A.112 B.14 C.13 D.7127．已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋x ，x ≥0，－x 2－x ，x <0，则不等式f (x )>0的解的区间是( )．A ．(0,1)B ．(－1,0)∪(0,1)C ．(－1,1)D ．(－∞，－1)∪(1，＋∞)8．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0，x ＋y ≤1，0≤y ≤12，若目标函数z ＝ax ＋y (其中a 为常数)仅在点⎝ ⎛⎭⎪⎫12，12处取得最大值，则实数a 的取值范围是( )．A ．(－2,2)B ．(0,1)C ．(－1,1)D ．(－1,0)9．执行如图所示的程序框图，若p ＝4，则输出的S ＝( )．A.1516B.34C.1716D.517 10．已知数列{a n }满足log 3a n ＋1＝log 3a n ＋1(n ∈N *)，且a 2＋a 4＋a 6＝9，则log 13(a 5＋a 7＋a 9)的值是( )．A ．－15B ．－5C ．5 D.1511．某一随机变量ξ的分布列如下表，且E (ξ)＝1.5，则m －n 的值为( ).ξ 0 1 2 3 P0.2m n0.312．已知抛物线y 2＝2px (p >0)上一点M (1，m )(m >0)到其焦点的距离为5，双曲线x 2a－y 2＝1的左顶点为A ，若双曲线的一条渐近线与直线AM 平行，则实数a 的值为( )． A.19 B.14 C.13 D.12 二、填空题(本大题共4小题，每小题4分，共16分) 13．已知函数y ＝2sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω>0，|φ|<π2的部分图象如图，则φ＝________.14．设F 1，F 2为椭圆x 24＋y 2＝1的左、右焦点，过椭圆中心任作一直线与椭圆交于P ，Q 两点，当四边形PF 1QF 2面积最大时，PF 1→·PF 2→的值等于________．15．在△ABC 中，|BC |＝4，且BC 落在x 轴上，BC 中点为坐标原点，如果sin C －sin B ＝12sin A ，则顶点A 的轨迹方程是________． 16．方程2－x＋x 2＝3的实数解的个数为________．参考答案【小题狂练(六)】 1．A [⎝ ⎛⎭⎪⎫3－i 1＋i 2＝⎣⎢⎡⎦⎥⎤3－i1－i 22＝(1－2i)2＝－3－4i.]2．B [由题得命题p 是假命题，因为当向量a ·b ＝－1<0时，两个向量的夹角为180°，不是钝角．命题q 是假命题，如函数y ＝－1x，所以选B.]3．B [因为f ′(x )＝6x 2－12x ＝6x (x －2)，由f ′(x )>0，得x >2或x <0；由f ′(x )<0得0<x <2.所以函数f (x )在(0,2)上是减函数，而f (0)＝7>0，f (2)＝－1<0，由零点存在定理可知，函数f (x )＝2x 3－6x 2＋7在(0,2)内零点的个数为1.] 4．B [由题意知，a·b ＝x －1＝0，解得x ＝1，故|b |＝ 2.]5．A [3sin α＋cos α＝0，则tan α＝－13，1cos 2α＋sin 2α＝sin 2α＋cos 2αcos 2α＋2sin αcos α＝tan 2α＋11＋2tan α＝⎝ ⎛⎭⎪⎫－132＋11＋2⎝ ⎛⎭⎪⎫－13＝103.] 6．A [S ＝ (x 2－x 3)d x ＝⎝ ⎛⎭⎪⎫13x 3－14x 4⎪⎪⎪10＝112.]7．B [原不等式等价于⎩⎪⎨⎪⎧x ≥0，－x 2＋x >0或⎩⎪⎨⎪⎧x <0，－x 2－x >0⇒0<x <1或－1<x <0.所以解的区间为(－1,0)∪(0,1)．]8．C [由x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0，x ＋y ≤1，0≤y ≤12，画出此不等式组表示的平面区域如图中阴影部分所示．由目标函数z ＝ax ＋y ，得y ＝－ax ＋z ，因为z 仅在点⎝ ⎛⎭⎪⎫12，12处取得最大值，所以得－1<－a <1，得实数a 的取值范围是(－1,1)．]9．A [由题意可知，S ＝12＋122＋123＋124＝12×⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫1241－12＝1516，所以输出S 的值是1516.]10．B [由log 3a n ＋1＝log 3a n ＋1(n ∈N *)，得a n ＋1＝3a n ，所以数列{a n }是公比等于3的等比数列，a 5＋a 7＋a 9＝(a 2＋a 4＋a 6)×33＝35，所以log 13(a 5＋a 7＋a 9)＝－log 335＝－5，故选B.]11．C [依题意得⎩⎪⎨⎪⎧m ＋n ＝0.5，m ＋2n ＋0.9＝1.5，由此解得m ＝0.4，n ＝0.1，所以m －n ＝0.3，选C.]12．A [由于M (1，m )在抛物线上，∴m 2＝2p ，而M 到抛物线的焦点的距离为5，根据抛物线的定义知点M 到抛物线的准线x ＝－p 2的距离也为5，∴1＋p2＝5，∴p ＝8，由此可以求得m ＝4，双曲线的左顶点为A (－a ，0)，∴k AM ＝41＋a ，而双曲线的渐近线方程为y ＝±x a ，根据题意得，41＋a ＝1a，∴a ＝19.]13．解析从题中图象中可以看出T ＝4⎝ ⎛⎭⎪⎫7π12－π4＝4π3，所以ω＝2πT ＝2π×34π＝32，又当x ＝π4时，y ＝2，所以2＝2sin ⎝ ⎛⎭⎪⎫32×π4＋φ，即sin ⎝ ⎛⎭⎪⎫3π8＋φ＝1，因为|φ|<π2，所以3π8＋φ＝π2，解得φ＝π8.答案 π814．解析易知当P ，Q 分别在椭圆短轴端点时，四边形PF 1QF 2面积最大．此时，F 1(－3，0)，F 2(3，0)，不妨设P (0,1)，∴PF 1→＝(－3，－1)，PF 2→＝(3，－1)， ∴PF 1→·PF 2→＝－2. 答案－215．解析因为sin C －sin B ＝12sin A ，所以|AB |－|AC |＝12|BC |.因为|BC |＝4，所以|AB |－|AC |＝2，所以a ＝1，c ＝2，b ＝3，即x 2－y 23＝1的右半支．答案 x 2－y 23＝1(x >1)16．解析方程变形为3－x 2＝2－x ＝⎝ ⎛⎭⎪⎫12x ，令y ＝3－x 2，y ＝⎝ ⎛⎭⎪⎫12x .在同一坐标系下作出y＝3－x 2与y ＝⎝ ⎛⎭⎪⎫12x 的图象．由图象可知两函数图象有2个交点．答案 2{DK30656 77C0 矀Y22088 5648 噈23428 5B84 宄35483 8A9B 誛29679 73EF 珯'21642 548A 咊40310 9D76 鵶 40757 9F35 鼵。

【拿高分选好题】(新课程)高中数学二轮复习精选第二部分洞察高考热点32题《专题一70分填空

解析由|x－a|＜1得－1
＜x－a＜1，即a－1＜x ＜a＋1.如图，要使A∩B＝ ∅成立，由图可知a＋1≤1或a－1≥5，所以a≤0或a≥6. 答案 a≤0或a≥6
解题方法技巧：数形结合法对于一些含有几何背景的填空题，若能根据题目条件的特点，
作出符合题意的图形，做到数中思形，以形助数，并通过对图
________．
解析 A＝{1,2}，B＝{1,2,3,4}，故满足条件A⊆C⊆B的集合
C的个数即为集合{3,4}的子集个数22＝4(个)．答案 4
解题方法技巧：直接求解法直接从题设条件出发，利用定义、性质、定理、公式等，经过
变形、推理、计算、判断得到结论的一种解题方法．它是解填
空题常用的基本方法，使用直接法解填空题，要善于透过现象抓本质，自觉地、有意识地采取灵活、简捷的解法．
专题一 70分填空题大
突破与解题技法
专题一 70分填空题大突破与解题技法
【专题定位】
江苏高考对填空题知识点的考查相对稳定，共有14道，分值70分，填空题的得分多少，决定了整个试卷的成败，本专题通过对高考填空题的题型进行分类，同时穿插方法的指导，提高解题的速度和正确率．
填空题没有备选项．因此，解答时既有不受诱误的干扰之
好处，又有缺乏提示的帮助之不足，对考生独立思考和求解，在能力要求上会高一些，只要求写出结果，不要求写出解答过程，不设中间分，更易失分，因而在解答过程中应力求准确无误．
【应对策略】解填空题时，要有合理的分析和判断，要求推理、运算的
每一步骤都正确无误，还要求将答案表达得准确、完整. 合情推理、优化思路、少算多思将是快速、准确地解答填空题的基本要求．数学填空题，绝大多数是计算型(尤其是推理计算型) 和概念(性质)判断型的试题，应答时必须按规则进行切实的计

【拿高分，选好题第二波】（新课程）高中数学二轮复习精选第二部分洞察高考热点39题《专题二 90分

专题二90分解答题大冲关与评分细则【专题定位】数学解答题是高考数学试卷中的一类重要题型，这些题涵盖了中学数学的主要内容，具有知识容量大、解题方法多、能力要求高、突显数学思想方法的运用以及要求考生具有一定的创新意识和创新能力等特点，解答题综合考查学生的运算能力、逻辑思维能力、空间想象能力和分析问题、解决问题的能力，分值占90分，主要分六块：三角函数(或与平面向量交汇)、立体几何、应用问题、函数与导数(或与不等式交汇)、数列(或与不等式交汇)、解析几何(或与平面向量交汇)．从历年高考题看综合题这些题型的命制都呈现出显著的特点和解题规律，从阅卷中发现考生“会而得不全分”的现象大有人在，针对以上情况，在高考数学备考中认真分析这些解题特点及时总结出来，这样有针对性的进行复习训练，能达到事半功倍的效果．【应对策略】解答题是高考数学试卷的重头戏，占整个试卷分数的半壁江山，考生在解答解答题时，应注意正确运用解题技巧．(1)对会做的题目：要解决“会而不对，对而不全”这个老大难的问题，要特别注意表达准确，考虑周密，书写规范，关键步骤清晰，防止分段扣分．解题步骤一定要按教科书要求，避免因“对而不全”失分．(2)对不会做的题目：对绝大多数考生来说，更为重要的是如何从拿不下来的题目中分段得分．我们说，有什么样的解题策略，就有什么样的得分策略．对此可以采取以下策略：①缺步解答：如遇到一个不会做的问题，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步．特别是那些解题层次明显的题目，每一步演算到得分点时都可以得分，最后结论虽然未得出，但分数却已过半．②跳步解答：解题过程卡在某一过渡环节上是常见的．这时，我们可以先承认中间结论，往后推，看能否得到结论．若题目有两问，第(1)问想不出来，可把第(1)问作“已知”，先做第(2)问，跳一步再解答．③辅助解答：一道题目的完整解答，既有主要的实质性的步骤，也有次要的辅助性的步骤．实质性的步骤未找到之前，找辅助性的步骤是明智之举．如：准确作图，把题目中的条件翻译成数学表达式，根据题目的意思列出要用的公式等．罗列这些小步骤都是有分的，这些全是解题思路的重要体现，切不可以不写，对计算能力要求高的，实行解到哪里算哪里的策略．书写也是辅助解答，“书写要工整，卷面能得分”是说第一印象好会在阅卷老师的心理上产生光环效应．④逆向解答：对一个问题正面思考发生思维受阻时，用逆向思维的方法去探求新的解题途径，往往能得到突破性的进展．顺向推有困难就逆推，直接证有困难就间接证．细心计算，规范解答，全面拿下三角与向量题【示例】► (2012·苏锡常镇调研测试)如图，在四边形ABCD 中，已知AB ＝13，AC ＝10，AD ＝5，CD ＝65，AB →·AC →＝50. (1)求cos ∠BAC 的值；(2)求sin ∠CAD 的值；(3)求△BAD 的面积．解题突破 (1)根据数量积的定义式的变形式求；(2)在△ACD 中，利用余弦定理求cos ∠CAD ，再利用平方关系求解；(3)利用两角和公式求∠BAD 的正弦值，代入三角形面积公式求解．解 (1)因为AB →·AC →＝|AB →||AC →|cos ∠BAC ，所以cos ∠BAC ＝AB →·AC →|AB →||AC →|＝5013×10＝513.(2分) (2)在△ADC 中，AC ＝10，AD ＝5，CD ＝65，由余弦定理，得cos ∠CAD ＝AC 2＋AD 2－CD 22AC ·AD ＝102＋52－6522×10×5＝35.(4分) 因为∠CAD ∈(0，π)，所以sin ∠CAD ＝ 1－cos 2∠CAD ＝1－⎝ ⎛⎭⎪⎫352＝45.(6分) (3)由(1)知，cos ∠BAC ＝513. 因为∠BAC ∈(0，π)，所以sin ∠BAC ＝ 1－cos 2∠BAC ＝1－⎝ ⎛⎭⎪⎫5132＝1213.(8分) 从而sin ∠BAD ＝sin(∠BAC ＋∠CAD )＝sin ∠BAC cos ∠CAD ＋cos ∠BAC sin ∠CAD＝1213×35＋513×45＝5665.(11分) 所以S △BAD ＝12AB ·AD ·sin∠BAD ＝12×13×5×5665＝28.(14分)评分细则 1没有写cos ∠BAC ＝AB →·AC →|AB →||AC →|直接计算的，扣1分.,2不交代∠CAD 的范围的，扣1分；,3不交代∠BAC 范围的，扣1分. 【突破训练】 (2012·苏锡常镇调研测试(一))在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，向量m ＝⎝ ⎛⎭⎪⎫2cos C 2，－sin C ，n ＝⎝ ⎛⎭⎪⎫cos C 2，2sin C ，且m ⊥n . (1)求角C 的大小；(2)若a 2＝2b 2＋c 2，求tan A 的值．解 (1)∵m ⊥n ，∴m ·n ＝0.则2cos 2C 2－2sin 2C ＝0.(2分) (阅卷说明：无中间分)∵C ∈(0，π)，∴cos C 2＞0，sin C ＞0.∴cos C2＝sin C (4分) (阅卷说明：得到2cos 2C ＋cos C －1＝0也得2分) 则sin C 2＝12.(6分) 又C 2∈⎝ ⎛⎭⎪⎫0，π2，∴C 2＝π6.则C ＝π3.(8分) (阅卷说明：以上有一处写范围不扣分，否则扣1分)(2)∵C ＝π3，由余弦定理，得c 2＝a 2＋b 2－ab . 又∵a 2＝2b 2＋c 2，∴a 2＝2b 2＋a 2＋b 2－ab .则a ＝3b .(10分)由正弦定理，得sin A ＝3sin B ．(11分) ∵C ＝π3，∴sin A ＝3sin ⎝ ⎛⎭⎪⎫2π3－A .(12分) 即sin A ＝－33cos A ．(13分)∵cos A ＝0上式不成立，即cos A ≠0，∴tan A ＝－3 3.(14分)(阅卷说明：结果正确不扣分)【抢分秘诀】1．解决三角函数图象问题，主要从函数图象上的点入手，抓住函数图象上的关键点，而对于作图问题往往利用函数在一个周期内的五点确定函数图象的形状，识图问题需要利用关键点确定解析式中参数的取值，而图象的伸缩、平移变换也可以利用关键点帮助准确记忆相关规律．2．解决三角函数的最值与范围问题，要从三角函数的性质入手，常常转化为两类问题求解：一是通过化简、变换及换元转化为正弦、余弦函数的最值与范围问题求解；二是通过换元分解为基本初等函数和正弦、余弦函数的最值、三角函数的有界性和基本初等函数的单调性问题解决．3．解决三角函数的化简、求值与证明问题的基本思路是：第一，观察角与角之间的关系，注意角的变形应用，角的变换是三角函数变换的核心；第二，看函数名称之间的关系，通常是统一为正弦、余弦函数的形式；第三，观察代数式的结构特点，对于三角公式要记忆准确，应用公式要认真分析，合理转化，避免盲目性．4．解三角形或多边形问题均以三角形为载体，其解题过程的实质是将三角形中的问题转化为代数问题或方程问题，解题要从三角形的边角关系入手，依据题设条件合理设计解题程序，灵活进行边角之间的互化．善于观察，注意转化，做好立体几何不是难事【示例】► (2012·南师大附中阶段检测)如图，四棱椎P ABCD 的底面为矩形，且AB ＝2，BC ＝1，E ，F 分别为AB ，PC 中点．(1)求证：EF ∥平面PAD ；(2)若平面PAC ⊥平面ABCD ，求证：平面PAC ⊥平面PDE .解题突破 (1)由E ，F 分别为AB ，PC 中点．取PD 的中点M ，再证四边形AEMF 是平行四边形．(2)在矩形ABCD 中，根据AB ＝2BC ，可得DA AE ＝CD DA，从而可证△DAE ∽△CDA .再证明DE ⊥AC ，根据面面垂直的性质和判定可得平面PAC ⊥平面PDE .证明 (1)法一取线段PD 的中点M ，连接FM ，AM .因为F 为PC 的中点，所以FM ∥CD ，且FM ＝12CD . 因为四边形ABCD 为矩形，E 为AB 的中点，所以EA ∥CD ，且EA ＝12CD .所以FM∥EA，且FM＝EA.所以四边形AEFM为平行四边形．所以EF∥AM.(5分)又AM⊂平面PAD，EF⊄平面PAD，所以EF∥平面PAD.(7分)法二连接CE并延长交DA的延长线于N，连接PN.因为四边形ABCD为矩形，所以AD∥BC，所以∠BCE＝∠ANE，∠CBE＝∠NAE.又AE＝EB，所以△CEB≌△NEA，所以CE＝NE.又F为PC的中点，所以EF∥NP.(5分)又NP⊂平面PAD，EF⊄平面PAD，所以EF∥平面PAD.(7分)法三取CD的中点Q，连接FQ，EQ.在矩形ABCD中，E为AB的中点，所以AE＝DQ，且AE∥DQ.所以四边形AEQD为平行四边形，所以EQ∥AD.又AD⊂平面PAD，EQ⊄平面PAD，所以EQ∥平面PAD.(2分)因为Q，F分别为CD，CP的中点，所以FQ∥PD.又PD⊂平面PAD，FQ⊄平面PAD，所以FQ∥平面PAD.又FQ，EQ⊂平面EQF，FQ∩EQ＝Q，所以平面EQF∥平面PAD.(5分) 因为EF⊂平面EQF，所以EF∥平面PAD.(7分)(2)设AC，DE相交于G.在矩形ABCD中，因为AB＝2BC，E为AB的中点．所以DAAE ＝CDDA＝ 2.又∠DAE＝∠CDA，所以△DAE∽△CDA，所以∠ADE＝∠DCA.又∠ADE＋∠CDE＝∠ADC＝90°，所以∠DCA＋∠CDE＝90°.由△DGC的内角和为180°，得∠DGC＝90°.即DE⊥AC.(9分) 因为平面PAC⊥平面ABCD因为DE ⊂平面ABCD ，所以DE ⊥平面PAC ，(12分)又DE ⊂平面PDE ，所以平面PAC ⊥平面PDE .(14分)评分细则 1第一问，方法1和2，下结论时：不交代平面外一条直线与平面内一条直线平行，一律扣2分；方法3，直接由线线平行→面面平行，扣3分； 2第二问，不用平面几何知识证明DE ⊥AC ，扣2分.【突破训练】 (2012·南师附中统测)如图，在四棱锥P ABCD 中，PD ⊥平面ABCD ，四边形ABCD 是菱形，AC ＝6，BD ＝63，E 是PB 上任意一点．(1)求证：AC ⊥DE ；(2)当△AEC 面积的最小值是9时，求证：EC ⊥平面PAB .(1)证明连接BD ，设AC 与BD 相交于点F .因为四边形ABCD 是菱形，所以AC ⊥BD .(4分)又因为PD ⊥平面ABCD ，AC ⊂平面PDB ，E 为PB 上任意一点，DE ⊂平面PBD ，所以AC ⊥DE .(7分)(2)解连ED .由(1)知AC ⊥平面PDB ，EF ⊂平面PBD ，所以AC ⊥EF .S △ACE ＝12AC ·EF ，在△ACE 面积最小时，EF 最小，则EF ⊥PB .S △ACE ＝12×6×EF ＝9，解得EF ＝3，(10分)由PB ⊥EF 且PB ⊥AC 得PB ⊥平面AEC ，则PB ⊥EC ，又由EF ＝AF ＝FC ＝3得EC ⊥AE ，而PB ∩AE ＝E ，故EC ⊥平面PAB .(14分)【抢分秘诀】(1)在解答中，遵循先证明后计算的原则．注重考查立体问题平面化，面面问题，线面化再线线化的化归过程．(2)根据题目的条件画出图形，注意图形的合理性、美观性和直观性．有些性质的判定和长度的计算及点的位置的确定，往往需借助图形的直观性而估算一个大概，而且有利于经过计算或论证得到的最后的结果的验证．(3)要注意立体几何语言的表达方法，要简明扼要、清楚明白、符合逻辑的进行表述，要以课本上的表述为示范，尽快地掌握要领．各个命题的因果关系要明明白白，计算过程清晰明了，保证无误．重视立体几何语言的严谨性、科学性和简捷性，往往思路正确，而表述有误，因此失分真是太可惜！(4)立体几何的概念、公理、定理、计算公式等，应牢固掌握，同时尽可能多的掌握一些重要结论．因为这些知识都是学习立体几何的基本工具，它是思维浓缩的精华内容，是规律的总结，也是进行推理、论证和计算的基础．看似复杂，实则简单，带你融会贯通应用题【例1】► (2012·南京高三调研)经销商用一辆J 型卡车将某种水果从果园运送(满载)到相距400 km 的水果批发市场．据测算，J 型卡车满载行驶时，每100 km 所消耗的燃油量u (单位：L)与速度v (单位：km/h)，的关系近似地满足u ＝⎩⎪⎨⎪⎧ 100v ＋23，0＜v ≤50，v 2500＋20，v ＞50.除燃油费外，人工工资、车损等其他费用平均每小时300元．已知燃油价格为每升(L)7.5元．(1)设运送这车水果的费用为y (元)(不计返程费用)，将y 表示成速度v 的函数关系式；(2)卡车该以怎样的速度行驶，才能使运送这车水果的费用最少？解题突破由u 是关于v 的分段函数，得y 也是关于v 的分段函数，求出各段函数的最小值，再比较大小，而求函数最值的方法可以有函数图象法、单调性法、导数法等，其中导数法是求函数最值的一种相当重要的方法．解 (1)由题意，当0＜v ≤50时，y ＝7.5·400100u ＋300·400v ＝30·⎝ ⎛⎭⎪⎫100v ＋23＋300·400v ＝123 000v＋690，当v ＞50时，y ＝7.5·400100u ＋300·400v ＝30·⎝ ⎛⎭⎪⎫v 2500＋20＋300·400v ＝3v 250＋120 000v ＋600，所以y ＝⎩⎪⎨⎪⎧ 123 000v ＋690，0＜v ≤50，3v 250＋120 000v ＋600，v ＞50.(8分)(2)当0＜v ≤50时，y ＝123 000v＋690是单调减函数，故v ＝50时，y 取得最小值y min ＝123 00050＋690＝3 150；当v ＞50时，y ＝3v 250＋120 000v＋600(v ＞50) 由y ′＝3v 25－120 000v 2＝3v 3－10625v2＝0，得v ＝100 当50＜v ＜100时，y ′＜0，函数y ＝3v 250＋120 000v＋600单调递减．所以当v ＝100时，y 取得最小值y min ＝3×100250＋120 000100＋600＝2 400由于3 150＞2 400，所以当v ＝100时，y 取得最小值．答当卡车以100 km/h 的速度驶时，运送这车水果的费用最少．(16分)评分细则 1第一问，有一段求解错误的，扣4分； 2第二问，有一段函数最值求解错误的，扣2分；没有将两个最小值比较的，扣2分，不写答案的，扣1分.【例2】► (2012·南通市数学学科基地密卷(一)，18)如图所示：一吊灯的下圆环直径为4 m ，圆心为O ，通过细绳悬挂在天花板上，圆环呈水平状态，并且与天花板的距离(即OB )为2 m ，在圆环上设置三个等分点A 1，A 2，A 3.点C 为OB 上一点(不包含端点O 、B )，同时点C 与点A 1，A 2，A 3，B 均用细绳相连接，且细绳CA 1，CA 2，CA 3的长度相等。

【拿高分,选好题第二波】(新课程)高中数学二轮复习 精选考前小题狂练3 新人教版

【拿高分,选好题第二波】(新课程)高中数学二轮复习精选第一部分25个必考问题专项突破专题训练16算法

高中新课程数学(苏教)二轮复习精选考前小题狂练

【拿高分,选好题第二波】(新课程)高中学数二轮复习 精选第二部分 洞察高考热点39题《专题三 4

(新课程)高中数学二轮复习精选考前小题狂练3理新人教版.doc

【拿高分，选好题第二波】（新课程）高中数学二轮复习 精选第二部分 洞察高考热点39题《专题三 40分

【拿高分,选好题第二波】(新课程)高中数学二轮复习 精选考前小题狂练1 新人教版

【拿高分,选好题】高中新课程数学(苏教)二轮复习精选第二部分 洞察高考热点32题《专题一 70分

【拿高分,选好题第二波】(新课程)高中学数二轮复习 精选第二部分 洞察高考热点39题《专题三 40分

(新课程)高中数学二轮复习 精选考前小题狂练4 理 版

【拿高分,选好题第二波】(新课程)高中数学二轮复习 精选大题冲关解答题规范训练1 新人教版

2021-2022年(新课程)高中数学二轮复习 精选考前小题狂练6 理 新人教版

【拿高分 选好题】(新课程)高中数学二轮复习 精选第二部分 洞察高考热点32题《专题一70分填空

【拿高分，选好题第二波】（新课程）高中数学二轮复习 精选第二部分 洞察高考热点39题《专题二 90分