宁夏银川市2020版七年级上学期数学期中考试试卷C卷
宁夏银川市2020年(春秋版)七年级上学期期末数学试卷C卷

宁夏银川市2020年(春秋版)七年级上学期期末数学试卷C卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2020七上·椒江期末) 四个有理数-1,0,-3,4,其中最小的有理数是()A . -1B . 0C . -3D . 42. (2分) (2017七下·乌海期末) 下列调查中,适宜采用全面调查方式的是()A . 对乌达区中学生心理健康现状的调查B . 对冷饮市场上冰淇淋质量情况的调查C . 审核书稿中的错别字D . 调查乌达区中学生社会主义核心价值观的背诵情况3. (2分)长方体的主视图与俯视图如图所示,则这个长方体的体积是()A . 52B . 32C . 24D . 94. (2分)如图,是苏步青学校食堂甲、乙、丙、丁四种早餐受欢迎程度的扇形统计图,则最受欢迎的早餐是()A . 甲B . 乙C . 丙D . 丁5. (2分)下列计算正确的是()A . (a2)3=a5B . 2a-a=2C . (2a)2=4aD . a•a3=a46. (2分)下列说法正确的是()A . 单项式﹣的系数是﹣3B . 单项式2πa3的次数是4C . 多项式x2y2﹣2x2+3是四次三项式D . 多项式x2﹣2x+3的项分别是x2、2x、37. (2分)甲组人数是乙组人数的2倍,从甲组抽调8人到乙组,这时甲组剩下的人数恰比乙组人数的一半多2个,设乙组原有x人,则可列方程().A .B .C .D .8. (2分) (2017七上·潮南期末) 如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于()A . 0.5B . 1C . 1.5D . 29. (2分)若关于x的方程ax+3x=2的解是x=1,则a的值是()A . -1B . 5C . 1D . -510. (2分)如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出“树枝”()A . 64B . 60C . 56D . 32二、填空题 (共15题;共24分)11. (3分)计算:①x2•x3=________;②(﹣2y2)3=________;③ =________.12. (1分) (2016七下·盐城开学考) 已知两个单项式﹣2a2bm+1与na2b4的和为0,则m+n的值是________.13. (1分)关于x的方程(k+1)x2+4kx﹣5k=0是一元一次方程,则方程的解是________.14. (1分) (2015七上·市北期末) 用科学记数法表示:5678000000=________.15. (1分)2700″=________°.16. (1分)某校的早读时间是7:30﹣7:50,在这个时间中,分针旋转的角度为________ 度.17. (1分) (2015七上·莆田期末) 已知x=﹣1是关于x的方程2x﹣3a=﹣4的解,则a为________.18. (1分)(2020·拉萨模拟) 已知实数x,y满足|x﹣4|+ =0,则以x,y的值为两边长的直角三角形的周长是________.19. (1分)(2014·盐城) 已知x(x+3)=1,则代数式2x2+6x﹣5的值为________.20. (1分) (2016七上·崇仁期中) 化简x﹣y﹣(x+y)的最后结果是________.21. (1分) (2020七上·北仑期末) 将两个正方形与直角三角板的一个直角顶点重合放置如图所示,则∠1的度数为________。
银川市2020年七年级上学期数学期末考试试卷C卷

银川市2020年七年级上学期数学期末考试试卷C卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)有1000个数排一行,其中任意相邻的三个数中,中间的数等于它前后两数的和,若第一个数和第二个数都是1,则1000个数的和等于()A . 1000B . 1C . 0D . -12. (2分)下列各式计算正确的是()A .B .C .D .3. (2分)如图,A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使PA+PB最短.下面四种选址方案符合要求的是()A .B .C .D .4. (2分)(2019·桂林模拟) 下列说法:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程中的分母化为整数,得=12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有()A . 1个B . 2个C . 3个D . 4个5. (2分)下列结论正确的有()①任何数都不等于它的相反数;②符号相反的数互为相反数;③表示互为相反数的两个数的点到原点的距离相等;④若有理数a,b互为相反数,那么a+b=0;⑤若有理数a,b互为相反数,则它们一定异号。
A . 2个B . 3个C . 4个D . 5个6. (2分) (2020七下·温州月考) 如图,直线c截两平行直线a、b,则下列式子中一定不成立的是()A . ∠1=∠2B . ∠2+∠5=180°C . ∠4=∠5D . ∠4>∠37. (2分) (2015七上·宝安期末) 一家商店将某种服装按成本价提高20%后标价,又以9折优惠卖出,结果每件服装仍可获利8元,则这种服装每件的成本是()A . 100元B . 105元C . 110元D . 115元8. (2分)52°24'的余角和补角分别是()A . 37°36',127°36'B . 127°36',37°36'C . 38°24',128°24'D . 128°24',38°24'9. (2分)(2017·东莞模拟) 如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是()A . ∠1=50°B . ∠2=50°C . ∠4=130°D . ∠5=30°10. (2分) (2019八上·长沙开学考) 点 D 、 E 分别在∠BAC 的边 AB 、 AC 上,沿 DE 将△ADE 折叠到△A'DE 的位置,若A'D ⊥ AC ,∠BAC = 28° ,则∠ADE 的大小为()A . 28°B . 31°C . 36°D . 62°11. (2分) (2018七上·翁牛特旗期末) 如图,是正方体的平面展开图,每个面上都标有一个汉字,与“信”字相对的面上的字为()A . 文B . 明C . 法D . 治12. (2分)下列计算正确的一项是()A . a5+a5=2a10B . (a+2)(a﹣2)=a2﹣4C . (a﹣b)2=a2﹣b2D . 4a﹣2a=2二、填空题 (共9题;共9分)13. (1分)(2020·平度模拟) 2020年3月11日,全国绿化委员会办公室发布《2019年中国国土绿化状况公报》显示,2019年我国国土绿化工作取得新成绩,全年共完成造林7067000公顷。
宁夏银川市2020年七年级上学期数学期末考试试卷C卷

宁夏银川市2020年七年级上学期数学期末考试试卷C卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2020·临海模拟) ﹣2+5的结果是()A . ﹣3B . -2C . +2D . 32. (2分) 2011年3月5日上午9时,第十一届全国人民代表大会第四次会议在人民大会堂开幕,国务院总理温家宝在年度计划报告中指出,今年中央财政用于“三农”的投入拟安排9884.5亿元.将9884.5用科学记数法表示应为()A . 98.845×102B . 0.98845×104C . 9.8845×104D . 9.8845×1033. (2分) (2020九下·哈尔滨月考) 如图是5个完全相同的小正方体搭成的的几何体,则该几何体的俯视图是()A .B .C .D .4. (2分) (2017七下·泗阳期末) 下列各式正确的是()A . a2·a3=a6B . a3÷a2=aC . (a3)2=a5D . a2+a2=2a45. (2分)﹣a﹣b+c的相反数是()A . a+b+cB . a﹣b+cC . a+b﹣cD . c+a﹣b6. (2分)(2019·中山模拟) 如图,点A所表示的数的绝对值是()A . 3B . ﹣3C .D .7. (2分) (2018七上·鄂州期末) 若方程2x+1=﹣3的解是关于x的方程7﹣2(x﹣a)=3的解,则a的值为()A . ﹣2B . ﹣4C . ﹣5D . ﹣68. (2分) (2016七上·龙海期末) 如图,D为AB的中点,E为BC的中点,AD=1cm,EC=1.5cm,则DE的长是()A . 1.5cmB . 2cmC . 2.5cmD . 3cm9. (2分)绝对值不大于4的整数的积是()A . 6B . -6C . 0D . 2410. (2分) (2019七下·香坊期末) 如图,点位于点的().A . 南偏东方向上B . 北偏西方向上C . 南偏东方向上D . 南偏西方向上二、填空题 (共6题;共6分)11. (1分) (2019七上·厦门月考) 计算:⑴ ________;⑵ ________;⑶________;⑷ ________;12. (1分)(2011·湛江) 已知∠1=30°,则∠1的补角的度数为________度.13. (1分) (2018七上·辽阳期末) 已知单项式-2xm+1y2和5x5-ny2m是同类项,则(-m)n的值是________.14. (1分) (2018七上·泰州期末) 钢笔每支18元,圆珠笔每只3元,n支钢笔和m支圆珠笔共________元.15. (1分) (2019七上·崂山月考) 如图,点C、D在线段AB上,D是线段AB的中点,AC= AD , CD=4cm ,则线段AB的长为________cm16. (1分) (2016七上·太原期末) 若方程4x﹣1=□x+2的解是x=3,则“□”处的数为________.三、解答题 (共8题;共62分)17. (10分) (2018七上·召陵期末) 如图所示,已知线段a、b,求做线段AB=2a-b,并写出作图步骤.18. (15分)(2018·嘉兴模拟) 解答题(1)计算:()2—2-1×(-6):(2)解不等式:5x+2≤3(2+x),并把解在数轴上表示出来.19. (10分) (2019七上·海南月考) 已知A﹣2B=7a2﹣7ab,且B=﹣4a2+6ab+7.(1)求A.(2)若|a+1|+(b﹣2)2=0,求A的值.20. (10分) (2019七上·西安月考) 解下列方程(1) 3x-7(x-1)=3-2(x+3)(2) 2x-(x+10)=6x(3)(4)21. (5分) (2017七上·东城期末) (列方程解应用题)互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品进价为180元,按标价的八折销售,仍可获利60元,求这件商品的标价.22. (5分) (2020七上·三门峡期末) 已知关于x的方程:2(x﹣1)+1=x与3(x+m)=m﹣1有相同的解,求以y为未知数的方程的解.23. (5分)如图,在梯形ABCD中,AD∥BC,∠ABC、∠BCD的平分线正好相交于梯形的中位线EF上的点G。
宁夏银川市2020年七年级上学期数学期末考试试卷C卷

宁夏银川市2020年七年级上学期数学期末考试试卷C卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2019七上·花都期中) -42可表示为()A . (-4)×2B . -(4×4)C . (-4)+(-4)D . (-4)×(-4)2. (2分)“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是()A . 两点确定一条直线B . 直线比曲线短C . 两点之间直线最短D . 两点之间线段最短3. (2分)下列各数中,互为相反数的是()A . ﹣(﹣2)与﹣(+2)B . +(﹣5)与﹣|﹣5|C . |﹣3|与|+3|D . |a|与|﹣a|4. (2分)甲、乙两个工程队共有100人,且甲队的人数比乙队的人数的4倍少10人.如果设乙队的人数为x人,则所列的方程为()A . 4x+x=100B . 4x+x-10=100C . x+4(x-10)=100D . x-10+x=1005. (2分)有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车,若每辆客车乘43人,则只有1人不能上车,有下列四个等式:①40m+10=43m-1;②;③;④40m+10=43m+1,其中符合题意的是()A . ①②B . ②④C . ①③6. (2分)在0,﹣1,﹣0.5,1这四个数中,最小的数是()A . 0B . -1C . -0.5D . 17. (2分) (2018九上·镇海期末) 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面的相对面上标的字是()A . 美B . 丽C . 镇D . 海8. (2分)毕节地区水能资源丰富,理论蕴藏量达221.21万千瓦,已开发156万千瓦,把已开发水能资源用四舍五入法保留两个有效数字并且用科学记数法表示应记为()千瓦.A .B .C .D .9. (2分)用一副三角尺,你能画出下面那个度数的角()A . 65度B . 105度C . 85度D . 95度10. (2分) (2019七上·凤山期中) 式子-7,x,,,,,中,整式的个数是()A . 7个B . 6个D . 4个二、填空题 (共8题;共8分)11. (1分) (2016七上·瑞安期中) 已知3与一个数的差为-7 ,则这个数为________.12. (1分)(2010·华罗庚金杯竞赛) 分数,,,,中最小的一个是________。
2020年宁夏银川芦花中学人教版七年级上学期期中考试数学试题(A卷全套)

芦花学校2020—2020学年第一学期七年级数学期中考试班级 姓名 成绩(备注:不准使用计算器) 成绩一、选择题(只有一个正确答案,认真思考啊!每小题3分,共24分) 1、-3的相反数是( )(A)-3 (B)13-(C)13(D)3 2、若2||=a ,则a =( )(A)2 (B)2- (C)2 或2- (D)以上答案都不对 3、下列各式中,正确的是( )(A)y x y x y x 2222-=- (B)2a +3b =5ab (C)7ab -3ab =4 (D)523a a a =+ 4、下列说法不正确的是( )(A)0既不是正数,也不是负数 (B) 1是绝对值最小的数 (C)一个有理数不是整数就是分数 (D) 0的绝对值是0 5、下列说法正确的是( )(A)a 是代数式,1不是代数式;(B)表示a 、b 的积的2倍的代数式为ab2; ( C)a 、b 两数差的平方与a 、b 两数的积的4倍的和表示为(a-b)2+4ab (D)xy 的系数是0.6、右图是一数值转换机,若输入的x 为-5,则输出的结果为A. 11B. -9C. -17D. 217、比较2-, 0, ()2-- ,3-的大小,下列正确的( )。
(A)0 >3-> ()2--> -2 (B) ()2-- >3- > -2> 0 (C)()2-- > 0 > -2 >3- (D)3-> ()2--> -2> 0 8、若a+b <0, 且ab <0,则下列正确的是( )A. a,b 异号,负数的绝对值大。
B. a,b 异号,且a >bC. a,b 异号,且 ∣a ︳>∣b ∣D. a,b 异号,正数的绝对值大。
二、填空题(简洁的结果,表达的是你敏锐的思维,需要的是细心!每小题3分,共24分)9、如果运进72吨记作+72吨,那么运出56吨记作_________; 10、观察下列数字的排列规律,然后在括号内填入适当的数:3,-7,11,15-,19,-23,( ),( ).11、某日傍晚,黄山的气温由中午的零上2℃下降了7℃,这天傍晚的气温是_________。
【解析版】银川市初中数学七年级上期中经典测试卷(专题培优)(1)
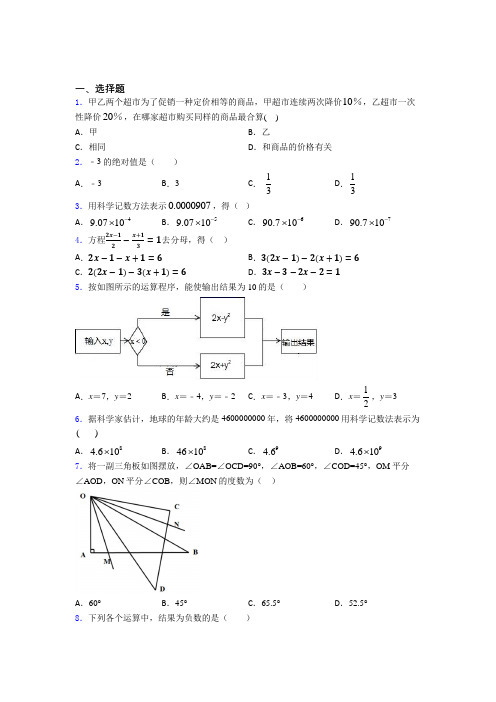
一、选择题1.甲乙两个超市为了促销一种定价相等的商品,甲超市连续两次降价10%,乙超市一次性降价20%,在哪家超市购买同样的商品最合算( ) A .甲 B .乙C .相同D .和商品的价格有关2.﹣3的绝对值是( ) A .﹣3B .3C .-13D .133.用科学记数方法表示0.0000907,得( ) A .49.0710-⨯ B .59.0710-⨯C .690.710-⨯D .790.710-⨯4.方程2x−12−x+13=1去分母,得( )A .2x −1−x +1=6B .3(2x −1)−2(x +1)=6C .2(2x −1)−3(x +1)=6D .3x −3−2x −2=15.按如图所示的运算程序,能使输出结果为10的是( )A .x =7,y =2B .x =﹣4,y =﹣2C .x =﹣3,y =4D .x =12,y =3 6.据科学家估计,地球的年龄大约是4600000000年,将4600000000用科学记数法表示为( )A .84.610⨯B .84610⨯C .94.6D .94.610⨯7.将一副三角板如图摆放,∠OAB=∠OCD=90°,∠AOB=60°,∠COD=45°,OM 平分∠AOD ,ON 平分∠COB ,则∠MON 的度数为( )A .60°B .45°C .65.5°D .52.5°8.下列各个运算中,结果为负数的是( )A .2-B .()2--C .2(2)-D .22-9.已知x =2是关于x 的一元一次方程mx+2=0的解,则m 的值为( ) A .﹣1 B .0 C .1 D .210.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b )n 的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b )20的展开式中第三项的系数为( ) A .2017B .2016C .191D .19011.下列等式变形正确的是( ) A .由a =b ,得5+a =5﹣b B .如果3a =6b ﹣1,那么a =2b ﹣1 C .由x =y ,得x y m m= D .如果2x =3y ,那么262955x y--= 12.下列等式变形错误的是( )A .若x =y ,则x -5=y -5B .若-3x =-3y ,则x =yC .若x a =ya,则x =yD .若mx =my ,则x =y 13.如果||a a =-,下列成立的是( )A .0a >B .0a <C .0a ≥D .0a ≤14.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496亿km .用科学记数法表示1.496亿是( ) A .71.49610⨯ B .714.9610⨯C .80.149610⨯D .81.49610⨯15.解方程2153132x x +--=,去分母正确的是( ) A .2(21)3(53)1x x +--= B .21536x x +--=C .2(21)3(53)6x x +--=D .213(53)6x x +--=二、填空题16.若代数式5x -5与2x -9的值互为相反数,则x =________.17.填在下列各图形中的三个数之间都有相同的规律,根据此规律,a 的值是____.18.如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n 个图案中白色正方形比黑色正方形多________个.(用含n 的代数式表示)19.有一列数,按一定规律排列成1,2,4,8,16,32,,---⋅⋅⋅其中某三个相邻数的积是124,则这三个数的和是_____.20.30万=42.3010⨯ ,则2.30中“0”在原数中的百位,故近似数2.30万精确到百位.21.下面每个表格中的四个数都是按相同规律填写的:根据此规律确定x 的值为_______.22.2018年2月3日崂山天气预报:多云,-1°C~-9°C ,西北风3级,则当天最高气温比最低气温高_______℃23.正整数按如图的规律排列,请写出第10行,第10列的数字_____.24.将从1开始的连续自然数按以下规律排列: 第1行1第2行2 3 4第3行9 8 7 6 5第4行10 11 12 13 14 15 16第5行252423222120191817…则2018在第_____行.25.若233m x y -与42n x y 是同类项,则n m =__________.三、解答题26.我们规定,若关于x 的一元一次方程ax =b 的解为b ﹣a ,则称该方程为“差解方程”,例如:2x =4的解为2,且2=4﹣2,则该方程2x =4是差解方程. 请根据上边规定解答下列问题: (1)判断3x =4.5是否是差解方程;(2)若关于x 的一元一次方程6x =m +2是差解方程,求m 的值.27.先化简,再求值:5(3a 2b ﹣ab 2﹣1)﹣(ab 2+3a 2b ﹣5),其中a =﹣12,b =13.28.有个填写运算符号的游戏:在“1269”中的每个□内,填入+⨯÷,﹣,,中的某一个(可重复使用),然后计算结果. (1)计算:1269+﹣﹣;(2)若请推算12696÷⨯=﹣,□内的符号;(3)在“1269﹣”的□内填入符号后,使计算所得数最小,直接写出这个最小数. 29.如图是某种产品展开图,高为3cm.(1)求这个产品的体积.(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积. 30.某鱼池捕鱼8袋,以每袋25千克为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,-3, 2, -0.5, 1, -2, -2, -2.5.这8袋鱼一共多少千克?【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题二、填空题16.2【解析】【分析】由5x-5的值与2x-9的值互为相反数可知:5x-5+2x-9=0解此方程即可求得答案【详解】由题意可得:5x-5+2x-9=0移项得7x=14系数化为1得x=2【点睛】本题考查了17.【解析】寻找规律:上面是1234…;左下是14=229=3216=42…;右下是:从第二个图形开始左下数字减上面数字差的平方:(4-2)2(9-3)2(16-4)2…∴a=(36-6)2=90018.4n+3【解析】【分析】利用给出的三个图形寻找规律发现白色正方形个数=总的正方形个数-黑色正方形个数而黑色正方形个数第1个为1第二个为2由此寻找规律总个数只要找到边与黑色正方形个数之间关系即可依此类19.-384【解析】【分析】根据题目中的数字可以发现它们的变化规律再根据其中某三个相邻数的积是可以求得这三个数从而可以求得这三个数的和【详解】一列数为这列数的第个数可以表示为其中某三个相邻数的积是设这三20.无21.301【解析】【分析】根据所给图形的数字的规律进行求解即可【详解】解:由图像的:表格中中的左上的数字分别为:1234可得第n个表格中的数字为:n;表格中中的右上的数字分别为:36912可得第n个表格22.8【解析】【分析】根据有理数的减法解答即可【详解】-1-(-9)=8所以当天最高气温是比最低气温高8℃故答案为:8【点睛】此题考查有理数的减法关键是根据有理数的减法解答23.91【解析】【分析】观察如图的正整数排列可得到第一列的数分别是1491625…可得出一个规律:第一列每行的数都等于行数的2次方且每行的数个数与对应列的数的个数相等【详解】解:由第一列数149162524.45【解析】【分析】分析可得各行最大数依次为1491625可得每行的最大数为行数的平方接下来求得2018两边的平方数再结合结论即可得到答案【详解】观察可知:各行最大数依次为1491625可得每行的最25.8【解析】【分析】利用同类项的定义得出mn的值进而得出答案【详解】∵与是同类项∴∴∴故答案为:8【点睛】此题主要考查了同类项正确得出mn的值是解题关键三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题二、填空题16.2【解析】【分析】由5x-5的值与2x-9的值互为相反数可知:5x-5+2x-9=0解此方程即可求得答案【详解】由题意可得:5x-5+2x-9=0移项得7x=14系数化为1得x=2【点睛】本题考查了解析:2【解析】【分析】由5x-5的值与2x-9的值互为相反数可知:5x-5+2x-9=0,解此方程即可求得答案.【详解】由题意可得:5x-5+2x-9=0,移项,得7x=14,系数化为1,得x=2.【点睛】本题考查了相反数的性质以及一元一次方程的解法.17.【解析】寻找规律:上面是1234…;左下是14=229=3216=42…;右下是:从第二个图形开始左下数字减上面数字差的平方:(4-2)2(9-3)2(16-4)2…∴a=(36-6)2=900解析:【解析】寻找规律:上面是1,2 ,3,4,…,;左下是1,4=22,9=32,16=42,…,;右下是:从第二个图形开始,左下数字减上面数字差的平方:(4-2)2,(9-3)2,(16-4)2,…∴a=(36-6)2=900.18.4n+3【解析】【分析】利用给出的三个图形寻找规律发现白色正方形个数=总的正方形个数-黑色正方形个数而黑色正方形个数第1个为1第二个为2由此寻找规律总个数只要找到边与黑色正方形个数之间关系即可依此类解析:4n+3【解析】【分析】利用给出的三个图形寻找规律,发现白色正方形个数=总的正方形个数-黑色正方形个数,而黑色正方形个数第1个为1,第二个为2,由此寻找规律,总个数只要找到边与黑色正方形个数之间关系即可,依此类推,寻找规律.【详解】解:方法一:第1个图形黑、白两色正方形共3×3个,其中黑色1个,白色3×3-1个,第2个图形黑、白两色正方形共3×5个,其中黑色2个,白色3×5-2个,第3个图形黑、白两色正方形共3×7个,其中黑色3个,白色3×7-3个,依此类推,第n个图形黑、白两色正方形共3×(2n+1)个,其中黑色n个,白色3×(2n+1)-n 个,即:白色正方形5n+3个,黑色正方形n个,故第n个图案中白色正方形比黑色正方形多4n+3个,第1个图形白色正方形共8个,黑色1个,白色比黑色多7个,第2个图形比第1个图形白色比黑色又多了4个,即白色比黑色多(7+4)个, 第3个图形比第2个图形白色比黑色又多了4个,即白色比黑色多(7+4×2)个, 类推,第n 个图案中白色正方形比黑色正方形多[7+4(n-1)]个,即(4n+3)个, 故第n 个图案中白色正方形比黑色正方形多4n+3个. 【点睛】本题考查了几何图形的变化规律,是探索型问题,图中的变化规律是解题的关键.19.-384【解析】【分析】根据题目中的数字可以发现它们的变化规律再根据其中某三个相邻数的积是可以求得这三个数从而可以求得这三个数的和【详解】一列数为这列数的第个数可以表示为其中某三个相邻数的积是设这三解析:-384 【解析】 【分析】根据题目中的数字,可以发现它们的变化规律,再根据其中某三个相邻数的积是124,可以求得这三个数,从而可以求得这三个数的和. 【详解】一列数为1,24,816,32---⋯,,,, ∴这列数的第n 个数可以表示为1(2)n --,其中某三个相邻数的积是124,∴设这三个相邻的数为11222n n n +﹣(﹣)、(﹣)、(﹣),则11122)2)2)4(((n n n +••﹣--﹣=,即32122)2)n(-=(,32424=((2)22)n ∴-=-,324n ∴=,解得,8n =,∴这三个数的和是: 7892)(2)(2)++(---=72)(124)128)3⨯-+⨯(-=(-384=-,故答案为:384-. 【点睛】本题考查数字的变化类,解答本题的关键是明确题意,发现题目中数字的变化规律.20.21.301【解析】【分析】根据所给图形的数字的规律进行求解即可【详解】解:由图像的:表格中中的左上的数字分别为:1234可得第n 个表格中的数字为:n ;表格中中的右上的数字分别为:36912可得第n 个表格 解析:301【解析】根据所给图形的数字的规律进行求解即可.【详解】解:由图像的:表格中中的左上的数字分别为:1、2、3、4,可得第n个表格中的数字为:n;表格中中的右上的数字分别为:3、6、9、12,可得第n个表格中的数字为:3n,得最后一个中右上数字为21,可得为第7个表格,故a=7;表格中中的右上的数字分别为:2、4、6、8,可得第n个表格中的数字为:2n,故b=14;结合前4个表格可知,右下的数值=左下×右上+左下,故x=21×14+7=301,故【点睛】本题主要考查规律形数字的变化,能熟练找出规律是解题的关键.22.8【解析】【分析】根据有理数的减法解答即可【详解】-1-(-9)=8所以当天最高气温是比最低气温高8℃故答案为:8【点睛】此题考查有理数的减法关键是根据有理数的减法解答解析:8【解析】【分析】根据有理数的减法解答即可.【详解】-1-(-9)=8,所以当天最高气温是比最低气温高8℃,故答案为:8【点睛】此题考查有理数的减法,关键是根据有理数的减法解答.23.91【解析】【分析】观察如图的正整数排列可得到第一列的数分别是1491625…可得出一个规律:第一列每行的数都等于行数的2次方且每行的数个数与对应列的数的个数相等【详解】解:由第一列数1491625解析:91【解析】【分析】观察如图的正整数排列可得到,第一列的数分别是1,4,9,16,25,…可得出一个规律:第一列每行的数都等于行数的2次方.且每行的数个数与对应列的数的个数相等.【详解】解:由第一列数1,4,9,16,25,…得到:1=124=229=32 16=42 25=52…所以第10行第1列的数为:102=100. 又每行的数个数与对应列的数的个数相等. 所以第10行第9列的数为100﹣9=91. 故答案为:91. 【点睛】此题考查规律型:数字的变化类的知识,解题关键是找出两个规律,即第一列每行的数都等于行数的2次方和每行的数个数与对应列的数的个数相等.24.45【解析】【分析】分析可得各行最大数依次为1491625可得每行的最大数为行数的平方接下来求得2018两边的平方数再结合结论即可得到答案【详解】观察可知:各行最大数依次为1491625可得每行的最解析:45 【解析】 【分析】分析可得各行最大数依次为1、4、9、16、25,可得每行的最大数为行数的平方,接下来求得2018两边的平方数,再结合结论即可得到答案. 【详解】观察可知:各行最大数依次为1、4、9、16、25,可得每行的最大数为行数的平方. 22441936452025==,, 因为1936<2018<2025, 所以2018是第45行的数. 故答案为45. 【点睛】本题属于探究规律类题目,解答本题需掌握题目中数的排列规律,考虑从最大数与行数入手.25.8【解析】【分析】利用同类项的定义得出mn 的值进而得出答案【详解】∵与是同类项∴∴∴故答案为:8【点睛】此题主要考查了同类项正确得出mn 的值是解题关键解析:8 【解析】 【分析】利用同类项的定义得出m ,n 的值进而得出答案. 【详解】 ∵233mxy -与42n x y 是同类项∴24m =,3n = ∴2m =∴328n m ==.故答案为:8.【点睛】此题主要考查了同类项,正确得出m ,n 的值是解题关键.三、解答题26.(1)是;见解析;(2)265. 【解析】【分析】(1)求出方程的解,再根据差解方程的意义得出即可;(2)根据差解方程得出关于m 的方程,求出方程的解即可.【详解】解:(1)∵3x =4.5,∴x =1.5,∵4.5﹣3=1.5,∴3x =4.5是差解方程;(2)∵关于x 的一元一次方程6x =m +2是差解方程,∴m +2﹣6=26m +, 解得:m =265. 【点睛】本题考查了一元一次方程的解的应用,能理解差解方程的意义是解此题的关键. 27.原式=12a 2b ﹣6ab 2=43. 【解析】试题分析:去括号,合并同类项,把字母的值代入运算即可.试题解析:原式2222155535,a b ab ab a b =----+ 22126.a b ab =- 当1123a b =-=,时,原式1111141261.432933⎛⎫=⨯⨯-⨯-⨯=+= ⎪⎝⎭ 28.(1)-2;(2)-;(3)-20,理由详见解析.【解析】【分析】(1)根据有理数的加减法法则解答即可;(2)根据题目中式子的结果,可以得到□内的符号;(3)先写出结果,然后说明理由即可.【详解】(1)1+2﹣6﹣9=3﹣6﹣9=﹣3﹣9=﹣12;(2)∵1÷2×6□9=﹣6,∴112⨯⨯6□9=﹣6,∴3□9=﹣6,∴□内的符号是“﹣”;(3)这个最小数是﹣20,理由:∵在“1□2□6﹣9”的□内填入符号后,使计算所得数最小,∴1□2□6的结果是负数即可,∴1□2□6的最小值是1﹣2×6=﹣11,∴1□2□6﹣9的最小值是﹣11﹣9=﹣20,∴这个最小数是﹣20.【点睛】本题考查了有理数的混合运算,明确有理数混合运算的计算方法是解答本题的关键.29.(1)长方形的体积为144cm3;(2)纸箱的表面积为516cm2.【解析】【分析】(1)根据已知图形得出长方体的高进而得出答案;(2)设计的包装纸箱为15×6×8规格.【详解】(1)长方体的高为3cm,则长方形的宽为(12-2×3)cm,长为12(25-3-6)cm,根据题意可得:长方形的体积为:8×6×3=144(cm3);(2)因为长方体的高为3cm,宽为6cm,长为8cm,所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:8×6=48(cm2),8×15=120(cm2),6×15=90(cm2)纸箱的表面积为:2(120+48+90)=516(cm2).【点睛】本题考查几何体的展开图、几何体的表面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.30.5【解析】【分析】用25乘以8的积,加上称后记录的八个数的和即可求得.【详解】25×8+(1.5−3+2−0.5+1−2−2−2.5)=200+4.5−10=194.5(千克).答:这8袋鱼一共194.5千克.【点睛】此题考查正数和负数,解题关键在于掌握运算法则.。
2021-2022学年-有答案-宁夏回族自治区银川市某校初一(上)期中考试数学试卷

2021-2022学年宁夏回族自治区银川市某校初一(上)期中考试数学试卷一、选择题1. 如果向东走2m记为+2m,那么向西走3m可记为( )A.+2mB.−2mC.+3mD.−3m2. 既能使截面是长方形,又能使截面是圆,则这个几何体可能是( )A.圆锥B.棱柱C.圆柱D.球3. 在数轴上表示数a的点在原点左侧,并且到原点的距离为3个单位长度,则a的相反数是( )A.3B.−3C.13D.−134. 如图是一个正方体的表面展开图,则在原正方体中与“唐”字相对的面上的字为( )A.银B.徕C.回D.中5. 多项式2a2b−ab2+ab的项数及次数分别是()A.3,2B.3,3C.2,3D.2,26. 若|x|=2,|y|=5,xy<0,则x+y的值为( )A.7B.7或−7C.3或−3D.±7或±37. 若a是最大的负整数,b是绝对值最小的数,c是最小的正整数,那么a+b+c的值为()A.−1B.0C.1D.28. 用八个同样大小的小立方体粘成一个大立方体如图1,从正面、左面和上面看到的形状图都一样,如图2所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体从正面、左面和上面看到的形状图仍是图2,则他取走的小立方体最多可以是( )个A.1B.2C.3D.4二、填空题五棱柱有________个顶点,有________条棱,有________个面.保护水资源,人人有责.我国是世界上严重缺水的国家之一. 目前国家可利用淡水资源总量仅约899000亿立方米,用科学记数法表示为________亿立方米.比较大小:−67________−78(填“<”或“>”).−6ab 45的系数是________,次数是________.1米长的绳子,第1次剪去一半,第2次剪去剩下的一半,如此剪下去,第五次后剩下的绳子的长度为________米.如图一个几何体从正面、左面和上面看到的图形,根据图中提供的数据计算这个几何体的体积是________(结果保留π).下列图形是由一些小正方形和实心圆按一定规律排列而成的,如图所示,按此规律排列下去,第20个图形中有________个实心圆.用“+,−,×,÷”将−3,5,−4,3连成一个等式,使其结果是24:________=24. (每个数只能使用一次,可以使用括号)三、解答题小明学完有理数后,对下列各数:7,−0.618,−28,−312,−1,0,10%进行了分类,但小亮检查后发现小明的填写有错误,请你将正确的分类填入后面的集合内. 整数集合:{7,−28,−1, ⋯} 整数集合:{ ⋯}分数集合:{−0.618,−312,⋯}分数集合:{⋯}正数集合:{7,0,10%,⋯}正数集合:{⋯}负有理数集合:{−28,−1,⋯}负有理数集合:{⋯}计算.(1)(−16)+(−8)−(−12);(2)23−38−(−13)+(−18);(3)(−36)÷3×(−13);(4)(−12−13+34)×(−60);(5)−32×12+(−3)2÷(−3).在数轴上把下列各数表示出来,并用“<”将它们连接起来.3,−52,−22,|−5|,(−1)3如图,这是一个由一些大小相同的小立方块搭成的几何体,从上面看到的几何体形状图如图所示,小正方形中的数字表示该位置的小立方块的个数.请你画出这个几何体从正面、左面看到的平面图形.有两个数−4和+6,它们的相反数的和为a,它们的倒数的和为b,它们的和的绝对值为c,求a×b÷c的值.如图,长和宽分别是a ,b 的长方形纸片的四个角都剪去一个边长为x 的正方形.(单位:厘米)(1)用含a ,b ,x 的代数式表示纸片剩余部分的面积;(2)当a =8,b =6,x =1时,求剩余部分的面积.初一(1)班共有50名学生,在一次数学测试中以90分为标准,超过的记为正,不足的记为负,成绩如下:请你算出这次考试的平均成绩.抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从A 地出发,晚上到达B 地,约定向东为正方向,当天的航行路程记录如下(单位:千米): 14,−9,+8,−7,13,−6,+12,−5.(1)B 在A 地的什么方向,距离A 地多远?(2)救灾过程中,冲锋舟离出发点A 最远处有多远?(3)若冲锋舟每千米耗油0.5升,油箱容量为28升,求冲锋舟当天救灾过程中至少还需补充多少升油?规定:若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(−3)÷(−3)÷(−3)÷(−3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(−3)÷(−3)÷(−3)÷(−3)记作(−3)④,读作“−3的圈4次方”,一般地,把n 个a 相除记作a ⓝ,读作“a 的圈n 次方”.请你阅读以上材料并完成下列问题:(1)直接写出计算结果:2③=________,(−13)④________;(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算;那么有理数的除方运算能否转化为乘方运算呢?我们可以进行下列计算:如:2④=2÷2÷2÷2=2×12×12×12=(12)2;(−3)⑤=(−3)÷(−3)÷(−3)÷(−3)÷(−3) =(−3)×(−13)×(−13)×(−13)×(−13)=(−13)3;仔细思考上述计算过程,将下列运算结果直接写成幂的形式:5⑤=________,(−2)⑥=________;(3)想一想,将一个非零有理数a的圈n次方写成幂的形式为aⓝ=________;(4)算一算:122÷(−1)④×(−2)⑤.3参考答案与试题解析2021-2022学年宁夏回族自治区银川市某校初一(上)期中考试数学试卷一、选择题1.【答案】D【考点】正数和负数的识别【解析】根据正负数的概念,向东走跟向西走是相反的概念,向东走记为正数,则向西走记为负数.【解答】解:根据正负数的概念,向东走跟向西走是相反的概念,所以向东走2m记作+2m,则向西走3m记作−3m.故选D.2.【答案】C【考点】由三视图判断几何体【解析】用一个平面截一个几何体得到的面叫做几何体的截面,根据截面是长方形、圆,即可得.【解答】解:既能使截面是长方形,又能使截面是圆,则这个几何体可能是圆柱.故选C.3.【答案】A【考点】数轴相反数【解析】由数轴可求a的值,再求相反数.【解答】解:由表示数a的点在原点左侧,并且到原点的距离为3个单位,则a=−3,所以−3的相反数为3.故选A.【答案】D【考点】正方体相对两个面上的文字【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,原正方体中与“唐”字所在面相对的面上标的字是“中”.故选D.5.【答案】B【考点】多项式的概念的应用【解析】多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数,根据这个定义即可判定.【解答】解:2a2b−ab2+ab是三次三项式,故次数是3,项数是3.故选B.6.【答案】C【考点】绝对值有理数的加法【解析】先由绝对值的性质得到x与y的值,然后再由xy<0得出x、y异号,从而得出x+y的值. 【解答】解:∵|x|=2,|y|=5,∴x=±2,y=±5,∵xy<0,∴当x=−2时,y=5,此时x+y=3;当x=2时,y=−5,此时x+y=−3.故选C.7.【答案】B【考点】有理数的概念及分类有理数的加法根据题意确定出a,b,c的值,代入原式计算即可得到结果.【解答】解:由题意,得a=−1,b=0,c=1,则a+b+c=−1+0+1=0.故选B.8.【答案】D【考点】由三视图判断几何体【解析】由于从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图都相同,由主视图可知有2层2列,由左视图可知有2层2行,由俯视图可知最少有2个小立方体.【解答】解:由主视图和左视图可得每一层的每一行每一列都要保留一个立方体,故取走的小立方体最多可以是4个,如图所示.故选D.二、填空题【答案】10,15,7【考点】认识立体图形【解析】根据五棱柱的概念和特性可解题.【解答】解:由棱柱的特点可知,n棱柱有2n个顶点,3n条棱,(n+2)个面,故5棱柱有10个顶点,15条棱,7个面.故答案为:10;15;7.【答案】8.99×105【考点】科学记数法--表示较大的数【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数解:科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数. 故899000用科学记数法表示为8.99×105.故答案为:8.99×105.【答案】>【考点】有理数大小比较【解析】根据两个负数比较大小,绝对值大的反而小,即可解答.【解答】解:|−67|=67=4856,|−78|=78=4956.∵ 4856<4956,即|−67|<|−78|,∴ −67>−78.故答案为:>.【答案】−65,5【考点】单项式的系数与次数【解析】根据单项式的次数、系数的定义解答.【解答】解:单项式−6ab 45的系数是−65,次数是 4+1=5. 故答案为:−65;5 .【答案】1 【考点】有理数的乘方【解析】根据题意归纳总结得到一般性规律,确定出所求即可.【解答】解:第一次剪去全长的12,剩下全长的12, 第二次剪去剩下的12,剩下全长的12×12=122,第三次再剪去剩下的12,剩下全长的122×12=123,⋯如此剪下去,第5次后剩下的绳子的长为125=132. 故答案为:132 .【答案】3π【考点】由三视图确定几何体的体积或面积【解析】首先根据三视图判定该几何体为圆柱体,再根据三视图中标注的数据及圆柱体积=底面积×高进行计算即可.【解答】解:由三视图可知,该几何体是底面直径为2,高为3的圆柱体,故V =π×(22)2×3=3π.故答案为:3π.【答案】42【考点】规律型:图形的变化类【解析】根据图形中实心圆的数量变化,得出变化规律,进而求出即可.【解答】解:由图可知,第1个图形中有2×1+2=4个实心圆,第2个图形中有2×2+2=6个实心圆,第3个图形中有2×3+2=8个实心圆,⋯则第n 个图形中有2n +2个实心圆,故第20个图形中有2×20+2=42个实心圆.故答案为:42.【答案】(−3)×(−4)×(5−3)【考点】有理数的混合运算【解析】根据题意可以写出相应的式子,本题得以解决.【解答】解:由题意,得(−3)×(−4)×(5−3)=24(答案不唯一).故答案为:(−3)×(−4)×(5−3).三、解答题【答案】解: 整数集合:{7,−28,−1,0,⋯};分数集合:{−0.618,−312,10%,⋯};正数集合:{7,10%,⋯};负有理数集合:{−0.618,−28,−312,−1,⋯}. 【考点】有理数的概念及分类【解析】根据整数、正数、分数、负有理数的定义正确分类即可.【解答】解: 整数集合:{7,−28,−1,0,⋯};分数集合:{−0.618,−312,10%,⋯};正数集合:{7,10%,⋯};负有理数集合:{−0.618,−28,−312,−1,⋯}. 【答案】解:(1)原式=−16−8+12=−24+12=−12.(2)原式=23−38+13−18=2+1−3−1 =1−12=12. (3)原式=(−36)×13×(−13) =(−12)×(−13) =4.(4)原式=(−12)×(−60)−13×(−60)+34×(−60)=30+20−45=50−45=5.(5)原式=−9×12+9÷(−3) =−92+(−3) =−152.【考点】有理数的加法有理数的加减混合运算有理数的乘除混合运算有理数的除法有理数的乘法有理数的混合运算【解析】此题暂无解析【解答】解:(1)原式=−16−8+12=−24+12=−12.(2)原式=23−38+13−18=23+13−38−18 =1−12=12.(3)原式=(−36)×13×(−13)=(−12)×(−13) =4.(4)原式=(−12)×(−60)−13×(−60)+34×(−60) =30+20−45=50−45=5.(5)原式=−9×12+9÷(−3)=−92+(−3) =−152.【答案】解:由题意可知,−22=−4,|−5|=5,(−1)3=−1,在数轴上表示如图所示.故−22<−52<(−1)3<3<|−5|.【考点】有理数大小比较数轴有理数的乘法绝对值【解析】先化简各数,再把各数表示在数轴上,然后再用“<”连接起来.【解答】解:由题意可知,−22=−4,|−5|=5,(−1)3=−1,在数轴上表示如图所示.故−22<−52<(−1)3<3<|−5|.【答案】解:根据三视图的法则可知,从正面看从左往右小正方形的个数分别为1个,2个和3个,从左面看从左往右小正方形的个数分别为2个,3个和1个.故几何体从正面、左面看到的平面图形如图所示.【考点】简单几何体的三视图【解析】此题暂无解析【解答】解:根据三视图的法则可知,从正面看从左往右小正方形的个数分别为1个,2个和3个,从左面看从左往右小正方形的个数分别为2个,3个和1个.故几何体从正面、左面看到的平面图形如图所示.【答案】解:由题意可知,a=4+(−6)=−2,b=−14+16=−112,c=|(−4)+6|=2,故a×b÷c=(−2)×(−112)÷2=112.【考点】相反数倒数绝对值有理数的乘除混合运算【解析】【解答】解:由题意可知,a=4+(−6)=−2,b=−14+16=−112,c=|(−4)+6|=2,故a×b÷c=(−2)×(−112)÷2=112.【答案】解:(1)由题意可知,剩余部分面积为S长方形−4S小正方形=(ab−4x2)cm2.(2)由(1)可知,剩余部分面积为S长方形−4S小正方形=ab−4x2,则当a=8,b=6,x=1时,剩余部分面积为8×6−4×12=48−4=44(cm2).答:剩余部分的面积为44cm2.【考点】列代数式列代数式求值【解析】由剩余部分面积为S长方形−4S小正方形作答.(2)由(1)中式子代入求值.【解答】解:(1)由题意可知,剩余部分面积为S长方形−4S小正方形=(ab−4x2)cm2.(2)由(1)可知,剩余部分面积为S长方形−4S小正方形=ab−4x2,则当a=8,b=6,x=1时,剩余部分面积为8×6−4×12=48−4=44(cm2).答:剩余部分的面积为44cm2.【答案】解:3×(−5)+6×(+3)+5×(−1)+4×(+10)+11×(+2)+3×0 +6×(−2)+8×(+4)+3×(−6)+1×(−12)=50(分),则这次考试的总成绩为50×90+50=4550(分),故这次考试的平均成绩为4550÷50=91(分).答:这次考试的平均成绩为91分.【考点】正数和负数的识别有理数的混合运算【解析】【解答】解:3×(−5)+6×(+3)+5×(−1)+4×(+10)+11×(+2)+3×0 +6×(−2)+8×(+4)+3×(−6)+1×(−12)=50(分),则这次考试的总成绩为50×90+50=4550(分),故这次考试的平均成绩为4550÷50=91(分).答:这次考试的平均成绩为91分.【答案】解:(1)由题意,得14−9+8−7+13−6+12−5=20(千米),又20为正数,则B地在A地的正东方向.答:B地在A地的正东方向,距离20千米.(2)由题意可知,第一次离出发点的距离为14千米;第二次离出发点的距离为14−9=5(千米);第三次离出发点的距离为5+8=13(千米);第四次离出发点的距离为13−7=6(千米);第五次离出发点的距离为6+13=19(千米);第六次离出发点的距离为19−6=13(千米);第七次离出发点的距离为13+12=25(千米);第八次离出发点的距离为25−5=20(千米).答:救灾过程中,冲锋舟离出发点A最远处有25千米.(3)由题意可知,这一天走的总路程为14+|−9|+8+|−7|+13+|−6|+12|+|−5|=74(千米),则耗油为74×0.5=37(升),故还需补充的油量为37−28=9(升).答:冲锋舟当天救灾过程中至少还需补充9升油.【考点】正数和负数的识别有理数的加法有理数的乘除混合运算【解析】(1)把题目中所给数值相加,若结果为正数则B地在A地的东方,若结果为负数,则B地在A地的西方;(2)分别计算出各点离出发点的距离,取数值较大的点即可;(3)先求出这一天走的总路程,再计算出一共所需油量,减去油箱容量即可求出途中还需补充的油量.【解答】解:(1)由题意,得14−9+8−7+13−6+12−5=20(千米),又20为正数,则B地在A地的正东方向.答:B地在A地的正东方向,距离20千米.(2)由题意可知,第一次离出发点的距离为14千米;第二次离出发点的距离为14−9=5(千米);第三次离出发点的距离为5+8=13(千米);第四次离出发点的距离为13−7=6(千米);第五次离出发点的距离为6+13=19(千米);第六次离出发点的距离为19−6=13(千米);第七次离出发点的距离为13+12=25(千米);第八次离出发点的距离为25−5=20(千米).答:救灾过程中,冲锋舟离出发点A 最远处有25千米.(3)由题意可知,这一天走的总路程为14+|−9|+8+|−7|+13+|−6|+12|+|−5|=74(千米), 则耗油为74×0.5=37(升),故还需补充的油量为37−28=9(升).答:冲锋舟当天救灾过程中至少还需补充9升油.【答案】12,9(15)3,(−12)4(1)n−2(4)122÷(−1)④×(−2)⑤ =144÷(−3)2×(−12)3 =144×19×(−18)=−2.【考点】有理数的除法规律型:数字的变化类定义新符号有理数的乘方有理数的混合运算【解析】阅读理解,进行计算;阅读,由有理数的乘除法以及乘方运算求解;由有理数的除法运算以及乘方运算求解;由有理数的运算求解.【解答】解:(1)由题意可知,2③=2÷2÷2=12, (−13)④=(−13)÷(−13)÷(−13)÷(−13)=9. 故答案为:12;9.(2)5⑤=5÷5÷5÷5÷5=5×15×15×15×15=(15)3,(−2)⑥=(−2)×(−12)×(−12)×(−12)×(−12)×(−12)=(−12)4. 故答案为:(15)3;(−12)4.(3)由(2)可知,a n=a÷a÷a÷...÷a=a×1a ×...×1a=(1a)n−2.故答案为:(1a )n−2.(4)122÷(−13)④×(−2)⑤=144÷(−3)2×(−1 2 )3=144×19×(−18)=−2.。
2022年宁夏银川兴庆区银川市第一中学(南熏路校区)七年级上学期期中数学试卷(含答案)

2022年宁夏银川兴庆区银川市第一中学(南熏路校区)七上期中数学试卷1.大型记录电影《厉害了,我的国》3月2日在全国上映,在上映首日收获了41320000人民币的票房,数据“41320000”用科学记数法表示为( )A.41.32×106B.4.132×106C.41.32×107D.4.132×1072.下列运算正确的是( )A.3a+2a=5a2B.2a+2b=2abC.a2−a2=a2D.2a2bc−a2bc=a2bc3.如图中,是正方体的表面展开图的是( )A.B.C.D.4.用一平面去截下列几何体,其截面可能是长方形的有( )A.1个B.2个C.3个D.4个按从小到大的顺序排列是( )5.有理数−32,(−3)2,∣−3∣,−13<−32<(−3)2<∣−3∣A.−13<−32<∣−3∣<(−3)2B.−13<(−3)2C.−32<∣−3∣<−13D . −32<−13<∣−3∣<(−3)26. 下列说法不正确的是 ( )A . 0 既不是正数,也不是负数B . 1 是绝对值最小的数C .一个有理数不是整数就是分数D . 0 的相反数是 07. 【例 3 】 1 米长的彩带,第 1 次剪去 13,第二次剪去剩下的 13,如此剪下去,剪 7 次后剩下的彩带长(不计损耗)为 ( ) A . (13)6米B . (13)7米C . (23)6米D . (23)7米8. 已知 ∣x +1∣+(y −3)2=0 则 x y 的值是 ( ) A . 1 B . −1 C . 3 D . −39. 若 x 的相反数是 3,∣y ∣=5,则 x +y 的值为 .10. 绝对值小于 3 的整数有 个.11. 单项式 −2ab 23的系数是 .12. 若 −3x m y 2 与 2x 4y n 是同类项,则 m −n = .13. 设一个三位数的个位数字为 a ,十位数字为 b ,百位数字为 c ,请你用含 a ,b ,c 的代数式表示这个三位数 .14. “∗”是规定的一种运算法则:a ∗b =a 2−b ,则 5∗(−1) 的值是 .15. 已知:a ,b 互为相反数,c ,d 互为倒数,m 的平方等于 4,则代数式 2022(a +b )−3cd +2m 的值是 .16. 如图所示,a ,b 是有理数,则式子 ∣a ∣+∣b ∣+∣a +b ∣+∣b −a ∣ 化简的结果为 .17. 将下列各数填在相应的集合里.−3.8,4.3,−∣∣−207∣∣,42,0,−(−35),−32.(1) 分数集合:{ ⋯}. (2) 非负数集合:{ ⋯}.18. 计算:(1) 26+(−14)+(−16)+8. (2) (−5)×(−7)−5÷(−16).19. 一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数,请画出从左面看到的这个几何体的形状图.20. 简便计算.(1) (−24)×(34−56+712).(2) (−2)18×(12)19.21. 如图,长方体的长为 4 厘米,宽为 3 厘米,高为 5 厘米.(1) 求此长方体所有棱长的和.(2) 若它是一个无盖的精致包装盒,制作这种包装盒的每平方厘米是 0.1 元,那么制作 8 个这样的包装盒共需多少元.(不考虑接缝之间的材料)22. 化简下列格式.(1) 3x 2y −3xy 2−12xy 2+23x 2y .(2) 3(4x +2y )−4(−y +8x ).23.某检修小组乘汽车检修供电线路,向南记为正,向北记为负.某天自A地出发,所走路程(单位:千米)为:+22,−3,+4,−2,−8,+17,−2,+12,+7,−5.(1) 最后他们是否回到出发点?若没有,则在A地的什么地方?距离A地多远?(2) 若每千米耗油0.06升,则今天共耗油多少升?24.先化简,再求值.(1) 6a+2a2−3a+a2+1的值,其中a=−1.(2) 4x2−(23y2+2x2)+2(3xy+13y2),其中x=3,y=−1.25.填空.(1) 如果想求1+3+32+33+⋯+32022的值,可按以下步骤完成.设s=1+3+32+33+⋯+32022,则3s=,3s−s=.因此s=.(2) 仿照以上推理,计算出1+5+52+53+⋯+599值.26.小红做一道数学题“两个多项式A,B,B为4x2−5x−6,试求A+2B的值”小红误将A+2B看成A−2B,结果答案为−7x2+10x+12.(1) 试求A+2B的正确结果.(2) 求出当x=−3时,A+2B的值.答案1. 【答案】D【解析】41320000=4.132×107.2. 【答案】D3. 【答案】A【解析】正方体的表面展开图不能有田字型,一行最多不超过4个小正方形,正方体的表面展开图的是图形A.4. 【答案】C【解析】根据圆柱、长方体、圆锥、四棱柱、圆台的形状判断,圆锥与圆台不可能得到长方形截面,能得到长方形截面的几何体有:长方体、圆柱、四棱柱,一共有3个.5. 【答案】D【解析】∵−32=−9,(−3)2=9,∣−3∣=3,又∵−9<−13<3<9,∴−32<−13<∣−3∣<(−3)2.6. 【答案】B7. 【答案】D【解析】第1次剩下1−13=23米;第2次剩下23×(1−13)=(23)2米;⋯,依此类推,剪7次剩下的彩带长为(23)7米.故选:D.8. 【答案】B【解析】∵∣x+1∣+(y−3)2=0,∴x+1=0,y−3=0,∴x=−1,y=3.∴x y=(−1)3=−1.9. 【答案】−8或2【解析】−8或210. 【答案】5【解析】绝对值小于3的整数有±2,±1,0,一共5个.11. 【答案】−23【解析】题中单项式的系数是常数项−23.12. 【答案】2【解析】由同类项定义可知:m=4,n=2,∴m−n=4−2=2.13. 【答案】100c+10b+a【解析】一个三位数个位数字是a,十位数字是b,百位数字是c,则这个三位数是100c+ 10b+a.14. 【答案】26【解析】∵a∗b=a2−b,∴5∗(−1)=52−(−1)=25+1=26.15. 【答案】1或−7【解析】∵a,b互为倒数,∴a+b=0,∵c,d互为倒数,∴cd=1,∵m的平方等于4,∴m=±2,∴原式=2022×0−3×1±2×2=−3±4=1或−7.16. 【答案】3b−a【解析】∵由数轴上a,b两点的位置可知,−1<a<0,b<1,∴a+b>0,b−a>0,∴原式=−a+b+a+b+b−a=3b−a.17. 【答案】(1) 分数集合:{−3.8,4.3,−∣∣−207∣∣,−(−35)⋯}.(2) 非负数集合:{4.3,42,0,−(−35)⋯}.18. 【答案】(1) 原式=(26+8)−(14+16) =34−30=4.(2) 原式=35+30=65.19. 【答案】由已知条件可知,从正面看有3列,每列小正方数形数目分别为4,3,2;从左面看有3列,每列小正方形数目分别为1,4,3.据此可画出图形.该几何体的左视图为:20. 【答案】(1) 原式=−24×34+24×56−24×712 =−18+20−14=−12.(2) 原式=(−2)18×(12)19=(−2)18×(12)18×12=(−2×12)18×12=(−1)18×12=1×12=12.21. 【答案】(1) ∵长方体的长为4厘米,宽为3厘米,高为5厘米,这个长方体的棱长总和为4×(4+3+5)=48(厘米),故长方体所有棱长的和为48厘米.(2) 表面积为:2×(4×3+4×5+3×5)−4×3=2×47−12=82(平方厘米).制作10个这样的包装盒共需:0.1×82×8=65.6(元).∴制作8个这样的包装盒共需65.6元.22. 【答案】(1) 原式=(3x2y+23x2y)−(3xy2+12xy2)=113x2y−72xy2.(2) 原式=12x+6y+4y−32x =−20x+10y.23. 【答案】(1) ∵+22−3+4−2−8+17−2+12+7−5=42,∴最后他们没有回到出发点,在A地那边42千米的地方.(2) ∵22+3+4+2+8+17+2+12+7+5=82,∵每千米耗油0.06升,∴今天共耗油82×0.06=4.92(升).答:今天共耗油4.92升.24. 【答案】(1) 原式=(2a 2+a2)+(6a−3a)+1=3a2+3a+1.当a=1时,原式=3×(−1)2+3×(−1)+1 =3−3+1=1.(2) 原式=4x2−23y2−2x2+6xy+23y2 =2x2+6xy.当x=3,y=−1时,原式=2×32+6×3×(−1)=18−18=0.25. 【答案】(1) 3+32+33+⋯+32022;(3+32+33+⋯+32022)−(1+3+32+33+⋯+32022)=32022−1;32022−12(2) {s =1+5+52+53+⋯+599, ⋯⋯①5s =5+52+53+54+⋯+599+5100. ⋯⋯②② − ①得 4s =5100−1,s =5100−14.【解析】(1) 3s =3+32+33+⋯+32022, 3s −s=(3+32+33+⋯+32022)−(1+3+32+33+⋯+32022)=32022−1,因此 s =32022−12.26. 【答案】(1) ∵A −2B =−7x 2+10x +12,B =4x 2−5x −6, ∴A =−7x 2+10x +12+2(4x 2−5x −6)=x 2, ∴A +2B =x 2+2(4x 2−5x −6)=9x 2−10x −12.(2) 当 x =−3 时,A +2B =9×(−3)2−10×(−3)−12=99.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁夏银川市2020版七年级上学期数学期中考试试卷C卷
姓名:________ 班级:________ 成绩:________
一、单选题 (共9题;共9分)
1. (1分) (2020七上·长兴期末) 2020的相反数是()
A . -2020
B . 2020
C .
D .
2. (1分)下列说法中正确的是()
A . 负有理数是负分数
B . -1是最大的负数
C . 正有理数和负有理数组成全体有理数
D . 零是整数
3. (1分)(2016·资阳) 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为()
A . 7.6×
B . 7.6×
C . 7.6×
D . 7.6×
4. (1分) (2017七上·深圳期中) 下列各式正确的是()
A . a﹣(b﹣c+d)=a﹣b﹣c+d
B . a﹣2(b﹣c+d)=a﹣2b+2c+d
C . a﹣(b﹣c+d)=a﹣b+c+d
D . a﹣(b﹣c+d)=a﹣b+c﹣d
5. (1分) (2019七上·淮滨月考) 下列判断中正确的是()
A . 与不是同类项
B . 不是整式
C . 单项式的系数是 -1
D . 是二次三项式
6. (1分)(2017·衡阳模拟) 下列各数中,负数是()
A . ﹣(﹣2)
B . ﹣|﹣1|
C . (﹣1)0
D . 1﹣2
7. (1分)一个三位数,百位数字是a,十位数字是b,个位数字是c,那么这个三位数的十位数字和百位数字对调后所得的三位数是()
A . a+b+c
B . bca
C . 100c+10b+a
D . 100b+10c+a
8. (1分)北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:
如果将两地国际标准时间的差简称为时差,那么()
A . 汉城与纽约的时差为13小时
B . 汉城与多伦多的时差为13小时
C . 北京与纽约的时差为14小时
D . 北京与多伦多的时差为14小时
9. (1分)(2017·百色) 观察以下一列数的特点:0,1,﹣4,9,﹣16,25,…,则第11个数是()
A . ﹣121
B . ﹣100
C . 100
D . 121
二、填空题 (共5题;共5分)
10. (1分) (2020八上·淅川期末) 计算: ________.
11. (1分)若2m=5,8n=2,则22m+3n=________。
12. (1分) (2017九上·岑溪期中) 若,则=________.
13. (1分) (2019七上·天台期中) 若一个多项式与多项式4x2﹣4xy﹣2y2的和是5x2﹣6xy﹣y2 .则这个多项式是________ .
当x=,y=时,这个多项式的值是________.
14. (1分)(2014·成都) 在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中三角形ABC是格点三角形,其中S=2,N=0,L=6;图中格点多边形DEFGHI所对应的S,N,L分别是________.经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S=________.(用数值作答)
三、解答题 (共8题;共16分)
15. (3分) (2018七上·港南期中) 计算题
(1)计算:- ×(-1 )÷(-2 )
(2)化简:(x2-y2)-3(x2-2y2)
16. (2分)、化简(1)2x2y-2xy-4xy2+xy+4x2y-3xy2 (2) 3 (4x2-3x+2)-2 (1-4x2+x)
(3)5abc-2a2b-[ 3abc-3 (4ab2+a2b)] (4) (2x2+x)-2[x2-2(3 x2-x)]
17. (1分) (2020七上·鹿邑期末) 先化简,再求值:,其中 .
18. (1分)计算:
(1);
(2);
(3);
(4)先化简,再求值:,其中x=-1,y=2.
19. (3分) (2019七上·海曙期中) 在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p .
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值;
(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x的值.
20. (1分) (2018七下·明光期中) 对于任意实数a、b、c、d,我们规定 =ad-bc,若-8<
<4,求整数x的值.
21. (2分) (2018七上·阆中期中) 按要求求值
(1)化简求值:其中 .
(2)若化简的结果与x的取值无关,求m的值.
22. (3分) (2020七上·西湖期末) 图 1为奇数排成的数表,用十字框任意框出 5个数,记框内中间这个数为 m ,其它四个数分别记为 a , b , c , d (如图);图 3为按某一规律排成的另一个数表,用十字框任意框出 5个数,记框内中间这个数为 n ,其它四个数记为 e , f , g , h (如图 4).
(1)请你含 m 的代数式表示 b .
(2)请你含 n 的代数式表示 e .
(3)若,,求的值.
参考答案一、单选题 (共9题;共9分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
二、填空题 (共5题;共5分)
10-1、
11-1、
12-1、
13-1、
14-1、
三、解答题 (共8题;共16分)
15-1、
15-2、
16-1、17-1、
18-1、19-1、19-2、
20-1、21-1、21-2、
22-1、22-2、
22-3、。
