In-medium vector meson masses in a Chiral SU(3) model
The Subleading Isgur-Wise Form Factor $chi_3(vcdot v')$ to Order $alpha_s$ in QCD Sum Rules

a rXiv:h ep-ph/9212266v116Dec1992SLAC–PUB–6017WIS–92/99/Dec–PH December 1992T/E The Subleading Isgur-Wise Form Factor χ3(v ·v ′)to Order αs in QCD Sum Rules Matthias Neubert Stanford Linear Accelerator Center Stanford University,Stanford,California 94309Zoltan Ligeti and Yosef Nir Weizmann Institute of Science Physics Department,Rehovot 76100,Israel We calculate the contributions arising at order αs in the QCD sum rule for the spin-symmetry violating universal function χ3(v ·v ′),which appears at order 1/m Q in the heavy quark expansion of meson form factors.In particular,we derive the two-loop perturbative contribution to the sum rule.Over the kinematic range accessible in B →D (∗)ℓνdecays,we find that χ3(v ·v ′)does not exceed the level of ∼1%,indicating that power corrections induced by the chromo-magnetic operator in the heavy quark expansion are small.(submitted to Physical Review D)I.INTRODUCTIONIn the heavy quark effective theory(HQET),the hadronic matrix elements describing the semileptonic decays M(v)→M′(v′)ℓν,where M and M′are pseudoscalar or vector mesons containing a heavy quark,can be systematically expanded in inverse powers of the heavy quark masses[1–5].The coefficients in this expansion are m Q-independent,universal functions of the kinematic variable y=v·v′.These so-called Isgur-Wise form factors characterize the properties of the cloud of light quarks and gluons surrounding the heavy quarks,which act as static color sources.At leading order,a single functionξ(y)suffices to parameterize all matrix elements[6].This is expressed in the compact trace formula[5,7] M′(v′)|J(0)|M(v) =−ξ(y)tr{(2)m M P+ −γ5;pseudoscalar meson/ǫ;vector mesonis a spin wave function that describes correctly the transformation properties(under boosts and heavy quark spin rotations)of the meson states in the effective theory.P+=1g s2m Q O mag,O mag=M′(v′)ΓP+iσαβM(v) .(4)The mass parameter¯Λsets the canonical scale for power corrections in HQET.In the m Q→∞limit,it measures thefinite mass difference between a heavy meson and the heavy quark that it contains[11].By factoring out this parameter,χαβ(v,v′)becomes dimensionless.The most general decomposition of this form factor involves two real,scalar functionsχ2(y)andχ3(y)defined by[10]χαβ(v,v′)=(v′αγβ−v′βγα)χ2(y)−2iσαβχ3(y).(5)Irrespective of the structure of the current J ,the form factor χ3(y )appears always in the following combination with ξ(y ):ξ(y )+2Z ¯Λ d M m Q ′ χ3(y ),(6)where d P =3for a pseudoscalar and d V =−1for a vector meson.It thus effectively renormalizes the leading Isgur-Wise function,preserving its normalization at y =1since χ3(1)=0according to Luke’s theorem [10].Eq.(6)shows that knowledge of χ3(y )is needed if one wants to relate processes which are connected by the spin symmetry,such as B →D ℓνand B →D ∗ℓν.Being hadronic form factors,the universal functions in HQET can only be investigated using nonperturbative methods.QCD sum rules have become very popular for this purpose.They have been reformulated in the context of the effective theory and have been applied to the study of meson decay constants and the Isgur-Wise functions both in leading and next-to-leading order in the 1/m Q expansion [12–21].In particular,it has been shown that very simple predictions for the spin-symmetry violating form factors are obtained when terms of order αs are neglected,namely [17]χ2(y )=0,χ3(y )∝ ¯q g s σαβG αβq [1−ξ(y )].(7)In this approach χ3(y )is proportional to the mixed quark-gluon condensate,and it was estimated that χ3(y )∼1%for large recoil (y ∼1.5).In a recent work we have refined the prediction for χ2(y )by including contributions of order αs in the sum rule analysis [20].We found that these are as important as the contribution of the mixed condensate in (7).It is,therefore,worthwhile to include such effects also in the analysis of χ3(y ).This is the purpose of this article.II.DERIV ATION OF THE SUM RULEThe QCD sum rule analysis of the functions χ2(y )and χ3(y )is very similar.We shall,therefore,only briefly sketch the general procedure and refer for details to Refs.[17,20].Our starting point is the correlatord x d x ′d ze i (k ′·x ′−k ·x ) 0|T[¯q ΓM ′P ′+ΓP +iσαβP +ΓM+Ξ3(ω,ω′,y )tr 2σαβ2(1+/v ′),and we omit the velocity labels in h and h ′for simplicity.The heavy-light currents interpolate pseudoscalar or vector mesons,depending on the choice ΓM =−γ5or ΓM =γµ−v µ,respectively.The external momenta k and k ′in (8)are the “residual”off-shell momenta of the heavy quarks.Due to the phase redefinition of the effective heavy quark fields in HQET,they are related to the total momenta P and P ′by k =P −m Q v and k ′=P ′−m Q ′v ′[3].The coefficient functions Ξi are analytic in ω=2v ·k and ω′=2v ′·k ′,with discontinuities for positive values of these variables.They can be saturated by intermediate states which couple to the heavy-light currents.In particular,there is a double-pole contribution from the ground-state mesons M and M ′.To leading order in the 1/m Q expansion the pole position is at ω=ω′=2¯Λ.In the case of Ξ2,the residue of the pole is proportional to the universal function χ2(y ).For Ξ3the situation is more complicated,however,since insertions of the chromo-magnetic operator not only renormalize the leading Isgur-Wise function,but also the coupling of the heavy mesons to the interpolating heavy-light currents (i.e.,the meson decay constants)and the physical meson masses,which define the position of the pole.1The correct expression for the pole contribution to Ξ3is [17]Ξpole 3(ω,ω′,y )=F 2(ω−2¯Λ+iǫ) .(9)Here F is the analog of the meson decay constant in the effective theory (F ∼f M√m QδΛ2+... , 0|j (0)|M (v ) =iF2G 2tr 2σαβΓP +σαβM (v ) ,where the ellipses represent spin-symmetry conserving or higher order power corrections,and j =¯q Γh (v ).In terms of the vector–pseudoscalar mass splitting,the parameter δΛ2isgiven by m 2V −m 2P =−8¯ΛδΛ2.For not too small,negative values of ωand ω′,the coefficient function Ξ3can be approx-imated as a perturbative series in αs ,supplemented by the leading power corrections in 1/ωand 1/ω′,which are proportional to vacuum expectation values of local quark-gluon opera-tors,the so-called condensates [22].This is how nonperturbative corrections are incorporated in this approach.The idea of QCD sum rules is to match this theoretical representation of Ξ3to the phenomenological pole contribution given in (9).To this end,one first writes the theoretical expression in terms of a double dispersion integral,Ξth 3(ω,ω′,y )= d νd ν′ρth 3(ν,ν′,y )1Thereare no such additional terms for Ξ2because of the peculiar trace structure associated with this coefficient function.possible subtraction terms.Because of theflavor symmetry it is natural to set the Borel parameters associated withωandω′equal:τ=τ′=2T.One then introduces new variables ω±=12T ξ(y) F2e−2¯Λ/T=ω0dω+e−ω+/T ρth3(ω+,y)≡K(T,ω0,y).(12)The effective spectral density ρth3arises after integration of the double spectral density over ω−.Note that for each contribution to it the dependence onω+is known on dimensionalgrounds.It thus suffices to calculate directly the Borel transform of the individual con-tributions toΞth3,corresponding to the limitω0→∞in(12).Theω0-dependence can be recovered at the end of the calculation.When terms of orderαs are neglected,contributions to the sum rule forΞ3can only be proportional to condensates involving the gluonfield,since there is no way to contract the gluon contained in O mag.The leading power correction of this type is represented by the diagram shown in Fig.1(d).It is proportional to the mixed quark-gluon condensate and,as shown in Ref.[17],leads to(7).Here we are interested in the additional contributions arising at orderαs.They are shown in Fig.1(a)-(c).Besides a two-loop perturbative contribution, one encounters further nonperturbative corrections proportional to the quark and the gluon condensate.Let usfirst present the result for the nonperturbative power corrections.WefindK cond(T,ω0,y)=αs ¯q q TT + αs GG y+1− ¯q g sσαβGαβq√y2−1),δn(x)=1(4π)D×1dλλ1−D∞λd u1∞1/λd u2(u1u2−1)D/2−2where C F=(N2c−1)/2N c,and D is the dimension of space-time.For D=4,the integrand diverges asλ→0.To regulate the integral,we assume D<2and use a triple integration by parts inλto obtain an expression which can be analytically continued to the vicinity of D=4.Next we set D=4+2ǫ,expand inǫ,write the result as an integral overω+,and introduce back the continuum threshold.This givesK pert(T,ω0,y)=−αsy+1 2ω0dω+ω3+e−ω+/T(16)× 12−23∂µ+3αs9π¯Λ,(17)which shows that divergences arise at orderαs.At this order,the renormalization of the sum rule is thus accomplished by a renormalization of the“bare”parameter G2in(12).In the9π¯Λ 1µ2 +O(g3s).(18)Hence a counterterm proportional to¯Λξ(y)has to be added to the bracket on the left-hand side of the sum rule(12).To evaluate its effect on the right-hand side,we note that in D dimensions[17]¯Λξ(y)F2e−2¯Λ/T=3y+1 2ω0dω+ω3+e−ω+/T(19)× 1+ǫ γE−ln4π+2lnω+−ln y+12T ξ(y) F2e−2¯Λ/T=αsy+1 2ω0dω+ω3+e−ω+/T 2lnµ6+ y r(y)−1+ln y+1According to Luke’stheorem,theuniversalfunction χ3(y )vanishes at zero recoil [10].Evaluating (20)for y =1,we thus obtain a sum rule for G 2(µ)and δΛ2.It reads G 2(µ)−¯ΛδΛ224π3ω00d ω+ω3+e −ω+/T ln µ12 +K cond (T,ω0,1),(21)where we have used that r (1)=1.Precisely this sum rule has been derived previously,starting from a two-current correlator,in Ref.[16].This provides a nontrivial check of our ing the fact that ξ(y )=[2/(y +1)]2+O (g s )according to (19),we find that the µ-dependent terms cancel out when we eliminate G 2(µ)and δΛ2from the sum rule for χ3(y ).Before we present our final result,there is one more effect which has to be taken into account,namely a spin-symmetry violating correction to the continuum threshold ω0.Since the chromo-magnetic interaction changes the masses of the ground-state mesons [cf.(10)],it also changes the masses of higher resonance states.Expanding the physical threshold asωphys =ω0 1+d M8π3 22 δ3 ω032π2ω30e −ω0/T 26π2−r (y )−ξ(y ) δ0 ω096π 248T 1−ξ(y ).It explicitly exhibits the fact that χ3(1)=0.III.NUMERICAL ANALYSISLet us now turn to the evaluation of the sum rule (23).For the QCD parameters we take the standard values¯q q =−(0.23GeV)3,αs GG =0.04GeV4,¯q g sσαβGαβq =m20 ¯q q ,m20=0.8GeV2.(24) Furthermore,we useδω2=−0.1GeV from above,andαs/π=0.1corresponding to the scale µ=2¯Λ≃1GeV,which is appropriate for evaluating radiative corrections in the effective theory[15].The sensitivity of our results to changes in these parameters will be discussed below.The dependence of the left-hand side of(23)on¯Λand F can be eliminated by using a QCD sum rule for these parameters,too.It reads[16]¯ΛF2e−2¯Λ/T=9T4T − ¯q g sσαβGαβq4π2 2T − ¯q q +(2y+1)4T2.(26) Combining(23),(25)and(26),we obtainχ3(y)as a function ofω0and T.These parameters can be determined from the analysis of a QCD sum rule for the correlator of two heavy-light currents in the effective theory[16,18].Onefinds good stability forω0=2.0±0.3GeV,and the consistency of the theoretical calculation requires that the Borel parameter be in the range0.6<T<1.0GeV.It supports the self-consistency of the approach that,as shown in Fig.2,wefind stability of the sum rule(23)in the same region of parameter space.Note that it is in fact theδω2-term that stabilizes the sum rule.Without it there were no plateau.Over the kinematic range accessible in semileptonic B→D(∗)ℓνdecays,we show in Fig.3(a)the range of predictions forχ3(y)obtained for1.7<ω0<2.3GeV and0.7<T< 1.2GeV.From this we estimate a relative uncertainty of∼±25%,which is mainly due to the uncertainty in the continuum threshold.It is apparent that the form factor is small,not exceeding the level of1%.2Finally,we show in Fig.3(b)the contributions of the individual terms in the sum rule (23).Due to the large negative contribution proportional to the quark condensate,the terms of orderαs,which we have calculated in this paper,cancel each other to a large extent.As a consequence,ourfinal result forχ3(y)is not very different from that obtained neglecting these terms[17].This is,however,an accident.For instance,the order-αs corrections would enhance the sum rule prediction by a factor of two if the ¯q q -term had the opposite sign. From thisfigure one can also deduce how changes in the values of the vacuum condensates would affect the numerical results.As long as one stays within the standard limits,the sensitivity to such changes is in fact rather small.For instance,working with the larger value ¯q q =−(0.26GeV)3,or varying m20between0.6and1.0GeV2,changesχ3(y)by no more than±0.15%.In conclusion,we have presented the complete order-αs QCD sum rule analysis of the subleading Isgur-Wise functionχ3(y),including in particular the two-loop perturbative con-tribution.Wefind that over the kinematic region accessible in semileptonic B decays this form factor is small,typically of the order of1%.When combined with our previous analysis [20],which predicted similarly small values for the universal functionχ2(y),these results strongly indicate that power corrections in the heavy quark expansion which are induced by the chromo-magnetic interaction between the gluonfield and the heavy quark spin are small.ACKNOWLEDGMENTSIt is a pleasure to thank Michael Peskin for helpful discussions.M.N.gratefully acknowl-edgesfinancial support from the BASF Aktiengesellschaft and from the German National Scholarship Foundation.Y.N.is an incumbent of the Ruth E.Recu Career Development chair,and is supported in part by the Israel Commission for Basic Research and by the Minerva Foundation.This work was also supported by the Department of Energy,contract DE-AC03-76SF00515.REFERENCES[1]E.Eichten and B.Hill,Phys.Lett.B234,511(1990);243,427(1990).[2]B.Grinstein,Nucl.Phys.B339,253(1990).[3]H.Georgi,Phys.Lett.B240,447(1990).[4]T.Mannel,W.Roberts and Z.Ryzak,Nucl.Phys.B368,204(1992).[5]A.F.Falk,H.Georgi,B.Grinstein,and M.B.Wise,Nucl.Phys.B343,1(1990).[6]N.Isgur and M.B.Wise,Phys.Lett.B232,113(1989);237,527(1990).[7]J.D.Bjorken,Proceedings of the18th SLAC Summer Institute on Particle Physics,pp.167,Stanford,California,July1990,edited by J.F.Hawthorne(SLAC,Stanford,1991).[8]M.B.Voloshin and M.A.Shifman,Yad.Fiz.45,463(1987)[Sov.J.Nucl.Phys.45,292(1987)];47,801(1988)[47,511(1988)].[9]A.F.Falk,B.Grinstein,and M.E.Luke,Nucl.Phys.B357,185(1991).[10]M.E.Luke,Phys.Lett.B252,447(1990).[11]A.F.Falk,M.Neubert,and M.E.Luke,SLAC preprint SLAC–PUB–5771(1992),toappear in Nucl.Phys.B.[12]M.Neubert,V.Rieckert,B.Stech,and Q.P.Xu,in Heavy Flavours,edited by A.J.Buras and M.Lindner,Advanced Series on Directions in High Energy Physics(World Scientific,Singapore,1992).[13]A.V.Radyushkin,Phys.Lett.B271,218(1991).[14]D.J.Broadhurst and A.G.Grozin,Phys.Lett.B274,421(1992).[15]M.Neubert,Phys.Rev.D45,2451(1992).[16]M.Neubert,Phys.Rev.D46,1076(1992).[17]M.Neubert,Phys.Rev.D46,3914(1992).[18]E.Bagan,P.Ball,V.M.Braun,and H.G.Dosch,Phys.Lett.B278,457(1992);E.Bagan,P.Ball,and P.Gosdzinsky,Heidelberg preprint HD–THEP–92–40(1992).[19]B.Blok and M.Shifman,Santa Barbara preprint NSF–ITP–92–100(1992).[20]M.Neubert,Z.Ligeti,and Y.Nir,SLAC preprint SLAC–PUB–5915(1992).[21]M.Neubert,SLAC preprint SLAC–PUB–5992(1992).[22]M.A.Shifman,A.I.Vainshtein,and V.I.Zakharov,Nucl.Phys.B147,385(1979);B147,448(1979).FIGURESFIG.1.Diagrams contributing to the sum rule for the universal form factorχ3(v·v′):two-loop perturbative contribution(a),and nonperturbative contributions proportional to the quark con-densate(b),the gluon condensate(c),and the mixed condensate(d).Heavy quark propagators are drawn as double lines.The square represents the chromo-magnetic operator.FIG.2.Analysis of the stability region for the sum rule(23):The form factorχ3(y)is shown for y=1.5as a function of the Borel parameter.From top to bottom,the solid curves refer toω0=1.7,2.0,and2.3GeV.The dashes lines are obtained by neglecting the contribution proportional toδω2.FIG.3.(a)Prediction for the form factorχ3(v·v′)in the stability region1.7<ω0<2.3 GeV and0.7<T<1.2GeV.(b)Individual contributions toχ3(v·v′)for T=0.8GeV and ω0=2.0GeV:total(solid),mixed condensate(dashed-dotted),gluon condensate(wide dots), quark condensate(dashes).The perturbative contribution and theδω2-term are indistinguishable in thisfigure and are both represented by the narrow dots.11。
Meson-nucleon scattering and vector mesons in nuclear matter

a r X i v :n u c l -t h /9808071v 1 27 A u g 1998(1)Meson-nucleon scattering and vector mesonsin nuclear matter ∗Bengt FrimanGesellschaft f¨u r Schwerionenforschung (GSI)D-64220Darmstadt,Germany&Institut f¨u r Kernphysik,TU DarmstadtD-64289Darmstadt,Germany(Received February 9,2008)The properties of vector mesons in nuclear matter are discussed.I examine the constraints imposed by elementary processes on the widths of ρand ωmesons in nuclear matter.Furthermore,results for the ρ-and ω-nucleon scattering amplitudes obtained by fitting meson-nucleon scattering data in a coupled-channel approach are presented.1.IntroductionThe electromagnetic decay of the vector mesons into e +e −and µ+µ−pairs makes them particularly well suited for exploring the conditions in dense and hot matter in nuclear collisions.The lepton pairs provide virtually undistorted information on the mass distribution of the vector mesons in the medium.The lepton-pair spectrum in nucleus-nucleus collisions at SPS energies exhibits a low-mass enhancement compared to proton-proton and proton-nucleus collisions [2].A quantitative interpretation of the lepton-pair data can be obtained within a scenario,where the effective vector-meson masses are reduced in a hadronic environment [3,4,5,6].On the other hand,attempts to interpret the low-mass enhancement of lepton pairs in terms of many-body effects also yield good agreement with the data [7,8].In these calculations the broadening of the ρmeson in nuclear matter due to the interactions of its pion cloud with the medium [9,10,11,12]and the momentum dependence of the ρ-meson self energy due to the coupling with baryon-resonance–nucleon-hole states [13,14]are taken intoaccount.2proc printed on February9,2008Through the low-density theorem hadron-nucleon scattering data can be used to determine the self-energies of hadrons in nuclear matter at low densities.In this talk I discuss the the constraints on the imaginary part of the vector-meson self energy in nuclear matter that can be derived from elementary reactions,and present results of a coupled channel calculation of meson-nucleon scattering.The latter provides a model for the vector-meson–nucleon scattering amplitude.2.Constraints from elementary processesThe low-density theorem states that the self energy of e.g.a vector meson V in nuclear matter is given by[15]ΣV(ρN)=−4π(1+m Vk2πIm¯f(π−p)ωn→ωn(θ=0),(2)where¯f denotes the spin-averaged scattering amplitude.Close to theωn threshold,the scattering amplitude can be expanded in powers of the rel-ative momentum in theωn channel qω.An excellentfit to the data from threshold up to q=120MeV/c2is obtained with Im¯f(π−p)ωn→ωn=a+bq2ω+cq4ω, where a=0.013fm,b=0.10fm3and c=−0.08fm5(see Fig.1).The co-efficient a is the imaginary part of the scattering length.The corresponding contribution of theπ-nucleon channel to the width of theωmeson at rest in nuclear matter can now be obtained by using theproc printed on February9,20083Fig.1.Theπamplitudelow-densityω24proc printed on February9,2008Fig.2.The line shows the best fit,while the[22]. amplitude energy of a vector-mesonSince we close to threshold,it is sufficient to consider only s-wave scattering in theρN andωN channels.This implies that in theπN andπ∆channels we need only s-and d-waves.In particular,we consider the S11,S31,D13and D33 partial waves ofπN scattering.Furthermore,we consider the pion-induced production ofη,ωandρmesons offnucleons.In order to learn something about the momentum dependence of the vector-meson self energy,vector-meson–nucleon scattering also in higher partial waves would have to be considered.In accordance with the approach outlined above only data in the relevant kinematical range will be used in the analysis.The threshold for vector-proc printed on February9,20085 Fig.3.The points are fromref.[18],as√mesonwith 4-point the reader is referred to ref.[21].In Fig.2ourfit to theπN scattering data is illustrated by the D13channel.In the remaining channels the quality of thefit is in general better.Furthermore,in Fig.3the cross section for the reactionπ−p→ρ0n is shown.The bumps at s1/2below1.6GeV are due to the coupling to res-onances below the threshold,like the N⋆(1520).This indicates that these resonances may play an important role in theρ-nucleon dynamics,in agree-ment with the results of Manley and Saleski[20].However,the strength of the coupling is uncetrain,due to the ambiguity in theρ-production cross section close to threshold mentioned above.Wefind that also theωmeson couples strongly to these resonances.The pion-inducedη-production cross section is well described up to s1/2≃1.65GeV.At higher energies presumably higher partial waves,not included in our model,become important.Similarly,the pion-induced pro-duction ofωmesons is reasonably well represented close to threshold,al-though the strong energy dependence of the amplitude shown in Fig.1is not reproduced by the model.This may be due to the coupling to channels not included at present,like the K−Σchannel.The resultingρ-andω-nucleon scattering amplitudes are shown in Fig.4. Theρ−N andω−N scattering lengths are(-0.2+0.7i)fm and(-0.5+0.1i) fm respectively.To lowest order in the density,this corresponds to the following in-medium modifications of masses and widths at nuclear matter density:∆mρ≃20MeV,∆mω≃50MeV,∆Γρ≃140MeV and∆Γω≃206proc printed on February9,2008Fig.4.The over spin and isospin.MeV.resonances below of the amplitudes,will be split into a meson a resonance-hole like mode,which is pushed down in energy.The downward shift of vector-meson strength would contribute to the low-mass enhancement in the lepton-pair spectra.Thus,our results support the dynamical scenario discussed in ref.[23].AcknowledgmentsI thank M.Lutz and G.Wolf for valuable discussions.I am grateful to W.Florkowski and M.Nowak for their warm hospitality during my stay in Cracow and I acknowledge the partial support by the Polish Governmentproc printed on February9,20087 Project(KBN)grant2P03B00814as well as by the Institute of Nuclear Physics in Cracow.REFERENCES[1]CERES,G.Agakichiev et al.,Phys.Rev.Lett.75,1272(1995);Nucl.Phys.A610,317c(1996);A.Drees,Nucl.Phys.A610,536c(1996);P.Wurm,in Proc.Workshop on Astro-Hadron Physics,Seoul,Korea,Oct.,1997[2]Helios-3,M.Masera et al.,Nucl.Phys.A590,93c(1992)[3]G.Q.Li,C.M.Ko and G.E.Brown,Phys.Rev.Lett.75,4007(1995)[4]W.Cassing,W.Ehehalt and C.M.Ko,Phys.Lett.B363,35(1995);W.Cass-ing,W.Ehehalt and I.Kralik,Phys.Lett.B377,5(1995)[5]G.E.Brown and M.Rho,Phys.Rev.Lett.66,2720(1991)[6]T.Hatsuda and S.H.Lee,Phys.Rev.C46,R34(1992)[7]R.Rapp,G.Chanfray and J.Wambach,Phys.Rev.Lett.76,368(1996);Nucl.Phys.A617,472(1997)[8]W.Cassing,E.L.Bratkovskaya,R.Rapp and J.Wambach,nucl-th/9708020[9]M.Herrmann,B.Friman and W.N¨o renberg,Nucl.Phys.A560,411(1993)[10]G.Chanfray and P.Schuck,Nucl.Phys.A545,271c(1992)[11]M.Asakawa,C.M.Ko,P.Levai and X.J.Qiu,Phys.Rev.C46,R1159(1992)[12]F.Klingl,N.Kaiser and W.Weise,Nucl.Phys.A624,527(1997)[13]B.Friman and H.J.Pirner,Nucl.Phys.A617,496(1997)[14]W.Peters,M.Post,H.Lenske,S.Leupold and U.Mosel,Nucl.Phys.A628,109(1998)[15]W.Lenz,Z.Phys.56,778(1929);C.D.Dover,J.H¨u fner and R.H.Lemmer,Ann.Phys.66,248(1971)[16]B.Friman,in Proc.Workshop on Astro-Hadron Physics,Seoul,Korea,Oct.,1997,nucl-th/9801053[17]J.Keyne et al.,Phys.Rev.D14,28(1976);H.Karami et al.,Nucl.Phys.B154,503(1979)[18]A.D.Brody et al.,Phys.Rev.D4,2693(1971)[19]Handbook of Physics,Landolt and B¨o rnstein,vol.1/12a(Springer,Ber-lin,1987)[20]D.M.Manley and E.M.Saleski,Phys.Rev.C45,4002(1992)[21]M.Lutz,G.Wolf and B.Friman,to be published[22]R.A.Arndt et al.,Phys.Rev.C52,2120(1995)[23]G.E.Brown et al,to be published in Proceedings International Workshopon the Structure of Mesons,Baryons,and Nuclei,Cracow,May,1998,nucl-th/9806026。
显微硬度英语

显微硬度英语Microhardness, a concept often discussed in materials science, is the measure of a material's resistance to deformation under a small, localized load. It's an essential tool for understanding the properties of materials at a microscopic level.In the realm of metallurgy, microhardness testing is pivotal for evaluating the strength and durability of alloys.A diamond-tipped indenter is used to press into the material, leaving an indentation whose size is then measured to determine hardness.The process is delicate, requiring precision and a keen eye for detail. It's not just about the numbers; it's about the story the indentation tells about the material's internal structure.Advancements in technology have led to automated microhardness testing, which increases the accuracy and reproducibility of results. This innovation has been a boon for industries that rely on the precise engineering of materials.For students and researchers alike, understanding microhardness is crucial for designing materials withspecific properties. Whether it's improving the wear resistance of a tool or enhancing the fracture toughness of acomponent, microhardness plays a key role.Educational institutions often incorporate microhardness testing into their curriculum to prepare students for the practical challenges of material science. Hands-on experience with this testing method is invaluable for future engineers and scientists.In conclusion, microhardness is more than just ascientific measurement; it's a language that materials scientists use to communicate the intrinsic qualities of the substances they study. It's a testament to the meticulous nature of scientific inquiry and the pursuit of knowledge at the most fundamental level.。
化学化工英语试题及答案

化学化工英语试题及答案一、选择题(每题2分,共20分)1. Which of the following is a chemical element?A. WaterB. OxygenC. HydrogenD. Carbon答案:B, C, D2. The chemical formula for table salt is:A. NaOHB. NaClC. HClD. NaHCO3答案:B3. What is the process called when a substance changes from a solid to a liquid?A. SublimationB. VaporizationC. MeltingD. Condensation答案:C4. In the periodic table, which group contains alkali metals?A. Group 1B. Group 2C. Group 17D. Group 18答案:A5. What is the name of the process where a substance decomposes into two or more substances due to heat?A. CombustionB. OxidationC. ReductionD. Decomposition答案:D6. Which of the following is a physical property of a substance?A. ColorB. TasteC. SolubilityD. Reactivity答案:A7. What is the term for a compound that releases hydrogen ions (H+) when dissolved in water?A. BaseB. AcidC. SaltD. Neutral答案:B8. The law of conservation of mass states that in a chemical reaction:A. Mass is lostB. Mass is gainedC. Mass remains constantD. Mass can be converted into energy答案:C9. Which of the following is a type of chemical bond?A. Ionic bondB. Covalent bondC. Hydrogen bondD. All of the above答案:D10. What is the name of the process where a substance absorbs energy and changes from a liquid to a gas?A. MeltingB. VaporizationC. SublimationD. Condensation答案:B二、填空题(每题2分,共20分)1. The symbol for the element iron is ________.答案:Fe2. The pH scale ranges from ________ to ________.答案:0 to 143. A compound that produces a basic solution when dissolvedin water is called a ________.答案:base4. The smallest particle of an element that retains its chemical properties is called a ________.答案:atom5. The process of separating a mixture into its individual components is known as ________.答案:separation6. The study of the composition, structure, and properties of matter is called ________.答案:chemistry7. The process of a substance changing from a gas to a liquid is called ________.答案:condensation8. A(n) ________ reaction is a type of chemical reactionwhere two or more substances combine to form a single product. 答案:synthesis9. The volume of a gas at constant temperature and pressureis directly proportional to the number of ________.答案:moles10. The process of converting a solid directly into a gas without passing through the liquid phase is known as ________. 答案:sublimation三、简答题(每题10分,共30分)1. Explain what is meant by the term "stoichiometry" in chemistry.答案:Stoichiometry is the calculation of the relative quantities of reactants and products in a chemical reaction.It is based on the law of conservation of mass and involvesthe use of balanced chemical equations and the molar massesof substances to determine the amounts of reactants needed to produce a certain amount of product or the amounts ofproducts formed from a given amount of reactant.2. Describe the difference between a physical change and a chemical change.答案:A physical change is a change in the state or form of a substance without altering its chemical composition. Examples include melting, freezing, and boiling. A chemical change, on the other hand, involves a change in the chemical composition of a substance, resulting in the formation of new substances. Examples include combustion and rusting.3. What are the three main types of chemical bonds, and givean example of each.答案:The three main types of chemical bonds are ionic bonds, covalent bonds, and metallic bonds. An ionic bond is formed when electrons are transferred from one atom to another, resulting in the formation of oppositely charged ions. An example is the bond between sodium (Na) and chloride (Cl) in table salt (NaCl). A covalent bond is formed when two atoms share electrons, as seen in water (H2O) where hydrogen atoms share electrons with oxygen. Metallic bonds occur in metals, where a "sea" of delocalized electrons is shared among positively charged metal ions, as in sodium metal。
质荷比272的英文

质荷比272的英文The concept of mass-to-charge ratio, or m/z, is a fundamental aspect of mass spectrometry, a technique used to identify and quantify molecules based on their mass and charge.In the realm of scientific inquiry, the discovery of a molecule with a specific m/z of 272 could signify a breakthrough in the field of biochemistry, where such a ratio might correspond to a novel compound or a previously unknown substance.For students of chemistry, understanding the significance of m/z 272 involves grasping the principles of ionization and the separation of ions based on their mass-to-charge properties, which is crucial for analyzing complex mixtures.In the lab, observing a mass-to-charge ratio of 272 might lead to a series of experiments aimed at elucidating the structure and function of the associated molecule,potentially opening new avenues in pharmaceutical research.For those fascinated by the mysteries of the cosmos, the m/z 272 could represent a clue in the search for extraterrestrial life, where the detection of specific molecular signatures is key.In environmental science, the identification of acompound with this particular m/z could be pivotal in understanding pollution patterns or the metabolic pathways of certain organisms.For young learners, the idea of m/z 272 might serve as a stepping stone to the broader understanding of how scientists use mass spectrometry to explore the world at the molecular level.In the context of a high school science fair, a project centered around the mass-to-charge ratio of 272 could demonstrate the student's ability to apply scientific principles to real-world problems, showcasing creativity and analytical skills.Ultimately, the mass-to-charge ratio of 272, while a simple numerical value, encapsulates the potential for scientific discovery and the endless pursuit of knowledge in the field of chemistry and beyond.。
An origin for small neutrino masses in the NMSSM

1
I
Introduction
The most severe theoretical drawback of the Standard Model (SM) is probably the gauge hierarchy problem (see for example [1]). In well defined supersymmetric extensions of the SM, the property of cancellation of quadratic divergences allows to address this problem. With regard to the field content, the most economical candidate for such a realistic extension is the Minimal Supersymmetric Standard Model (MSSM). Nevertheless, within the MSSM, there are two unexplained hierarchies. The first one is intrinsic to supersymmetric models: it is named as the µ problem [2]. It arises from the presence of a mass (µ) term for the Higgs fields in the superpotential. The only two natural values for this µ parameter are either zero or the Planck energy scale. While the former value is excluded by experiments as it gives rise to the unacceptable existence of an axion, the latter one reintroduces the gauge hierarchy problem. The other hierarchy with an unknown origin is the one existing between the small neutrino masses and the electroweak symmetry breaking scale (∼ 100GeV). Indeed, during last years, neutrino oscillation experiments have confirmed that neutrinos are massive. Furthermore, the additional results, extracted from tritium beta decay experiments and cosmological data, indicate that the values of absolute neutrino masses are typically smaller than the eV scale. In this paper, we propose a supersymmetric scenario which has the virtue of addressing simultaneously both of these hierarchy questions: the µ value naturalness and the neutrino mass smallness. A nice feature of our scenario is that the mechanisms explaining the two hierarchy origins are connected, since they involve the same additional gauge-singlet superfield, providing thus a common source to the solutions of these two independent problems. Our framework is the Next to Minimal Supersymmetric Standard Model (NMSSM) [3] 1 . The NMSSM provides an elegant solution to the µ problem through the introduction of a new gauge-singlet superfield S entering the scale invariant superpotential. The scalar component of S acquires naturally a Vacuum Expectation Value (VEV) of the order of the supersymmetry breaking scale, generating an effective µ parameter of order of the electroweak scale. Another appealing feature of the NMSSM is to soften the “little fine tuning problem” of the MSSM [5]. The introduction of suitable non-renormalizable operators [6] can avoid the possibility of a cosmological domain wall problem [7]. There exist different explanations for a µ value of order of the electroweak scale, but those arise in extended frameworks. In supersymmetric extensions of the SM, there exist coupling terms violating the so-called R-parity symmetry [8, 9] which acts on fields like (−1)3B +L+2S , B , L and S being respectively the Baryon number, Lepton number and Spin. From a purely theoretical point of view, these terms must be considered, even if some phenomenological limits apply on the R-parity violating (Rp ) coupling constants [10, 11, 12, 13, 14]. As a matter of fact, these terms are supersymmetric, gauge invariant and some of them are renormalizable. Moreover, from the points of view of scenarios with discrete gauge symmetries [16], Grand Unified Theories (GUT) [17]-[18] as well as string theories [23], there exists no fundamental argument against the violation of the R-parity symmetry [10]. In the present work, we consider the ‘bilinear’ R-parity violating term Hu L appearing in the superpotential, Hu and L being respectively the up Higgs and lepton doublet superfields. The existence/influence of the other Rp terms will also be discussed. This bilinear interaction has been recently considered within the NMSSM context [15]. In particular, this type of interaction, which breaks the lepton number, mixes the higgsino and neutrinos together so that the neutrino field picks up a Majorana mass [24] (the generation of such a neutrino mass requires two units of L violation). Hence, no additional right
Quarks——介绍夸克的英文资料
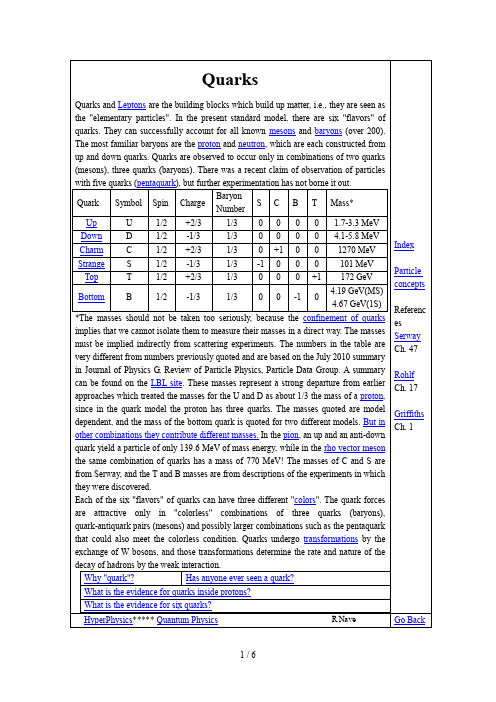
QuarksQuarks and Leptons are the building blocks which build up matter, i.e., they are seen as the "elementary particles". In the present standard model, there are six "flavors" of quarks. They can successfully account for all known mesons and baryons (over 200). The most familiar baryons are the proton and neutron, which are each constructed from up and down quarks. Quarks are observed to occur only in combinations of two quarks (mesons), three quarks (baryons). There was a recent claim of observation of particles with five quarks (pentaquark), but further experimentation has not borne it out.Quark Symbol Spin Charge BaryonNumberS C B T Mass*Up U 1/2 +2/3 1/3 0 0 0 0 1.7-3.3 MeV Down D 1/2 -1/3 1/3 0 0 0 0 4.1-5.8 MeV Charm C 1/2 +2/3 1/3 0 +1 0 0 1270 MeV Strange S 1/2 -1/3 1/3 -1 0 0 0 101 MeV Top T 1/2 +2/3 1/3 0 0 0 +1 172 GeVBottom B 1/2 -1/3 1/3 0 0 -1 0 4.19 GeV(MS) 4.67 GeV(1S)*The masses should not be taken too seriously, because the confinement of quarks implies that we cannot isolate them to measure their masses in a direct way. The masses must be implied indirectly from scattering experiments. The numbers in the table are very different from numbers previously quoted and are based on the July 2010 summary in Journal of Physics G, Review of Particle Physics, Particle Data Group. A summary can be found on the LBL site. These masses represent a strong departure from earlier approaches which treated the masses for the U and D as about 1/3 the mass of a proton, since in the quark model the proton has three quarks. The masses quoted are model dependent, and the mass of the bottom quark is quoted for two different models. But in other combinations they contribute different masses. In the pion, an up and an anti-down quark yield a particle of only 139.6 MeV of mass energy, while in the rho vector meson the same combination of quarks has a mass of 770 MeV! The masses of C and S are from Serway, and the T and B masses are from descriptions of the experiments in which they were discovered.Each of the six "flavors" of quarks can have three different "colors". The quark forces are attractive only in "colorless" combinations of three quarks (baryons), quark-antiquark pairs (mesons) and possibly larger combinations such as the pentaquark that could also meet the colorless condition. Quarks undergo transformations by the exchange of W bosons, and those transformations determine the rate and nature of the decay of hadrons by the weak interaction.Why "quark"?Has anyone ever seen a quark?What is the evidence for quarks inside protons?What is the evidence for six quarks?IndexParticle conceptsReferenc es Serway Ch. 47Rohlf Ch. 17Griffiths Ch. 1HyperPhysics***** Quantum Physics R Nave Go BackWhy "Quark"?The name "quark" was taken by Murray Gell-Mann from the book "Finnegan's Wake"by James Joyce. The line "Three quarks for Muster Mark..." appears in the fancifulbook. Gell-Mann received the 1969 Nobel Prize for his work in classifying elementary particles.IndexParticleconceptsHyperPhysics ***** Quantum PhysicsR Nave Go BackUp and Down QuarksThe up and down quarks are the most common and least massive quarks, being the constituents of protons and neutrons and thus of most ordinary matter.The fact that the free neutron decaysand nuclei decay by beta decay in processes likeis thought to be the result of a more fundamental quark processTable of quark propertiesIndexParticle conceptsHyperPhysics ***** Quantum PhysicsR Nave Go BackThe Strange QuarkIn 1947 during a study of cosmic ray interactions, a product of a proton collision with a nucleus was found to live for much longer time than expected: 10-10 seconds instead of the expected 10-23 seconds! This particle was named the lambda particle (Λ0) and theproperty which caused it to live so long was dubbed "strangeness" and that name stuck to be the name of one of the quarks from which the lambda particle is constructed. The lambda is a baryon which is made up of three quarks: an up, a down and a strange quark.The shorter lifetime of 10-23 seconds was expected because the lambda as a baryon participates in the strong interaction, and that usually leads to such very short lifetimes. The long observed lifetime helped develop a new conservation law for such decays called the "conservation of strangeness". The presence of a strange quark in a particle is denoted by a quantum number S=-1. Particle decay by the strong or electromagnetic interactions preserve the strangeness quantum number. The decay process for the lambda particle must violate that rule, since there is no lighter particle which contains a strange quark - so the strange quark must be transformed to another quark in the process. That can only occur by the weak interaction , and that leads to a much longerlifetime. The decay processes show that strangeness is not conserved:The quark transformations necessary to accomplish these decay processes can be visualized with the help of Feynmann diagrams .The omega-minus , a baryon composed of three strange quarks, is a classic example of the need for the property called "color " in describing particles. Since quarks are fermions with spin 1/2, they must obey the Pauli exclusion principle and cannot exist in identical states. So with three strange quarks, the property which distinguishes them must be capable of at least three distinct values.Conservation of strangeness is not in fact an independent conservation law, but can be viewed as a combination of the conservation of charge, isospin , and baryon number . It is often expressed in terms of hypercharge Y , defined by:Isospin and either hypercharge or strangeness are the quantum numbers often used to draw particle diagrams for the hadrons. Table of quark propertiesIndexParticle conceptsHyperPhysics ***** Quantum PhysicsR Nave Go BackThe Charm QuarkIn 1974 a meson called the J/Psi particle was discovered. With a mass of 3100 MeV,over three times that of the proton, this particle was the first example of another quark, called the charm quark. The J/Psi is made up of a charm-anticharm quark pair.The lightest meson which contains a charm quark is the D meson. It provides interesting examples of decay since the charm quark must be transformed into a strange quark by the weak interaction in order for it to decay.One baryon with a charm quark is a called a lambda with symbol Λ+c . It has a composition udc and a mass of 2281 MeV/c2.Table of quark properties IndexParticle conceptsHyperPhysics***** Quantum Physics R Nave Go BackThe Top QuarkConvincing evidence for the observation of the top quark was reported by Fermilab's Tevatron facility in April 1995. The evidence was found in the collision products of 0.9 TeV protons with equally energetic antiprotons in the proton-antiproton collider. The evidence involved analysis of trillions of 1.8 TeV proton-antiproton collisions. The Collider Detector Facility group had found 56 top candidates over a predicted background of 23 and the D0 group found 17 events over a predicted background of 3.8. The value for the top quark mass from the combined data of the two groups after the completion of the run was 174.3 +/- 5.1 GeV. This is over 180 times the mass of a proton and about twice the mass of the next heaviest fundamental particle, the Z0 vector boson at about 93 GeV.The interaction is envisioned as follows: IndexParticle concept sReferen ce Ladbur yD-ZeroTable of quark propertiesHyperPhysics***** Quantum Physics R Nave Go BackConfinement of QuarksHow can one be so confident of the quark model when no one has ever seen an isolated quark? There are good reasons for the lack of direct observation. Apparently the color force does not drop off with distance like the other observed forces. It is postutated that it may actually increase with distance at the rate of about 1 GeV per fermi. A free quark is not observed because by the time the separation is on an observable scale, the energy is far above the pair production energy for quark-antiquark pairs. For the U and D quarks the masses are 10s of MeV so pair production would occur for distances much less thana fermi. You would expect a lot of mesons (quark-antiquark pairs) in very high energy collision experiments and that is what is observed.Basically, you can't see an isolated quark because the color force does not let them go, and the energy required to separate them produces quark-antiquark pairs long before they are far enough apart to observe separately.One kind of visualization of quark confinement is called the "bag model". One visualizes the quarks as contained in an elastic bag which allows the quarks to move freely around, as long as you don't try to pull them further apart. But if you try to pull a quark out, the bag stretches and resists.Another way of looking at quark confinement is expressed by Rohlf. "When we try to pull a quark out of a proton, for example by striking the quark with another energetic particle, the quark experiences a potential energy barrier from the strong interaction that increases with distance." As the example of alpha decay demonstrates, having a barrier higher than the particle energy does not prevent the escape of the particle - quantum mechanical tunneling gives a finite probability for a 6 MeV alpha particle to get through a 30 MeV high energy barrier. But the energy barrier for the alpha particle is thin enough for tunneling to be effective. In the case of the barrier facing the quark, the energy barrier does not drop off with distance, but in fact increases.Evidence for quarks in deep inelastic scattering IndexParticle conceptsReferenc eRohlf Sec 6-6HyperPhysics***** Quantum Physics R Nave Go Back The Bottom QuarkIn 1977, an experimental group at Fermilab led by Leon Lederman discovered a new resonance at 9.4 GeV/c^2 which was interpreted as a bottom-antibottom quark pair and called the Upsilon meson. From this experiment, the mass of the bottom quark is implied to be about 5 GeV/c^2. The reaction being studied waswhere N was a copper or platinum nucleus. The spectrometer had a muon-pair mass resolution of about 2%, which allowed them to measure an excess of events at 9.4 GeV/c^2. This resonance has been subsequently studied at other accelerators with a detailed investigation of the bound states of the bottom-antibottom meson.Table of quark properties IndexParticle conceptsReferenc eRohlf Ch. 17HyperPhysics***** Quantum Physics R Nave Go Back。
International Journal of Numerical Modelling

INTERNATIONAL JOURNAL OF NUMERICAL MODELLING:ELECTRONIC NETWORKS,DEVICES AND FIELDS Int.J.Numer.Model.2010;23:1–19Published online6July2009in Wiley InterScience().DOI:10.1002/jnm.720 Advanced models for transient analysis of lossy and dispersiveanisotropic planar layersGiulio AntoniniÃ,yUAq EMC Laboratory,Dipartimento di Ingegneria Elettrica e dell’Informazione,Universita`degli Studi dell’Aquila,Monteluco di Roio,67040L’Aquila,ItalySUMMARYA new model is proposed for the transient analysis of the electromagneticfield propagation through anisotropic lossy and dispersive layers.The propagation equations of the electromagneticfields are solved as a Sturm–Liouville problem leading to identify its dyadic Green’s function in a series rational form. Then,the corresponding poles and residues are obtained and a reduced order macromodel is generated, which can be easily embedded within existing three dimensional solvers.The model is applied to lossy and dispersive anisotropic layers with differently polarized plane–waves.Copyright r2009John Wiley& Sons,Ltd.Received1November2008;Revised23January2009;Accepted3June2009KEY WORDS:planar anisotropic layers;lossy and dispersive media;dyadic Green’s function;transient analysis1.INTRODUCTIONComposite materials have received an increasing interest in industrial and military applications and have been suggested as substitutes for metals in modern aircrafts systems by virtue of their superior mechanical properties in strength-to-weight and modulus-to-weight ratios.They are generally laminated,anisotropic and lossy.A pioneering investigation of the electromagnetic properties of advanced composite materials is reported in[1].More recently,the characteriza-tion of the reflection,transmission and shielding properties of such materials have been presented in several studies in the frequency domain[2–4].Transient analysis of anisotropic lossy slabs can be performed using an equivalent-transmission-line-circuit[5,6].This approach*Correspondence to:Giulio Antonini,UAq EMC Laboratory,Dipartimento di Ingegneria Elettrica e dell’Informazione, Universita degli Studi dell’Aquila,Monteluco di Roio,67040,L’Aquila,Italy.y E-mail:giulio.antonini@univaq.itContract/grant sponsor:Italian Ministry of University(MIUR)under a Program for the Development of Research of National Interest;contract/grant number:2006095890Copyright r2009John Wiley&Sons,Ltd.relies on the analogy between the field equations and the coupled transmission line equations [7]and,as a consequence,the standard halt-T ladder network (HTLN)is used.On the other hand,it is known that the HTLN model contains much more information than needed [8]and a reduced order model may be more suitable for a computer implementation.Such a limitation has been overcome in [9]by adopting the vector fitting technique [10],which allows the extraction of a reduced order rational macromodel,which is interfaced to a finite difference time domain solver.In this way,thin composite structures are modeled through the use of convolution integrals avoiding their spatial discretization,which is typically a cpu-time consuming process.In [11]a new methodology for the transient analysis of plane waves obliquely incident on a planar lossy and dispersive layer has been presented.The proposed model is based on the Sturm–Liouville problem associated with the propagation equations.The Green’s function is calculated in a rational series form and the open-end impedance matrix is obtained as the sum of infinite rational functions.The rational form permits an easy identification of poles and residues.The pole–residue representation is converted into a state-space model,which can be easily interfaced with ordinary differential equation solvers.The aim of this paper is to extend the previous approach to the transient analysis of plane waves impinging on planar anisotropic lossy and dispersive layers.The TM z –TE z mode coupling generated by the anisotropy leads to a multidimensional wave propagation problem.The propagation equation within the layer is solved as a Sturm–Liouville problem where tangential electric fields are considered as unknowns and tangential magnetic fields as sources.This allows one to write the dyadic Green’s function of the problem in a rational series form from which poles and residues can be easily identified.Hence,an arbitrary large rational macromodel can be generated and used to obtain a finite state-space representation,which is well suited for computer implementation.The paper is organized as follows.In Section 2,the propagation equations of electromagnetic fields through lossy and dispersive anisotropic layers are derived and re-cast as a Sturm–Liouville problem.Then,in Section 3,the dyadic Green’s function is obtained as solution of the corresponding Sturm–Liouville problem and the impedance matrix computed.The knowledge of the rational form of the impedance matrix pawns the way to the computation of a reduced order macromodel and,finally,to a state-space realization.Sections 4presents the numerical results validating the proposed method and Section 5draws the conclusions.2.PROPAGATION OF TANGENTIAL FIELDSLet us assume that the incident electromagnetic fields is described as a uniform plane wave with angle of incidence and polarization with respect to a spherical coordinate system as illustrated in Figure 1.Free space is assumed as the background medium.The propagation vector k of the wave is incident at angles y p from the x axis and /p from the projection onto the y –z plane from the y axis,as shown in Figure 1(a).The polarization of the electric field vector is described in terms of the unit vectors in the spherical coordinate system,a y and a f ,as illustrated in Figure 1(b).The general expression for the electric field vector in the Laplace domain is:E i ¼E 0e x a x þe y a y þe z a z ÀÁe Àk x x Àk y y Àk z z ð1ÞG.ANTONINI2Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmwhere the components of the incident electric field vector (e x ,e y ,e z )can be expressed in terms of the polarization angles y E ;y p ;f p [12].The propagation vector k ¼ðkx ;ky ;kz Þhas an amplitude k ¼s =c 0¼s ffiffiffiffiffiffiffiffiffim 0e 0p ,being s the complex frequency variable.Let us consider the propagation of a obliquely impinging plane wave through an anisotropic planar layer,as shown in Figure 2.Curl Maxwell’s equations,in the Laplace domain,read:H ÂE ðr ;s Þ¼Às m ðs ÞH ðr ;s Þð2a ÞH ÂH ðr ;s Þ¼s ðs ÞE ðr ;s Þþs e ðs ÞE ðr ;s Þð2b Þwhere m ðs Þ;e ðs Þ;s ðs Þare frequency dependent tensors of the magnetic permeability,electric permittivity and electric conductivity of the layer,respectively.Assuming that the anisotropyis Figure 1.Definitions of the parameters characterizing the incident field as a uniform plane wave.Figure 2.Global coordinates and principal coordinates for an anisotropic planar layer.ADVANCED MODELS FOR TRANSIENT ANALYSIS 3Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmin the transverse plane x–y only,they are given by:m sðÞ¼m xx m xy0m yx m yy000m zz26643775ð3Þe sðÞ¼e xx e xy0e yx e yy000e zz264375ð4Þs sðÞ¼s xx s xy0s yx s yy000s zz2435ð5Þwheree xx¼e0x cos f2þe0y sin f2ð6aÞe xy¼e yx¼ðe0x Àe0yÞcos f sin fð6bÞe yy¼e0x sin f2þe0ycos f2ð6cÞe zz¼e0zð6dÞThe dependence on the Laplace variable has been omitted for the sake of clarity.Here,ðe0x ;e0y;e0zÞare the permittivities with respect to the principal axis and f is the angle between the global and the principal axis of the layer.Similar expressions are used for the conductivities s xx;s xy;ð¼s yxÞ;s yy;s zz and permeabilities m xx;m xy;ð¼m yxÞ;m yy;m zz.Since we want to obtain impedance boundary conditions which connect tangential components on the interfaces,it is convenient to separate the tangentialfield components (E t(r,s),H t(r,s))from the normal ones(E n(r,s),H n(r,s)).Hence,we can write:E¼E tþE n n H¼H tþH n nð7ÞwhereE tÁn¼0H tÁn¼0ð8ÞAnalogously,the nabla operator H and the tensors of magnetic permeability,electric permittivity and conductivity can be split into their tangential and normal components[13].In the following,a standard approach is adopted[13]by equating separately the normal components of(2),eliminating the normal components and cross multiplying by n.Finally,a first-order state equation governing the electromagneticfields in the slab can be derived asd d zE xðzÞÀE yðzÞH yðzÞH xðzÞ26666643777775¼AÁE xðzÞÀE yðzÞH yðzÞH xðzÞ26666643777775ð9ÞG.ANTONINI4Copyright r2009John Wiley&Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmwhere the matrix A is as follows:A¼00Às m yyÀk2xs zzþs e zzÀs m xyþk x k ys zzþs e zz00Às m yxþk y k xs zzþs e zzÀs m xxÀk2ys zzþs e zz!Às xxþs e xxÀk2ys m zz!ÀÀs xyÀs e xyÀk x k ys m zz00ÀÀs yxÀs e yxÀk x k ys m zzÀs yyþs e yyÀk2xs m zz002 66 66 66 66 66 66 643 77 77 77 77 77 77 75ð10ÞHence,it is possible identifying the per-unit-length impedance and admittance matrices,respectively,as:Z0ðsÞ¼s m yyÀk2xs zzþs e zzs m xyþk x k ys zzþs e zzs m yxþk y k xs zzþs e zzs m xxÀk2ys zzþs e zz26643775ð11aÞY0ðsÞ¼s xxþs e xxÀk2ys m zzÀs xyÀs e xyÀk x k ys m zzÀs yxÀs e yxÀk x k ys m zzs yyþs e yyÀk2xs m zz26643775ð11bÞThe second-order wave equation for the transverse electricfield component~E t¼ðE x;ÀE yÞimmediately follows from the transmission line equations(9),after elimination of the magnetic field and it takes the form;@2 @z2~EtÀGðsÞ~E t¼0ð12Þwhere CðsÞ¼Z0ðsÞY0ðsÞ.It is to be pointed out that thefield pairs(E x,H y)and(ÀE x,H y) corresponds to TM z and TE z polarizations.Both the polarizations exhibit a Poynting vector along the z axis;a perfect analogy with coupled transmission lines can be established,as it is presented in[5–14].It is also clearly recognized that the model presented in those papers is a special case of the methodology proposed in this work.2.1.Boundary conditionsThe system of global coordinates x,y and z can always be chosen such that k y50,as in Figure3.In this case,the component k x of the propagation vector can be related to the Laplace variable ask x¼ssin y ið13Þwhere c0is the speed of light in the background homogenous medium and y i is the incidence angle of the incident plane wave.The incidence angle y i can be expressed in terms of the polarization angle y p as:y i¼pÀy pð14ÞADVANCED MODELS FOR TRANSIENT ANALYSIS5 Copyright r2009John Wiley&Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmHence,boundary conditions need to be enforced at the two interfaces z ¼0;z ¼d ;they read:ÀE y ð0;s Þ¼À2E i y ðs ÞÀZ 0cos y iH x ð0;s Þð15a ÞÀE y ðd ;s Þ¼Z 0cos y i H x ðd ;s Þð15b Þfor the TE z polarization andE x ð0;s Þ¼2E i x ðs ÞÀZ 0cos y i H y ð0;s Þð16a ÞE x ðd ;s Þ¼Z 0cos y i H y ðd ;s Þð16b Þfor the TM z polarization.2.2.Incorporation of interface magnetic fields as sourcesMagnetic (or electric)fields at abscissa z 50and z 5d can be regarded as external sources and described in terms of distributed sourcesH ys ðz ;s Þ¼H y ð0;s Þd ðz ÞþH y ðd ;s Þd ðz Àd Þð17a ÞH xs ðz ;s Þ¼H x ð0;s Þd ðz ÞþH x ðd ;s Þd ðz Àd Þð17b Þwhere d ðz Þrepresents the Dirac delta function.The sources can be written in a vector form asH s ðz ;s Þ¼H 0ðs Þd ðz ÞþH d ðs Þd ðz Àd Þð18Þwhere H 0ðs Þ¼½H y ð0;s Þ;H x ð0;s Þ T and H d ðs Þ¼½H y ðd ;s Þ;H x ðd ;s Þ T .Following the same approach described in [11],the incorporation of such distributed source in Telegrapher’s equations (12)permits to obtain@2~E t ÀG ðs Þ~E t ¼ÀZ 0ðs ÞH s ðz ;s Þð19ÞFrom (10)it is seen that the TM z and TE z modes are coupled by both the wave vector components k x and k y ,which depend on the system of coordinates,and the anisotropy,described by the off-diagonal terms oftensors.Figure 3.Incident plane wave to the planar structure:(a)TE z polarization mode and (b)TM z polarization mode.G.ANTONINI6Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnm3.DYADIC GREEN’S FUNCTION FOR A PLANAR ANISOTROPIC LAYER Equation(19)can be regarded as a vector Sturm–Liouville problem,which,in general,can be written as½Lþl rðzÞ yðzÞ¼fðzÞð20Þwhere0z d,L is the Sturm–Liouville operator,l is a z-independent matrix,r(z)is a diagonal z-dependent matrix and f(z)is the vector of distributed sources.The boundary conditions can be either of Dirichlet or Neumann or mixed type and,in general,we can writea1yðzÞþa2dd zyðzÞz¼0j¼0ð21aÞb1yðzÞþb2dd zyðzÞz¼dj¼0ð21bÞIn the specific case of oblique incidence of plane waves on anisotropic layers,it is easy to recognize that:L¼U d2d zð22aÞl¼ÀZ0ðsÞY0ðsÞð22bÞrðzÞ¼Uð22cÞfðzÞ¼ÀZ0ðsÞH sðz;sÞð22dÞwhere U represents the identity matrix.Furthermore,since the magneticfield at the interface is already modeled through the source vector(18),boundary conditions of the Neumann type can be adopted:d d z ~Et z¼0j¼dd z~Et z¼dj¼0ð23aÞSince both TE z and TM z modes can be excited separately,two vector Green’s functions,one for each mode,are ing a dyadic notation[15]yields:G jðz;z0Þ¼X2i¼1G ij z;z0ÀÁu i j¼1;2ð24ÞThe two Green’s functions G jðz;z0Þare the solution of the equations:A G jðz;z0Þ¼½Lþl rðzÞ G jðz;z0Þ¼dðz;z0Þu j j¼1;2ð25Þwhere dðz;z0Þis the one-dimensional Dirac delta function.The dyadic Green’s function G z;z0ðÞis given by:Gðz;z0Þ¼X2j¼1G jðz;z0Þu j¼X2j¼1X2i¼1G ijðz;z0Þu i u jð26ÞADVANCED MODELS FOR TRANSIENT ANALYSIS7 Copyright r2009John Wiley&Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmwhich,with a matrix notation,can be written as:G ðz ;z 0Þ¼G 11G 12G 21G 22"#ð27ÞSince the Sturm–Liouville problem (22),along with the boundary conditions (23)is self-adjoint[16],it is possible to expand the vector Green’s function in terms of a set of basis functionsf n ðz Þas:G j ðz ;z 0Þ¼X 1n ¼0a nj ðz 0Þf n ðz Þð28Þwhere a nj is the amplitude coefficient vector.Eigenfunctions f n ðx Þsatisfy the corresponding eigenvalue problem d 2d x þk 2n !f n ðx Þ¼0ð29Þwhere the eigenvalues are all positive k 2n ¼l n 40since the Sturm–Liouville problem is self-adjoint.Furthermore,the boundary conditions are of the Neumann type:d f n ðx Þz ¼0j ¼d f nðz Þz ¼d j ¼0ð30ÞEigenvalues k n and eigenfunctions f n ðz Þ;n ¼0;1;ÁÁÁ1can be easily found as [17]:k n ¼n p d n ¼0;1;ÁÁÁ;1ð31a Þf 0ðz Þ¼ffiffiffi1dr n ¼0ð31b Þf n ðz Þ¼ffiffiffi2d r cos n p dz n ¼1;ÁÁÁ;1ð31c Þwhere the magnitude of the eigenfunctions has been computed enforcing their orthonormality Z df m ðz Þf n ðz Þd z ¼d mn ð32ÞForcing the vector Green’s function G j ðz ;z 0Þto be the solution of (25)and using the orthonormality conditions of the eigenfunctions (32),the coefficient vector a nj z 0ðÞis obtained a nj z 0ÀÁ¼l Àl n ðÞÀ1f n ðz 0Þu j j ¼1;2ð33ÞApplying the right dyadic product [15]to (33),multiplying it by u j ,and taking the sum over index j ,yields:X2j ¼1a mj z 0ÀÁu j ¼a n ðz 0Þ¼l Àl n ðÞÀ1f n ðz 0ÞX 2j ¼1u j u j¼l Àl n ðÞÀ1U f n ðz 0Þ¼l Àl n ðÞÀ1f n ðz 0ÞHence,the dyadic Green’s function (27)can be written as:G z ;z 0ÀÁ¼X 1n ¼0a n ðz 0Þf n ðz Þ¼X 1n ¼0l Àl n ðÞÀ1f n ðz 0Þf n ðz ÞG.ANTONINI8Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnm3.1.Rational macromodel of the Z impedanceThe knowledge of the dyadic Green’s function G z ;z 0ðÞin the rational form (34)pawns the way to the development of a rational macromodel of the layer.In fact,the electric field vector ~E t ¼ðE x ;ÀE y Þcan be computed as:~E t ðz ;s Þ¼Z d 0G ðz ;z 0Þf ðz 0Þd z 0ð34ÞEvaluating ~E t ðz ;s Þin correspondence to the interfaces z 50and z 5d yields ~E t ð0;s Þ~Et ðd ;s Þ2435¼Z 11Z 12Z 21Z 222435ÁH ð0;s ÞH ðd ;s Þ2435ð35Þwhere the impedance matrix Z (s )entries are:Z 11¼Z 22¼X 1n ¼0G 2ðs Þþn p d 2U !À1ÁA 2n Z 0ðs Þð36a ÞZ 21¼Z 12¼X 1n ¼0G 2ðs Þþn p d 2U !À1ÁA 2n Z 0ðs ÞÀ1ðÞn ð36b ÞIf dispersive media are considered,we assume that the physical properties of the layer are known as tabulated data,at discrete frequencies.A rational model of the per-unit-length impedance Z 0(s )and admittance Y 0(s )can be obtained by using the vector fitting algorithm [10]:Z 0ðs Þ¼s ~lþX P Z q ¼1R Z s Àp q ;Z ¼B p ðs ÞA p ðs Þ¼b 1s P Z þ1þb 2s P Z s þÁÁÁþb P Z s þb P Z þ11Z 2Z P Z À1P Zð37a ÞE x (0,s -E y (0,s )E x (d ,s )-E y (d,s )Figure 4.Planar layer macromodel.ADVANCED MODELS FOR TRANSIENT ANALYSIS 9Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmY 0s ðÞ¼~sþs ~e þX P Y q ¼1R Y s Àp q ;Y ¼D p ðs ÞC p ðs Þ¼d 1s P Y þ1þd 2s P Y s þÁÁÁþd P Y s þd P Y þ1c 1s Y þc 2s Y þÁÁÁþc P Y À1s þc P Yð37b Þ02468x 1013Real(poles)Order 20 model Reduced order model 00.51 1.5024681012141618x 1013x 1011Frequency [GHz]I m a g (p o l e s )M a g n i t u d e o f r e s i d u e s Order 20 model Reduced order modelx 104Figure 5.Location of poles in the complex plane (top)and magnitude spectrum of residues of impedance Z 14(bottom)(Section 4.1).The circle refer to the poles of the order 20model,the stars refers to the polesselected as dominant.G.ANTONINI10Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmwhere P z and P Y represent the number of poles used in the rational approximation,B p (s )and D p (s )are polynomial matrices and A p (s )and C p (s )can be made strictly Hurwitz polynomials by enforcing their zeros to be on the left complex plane,when using the vector fitting algorithm.Impedance matrix Z(s )can be recast as Z ðs Þ¼X 1n ¼0B p ðs ÞA p ðs ÞD p ðs ÞC p ðs Þþn p d 2U !À1ÁA 2n B p ðs ÞA p ðs Þ1À1ðÞn À1ðÞn 12435¼X1n ¼0B p ðs ÞD p ðs ÞþA p ðs ÞC p ðs Þn p d 2U !À1ÁA 2n B p ðs ÞC p ðs Þ1À1ðÞn À1ðÞn 12435¼X1n ¼0E p s ðÞÀ1A 2n B p ðs ÞC p ðs Þ1À1ðÞn À1ðÞn 12435ð38Þwhere E p ðs Þ¼B p ðs ÞD p ðs ÞþA p ðs ÞC p ðs Þn p d ÀÁ2U .The entries of impedance matrix Z (s )are strictlyproper rational functions and share the same poles,which can be evaluated as the zeros of the characteristic polynomial Q n (s):Q n ðs Þ¼det B p ðs ÞD p ðs ÞþA p ðs ÞC p ðs Þn p d2U !¼0ð39Þfor n ¼0;...;1.Each mode n generates a number of poles depending on the order of the rational approximations (37a)and (37b):~n poles ;n ¼order conv ðB p ;D p ÞÂÃÁ2¼P Z þP Y þ2ðÞÁ2ð40Þ05101520100Frequency [GHz]|G 14|Figure 6.Magnitude spectrum of the Green’s function G 14(Section 4.1).The solid line refers to the result obtained considering all the poles (GF),the dashed line refers to the reduced order model (GF-mor).Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmwhere conv denotes the product of polynomials in argument and order is the order of the polynomial in argument.The corresponding residues can be computed,using standard techniques [18],asR k ¼adj E ðs ÞðÞA 2n B p ðs ÞC p ðs Þs ¼p n ðk ÞQ n 1Q poles l ¼1ð77Þl ¼k p n ðk ÞÀp n ðl Þ½Á1À1ðÞn À1ðÞn 1"#ð41Þ202530354045500.20.40.60.81Time [ns]E i [V /m ]Figure 8.Incident electric field (Section 4.1).05101520101.895101.896Frequency [GHz]|Z 14| []Figure 7.Magnitude spectrum of impedance Z 14(Section 4.1).The solid line corresponds to the result obtained with use of the plane waves theory (PWT),the dashed line refers to the results obtained by using the proposed methodology (GF),the dashdot line refers to the proposed methodology considering only thedominant poles (GF-mor).Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmfor k ¼0;...;n poles ,where adj ðÁÞrepresents the adjoint operator of the matrix in argument,p n (k )is the k -th pole generated by the n -th mode and Q n 1denotes the coefficient of the highest power in s in polynomial matrix E p (s ).Once poles and residues of the rational representation of matrix Z(s )are obtained,a pole pruning can be performed and the n d poles dominant poles identified,following the criteria illustrated in [8].The impedance matrix Z(s )can be re-written in a pole/residue form asZ ðs Þ¼Xn d polesk ¼1R k s Àp k ð42Þ0.020.040.060.08Time [ns]E [V /m ]0.020.04Time [ns]E [V /m ]Figure 9.Transmitted electric field for the TE z (top)and TM z (bottom)polarizations (Section 4.1).The solid line corresponds to the result obtained with use of the PWT via IFFT,the dashdot line refers to theresults obtained using the proposed methodology in the time domain (GF-TD).Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmwhich is suited for both circuit synthesis [19]and state-space realization [20,21].The equivalent circuit can be analyzed by means of SPICE-like solvers [22];the state-space equations can be written as_x ðt Þ¼Ax ðt ÞþBH ðt Þð43a Þ~Et ðt Þ¼Cx ðt ÞþDH ðt Þð43b Þwhere A 2<n d poles Ân d poles ,B 2<n d poles Â4,C 2<4Ân d poles ,D 2<4Â4,n d poles being the number of theselected dominant poles (Figure 4).4.NUMERICAL RESULTS4.1.Anisotropic lossy layer-TE polarizationIn the first example,a TE z polarized plane wave is assumed impinging with incidence angle y i ¼p =3on a planar composite layer exhibiting anisotropy due to the presence of conducting fibers (see Figure 2).The planar layer is 0.5mils thick and characterized by electrical conductivity s x 54Â104S/m and s y 5s z 550S/m and permittivity e x ¼e y ¼e z ¼5e 0,in the local system of coordinates.The orientation of fibers,with respect to the global system of coordinates,is defined by f ¼p =4.The magnetic permeability is assumed equal to that of vacuum.A rational model of order 21has been generated;the computation has been carried out on a AMD Athlon 2GHz processor,equipped with 1.5Gb RAM and took 2.5s,leading to 84poles among which only 29have been selected as dominant.Figure 5(top)shows the location of poles in the complex plane.The selection of the dominant poles has been accomplished on the base of their resonance frequency and the magnitude of the corresponding residues,as shown in Figure 5(bottom).0246810103104105106Frequency [GHz]|Z 13| []PWTGFFigure 10.Magnitude spectrum of impedance Z 13(Section 4.2).The solid line corresponds to the result obtained with use of the PWT,the dashed line refers to the results obtained by using the proposedmethodology (GF).Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnmFigure 6shows the comparison of the magnitude spectrum of the Green’s function G 14as evaluated considering all the poles and only the dominant ones.Figure 7shows a sample of the magnitude spectrum of impedance Z 14as evaluated by the plane wave theory (PWT)and the proposed Green’s function-based methodology.A satisfactory agreement is obtained over the entire frequency bandwidth of interest.The layer is excited by a TE z polarized plane wave whose time behavior is shown in Figure 8.Due to the anisotropy,transmitted electric field is characterized by both TE z and TM z modes,shown in Figure 9.The results have been computed by using the PWT via IFFT4550550.10.20.30.40.5Time [ns]E [V /m]45505512345Time [ns]E [V /m]Figure 11.Transmitted electric field for the TM z (top)and TE z (bottom)polarizations (Section 4.2).The solid line corresponds to the result obtained with use of the PWT via IFFT,the dashdot line refers to theresults obtained using the proposed methodology in the time domain (GF-TD).Copyright r 2009John Wiley &Sons,Ltd.Int.J.Numer.Model.2010;23:1–19DOI:10.1002/jnm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :n u c l -t h /0302073v 2 7 M a r 2003In-medium vector meson masses in a Chiral SU(3)modelD.Zschiesche,1,∗A.Mishra,1,†S.Schramm,2H.St¨o cker,1and W.Greiner 11Institut f¨u r Theoretische Physik,Robert Mayer Str.8-10,D-60054Frankfurt am Main,Germany2Argonne National Laboratory,9700S.Cass Avenue,Argonne IL 60439,USA(Dated:February 8,2008)Abstract A significant drop of the vector meson masses in nuclear matter is observed in a chiral SU(3)model due to the effects of the baryon Dirac sea.This is taken into account through the summation of baryonic tadpole diagrams in the relativistic Hartree approximation.The appreciable decrease of the in-medium vector meson masses is due to the vacuum polarisation effects from the nucleon sector and is not observed in the mean field approximation.1.INTRODUCTIONThe medium modifications of the vector mesons(ρandω)in hot and dense matter have recently been a topic of great interest in the strong interaction physics research,both experimentally[1,2,3,4,5]and theoretically[6,7,8,9,10,11,12].One of the explanations of the experimental observation of enhanced dilepton production[1,2,3]in the low invariant mass regime could be a reduction in the vector meson masses in the medium.It wasfirst suggested by Brown and Rho that the vector meson masses drop in the medium according to a simple(BR)scaling law[6],given as m∗V/m V=f∗π/fπ.fπis the pion decay constant and the asterisk refers to in-medium quantities.There have also been QCD sum rule approaches extensively used in the literature[8,9,10,11]for consideration of the in-medium vector meson properties.In the framework of Quantum Hadrodynamics(QHD)[13]as a description of the hadronic matter,it is seen that the dropping of the vector meson masses has its dominant contribution arising from the vacuum polarisation effects in the baryon sector [14,15,16,17].This drop is not observed in the meanfield approximation.The vector meson properties[18]and their effects on the low mass dilepton spectra[19]have been investigated recently including the quantum correction effects from the baryon as well as the scalar meson sectors in the Walecka model[20].In the present investigation we use the SU(3)chiral model[21,22]for the description of the hadronic matter.This model has been shown to successfully describe hadronic properties in the vacuum as well as nuclear matter,finite nuclei and neutron star properties.Furthermore the model consistently includes the lowest lying baryon and meson multiplets,including the vector mesons.In the meanfield approximation the vector meson masses do not show any significant drop,similar to results in the Walecka model.The effect of the Dirac sea is taken into account by summing over baryonic tadpole diagrams in the relativistic Hartree approximation(RHA).It is seen that an appreciable decrease of the vector meson masses arises from the nucleon Dirac sea.This shows the importance of taking into account these contributions.We organize the paper as follows:In section2we introduce the chiral SU(3)model used in the present investigation.Section3describes the meanfield approximation for nuclear matter.In section4the nuclear matter properties are considered in the relativistic Hartree approximation.Section5gives the in-medium vector meson properties due to thecontributions from the nucleon Dirac sea.The results are presented and discussed in section 6.Finally,in section7we summarize thefindings of the present work.2.THE HADRONIC CHIRAL SU(3)×SU(3)MODELWe consider a relativisticfield theoretical model of baryons and mesons built on chiral symmetry and broken scale invariance[21,22].A nonlinear realization of chiral symmetry is adopted,that has been successful in a simultaneous description offinite nuclei and hyperon potentials[21].The general form of the Lagrangian is as follows:L=L kin+ W=X,Y,V,A,u L BW+L VP+L vec+L0+L SB.(1) L kin is the kinetic energy term,L BW includes the interaction terms of the baryons with the spin-0and spin-1mesons,the former generating the baryon masses.L VP contains the inter-action terms of vector mesons with pseudoscalar mesons.L vec generates the masses of the spin-1mesons through interactions with spin-0fields and contains quartic self-interactions of the vector-fields.L0gives the meson-meson interaction terms which induce the sponta-neous breaking of chiral symmetry.It also includes a scale-invariance breaking logarithmic potential.Finally,L SB introduces an explicit symmetry breaking of the U(1)A,SU(3)V and chiral symmetry.2.1.Kinetic TermsThe kinetic energy terms are given as[21]L kin=i Tr2Tr DµXDµX+Tr(uµXuµX+XuµuµX)+12DµχDµχ−14Tr(FµνFµν)−11As described in section2.3,the vector mesons need to be renormalized.The physicalfields will be denoted as Vµandρµ,ωµ,φµrespectively and the unrenormalized,mathematicalfields as˜Vµand˜ρµ,˜ωµ,˜φ.of the axial vector uµ=−iπaλaγ5 is the unitary2σ0transformation operator[21].The pseudoscalar mesons are given as parameters of the symmetry transformation.Since thefields in the nonlinear realization of chiral symmetry contain the local unitary transformation operator,covariant derivatives Dµ=∂µ+i[Γµ,], withΓµ=−i2g W8 αW[B O BW]D −g W113Tr(B O BW]F:=Tr(B O BW)and[B O W B+Tr(36g S8.In this case the nucleon mass does depend only on the nonstrange condensateσ.Furthermore,the coupling constants between the baryons and the two scalar condensates are related to the additive quark model.Thisleaves only one coupling constant free that is adjusted to give the correct nucleon mass [21].For a fine-tuning of the remaining masses,it is necessary to introduce an explicit symmetry breaking term,which breaks the SU(3)-symmetry along the hypercharge direction (for details see [21]).Therefore the resulting baryon octet masses for the current investigation read:m N =−g Nσσ0m Λ=−g Nσ 23√3m Σ=−g Nσ 23√3σ0−22ζ0 +m 1+m 2.(5)Alternative ways of mass generation have also been considered earlier [21].2.2.2.Baryon -vector meson interactionTwo independent interaction terms of baryons with spin-1mesons can be constructed in analogy with the baryon-spin-0-meson interaction.They correspond to the antisymmetric (f -type)and symmetric (d -type)couplings,respectively.The general couplings are shown in [21].From the universality principle [23]and the vector meson dominance model one may conclude that the d -type coupling should be small.Here we will use pure f -type coupling,i.e.αV =1for all fits,even though a small admixture of d-type coupling allows for some fine-tuning of the single particle energy levels of nucleonsin nuclei (see [21]).As for thecase with scalar mesons,we furthermore set g V 1=√sγµs does not couple to the nucleon.The resulting Lagrangian reads:L BV =−√BγµB ˜V µ]F +Tr(ψN γµψN +g V 8˜ ρµ2.3.Meson-meson interactions2.3.1.Vector mesonsThe vector meson-meson interactions contain the mass terms of the vector mesons and higher order vector meson self-interactions.The simplest scale invariant mass term isL(1)vec=1χ2Tr˜Vµ˜Vµ.(8)It implies a mass degeneracy for the vector meson nonet.The scale invariance is assured by the square of the glueballfieldχ(see sec. 2.3.2for details).To split the masses,one can add the chiral invariants[24,25]L(2)vec=112λV Tr ˜Vµν 2.(10) Note that in9,we replace the scalar multiplet X by its vacuum expectation -bining the contributions(9,10)with the kinetic energy term(2),one obtains the following terms for the vector mesons in the vacuum−14Z−1ω ˜Vµν˜ω 2−12 ;Z−1ω,φ= 1−µ(σ20+2ξ20)−2λV2D1/2 (12)whereD=µ23µ(σ20−2ξ20).(13)Then the Lagrangian for the newfields in the vacuum reads L vac vec==−12χ2denote the vector meson masses in the ing m V=687.33MeV,µσ20=0.41andλV=−0.041,the correctω-,ρ-andφ-masses are obtained.The vector meson self-interactions[26]readL(4)vec=2(˜g4)4Tr(˜Vµ˜Vµ)2.(16) The coupling of this self-interaction term is also modified by the redefinition of thefields.Theredefined coupling corresponding to the quartic interaction for theωfield can be expressed interms of the coupling˜g4of the term(16).This term gives a contribution to the vector-mesonmasses in the medium,i.e.forfinite values of theωorρ-fields.The resulting expressionsfor the vector meson masses in the medium(isospin symmetric)arem∗ω2=m2ω+12g44ω2(17)Zρm∗ρ2=m2ρ+12g44φ2,(19)Z2ω√with g4=Zωandg Nρ≡g8Vk0χ2I2+k1(I2)2+k2I4+2k3χI3,(20)2with I2=Tr(X+iY)2,I3=det(X+iY)and I4=Tr(X+iY)4.Furthermoreχdenotesa scalar color-singlet gluonfield.It is introduced to construct the model to satisfy theQCD trace anomaly,i.e.the nonvanishing of the trace of the energy-momentum tensorθµµ=βQCDAll the terms in the Lagrangian are multiplied by appropriate powers of the glueball-field to obtain a dimension(Mass)4in thefields.Then all coupling constants are dimensionless and therefore the model is scale invariant[28].Then,a scale breaking potentialL scalebreak=−1χ40+δdet X 0(21)is introduced.This yieldsθµµ=(1−δ)χ4.By identifying theχ-field with the gluon condensate and the choiceδ=6/33for threeflavors and three colors withβQCD as given by the one loop level,the correct trace anomaly is obtained.Thefirst term in(21)corresponds to the contribution of the gluons and the second term describes the contribution from the quarks to the trace anomaly.Finally the termLχ=−k4χ4(22) generates a phenomenologically consistentfinite vacuum expectation value.The parameters k0,k2and k4,are used to ensure an extremum in the vacuum for the σ-,ζ-andχ-field equations,respectively.As for the remaining constants,k3is constrained by theηandη′-masses,which take the values mη=520MeV and mη′=999MeV in all parameter sets.k1isfixed in the meanfieldfit with quartic vector meson interaction such that the effective nucleon mass at saturation density is around0.65m N and theσ-mass is of the order of500MeV.Then it is kept constant in all the otherfits,since a change in k1yields quite a strong modification of the other coupling constants in the selfconsistency calculation.Since we want to focus on the influence of the Hartree terms,we try to keep everything else as less modified as possible.Since the shift in theχin the medium is rather small[21],we will in good approximation setχ=χ0.We will refer to this case as the frozen glueball limit.The VEV of the gluon condensate,χ0,isfixed tofit the pressure p=0at the saturation densityρ0=0.15fm−3.2.4.Explicitly broken chiral symmetryIn order to eliminate the Goldstone modes from a chiral effective theory,explicit symmetry breaking terms have to be introduced.Here,we again take the corresponding term of the linearσ-modelL SB=1with A p =1/√√ψN [g Nωγ0ω+m ∗N ]ψN(25)L vec =1χ20ω2+g 44ω4(26)V 0=12+ζ4)−k 3χσ2ζ+k 4χ4+1χ40−δσ20ζ0(27)V SB =χ2m 2K f K −12m 2πf π)ζ ,(28)where m ∗N is the effective mass of the nucleon.Only the scalar (L BX )and the vector meson terms (L BV )contribute to the baryon-meson interaction.For all other mesons,the expec-tation value vanishes in the mean-field approximation.Now it is straightforward to write down the expression for the thermodynamical potential of the grand canonical ensemble,Ω,per volume V at a given chemical potential µand at zero temperature:Ω(2π)3√k 2N +m ∗N2and the effective chemical potential reads µ∗N =µN −g Nωω.The mesonic fields are determined by extremizing the thermodynamic potential.Since weuse the frozen glueball approximation(i.eχ=χ0),we have coupled equations only for the fieldsσ,ζandωin the selfconsistent calculation given as∂(Ω/V)3σ++m2πfπ+∂m∗N∂ζ=k0χ2ζ−4k1(σ2+ζ2)ζ−4k2ζ3−k3χσ2−δχ42m2K f K−12m2πfπ=0,(31)∂(Ω/V)(2π)3m∗N4π2 k F N E∗F N−m∗2N lnk F N+E∗F N(2π)3=γN k3F N16π2 m∗N4ln m∗N2m2N(m N−m∗N)2+1312(m N−m∗N)4 ,(35)ParameterLagrange-term L BM2Tr(BBX ]Fg V 8g V 8√BγµB )Tr V µ+[E/A (ρ0)=−16MeV ,g Nω≡3g V 8Z ωL (1)vec2m 2Vχ2µ1m ω,m ρ,m φλV 1g 42g 44Tr V µV µk 0−1∂Ωm ∗N /m N ,m σk 2k 2I 4∂ζ|vac=0k 32k 3χI 3∂Ω3χ4lnI 3βQCDχ0m π,m KL esb2Tr A p u (X +iY )u +u †(X +iY )u † 3σ+m 2πf π+∂m ∗N4π2 m ∗N3ln m ∗N 2m N (m N −m ∗N )2+11equations forσ,ζandχhave minima at the vacuum expectation values of thefields.Table II shows the parameters corresponding to the the Mean-field and the Hartree approximations.Parameter Hartree2.701.4 1.4g Nω10.519.37g Nρ 3.50 3.12χ0430.2446k3-2.07-1.732.37 2.07-5.55-5.55-0.23-0.230.640.71475.6560.2266.1359.529.027.4TABLE II:Parameters for the Mean-Field and the Hartree Fit5.VECTOR MESON PROPERTIES IN THE MEDIUM5.1.In-medium vector meson massesWe now examine how the Dirac sea effects discussed in section4modify the masses of the vector mesons.Rewriting the expression for the vector interaction of these mesons given in equation(6)in terms of the renormalized couplings g Nωand g NρyieldsL N BV=g NωωµψNγµ τψN.(38) Furthermore a tensor coupling is introduced:L tensor=−g NVκVwhere (g NV ,κV )=(g Nω,κω)or (g Nρ,κρ)and τa =1or τ,for V µa =ωµor ρµa , τbeing the Pauli matrices.The vector meson self energy is given asΠµνV (k )=−γI g 2NVi¯k 2−m ∗2N+iǫ+iπ3Re(Πren F )µµ=−g 2Nωm N 2−k 2z (1−z ).(43)and for the ρmeson,ΠρF (k 2)=−g 2Nρ2m NI 2+12m N2(k 2I 1+m ∗N 2I 2)(44)where,I 1=1dzz (1−z )lnm ∗N2−k 2z (1−z )m N 2−k 2z (1−z ).(45)The density dependent part for the self energy is given as ΠD(k0,k→0)=−4g2NVǫ∗(p)(4ǫ∗(p)2−k20) 22mN+22m N 2(|p|2+3m∗N2)(47)whereǫ∗(p)=(p2+m∗N2)1/2is the effective energy for the nucleon.The effective mass of the vector meson is then obtained by solving the equation,withΠ=ΠF+ΠD,k20−m2V+ReΠ(k0,k=0)=0.(48)5.2.Meson decay propertiesWe next proceed to study the vector meson decay widths as modified due to the effect of vacuum polarisation effects through RHA.The decay width for the processρ→ππis calculated from the imaginary part of the self energy and in the rest frame of theρ-meson, it becomesΓρ(k0)=g2ρππk201+f(k02) −f(k02) (49)where,f(x)=[eβx−1]−1is the Bose-Einstein distribution function.Thefirst and the second terms in the above equation represent the decay and the formation of the resonance,ρ.The medium effects have been shown to play a very important role for theρ-meson decay width.In the calculation for theρdecay width,the pion has been treated as free,i.e. any modification of the pion propagator due to effects like delta-nucleon hole excitation[30] have been neglected.The coupling gρππisfixed from the decay width ofρmeson in vacuum (Γρ=151MeV)decaying into two pions.For the nucleon-rho couplings,the vector and tensor couplings as obtained from the N-N forward dispersion relation[15,17,31]are used.With the couplings as described above,we consider the modification ofωandρmeson properties in nuclear matter due to quantum correction effects.To calculate the decay width for theω-meson,we consider the following interaction Lagrangian for theωmeson[32,33,34]Lω=gωπρm3ǫµναβǫijkωµ∂νπi∂απj∂βπk.(50)πThe decay width of theω-meson in vacuum is dominated by the channelω→3π.In the medium,the decay width forω→3πis given as(2π)4Γω→3π=,p i and E i’s are4-momenta and energies for the pions,and f(E i)’s are (2π)32E itheir thermal distributions.The matrix element M fi has contributions from the channels ω→ρπ→3π(described by thefirst term in(50))and the direct decayω→3πresulting from the contact interaction(second term in(50))[34,35,36].For theωρπcoupling we take the value gωρπ=2which is compatible to the vacuum decay widthω→πγ[17].Wefix the point interaction coupling gω3πbyfitting the partial decay widthω→3πin vacuum(7.49 MeV)to be0.24.The contribution arising from the direct decay turns out to be marginal, being of the order of upto5%of the total decay width forω→3π.With the modifications of the vector meson masses in the hot and dense medium,a new channel becomes accessible,the decay modeω→ρπfor m∗ω>m∗ρ+mπ.This has been taken into account in the present investigation.6.RESULTS AND DISCUSSIONSWe shall now discuss the results of the present investigation:the nucleon properties as modified due to the Dirac sea contributions through the relativistic Hartree approximation and their effects on vector meson properties in the dense hadronic matter.Figure1shows the equation of state in the Mean-Field-and in the Hartree-approximation with and without quartic self-interaction for theω-field.In both cases we observe that the additional terms resulting from the Hartree approximation lead to a softening of the equation of state at higher densities.However,the compressibilty in the relativistic Hartree-approximation is higher than the mean-field value,as shown in table II.Furthermore,the influence of the finite value for the quarticωcoupling,g4is clearly visible.In this case the compressibilityB /0E /A -m N [M e V ]B /0E /A -m N [M e V ]FIG.1:Binding energy per particle as a function of density in the Mean-Field and in the Hartree-Approximation.at nuclear saturation is strongly reduced (table II).Also,the resulting equation of state is much softer in particular at higher densities.The reason for this can be seen from figure 2.The vector field ω,which causes the repulsion in the system,rises much more steeply as a function of density for g 4=0than for the case of g 4=2.7,because the quartic self-interaction attenuates the ω-field.The effective nucleon mass for the different cases is depicted in figure 3.Here the RHA predicts higher nucleon masses than the Mean-Field case.At higher densities these contribu-tions become increasingly important.This is also reflected in the density dependence of the non-strange σfield,showing a considerable increase due to the Hartree contributions (fig-ure2).In contrast,the strange condensate,ζ,which does not couple to the nucleons,takes only slightly lower values in the MF-case.The in-medium properties of the vector mesons are modified due to the vacuum polarization effects.The nucleon-ωvector coupling,g Nω,is calculated from the nuclear matter saturation properties.As already stated,the N-ωtensor coupling is neglected.Figure 4shows the resulting modification of the ω–meson mass in the Hartree approximation as compared to the mean field case.For g 4=0,the ωmass has no density dependence,because of the frozen glueball approximation.In contrast,a strong re-B /0F i e l d sB /0F i e l d sFIG.2:Scalar fields σ,ζand vector field ωas a function of density in the Mean-Field and in the Hartree-Approximation.B /m N */m NB /m N */m NFIG.3:Effective nucleon mass as a function of density in the Mean-Field and in the Hartree-Approximation.B /01.01.2m */B /0m */FIG.4:Effective ωmeson mass in the mean field approximation and including the Hartreecontributions.Left:no quartic vector-meson interaction.Right:Including ω4interaction.There is significant drop of the vector meson mass due to the Dirac sea effect,which is not seen in the mean field approximation.duction due to the Dirac sea polarization is found for densities up to around normal nuclear matter density.At higher densities,the Fermi polarization part of the ω-self-energy starts to become important,leading to an increase in the mass.A similar behaviour has been observed in the Walecka model [14,15,16].The quartic term in the ω-field considerably enhances the ωmass with increasing density.Thus in the mean field case,the mass rises monotonically.For the Hartree approximation a decrease of the ωmass for small densities can still be found.But at higher densities the contribution from the quartic term becomes more important and leads to an increase of the in-medium mass.In figure 5,we illustrate the medium modification for the ρmeson mass with the vector and tensor couplings to the nucleons being fixed from the NN forward dispersion relation[15,17,31].The values for these couplings are given as g 2Nρ/4π=0.55and κρ=6.1.We noticethat the decrease in the ρmeson with increasing density is much sharper than that of the ωmeson.Such a behaviour of the ρmeson undergoing a much larger medium modification was also observed earlier [17]within the relativistic Hartree approximation in the WaleckaB /0m */mB /0m /mFIG.5:Effective ρmeson mass without and with the Hartree contributions,with the nucleon-rho vector and tensor couplings,as fitted from the NN scattering data (g Nρ=2.63,κρ=6.1).The Hartree approximation gives rise to the decrease of the ρmass in the medium.model.This indicates that the tensor coupling,which is negligible for the ωmeson,plays a significant role for the ρmeson.The in-medium decay width for ρ→ππ,Γ∗ρreflects the behaviour of the in-medium ρmass.This is because in the present work only the case T =0is considered,and so there is no Bose-enhancement effect.Therefore in the absence of the quartic vector-meson interaction,the significant drop of the mass of the ρmeson in the medium leads to a decrease of the ρdecay width.This is shown in figure 6.Since the quartic self-interaction yields an increase in the mass at higher densities,it leads to an increase of the ρdecay width.In the previous calculations,the ρ-N coupling strengths were used as determined from the NN forward scattering data [31].Now we consider the mass modification for the ρmeson,with the nucleon ρcoupling,g Nρas determined from the symmetry relations (table II).The symmetry energy coefficient a sym is given as [37]a sym =1∂t 2ǫρ0.The resulting values for the symmetry energy for the different cases areB /0150*B /0FIG.6:Decay width of ρmeson in the absence and presence of the Dirac sea effect with thecouplings fitted from the NN scattering data.shown in table II.They are compatible with the experiment.We take the tensor coupling as a parameter in our calculations since this coupling cannot be fixed from infinite nuclear matter properties.However,it influences the properties of finite nuclei.The resulting in-medium mass of the ρmeson is plotted in figure 7as a function of baryon density ρB /ρ0.It is observed that the ρmeson mass has a strong dependence on the tensor coupling.In the Hartree approximation the ρ-nucleon vector coupling does not differ too much in the two cases,i.e.depending on whether it is obtained fromm NN scattering data or from the symmetry relations.Thus we find a similar behaviour for the ρmass,if in the latter case we choose κρ=6,i.e.close to the value from scattering data.Figure 8shows the decay width for the ρmeson when we take the Nρvector coupling as determined from symmetry relations and the tensor coupling taken as a parameter.The decay width of the ωmeson is plotted as a function of density in figure 9.In the vacuum the process ω→3πis the dominant decay mode.However,in the medium the channel ω→ρπalso opens up,since the ρ-meson has a stronger drop in the medium as compared to the ωmeson mass.The mean field approximation,does not have a contribution from the latter decay channel,B /0m */mB /0m /mFIG.7:Effective ρmeson mass without and with the Hartree contributions,with the nucleon-rho vector coupling,g Nρ,as from the chiral model,which is compatible with the symmetry energy.Since we do not know the medium dependent tensor coupling,κρ,it is taken as a parameter.The Hartree approximation gives rise to the decrease of the ρmass in the medium,which is seen to be quite sensitive to the nucloen-rho tensor coupling.whereas the inclusion of relativistic Hartree approximation permits both processes in the medium.In the presence of the quartic vector meson interaction,the channel ω→ρπ,which opens up at around 0.3ρ0,no longer remains kinematically accessible at higher densities.This is due to the increased importance of ω4contributions to the vector meson masses at high densities.The strong enhancement of the ωmeson mass in the presence of a quartic self interactionterm for the ωfield,makes also the decay channel ω→N ¯Nkinematically accessible in the mean field approximation.In the present investigation the vector meson properties are considered at rest.Vector mesons with a finite three momentum can also have additional decay channels to particle hole pairs.These decay modes,e.g,have significant contributions,to the ∆decay width [38].Additional channels that open up in the mean field approximation in the presence of a quartic term for ω,however,have not been taken into consideration in the present work.Here the emphasis is on the effect due to the relativistic HartreeB /0150 *B /0150FIG.8:Decay width ofρmeson in the absence and presence of the Dirac sea effect with the nucleon-rho vector coupling,gρN,as from the chiral model,which is compatible with the symmetry energy.The tensor coupling,κρis taken as a parameter.approximation on the in-medium vector meson properties.Figure10illustrates the decay width of theω-meson when the medium dependence of the ρN vector coupling is taken into account and the tensor coupling is taken as a parameter. The strong dependence of theρmeson properties on the tensor coupling are reflected in the ω-decay width through the channelω→ρπ.7.SUMMARYTo summarize,in the present paper we have considered the modification of the vector meson properties due to vacuum polarisation effects arising from the Dirac sea in nuclear matter in the chiral SU(3)model.The baryonic properties as modified due to such effects determine the vector meson masses in dense hadronic matter.A significant reduction of these masses in the medium is found,where the Dirac sea contribution dominates over the Fermi sea part.This shows the importance of the vacuum polarisation effects for the vector meson properties,as has been emphasized earlier within the framework of QuantumB /0100 *B /0100*FIG.9:Effective decay width ofωmeson without and with the Hartree contributions.The decay width has contributions fromω→3πas well asω→ρπ.The latter becomes accessible due to stronger medium modification of theρmeson mass as compared to theωmass.The MFT has no contribution from the processω→ρπ.Hadrodynamics[15,16].Theρ-meson mass is seen to have a sharper drop as compared to theω-meson mass in the medium.This reflects the fact that the vector meson-nucleon tensor coupling,which is absent for theω-meson,plays an important role for theρ-mass.The decay width ofρ→ππis modified appreciably due to the modification of theρmass.The effects discussed above influence observables infinite nuclei,stellar objects and rela-tivistic heavy ion collisions.For example the modified vector meson properties in a medium play an important role in the dilepton emission rates in relativistic heavy ion collisions[39]. This is reflected by the shift and broadening of the peaks in the low invariant mass regime in the dilepton spectra.Therefore,it will be important to investigate how the dilepton rates are modified by the in-medium vector meson properties in the hot and dense hadronic mat-ter.This necessitates the extension of the current work tofinite temperatures.Furthermore, it will be worthwhile to study,how the analysis of particle ratios for relativistic heavy ion collisions in[40]is affected by the Hartree contributions.These and related problems are。
