2021年中考数学重难点专项突破专题50 圆中的翻折综合问题(解析版)
2021年九年级数学中考复习专题之圆的综合(考察切线证明、长度、面积、动点问题等)(含答案)

2021年九年级数学中考复习专题之圆的综合(考察切线证明、长度、面积、动点问题等)1.如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.(1)求证:∠ADC=∠ABD;(2)求证:AD2=AM•AB;(3)若AM=,sin∠ABD=,求线段BN的长.2.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.3.如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.(1)求证:PA是⊙O的切线;(2)若=,且OC=4,求PA的长和tan D的值.4.如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.(1)求证:直线CD为⊙O的切线;(2)若AB=5,BC=4,求线段CD的长.5.如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE(1)求证:△ABC∽△CBD;(2)求证:直线DE是⊙O的切线.6.如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.(1)求证:四边形ABCE是平行四边形;(2)若AE=6,CD=5,求OF的长.7.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.8.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状: ;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.9.如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°.①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)10.如图,△ABC中,∠C=90°,点G是线段AC上的一动点(点G不与A、C重合),以AG为直径的⊙O交AB于点D,直线EF垂直平分BD,垂足为F,EF交BC于点E,连结DE.(1)求证:DE是⊙O的切线;(2)若cos A=,AB=8,AG=2,求BE的长;(3)若cos A=,AB=8,直接写出线段BE的取值范围.答案1.(1)证明:连接OD,∵直线CD切⊙O于点D,∴∠CDO=90°,∵AB为⊙O的直径,∴∠ADB=90°,∴∠1+∠2=∠2+∠3=90°,∴∠1=∠3,∵OB=OD,∴∠3=∠4,∴∠ADC=∠ABD;(2)证明:∵AM⊥CD,∴∠AMD=∠ADB=90°,∵∠1=∠4,∴△ADM∽△ABD,∴,∴AD2=AM•AB;(3)解:∵sin∠ABD=,∴sin∠1=,∵AM=,∴AD=6,∴AB=10,∴BD==8,∵BN⊥CD,∴∠BND=90°,∴∠DBN+∠BDN=∠1+∠BDN=90°,∴∠DBN=∠1,∴sin∠NBD=,∴DN=,∴BN==.2.解:(1)∵⊙M经过O、A、B三点,且∠AOB=90°,∴AB为直径∵点A为(,0),点B为(0,﹣),∴OA=,OB=,∴AB==2,∴⊙M的半径为:;(2)∵∠COD=∠CBO,∠COD=∠CBA,∴∠CBO=∠CBA,即BD平分∠ABO;(3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA 于点F,即AE是切线,∵在Rt△AOB中,tan∠OAB===,∴∠OAB=30°,∴∠ABO=90°﹣∠OAB=60°,∴∠ABC=∠OBC=∠ABO=30°,∴OC=OB•tan30°=×=,∴AC=OA﹣OC=,∴∠ACE=∠ABC+∠OAB=60°,∴∠EAC=60°,∴△ACE是等边三角形,∴AE=AC=,∴AF=AE=,EF=AE=,∴OF=OA﹣AF=,∴点E的坐标为:(,).3.(1)证明:连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵=,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO==2,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC•PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3,∴PB=PA=3,∵AC=BC,OA=OE,∴OC=BE,OC∥BE,∴BE=2OC=8,BE∥OP,∴△DBE∽△DPO,∴,即,解得:BD=,在Rt△OBD中,tan∠D===.(补充方法:可以证明△DBE∽△DAB,可得===,由此解决问题,可以简单一些)4.(1)证明:连接OC,∵∠CEA=∠CBA,∠AEC=∠ODC,∴∠CBA=∠ODC,又∵∠CFD=∠BFO,∴∠DCB=∠BOF,∵CO=BO,∴∠OCF=∠B,∵∠B+∠BOF=90°,∴∠OCF+∠DCB=90°,∴直线CD为⊙O的切线;(2)解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠DCO=∠ACB,又∵∠D=∠B∴△OCD∽△ACB,∵∠ACB=90°,AB=5,BC=4,∴AC=3,∴=,即=,解得;DC=.5.(1)证明:∵AC为⊙O的直径,∴∠ADC=90°,∴∠BDC=90°,又∵∠ACB=90°,∴∠ACB=∠BDC,又∵∠B=∠B,∴△BCD∽△BAC;(2)连结DO,如图,∵∠BDC=90°,E为BC的中点,∴DE=CE=BE,∴∠EDC=∠ECD,又∵OD=OC,∴∠ODC=∠OCD,而∠OCD+∠DCE=∠ACB=90°,∴∠EDC+∠ODC=90°,即∠EDO=90°,∴DE⊥OD,∴DE与⊙O相切.6.(1)证明:∵AE与⊙O相切于点A,∴∠EAC=∠ABC,∵AB=AC∴∠ABC=∠ACB,∴∠EAC=∠ACB,∴AE∥BC,∵AB∥CD,∴四边形ABCE是平行四边形;(2)解:如图,连接AO,交BC于点H,双向延长OF分别交AB,CD与点N,M,∵AE是⊙O的切线,由切割线定理得,AE2=EC•DE,∵AE=6,CD=5,∴62=CE(CE+5),解得:CE=4,(已舍去负数),∵AB∥CD,∴∠BAD=∠ADC,∴=,∴AC=BD,∴AB=AC=BD=CE=4,又根据对称性和垂径定理,得AO垂直平分BC,MN垂直平分AB,DC,设OF=x,OH=Y,FH=z,∵AB=4,BC=6,CD=5,∴BF=BC﹣FH=3﹣z,DF=CF=BC+FH=3+z,易得△OFH∽△DFM∽△BFN,∴,,即,①②,①+②得:,①÷②得:,解得,∵x2=y2+z2,∴,∴x=,∴OF=.7.(1)证明:连接OD,∵OB=OD,∴∠ABC=∠ODB,∵AB=AC,∴∠ABC=∠ACB,∴∠ODB=∠ACB,∴OD∥AC,∵DF是⊙O的切线,∴DF⊥OD,∴DF⊥AC.(2)解:连接OE,∵DF⊥AC,∠CDF=22.5°,∴∠ABC=∠ACB=67.5°,∴∠BAC=45°,∵OA=OE,∴∠AOE=90°,∵⊙O的半径为4,∴S扇形AOE=4π,S△AOE=8 ,∴S阴影=4π﹣8.8.证明:(1)△ABC是等边三角形.证明如下:在⊙O中∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;(2)在PC上截取PD=AP,如图1,又∵∠APC=60°,∴△APD是等边三角形,∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,在△APB和△ADC中,,∴△APB≌△ADC(AAS),∴BP=CD,又∵PD=AP,∴CP=BP+AP;(3)当点P为的中点时,四边形APBC的面积最大.理由如下,如图2,过点P作PE⊥AB,垂足为E.过点C作CF⊥AB,垂足为F.∵S△APB=AB•PE,S△ABC=AB•CF,∴S四边形APBC=AB•(PE+CF),当点P为的中点时,PE+CF=PC,PC为⊙O的直径,∴此时四边形APBC的面积最大.又∵⊙O的半径为1,∴其内接正三角形的边长AB=,∴S四边形APBC=×2×=.9.解:(1)直线BC与⊙O相切;连结OD,∵OA=OD,∴∠OAD=∠ODA,∵∠BAC的角平分线AD交BC边于D,∴∠CAD=∠OAD,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.又∵直线BC过半径OD的外端,∴直线BC与⊙O相切.(2)设OA=OD=r,在Rt△BDO中,∠B=30°,∴OB=2r,在Rt△ACB中,∠B=30°,∴AB=2AC=6,∴3r=6,解得r=2.(3)在Rt△ACB中,∠B=30°,∴∠BOD=60°.∴.∵∠B=30°,OD⊥BC,∴OB=2OD,∴AB=3OD,∵AB=2AC=6,∴OD=2,BD=2S △BOD=×OD•BD=2,∴所求图形面积为.10.(1)证明:连接OD,如图,∵△ABC中,∠C=90°,∴∠A+∠B=90°,∵直线EF垂直平分BD,∴ED=EB,∴∠B=∠EDB,∵OA=OD,∴∠A=∠ODA,∴∠ODA+∠EDB=90°,∴∠ODE=90°,∴OD⊥DE,∴DE是⊙O的切线;(2)解:连接GD,∵AG为直径,∴∠ADG=90°,∵cos A=,∴∠A=60°,∴∠AGD=30°,∴AD=AG=,∵AB=8,∴BD=AB﹣AD=8﹣=7,∵直线EF垂直平分BD,∴BF=BD=,在Rt△BEF中,∠B=30°,∴EF=BF=,∴BE=2EF=7;(3)解:∵cos A=,∴∠A=60°,∴∠B=30°,∴AC=AB=4,由(2)得AD=AG,BF =(AB﹣AD)=4﹣AG,在Rt△BEF中,∠B=30°,∴EF=BF,∴BE=2EF=BF=(4﹣AG)=8﹣AG,∵0<AG<AC,即0<AG<4,∴6<BE<8.。
2021年九年级数学中考一轮复习专题突破训练:几何压轴—圆的综合(二)及答案

2021年九年级数学中考一轮复习专题突破训练:几何压轴—圆的综合1.如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE.(1)求证:直线PQ为⊙O的切线;(2)若直径AB的长为4.①当PE=时,四边形BOPQ为正方形;②当PE=时,四边形AEOP为菱形.2.已知AB是⊙O的直径,DA为⊙O的切线,切点为A,过⊙O上的点C作CD∥AB交AD于点D,连接BC、AC.(1)如图①,若DC为⊙O的切线,切点为C,求∠ACD和∠DAC的大小.(2)如图②,当CD为⊙O的割线且与⊙O交于点E时,连接AE,若∠EAD=30°,求∠ACD和∠DAC的大小.3.已知AB为⊙O的直径,点C为⊙O上一点,点D为AB延长线一点,连接AC.(Ⅰ)如图①,OB=BD,若DC与⊙O相切,求∠D和∠A的大小;(Ⅱ)如图②,CD与⊙O交于点E,AF⊥CD于点F连接AE,若∠EAB=18°,求∠FAC 的大小.4.如图,在等腰三角形ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,过点C作⊙O的切线交AB的延长线于点P.(1)求证:∠CAB=2∠BCP;(2)若⊙O的直径为5,sin∠BCP=,求△ABC内切圆的半径;(3)在(2)的条件下,求△ACP的周长.5.如图,△ABC中,∠ACB=90°,AC=3,BC=4,延长BC到点D,使BD=BA,P是BC边上一点.点Q在射线BA上,PQ=BP,以点P为圆心,PD长为半径作⊙P,交AC 于点E,连接PQ,设PC=x.(1)AB=,CD=,当点Q在⊙P上时,求x的值;(2)x为何值时,⊙P与AB相切?(3)当PC=CD时,求阴影部分的面积;(4)若⊙P与△ABC的三边有两个公共点,直接写出x的取值范围.6.如图1,以AB为直径作⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C作∠ACB的平分线交⊙O于点D,过点D作AB的平行线交CB的延长线于点E.(1)如图1,连结AD,求证:∠ADC=∠DEC.(2)若⊙O的半径为5,求CA•CE的最大值.(3)如图2,连结AE,设tan∠ABC=x,tan∠AEC=y,①求y关于x的函数解析式;②若=,求y的值.7.如图,AB是⊙O的直径,CD是⊙O的一条弦,=,CO的延长线交⊙O于点E,交BD的延长线于点F,连接FA,且恰好FA∥CD,连接BE交CD于点P,延长BE交FA于点G,连接DE.(1)求证:FA是⊙O的切线;(2)求证:点G是FA的中点;(3)当⊙O的半径为6时,求tan∠FBE的值.8.如图1,Rt△ABC中,∠ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点为E(点E在点P右侧),连结DE、BE,已知AB=3,BC=6.(1)求线段BE的长;(2)如图2,若BP平分∠ABC,求∠BDE的正切值;(3)是否存在点P,使得△BDE是等腰三角形,若存在,求出所有符合条件的CP的长;若不存在,请说明理由.9.如图,AB是半圆O的直径,C是半圆O上一点(不与点A、B重合),D是的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.(1)求证:∠FCD=∠ADE;(2)填空:①当∠FCD的度数为时,四边形OADC是菱形;②若AB=2,当CF∥AB时,DF的长为.10.如图,在∠DAM内部做Rt△ABC,AB平分∠DAM,∠ACB=90°,AB=10,AC=8,点N为BC的中点,动点E由A点出发,沿AB运动,速度为每秒5个单位,动点F由A 点出发,沿AM运动,速度为每秒8个单位,当点E到达点B时,两点同时停止运动,过A、E、F作⊙O.(1)判断△AEF的形状为,并判断AD与⊙O的位置关系为;(2)求t为何值时,EN与⊙O相切?求出此时⊙O的半径,并比较半径与劣弧长度的大小;(3)直接写出△AEF的内心运动的路径长为;(注:当A、E、F重合时,内心就是A点)(4)直接写出线段EN与⊙O有两个公共点时,t的取值范围为.(参考数据:sin37°=,tan37°=,tan74°≈,sin74°≈,cos74°≈)参考答案1.(1)证明:∵OQ∥AP,∴∠EOC=∠OAP,∠POQ=∠APO,又∵OP=OA,∴∠APO=∠OAP,又∵∠BOQ=∠EOA=∠OAP,∴∠POQ=∠BOQ,在△BOQ与△POQ中,,∴△POQ≌△BOQ(SAS),∴∠OPQ=∠OBQ=90°,∵点P在⊙O上,∴PQ是⊙O的切线;(2)解:①∵△POQ≌△BOQ,∴∠OBQ=∠OPQ=90°,当∠BOP=90°,四边形OPQB为矩形,而OB=OP,则四边形OPQB为正方形,此时点C、点E与点O重合,PE=PO=AB =2;②∵PE⊥AB,∴当OC=AC,PC=EC,四边形AEOP为菱形,∵OC=OA=1,∴PC===,∴PE=2PC=2.故答案为:2;2.2.解:(1)∵AB是⊙O的直径,DA为⊙O的切线,切点为A,∴DA⊥AB,∴∠DAB=90°,∵DC为⊙O的切线,切点为C,∴DC=DA,∵CD∥AB,∴∠D+∠DAB=180°,∴∠D=90°,∴∠ACD=∠DAC=45°;(2)∵AB是⊙O的直径,DA为⊙O的切线,切点为A,∴DA⊥AB,∴∠DAB=90°,∠DEA=∠EAB,∴∠ADC=90°,∵∠EAD=30°,∴∠DEA=60°,∴∠EAB=60°,∴∠BCE=120°,∵AB是⊙O的直径,∴∠BCA=90°,∴∠ACD=30°,∴∠DAC=60°.3.解:(Ⅰ)如图①,连接OC,BC,∵AB为⊙O的直径,∴∠ACB=90°,∵DC与⊙O相切,∴∠OCD=90°,∵OB=BD,∴BC=OD=OB=BD,∴BC=OB=OC,∴△OBC是等边三角形,∴∠OBC=∠OCB=∠COB=60°,∴∠BCD=∠OCA=30°,∴∠D=∠A=30°;(Ⅱ)如图②,连接BE,∵AB为⊙O的直径,∴∠AEB=90°,∵AF⊥CD,∴∠AFC=90°,∵∠ACF是圆内接四边形ACEB的外角,∴∠ACF=∠ABE,∴∠FAC=∠EAB=18°,答:∠FAC的大小为18°.4.解:(1)如图,连接AN,∵AC为直径,∴AN⊥BC,∵AB=AC,∴AN平分∠BAC,∵PC是圆的切线,∴∠ACP=90°,∵∠NAC+∠ACB=∠PCB+∠ACB=90°,∴∠NAC=∠BCP,即∠BAC=2∠BCP;(2)由(1)知,AN平分∠BAC,则∠NAC=∠BCP,故sin∠NAC=sin∠BCP=,则tan∠NAC=,在Rt△NAC中,AC=5,NC=AC•sin∠NAC=5×=,同理AN=2,则BC=2NC=2;S=×BC•AN=2×2=10,△ABC设△ABC内切圆的半径为r,则S=(AB+AC+BC)•r=×(5+5+2)•r=10,△ABC解得:r=;故△ABC内切圆的半径为;(3)在△ABC中,设AC边长的高为h,则S=AC•h=×5×h=10,解得:h=4,△ABCsin∠BAC==,在Rt△ACP中,∵sin∠BAC==,设PC=4m,则AP=5m,则AC=3m=5,解得m=,△ACP的周长=3m+4m+5m=12m=20.5.解:(1)∵△ABC中,∠ACB=90°,AC=3,BC=4,∴AB=5,∵BD=BA,∴BD=5,∴CD=1.故答案为:5,1;当点Q在⊙P上时,如图1,PQ=PD.∴BP=PD,即4﹣x=x+1.解得x=.(2)作PF⊥AB于点F,当PF=PD时,⊙P与AB相切,如图2,则PF=PD=x+1,sin B==,∴=.解得x=.经检验,x=是分式方程的解,且满足题意.∴x=时,⊙P与AB相切.(3)如图3,连接PE,∵Rt△PEC中,PC=CD=1,PE=PD=1+1=2,∴∠EPC=60°,EC=.∴S阴影=S扇形PDE﹣S△PCE=﹣×1×=﹣.(4)由图2可知,当0≤x<时,⊙P与△ABC的三边有两个公共点;由图1可知,当<x<4时,⊙P与△ABC的三边有两个公共点.∴x的取值范围为:0≤x<或<x<4.6.(1)证明:∵AB∥DE,∴∠ABC=∠E,∵∠ADC=∠ABC,∴∠ADC=∠E;(2)解:∵CD平分∠ACB,∴∠ACD=∠DCE,又∠ADC=∠E,∴△ADC∽△DEC,∴,即CD2=CA•CE,又∵⊙O的半径为5,∴CA•CE=CD2≤102=100.即CA•CE的最大值为100.(3)解:①连接AD,∵△ADC∽△DEC,,∴y=tan∠AEC=,过点D作DF⊥CE,不妨设EF=a,∵∠CED=∠CBA,∠DCE=45°,∴CF=DF=ax,∴CD=ax,∴y==.②∵,∴,∴=9:4,即x:y=9:4,将y=x代入y=得,,解得,x1=2,x2=,当x=2时,y=,当x=时,y=,∴y=或.7.(1)证明:∵AB是⊙O的直径,CD是⊙O的一条弦,=,∴AB⊥CD,又∵FA∥CD,∴FA⊥AB,∵OA过O,∴FA是⊙O的切线;(2)证明:连接AE,∵AB是⊙O的直径,∴AE⊥BG,又∵FA⊥AB,∴∠GEA=∠BAG,又∵∠BGA=∠EGA,∴△GAB∽△GEA,∴=,∴GA2=GB×EG,∵FA∥CD,∴∠C=∠EFG,又∵∠C=∠FBE,∴∠EFG=∠FBE,又∵∠FGE=∠BGF,∴△FEG∽△BFG,∴=,∴GF2=GB×GE,∴GF=GA,∴G为AF的中点;(3)解:∵FA∥CD,∴==,又∵GF=GA,∴DP=HP,又∵CE是⊙O的直径,D在圆上,∴CD⊥DE,又∵AB⊥CD于点H,EO=OC,∴点H是CD的中点,AB∥DE,又∵DP=HP,∴DE=BH,又∵点O是CE中点,点H是CD的中点,∴OH=DE=BH,又∵⊙O的半径为6,∴OH=2,CH===4,∴tan∠FBE=tan C===.8.解:(1)∵∠ABC=90°,AB=3,BC=6,∴AC===3,∵BP为⊙O的直径,∴∠BEP=90°,∴BE⊥AC,∵S=×AB×AC,△ABC∴BE=;(2)∵BP平分∠ABC,∴∠DBP=∠ABC=45°,连接DP,如图1,∵BP为⊙O的直径,∴∠DBP=∠DPB=45°,∴可设DP=BD=x,∵∠CDP=∠ABC=90°∴PD∥AB,∴△CPD∽△CAB,∴=2,∴CD=2x,∴CB=3x=6,∴x=2,∴DP=BD=2,CD=4,∴CP===2,∴CE===,∴tan∠BDE=tan∠BPE===3.(3)解:存在这样的点P.由△DCP∽△BCA,得,,∴CP=CD,若△BDE是等腰三角形,可分三种情况:①当BD=BE时,BD=BE=,∴CD=BC﹣BD=6﹣,∴CP==3﹣3.②当BD=DE时,此时点D是Rt△CBE斜边的中点,∴CD=BC=3,∴CP=;③当DE=BE时,作EH⊥BC于点H,则H是BD的中点,∵∠ABC=∠EHC=90°,∴EH∥AB,∴,又∵AE=AC﹣CE=3﹣=,∴BH=DH==,∴CD=6﹣=,∴CP=.综上所述,△BDE是等腰三角形,符合条件的CP的长为3﹣3或或.9.(1)证明:连接OC、AC.如图1所示:∵D是的中点,∴=,∴DA=DC,∴∠DAC=∠DCA.∵OA=OC,∴∠OAC=∠OCA.∴∠DAC+∠OAC=∠DCA+∠OCA,即∠OAD=∠OCD.∵CF是半圆O的切线,∴CF⊥OC,∴∠FCD+∠OCD=90°,∵DE⊥AB,∴∠ADE+∠OAD=90°,∴∠FCD=∠ADE.(2)解:①当∠FCD的度数为30°时,四边形OADC是菱形;理由如下:连接OD,如图2所示:∵∠FCD=30°,∴∠ADE=30°,∵DE⊥AB,∴∠OAD=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OA,∠AOD=60°,∵D是的中点,∴=,∴∠AOD=∠COD=60°,∵OC=OD,∴△COD是等边三角形,∴CD=OD=OC,∴OA=AD=CD=OC,∴四边形OADC是菱形;故答案为:30°;②连接OD,如图3所示:∵AB=2,∴OA=OD=,∵CF∥AB,DE⊥AB,∴CF⊥EF,∴∠CFD=90°=∠DEA,在△ADE和△DCF中,,∴△ADE≌△DCF(AAS),∴AE=DF,DE=CF,∵CF半圆O的切线,∴CF⊥OC,∴四边形OCFE是矩形,∴CF=OE,∴DE=OE,∴△ODE是等腰直角三角形,∴OE=OD=1,∴DF=AE=OA﹣OE=﹣1;故答案为:﹣1.10.解:(1)过点E作EH⊥AF于H,连接OA、OE、OH,如图1所示:∵∠ACB=90°,AB=10,AC=8,∴BC===6,设运动时间为t,则AE=5t,AF=8t,∵∠AHE=∠ACB=90°,∠EAH=∠BAC,∴△EAH∽△BAC,∴=,即:=,∴AH=4t,∴FH=AF﹣AH=8t﹣4t=4t,∴AH=FH,∵EH⊥AF,∴△AEF是等腰三角形,∴E为的中点,∠EAF=∠EFA,∵AH=FH,∴OH⊥AC,∴E、H、O三点共线,∴∠OAF+∠AOE=90°,∵AB平分∠DAM,∴∠DAE=∠EAF=∠EFA,∵∠AOE=2∠EFA,∴∠AOE=∠DAE+∠EAF=∠DAF,∴∠DAF+∠OAF=90°=∠DAO,即OA⊥AD,∵OA为⊙O的半径,∴AD与⊙O相切;故答案为:等腰三角形,相切;(2)连接OA、OF、OE,OE于AC交于H,如图2所示:由(1)知:EH⊥AC,∵EN与⊙O相切,∴∠OEN=90°,∵∠ACB=90°,∴四边形EHCN为矩形,∴EH=NC,在Rt△AHE中,EH===3t,∴NC=3t,∵点N为BC的中点,∴BC=2NC=6t,∵BC=6,∴6t=6,∴t=1,∴AH=4,EH=3,设⊙O的半径为x,则OH=x﹣3,在Rt△AOH中,由勾股定理得:OA2=OH2+AH2,即x2=(x﹣3)2+42,解得:x=,∴⊙O的半径为,∴OH=,∴tan∠AOH==,∴∠AOH=74°,∵∠AOH=60°时,△AOE是等边三角形,AE=OA,74°>60°,∴AE>OA,∴劣弧长度的大于半径;(3)当点E运动到B点时,t=10÷5=2,∴AF =2×8=16,AE =EF =AB =10, 此时△AEF 的内心记为G ,当A 、E 、F 重合时,内心为A 点,∴△AEF 的内心运动的路径长为AG ,作GP ⊥AE 于P ,GQ ⊥EF 于Q ,连接AG 、GF ,则CG =PG =NQ ,如图3所示: S △AEF =AF •BC =×16×6=48,设CG =PG =NQ =a ,则S △AEF =S △AGF +S △AEB +S △FEG =AF •CG +AE •PG +EF •GQ =×(16+10+10)a =48,解得:a =,在Rt △AGC 中,AC 2+CG 2=AG 2,即82+()2=AG , ∴AG =, 故答案为:;(4)分别讨论两种极限位置,①当EN 与⊙O 相切时,由(2)知,t =1;②当N 在⊙O 上,即ON 为⊙O 的半径,连接OA 、ON 、OE ,OE 交AC 于H ,过点O 作OK ⊥BC 于K ,如图4所示: 则四边形OKCH 为矩形,OA =OE =ON ,∴OH =CK ,AH =4t ,EH =3t ,设⊙O 的半径为x ,则在Rt △AOH 中,AH 2+OH 2=OA 2,即(4t )2+(x ﹣3t )2=x 2,解得:x =t , ∴OH =CK =t ﹣3t =t ,在Rt △OKN 中,OK 2+KN 2=ON 2,即(8﹣4t )2+(3+t )2=(t )2, 解得:t =,∴线段EN 与⊙O 有两个公共点时,t 的取值范围为:1<t ≤,故答案为:1<t≤.。
专题50 圆中的翻折综合问题(解析版)
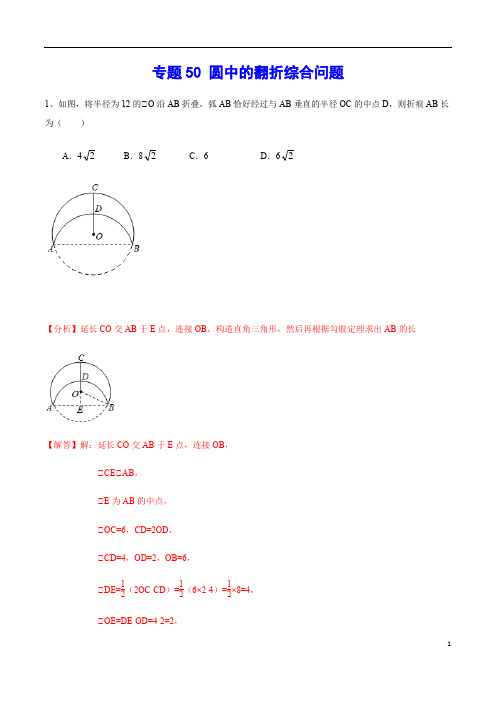
专题50 圆中的翻折综合问题1、如图,将半径为12的⊙O 沿AB 折叠,弧AB 恰好经过与AB 垂直的半径OC 的中点D ,则折痕AB 长为( )A .42B .82C .6D .62【分析】延长CO 交AB 于E 点,连接OB ,构造直角三角形,然后再根据勾股定理求出AB 的长【解答】解:延长CO 交AB 于E 点,连接OB ,⊙CE⊙AB ,⊙E 为AB 的中点,⊙OC=6,CD=2OD ,⊙CD=4,OD=2,OB=6,⊙DE=12(2OC -CD )=12(6×2-4)=12×8=4,⊙OE=DE -OD=4-2=2,在Rt⊙OEB 中,⊙OE 2+BE 2=OB 2, ⊙BE=22OE OB -=2246-42 ⊙AB=2BE=82.故选:B .【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.2、已知如图:⊙O 的半径为8cm ,把弧AmB 沿AB 折叠使弧AmB 经过圆心O ,再把弧AOB 沿CD 折叠,使弧COD 经过AB 的中点E ,则折线CD 的长为( )A .8cmB .38cmC .72cmD .47cm【分析】连接OE 并延长交CD 于点F ,交C′D′于点F′,交弧AmB 于点G ,根据翻折的性质得出OF′=6,再由勾股定理得出.【解答】解:连接OE 并延长交CD 于点F ,交C′D′于点F′,交弧AmB 于点G ,⊙OC′=8cm ,⊙OF′=6cm ,⊙C′F′=CF=2268 =27cm ,F ⊙CD=2CD=47cm .故选:D .【点评】本题考查了垂径定理和勾股定理以及翻折的性质,是基础知识要熟练掌握.3、如图,AB 是⊙O 的直径,且AB=4,C 是⊙O 上一点,将弧AC 沿直线AC 翻折,若翻折后的圆弧恰好经过点O ,π≈314,2≈1.41,3≈1.73,那么由线段AB 、AC 和弧BC 所围成的曲边三角形的面积与下列四个数值最接近的是( )A .3.2B .3.6C .3.8D .4.2【分析】作OE⊙AC 交⊙O 于F ,交AC 于E ,根据折叠的性质得到OE=12OF ,求出⊙ACB 的度数即可解决问题.【解答】解:作OE⊙AC 交⊙O 于F ,交AC 于E .连接OB ,BC .由折叠的性质可知,EF=OE=12OF , ⊙OE=12OA ,在Rt⊙AOE 中,OE=12OA , ⊙⊙CAB=30°,⊙AB 是直径,⊙⊙ACB=90°,⊙BOC=2⊙BAC=60°,⊙AB=4,⊙BC=12AB=2,AC=3BC=23, ⊙线段AB 、AC 和弧BC 所围成的曲边三角形的面积为S=12•AC•BC+S 扇形OBC -S ⊙OBC =12×23×2+60π•22360-43×22=3+23π≈3.8,故选:C .【点评】本题考查的是翻折变换的性质、圆周角定理,折叠是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.4、如图,将⊙O 的劣弧︵ AB 沿AB 翻折,D 为优弧︵ADB 上一点,连接AD ,交︵ AB 于点C ,连接BC 、BD ;若BC=5,则BD= .【分析】根据圆周角定理、翻转变换的性质得到⊙ADB=⊙BCD ,根据等腰三角形的判定定理解答.【解答】解:由翻转变换的性质可知,⊙ADB 所对的弧是劣弧︵ AB ,⊙CAB 所对的弧是劣弧︵ BC ,⊙CBA 所对的弧是劣弧︵ AC ,⊙⊙ADB=⊙CAB+⊙CBA ,由三角形的外角的性质可知,⊙BCD=⊙CAB+⊙CBA ,⊙⊙ADB=⊙BCD ,⊙BD=BC=5,故答案为:5.【点评】本题考查的是翻转变换的性质、圆周角定理的应用,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.5、如图,AB 是⊙O 的直径,且AB=4,C 是⊙O 上一点,将弧AC 沿直线AC 翻折,若翻折后的圆弧恰好经过点O ,π≈314,2≈1.41,3≈1.73,那么由线段AB 、AC 和弧BC 所围成的曲边三角形的面积与下列四个数值最接近的是( )A .3.2B .3.6C .3.8D .4.2【分析】作MN 关于直线AN 的对称线段M′N ,交半圆于B',连接AM 、AM′,构造全等三角形,然后利用勾股定理、割线定理解答.【解答】解:如图,作MN 关于直线AN 的对称线段M′N ,交半圆于B',连接AM 、AM′,可得M 、A 、M′三点共线,MA=M′A ,MB=M′B′=4,M′N=MN=10.连接AB',⊙四边形AMNB'是圆内接四边形,⊙⊙M'AB'=⊙M'NM ,⊙⊙M'=⊙M',⊙⊙M'AB'⊙⊙M'NM ,⊙M′A M′N =M′B′M′M⊙M′A•M′M=M′B′•M′N ,即M′A•2M′A=4×10=40.则M′A 2=20,又⊙M′A 2=M′N 2-AN 2,⊙20=100-AN 2, ⊙AN=45.故选:B .【点评】此题将翻折变换、勾股定理、割线定理相结合,考查了同学们的综合应用能力,要善于观察图形特点,然后做出解答.6、如图,是一个圆心角为90°的扇形,AO=2cm ,点P 在半径AO 上运动,点Q 在弧AB 上运动,沿PQ 将它以上的部分向下翻折,使翻折后的弧恰好过点O ,则OP 的最大距离为 .【分析】作O 关于PQ 的对称点O′,O′恰好落在⊙O 上,于是得到OP=12R cos⊙POE,推出⊙OO′Q 为等边三角形,根据等边三角形的性质得到OQ=O′Q=OO′=R ,当cos⊙POE 最小时,⊙POE 最大,当⊙QOB=0°时,⊙POE=30°于是得到结论.【解答】解:作O 关于PQ 的对称点O′,O′恰好落在⊙O 上,⊙OP=12R cos⊙POE, ⊙⊙OO′Q 为等边三角形,⊙OQ=O′Q=OO′=R ,⊙POE+⊙QOB=30°,当cos⊙POE 最小时,⊙POE 最大,当⊙QOB=0°时,⊙POE=30°,⊙OP=1cos30°=332.故答案为:332.【点评】本题考查了翻折变换-折叠问题,等边三角形的判定和性质,正确的在才辅助线是解题的关键.7、如图,⊙O的半径为5,弦AB的长为8,将沿直线AB折叠,折叠后如右图,则⊙O到所作的圆的切线OC的长为()A.22B.5 C.3 D.11【分析】根据题意先画出图形,可知翻转过后的弧AB所在的圆和⊙O全等,且两个圆的圆心相距为6,又已知圆的半径,故根据勾股定理即可求出答案.【解答】解:根据题意画出图形如下所示:BD=4,OB=5,点O′为翻转过后的弧AB所在圆的圆心,则有O′D=OD=2245-=3.又O′C=5,O′O=6, ⊙OC=22C ′O O ′O -=2256-=11.故选:D .【点评】本题考查了翻转变换、垂径定理及圆的切线的性质,难度不大,找出翻转过后的弧AB 所在圆的圆心是解题关键.8、如图,将弧BC 沿弦BC 折叠交直径AB 于点D ,若AD=6,DB=7,则BC 的长是( )A .91B .37C .134D .130【分析】连接CA 、CD ,根据翻折的性质可得弧CD 所对的圆周角是⊙CBD ,再根据AC 弧所得的圆周角也是⊙CBA ,然后求出AC=CD ,过点C 作CE⊙AB 于E ,根据等腰三角形三线合一的性质可得AE=ED=12AD ,根据直径所对的圆周角是直角可得⊙ACB=90°,然后求出⊙ACE 和⊙CBE 相似,根据相似三角形对应边成比例求出CE 2,再求出BE ,然后利用勾股定理列式计算即可求出BC .【解答】解:如图,连接CA 、CD , 根据折叠的性质,弧CD 所对的圆周角是⊙CBD , ⊙弧AC 所对的圆周角是⊙CBA ,⊙CBA=⊙CBD ,⊙AC=CD (相等的圆周角所对的弦相等),过点C 作CE⊙AB 于E , 则AE=ED=12AD=12×6=3, ⊙BE=BD+DE=7+3=10, ⊙AB 是直径,⊙⊙ACB=90°, ⊙CE⊙AB ,⊙⊙ACB=⊙AEC=90°,⊙⊙A+⊙ACE=⊙ACE+⊙BCE=90°,⊙⊙A=⊙BCE ,⊙⊙ACE⊙⊙CBE ,⊙AE CE = CE BE, 即CE 2=AE•BE=3×10=30, 在Rt⊙BCE 中,BC=22CE BE + =30102+= 130,故选:D .【点评】本题考查了翻折的性质,相似三角形的判定与性质,圆的性质,等腰三角形的判定与性质,作辅助线并求出AC=CD 是解题的关键.9、如图,在⊙O 中,点C 在优弧 AB ︵ 上,将弧︵ BC 沿BC 折叠后刚好经过AB 的中点D ,连接AC ,CD .则下列结论中错误的是( )A .AC=CDB .︵ AC +︵ BD =︵ BCC .OD⊙ABD .CD 平分⊙ACB【分析】A 、作辅助线,构建折叠的性质可得AD=CD ;B 、相等两弧相加可作判断;C 、根据垂径定理可作判断;D 、延长OD 交⊙O 于E ,连接CE ,根据垂径定理可作判断.【解答】解:A 、过D 作DD'⊙BC ,交⊙O 于D',连接CD'、BD',由折叠得:CD=CD',⊙ABC=⊙CBD',⊙AC=CD'=CD ,故⊙正确;B 、⊙AC=CD',⊙︵ AC =︵ CD′ ,由折叠得:︵ BD =︵ BD ′,⊙︵ AC +︵ BD =︵ BC ,故⊙正确;C 、⊙D 为AB 的中点,⊙OD⊙AB ,故⊙正确;D 、延长OD 交⊙O 于E ,连接CE ,⊙OD⊙AB ,⊙⊙ACE=⊙BCE ,⊙CD 不平分⊙ACB ,故⊙错误;故选:D .【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理和垂径定理.11、如图,⊙ABC 内接于⊙O ,BC=22,⊙BAC=45°,将劣弧︵ AB 和︵ AC 分别沿直线AB 、AC 折叠后交于点M ,点S 、T 是弦AB 、AC 上的动点,则⊙MST 的周长的最小值为( )A .22B .4C .24D .8【分析】作点M关于AB的对称点M′,关于AC的对称点M″,根据折叠的性质得到点M′,M″在圆周上,连接M′M″,交AB于S,交AC于T,则⊙MST的周长最小,连接AM′,AM″,OB,OC,根据圆周角定理得到M′M″是⊙O的直径,即可得到结论.【解答】解:作点M关于AB的对称点M′,关于AC的对称点M″,⊙将劣弧AB和AC分别沿直线AB、AC折叠后交于点M,⊙点M′,M″在圆周上,连接M′M″,交AB于S,交AC于T,则⊙MST的周长最小,连接AM′,AM″,OB,OC,则⊙M′AM″=2⊙BAC,⊙⊙BAC=45°,⊙⊙M′AM″=⊙BOC=90°,⊙BC=22,⊙OB=2,⊙M′M″=2OB=4,⊙⊙MST的周长的最小值为4,故选:B.【点评】本题考查了三角形的外接圆与外心,轴对称-最短路线问题,翻折变换(折叠问题),圆周角定理,勾股定理,正确的作出辅助线是解题的关键.12、如图,在⊙O 中,点C 在优弧⊙ACB 上,将弧沿⊙BC 折叠后刚好经过AB 的中点D ,若⊙O 的半径为5,AB=4,则BC 的长是 .【分析】连接OD 、AC 、DC 、OB 、OC ,作CE⊙AB 于E ,OF⊙CE 于F ,如图,利用垂径定理得到OD⊙AB ,则AD=BD=12AB=2,于是根据勾股定理可计算出OD=1,再利用折叠的性质可判断弧AC 和弧CD 所在的圆为等圆,则根据圆周角定理得到︵ AC =︵ CD ,所以AC=DC ,利用等腰三角形的性质得AE=DE=1,接着证明四边形ODEF 为正方形得到OF=EF=1,然后计算出CF 后得到CE=BE=3,于是得到BC=32.【解答】解:连接OD 、AC 、DC 、OB 、OC ,作CE⊙AB 于E ,OF⊙CE 于F ,如图,⊙D 为AB 的中点,⊙OD⊙AB ,⊙AD=BD=12AB=2, 在Rt⊙OBD 中,OD=22BD OB -=222)5(-=1,⊙将弧︵ BC 沿BC 折叠后刚好经过AB 的中点D .⊙︵ AC 和︵ CD 所在的圆为等圆,⊙︵ AC =︵ CD ,⊙AC=DC ,⊙AE=DE=1,易得四边形ODEF 为正方形,⊙OF=EF=1,在Rt⊙OCF 中,CF=22OF CO -=221)5(-=2,⊙CE=CF+EF=2+1=3,而BE=BD+DE=2+1=3, ⊙BC=32.故答案为32.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理和垂径定理.14、如图,AB 是半径为2的⊙O 的弦,将︵ AB 沿着弦AB 折叠,正好经过圆心O ,点C 是折叠后的︵ AB 上一动点,连接并延长BC 交⊙O 于点D ,点E 是CD 的中点,连接AC ,AD ,EO .则下列结论:⊙⊙ACB=120°,⊙⊙ACD 是等边三角形,⊙EO 的最小值为1,其中正确的是 .(请将正确答案的序号填在横线上)【分析】根据折叠的性质可知,结合垂径定理、三角形的性质、同圆或等圆中圆周角与圆心的性质等可以判断⊙⊙是否正确,EO 的最小值问题是个难点,这是一个动点问题,只要把握住E 在什么轨迹上运动,便可解决问题.【解答】解:如图1,连接OA 和OB ,作OF⊙AB .由题知:︵ AB 沿着弦AB 折叠,正好经过圆心O⊙OF=OA=12OB ⊙⊙AOF=⊙BOF=60°⊙⊙AOB=120°⊙⊙ACB=120°(同弧所对圆周角相等)⊙D=12⊙AOB=60°(同弧所对的圆周角是圆心角的一半) ⊙⊙ACD=180°-⊙ACB=60°⊙⊙ACD是等边三角形(有两个角是60°的三角形是等边三角形)故,⊙⊙正确下面研究问题EO的最小值是否是1如图2,连接AE和EF⊙⊙ACD是等边三角形,E是CD中点⊙AE⊙BD(三线合一)又⊙OF⊙AB⊙F是AB中点即,EF是⊙ABE斜边中线⊙AF=EF=BF即,E点在以AB为直径的圆上运动.所以,如图3,当E、O、F在同一直线时,OE长度最小此时,AE=EF,AE⊙EF⊙⊙O的半径是2,即OA=2,OF=1⊙AF=3(勾股定理)⊙OE=EF-OF=AF-OF=3-1所以,⊙不正确综上所述:⊙⊙正确,⊙不正确.故答案为⊙⊙.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.14、如图,将︵ AB 沿着弦AB 翻折,C 为翻折后的弧上任意一点,延长AC 交圆于D ,连接BC .(1)求证:BC=BD ;(2)若AC=1,CD=4,︵ AB =120°,求弦AB 的长和圆的半径.【分析】(1)作点C 关于AB 的对称点C′,连接AC′,BC′.利用翻折不变性,以及圆周角定理即可解决问题;(2)连接OA ,OB ,作OM⊙AB 于M ,AH⊙BC 交BC 的延长线于H .解直角三角形求出AB ,OA 即可;【解答】(1)证明:作点C 关于AB 的对称点C′,连接AC′,BC′.由翻折不变性可知:BC=BC′,⊙CAB=⊙BAC′,⊙︵ BD =︵BC ′,⊙BD=BC′,⊙BC=BD .(2)解:连接OA ,OB ,作OM⊙AB 于M ,AH⊙BC 交BC 的延长线于H .⊙︵AB =120°,⊙⊙D=12×120°=60°,⊙⊙AOB=⊙ACB=2⊙D=120°,⊙BC=BD ,⊙⊙BCD 是等边三角形,⊙BC=DC=4,在Rt⊙ACH 中,⊙⊙H=90°,⊙ACH=60°,AC=1,⊙CH=12,AH=23, ⊙AB=22BH AH +=22)29()23(+=21,⊙OM⊙AB , ⊙AM=BM=221,在Rt⊙AOM 中,⊙⊙OAM=30°,⊙AMO=90°, ⊙OA=AMcos30°=7【点评】本题考查圆心角、弧、弦之间的关系,垂径定理,勾股定理,翻折变换,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.15、如图,已知⊙O 的半径为2,AB 为直径,CD 为弦.AB 与CD 交于点M ,将︵ CD 沿CD 翻折后,点A与圆心O 重合,延长OA 至P ,使AP=OA ,连接PC(1)求CD 的长;(2)求证:PC 是⊙O 的切线;(3)点G 为︵ADB 的中点,在PC 延长线上有一动点Q ,连接QG 交AB 于点E .交︵ BC 于点F (F 与B 、C 不重合).问GE•GF 是否为定值?如果是,求出该定值;如果不是,请说明理由.【分析】(1)连接OC ,根据翻折的性质求出OM ,CD⊙OA ,再利用勾股定理列式求解即可;(2)利用勾股定理列式求出PC ,然后利用勾股定理逆定理求出⊙PCO=90°,再根据圆的切线的定义证明即可;(3)连接GA 、AF 、GB ,根据等弧所对的圆周角相等可得⊙BAG=⊙AFG ,然后根据两组角对应相等两三角相似求出⊙AGE 和⊙FGA 相似,根据相似三角形对应边成比例可得AG GE =FG AG,从而得到GE•GF=AG 2,再根据等腰直角三角形的性质求解即可.【解答】(1)解:如图,连接OC ,⊙︵CD 沿CD 翻折后,点A 与圆心O 重合, ⊙OM=12OA=12×2=1,CD⊙OA ,⊙OC=2, ⊙CD=2CM=222OM OC -=22212-=23;(2)证明:⊙PA=OA=2,AM=OM=1,CM=12CD=3,⊙CMP=⊙OMC=90°,⊙PC=22PM MC +=223)3(+=23, ⊙OC=2,PO=2+2=4,⊙PC 2+OC 2=(23)2+22=16=PO 2, ⊙⊙PCO=90°,⊙PC 是⊙O 的切线;21(3)解:GE•GF 是定值,证明如下,连接GO 并延长,交⊙O 于点H ,连接HF⊙点G 为︵ADB 的中点⊙⊙GOE=90°,⊙⊙HFG=90°,且⊙OGE=⊙FGH⊙⊙OGE⊙⊙FGH⊙OG GF = GE GH⊙GE•GF=OG•GH=2×4=8.【点评】本题是圆的综合题型,主要利用了翻折变换的性质,垂径定理,勾股定理,勾股定理逆定理,圆的切线的定义,相似三角形的判定与性质,难点在于(3)作辅助线构造出相似三角形.。
2021年中考数学高频考点:《圆的综合》解答题专题练习(二)含答案

2021年中考数学复习高频考点精准练:《圆的综合》解答题专题练习(二)1.在Rt△ABC中,∠ABC=90°,tan A=,AC=5,点M是射线AB上一点,以MC为半径的⊙M交直线AC于点D.(1)如图,当MC=AC时,求CD的长;(2)当点D在线段AC的延长线上时,设BM=x,四边形CBMD的面积为y,求y关于x的函数解析式,并写出它的定义域;(3)如果直线MD与射线BC相交于点E,且△ECD与△EMC相似,求线段BM的长.2.如图,PA、PB为⊙O的切线,A、B为切点,点C为半圆弧的中点,连AC交PO于E 点.(1)求证:PB=PE;(2)若tan∠CPO=,求sin∠PAC的值.3.在梯形ABCD中,AD∥BC,AB⊥BC,AD=3,CD=5,cos C=(如图).M是边BC 上一个动点(不与点B、C重合),以点M为圆心,CM为半径作圆,⊙M与射线CD、射线MA分别相交于点E、F.(1)设CE=,求证:四边形AMCD是平行四边形;(2)联结EM,设∠FMB=∠EMC,求CE的长;(3)以点D为圆心,DA为半径作圆,⊙D与⊙M的公共弦恰好经过梯形的一个顶点,求此时⊙M的半径长.4.已知如图,⊙O的直径BC=4,==,点P是射线BD上的一个动点.(1)如图1,求BD的长;(2)如图1,若PB=8,连接PC,求证PC为⊙O的切线;(3)如图2,连接AP,点P在运动过程中,求AP+PB的最小值.5.如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PB=PA,射线PO交⊙O于C、D两点.(1)求证:PB是⊙O的切线;(2)求证:AC平分∠PAB;(3)若⊙O的直径是6,AB=2,则点D与△PAB的内切圆上各点之间距离的最大值为.6.国庆假期,小明做数学题时遇到了如下问题:如图1,四边形ABCD是⊙O的内接四边形,BC是⊙O的直径,直线l经过点A,∠ABD =∠DAE=30°.试说明直线l与⊙O相切.小明添加了适当的辅助线后,得到了图2的图形,并利用它解决了问题.(1)请你根据小明的思考,写出解决这一问题的过程;(2)图2中,若AD=,AB=4,求DC的长.7.如图,直线l1⊥l2,O为垂足,以O圆心,的半径作圆,交l1于点M,N,交l2于点P,Q.在⊙O上任取一点A,作△ABC,使∠A=90°,∠ACB=30°,顶点A,B,C按顺时针方向分布,点C落在射线ON上,且不在⊙O内.若△ABC的某一边所在直线与⊙O相切,我们称该边为⊙O的“相伴切边”.(1)如图1,CA为⊙O的“相伴切边”,CA平分∠OCB,求OC的长;(2)是否存在△ABC三边中两边都是⊙O的“相伴切边”的情形?若存在,请求出AC的长;若不存在,请说明理由.8.如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AC平分∠DAB,AC 与BD相交于点F,延长AC到点E,使CE=CF.(1)求证:BE是半圆O所在圆的切线;(2)若BC=AD=6,求⊙O的半径.9.如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,以AD为直径作⊙O交AB于点E,连接CE,且CB=CE.(1)求证:CE是⊙O的切线;(2)若CD=2,AB=4,求⊙O的半径.10.如图,⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于D.(1)判断△ABD的形状,并说明理由;(2)求点O到弦BD的距离.(3)求CD的长.11.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连接OA,此时有OA∥PE.(1)求证:AP=AO;(2)若,求弦AB的长;12.如图,在Rt△ABC中,∠ABC=90°.以AB为直径作⊙O交AC于点D,过点D作DE ⊥AB于点E,F为DE中点,连接AF并延长交BC于点G,连接DG.求证:(1)BG=CG;(2)DG是⊙O的切线.13.如图,直线AF与⊙O相切于点A,弦BC∥AF,连接BO并延长,交⊙O于点E,连接CE并延长,交AF于点D.(1)求证:CE∥OA;(2)若⊙O的半径R=13,BC=24,求DE的长.14.如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O,交BC于E,过点B作∠CBD =∠A,过点C作CD⊥BD于D.(1)求证:BD是⊙O的切线;(2)若CD=2,BC=2,求⊙O的直径.15.如图,AB是⊙O的直径.四边形ABCD内接于⊙O,AD=CD,对角线AC与BD交于点E,在BD的延长线上取一点F,使DF=DE,连接AF.(1)求证:AF是⊙O的切线.(2)若AD=5,AC=8,求⊙O的半径.参考答案1.解:在Rt△ABC中,tan A=,AC=5,设∠A=α,则BC=3,AB=4=BM,sin A==sinα,cos A==cosα,(1)如图1,∵MC=MA=5,过点M作MN⊥CD于点N,∵MC=MD,则CN=CD,在Rt△AMN中,MN=AM sin A=(4+4)×=,则CD=2CN=2=2=;(2)如图1,设CD=2m,则CM2=BC2+MB2=9+x2,则MN2=CM2﹣m2=x2+9﹣m2,在Rt△AMN中,AN2+MN2=AM2,即(5+m)2+9+x2﹣m2=(4+x)2,解得m=(4x﹣9),则MN==(x+4);则S=CD•MN+×AM•BC=(8x2+39x﹣72);∵m=(4x﹣9)>0,∴x>;(3)如图2,过点M作MN⊥CD于点N,过点P作PD⊥CM于点P,设圆的半径为r,∵△ECD与△EMC相似,则∠ECD=∠EMC=∠ACB=α,在Rt△DPM中,DP=DM sin∠EMC=r sinα=r,MP=r cosα=r,则CP=r﹣MP=r﹣r=r,CD==r=2CN,∴MN==r,∵tan A==,解得r=3,则BM===6.2.(1)证明:连接OA,OC,∵OA=OC,∴∠OAC=∠OCA,∵点C为半圆弧的中点,∴∠COE=90°,∴∠OCA+∠OEC=90°,∵PA为⊙O的切线,∴∠PAO=90°,∴∠OAC+∠PAE=90°,∴∠PAE=∠OEC,∵∠OEC=∠AEP,∴∠PAE=∠AEP,∵PA、PB为⊙O的切线,∴PA=PE=PB;(2)解:∵tan∠CPO==,设OC=3k,OP=5k,∴OA=OC=3k,∴PA=PE=4k,过A作AH⊥PO于H,∴OP•AH=PA•OA,∴AH==k,∴OH==k,∵∠AHE=∠COE=90°,∠AEH=∠CEO,∴△AHE∽△COE,∴,∴OE=k,∴CE==k,∴sin∠PAC=sin∠CEO===.3.(1)证明:如图1中,连接EM,过点M作MG⊥CD于G,则EG=CG=,在Rt△CGM中,CM===3,∴AD=CM,∵AD∥CM,∴四边形AMCD是平行四边形.(2)解:如图2中,过点E作EH⊥BC于H,过点M作MT⊥EC于T.∵ME=MC,MT⊥EC,∴CT=ET,∴cos C==,设EC=6k,则CT=ET=3k,MC=ME=5k,在Rt△CEH中,EH=CE=k,CH=EC=k,∴MH=CM﹣CH=k,∴tan∠EMH=,∵∠FMB=∠EMC,∴tan∠FMB===,∴BM=,∴CM=BC﹣BM==5k,∴CE=6k=.(3)如图3﹣1中,当公共弦经过点A时,过点D作DP⊥BC于P,则四边形ABPD是矩形.∴AD=BP=3,在Rt△CDP中,cos C==,∵CD=5,∴PC=3,AB=PD=4,∴BC=3+3=6,设CM=AM=x,在Rt△ABM中,则有x2=42+(6﹣x)2,解得x=,∴⊙M的半径为.如图3﹣2中,当公共弦经过点D时,连接MD,MP,过点M作MN⊥AD于N.设CM=ME=MP=x,则DN=x﹣3,∵DM2=MN2+DN2=MP2﹣DP2,∴42+(x﹣3)2=x2﹣32,∴x=,综上所述,满足条件的⊙M的半径为或.4.解:(1)∵BC是直径,==,则、、均为60°的弧,则∠DBC=30°,连接OA交BD于点H,∵BC=4,则BO=CO=2,在Rt△BOH中,BH=BO cos∠DBC=2×=3,则BD=2BH=6;(2)在Rt△BCD中,BC=4,∠DBC=30°,则CD=CB=2,PD=PB﹣BD=8﹣6=2,在Rt△CDP中,PC2=CD2+PD2=4+(2)2=16,在△BCP中,BC2=(4)2=48,BP2=64,则PB2=CB2+PC2,故△BPC为直角三角形,故PC⊥CB,故PC为⊙O的切线;(3)过点A作AH⊥BC交BD于点P,在Rt△PBH中,∠DBC=30°,则PH=PB,即AP+PB=AP+PH=AH为最小,∵、均为60°的弧,则∠ABO=60°,而AO=BO,故△ABO为边长为2的等边三角形,则AH=AB sin60°=2×=3,即AP+PB的最小值为3.5.(1)证明:如图1中,连接OA,OB.∵PA是切线,∴PA⊥OA,∴∠PAO=90°,在△PAO和△PBO中,,∴△PAO≌△PBO(SSS),∴∠PBO=∠PAO=90°,∴PB⊥OB,∴PB是⊙O的切线.(2)证明:如图1中,设∠PAC=α.∵∠PAO=90°,∴∠OAC=90°﹣α,∵OA=OC,∴∠OCA=∠OAC=90°﹣α,∵PA=PB,OA=OB,∴PO垂直平分线段AB,∴∠CAB=90°∠ACO=90°﹣(90°﹣α)=α,∴∠PAC=∠CAB,∴AC平分∠PAB.(3)解:如图2中,设AB交OP于点M.∵PA,PB是⊙O的切线,∴OP平分∠APB,∵AC平分∠PAB,∴点C是△PAB的内心,设△PAB的内切圆⊙C交PC于H,∵⊙O的直径为6,∴OA=3,∵OP垂直平分线AB,AB=2,∴AM=BM=,∴OM===2,∵OC=3,∴CH=CM=3﹣2=1,∵点D到⊙C上各点的最大距离为DH,∴最大距离DH=CD+CH=6+1=7.故答案为7.6.(1)证明:过A作直径AF,连接DF,如图2所示:∵AF是⊙O的直径,∴∠ADF=90°,∴∠AFD+∠FAD=90°,∵∠ABD=∠AFD,∠ABD=∠DAE,∴∠AFD=∠DAE,∴∠DAE+∠DAF=90°,即∠OAE=90°,∴OA⊥AE,∵点A是半径OA的外端,∴直线l与⊙O相切;(2)解:过点A作AG⊥BD,垂足为点G,∴∠AGB=∠AGD=90°,∵∠ABD=30°,∴∠AFD=30°,∴直径AF=2AD==BC,∵∠ABD=30°,AB=4,∴AG==2,BG=AG=2,∴DG===,∴BD=BG+DG=,∵BC是直径,∴∠BDC=90°,∴.7.解:(1)如图1,连接OA,则OA=,∵CA为⊙O的“相伴切边”,∴OA⊥AC,即∠OAC=90°,∵∠ACB=30°,CA平分∠OCB,∴∠OCA=∠ACB=30°,则在Rt△AOC中,OC=2OA=2;(2)存在.由题意可分三种情况,①当边AB,BC都是⊙O的“相伴切边”时,即OA⊥AB,∵∠BAC=90°,即AC⊥AB,∴O,A,C三点共线,又∵点C落在射线ON上,且不在⊙O内,∴点A只能在点M或点N处,如图2,当点A在点N处时,设BC与⊙O相切于点D,连接OD,则OD⊥CD,∵∠ACB=30°,∴OC=2OD=2,∴AC=OC﹣AO=,当点A在点M处时,如图3,设BC与⊙O相切于点D,连接OD,则OD⊥CD,∵∠ACB=30°,∴OC=2OD=2,∴AC=OC+AO=3,②当边AC,BC都是⊙O的“相伴切边”时,则OA⊥AC,∵∠BAC=90°,∴∠OAB=180°,即O,A,B三点共线,如图4,设BC与⊙O相切于点D,连接OD,则OD⊥CD,设AB=x,则BC=2x,AC==x,∴OB=OA+AB=+x,∵∠BAC=∠BDO=90°,∠B=∠B,∴△ABC∽△DBO,∴,即,解得,x=2﹣或x=0(舍去),经检验,x=2﹣是所列方程的解.∴AC=x=2﹣3.③当边AC,AB都是⊙O的“相伴切边”时,∵AC是⊙O的“相伴切边”,∴OA⊥AC,即∠OAC=90°,∵∠BAC=90°,∴∠OAB=180°,即O,A,B三点共线,∴AB不可能是⊙O的“相伴切边”,则AC,AB不能同时是⊙O的“相伴切边”;综上可得,AC的长是或3或2﹣3.8.(1)证明:∵AB是半圆O的直径,∴∠ACB=∠ADB=90°,∵CE=CF,∴BE=BF,∴∠E=∠BFE,∵AC平分∠DAB,∴∠DAF=∠BAF,∵∠DAF+∠AFD=90°,∴∠BAF+∠E=90°,∴BE是半圆O所在圆的切线;(2)解:∵∠DAF=∠BAF,∴=,∵BC=AD,∴=,∴==,∴∠CAB=30°,∴AB=2BC=12,∴⊙O的半径为6.9.(1)证明:如图,连接OE,DE,∵∠ACB=90°,∴∠A+∠B=90°,∵AD是⊙O的直径,∴∠AED=∠DEB=90°,∴∠DEC+∠CEB=90°,∵CE=BC,∴∠B=∠CEB,∴∠A=∠DEC,∵OE=OD,∴∠OED=∠ODE,∵∠A+∠ADE=90°,∴∠DEC+∠OED=90°,即∠OEC=90°,∴OE⊥CE.∵OE是⊙O的半径,∴CE是⊙O的切线;(2)解:在Rt△ABC中,∠ACB=90°,CD=2,AB=4,BC=CE,设⊙O的半径为r,则OD=OE=r,OC=r+2,AC=2r+2,∴AC2+BC2=AB2,∴(2r+2)2+BC2=(4)2,在Rt△OEC中,∠OEC=90°,∴OE2+CE2=OC2,∴r2+BC2=(r+2)2,∴BC2=(r+2)2﹣r2,∴(2r+2)2+(r+2)2﹣r2=(4)2,解得r=3,或r=﹣6(舍去).∴⊙O的半径为3.10.解:(1)△ABD是等腰直角三角形,理由如下:∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,∵∠ACB的平分线交⊙O于D,∴∠ACD=∠BCD=45°,∴,∴AD=BD,∴△ABD是等腰直角三角形;(2)过O作OE⊥DB于E,如图所示:则∠OEB=90°,∵AB=10cm,∴OB=AB=5(cm),由(1)得:△ABD是等腰直角三角形,∴∠ABD=45°,∴△OBE是等腰直角三角形,∴OE=OB=(cm),即点O到弦BD的距离为cm;(3)过B作BF⊥CD于F,如图所示:则∠BFC=∠BFD=90°,∵∠ACB=90°,∴BC===8(cm),∵∠BCD=45°,∴△BCF是等腰直角三角形,∴CF=BF=BC=4(cm),由(1)得:△ABD是等腰直角三角形,∴BD=AB=5(cm),∴DF===3,∴CD=CF+DF=4+3=7(cm).11.(1)证明:∵PG平分∠EPF,∴∠DPO=∠BPO,∵OA∥PE,∴∠DPO=∠POA,∴∠BPO=∠POA,∴PA=OA;(2)过点O作OH⊥AB于点H,如图,则AH=BH,在Rt△OPH中,tan∠OPH==,设OH=x,则PH=2x,由(1)可知PA=OA=10,∴AH=PH﹣PA=2x﹣10,∵AH2+OH2=OA2,∴(2x﹣10)2+x2=102解得x1=0(不合题意,舍去),x2=8,∴AH=6,∴AB=2AH=12.12.证明:(1)∵DE⊥AB,∴∠AED=∠ABC=90°,∴DE∥BC,∴△AEF∽△ABG,△ADF∽△ACG,∴,=,∴,∵F为DE中点,∴EF=DF,∴BG=CG;(2)连接OD,BD,OG,∵AB为⊙O的直径,∴AD⊥BD,∵AO=BO,BG=CG,∴OG∥AC,∴OG⊥BD,∴BF=DF,∴DG=BG,在△ODG与△OBG中,,∴△ODG≌△OBG(SSS),∴∠ODG=∠OBG=90°,∴DG是⊙O的切线.13.(1)证明:∵BE是⊙O的直径,∴∠BCE=90°,∵BC∥AF,∴∠CDF=∠ACE=90°,∵AF与⊙O相切于点A,∴∠OAF=90°,∴∠OAF=∠CDF,∴CE∥OA;(2)解:如图,作OH⊥CE于点H,由垂径定理知:CH=EH,∵OB=OE,∴OH是△ECB的中位线,∴OH=BC=24=12,在Rt△OEH中,根据勾股定理,得EH===5,∵OH⊥CE,∴∠OHD=90°,由(1)知:∠CDA=∠OAD=90°,∴四边形OADH是矩形,∴DH=OA=13,∴DE=DH﹣EH=13﹣5=8.14.解:(1)如图,连接AE,∵AB为直径,∴∠AEB=90°,∵△ABC是等腰三角形,AB=AC,∴∠BAE=BAC,∵∠CBD=∠BAC,∴∠BAE=∠CBD,∵∠ABE+∠BAE=90°,∴∠ABE+∠CBD=90°,∴∠ABD=90°,∴AB⊥BD,∵AB为直径,∴BD是⊙O的切线;(2)由(1)知:△ABC是等腰三角形,AE⊥BC,∴BE=CE=BC=,∵CD⊥BD,∴∠CDB=∠AEB=90°,∵∠CBD=∠BAE,∴△CBD∽△BAE,∴=,∴=,∴AB=3.∴⊙O的直径为3.15.解:(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥EF,∠BAD+∠ABD=90°,又∵DF=DE,∴AF=AE,∴∠FAD=∠EAD.∴∠FAD=∠EAD=∠ACD=∠ABD,∴∠FAB=∠FAD+∠BAD=∠BAD+∠ABD=90°,∴AF是⊙O的切线.(2)如图,连接OD交AC于M,∵AD=CD,∴,∴OD⊥AC,AM=CM=AC=4,∴AD=CD=5,在Rt△DMC中,DM==3.设⊙O的半径为x,则OM=x﹣3,∵OM2+AM2=OA2,∴(x﹣3)2+42=x2,∴x=.⊙O的半径即OA=.。
2020-2021中考数学专题复习分类练习 圆的综合综合解答题含答案解析

2020-2021中考数学专题复习分类练习圆的综合综合解答题含答案解析一、圆的综合1.图1和图2,半圆O的直径AB=2,点P(不与点A,B重合)为半圆上一点,将图形延BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.(1)当α=15°时,过点A′作A′C∥AB,如图1,判断A′C与半圆O的位置关系,并说明理由.(2)如图2,当α= °时,BA′与半圆O相切.当α= °时,点O′落在上.(3)当线段BO′与半圆O只有一个公共点B时,求α的取值范围.【答案】(1)A′C与半圆O相切;理由见解析;(2)45;30;(3)0°<α<30°或45°≤α<90°.【解析】试题分析:(1)过O作OD⊥A′C于点D,交A′B于点E,利用含30°角的直角三角形的性质可求得DE+OE=A′B=AB=OA,可判定A′C与半圆相切;(2)当BA′与半圆相切时,可知OB⊥A′B,则可知α=45°,当O′在上时,连接AO′,则可知BO′=AB,可求得∠O′BA=60°,可求得α=30°;(3)利用(2)可知当α=30°时,线段O′B与圆交于O′,当α=45°时交于点B,结合题意可得出满足条件的α的范围.试题解析:(1)相切,理由如下:如图1,过O作OD过O作OD⊥A′C于点D,交A′B于点E,∵α=15°,A′C∥AB,∴∠ABA′=∠CA′B=30°,∴DE=A′E ,OE=BE ,∴DO=DE+OE=(A′E+BE )=AB=OA ,∴A′C 与半圆O 相切;(2)当BA′与半圆O 相切时,则OB ⊥BA′,∴∠OBA′=2α=90°,∴α=45°,当O′在上时,如图2,连接AO′,则可知BO′=AB ,∴∠O′AB=30°,∴∠AB O′=60°,∴α=30°,(3)∵点P ,A 不重合,∴α>0,由(2)可知当α增大到30°时,点O′在半圆上,∴当0°<α<30°时点O′在半圆内,线段BO′与半圆只有一个公共点B ;当α增大到45°时BA′与半圆相切,即线段BO′与半圆只有一个公共点B .当α继续增大时,点P 逐渐靠近点B ,但是点P ,B 不重合,∴α<90°,∴当45°≤α<90°线段BO′与半圆只有一个公共点B .综上所述0°<α<30°或45°≤α<90°.考点:圆的综合题.2.已知O e 的半径为5,弦AB 的长度为m ,点C 是弦AB 所对优弧上的一动点. ()1如图①,若m 5=,则C ∠的度数为______o ;()2如图②,若m 6=.①求C ∠的正切值;②若ABC V 为等腰三角形,求ABC V 面积.【答案】()130;()2C ∠①的正切值为34;ABC S 27=V ②或43225. 【解析】【分析】 ()1连接OA ,OB ,判断出AOB V 是等边三角形,即可得出结论;()2①先求出10AD =,再用勾股定理求出8BD =,进而求出tan ADB ∠,即可得出结论;②分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.【详解】()1如图1,连接OB ,OA ,OB OC 5∴==,AB m 5==Q ,OB OC AB ∴==,AOB ∴V 是等边三角形,AOB 60∠∴=o ,1ACB AOB 302∠∠∴==o , 故答案为30;()2①如图2,连接AO 并延长交O e 于D ,连接BD ,AD Q 为O e 的直径,AD 10∴=,ABD 90∠=o ,在Rt ABD V 中,AB m 6==,根据勾股定理得,BD 8=, AB 3tan ADB BD 4∠∴==, C ADB ∠∠=Q ,C ∠∴的正切值为34; ②Ⅰ、当AC BC =时,如图3,连接CO 并延长交AB 于E ,AC BC =Q ,AO BO =,CE ∴为AB 的垂直平分线,AE BE 3∴==,在Rt AEO V 中,OA 5=,根据勾股定理得,OE 4=,CE OE OC 9∴=+=,ABC 11S AB CE 692722∴=⨯=⨯⨯=V ; Ⅱ、当AC AB 6==时,如图4,连接OA 交BC 于F ,AC AB =Q ,OC OB =,AO ∴是BC 的垂直平分线,过点O 作OG AB ⊥于G , 1AOG AOB 2∠∠∴=,1AG AB 32==, AOB 2ACB ∠∠=Q ,ACF AOG ∠∠∴=,在Rt AOG V 中,AG 3sin AOG AC 5∠==, 3sin ACF 5∠∴=, 在Rt ACF V 中,3sin ACF 5∠=, 318AF AC 55∴==, 24CF 5∴=, ABC 111824432S AF BC 225525∴=⨯=⨯⨯=V ; Ⅲ、当BA BC 6==时,如图5,由对称性知,ABC 432S 25=V .【点睛】圆的综合题,主要圆的性质,圆周角定理,垂径定理,等腰三角形的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.3.如图,PA 、PB 是⊙O 的切线,A ,B 为切点,∠APB=60°,连接PO 并延长与⊙O 交于C 点,连接AC 、BC .(Ⅰ)求∠ACB 的大小;(Ⅱ)若⊙O 半径为1,求四边形ACBP 的面积.【答案】(Ⅰ)60°;(Ⅱ)33【解析】分析:(Ⅰ)连接AO,根据切线的性质和切线长定理,得到OA⊥AP,OP平分∠APB,然后根据角平分线的性质和三角形的外角的性质,30°角的直角三角形的性质,得到∠ACB的度数;(Ⅱ)根据30°角的直角三角形的性质和等腰三角形的性质,结合等底同高的性质求三角形的面积即可.详解:(Ⅰ)连接OA,如图,∵PA、PB是⊙O的切线,∴OA⊥AP,OP平分∠APB,∴∠APO=12∠APB=30°,∴∠AOP=60°,∵OA=OC,∴∠OAC=∠OCA,∴∠ACO=12AOP=30°,同理可得∠BCP=30°,∴∠ACB=60°;(Ⅱ)在Rt△OPA中,∵∠APO=30°,∴33,OP=2OA=2,∴OP=2OC,而S△OPA=123∴S△AOC=12S△PAO=34,∴S△ACP=33,4∴四边形ACBP的面积=2S△ACP=33.点睛:本题考查了切线的性质,解直角三角形,等腰三角形的判定,熟练掌握切线的性质是解题的关键.4.已知:如图,△ABC中,AC=3,∠ABC=30°.(1)尺规作图:求作△ABC的外接圆,保留作图痕迹,不写作法;(2)求(1)中所求作的圆的面积.【答案】(1)作图见解析;(2)圆的面积是9π.【解析】试题分析:(1)按如下步骤作图:①作线段AB的垂直平分线;②作线段BC的垂直平分线;③以两条垂直平分线的交点O为圆心,OA长为半圆画圆,则圆O即为所求作的圆.如图所示(2)要求外接圆的面积,需求出圆的半径,已知AC=3,如图弦AC所对的圆周角是∠ABC=30°,所以圆心角∠AOC=60°,所以∆AOC是等边三角形,所以外接圆的半径是3故可求得外接圆的面积.(2)连接OA,OB.∵AC=3,∠ABC=30°,∴∠AOC=60°,∴△AOC是等边三角形,∴圆的半径是3,∴圆的面积是S=πr2=9π.5.函数是描述客观世界运动变化的重要模型,理解函数的本质是重要的任务。
2021年中考数学第三轮:圆的综合 解答题专题复习(含答案)

2021年中考数学第三轮:圆的综合解答题专题复习1、如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.(2)若CD的长.2、如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.(1)求证:ED是⊙O的切线;(2)当OE=10时,求BC的长.3、如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.(1)求证:CD是⊙O的切线;(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.4、如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC(1)求证:DE与⊙O相切;(2)若BF=2,DF=,求⊙O的半径.5、如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.(1)求证:PF平分∠BFD.(2)若tan∠FBC=,DF=,求EF的长.6、如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF ⊥AC,垂足为F,线段FD,AB的延长线相交于点G.(1)求证:DF是⊙O的切线;(2)若CF=1,DF=,求图中阴影部分的面积.7、如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).8、如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,过点A作AF⊥CE于点F,延长AF交BC于点P.(1)求证:CA=CP;(2)连接OF,若AC=,∠D=30°,求线段OF的长.9、如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC 的外接圆于点F,连接FB,FC.(1)求证:∠FBC=∠FCB;(2)已知FA•FD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.10、如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.(1)判断AB与⊙O的位置关系,并说明理由;(2)若PF:PC=1:2,AF=5,求CP的长.11、如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O 是△ABD的外接圆.(1)求证:AC是⊙O的切线;(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.12、如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点M、N,过点A作PO的垂线AB,垂足为C,变⊙O于点B,延长BO与⊙O交于点D,连接AD、BM.(1)等式OD2=OC•OP成立吗?若成立,请加以证明;若不成立,请说明理由.(2)若AD=6,tan∠M=,求sin∠D的值.13、如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.(1)试判断△ABC的形状,并说明理由;(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣,求⊙O 的半径和BF的长.14、如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l ∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.15、如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF ⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.(1)求证:BO=2OM.(2)设EF>HE,当矩形EFGH的面积为24,求⊙O的半径.(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.参考答案2021年中考数学第三轮:圆的综合解答题专题复习1、如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.(2)若sinB=,CD的长.5解:(1)证明:连接DE,∵BD是⊙O的直径,∴∠DEB=90°,∵E是AB的中点,∴DA=DB,∴∠1=∠B,∵∠B=∠F,∴∠1=∠F;(2)∵∠1=∠F,∴在Rt△ABC中,AC=AB•sinB=4,∴,设CD=x,则AD=BD=8﹣x,∵222+=,AC CD AD即222+=-,∴x=3,即CD=3.x x4(8)2、如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.(1)求证:ED是⊙O的切线;(2)当OE=10时,求BC的长.【解答】(1)证明:如图,连接OD.∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°.在△AOE与△DOE中,,∴△AOE≌△DOE(SSS),∴∠OAE=∠ODE=90°,即OD⊥ED.又∵OD是⊙O的半径,∴ED是⊙O的切线;(2)解:如图,∵OE=10.∵AB是直径,∴∠ADB=90°,即AD⊥BC.又∵由(1)知,△AOE≌△DOE,∴∠AEO=∠DEO,又∵AE=DE,∴OE⊥AD,∴OE∥BC,∴=,∴BC=2OE=20,即BC的长是20.3、如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.(1)求证:CD是⊙O的切线;(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.【解答】解:(1)连接OC.∵OA=OC.∴∠OAC=∠OCA,∵∠MAC=∠OAC,∴∠MAC=∠OCA,∴OC∥AM,∵CD⊥AM,∴OC⊥CD,∴CD是⊙O的切线.(2)在RT△ACD中,∵∠ACD=30°,AD=4,∠ADC=90°,∴AC=2AD=8,CD=AD=4,∵∠MAC=∠OAC=60°,OA=OC,∴△AOC是等边三角形,∴S阴=S△ACD﹣(S扇形OAC﹣S△AOC)=×4×4﹣(﹣×82)=24﹣π.4、如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC(1)求证:DE与⊙O相切;(2)若BF=2,DF=,求⊙O的半径.【解答】(1)证明:连接OD,∵AB是⊙O的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵∠BOD=2∠BCD,∠A=2∠BCD,∴∠BOD=∠A,∵∠AED=∠ABC,∴∠BOD+∠AED=90°,∴∠ODE=90°,即OD⊥DE,∴DE与⊙O相切;(2)解:连接BD,过D作DH⊥BF于H,∵DE与⊙O相切,∴∠BDE=∠BCD,∵∠AED=∠ABC,∴∠AFC=∠DBF,∵∠AFC=∠DFB,∴△ACF与△FDB都是等腰三角形,∴FH=BH=BF=1,则FH=1,∴HD==3,在Rt△ODH中,OH2+DH2=OD2,即(OD﹣1)2+32=OD2,∴OD=5,∴⊙O的半径是5.5、如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.(1)求证:PF平分∠BFD.(2)若tan∠FBC=,DF=,求EF的长.【解答】解:(1)连接OP,BF,PF,∵⊙O与AD相切于点P,∴OP⊥AD,∵四边形ABCD的正方形,∴CD⊥AD,∴OP∥CD,∴∠PFD=∠OPF,∵OP=OF,∴∠OPF=∠OFP,∴∠OFP=∠PFD,∴PF平分∠BFD;(2)连接EF,∵∠C=90°,∴BF是⊙O的直径,∴∠BEF=90°,∴四边形BCFE是矩形,∴EF=BC,∵AB∥OP∥CD,BO=FO,∴OP=AD=CD,∵PD2=DF•CD,即()2=•CD,∴CD=4,∴EF=BC=4.6、如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF ⊥AC,垂足为F,线段FD,AB的延长线相交于点G.(1)求证:DF是⊙O的切线;(2)若CF=1,DF=,求图中阴影部分的面积.【解答】(1)证明:连接AD、OD,如图所示.∵AB为直径,∴∠ADB=90°,∴AD⊥BC,∵AC=AB,∴点D为线段BC的中点.∵点O为AB的中点,∴OD为△BAC的中位线,∴OD∥AC,∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线.(2)解:在Rt△CFD中,CF=1,DF=,∴tan∠C==,CD=2,∴∠C=60°,∵AC=AB,∴△ABC为等边三角形,∴AB=4.∵OD∥AC,∴∠DOG=∠BAC=60°,∴DG=OD•tan∠DOG=2,∴S阴影=S△ODG﹣S扇形OBD=DG•OD﹣πOB2=2﹣π.7、如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).【解答】(1)证明:连接OD,如图所示.∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∴∠CFD=∠ODF=90°,∴DF⊥AC.(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴的长===π.8、如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,过点A作AF⊥CE于点F,延长AF交BC于点P.(1)求证:CA=CP;(2)连接OF,若AC=,∠D=30°,求线段OF的长.【解答】解:(1)如图1,连接AE,∵OE⊥AB,∴∠AOE=90°,∠AEO=45°,∴∠OEG+∠OGE=90°,∵AF⊥CE,∴∠AFG=90°,∴∠FAG+∠AGF=90°,∵∠AGF=∠OGE,∴∠OEG=∠BAP,∵∠AEC=∠ABC,∴∠APC=∠ABC+∠BAP=∠AEC+∠OEG=∠AEO=45°,∵AB是⊙O直径,∴∠ACB=90°,∴∠BAC=90°﹣∠APC=45°=∠APC,∴CA=CP;(2)如图2,连接OC,∵CD是⊙O的切线,∴∠DCO=90°,∵∠D=30°,∴∠AOC=60°,∵OA=OC,∴∠BAC=60°在Rt△ABC中,AC=,∴BC=ACtan∠BAC=ACtan60°=×=3,由(1)知,CP=AC=,∴BP=BC﹣CP=3﹣,由(1)知AC=CP,∵AF⊥CE,∴AF=PF,∵OA=OB,∴OF=BP=(3﹣).9、如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC 的外接圆于点F,连接FB,FC.(1)求证:∠FBC=∠FCB;(2)已知FA•FD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.【解答】(1)证明:∵四边形AFBC内接于圆,∴∠FBC+∠FAC=180°,∵∠CAD+∠FAC=180°,∴∠FBC=∠CAD,∵AD是△ABC的外角∠EAC的平分线,∴∠EAD=∠CAD,∵∠EAD=∠FAB,∴∠FAB=∠CAD,又∵∠FAB=∠FCB,∴∠FBC=∠FCB;(2)解:由(1)得:∠FBC=∠FCB,又∵∠FCB=∠FAB,∴∠FAB=∠FBC,∵∠BFA=∠BFD,∴△AFB∽△BFD,∴,∴BF2=FA•FD=12,∴BF=2,∵FA=2,∴FD=6,AD=4,∵AB为圆的直径,∴∠BFA=∠BCA=90°,∴tan∠FBA===,∴∠FBA=30°,又∵∠FDB=∠FBA=30°,∴CD=AD•cos30°=4×=2.10、如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.(1)判断AB与⊙O的位置关系,并说明理由;(2)若PF:PC=1:2,AF=5,求CP的长.【解答】解:(1)AB是⊙O切线.理由:连接DE、CF.∵CD是直径,∴∠DEC=∠DFC=90°,∵∠ACB=90°,∴∠DEC+∠ACE=180°,∴DE∥AC,∴∠DEA=∠EAC=∠DCF,∵∠DFC=90°,∴∠FCD+∠CDF=90°,∵∠ADF=∠EAC=∠DCF,∴∠ADF+∠CDF=90°,∴∠ADC=90°,∴CD⊥AD,∴AB是⊙O切线.(2)∵∠CPF=∠CPA,PCF=∠PAC,∴△PCF∽△PAC,∴=,∴PC2=PF•PA,设PF=a.则PC=2a,∴4a2=a(a+5),∴a=,∴PC=2a=.11、如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O 是△ABD的外接圆.(1)求证:AC是⊙O的切线;(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.【解答】(1)证明:连接AO,延长AO交⊙O于点E,则AE为⊙O的直径,连接DE,如图所示:∵∠ABC:∠ACB:∠ADB=1:2:3,∠ADB=∠ACB+∠CAD,∴∠ABC=∠CAD,∵AE为⊙O的直径,∴∠ADE=90°,∴∠EAD=90°﹣∠AED,∵∠AED=∠ABD,∴∠AED=∠ABC=∠CAD,∴∠EAD=90°﹣∠CAD,即∠EAD+∠CAD=90°,∴EA⊥AC,∴AC是⊙O的切线;(2)解:∵BD是⊙O的直径,∴∠BAD=90°,∴∠ABC+∠ADB=90°,∵∠ABC:∠ACB:∠ADB=1:2:3,∴4∠ABC=90°,∴∠ABC=22.5°,由(1)知:∠ABC=∠CAD,∴∠CAD=22.5°.12、如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点M、N,过点A作PO的垂线AB,垂足为C,变⊙O于点B,延长BO与⊙O交于点D,连接AD、BM.(1)等式OD2=OC•OP成立吗?若成立,请加以证明;若不成立,请说明理由.(2)若AD=6,tan∠M=,求sin∠D的值.【解答】解:(1)等式OD2=OC•OP成立;理由如下连接OA,如图1所示:∵PA为⊙O的切线,A为切点,过点A作PO的垂线AB,垂足为C,∴∠OAP=∠ACO=90°,∵∠AOC=∠POA,∴△OAC∽△OPA,∴=,即OA2=OC•OP∵OD=OA,∴OD2=OC•OP;(2)连接BN,如图2所示:则∠MBN=90°.∵tan∠M=,∴=,∴设BN=x,BM=2x,则由勾股定理,得MN==x,∵BM•BN=MN•BC,∴BC=x,又∵AB⊥MN,∴AB=2BC=x,∴Rt△ABD中,BD=MN=x,AD2+AB2=BD2,∴62+(x)2=(x)2,解得:x=2,∴BD=×2=10,AB=8,∴sin∠D===.13、如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.(1)试判断△ABC的形状,并说明理由;(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣,求⊙O 的半径和BF的长.【解答】解:(1)△ABC是等腰三角形,理由是:如图1,连接OE,∵DE是⊙O的切线,∴OE⊥DE,∵ED⊥AC,∴AC∥OE,∴∠1=∠C,∵OB=OE,∴∠1=∠B,∴∠B=∠C,∴△ABC是等腰三角形;(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,∵△ABC是等腰三角形,∴∠B=∠C=75°,∴∠A=180°﹣75°﹣75°=30°,设OG=x,则OA=OB=OE=2x,AG=x,∴DG=0E=2x,根据AC=AB得:4x=x+2x+2﹣,x=1,∴0E=OB=2,在直角△OEF中,∠EOF=∠A=30°,cos30=,OF==2÷=,∴BF=﹣2,⊙O的半径为2.14、如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l ∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.【解答】解:(1)直线l与⊙O相切.理由:如图1所示:连接OE、OB、OC.∵AE平分∠BAC,∴∠BAE=∠CAE.∴.∴∠BOE=∠COE.又∵OB=OC,∴OE⊥BC.∵l∥BC,∴OE⊥l.∴直线l与⊙O相切.(2)∵BF平分∠ABC,∴∠ABF=∠CBF.又∵∠CBE=∠CAE=∠BAE,∴∠CBE+∠CBF=∠BAE+∠ABF.又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB.∴BE=EF.(3)由(2)得BE=EF=DE+DF=7.∵∠DBE=∠BAE,∠DEB=∠BEA,∴△BED∽△AEB.∴,即,解得;AE=.∴AF=AE﹣EF=﹣7=.15、如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF ⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.(1)求证:BO=2OM.(2)设EF>HE,当矩形EFGH的面积为24,求⊙O的半径.(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.【详细解答】(1)如图1所示:设⊙O切AB于点P,连接OP,则∠OPB=90°.∵四边形ABCD为菱形,∴∠ABD=12∠ABC=30°.∴OB=2OP.∵OP=OM,∴OP=2OM.(2)如图2所示:设GH交BD于点N,连接AC,交BD于点Q.∵四边形ABCD是菱形,∴AC⊥BD.∴BD=2BQ=2AB•cos∠ABQ=.设⊙O的半径为r,则OB=2r,MB=3r.∵EF>HE,∴点E,F,G,H均在菱形的边上.①如图2所示,当点E在AB上时.在Rt△BEM中,EM=BM•tan∠EBM=.由对称性得:EF=2EM=2,ND=BM=3r.∴MN=18﹣6r.∴S矩形E F G H=EF•MN=2(18﹣6r)=24解得:1r=1,2r=2.当r=1时,EF<HE,∴r=1时,不合题意舍,当r=2时,EF>HE,∴⊙O的半径为2.∴BM=3r=6.如图3所示:当点E在AD边上时.BM=3r,则MD=18﹣3r.由对称性可知:NB=MD=6.∴MB=3r=18﹣6=12.解得:r=4.综上所述,⊙O的半径为2或4.(3)解设GH交BD于点N,⊙O的半径为r,则BO=2r.当点E在边BA上时,显然不存在HE或HG与⊙O相切.①如图4所示,点E在AD上时.∵HE与⊙O相切,∴ME=r,DM=.∴3r+.解得:r=9﹣3∴OB=18﹣6②如图5所示;由图形的对称性得:ON=OM,BN=DM.∴OB=12BD=9.③如图6所示.∵HG与⊙O相切时,MN=2r.∵BN+MN=BM=3r.∴BN=r.∴DM=.∴D与O重合.∴BO=BD=18.④如图7所示:∵HE与⊙O相切,∴EM=r,DM=.∴3r﹣.∴r=9+3∴OB=2r=18+6综上所述,当HE或GH与⊙O相切时,OB的长为18﹣6或9或18或18+6.。
2021年中考专题--翻折圆特训(含详细解析)

翻折圆专题一.选择题1.如图,将AB ⌒ 沿弦AB 翻折过圆心O 点,交弦AC 于D ,AD =1,CD =2,则AB 长为( )A .25 B .223 C .5 D .72.已知⌒O 的半径为5,弦AB 的长为8,将AB ⌒ 沿直线AB 翻折得到ACB ⌒ ,如图所示,则点O 到ACB⌒ 所在圆的切线长OC 为( )A .11B .22C .5D .33.如图,在⌒O 中,将AB ⌒ 沿弦AB 翻折交半径AO 的延长线于点D ,延长BD 交⌒O 于点C ,AC 切ADB⌒ 所在的圆于点A ,则tan⌒C 的值是( )A .3B .34 C .2+3 D .1+24.以半圆中的一条弦BC (非直径)为对称轴将弧BC 折叠后与直径AB 交于点D ,若32DB AD ,且AB =10,则CB 的长为( )A .54B .34C .24D .45.如图,在⌒O 中,点C 在优弧AB⌒ 上,将弧BC ⌒ 沿BC 折叠后刚好经过AB 的中点D .若⌒O 的半径为5,AB =4,则BC 的长是( )A .32B .23C .235 D .265 二.填空题6.如图,等腰⌒ABC 中,AC =BC =32.⌒ACB =120°,以AB 为直径在⌒ABC 另一侧作半圆,圆心为O ,点D 为半圆上的动点,将半圆沿AD 所在直线翻叠,翻折后的弧AD 与直径AB 交点为F ,当弧AD 与BC 边相切时,AF 的长为 .7.如图,AB是⌒O的弦,点C在AB⌒上,点D是AB的中点.将AC⌒沿AC折叠后恰好经2,AB=8.则AC的长是.过点D,若⌒O的半径为58.一张半径为R的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O为半圆圆心,如果切点分直径之比为3:2,则折痕长为.⌒上一点,连接AD,交AB⌒于点C,9.如图,将⌒O的劣弧AB⌒沿AB翻折,D为优弧ADB连接BC、BD;若BC=5,则BD=.10.如图,将BC⌒沿弦BC折叠交直径AB于点D,若AD=4,DB=8,则BC的长是.11.已知:如图,在半径为8的⌒O中,AB为直径,以弦AC(非直径)为对称轴将AC⌒折叠后与AB 相交于点D ,如果AD =3DB ,那么AC 的长为 .12.如图,AB 是半圆O 的直径,将半圆沿弦BC 折叠,折叠后的圆弧与AB 交于点D ,再将弧BD 沿AB 对折后交弦BC 于E ,若E 恰好是BC 的中点,则BC :AB = .13.如图,已知⌒O 中,点C 在优弧AB 上,将弧BC 沿BC 折叠后刚好经过AB 的中点D ,若BC =23,AB =4,则⌒O 的半径为 .14.以半圆的一条弦BC (非直径)为对称轴将弧BC 折叠后与直径AB 交于点D ,若tan B =21,且AD =4,则AB = .15.如图,已知半圆O 的直径AB =4,沿它的一条弦折叠.若折叠后的圆弧与直径AB 相切于点D ,且AD :DB =3:1,则折痕EF 的长 .16.如图,扇形OAB的半径为4,⌒AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.(1)当P是OB中点,且PQ⌒OA时(如图1),弧AQ的长为;(2)将扇形OAB沿PQ对折,使折叠后的弧QB′恰好与半径OA相切于C点(如图2).若OP=3,则O到折痕PQ的距离为.三.解答题17.如图,将弧AB⌒沿着弦AB翻折,C为翻折后的弧上任意一点,延长AC交圆于D,连接BC.(1)求证:BC=BD;⌒=120°,求弦AB的长和圆的半径.(2)若AC=1,CD=4,弧AB18.如图1和图2,AB是⌒O的直径,AB=10,C是⌒O上的一点,将BC⌒沿弦BC翻折,交AB于点D.(1)若点D与圆心O重合,直接写出⌒B的度数;(2)设CD交⌒O于点E,若CE平分⌒ACB,⌒求证:⌒BDE是等腰三角形;⌒求⌒BDE的面积;⌒沿直径AB翻折,得到图2,若点F恰好是翻折后的BD⌒的中点,(3)将图1中的BD直接写出⌒B的度数.19.如图1,AB是⌒O的直径,AB=10,C是⌒O上的一点,将弧BC沿弦BC翻折,交AB 于点D,连接CD并延长,交⌒O于点E,连接BE.(1)当AD=2时,BE的长是.(2)当点D位于线段OA上时(不与点A重合),设⌒ABC=a,则a的取值范围是.(3)当⌒ABC=15°时,点D和点O的距离是.⌒所在圆的圆心是O′,当BE与⌒O′相切时,求BE的长.(4)如图2,设BDC20.如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为AB⌒,P是⌒上的一动点,连接PQ.半径OB上一动点,Q是AB(1)当⌒POQ=度时,PQ有最大值,最大值为.⌒的长;(2)如图2,若P是OB中点,且QP⌒OB于点P,求BQ(3)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在AO的延长线上,求阴影部分面积.(4)如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.21.如图,AB为⌒O的直径,点C为⌒O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作⌒MPB=⌒ADC.(1)判断PM与⌒O的位置关系,并说明理由;(2)若PC=3,求四边形OCDB的面积.22.如图,AB为⌒O的直径,点C是⌒O上一点,CD是⌒O的切线,⌒CDB=90°,BD交⌒O于点E.⌒=CE⌒.(1)求证:AC(2)若AE=12,BC=10.⌒求AB的长;⌒如图2,将BC⌒沿弦BC折叠,交AB于点F,则AF的长为23.已知半圆O的直径AB=4,沿它的一条弦折叠.(1)如图,若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,求折痕EF的长;(2)在使折叠后的圆弧与直径AB相切的过程中,请直接写出折痕EF的最大值和最小值.24.如图,⌒O的半径为2,弧AB等于120°,E是劣弧AB的中点.(1)如图⌒,试说明:点O、E关于AB对称(即AB垂直平分OE.);(2)把劣弧AB沿直线AB折叠(如图⌒)⌒O的动弦CD始终与折叠后的弧AB相切,求CD的长度的变化范围.25.如图1,半圆的直径AB长为6,点C在AB上,以BC为一边向半圆内部作一正方形BCDE,连接AD并延长交半圆于F点,连接BF.设BC的长为x(0<x<3),AF的长为y,(1)求y与x的函数关系式;(2)当x=2时,⌒求BF的长;⌒如图2,若将弧AF沿直线AF翻折与直径AB交于点G,试求AG的长.翻折圆小专题 参考答案与试题解析一.选择题1.如图,将AB ⌒ 沿弦AB 翻折过圆心O 点,交弦AC 于D ,AD =1,CD =2,则AB 长为( )A .25 B .223 C .5 D .7【分析】求出⌒CDB 为等边三角形,求出BE 和DE 的长,求出AE ,再根据勾股定理求出AB 即可.【解答】解:过点O 作OF ⌒AB 于F ,过点B 作BE ⌒AC 于E ,连接OA 、OB 、BD 、BC , ⌒OF =21OA , ⌒⌒AOF =⌒BOF =60°, ⌒⌒ADB =⌒AOB =120°,⌒ACB =21⌒AOB =60°, ⌒⌒CDB =⌒ACB =60°, ⌒⌒CDB 为等边三角形,⌒CD =2,⌒DE =1,BE =3,⌒AB =22BE AE +=()()22311++=7, 故选:D .【点评】本题考查了勾股定理、等边三角形的性质和判定,圆周角定理和垂径定理,能构造直角三角形是解此题的关键,注意:垂直于弦的直径平分这条弦.2.已知⌒O 的半径为5,弦AB 的长为8,将AB⌒ 沿直线AB 翻折得到ACB ⌒ ,如图所示,则点O 到ACB⌒ 所在圆的切线长OC 为( )A .11B .22C .5D .3【分析】首先作出ACB⌒ 所在圆,圆心为O ′,连接OO ′交AB 于点E ,连接,O ′C ,OB ,由垂径定理,可求得OE 的长,即可求得OO ′的长,由切线的性质,利用勾股定理即可求得答案.【解答】解:作出ACB⌒ 所在圆,圆心为O ′,连接OO ′交AB 于点E ,连接O ′C ,OB , ⌒OC 是⌒O ′的切线, ⌒O ′C ⌒OC ,⌒BE =21AB =21×8=4, ⌒OE =22BE OB -=3,⌒OO ′=2OE =6,⌒OC =22C O O O '+'=115622=-.故选:A .【点评】此题考查了切线的性质、垂径定理以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.3.如图,在⌒O 中,将AB ⌒ 沿弦AB 翻折交半径AO 的延长线于点D ,延长BD 交⌒O 于点C ,AC 切ADB⌒ 所在的圆于点A ,则tan⌒C 的值是( )A .3B .34C .2+3D .1+2【分析】作点D 关于AB 的对称点H ,连接AH ,BH ,CH .首先证明CH 是⌒O 的直径,⌒ACH ,⌒BDH 都是等腰直角三角形,再证明⌒ACD =⌒CHB =67.5即可解决问题;【解答】解:作点D 关于AB 的对称点H ,连接AH ,BH ,CH .⌒所在圆的圆心在直线AH上,根据对称性可知,ADB⌒所在的圆于点A,⌒AC切ADB⌒AC⌒AH,⌒⌒CAH=90°,⌒CH是⌒O的直径,⌒⌒CBH=90°,⌒⌒ABD=⌒ABH=45°,⌒⌒AHC=⌒ABC=45°,⌒⌒ACH=⌒AHC=45°,⌒AC=AH,⌒OC=OH,⌒AD垂直平分线段CH,⌒DC=DH,⌒⌒DCH=⌒DHC,⌒BD=BH,⌒⌒BDH=⌒BHD=45°,⌒⌒BDH=⌒DCH+⌒DHC,⌒⌒DCH =22.5°,⌒⌒ACD =⌒CHB =67.5°,设BD =BH =a ,则CD =DH =2a ,⌒tan⌒ACB =tan⌒CHB =212+=+=aa a BH BC 故选:D .【点评】本题考查切线的性质、圆周角定理、翻折变换、等腰直角三角形的判定和性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明CH 是直径,⌒ACH ,⌒BDH 都是等腰直角三角形.4.以半圆中的一条弦BC (非直径)为对称轴将弧BC 折叠后与直径AB 交于点D ,若32=DB AD ,且AB =10,则CB 的长为( )A .54B .34C .24D .4【分析】作AB 关于直线CB 的对称线段A ′B ,交半圆于D ′,连接AC 、CA ′,构造全等三角形,然后利用勾股定理、割线定理解答.【解答】解:如图,若32=DB AD ,且AB =10, ⌒AD =4,BD =6,作AB 关于直线BC 的对称线段A ′B ,交半圆于D ′,连接AC 、CA ′,可得A 、C 、A ′三点共线,⌒线段A ′B 与线段AB 关于直线BC 对称,⌒AB =A ′B ,⌒AC =A ′C ,AD =A ′D ′=4,A ′B =AB =10.而A ′C •A ′A =A ′D ′•A ′B ,即A ′C •2A ′C =4×10=40.则A ′C 2=20,又⌒A ′C 2=A ′B 2﹣CB 2,⌒20=100﹣CB 2,⌒CB =45.故选:A .【点评】此题将翻折变换、勾股定理、割线定理相结合,考查了同学们的综合应用能力,要善于观察图形特点,然后做出解答.5.如图,在⌒O 中,点C 在优弧AB⌒ 上,将弧BC ⌒ 沿BC 折叠后刚好经过AB 的中点D .若⌒O 的半径为5,AB =4,则BC 的长是( )A .32B .23C .235D .265 【分析】连接OD 、AC 、DC 、OB 、OC ,作CE ⌒AB 于E ,OF ⌒CE 于F ,如图,利用垂径定理得到OD ⌒AB ,则AD =BD =21AB =2,于是根据勾股定理可计算出OD =1,再利用折叠的性质可判断弧AC 和弧CD 所在的圆为等圆,则根据圆周角定理得到AC⌒ =CD ⌒ ,所以AC =DC ,利用等腰三角形的性质得AE =DE =1,接着证明四边形ODEF 为正方形得到OF =EF =1,然后计算出CF 后得到CE =BE =3,于是得到BC =32.【解答】解:连接OD 、AC 、DC 、OB 、OC ,作CE ⌒AB 于E ,OF ⌒CE 于F ,如图, ⌒D 为AB 的中点,⌒OD ⌒AB ,⌒AD =BD =21AB =2, 在Rt⌒OBD 中,OD =()2225-=1,⌒将弧BC⌒ 沿BC 折叠后刚好经过AB 的中点D . ⌒弧AC 和弧CD 所在的圆为等圆,⌒AC⌒ =CD ⌒ , ⌒AC =DC ,⌒AE =DE =1,易得四边形ODEF 为正方形,⌒OF =EF =1,在Rt⌒OCF 中,CF =()2225-=2,⌒CE =CF +EF =2+1=3,而BE =BD +DE =2+1=3,⌒BC =32.故选:B.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理和垂径定理.二.填空题2.⌒ACB=120°,以AB为直径在⌒ABC另一侧作6.如图,等腰⌒ABC中,AC=BC=3半圆,圆心为O,点D为半圆上的动点,将半圆沿AD所在直线翻叠,翻折后的弧AD与直径AB交点为F,当弧AD与BC边相切时,AF的长为【分析】作点O关于AD的对称点O′,连接O′A,延长BC交⌒O于点E,设⌒O′与BC 相切于点G,证明四边形O′AEG为平行四边形,得AO′⌒BE,即⌒O′AB=⌒ABC=30°,作O′M⌒AF于M,在Rt⌒O′AM中,O′A=3,⌒O′AB=30°,可求得AM的长,进而得出AF的长.【解答】解:如图,作点O关于AD的对称点O′,连接O′A,⌒AC=BC=23.⌒ACB=120°,⌒AB=6,⌒O′A=OA=3,延长BC交⌒O于点E,⌒AB是⌒O的直径,⌒⌒E=90°,设⌒O′与BC相切于点G,则⌒O′GB=90°,⌒⌒E=⌒O′GB,⌒AE⌒O′G,⌒⌒ABC=30°,AB=6,⌒AE=O′G=3,⌒四边形O′AEG为平行四边形,⌒AO′⌒BE,⌒⌒O′AB=⌒ABC=30°,作O′M⌒AF于M⌒O′A=3,⌒O′AB=30°,⌒AM=MF=233,⌒AF=2AM=33.故答案为:33.【点评】本题考查圆的切线的性质,垂径定理,直角三角形的性质,平行四边形的判定和性质,解题的关键是掌握圆的切线的性质.7.如图,AB 是⌒O 的弦,点C 在AB⌒ 上,点D 是AB 的中点.将AC ⌒ 沿AC 折叠后恰好经过点D ,若⌒O 的半径为52,AB =8.则AC【分析】如图,延长BO 交⌒O 于E ,连接AE ,OA ,OD ,OC ,BC ,作CH ⌒AB 于H .首先证明⌒CAE =⌒CAH =45°,推出⌒BOC =90°,推出BC =210,设AH =CH =x ,则BH =8﹣x ,在Rt⌒BCH 中,根据CH 2+BH 2=BC 2,构建方程求出x 即可解决问题;【解答】解:如图,延长BO 交⌒O 于E ,连接AE ,OA ,OD ,OC ,BC ,作CH ⌒AB 于H .⌒AD =DB ,⌒OD ⌒AB , ⌒⌒ADO =90°,⌒OA =25,AD =DB =4,⌒OD =22AD OA =2,⌒BE 是直径,⌒⌒BAE =90°,⌒AD =DB ,EO =OB , ⌒OD ⌒AE ,AE =2OD =4,⌒AE =AD ,⌒AD⌒ =AE ⌒ , ⌒EC⌒ =CD ⌒ , ⌒⌒CAE =⌒CAH =45°,⌒⌒BOC =2⌒CAB =90°,⌒BC =2OC =210,⌒CH ⌒AB ,⌒⌒CAH =⌒ACH =45°,⌒AH =CH ,设AH =CH =x ,则BH =8﹣x , 在Rt⌒BCH 中,⌒CH 2+BH 2=BC 2, ⌒x 2+(8﹣x )2=(210)2,⌒x =6或2(舍弃),在Rt⌒ACH 中,⌒AC =22CH AH , ⌒AC =62.故答案为62.【点评】本题考查圆周角定理、垂径定理、勾股定理、解直角三角形等知识,综合性比较强,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题.属于中考填空题中的压轴题.8.一张半径为R 的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O 为半圆圆心,如果切点分直径之比为3:2【分析】如图,作O 点关于AB 的对称点O ′,则点O ′为弧ADB 所在圆的圆心,连结O ′D ,则O ′D ⌒EF ,O ′D =R ,先利用ED :DF =3:2计算出DF =52•2R =54R ,则OD =51R ,再在Rt⌒O ′OD 中利用勾股定理计算出O ′=526R ,则OC =21O ′O =1026R ,然后在Rt⌒AOC 中根据勾股定理可计算出AC =1074R ,再利用垂径定理可得AB =2AC =574R . 【解答】解:如图,作O 点关于AB 的对称点O ′,则点O ′为弧ADB 所在圆的圆心, 连结O ′D ,则O ′D ⌒EF ,O ′D =R ,⌒ED :DF =3:2, ⌒DF =52•2R =54R , ⌒OD =51R , 在Rt⌒O ′OD 中,OO ′=2251R R +⎪⎭⎫ ⎝⎛=526R ,⌒OC =21O ′O =1026R , 在Rt⌒AOC ,AC =22526⎪⎪⎭⎫ ⎝⎛-R R =1074R , ⌒OC ⌒AB ,⌒AC =BC ,⌒AB =2AC =574R . 即折痕长为574R . 故答案为574R .【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理.9.如图,将⌒O 的劣弧AB⌒ 沿AB 翻折,D 为优弧ADB ⌒ 上一点,连接AD ,交AB ⌒ 于点C ,连接BC 、BD ;若BC =5,则BD = 5 .【分析】根据圆周角定理、翻转变换的性质得到⌒ADB =⌒BCD ,根据等腰三角形的判定定理解答.【解答】解:由翻转变换的性质可知,⌒ADB 所对的弧是劣弧AB⌒ , ⌒CAB 所对的弧是劣弧BC⌒ ,⌒CBA 所对的弧是劣弧AC ⌒ , ⌒⌒ADB =⌒CAB +⌒CBA ,由三角形的外角的性质可知,⌒BCD =⌒CAB +⌒CBA ,⌒⌒ADB =⌒BCD ,⌒BD =BC =5,故答案为:5.【点评】本题考查的是翻转变换的性质、圆周角定理的应用,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.10.如图,将BC⌒ 沿弦BC 折叠交直径AB 于点D ,若AD =4,DB =8,则BC 的长是【分析】根据折叠的性质可得BC⌒ =BDC ⌒ ,再根据在同圆或等圆中,等弧所对的圆周角相等可得⌒BAC =⌒BCD +⌒CBD ,根据三角形的一个外角等于与它不相邻的两个内角的和可得⌒ADC =⌒BCD +⌒CBD ,从而得到⌒BAC =⌒ADC ,根据等角对等边可得AC =CD ,过点C 作CE ⌒AD 于E ,根据等腰三角形三线合一的性质可得AE =DE =21AD ,然后利用⌒ACE 和⌒CBE 相似,根据相似三角形对应边成比例列式求出CE ,在Rt⌒BCE 中,利用勾股定理列式计算即可得解.【解答】解:⌒弧BC 沿弦BC 折叠交直径AB 于点D ,⌒BC⌒ =BDC ⌒ , ⌒⌒BAC =⌒BCD +⌒CBD ,在⌒BCD 中,⌒ADC =⌒BCD +⌒CBD ,⌒⌒BAC =⌒ADC ,⌒AC =CD ,过点C 作CE ⌒AD 于E ,则AE =DE =21AD =21×4=2, ⌒BE =BD +DE =8+2=10,⌒AB 是直径,⌒⌒ACB =90°,⌒⌒ACE +⌒BCE =⌒ACB =90°,⌒⌒ACE +⌒CAE =180°﹣90°=90°,⌒⌒CAE =⌒BCE ,又⌒⌒AEC =⌒BEC =90°,⌒⌒ACE ⌒⌒CBE , ⌒BECE CE AE ,⌒CE =52102=⨯=•BE AE在Rt⌒BCE 中,BC =()30210522222=+=+BE CE 故答案为:2302.【点评】本题考查了翻折变换的性质,勾股定理的应用,相似三角形的判定与性质,等腰三角形三线合一的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线构造出等腰三角形和直角三角形是解题的关键,难点在于求出AC =CD .11.已知:如图,在半径为8的⌒O 中,AB 为直径,以弦AC (非直径)为对称轴将AC⌒ 折叠后与AB 相交于点D ,如果AD =3DB ,那么AC【分析】根据翻折变换的性质和圆周角定理可得⌒ABC =⌒ACD +⌒CAD ,根据三角形的外角的性质可得⌒BDC =⌒ACD +⌒CAD ,从而得到⌒ABC =⌒BDC ,根据等角对等边可得BC =CD ,过点C 作CE ⌒BD 于E ,根据等腰三角形三线合一的性质可得BE =DE =21BD ,然后利用⌒ACE 和⌒CBE 相似,根据相似三角形对应边成比例列式求出CE ,在Rt⌒BCE 中,利用勾股定理列式计算即可.【解答】解:连接CD 、CB ,作CE ⌒AB 于E ,⌒弧AC 沿弦AC 折叠交直径AB 于点D ,⌒⌒ABC =⌒ACD +⌒CAD ,在⌒BCD 中,⌒BDC =⌒ACD +⌒CAD ,⌒⌒ABC =⌒BDC ,⌒BC =CD ,又CE ⌒AB ,⌒BE =DE =21BD , ⌒AD =3DB ,AD +BD =16,⌒BD =4,AD =12,⌒AE =AD +DE =12+2=14,⌒AB 是直径,⌒⌒ACB =90°,⌒⌒ACE +⌒CAD =⌒ACB =90°,⌒⌒ACE +⌒BCE =90°,⌒⌒CAD =⌒BCE ,又⌒⌒AEC =⌒BEC =90°,⌒⌒ACE ⌒⌒CBE , ⌒BECE CE AE = ⌒CE =27,⌒AC =14422=+CE AE 故答案为:144.【点评】本题考查了翻折变换的性质,勾股定理的应用,相似三角形的判定与性质,等腰三角形三线合一的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线构造出等腰三角形和直角三角形是解题的关键.12.如图,AB 是半圆O 的直径,将半圆沿弦BC 折叠,折叠后的圆弧与AB 交于点D ,再将弧BD 沿AB 对折后交弦BC 于E ,若E 恰好是BC 的中点,则BC :AB .【分析】过D 点作BC 的垂线,垂足为M ,延长DM 交AB⌒ 于D ′,连接CD 、DE 、BD ′,过点C 作CF ⌒AB 于点F ,由圆周角定理得出AC ⌒ =CD'⌒ =CD ⌒ =DE ⌒ ,得出AC =CD =DE ,证出CM =EM ,延长CM =41BC ,证出DM ⌒AC ,⌒AD =41AB ,设⌒ABC =α,则⌒ACF =α,得出AD =2AF ,由三角函数得出AD =2AB •sin 2α,因此41AB =2AB •sin 2α,求出sinα=42,由勾股定理和三角函数得出cosα=AB BC =414,即可得出结果. 【解答】解:过D 点作BC 的垂线,垂足为M ,延长DM 交于D ′,连接CD 、DE 、BD ′,过点C 作CF ⌒AB 于点F ,如图所示:由等圆中圆周角相等所对的弧相等得:AC⌒ =CD'⌒ =CD ⌒ =DE ⌒ , ⌒AC =CD =DE ,⌒CM =EM ,⌒E 是BC 的中点,⌒CM =41BC , ⌒AB 是半圆O 的直径,⌒AC ⌒BC ,⌒DM ⌒BC ,⌒DM ⌒AC ,⌒AD =41AB , 设⌒ABC =α,则⌒ACF =α,⌒AC =CD ,⌒AD =2AF ,⌒AF =AC •sinα,AC =AB •sinα,⌒AD =2AB •sin 2α, ⌒41AB =2AB •sin 2α, ⌒sinα=42,即AB AC =42, ⌒AB =22AC ,BC =22AC AB =7AC ,⌒cosα=AB BC =414, ⌒BC :AB =414;故答案为:414.【点评】本题考查了翻折变换的性质、圆周角定理、勾股定理、三角函数等知识;熟练掌握圆周角定理,求出cosα是解决问题的关键.13.如图,已知⌒O 中,点C 在优弧AB 上,将弧BC 沿BC 折叠后刚好经过AB 的中点D ,若BC =23,AB =4,则⌒O【分析】连接OD 、AC 、DC 、OB 、OC ,作CE ⌒AB 于E ,OF ⌒CE 于F ,首先证明AC =CD ,推出AE =DE =1,再证明四边形OFED 是正方形即可解决问题.【解答】解:连接OD 、AC 、DC 、OB 、OC ,作CE ⌒AB 于E ,OF ⌒CE 于F ,如图, ⌒D 为AB 的中点,⌒OD ⌒AB ,⌒AD =BD =21AB =2, 沿BC 折叠后刚好经过AB 的中点D .⌒弧AC 和弧CD 所在的圆为等圆,⌒AC⌒ =CD ⌒ , ⌒AC =DC ,⌒AE =DE =1,⌒BE =3,EC =22BE BC -=3,⌒EC =EB ,⌒⌒ECB =⌒EBC =45°,⌒OC =OB ,⌒⌒OCB =⌒OBC ,⌒⌒OCE =⌒OBD ,⌒⌒OFC =⌒ODB =90°,OC =OB ,⌒⌒OCF ⌒⌒OBD (AAS ),⌒OF =OD ,可得四边形ODEF 为正方形,⌒OF =EF =1,在Rt⌒OBD 中,OB =22BD OD +=5【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理和垂径定理.14.以半圆的一条弦BC (非直径)为对称轴将弧BC 折叠后与直径AB 交于点D ,若tan B=21,且AD =4,则AB = 10 .【分析】作线段AB 关于直线BC 的对称线段BA ′,交⌒O 于D ′,连接AC 、CA ′,设AC =a ,BC =2a ,则AB =5a ,由A ′C •A ′A =A ′D ′•A ′B ,列出方程解决.【解答】解:作线段AB 关于直线BC 的对称线段BA ′,交⌒O 于D ′,连接AC 、CA ′. ⌒AB 是直径,⌒⌒ACB =⌒BCA ′=90°,⌒A 、C 、A ′共线,根据对称性可知:AD =A ′D =4,⌒tan⌒ABC =21=BC AC ,设AC =a ,BC =2a ,则AB =5a ,由A ′C •A ′A =A ′D ′•A ′B ,⌒a •2a =45a ,⌒a =25.AB =525•=10.故答案为10.【点评】本题考查翻折变换、相交弦定理,解题的关键是作线段AB 关于直线BC 的对称线段BA ′,转化为相交弦定理解决问题.15.如图,已知半圆O 的直径AB =4,沿它的一条弦折叠.若折叠后的圆弧与直径AB 相切于点D ,且AD :DB =3:1,则折痕EF【分析】设折叠后的圆弧所对圆心为O ′,连接O ′O 、O ′D 、OE ,O ′O 与EF 交于点M ,根据相交圆的性质就可以得出O ′O 与EF 互相垂直平分,由勾股定理就可以求出OO ′和EM 的值,从而得出结论.【解答】解:设折叠后的圆弧所对圆心为O ′,连接O ′O 、O ′D 、OE ,O ′O 与EF 交于点M , ⌒O ′O 与EF 互相垂直平分.⌒OM =21OO ′,EF =2EM . ⌒AB =4,⌒OA =OB =OE =2.⌒AD :DB =3:1,⌒DB =41AB =1, ⌒OD =1⌒O ′O =522='+D O OD ⌒OM =25 ⌒EM =21122=-OM OE ⌒EF =2EM =11,即折痕EF 的长为11. 故答案为:11.【点评】本题考查了翻折的性质的运用,相交圆的性质的运用,勾股定理的运用,垂直平分线的性质的运用,解答时求出根据相交圆的性质求解是关键.16.如图,扇形OAB 的半径为4,⌒AOB =90°,P 是半径OB 上一动点,Q 是弧AB 上的一动点.(1)当P 是OB 中点,且PQ ⌒OA 时(如图1),弧AQ 的长为 π3; (2)将扇形OAB 沿PQ 对折,使折叠后的弧QB ′恰好与半径OA 相切于C 点(如图2).若OP =3,则O 到折痕PQ .【分析】(1)要想求弧长,就得求AQ⌒ 所对的圆心角的度数,所以要连接OQ ,构成圆心角,利用直角三角形直角边是斜边的一半,则这条直角边所对的锐角为30°求出⌒1=30°,再利用平行线截得内错角相等得出⌒2的度数,代入弧长公式计算即可.(2)先找点O 关于PQ 的对称点O ′,连接OO ′、O ′B 、O ′C 、O ′P ,证明四边形OCO ′B 是矩形,由勾股定理求O ′B ,从而求出OO ′的长,则OM =21OO ′=6. 【解答】解:(1)如图1,连接OQ ,⌒扇形OAB 的半径为4且P 是OB 中点,⌒OP =2,OQ =4,⌒PQ ⌒OA ,⌒⌒BPQ =⌒AOB =90°,⌒⌒1=30°,⌒⌒2=⌒1=30°,由弧AQ 的长=180430⨯⨯π=π32, 故答案为:π32; (2)如图2,找点O 关于PQ 的对称点O ′,连接OO ′、O ′B 、O ′C 、O ′P ,ON ,则OM =O ′M ,OO ′⌒PQ ,O ′P =OP =3,点O ′是B'Q⌒ 所在圆的圆心, ⌒O ′C =OB =4,⌒折叠后的弧QB ′恰好与半径OA 相切于C 点,⌒O ′C ⌒AO ,⌒O ′C ⌒OB ,⌒⌒POO '=⌒CO 'M =⌒PO 'M ,⌒⌒PMO '=⌒QMO '=90°,⌒⌒O 'PM =⌒MNO ',⌒O 'P =O 'N =OP =3,⌒四边形OPO 'N 是平行四边形,⌒O 'P =ON ,⌒O 与O '对称,⌒ON =O 'N =3,⌒BP =CN =4﹣3=1,⌒PN ⌒OO ',⌒⌒MNO '=⌒MNO ,⌒⌒BPO '=⌒CNO ,⌒⌒O 'BP ⌒⌒OCN (SAS ),⌒⌒O 'BP =⌒OCN =90°,⌒四边形OCO ′B 是矩形,在Rt⌒O ′BP 中,O ′B =2213-=22,在Rt⌒OBO ′中,OO ′=()22224-=26, ⌒OM =21OO ′=21×26=6, 即O 到折痕PQ 的距离为6,故答案为:6.【点评】本题考查了折叠问题和圆的切线的性质、矩形的性质和判定,熟练掌握弧长公式l =180n R π(n 为圆心角度数,R 为圆半径),明确过圆的切线垂直于过切点的半径,这是常考的性质;对称点的连线被对称轴垂直平分.三.解答题17.如图,将弧AB⌒ 沿着弦AB 翻折,C 为翻折后的弧上任意一点,延长AC 交圆于D ,连接BC .(1)求证:BC =BD ;(2)若AC =1,CD =4,弧AB⌒ =120°,求弦AB 的长和圆的半径.【分析】(1)作点C 关于AB 的对称点C ′,连接AC ′,BC ′.利用翻折不变性,以及圆周角定理即可解决问题;(2)连接OA ,OB ,作OM ⌒AB 于M ,AH ⌒BC 交BC 的延长线于H .解直角三角形求出AB ,OA 即可;【解答】(1)证明:作点C 关于AB 的对称点C ′,连接AC ′,BC ′.由翻折不变性可知:BC =BC ′,⌒CAB =⌒BAC ′,⌒BD⌒ =BC'⌒ , ⌒BD =BC ′,⌒BC =BD .(2)解:连接OA ,OB ,作OM ⌒AB 于M ,AH ⌒BC 交BC 的延长线于H .⌒弧AB⌒ =120°, ⌒⌒D =21×120°=60°, ⌒⌒AOB =⌒ACB =2⌒D =120°,⌒BC =BD ,⌒⌒BCD 是等边三角形,⌒BC =DC =4,在Rt⌒ACH 中,⌒⌒H =90°,⌒ACH =60°,AC =1,⌒CH =21,AH =23, ⌒AB =2129232222=⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+BH AH⌒OM ⌒AB ,⌒AM =BM =221, 在Rt⌒AOM 中,⌒⌒OAM =30°,⌒AMO =90°,⌒OA =30cos AM =7 【点评】本题考查圆心角、弧、弦之间的关系,垂径定理,勾股定理,翻折变换,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.18.如图1和图2,AB 是⌒O 的直径,AB =10,C 是⌒O 上的一点,将BC⌒ 沿弦BC 翻折,交AB 于点D .(1)若点D 与圆心O 重合,直接写出⌒B 的度数;(2)设CD 交⌒O 于点E ,若CE 平分⌒ACB ,⌒求证:⌒BDE 是等腰三角形;⌒求⌒BDE 的面积;(3)将图1中的BD⌒ 沿直径AB 翻折,得到图2,若点F 恰好是翻折后的BD ⌒ 的中点,直接写出⌒B 的度数.【分析】(1)如图所示:将⌒O 沿BC 翻折得到⌒O ′,则⌒O 与⌒O ′为等圆,然后证明AC⌒ =CD⌒ =BD ⌒ ,则可得到AC ⌒ 的弧度,从而可求得⌒B 的度数; (2)⌒将⌒O 沿BC 翻折得到⌒O ′,则⌒O 与⌒O ′为等圆,在⌒O ′上取点E ′,连接CE ′,BE ′.由等弧所对的圆周角相等可得到⌒CEB =⌒E ′,依据圆内接四边形的性质可得到E ′=⌒BDE ,故此可证明⌒CEB =⌒BDE ;⌒连接OE .先证明⌒BOE 为直角,依据勾股定理可求得BE 的长,从而得到BD 的长,最后依据⌒DBE 的面积=21BD •OE 求解即可; (3)将⌒O 沿BC 翻折得到⌒O ′,将⌒O ′沿BD 翻折得到⌒O ″,则⌒O 、⌒O ′、⌒O ″为等圆.依据在同圆或等圆中相等的圆周角所对的弧相等可证明AC⌒ =CD ⌒ =DF ⌒ =FB ⌒ ,从而可得到弧AC 的度数,由弧AC 的度数可求得⌒B 的度数.【解答】解:(1)如图所示:将⌒O 沿BC 翻折得到⌒O ′,则⌒O 与⌒O ′为等圆.⌒AC⌒ 与CD ⌒ 所对的角均为⌒CBA ,⌒O 与⌒O ′为等圆, ⌒AC⌒ =CD ⌒ . 又⌒CD =BC ,⌒CD⌒ =BD ⌒ . 又⌒CDB⌒ =CO'B ⌒ , ⌒AC ⌒ =31ACB ⌒ , ⌒⌒ADC =31×180°=60°.⌒⌒B =30°.(2)⌒将⌒O 沿BC 翻折得到⌒O ′,则⌒O 与⌒O ′为等圆,在⌒O ′上取点E ′,连接CE ′,BE ′.由翻折的性质可知:CFB⌒ =CDB ⌒ , ⌒⌒CEB =⌒E ′.⌒四边形CDBE ′是圆内接四边形,⌒⌒E ′=⌒BDE .⌒⌒CEB =⌒BDE .⌒BE =BD .⌒⌒BDE 为等腰三角形.⌒如图2所示:连接OE .⌒AB 是⌒O 的直径,⌒⌒ACB =90°.⌒CE 是⌒ACB 的角平分线,⌒⌒BCE =45°.⌒⌒BOE =90°.在Rt⌒OBE 中,BE =2522=+OB OE .⌒BD =52.⌒⌒DBE 的面积=21BD •OE =21×52×5=2225.(3)将⌒O 沿BC 翻折得到⌒O ′,将⌒O ′沿BD 翻折得到⌒O ″,则⌒O 、⌒O ′、⌒O ″为等圆.⌒⌒O 与⌒O ′为等圆,劣弧AC 与劣弧CD 所对的角均为⌒ABC , ⌒AC⌒ =CD ⌒ . 同理:DF⌒ =CD ⌒ . 又⌒F 是劣弧BD 的中点, ⌒DF⌒ =BF ⌒ . ⌒AC⌒ =CD ⌒ =DF ⌒ =FB ⌒ . ⌒弧AC 的度数=180°÷4=45°. ⌒⌒B =21×45°=22.5°. 【点评】本题主要考查的是圆的综合应用,解答本题主要应用了翻折的性质、弧、弦、圆周角之间的关系、圆内接四边形的性质,等腰三角形的判定,找出图形中的等弧是解题的关键.19.如图1,AB是⌒O的直径,AB=10,C是⌒O上的一点,将弧BC沿弦BC翻折,交AB 于点D,连接CD并延长,交⌒O于点E,连接BE.(1)当AD=2时,BE的长是8.(2)当点D位于线段OA上时(不与点A重合),设⌒ABC=a,则a的取值范围是0<a≤30°.(3)当⌒ABC=15°时,点D和点O(4)如图2,设BCD⌒所在圆的圆心是O′,当BE与⌒O′相切时,求BE的长.【分析】(1)由折叠的性质以及圆周角定理的推理可知AC⌒=CD⌒,从而可知AC=DC,根据等腰三角形的性质可知:⌒CAD=⌒CDA,然后再证明⌒BDE=⌒BED,可推出BE=BD,最后根据BE=AB﹣AD求解即可;(2)当点D与点A重合时,点C与点A重合,此时,⌒ABC=a=0°;当点D与点O重合时,可证得⌒AOC为等边三角形,从而可知⌒ABC=30°,进而可确定出a的取值范围;(3)如图2所示:过点C作CF⌒AB,垂足为F,连接OC,先征得⌒COF=30°,在Rt⌒CFO中,根据特殊锐角三角函数值,可求得OF=235,然后根据等腰三角形三线合一可知AF=DF,从而可求得AD的长,最后根据DO=OA﹣AD求解即可.(4)如图3,作⌒O'的直径BF,连接FD、OE.由切线的性质可知⌒FBD+⌒DBE=90°,根据直径所对的圆周角等于90度可知:⌒FDB=90°,从而可证得⌒DBE=⌒DFB,根据同弧所对的圆周角相等可知:⌒DFB=⌒DCB,⌒DBE=⌒ACE,从而可得到⌒DBE=⌒DFB=⌒DCB=⌒ACE=45°,进而可证明⌒OBE为等腰直角三角形,然后可求得BE的长.【解答】解:(1)⌒⌒ABC=⌒DBC,⌒AC⌒=CD⌒.⌒AC=DC.⌒⌒CAD=⌒CDA⌒⌒CAD=⌒DEB,⌒CDA=⌒BDE,⌒⌒BDE=⌒BED.⌒BE=BD.⌒BE=AB﹣AD=10﹣2=8;(2)当点D与点A重合时,点C与点A重合,此时,⌒ABC=a=0°,如图1,当点D与点O重合时.则DC=DA.由(1)可知:AC=DC,又⌒DC=AD,⌒AC=DC=AD.⌒⌒ADC=60°.⌒⌒ABC=30°.⌒0°<α≤30°(3)如图2所示:过点C 作CF ⌒AB ,垂足为F ,连接OC .⌒⌒ABC =15°, ⌒⌒COF =30°.在Rt⌒CFO 中,cos⌒COF =23OC OF ⌒OF =235. ⌒AC =DC ,CF ⌒AD , ⌒AF =DF .⌒AD =2AF =2(OA ﹣OF )=2(5﹣235)=10﹣53. ⌒OD =OA ﹣AD =5﹣(10﹣53)=53﹣5; (4)如图3,作⌒O '的直径BF ,连接FD 、OE .⌒BE 与⌒O '相切, ⌒BE ⌒BF .⌒⌒FBD +DBE =90°. ⌒BF 是⌒O '的直径, ⌒⌒FDB =90°. ⌒⌒FBD +⌒DFB =90°. ⌒⌒DBE =⌒DFB .⌒⌒DFB =⌒DCB ,⌒DBE =⌒ACE , ⌒⌒DBE =⌒DFB =⌒DCB =⌒ACE . ⌒⌒ACB =90°,⌒⌒DBE =⌒DFB =⌒DCB =⌒ACE =45°. ⌒OB =OE ,⌒ABE =45°, ⌒⌒OEB =45°. ⌒⌒BOE =90°.在Rt⌒OBE 中,BE =22OB OE =52.【点评】本题主要考查的是圆的综合应用,解答本题主要应用了圆周角定理以及圆周角定理的推理、等腰三角形的性质和判断、特殊锐角三角函数,以及等边三角形的性质和判定,证得⌒ACD 为等腰三角形和⌒OBE 为等腰直角三角形是解答本题的关键. 20.如图1,将长为10的线段OA 绕点O 旋转90°得到OB ,点A 的运动轨迹为AB ⌒ ,P 是半径OB 上一动点,Q 是AB⌒ 上的一动点,连接PQ .(1)当⌒POQ = 90 度时,PQ(2)如图2,若P 是OB 中点,且QP ⌒OB 于点P ,求BQ⌒ 的长; (3)如图3,将扇形AOB 沿折痕AP 折叠,使点B 的对应点B ′恰好落在AO 的延长线上,求阴影部分面积.(4)如图4,将扇形OAB 沿PQ 折叠,使折叠后的弧QB ′恰好与半径OA 相切,切点为C ,若OP =6,求点O 到折痕PQ 的距离.【分析】(1)先判断出当PQ 取最大时,点Q 与点A 重合,点P 与点B 重合,即可得出结论;(2)先判断出⌒POQ =60°,最后用弧长用弧长公式即可得出结论;(3)先在Rt⌒B 'OP 中,OP 2+(102﹣10)2=(10﹣OP )2,解得OP =102﹣10,最后用面积的和差即可得出结论.(4)先找点O 关于PQ 的对称点O ′,连接OO ′、O ′B 、O ′C 、O ′P ,证明四边形OCO ′B 是矩形,由勾股定理求O ′B ,从而求出OO ′的长,进而得出OP . 【解答】解:(1)⌒P 是半径OB 上一动点,Q 是AB ⌒ 上的一动点, ⌒当PQ 取最大时,点Q 与点A 重合,点P 与点B 重合,此时,⌒POQ =90°,PQ =22OB OA =102,故答案为:90,102;(2)如图2,连接OQ , ⌒点P 是OB 的中点, ⌒OP =21OB =21OQ . ⌒QP ⌒OB , ⌒⌒OPQ =90°在Rt⌒OPQ 中,cos⌒QOP =21=OQ OP , ⌒⌒QOP =60°,⌒l BQ ⌒ =ππ3101801060=⨯ ;(3)由折叠的性质可得,BP =B 'P ,AB '=AB =102,在Rt⌒B 'OP 中,OP 2+(102﹣10)2=(10﹣OP )2解得OP =102, S 阴影=S 扇形AOB ﹣2S ⌒AOP =()100210025102101021210360902+-=-⨯⨯-⨯ππ. (4)找点O 关于PQ 的对称点O ′,连接OO ′、O ′B 、O ′C 、O ′P ,如图4, 则OP =O ′P ,OO ′⌒PQ ,O ′P =OP =6,点O ′是B'Q⌒ 所在圆的圆心,⌒O ′C =OB =10,⌒折叠后的弧QB ′恰好与半径OA 相切于C 点, ⌒O ′C ⌒AO , ⌒O ′C ⌒OB ,⌒四边形OCO ′B 是矩形,在Rt⌒O ′BP 中,O ′B =524622=-,在Rt⌒OBO ′,OO ′=()302521022=+,⌒OP =21OO ′=21×230=30, 即O 到折痕PQ 的距离为30,【点评】此题是圆的综合题,主要考查了圆的性质,弧长公式,扇形的面积公式,熟记公式是解本题的关键.21.如图,AB 为⌒O 的直径,点C 为⌒O 上一点,将弧BC 沿直线BC 翻折,使弧BC 的中点D 恰好与圆心O 重合,连接OC ,CD ,BD ,过点C 的切线与线段BA 的延长线交于点P ,连接AD ,在PB 的另一侧作⌒MPB =⌒ADC . (1)判断PM 与⌒O 的位置关系,并说明理由;(2)若PC =3,求四边形OCDB 的面积.。
2021年中考数学高频考点:《圆的综合》解答题专题练习(一)含答案

2021年中考数学复习高频考点精准练:《圆的综合》解答题专题练习(一)1.如图1,在△ABC中,AB=AC=5,以AB为直径作⊙O,分别交AC,BC于点E,F,连接EF,OE.(1)求证:∠OEF=∠ABC;(2)如图2,连接BE,若点D是线段BE上的一个动点,且tan∠CFE=2,求CD+BD 的最小值.2.在⊙O中,AB为直径,点P在BA的延长线上,PC为⊙O的切线,过点A作AH⊥PC于点H,交⊙O于点D,连接BC、BD、AC.(1)如图1,求证:∠CAH=∠CAB;(2)如图2,过点C作CE⊥AB于点E,求证:BD=2CE;(3)如图3,在(2)的条件下,点F在BC上,连接DF、EF,若BG=2AE,∠CFE=45°,OG=1,求线段EF的长.3.如图,在⊙O中,弦BC⊥半径OA于点D,点F是CD上一点,AF交⊙O于点E,点P为BC延长线上一点,PF=PE.(1)求证:PE是⊙O的切线;(2)若AD=2,BC=8,DF=1,求PE的长.4.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,过D作直线DG∥BC.(1)求证:DG是⊙O的切线;(2)若DE=6,BC=6,求阴影部分的面积.5.在等边三角形ABC中,经过点B有一个圆与AC,AB,BC分别交于点D,E,F,连接BD,DE,DF.(1)如图(1),若BD是圆的直径,AE=CF时,求证:DE=DF;(2)如图(2),若=,AD=4时,求AB的长.6.如图,AB是⊙O的直径,D是AB延长线上的一点,点C在⊙O上,BC=BD,AE⊥CD交DC 的延长线于点E,AC平分∠BAE.(1)求证:CD是⊙O的切线;(2)若CD=6,求⊙O的直径.7.如图,AB是⊙O的直径,点C在⊙O上,点D为弦BC的中点,射线OD与圆周及切线BE 分别交于点M和点E,连接CE.(1)求证:直线CE是⊙O的切线;(2)若直径AB=4,填空:①连接CM,CO,当∠ABC=°时,四边形ACMO是菱形;②当ME=时,四边形OCEB是正方形.8.如图,AB是⊙O的弦,连接OA,过点O作OC⊥OA,OC交AB于点P,延长OP到C,连接BC,且CP=CB.(1)求证:BC是⊙O的切线;(2)若∠BAO=25°,OA=18,点Q是上的一点,求的长(结果用π表示).9.(1)如图1,求证:∠AOD=2∠ACD;(2)如图2,AC⊥BD,M是AB中点,求证:①EM⊥CD;②CD=2OM.10.如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB.(1)求证:直线AB是⊙O的切线;(2)求证:∠FDC=∠EDC;(3)已知:DE=10,DF=6,求DC的长.11.如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;(2)若∠PAC=90°,AB=2,求PD的长.12.如图,AB为⊙O的直径,直线l与⊙O相切于D,⊙O的弦BC∥l,连接AD、AC,过D 作DE⊥AB于E点.(1)求证:BC=2DE;(2)过D作DG∥AB交AC于点G,GF⊥AB于点F.且BC=BF,求tan∠DAB的值.13.如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过A作⊙O的切线,过C作DA的平行线,两直线交于F,FC的延长线交AB的延长线于点G.(1)填空:∠D=°;(2)求证:FG与⊙O相切;(3)连接EF,求tan∠EFC的值.14.如图.⊙O过长方形ABCD的顶点D和BC上一点E.且与BA相切于点F,⊙O分别交AD,CD于G,H两点,BF=BE.(1)求证:BC是⊙O的切线;(2)连接FE,ED.若AG=1,BF=5,CH=2.求tan∠FED的值.15.在锐角△ABC中,AB=AC,以AB为直径的⊙O分别交边BC、AC于点D、E,AF⊥DE于点F.(1)求证:∠EDC=2∠CAF;(2)若直线AF是⊙O的切线,试判断△ABC的形状,并说明理由;(3)若=,求的值.参考答案1.(1)证明:如图1中,连接AF,OF.∵AB是直径,∴∠AFB=90°,∴AF⊥BC,∵AB=AC,∴∠EAF=∠FAB,∵∠EOF=2∠EAF,∠FOB=2∠FAB,∴∠EOF=∠FOB,∵OE=OF=OB,∴∠OEF=∠OFE=∠OFB=∠ABC,∴∠OEF=∠ABC.(2)解:如图2中,连接AF,过点C作CM⊥AB于M,过点D作DH⊥AB于H.∵四边形ABFE是圆内接四边形,∵∠CFE+∠EFB=180°,∴∠CFE=∠CAB,在Rt△AEB中,tan∠CAB=,tan∠CFE=2,∴=2,设AE=k,则BE=2k,∵AE2+BE2=AB2,∴k2+(2k)2=52,解得k=或﹣(舍弃),∴AE=,BE=2,∵AB=AC=5,AF⊥BC,BE⊥AC,又∵S=•AB•CM=•AC•BE,△ABC∴CM=BE=2,∵∠DHB=∠AEB=90°,∴sin∠DBH===,∴DH=BD,∵CD+DH≥CM=2,∴CD+BD=(CD+DH)≥×=10,∴CD+BD的最小值为10.2.(1)证明:连接OC,∵PC为⊙O的切线,∴OC⊥PC,∴∠PCO=90°,∵AH⊥PC,∴OC∥AH,∴∠CAH=∠ACO,∵OA=OC,∴∠OAC=∠OCA,∴∠CAH=∠CAB;(2)证明:连接OC,延长CO交BD于点M,∵∠CAH=∠CAB,CH⊥AH,CE⊥AB,∴CE=CH,∵AB为⊙O的直径,∴∠ADB=90°,∴∠DHC=∠HCM=∠ADB=90°,∴四边形HDMC为矩形,∴HC=DM,∠CMD=90°,CM⊥BD,∴BD=2DM=2CH=2CE;(3)解:连接CD,过点E作ES⊥BC于点S,ET⊥DF于点T,在Rt△CAH和Rt△CAE中,AC=AC,CH=CE,∴Rt△CAH≌Rt△CAE(HL),∴AH=AE,∵=,∴∠ABC=∠ADC,∵∠CAH=∠CEB=90°,CH=CE,∴△CHD≌△CEB(AAS),∴DH=BE,∵BG=2AE,设AE=a,则AH=AE=a,∵OG=1,∴OA=OB=2a+1,∴EO=OA﹣AE=a+1,EG=EO+OG=a+2,AG=OA+OG=2a+2,∴DH=BE=EG+BG=3a+2,∴AD=DH﹣AH=2a+2,∴AD=AG,∴∠ADG=∠AGD,∵∠HAE=∠ADG+∠AGD,∠HAE=∠HAC+∠EAC,由(1)知∠HAC=∠EAC,∴∠HAC=∠EAC=∠ADG=∠AGD,∴AC∥DF,∵AB为⊙O的直径,∴∠ACB=90°,∴∠DFC=∠DFB=∠ACB=90°,∵∠CFE=45°,∴∠EFC=∠EFD=45°,∵ES⊥BC,ET⊥DF,∴ES=ET,∠ESC=∠ETG=90°,∵∠CEG+∠CFG=180°,∴∠ECF+∠FGE=180°,∵∠EGT+∠EGF=180°,∴∠EGT=∠ECF.∴△ECS≌△EGT(AAS),∴CE=EG=a+2,在Rt△ADB中,AB=2OA=4a+2,BD=2CE=2a+4,AD=2a+2,∵AD2+BD2=AB2,∴(2a+2)2+(2a+4)2=(4a+2)2,解得a=2(a=﹣1舍去),∴CE=a+2=4,BE=3a+2=8,∴tan∠EBC==,∵BE=8,设ES=m,BS=2m,∴m2+(2m)2=82,解得m=(负值舍去),∴ES=,∵∠CFE=45°,∴EF=ES=.3.(1)证明:如图,连接OE,∵OA=OE,∴∠A=∠OEA,∵OA⊥BC,∴∠ADF=90°,∴∠A+∠AFD=90°,∵∠AFD=∠PFE,∴∠A+∠PFE=90°,∵PF=PE,∴∠PFE=∠PEF,∴∠A+∠PEF=∠OEA+∠PEF=90°,∴∠OEP=90°,∴OE⊥PE,OE是⊙O的半径,∴PE是⊙O的切线;(2)解:连接OC,OP,设OC=x,则OD=OA﹣AD=x﹣2,∵OA⊥BC,∴BD=CD=BC=4,在Rt△ODC中,根据勾股定理,得OC2=OD2+CD2,∴x2=(x﹣2)2+42,解得x=5,∴OC=5,OD=3,∵PE=PF,∴PD=PF+DF=PE+1,在Rt△OPD和Rt△OPE中,根据勾股定理,得OP2=OD2+PD2=OE2+PE2,∴9+(PE+1)2=25+PE2,解得PE=.4.(1)证明:连接OD交BC于H,连接OB、OC,如图,∵点E是△ABC的内心∴AD平分∠BAC,即∠BAD=∠CAD,∴∠BOD=∠COD,∴=,∴OD⊥BC,BH=CH,∵DG∥BC,∴OD⊥DG,∴DG是⊙O的切线;(2)解:∵点E是△ABC的内心,∴∠ABE=∠CBE,∵∠DBC=∠BAD,∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,∴DB=DE=6,∵BH=BC=3,在Rt△BDH中,sin∠BDH===,∴∠BDH=45°,∵OB=OD,∴△OBD为等腰直角三角形,∴∠BOD=90°,∵BD=6,∴OB=OD=3,∵∠DOC=∠BOD=90°,∴阴影部分的面积=S扇形DOC ﹣S△DOC=﹣3×3=π﹣9.5.(1)证明:如图1中,∵BD是直径,∴∠BED=∠BFD=90°,∵△ABC是等边三角形,∴BA=BC,∵AE=CF,∴BE=BF,∵BD=BD,∴Rt△BDE≌Rt△BDF(HL),∴DE=DF.(2)解:如图2中,过点D作DM⊥AB于M,DN⊥BC于N.∵∠AED+∠BED=180°,∠BED+∠BFD=180°,∴∠AED=∠DFB,∵∠DME=∠DNF=90°,∴△DME∽△DNF,∴==,在Rt△ADM中,∠AMD=90°,∠A=60°,AD=4,∴DM=AD•sin60°=2,∴DN=5,在Rt△DCN中,∠DNC=90°,∠C=60°,∴CD==10,∴AB=AC=AD+DC=4+10=14.6.(1)证明:连接OC,如图,∵AC平分∠EAB,∴∠OAC=∠EAC,∵OA=OC,∴∠OAC=∠OCA,∴∠EAC=∠ACO,∴OC∥AE,∵AE⊥DC,∴OC⊥CD,∴CD是⊙O的切线;(2)解:∵BC=BD,∴∠BCD=∠BDC,∵AB是⊙O的直径,∴∠ACB=∠ACO+∠OCB=90°,由(1)知OC⊥CD,∴∠OCD=∠BCD+∠OCB=90°,∴∠OAC=∠OCA=∠BCD=∠BDC,∵OC=OB,∴∠OBC=∠OCB,而∠OBC=∠BCD+∠D=2∠BCD,∴∠OCB=2∠BCD,而∠OCD=∠BCD+∠OCB=3∠BCD=90°,∴∠OAC=∠OCA=∠BCD=∠D=30°,设OC=x,则OD=2x,由勾股定理得4x2﹣x2=62,解得,所以.7.(1)证明:连接OC,∵BE为⊙O的切线,∴∠ABE=90°,∵点O为BC的中点,∴依据垂径定理得OE垂直平分BC,∴EC=EB,在△OEC和△OEB中,∵EC=EB,EO=EO,CO=BO,∴△OEC≌△OBC(SSS),∴∠ECO=∠EBO=90°,∵OC为半径,∴直线CE是⊙O的切线;(2)解:①30°;②,理由如下:①∵四边形ACMO为菱形,∴AC=AO,∵OC=OA,∴△CAO为等边三角形,∴∠CAO=60°,∴∠ABC=90°﹣60°=30°;②∵四边形OCEB为正方形,AB=4,∴OC=CE=2,∴,∵CM=2,∴ME=2﹣2,故答案为①30°;②.8.(1)证明:连接OB,∵OA,OB是⊙O的半径,∴∠OBA=∠OAB,∵CP=CB,∴∠CBP=∠CPB.∵∠CPB与∠APO是对顶角,∴∠APO=∠CPB,∴∠CBP=∠APO,∵OC⊥OA,交AB于点P,∴∠APO+∠PAO=90°,∴∠CBP+∠OBA=90°.∴OB⊥BC,∴BC是⊙O的切线.(2)解:∵∠BAO=25°,∴∠AOB=130°.∴所对的圆心角为230°,∵OA=18,∴.9.(1)证明:如图1中,连接CO,延长CO到T.∵∠TOD=∠D+∠DCO,∠AOT=∠A+∠AOC,∴∠AOD=∠TOD+∠TOA=∠D+∠DCO+∠ACO+∠A,∵OD=OC=OA,∴∠D=∠OCD,∠A=∠ACO,∴∠AOD=2∠ACD.(2)①证明:如图2﹣1中,延长ME交CD于H.∵AC⊥BD,∴∠AEB=90°,∵AM=BM,∴ME=AM=BM,∴∠A=∠D=∠AEM,∵∠AEM+∠MEB=90°,∠MEB=∠DEH,∴∠D+∠DEH=90°,∴∠DHE=90°,∴ME⊥CD.②证明:如图2﹣2中,延长BO交⊙O于P,连接PD,PA,AD.∵AM=MB,OP=OB,∴AP=2OM,∵PB是直径,∴∠PDB=90°,∵AC⊥BD,∴∠AEB=∠PDB=90°,∴PD∥AC,∴∠ADP=∠DAC,∴=,∴CD=AP,∴CD=2OM.10.(1)证明:连接OC,∵OA=OB,AC=CB,∴OC⊥AB,∵点C在⊙O上,∴AB是⊙O切线;(2)证明:∵OA=OB,AC=CB,∴∠AOC=∠BOC,∵OD=OF,∴∠ODF=∠OFD,∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,∴∠BOC=∠OFD,∴OC∥DF,∴∠CDF=∠OCD,∵OD=OC,∴∠ODC=∠OCD,∴∠ADC=∠CDF;(3)解:作ON⊥DF于N,延长DF交AB于M.∵ON⊥DF,∴DN=NF=3,在Rt△ODN中,∵∠OND=90°,OD=5,DN=3∴,∵∠OCM+∠CMN=180°,∠OCM=90°,∴∠OCM=∠CMN=∠MNO=90°,∴四边形OCMN是矩形,∴ON=CM=4,MN=OC=5,在Rt△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=9,∴.11.(1)证明:∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC是等边三角形.(2)解:∵△ABC是等边三角形,AB=2,∴AC=BC=AB=2,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=2,∴AP==.在Rt△DAC中,∠DAC=90°,AC=2,∠ACD=60°,∴AD=AC•tan∠ACD=2.∴PD=AD﹣AP=.12.(1)证明:连接OD,交BC于M,∵l是⊙O的切线,∴OD⊥l,∵BC∥l,∴BC⊥OD,∵O为AB的中点,∴M为BC中点,∴BC=2BM,在△OBM和△ODE中,,∴△OBM≌△ODE(ASA),∴DE=BM,∴BC=2DE;(2)解:连接BG,在Rt△BGC和Rt△BGF中,,∴Rt△BGC≌Rt△BGF(HL),∴BG平分∠CBF,CG=GF,设CG=GF=DE=a,则BC=BF=2a,∵∠GAF=∠CAB,∠AFG=∠ACB,∴△AFG∽△ACB,∴,∴,∴2AF=a+AG,又∵AG2=AF2+GF2,解得AF=a,AG=a,由(1)知,AD平分∠BAC,∴AG=GD=a,∴AE=a=3a,∴tan∠DAB==.13.解(1)∵AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,∴DE=DC,∵DC=AD,∴DE=AD,∴∠DAE=30°,∴∠D=60°;故答案为:60°;(2)如答图:连接OD、OC,∵OA=OD,∠DAE=30°,∴∠ADO=30°,∵∠ADC=60°,AD∥FG,∴∠CDO=30°,∠DCG=60°,∵OD=OC,∴∠DCO=30°,∴∠GCO=∠DCG+∠DCO=90°,∴OC⊥FG,∴FG与⊙O相切;(3)如答图2:连接EF、OF、OC,过E作EH⊥FG于H,设⊙O半径为R,∵AD∥FG,∠DAE=30°,FG与⊙O相切,∴∠G=30°,∠OCG=90°,∴OG=2R,CG=R,∵CD⊥AB,∴∠GEC=90°,GE=CG=R,∵EH⊥FG于H,∴EH=GE=R,∵∠DCG=60°,EH⊥FG于H,∴CH==R,∵CD⊥AB,AF是⊙O的切线,∴∠GEC=∠GAF=90°,∴CD∥AF,∴∠AFC=∠DCG=60°,∵FG、FA是是⊙O的切线,∴FA=FC,∠OCF=∠OAF,又OF=OF,∴△AOF≌△COF(HL),∴∠OFC=∠OFA=30°,∴CF=R,∴HF=CF+CH=R,在Rt△EHF中,tan∠EFC===.14.(1)证明:连接OF,OE,EF,如图1所示:∵⊙O与BA相切于点F,∴AB⊥OF,∴∠OFB=90°,∵四边形ABCD是矩形,∴∠B=90°,∵BF=BE,∴△BEF是等腰直角三角形,∴∠BFE=∠BEF=45°,∴∠OFE=90°45°=45°,又∵OE=OF,∴∠OEF=∠OFE=45°,∴∠OEB=45°+45°=90°,∴BC⊥OE,∴BC是⊙O的切线;(2)解:连接OG、FG,连接EO并延长交AD于P,如图2所示:则EP⊥AD,AP=BE=BF=5,∴GP=AP﹣AG=4,∵∠OFB=∠B=∠OEB=90°,∴四边形OFBE是矩形,∴OE=BF=5,在Rt△GPO中,由勾股定理得:PO===3,∴AF=OP=3,∵∠FGA=∠FED,∴,tan∠FED=tan∠FGA==3.15.证明:(1)∵AB是直径,∴∠ADB=90°,又∵AB=AC,∴BD=CD,∠B=∠C,∠BAD=∠CAD,∴=,∴BD=DE,∴BD=DE=DC,∴∠DEC=∠C=∠AEF,∵∠AEF+∠CAF=90°,∠C+∠DAC=90°,∴∠CAF=∠CAD,∵四边形ABDE是圆内接四边形,∴∠BAC+∠BDE=180°,又∵∠BDE+∠EDC=180°,∴∠EDC=∠BAC=2∠CAD=2∠CAF;(2)△ABC是等边三角形,理由如下:∵直线AF是⊙O的切线,∴∠BAF=90°,∵∠BAD=∠CAD=∠CAF,∴∠BAD=∠CAD=∠CAF=30°,∴∠BAC=60°,又∵AB=AC,∴△ABC是等边三角形;(3)∵=,∴设AD=25x,DF=24x,∴AF===7x,∵∠BAD=∠CAF,∠AFE=∠ADB=90°,∴△ADB∽△AFE,∴,∴,∴BD=x,∴BC=x,∵AB===x,∴.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题50 圆中的翻折综合问题1、如图,将半径为12的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为()A.42 B.82 C.6 D.62【分析】延长CO交AB于E点,连接OB,构造直角三角形,然后再根据勾股定理求出AB的长【解答】解:延长CO交AB于E点,连接OB,∵CE⊥AB,∴E为AB的中点,∵OC=6,CD=2OD,∴CD=4,OD=2,OB=6,∴DE=12(2OC-CD)=12(6×2-4)=12×8=4,∴OE=DE-OD=4-2=2,在Rt △OEB中,∵OE 2+BE 2=OB 2, ∴BE=22OE OB −=2246−42 ∴AB=2BE=82.故选:B .【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.2、已知如图:⊙O 的半径为8cm ,把弧AmB 沿AB 折叠使弧AmB 经过圆心O ,再把弧AOB 沿CD 折叠,使弧COD 经过AB 的中点E ,则折线CD 的长为( )A .8cmB .38cmC .72cmD .47cm【分析】连接OE 并延长交CD 于点F ,交C′D′于点F′,交弧AmB 于点G ,根据翻折的性质得出OF′=6,再由勾股定理得出.【解答】解:连接OE 并延长交CD 于点F ,交C′D′于点F′,交弧AmB 于点G ,∵OC′=8cm ,∴OF′=6cm ,∴C′F′=CF=2268−=27cm ,F ∴CD=2CD=47cm .故选:D .【点评】本题考查了垂径定理和勾股定理以及翻折的性质,是基础知识要熟练掌握.3、如图,AB 是⊙O 的直径,且AB=4,C 是⊙O 上一点,将弧AC 沿直线AC 翻折,若翻折后的圆弧恰好经过点O ,π≈314,2≈1.41,3≈1.73,那么由线段AB 、AC 和弧BC 所围成的曲边三角形的面积与下列四个数值最接近的是( )A .3.2B .3.6C .3.8D .4.2【分析】作OE⊥AC 交⊙O 于F ,交AC 于E ,根据折叠的性质得到OE=12OF ,求出∠ACB 的度数即可解决问题.【解答】解:作OE ⊥AC交⊙O 于F ,交AC 于E .连接OB ,BC . 由折叠的性质可知,EF=OE=12, ∴OE=12OA ,在Rt △AOE 中,OE=12OA , ∴∠CAB=30°,∵AB 是直径,∴∠ACB=90°,∠BOC=2∠BAC=60°,∵AB=4,∴BC=12AB=2,AC=3BC=23, ∴线段AB 、AC 和弧BC 所围成的曲边三角形的面积为S=12•AC•BC+S 扇形OBC -S △OBC =12×23×2+60π•22360-43×22=3+23π≈3.8,故选:C .【点评】本题考查的是翻折变换的性质、圆周角定理,折叠是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.4、如图,将⊙O 的劣弧︵ AB 沿AB 翻折,D 为优弧︵A DB 上一点,连接AD ,交︵ AB 于点C ,连接BC 、BD ;若BC=5,则BD= .【分析】根据圆周角定理、翻转变换的性质得到∠ADB=∠BCD ,根据等腰三角形的判定定理解答.【解答】解:由翻转变换的性质可知,∠ADB所对的弧是劣弧︵AB,∠CAB所对的弧是劣弧︵BC,∠CBA所对的弧是劣弧︵AC,∴∠ADB=∠CAB+∠CBA,由三角形的外角的性质可知,∠BCD=∠CAB+∠CBA,∴∠ADB=∠BCD,∴BD=BC=5,故答案为:5.【点评】本题考查的是翻转变换的性质、圆周角定理的应用,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.5、如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,将弧AC沿直线AC翻折,若翻折后的圆弧恰好经过点O,π≈314,2≈1.41,3≈1.73,那么由线段AB、AC和弧BC所围成的曲边三角形的面积与下列四个数值最接近的是()A.3.2 B.3.6 C.3.8 D.4.2【分析】作MN关于直线AN的对称线段M′N,交半圆于B',连接AM、AM′,构造全等三角形,然后利用勾股定理、割线定理解答.【解答】解:如图,作MN关于直线AN的对称线段M′N,交半圆于B',连接AM、AM′,可得M、A、M′三点共线,MA=M′A,MB=M′B′=4,M′N=MN=10.连接AB',∵四边形AMNB'是圆内接四边形,∴∠M'AB'=∠M'NM,∵∠M'=∠M',∴△M'AB'∽△M'NM,∴M′AM′N=M′B′M′M∴M′A•M′M=M′B′•M′N,即M′A•2M′A=4×10=40.则M′A2=20,又∵M′A2=M′N2-AN2,∴20=100-AN2,∴AN=45.故选:B.【点评】此题将翻折变换、勾股定理、割线定理相结合,考查了同学们的综合应用能力,要善于观察图形特点,然后做出解答.6、如图,是一个圆心角为90°的扇形,AO=2cm ,点P 在半径AO 上运动,点Q 在弧AB 上运动,沿PQ 将它以上的部分向下翻折,使翻折后的弧恰好过点O ,则OP 的最大距离为 .【分析】作O 关于PQ 的对称点O′,O′恰好落在⊙O 上,于是得到OP=12R cos ∠POE ,推出△OO′Q 为等边三角形,根据等边三角形的性质得到OQ=O′Q=OO′=R ,当cos∠POE 最小时,∠POE 最大,当∠QOB=0°时,∠POE=30°于是得到结论.【解答】解:作O 关于PQ 的对称点O′,O′恰好落在⊙O 上,∴OP=12R c os ∠POE , ∵△OO′Q 为等边三角形,∴OQ=O′Q=OO′=R ,∠POE+∠QOB=30°,当cos∠POE 最小时,∠POE 最大,当∠QOB=0°时,∠POE=30°,∴OP=1cos30°=332.故答案为:332.【点评】本题考查了翻折变换-折叠问题,等边三角形的判定和性质,正确的在才辅助线是解题的关键.7、如图,⊙O的半径为5,弦AB的长为8,将沿直线AB折叠,折叠后如右图,则⊙O到所作的圆的切线OC的长为()A.22 B.5 C.3 D.11【分析】根据题意先画出图形,可知翻转过后的弧AB所在的圆和⊙O全等,且两个圆的圆心相距为6,又已知圆的半径,故根据勾股定理即可求出答案.【解答】解:根据题意画出图形如下所示:BD=4,OB=5,点O′为翻转过后的弧AB所在圆的圆心,则有O′D=OD=2245−=3.又O′C=5,O′O=6, ∴OC=22C ′O O ′O −=2256−=11.故选:D .【点评】本题考查了翻转变换、垂径定理及圆的切线的性质,难度不大,找出翻转过后的弧AB 所在圆的圆心是解题关键.8、如图,将弧BC 沿弦BC 折叠交直径AB 于点D ,若AD=6,DB=7,则BC 的长是( ) A .91 B .37 C .134 D .130【分析】连接CA 、CD ,根据翻折的性质可得弧CD 所对的圆周角是∠CBD ,再根据AC 弧所得的圆周角也是∠CBA ,然后求出AC=CD ,过点C 作CE ⊥AB 于E ,根据等腰三角形三线合一的性质可得AE=ED=12AD ,根据直径所对的圆周角是直角可得∠ACB=90°,然后求出△ACE 和△CBE 相似,根据相似三角形对应边成比例求出CE 2,再求出BE ,然后利用勾股定理列式计算即可求出BC .【解答】解:如图,连接CA 、CD , 根据折叠的性质,弧CD 所对的圆周角是∠CBD , ∵弧AC 所对的圆周角是∠CBA ,∠CBA=∠CBD ,∴AC=CD (相等的圆周角所对的弦相等),过点C 作CE⊥AB 于E , 则AE=ED=12AD=12×6=3, ∴BE=BD+DE=7+3=10, ∵AB 是直径,∴∠ACB=90°, ∵CE⊥AB ,∴∠ACB=∠AEC=90°,∴∠A+∠ACE=∠ACE+∠BCE=90°,∴∠A=∠BCE ,∴△ACE∽△CBE ,∴AE CE = CE BE, 即CE 2=AE•BE=3×10=30, 在Rt △BCE 中,BC=22CE BE + = 30102+= 130,故选:D .【点评】本题考查了翻折的性质,相似三角形的判定与性质,圆的性质,等腰三角形的判定与性质,作辅助线并求出AC=CD 是解题的关键.9、如图,在⊙O 中,点C 在优弧 AB ︵ 上,将弧︵ BC 沿BC 折叠后刚好经过AB 的中点D ,连接AC ,CD .则下列结论中错误的是( )A .AC=CDB .︵ AC +︵ BD =︵ BCC .OD⊥AB D .CD 平分∠ACB【分析】A 、作辅助线,构建折叠的性质可得AD=CD ;B 、相等两弧相加可作判断;C 、根据垂径定理可作判断;D 、延长OD 交⊙O 于E ,连接CE ,根据垂径定理可作判断.【解答】解:A 、过D 作DD'⊥BC,交⊙O 于D',连接CD'、BD', 由折叠得:CD=CD',∠ABC=∠CBD',∴AC=CD'=CD ,故①正确;B 、∵AC=CD',∴︵ AC =︵ CD′ ,由折叠得:︵ BD =︵ BD ′,∴︵ AC +︵ BD =︵ BC ,故②正确;C 、∵D 为AB 的中点,∴OD⊥AB ,故③正确;D 、延长OD 交⊙O 于E ,连接CE ,∵OD⊥AB ,∴∠ACE=∠BCE ,∴CD 不平分∠ACB ,故④错误;故选:D .【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理和垂径定理.11、如图,△ABC 内接于⊙O ,BC=22,∠BAC=45°,将劣弧︵ AB 和︵ AC 分别沿直线AB 、AC 折叠后交于点M ,点S 、T 是弦AB 、AC 上的动点,则△M ST 的周长的最小值为( )A .22B .4C .24D .8【分析】作点M关于AB的对称点M′,关于AC的对称点M″,根据折叠的性质得到点M′,M″在圆周上,连接M′M″,交AB于S,交AC于T,则△M ST的周长最小,连接AM′,AM″,OB,OC,根据圆周角定理得到M′M″是⊙O的直径,即可得到结论.【解答】解:作点M关于AB的对称点M′,关于AC的对称点M″,∵将劣弧AB和AC分别沿直线AB、AC折叠后交于点M,∴点M′,M″在圆周上,连接M′M″,交AB于S,交AC于T,则△M ST的周长最小,连接AM′,AM″,OB,OC,则∠M′AM″=2∠BAC,∵∠BAC=45°,∴∠M′AM″=∠BOC=90°,∵BC=22,∴OB=2,∴M′M″=2OB=4,∴△M ST的周长的最小值为4,故选:B.【点评】本题考查了三角形的外接圆与外心,轴对称-最短路线问题,翻折变换(折叠问题),圆周角定理,勾股定理,正确的作出辅助线是解题的关键.12、如图,在⊙O 中,点C 在优弧⌢ACB 上,将弧沿⌢BC 折叠后刚好经过AB 的中点D ,若⊙O 的半径为5,AB=4,则BC 的长是 .【分析】连接OD 、AC 、DC 、OB 、OC ,作CE ⊥AB 于E ,OF ⊥CE 于F ,如图,利用垂径定理得到OD ⊥AB,则AD=BD=12AB=2,于是根据勾股定理可计算出OD=1,再利用折叠的性质可判断弧AC 和弧CD 所在的圆为等圆,则根据圆周角定理得到︵ AC=︵ CD ,所以AC=DC ,利用等腰三角形的性质得AE=DE=1,接着证明四边形ODEF 为正方形得到OF=EF=1,然后计算出CF 后得到CE=BE=3,于是得到BC=32.【解答】解:连接OD 、AC 、DC 、OB 、OC ,作CE⊥AB 于E ,OF ⊥CE 于F ,如图,∵D 为AB 的中点,∴OD⊥AB ,∴AD=BD=12AB=2, 在Rt △OBD中,OD=22BD OB −=222)5(−=1,∵将弧︵ BC 沿BC 折叠后刚好经过AB 的中点D .∴︵ AC 和︵ CD 所在的圆为等圆,∴︵ AC =︵ CD ,∴AC=DC ,∴AE=DE=1,易得四边形ODEF 为正方形,∴OF=EF=1,在Rt △OCF 中,CF=22OF CO −=221)5(−=2, ∴CE=CF+EF=2+1=3,而BE=BD+DE=2+1=3, ∴BC=32.故答案为32.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了圆周角定理和垂径定理.14、如图,AB 是半径为2的⊙O 的弦,将︵ AB 沿着弦AB 折叠,正好经过圆心O ,点C 是折叠后的︵ AB 上一动点,连接并延长BC 交⊙O 于点D ,点E 是CD 的中点,连接AC ,AD ,EO .则下列结论:①∠ACB=120°,②△ACD 是等边三角形,③EO 的最小值为1,其中正确的是 .(请将正确答案的序号填在横线上)【分析】根据折叠的性质可知,结合垂径定理、三角形的性质、同圆或等圆中圆周角与圆心的性质等可以判断①②是否正确,EO 的最小值问题是个难点,这是一个动点问题,只要把握住E 在什么轨迹上运动,便可解决问题.【解答】解:如图1,连接OA 和OB ,作OF ⊥AB. 由题知:︵ AB 沿着弦AB 折叠,正好经过圆心O∴OF=OA=12OB ∴∠AOF=∠BOF=60°∴∠AOB=120°∴∠ACB=120°(同弧所对圆周角相等)∠D=12∠AOB=60°(同弧所对的圆周角是圆心角的一半) ∴∠ACD=180°-∠ACB=60°∴△ACD是等边三角形(有两个角是60°的三角形是等边三角形)故,①②正确下面研究问题EO的最小值是否是1如图2,连接AE和EF∵△ACD是等边三角形,E是CD中点∴AE⊥BD(三线合一)又∵OF⊥AB∴F是AB中点即,EF是△ABE斜边中线∴AF=EF=BF即,E点在以AB为直径的圆上运动.所以,如图3,当E、O、F在同一直线时,OE长度最小此时,AE=EF,AE⊥EF∵⊙O的半径是2,即OA=2,OF=1∴AF=3(勾股定理)∴OE=EF-OF=AF-OF=3-1所以,③不正确综上所述:①②正确,③不正确.故答案为①②.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.14、如图,将︵ AB 沿着弦AB 翻折,C 为翻折后的弧上任意一点,延长AC 交圆于D ,连接BC .(1)求证:BC=BD ;(2)若AC=1,CD=4,︵ AB=120°,求弦AB 的长和圆的半径.【分析】(1)作点C 关于AB 的对称点C′,连接AC′,BC′.利用翻折不变性,以及圆周角定理即可解决问题;(2)连接OA ,OB ,作OM⊥AB 于M ,AH ⊥BC交BC 的延长线于H .解直角三角形求出AB ,OA 即可;【解答】(1)证明:作点C 关于AB 的对称点C′,连接AC′,BC′.由翻折不变性可知:BC=BC′,∠CAB=∠BAC′,∴︵ BD =︵BC ′,∴BD=BC′,∴BC=BD .(2)解:连接OA ,OB ,作OM ⊥AB 于M ,AH ⊥BC 交BC 的延长线于H .∵︵AB =120°,∴∠D=12×120°=60°,∴∠AOB=∠ACB=2∠D=120°,∵BC=BD ,∴△BCD 是等边三角形,∴BC=DC=4,在Rt △ACH 中,∵∠H=90°,∠ACH=60°,AC=1,∴CH=12,AH=23, ∴AB=22BH AH +=22)29()23(+=21,∵OM ⊥AB ,∴AM =BM =221,在Rt △AOM 中,∵∠OAM =30°,∠AM O=90°,∴OA=AM cos30°=7【点评】本题考查圆心角、弧、弦之间的关系,垂径定理,勾股定理,翻折变换,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.15、如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将︵CD沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC (1)求CD的长;(2)求证:PC是⊙O的切线;(3)点G为︵ADB 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交︵BC 于点F(F与B、C不重合).问GE•GF是否为定值?如果是,求出该定值;如果不是,请说明理由.【分析】(1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可;(3)连接GA、AF、GB,根据等弧所对的圆周角相等可得∠BAG=∠AFG,然后根据两组角对应相等两三角相似求出△AGE和△FGA相似,根据相似三角形对应边成比例可得AGGE=FGAG,从而得到GE•GF=AG2,再根据等腰直角三角形的性质求解即可.【解答】(1)解:如图,连接OC ,∵︵CD 沿CD 翻折后,点A 与圆心O 重合, ∴OM =12O A=12×2=1,CD ⊥OA ,∵OC=2,∴CD=2CM =222OM OC −=22212−=23;(2)证明:∵P A=OA=2,AM=OM=1,CM=12CD=3,∠CM P=∠OM C=90°,∴PC=22PM MC +=223)3(+=23, ∵OC=2,PO=2+2=4,∴PC 2+OC 2=(23)2+22=16=PO 2, ∴∠PCO=90°,∴PC 是⊙O 的切线;(3)解:GE•GF是定值,证明如下,连接GO并延长,交⊙O于点H,连接HF∵点G为︵A DB的中点∴∠GOE=90°,∵∠HFG=90°,且∠OGE=∠FGH ∴△OGE∽△FGH∴OGGF=GEGH∴GE•GF=OG•GH=2×4=8.【点评】本题是圆的综合题型,主要利用了翻折变换的性质,垂径定理,勾股定理,勾股定理逆定理,圆的切线的定义,相似三角形的判定与性质,难点在于(3)作辅助线构造出相似三角形.21。
