2020届新高考艺术生数学复习冲关训练:第三章 第3节三角函数的图象与性质
高考数学总复习 第三章 第3讲 三角函数的图象与性质课件 理

考点2 三角函数的对称性
例2:(1)函数y=cos2x+π3图象的对称轴方程可能是(
)
A.x=-π6
B.x=-1π2
C.x=6π
D.x=1π2
解析:(1)令2x+
π 3
=kπ(k∈Z),得x=
kπ 2
-
π 6
(k∈Z),令k=
0,得该函数的一条对称轴为x=-6π.
答案:A
(2)函数y=sin3x-4π的图象的一ห้องสมุดไป่ตู้对称中心是(
(0,0),π2,1,(π,0),32π,-1,(2π,0). (2)y=cosx的图象在[0,2π]上的五个关键点的坐标为 (0,1),π2,0,(π,-1),32π,0,(2π,1).
2.三角函数的图象和性质
函数
y=sinx
y=cosx
定义域
R
R
y=tanx
x|
xk2,kZ
图象
值域
[-1,1]
2.使 cosx=1-m 有意义的 m 值为( C )
A.m≥0
B.m≤0
C.0≤m≤2
D.-2≤m≤0
3.(2013 年上海)既是偶函数又在区间(0,π)上单调递减的
函数是( B )
A.y=sinx
B.y=cosx
C.y=sin2x
D.y=cos2x
4.函数 y=5tan(2x+1)的最小正周期为( B )
【规律方法】本题主要考查函数 y=Asin(wx+φ)的图象特 征,正弦函数的值域与最值.解题关键在于将已知的函数表达式 化为三角函数模型,再根据此三角函数模型的图象与性质进行 解题即可.
【互动探究】 3.已知函数 f(x)=2cos2x+sin2x-4cosx.
【金版教程】届高考数学总复习 第3章 第3讲 三角函数的图象与性质课件 理 新人教A版

求形如y=Asin(ωx+φ)(A>0,ω>0)的函数的单调区间,基
本思路是把ωx+φ看作一个整体,由-
π 2
+2kπ≤ωx+φ≤
π 2
+
2kπ(k∈Z)求得函数的增区间,由
π 2
+2kπ≤ωx+φ≤
3π 2
+2kπ(k
∈Z)求得函数的减区间.若在y=Asin(ωx+φ)中,ω<0,则应
先利用诱导公式将解析式转化,使x的系数变为正数,再进行
(1)y=cos(x+π3)(x∈[0,π])的值域________. (2)y=tan(4π-x)的单调递减区间__________.
1.f(x+T)=f(x) 最小 最小正周期
想一想:提示:f[(x+2)+2]=-f(x+2)=f(x),即f(x+4)
=f(x),所以f(x)是周期为4的函数.
____
________
________
____
y=tanx
无最值
____ ________ 无对称轴
____
判断以下命题的正误. ①y=sinx在第一象限是增函数.( ) ②y=cosx在[0,π]上是减函数.( ) ③y=tanx在定义域上为增函数.( ) ④y=|sinx|的周期为2π.( ) ⑤y=ksinx+1,x∈R则y的最大值为k+1.( )
Z)
π+2kπ(k∈Z)
奇
偶
奇
(kπ,0),k∈Z
(kπ+
π 2
,
0),k∈Z
(
kπ 2
,0),k∈Z
x=kπ+
π 2
,k∈Z
x=kπ,k∈Z
2π 2π π
判一判:①× ②√ ③× ④× ⑤×
2020新课标高考艺术生数学复习教师用书:第三章第3节 三角函数的图象与性质

第3节 三角函数的图象与性质最新考纲核心素养考情聚焦1.能画出y =sinx ,y =cosx ,y =tan x 的图象,了解三角函数的周期性、单调性、奇偶性、最大(小)值.2.借助图象理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x 轴的交点等),正切函数在上的性(-π2,π2)质1.三角函数的定义域与值域(最值),达成直观想象和数学运算的素养.2.三角函数的单调性,增强逻辑推理和数学运算的素养.3.三角函数的周期性、奇偶性和对称性,提升逻辑推理和数学运算的素养三角函数的奇偶性、周期性、单调性及最值是高考的热点,题型既有选择题、填空题,又有解答题,一般难度不会太大,属中低档题型,通常与三角恒等变换相结合,在考查三角函数性质的同时,又考查了三角恒等变换的方法与技巧.考查考生函数与方程、转化与化归、数形结合等数学思想的运用1.用五点法作正弦函数和余弦函数的简图正弦函数y =sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0),,(π,0),(π2,1),(2π,0).(3π2,-1)余弦函数y =cosx ,x ∈[0,2π]的图象中,五个关键点是:(0,1),,(π,-1),(π2,0),(2π,1).(3π2,0)2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )函数y =sin xy =cos xy =tan x图象定义域R R Error!Error! 值域 [-1,1] [-1,1] R 周期性2π 2π π 奇偶性 奇函数 偶函数奇函数递增区间 Error!Error! [2k π-π,2k π]Error!Error!递减区间 Error!Error! [2k π,2k π+π] 无对称中心 (k π,0) (k π+π2,0)(k π2,0)对称轴方程x =k π+π2 x =k π 无 若f (x )=A sin(ωx +φ)为偶函数,则φ=+k π(k ∈Z );若f (x )=A sin(ωx +φ)π2为奇函数,则φ=k π(k ∈Z ).[思考辨析] 判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.(1)函数y =sin x 的图象介于直线y =1与y =-1之间.( )(2)将余弦曲线向右平移个单位就得到正弦曲线.( )π2(3)函数y =sin是奇函数.( )(2x +3π2)(4)函数y =sin x 的对称轴方程为x =2k π+(k ∈Z ).( )π2(5)正切函数在整个定义域内是增函数.( )答案:(1)√ (2)√ (3)× (4)× (5)×[小题查验]1.(2017·全国Ⅱ卷)函数f (x )=sin的最小正周期为( )(2x +π3)A .4π B .2π C .π D.π2解析:C [函数f (x )=sin的最小正周期为T ==π.](2x +π3)2π22.(2019·全国Ⅱ卷)下列函数中,以为周期且在区间单调递增的是( )π2(π4,π2)A .f (x )=|cos 2x | B .f (x )=|sin 2x |C .f (x )=cos|x |D .f (x )=sin|x |解析:A [函数y =cos 2x 的周期为π,∴函数f (x )=|cos 2x |的周期为,当<x <时,π2π4π2<2x <π,y =cos 2x 递减且为负值,π2∴函数f (x )=|cos 2x |在区间上单调递增.](π4,π2)3.已知函数f (x )=sin(ω>0)的最小正周期为π,则该函数的图象( )(ωx +π3)A .关于直线x =对称 B .关于点对称π3(π3,0)C .关于直线x =-对称 D .关于点对称π6(π6,0)解析:B [∵f (x )=sin(ω>0)的最小正周期为π,∴ω=2,即f (x )=sin .(ωx +π3)(2x +π3)经验证可知f =sin=sin π=0,(π3)(2π3+π3)即是函数f (x )的一个对称点.](π3,0)4.函数y =tan的图象与x 轴交点的坐标是________.(2x +π4)解析:由2x +=k π(k ∈Z )得,x =-(k ∈Z ).∴函数y =tan的图象与x 轴交点π4k π2π8(2x +π4)的坐标是.(k π2-π8,0)答案:(k ∈Z )(k π2-π8,0)5.[人教A 版教材P46A 组T2改编]y =3sin在区间上的值域是________.(2x -π6)[0,π2]解析:当x ∈时,2x -∈,[0,π2]π6[-π6,5π6]sin ∈,故3sin ∈,即y =3sin 的值域为.(2x -π6)[-12,1](2x -π6)[-32,3](2x -π6)[-32,3]答案:[-32,3]考点一 三角函数的定义域、值域问题(自主练透)[命题角度1] 三角函数的定义域问题(1)函数y =的定义域为__________.sin x -cos x (2)函数y =lg(sin 2x )+的定义域为______________________________________.9-x 2解析:(1)法一(利用三角函数图象):要使函数有意义,必须使sin x -cos x ≥0.在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象,如图所示.在[0,2π]内,满足sin x =cos x 的x 为,,再结合正弦、余弦函数的周期是2π,所以函π45π4数y =的定义域为{x |2k π+≤x ≤2k π+,k ∈Z }.sin x -cos x π45π4法二(利用三角函数线):画出满足条件sin x ≥cos x 的角x 的终边范围(如图阴影部分所示),∴函数y =的定义域为{x |2k π+≤x ≤2k π+,k ∈Z }.sin x -cos x π45π4法三(利用整体思想):sin x -cos x =sin≥0,将x -视为一个整体,由正弦函数2(x -π4)π4y =sin x 的图象和性质可知2k π≤x -≤π+2k π,k ∈Z ,解得2k π+≤x ≤2k π+,k ∈Z .所π4π45π4以函数y =的定义域为{x |2k π+≤x ≤2k π+,k ∈Z }.sin x -cos x π45π4(2)由Error!得Error!∴-3≤x <-,或0<x <.π2π2∴函数y =lg(sin 2x )+的定义域为Error!.9-x 2答案:(1){x |2k π+≤x ≤2k π+,k ∈Z }π45π4(2)Error!求三角函数的定义域实际上就是解简单的三角不等式,常借助于三角函数线或三角函数图象来求解.[命题角度2] 三角函数的值域(最值)问题(1)(2019·全国Ⅰ卷)函数f (x )=sin-3cos x 的最小值为________.(2x +3π2)(2)函数y =sin x +cos x +sin x cos x 的值域为____________.解析:(1)f (x )=sin -3cos x =-cos 2x -3cos x ,(2x +3π2)∴f (x )min =-4.(2)设t =sin x +cos x ,则sin x cos x =(-≤t ≤),y =t +t 2-=(t +1)2-1.t 2-1222121212当t =时,y 取最大值+;当t =-1时,y 取最小值-1.2212∴函数的值域为.[-1,12+2]答案:(1)-4(2)[-1,12+2]1.求三角函数的定义域实际上就是解简单的三角不等式,常借助于三角函数线或三角函数图象来求解.2.求三角函数的值域(最值)的常见题型及求解策略:(1)形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+k 的形式,再求最值(值域);(2)形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);(3)形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).考点二 三角函数的单调性(师生共研)[典例] (1)y =sin 的单调递减区间为________.(π3 -2x )[解析] y =-sin的减区间是(2x -π3)y =sin的增区间.(2x -π3)由2k π-≤2x -≤2k π+,k ∈Z ,π2π3π2得k π-≤x ≤k π+,k ∈Z .π125π12故所给函数的减区间为,k ∈Z .[k π-π12,k π+5π12][答案] ,k ∈Z[k π-π12,k π+5π12](2)若f (x )=2sin ωx +1(ω>0)在区间上是增函数,则ω的取值范围是[-π2,2π3]____________.逻辑推理——三角函数单调性中应用的核心素养具体见下表:信息提取信息解读逻辑推理已知f (x )=2sin ωx +1(ω>0)在区间 上是增函数[-π2,2π3]解读一:是函数f (x )[-π2,2π3]单调递增区间的子区间.解读二:ωx 的取值范围是的子区间.[-π2,π2]解读三:原点到区间两端点的距离不超[-π2,2π3]过T4求参数ω的取值范围建立关于ω的不等式组推理一: 由函数y =sin x 在区间[2k π-π2,2k π+π2]上单调递增,求得f (x )=2sin ωx +1(ω>0)的单调递增区间.推理二:由不等式的基本性质求出ωx 的取值范围.推理三: 由正弦函数y =sin x 的图形与性质知原点到区间两端点的距离等于[-π2,π2]T 4[解析] 方法一:第一步,求出f (x )=2sin ωx +1(ω>0)的单调递增区间.由2k π-≤ωx ≤2k π+,k ∈Z ,π2π2得f (x )的增区间是,k ∈Z .[2k πω-π2ω,2k πω+π2ω]第二步,转化为集合之间的关系,即是函数f (x )单调递增区间的子区间.[-π2,2π3]∵f (x )在上是增函数,[-π2,2π3]∴⊆.[-π2,2π3][-π2ω,π2ω]第三步,利用数轴,列出关于ω的不等式组,解不等式组得ω的取值范围.∴-≥-且≤,∴ω∈.π2π2ω2π3π2ω(0,34]方法二:第一步,由x 的取值范围求出ωx (ω>0)的取值区间.∵x ∈,ω>0.∴ωx ∈,[-π2,2π3][-ωπ2,2πω3]第二步,由f (x )在区间上是增函数得ωx (ω>0)的取值区间是的子区间.[-π2,2π3][-π2,π2]又f (x )在区间上是增函数,[-π2,2π3]∴⊆,[-ωπ2,2πω3][-π2,π2]第三步,利用数轴,列出关于ω的不等式组,解不等式组得ω的取值范围.则Error!又ω>0,得0<ω≤.34方法三:第一步,由f (x )在区间上是增函数得原点到区间端点的距离不[-π2,2π3][-π2,2π3]超过.T 4∵f (x )在区间上是增函数,故原点到区间端点的距离不超过,[-π2,2π3]T 4第二步,列出关于ω的不等式组,解不等式组得ω的取值范围.所以Error!得T ≥,即≥.又ω>0,得0<ω≤.8π32πω8π334[答案] ω∈(0,34][互动探究]在本例(1)中函数不变,求函数在[-π,0]上的单调递减区间.解析:法一:x ∈R 时,y =sin 的减区间为,k ∈Z .令k =0得(π3-2x)[k π-π12,k π+5π12]-≤x ≤;π125π12令k =-1得-≤x ≤-,13π127π12故x ∈[-π,0]时,y =sin 的减区间为(π3-2x ),.[-π,-7π12][-π12,0]法二:因为-π≤x ≤0,所以-π≤2x -≤-,结合正弦曲线,73π3π3由-π≤2x -≤-π,解得-π≤x ≤-π;73π332712由-≤2x -≤-,解得-≤x ≤0,π2π3π3π12所以单调减区间为,.[-π,-7π12][-π12,0]求三角函数单调区间的两种方法(1)代换法:就是将比较复杂的三角函数处理后的整体当作一个角u (或t ),利用基本三角函数的单调性来求所要求的三角函数的单调区间.(2)图象法:函数的单调性表现在图象上是:从左到右,图象上升趋势的区间为单调递增区间,图象下降趋势的区间为单调递减区间,画出三角函数的图象,结合图象易求它的单调区间. 提醒:求解三角函数的单调区间时若x 的系数为负应先化为正,同时切莫漏掉考虑函数自身的定义域.[跟踪训练]1.函数f (x )=tan的单调递增区间是( )(2x -π3)A.(k ∈Z )[k π2-π12,k π2+5π12]B.(k ∈Z )(k π2-π12,k π2+5π12)C.(k ∈Z )(k π+π6,k π+2π3)D.(k ∈Z )[k π-π12,k π+5π12]解析:B [由k π-<2x -<k π+(k ∈Z )得,-<x <+(k ∈Z ),所以函数f (x )π2π3π2k π2π12k π25π12=tan的单调递增区间为(k ∈Z ),故选B.](2x -π3)(k π2-π12,k π2+5π12)2.(2018·全国Ⅱ卷)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( )A. B. C. D .ππ4π23π4解析:A [因为f (x )=cos x -sin x = cos ,所以由2k π≤x +≤π+2k π(k ∈Z )得-2(x +π4)π4+2k π≤x ≤+2k π(k ∈Z ),因此,[-a ,a ]π43π4⊆,∴-a <a ,-a ≥-,a ≤,∴0<a ≤从而a 的最大值为,选A.][-π4,3π4]π43π4π4π4考点三 三角函数的奇偶性、周期性和对称性(多维探究)[命题角度1] 三角函数的周期性1.(2017·山东卷)函数y =sin 2x +cos 2x 的最小正周期为( )3A. B. C .π D .2ππ22π3解析:C [由题意y =2sin,其周期T ==π.](2x +π6)2π22.若函数f (x )=2tan的最小正周期T 满足1<T <2,则自然数k 的值为(kx +π3)________.解析:由题意知,1<<2,即k <π<2k .又k ∈N ,πk 所以k =2或k =3.答案:2或3求三角函数周期的方法(1)利用周期函数的定义;(2)利用公式:y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为,y =tan(ωx +φ)的最2π|ω|小正周期为;π|ω|(3)利用图象:对含绝对值的三角函数的周期问题,通常要画出图象,结合图象进行判断.[跟踪训练](2018·全国Ⅰ卷)已知函数f (x )=2cos 2 x -sin 2 x +2,则( )A .f (x )的最小正周期为π,最大值为3B .f (x )的最小正周期为π,最大值为4C .f (x )的最小正周期为2π,最大值为3D .f (x )的最小正周期为2π,最大值为4解析:B [f (x )=2cos 2x -(1-cos 2x )+2=3cos 2x +1=cos 2x +,∴最小正周期为π,最3252大值为4.故选B.][命题角度2] 三角函数的对称轴或对称中心3.当x =时,函数f (x )=sin(x +φ)取得最小值,则函数y =f ( )π4(3π4-x )A .是奇函数且图象关于点对称(π2,0)B .是偶函数且图象关于点(π,0)对称C .是奇函数且图象关于直线x =对称π2D .是偶函数且图象关于直线x =π对称解析:C [∵当x =时,函数f (x )取得最小值,π4∴sin =-1,∴φ=2k π-(k ∈Z ).(π4+φ)3π4∴f (x )=sin=sin .(x +2k π-3π4)(x -3π4)∴y =f =sin(-x )=-sin x .(3π4-x )∴y =f 是奇函数,且图象关于直线x =对称.](3π4-x )π2若求f (x )=A sin(ωx +φ)的对称轴,只需令ωx +φ=+k π(k ∈Z ),求x ;若求f (x )π2=A sin(ωx +φ)的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z ),求x 即可.[跟踪训练]设函数f (x )=sin(2x +φ)+cos(2x +φ)(|φ|<),且其图象关于直线x =0对称,则( )3π2A .y =f (x )的最小正周期为π,且在上为增函数(0,π2)B .y =f (x )的最小正周期为π,且在上为减函数(0,π2)C .y =f (x )的最小正周期为,且在上为增函数π2(0,π4)D .y =f (x )的最小正周期为,且在上为减函数π2(0,π4)解析:B [∵函数f (x )=sin(2x +φ)+cos(2x +φ)=2sin 的图象关于直线3(2x +φ+π6)x =0对称,∴函数f (x )为偶函数,∴φ+=+k π(k ∈Z ).π6π2∵|φ|<,∴φ=,∴f (x )=2cos 2x ,π2π3∴T ==π.∵0<x <,∴0<2x <π,2π2π2∴函数f (x )在上为减函数.故选B.](0,π2)[命题角度3] 三角函数奇偶性、对称性的应用4.(2019·拉萨市一模)使函数f (x )=sin (2x +θ)+cos (2x +θ)是偶函数,且在上是3[0,π4]减函数的θ的一个值是( )A.B.C.D.π6π32π35π6解析:B [∵函数f (x )=sin(2x +θ)+cos (2x +θ)=2sin是偶函数,3(2x +θ+π6)∴θ+=k π+,即θ=k π+,k ∈Z ,因此可取θ=,π6π2π3π3此时,f (x )=2sin=cos 2x ,且在上,即2x ∈时,f (x )是减函数.故选B.](2x +π2)[0,π4][0,π2]5.(2019·雅安市模拟)函数f (x )=sin的图象在区间上的对称轴方程为3(2x +π3)(0,π2)________.解析:对于函数f (x )=sin的图象,令2x +=k π+,得x =+,k ∈Z ,令3(2x +π3)π3π2k π2π12k =0,可得函数在区间上的对称轴方程为x =.(0,π2)π12答案:x =π12函数f (x )=A sin(ωx +φ)的奇偶性、对称性的应用(1)若f (x )=A sin(ωx +φ)为偶函数,则当x =0时,f (x )取得最大或最小值;若f (x )=A sin(ωx +φ)为奇函数,则当x =0时,f (x )=0.(2)对于函数y =A sin(ωx +φ),其对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点,因此在判断直线x =x 0或点(x 0,0)是否是函数的对称轴或对称中心时,可通过检验f (x 0)的值进行判断.[跟踪训练](2019·全国Ⅰ卷)关于函数f (x )=sin|x |+|sin x |有下述四个结论:①f (x )是偶函数 ②f (x )在区间单调递增(π2,π)③f (x )在[-π,π]有4个零点 ④f (x )的最大值为2.其中所有正确结论的编号是( )A .①②④ B .②④C .①④D .①③解析:C [∵f (-x )=sin|-x |+|sin(-x )|=sin|x |+|sin x |,∴f (x )是偶函数,①对;f (x )在区间上单调递减,②错;(π2,π)f (x )在[-π,π]上有3个零点,③错;f (x )的最大值为2,④对.故选C.]1.(2018·全国卷Ⅲ)函数f (x )=的最小正周期为( )tan x1+tan2x A. B. C .π D .2ππ4π2解析:C [f (x )====sin x cos x =sin 2x ,∴f (x )的周期tan x1+tan2x sin x cos x1+sin2xcos2x sin x cos xsin2x +cos2x 12T ==π.故选C.]2π22.(2017·全国Ⅲ卷)函数f (x )=sin+cos 的最大值为( )15(x +π3)(x -π6)A.B .1C.D.653515解析:A [由诱导公式得cos=(x -π6)cos =sin ,则f (x )=[π2-(x +π3)](x +π3)sin +sin =sin ,所以函数f (x )的最大值为.故选A.]15(x +π3)(x +π3)65(x +π3)653.函数f (x )=1-2sin2是( )(x -π4)A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为的偶函数π2D .最小正周期为的奇函数π2解析:B [因为函数y =1-2sin 2=(x -π4)cos=sin 2x ,所以该函数是最小正周期为π的奇函数.故选B.](2x -π2)4.(2019·昆明市一模)若直线x =a π(0<a <1)与函数y =tan x 的图象无公共点,则不等式tan x ≥2a 的解集为( )A.{x |k π+π6≤x <k π+π2,k ∈Z }B.{x |k π+π4≤x <k π+π2,k ∈Z }C.{x |k π+π3≤x <k π+π2,k ∈Z }D.{x |k π-π4≤x ≤k π+π4,k ∈Z }解析:B [直线x =a π(0<a <1)与函数y =tan x 的图象无公共点,∴a =,∴不等式化12为tanx ≥1,解得k π+≤x <k π+,k ∈Z ;∴所求不等式的解集为π4π2{x |k π+≤x <k π+,k ∈Z }.]π4π25.(2019·长春市一模)已知函数f (x )=2sin (2x +φ)(0<φ<π),且f (0)=1,则下列结论中正确的是( )A .f (φ)=2B.是f (x )图象的一个对称中心(π6,0)C .∅=π3D .x =-是f (x )图象的一条对称轴π6解析:A [函数f (x )=2sin (2x +φ),且f (0)=2sin φ=1,∴sin φ=.又0<φ<π,∴φ=或;12π65π6当φ=时,f =2sin =2,当φ=时,f =2sin=2,故π6(π6)(2×π6+π6)5π6(5π6)(2×5π6+5π6)A 正确.]6.(2018·全国Ⅲ卷)函数f (x )=cos在[0,π]的零点个数为________.(3x +π6)解析:由f (x )=cos=0,有3x +=k π+(k ∈Z ),解得x =π+,由(3x +π6)π6π2k 3π90≤π+≤π得k 可取0,1,2,∴f (x )=cos在[0,π]上有3个零点.k 3π9(3x +π6)答案:37.函数f (x )=的定义域为________.3+2cos x 解析:要使函数f (x )=有意义,则+2cos x ≥0即cos x ≥-,由余弦函数3+2cos x 332的图象,得在一个周期[-π,π]上,不等式cos x ≥-的解集为,32{x |-5π6≤x ≤56π}所以,在实数集上不等式的解集为,{x |-56π+2k π≤x ≤56π+2k π,k ∈Z}即函数的定义域为.{x |-56π+2k π≤x ≤56π+2k π,k ∈Z}答案:{x |-56π+2k π≤x ≤56π+2k π,k ∈Z }8.(2019·鄂伦春自治旗一模)若函数f (x )=1+a sin (ax +(a >0))的最大值为3,则f (x )的π6最小正周期为______.解析:函数f (x )=1+a sin 的最大值为3,(ax +π6)∴1+a =3,解得a =2.∴f (x )=1+2sin,(2x +π6)∴f (x )的最小正周期为T ==π.2πω答案:π9.(2019·玉溪市模拟)设函数f (x )=2sin x cos x -cos 2x +1(1)求f (π2)(2)求f (x )的最大值和最小正周期.解:(1)函数f (x )=2sin x cos x -cos 2x +1=sin 2x -cos 2x +1=sin +1,2(2x -π4)∴f =sin+1=×+1=2.(π2)2(2×π2-π4)222(2)由f (x )=sin+1,2(2x -π4)当2x -=+2k π,k ∈Z ,即x =+k π,k ∈Z 时,π4π23π8f (x )取得最大值为+1,2最小正周期为T ==π.2πω10.(2019·泸州市模拟)已知函数f (x )=sin x cos x -cos 2x +a 的最大值为.22(1)求a 的值;(2)求使f (x )≥0成立的x 的集合.解:(1)∵f (x )=sin x cos x -cos 2x +a =sin 2x -+a =sin +a -,121+cos 2x222(2x -π4)12∴f (x )max =+a -=,∴a =.22122212(2)由(1)知,f (x )=sin.22(2x -π4)由f (x )≥0,得sin≥0,22(2x -π4)即2k π≤2x -≤π+2k π,k ∈Z ,π4∴+k π≤x ≤+k π,k ∈Z ,π85π8∴f (x )≥0成立的x 的集合为,k ∈Z .[π8+k π,5π8+k π]。
2020高考数学 课后作业 3-3 三角函数的图象与性质 新人教A版

2020高考数学人教A 版课后作业1.(文)(2020·四川文)将函数y =sin x 的图象上所有的点向右平行移动π10个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )A .y =sin ⎝⎛⎭⎪⎫2x -π10 B .y =sin ⎝⎛⎭⎪⎫2x -π5C .y =sin ⎝ ⎛⎭⎪⎫12x -π10D .y =sin ⎝ ⎛⎭⎪⎫12x -π20[答案] C[解析] ∵向右平移π10个单位,∴用x -π10代替y =sin x 中的x ;∵各点横坐标伸长到原来的2倍,∴用12x 代替y =sin ⎝ ⎛⎭⎪⎫x -π10中的x ,∴得y =sin ⎝ ⎛⎭⎪⎫12x -π10.(理)(2020·大纲全国卷理,5)设函数f (x )=cos ωx (ω>0),将y =f (x )的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ) A.13 B .3 C .6 D .9 [答案] C[解析] 由题意知,π3=2πω·k (k ∈Z),∴ω=6k ,令k =1,∴ω=6.2.(文)函数f (x )=sin 2x 的最小正周期和最小值分别为( ) A .2π,-1 B .2π,0 C .π,0 D .π,1 [答案] C[解析] ∵f (x )=sin 2x =1-cos2x 2,∴周期T =2π2=π,又f (x )=sin 2x ≥0,∴最小值为0,故选C.(理)(2020·济南模拟)函数f (x )=2cos 2x -3sin2x (x ∈R)的最小正周期和最大值分别为 ( )A .2π,3B .2π,1C .π,3D .π,1 [答案] C[解析] 由题可知,f (x )=2cos 2x -3sin2x =cos2x -3sin2x +1=2sin(π6-2x )+1,所以函数f (x )的最小正周期为T =π,最大值为3,故选C.3.(2020·衡水市高考模拟)设a =log 12tan70°,b =log 12sin25°,c =log 12cos25°,则它们的大小关系为( )A .a <c <bB .b <c <aC .a <b <cD .b <a <c [答案] A[解析] ∵tan70°>tan45°=1>cos25°>sin25°>0,log 12x 为减函数,∴a <c <b .4.(2020·衡水质检)函数y =3cos(x +φ)+2的图象关于直线x =π4对称,则φ的可能取值是( )A.3π4 B .-3π4 C.π4 D.π2[答案] A[解析] ∵y =cos x 的对称轴为x =k π(k ∈Z),∴x +φ=k π,即x =k π-φ,令π4=k π-φ得φ=k π-π4(k ∈Z),显然在四个选项中,只有3π4满足题意.故正确答案为A.5.(文)为了使函数y =sin ωx (ω>0)在区间[0,1]上至少出现50次最大值,则ω的最小值是( )A .98π B.1972π C.1992π D .100π [答案] B[解析] 由题意至少出现50次最大值即至少需用4914个周期,∴4914·T =1974·2πω≤1,∴ω≥1972π,故选B.(理)有一种波,其波形为函数y =sin ⎝ ⎛⎭⎪⎫π2x 的图象,若在区间[0,t ](t >0)上至少有2个波峰(图象的最高点),则正整数t 的最小值是( )A .3B .4C .5D .6[答案] C[解析] ∵y =sin ⎝ ⎛⎭⎪⎫π2x 的图象在[0,t ]上至少有2个波峰,函数y =sin ⎝ ⎛⎭⎪⎫π2x 的周期T =4,∴t ≥54T =5,故选C.6.(2020·安徽巢湖质检)函数f (x )=sin ⎝⎛⎭⎪⎫ωx -π3(ω>0)的最小正周期为π,则函数f (x )的单调递增区间为( )A.⎣⎢⎡⎦⎥⎤k π-π6,k π+5π6(k ∈Z)B.⎣⎢⎡⎦⎥⎤k π+5π6,k π+11π6(k ∈Z)C.⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z) D.⎣⎢⎡⎦⎥⎤k π+5π12,k π+11π12(k ∈Z) [答案] C[解析] 由条件知,T =2πω=π,∴ω=2,由2k π-π2≤2x -π3≤2k π+π2,k ∈Z 得,k π-π12≤x ≤k π+5π12,k ∈Z ,故选C. 7.(2020·福建质检)已知将函数f (x )=2sin π3x 的图象向左平移1个单位长度,然后向上平移2个单位长度后得到的图象与函数y =g (x )的图象关于直线x =1对称,则函数g (x )=________.[答案] 2sin π3x +2[解析] 将f (x )=2sin π3x 的图象向左平移1个单位长度后得到y =2sin[π3(x +1)]的图象,向上平移2个单位长度后得到y =2sin[π3(x +1)]+2的图象,又因为其与函数y =g (x )的图象关于直线x =1对称,所以y =g (x )=2sin[π3(2-x +1)]+2=2sin(π-π3x )+2=2sin π3x +2.8.(2011·济南调研)设函数y =2sin(2x +π3)的图象关于点P (x 0,0)成中心对称,若x 0∈[-π2,0],则x 0=________.[答案] -π6[解析] ∵函数y =2sin(2x +π3)的对称中心是函数图象与x 轴的交点,∴2sin(2x 0+π3)=0,∵x 0∈[-π2,0]∴x 0=-π6.1.(文)(2020·湖南张家界月考)若函数f (x )=(1+3tan x )cos x,0≤x <π2,则f (x )的最大值为( )A .1B .2 C.3+1 D.3+2 [答案] B[解析] f (x )=(1+3tan x )cos x=cos x +3sin x =2sin ⎝⎛⎭⎪⎫x +π6,∵0≤x <π2,∴π6≤x +π6<2π3,∴12≤sin ⎝⎛⎭⎪⎫x +π6≤1,∴f (x )的最大值为2.(理)(2020·湖北文,6)已知函数f (x )=3sin x -cos x ,x ∈R.若f (x )≥1,则x 的取值范围为( )A .{x |2k π+π3≤x ≤2k π+π,k ∈Z}B .{x |k π+π3≤x ≤k π+π,k ∈Z}C .{x |2k π+π6≤x ≤2k π+5π6,k ∈Z}D .{x |k π+π6≤x ≤k π+5π6,k ∈Z}[答案] A[解析] f (x )=3sin x -cos x =2sin(x -π6)≥1,即sin(x -π6)≥12,∴2k π+π6≤x -π6≤2k π+5π6k ∈Z , ∴2k π+π3≤x ≤2k π+π(k ∈Z).2.(文)(2020·北京大兴区模拟)已知函数f (x )=3sin πxR图象上相邻的一个最大值点与一个最小值点恰好都在圆x 2+y 2=R 2上,则f (x )的最小正周期为( )A .1B .2C .3D .4 [答案] D[解析] f (x )的周期T =2ππR=2R ,f (x )的最大值是3,结合图形分析知R >3,则2R >23>3,只有2R =4这一种可能,故选D.(理)(2020·北京西城模拟)函数y =sin(πx +φ)(φ>0)的部分图象如图所示,设P 是图象的最高点,A ,B 是图象与x 轴的交点,则tan ∠APB =( )A .10B .8 C.87 D.47 [答案] B[分析] 利用正弦函数的周期、最值等性质求解.[解析] 如图,过P 作PC ⊥x 轴,垂足为C ,设∠APC =α,∠BPC =β,∴∠APB =α+β,y =sin(πx +φ),T =2ππ=2,tan α=ACPC=121=12,tanβ=BCPC=321=32,则tan(α+β)=tanα+tanβ1-tanα·tanβ=12+321-12×32=8,∴选B.3.(文)(2020·湖南长沙一中月考)下列函数中,图象的一部分如图所示的是( ) A.y=sin(2x+π6)B.y=sin(2x-π6)C.y=cos(2x+π3)D.y=cos(2x-π6)[答案] D[解析] 将(-π6,0)代入选项逐一验证,对A项,y=sin(-π3+π6)≠0,A错;对B 项,y=sin(-π2)=-1≠0,B错;对C项y=cos0=1≠0,C错;对D项,y=cos(-π3-π6)=cosπ2=0符合,故选D.(理)(2020·吉林一中月考)函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则( )A .ω=π2,φ=π4B .ω=π3,φ=π6C .ω=π4,φ=π4D .ω=π4,φ=5π4[答案] C[解析] ∵T 4=3-1=2,∴T =8,∴ω=2πT =π4.令π4×1+φ=π2,得φ=π4,∴选C. 4.(2020·北京海淀期中)如果存在正整数ω和实数φ,使得函数f (x )=cos 2(ωx +φ)的图象如图所示(图象经过点(1,0)),那么ω的值为( )A .1B .2C .3D .4 [答案] B[解析] f (x )=12+12cos(2ωx +2φ),由图可知T2<1<34T ,∴43<T <2,43<2π2ω<2,π2<ω<34π, 又ω∈N *,∴ω=2.故选B.5.(2020·安徽百校论坛联考)已知f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π6-m 在x ∈[0,π2]上有两个不同的零点,则m 的取值范围是________.[答案] [1,2)[解析] f (x )在[0,π2]上有两个不同零点,即方程f (x )=0在[0,π2]上有两个不同实数解,∴y =2sin ⎝ ⎛⎭⎪⎫2x -π6,x ∈[0,π2]与y =m 有两个不同交点,∴1≤m <2. 6.(2020·长沙一中月考)已知f (x )=sin x +sin(π2-x ).(1)若α∈[0,π],且sin2α=13,求f (α)的值;(2)若x ∈[0,π],求f (x )的单调递增区间. [解析] (1)由题设知f (α)=sin α+cos α. ∵sin2α=13=2sin α·cos α>0,α∈[0,π],∴α∈(0,π2),sin α+cos α>0.由(sin α+cos α)2=1+2sin α·cos α=43,得sin α+cos α=233,∴f (α)=23 3.(2)由(1)知f (x )=2sin(x +π4),又0≤x ≤π, ∴f (x )的单调递增区间为[0,π4].7.(文)在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,向量m =(b,2a -c ),n =(cos B ,cos C ),且m ∥n .(1)求角B 的大小;(2)设f (x )=cos ⎝ ⎛⎭⎪⎫ωx -B 2+sin ωx (ω>0),且f (x )的最小正周期为π,求f (x )在区间[0,π2]上的最大值和最小值. [解析] (1)由m ∥n 得,b cos C =(2a -c )cos B , ∴b cos C +c cos B =2a cos B .由正弦定理得,sin B cos C +sin C cos B =2sin A cos B , 即sin(B +C )=2sin A cos B .又B +C =π-A ,∴sin A =2sin A cos B . 又sin A ≠0,∴cos B =12.又B ∈(0,π),∴B =π3.(2)由题知f (x )=cos(ωx -π6)+sin ωx =32cos ωx +32sin ωx =3sin(ωx +π6), 由已知得2πω=π,∴ω=2,f (x )=3sin(2x +π6),当x ∈[0,π2]时,(2x +π6)∈[π6,7π6],sin(2x +π6)∈[-12,1].因此,当2x +π6=π2,即x =π6时,f (x )取得最大值 3.当2x +π6=7π6,即x =π2时,f (x )取得最小值-32.(理)(2020·湖北黄冈)已知a =(3,cos x ),b =(cos 2x ,sin x ),函数f (x )=a ·b -32. (1)求函数f (x )的单调递增区间;(2)若x ∈⎣⎢⎡⎦⎥⎤0,π4,求函数f (x )的取值范围;(3)函数f (x )的图象经过怎样的平移可使其对应的函数成为奇函数? [解析] (1)函数f (x )=3cos 2x +sin x cos x -32=3⎝ ⎛⎭⎪⎫1+cos2x 2+12sin2x -32=32cos2x +12sin2x =sin ⎝⎛⎭⎪⎫2x +π3∴由-π2+2k π≤2x +π3≤π2+2k π,k ∈Z 得-5π12+k π≤x ≤π12+k π,k ∈Z 所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤-5π12+k π,π12+k π,(k ∈Z)(2)∵x ∈⎣⎢⎡⎦⎥⎤0,π4,∴2x +π3∈⎣⎢⎡⎦⎥⎤π3,5π6∴当2x +π3=π2即x =π12时f (x )max =1当2x +π3=5π6即x =π4时,f (x )min =12,∴12≤f (x )≤1.(3)将f (x )的图象上所有的点向右平移π6个单位长度得到y =sin2x 的图象,则其对应的函数即为奇函数.(答案不唯一)1.(2020·合肥质检)对任意x 1,x 2∈⎝ ⎛⎭⎪⎫0,π2,x 2>x 1,y 1=1+sin x 1x 1,y 2=1+sin x 2x 2,则( ) A .y 1=y 2 B .y 1>y 2 C .y 1<y 2D .y 1,y 2的大小关系不能确定 [答案] B[解析] 取函数y =1+sin x ,则1+sin x 1x 1的几何意义为过原点及点(x 1,1+sin x 1)的直线斜率,1+sin x 2x 2的几何意义为过原点及点(x 2,1+sin x 2)的直线斜率,由x 1<x 2,观察函数y =1+sin x 的图象可得y 1>y 2.选B.2.已知函数f (x )=A sin(ωx +φ),x ∈R(其中A >0,ω>0,0<φ<π2)的图象与x 轴的交点中,相邻两个交点之间的距离为π2,且图象上的一个最低点为M ⎝ ⎛⎭⎪⎫2π3,-2.则f (x )的解析式为( )A .f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6B .f (x )=2cos ⎝ ⎛⎭⎪⎫2x +π6C .f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3D .f (x )=cos ⎝ ⎛⎭⎪⎫2x +π3 [答案] A[解析] 由最低点为M ⎝⎛⎭⎪⎫2π3,-2得A =2.由x 轴上相邻两个交点之间的距离为π2得,T 2=π2,即T =π,∴ω=2πT =2ππ=2.由点M ⎝⎛⎭⎪⎫2π3,-2在函数图象上得,2sin ⎝ ⎛⎭⎪⎫2×2π3+φ=-2,即sin ⎝ ⎛⎭⎪⎫4π3+φ=-1,故4π3+φ=2k π-π2,k ∈Z ,∴φ=2k π-11π6.又φ∈⎝⎛⎭⎪⎫0,π2,∴φ=π6,故f (x )=2sin ⎝⎛⎭⎪⎫2x +π6.3.(2020·安徽马鞍山二中)函数f (x )=A sin(ωx +φ)+b 的图象如图所示,则f (1)+f (2)+…+f (2020)的值为( )A .2020 B.40172 C .2020 D.40192[答案] D[解析] 由f (x )的图象可以得到A =12,b =1,T =4,所以ω=π2,故f (x )=12sin(π2x +φ)+1,再由点⎝ ⎛⎭⎪⎫1,32在f (x )的图象上,可得φ=2k π,k ∈Z , 所以f (x )=12sin πx2+1.所以f (1)=12+1,f (2)=0+1,f (3)=-12+1,f (4)=0+1,所以f (1)+f (2)+f (3)+f (4)=4,所以f (1)+f (2)+…+f (2020)=2020+f (2020)=2020+f (1)=40192.4.(2020·浙江金华十校)M 、N 是曲线y =πsin x 与曲线y =πcos x 的两个不同的交点,则|MN |的最小值为( )A .π B.2π C.3π D .2π[答案] C[解析] 其中与原点最近的两交点M ⎝ ⎛⎭⎪⎫π4,2π2,N ⎝ ⎛⎭⎪⎫5π4,-2π2,∴|MN |=3π.5.已知函数f (x )=x ·sin x ,x ∈R.则f ⎝ ⎛⎭⎪⎫-π4,f (1)及f ⎝ ⎛⎭⎪⎫π3的大小关系为( ) A .f ⎝ ⎛⎭⎪⎫-π4>f (1)>f ⎝ ⎛⎭⎪⎫π3B .f (1)>f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫-π4C .f ⎝ ⎛⎭⎪⎫π3>f (1)>f ⎝ ⎛⎭⎪⎫-π4D .f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫-π4>f (1) [答案] C[解析] ∵f (x )为偶函数,且在⎣⎢⎡⎦⎥⎤0,π2上为增函数,∴f ⎝ ⎛⎭⎪⎫-π4=f ⎝ ⎛⎭⎪⎫π4,由于π3>1>π4,∴f ⎝ ⎛⎭⎪⎫π3>f (1)>f ⎝ ⎛⎭⎪⎫π4=f ⎝ ⎛⎭⎪⎫-π4,故选C.6.(2020·山东肥城联考)函数f (x )=2sin(ωx +φ)(其中ω>0,-π2<φ<π2)的图象如图所示,若点A 是函数f (x )的图象与x 轴的交点,点B 、D 分别是函数f (x )的图象的最高点和最低点,点C ⎝⎛⎭⎪⎫π12,0是点B 在x 轴上的射影,则AB →·BD →的值是( )A .8B .-8C.π28-8 D .-π28+8 [答案] C[解析] 由图可知T 4=π3-π12=π4,∴T =π,∴ω=2,由2·π3+φ=π知,φ=π3,从而A ⎝ ⎛⎭⎪⎫-π6,0,B ⎝ ⎛⎭⎪⎫π12,2,D ⎝ ⎛⎭⎪⎫7π12,-2,AB →=⎝ ⎛⎭⎪⎫π4,2,BD →=⎝ ⎛⎭⎪⎫π2,-4,∴AB →·BD →=π28-8.7.(2020·福建莆田市质检)某同学利用描点法画函数y =A sin(ωx +φ)(其中A >0,0<ω<2,-π2<φ<π2)的图象,列出的部分数据如下表:x 0 1 2 3 4 y11-1-2y =A sin(ωx +φ)的解析式应是________.[答案] y =2sin ⎝ ⎛⎭⎪⎫π3x +π6[解析] ∵(0,1)和(2,1)关于直线x =1对称,故x =1与函数图象的交点应是最高点或最低点,故数据(1,0)错误,从而由(4,-2)在图象上知A =2,由过(0,1)点知2sin φ=1,∵-π2<φ<π2,∴φ=π6,∴y =2sin ⎝ ⎛⎭⎪⎫ωx +π6,再将点(2,1)代入得,2sin ⎝⎛⎭⎪⎫2ω+π6=1, ∴2ω+π6=π6+2k π或2ω+π6=5π6+2k π,k ∈Z ,∵0<ω<2,∴ω=π3,∴解析式为y =2sin ⎝⎛⎭⎪⎫π3x +π6.8.(2020·福建四地六校联考)已知函数f (x )=-1+23sin x cos x +2cos 2x . (1)求f (x )的单调递减区间;(2)求f (x )图象上与原点最近的对称中心的坐标;(3)若角α,β的终边不共线,且f (α)=f (β),求tan(α+β)的值. [解析] f (x )=3sin2x +cos2x =2sin(2x +π6),(1)由2k π+π2≤2x +π6≤2k π+3π2(k ∈Z)得k π+π6≤x ≤k π+2π3(k ∈Z),∴f (x )的单调减区间为[k π+π6,k π+2π3](k ∈Z),(2)由sin(2x +π6)=0得2x +π6=k π(k ∈Z),即x =k π2-π12(k ∈Z), ∴f (x )图象上与原点最近的对称中心坐标是(-π12,0).(3)由f (α)=f (β)得:2sin(2α+π6)=2sin(2β+π6),又∵角α与β的终边不共线,∴(2α+π6)+(2β+π6)=2k π+π(k ∈Z),即α+β=k π+π3(k ∈Z),∴tan(α+β)= 3.。
2020年高三数学三轮复习回归基础专题三角函数的图像与性质
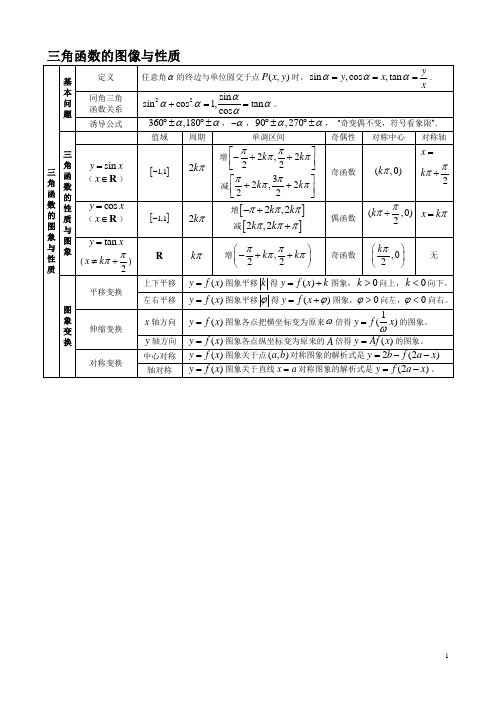
三角函数的图象与性质
基本问题
定义
任意角 的终边与单位圆交于点 时, .
同角三角
函数关系
。
诱导公式
, , ,“奇变偶不变,符号看象限”.
三角函数的性质与图象
值域
周期
单调区间
奇偶性
对称中心
对称轴
( )
增ห้องสมุดไป่ตู้
减
奇函数
( )
增
减
偶函数
( )
增
奇函数
无
图象变换
平移变换
上下平移
图象平移 得 图象, 向上, 向下。
左右平移
图象平移 得 图象, 向左, 向右。
伸缩变换
轴方向
图象各点把横坐标变为原来 倍得 的图象。
轴方向
图象各点纵坐标变为原来的 倍得 的图象。
对称变换
中心对称
图象关于点 对称图象的解析式是
轴对称
图象关于直线 对称图象的解析式是 。
金典艺术生高考数学复习资料--3三角函数性质与图像

三角函数性质与图像备注:以上性质的理解记忆关键是能想象或画出函数图象........... 函数sin()y A x ωϕ=+的图像和性质以函数sin y x =为基础,通过图像变换来把握. 如①sin y x=−−−−→图例变化为②sin()y A x ωϕ=+(A >0,ω>0)相应地,①的单调增区间2,222k k ππππ⎡⎤-++⎢⎥⎣⎦−−−→变为2222k x k πππωϕπ-+++≤≤的解集是②的增区间.注:⑴)sin(ϕω+=x y 或cos()y x ωϕ=+(0≠ω)的周期ωπ2=T ;⑵sin()y x ωϕ=+的对称轴方程是2x k ππ=+(Z k ∈),对称中心(,0)k π;cos()y x ωϕ=+的对称轴方程是x k π=(Z k ∈),对称中心1(,0)2k ππ+;)tan(ϕω+=x y 的对称中心(0,2πk ). 课前预习1.函数sin cos y x x =-的最小正周期是 . 2. 函数1π2sin()23y x =+的最小正周期T = .4.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是5.函数22cos()()363y x x πππ=-≤≤的最小值是6.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象向 平移 个单位长度7.将函数sin y x =的图象上各点的横坐标扩大为原来的2倍,纵坐标不变,再把所得图象上所有点向左平移3π个单位,所得图象的解析式是 .8. 函数sin y x x =在区间[0,2π]的最小值为______.9.已知f (x )=5sin x cos x -35cos 2x +325(x ∈R ) ⑴求f (x )的最小正周期; ⑵求f (x )单调区间;⑶求f (x )图象的对称轴, 典型例题例1、三角函数图像变换将函数12cos()32y x π=+的图像作怎样的变换可以得到函数cos y x =的图像? 变式1:将函数cos y x =的图像作怎样的变换可以得到函数2cos(2)4y x π=-的图像?例2、已知简谐运动ππ()2sin 32f x x ϕϕ⎛⎫⎛⎫=+<⎪⎪⎝⎭⎝⎭的图象经过点(01),,则该简谐运动的最 小正周期T 和初相ϕ分别为 例3、三角函数性质 求函数34sin(2)23y x ππ=+的最大、最小值以及达到最大(小)值时x 的值的集合 变式1:函数y =2sin x 的单调增区间是 变式2、下列函数中,既是(0,2π)上的增函数,又是以π为周期的偶函数是( )(A)y =lg x 2(B)y =|sin x | (C)y =cos x (D)y=x 2sin 2变式3、已知⎥⎦⎤⎢⎣⎡∈2,0πx ,求函数)125cos()12cos(x x y +--=ππ的值域变式4、已知函数12()log (sin cos )f x x x =-⑴求它的定义域和值域;⑵求它的单调区间;⑶判断它的奇偶性;⑷判断它的周期性.例4、三角函数的简单应用如图,某地一天从6时至14时的温度变化曲线近似满足函数y =A sin (ωx +ϕ)+b . (Ⅰ)求这段时间的最大温差; (Ⅱ)写出这段曲线的函数解析式. 例5、三角恒等变换函数y =xx cos sin 21++的最大值是 .π2sin 4α⎛⎫- ⎪⎝⎭变式2:已知函数2π()2sin 24f x x x ⎛⎫=+ ⎪⎝⎭,ππ42x ⎡⎤∈⎢⎥⎣⎦,.求()f x 的最大值和最小值. 实战训练1.函数x x f 2sin 21)(-=的最小正周期为2. 函数f x x x x ()cos sin cos =-223的最小正周期是____ 3.函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于 4.(07年浙江卷理2)若函数()2sin()f x x ωϕ=+,x ∈R (其中0ω>,2ϕπ<)的最小正周期是π,且(0)f =,则 5.(2007年辽宁卷7).若函数()y f x =的图象按向量a 平移后,得到函数(1)2y f x =--的图象,则向量a = 6.(2007年江西卷文2).函数5tan(21)y x =+的最小正周期为 7.(2007年湖北卷理2).将π2cos 36x y ⎛⎫=+ ⎪⎝⎭的图象按向量π24⎛⎫=-- ⎪⎝⎭,a 平移,则平移后所得图象的解析式为8.(2007年广东卷理3).若函数21()sin ()2f x x x R =-∈,则f(x)是最小正周期为 的 函数9.(2007年福建卷理5).已知函数()sin (0)f x x ωωπ⎛⎫=+> ⎪3⎝⎭的最小正周期为π,则该函数的图象( )A .关于点0π⎛⎫ ⎪3⎝⎭,对称 B .关于直线x π=4对称 C .关于点0π⎛⎫ ⎪4⎝⎭,对称D .关于直线x π=3对称 10.(2007年江苏卷1).下列函数中,周期为2π的是( ) A .sin2x y = B .sin 2y x = C .cos 4xy = D .cos 4y x = 11.(2007年江苏卷5).函数()sin ([,0])f x x x x π=∈-的单调递增区间是( )A .5[,]6ππ--B .5[,]66ππ--C .[,0]3π-D .[,0]6π- 12.(2007年天津卷文9)设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ,则()f x ( )A .在区间2736ππ⎡⎤⎢⎥⎣⎦,上是增函数 B .在区间2π⎡⎤-π-⎢⎥⎣⎦,上是减函数C .在区间84ππ⎡⎤⎢⎥⎣⎦,上是增函数D .在区间536ππ⎡⎤⎢⎥⎣⎦,上是减函数13.(07年山东卷文4).要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象( )A .向右平移π6个单位B .向右平移π3个单位 C .向左平移π3个单位D .向左平移π6个单位14.(07年全国卷二理2).函数sin y x =的一个单调增区间是( )A .ππ⎛⎫- ⎪44⎝⎭,B .3ππ⎛⎫ ⎪44⎝⎭,C .3π⎛⎫π ⎪2⎝⎭,D .32π⎛⎫π ⎪2⎝⎭,15.(2007年北京卷文3).函数()sin 2cos 2f x x x =-的最小正周期是16.(2007年重庆卷文)(18)已知函数)2sin(42cos 2ππ+⎪⎭⎫ ⎝⎛-x x 。
2020高考理数(北师大版)总复习 第3章 第3节 三角函数的图像与性质

区间
课
堂
题
型
全
奇偶性
突
k_∈__Z__ 奇__函__数__
k∈Z 偶__函__数__
无
课
后
限
时
_奇__函__数_
集 训
破
返 首 页
课
前 知
对称
识
全
中心
通
关
对称轴
方程
课
堂
周期性
题
型
全
突
破
_(k_π_,__0_)_,_k_∈__Z_ x_=__k_π_+__2π_(k_∈__Z_ )
2π
真
__k_π_+__π2_,__0_,__k_∈__Z_ ___k2_π_,__0_,__k_∈__Z___
课 后 限 时 集 训
破
返 首 页
(1)(2019·珠海模拟)已知 ω>0,函数 f(x)=sinωx+π4在π2,π
上递减,则 ω 的取值范围是( )
课
真
前
知 识
A.(0,2]
全
B.0,12
题 自 主 验
通 关
C.12,34
D.12,54
课
堂 题 型
(π,-1) ,32π,0,(2π,1).
全
突
课 后 限 时 集 训
破
返 首 页
2.正弦函数、余弦函数、正切函数的图像与性质
课
函数
y=sin x
前知Leabharlann 识图像全通
关
y=cos x
y=tan x
真
题
自
主
验
效
果
定义域
课
堂
题
型
2020届新高考艺术生数学复习冲关训练:第三章 第3节三角函数的图象与性质

第三章 第3节1.(2018·全国卷Ⅲ)函数f (x )=的最小正周期为( )tan x1+tan2x A. B. C .π D .2ππ4π2解析:C [f (x )====sin x cos x =sin 2x ,∴f (x )的周期tan x1+tan2x sin x cos x1+sin2xcos2x sin x cos xsin2x +cos2x 12T ==π.故选C.]2π22.(2017·全国Ⅲ卷)函数f (x )=sin+cos 的最大值为( )15(x +π3)(x -π6)A.B .1C. D.653515解析:A [由诱导公式得cos=(x -π6)cos =sin ,则f (x )=[π2-(x +π3)](x +π3)sin +sin =sin ,所以函数f (x )的最大值为.故选A.]15(x +π3)(x +π3)65(x +π3)653.函数f (x )=1-2sin2是( )(x -π4)A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为的偶函数π2D .最小正周期为的奇函数π2解析:B [因为函数y =1-2sin 2=(x -π4)cos=sin 2x ,所以该函数是最小正周期为π的奇函数.故选B.](2x -π2)4.(2019·昆明市一模)若直线x =a π(0<a <1)与函数y =tan x 的图象无公共点,则不等式tan x ≥2a 的解集为( )A.{x |k π+π6≤x <k π+π2,k ∈Z }B.{x |k π+π4≤x <k π+π2,k ∈Z }C.{x |k π+π3≤x <k π+π2,k ∈Z }D.{x |k π-π4≤x ≤k π+π4,k ∈Z }解析:B [直线x =a π(0<a <1)与函数y =tan x 的图象无公共点,∴a =,∴不等式12化为tanx ≥1,解得k π+≤x <k π+,k ∈Z ;∴所求不等式的解集为π4π2{x |k π+≤x <k π+,k ∈Z }.]π4π25.(2019·长春市一模)已知函数f (x )=2sin (2x +φ)(0<φ<π),且f (0)=1,则下列结论中正确的是( )A .f (φ)=2B.是f (x )图象的一个对称中心(π6,0)C .∅=π3D .x =-是f (x )图象的一条对称轴π6解析:A [函数f (x )=2sin (2x +φ),且f (0)=2sin φ=1,∴sin φ=.又0<φ<π,∴φ=或;12π65π6当φ=时,f =2sin =2,当φ=时,f =2sin=2,π6(π6)(2×π6+π6)5π6(5π6)(2×5π6+5π6)故A 正确.]6.(2018·全国Ⅲ卷)函数f (x )=cos 在[0,π]的零点个数为________.(3x +π6)解析:由f (x )=cos =0,有3x +=k π+(k ∈Z ),解得x =π+,由(3x +π6)π6π2k3π90≤π+≤π得k 可取0,1,2,∴f (x )=cos在[0,π]上有3个零点.k3π9(3x +π6)答案:37.函数f (x )=的定义域为________.3+2cos x解析:要使函数f (x )=有意义,则+2cos x ≥0即cos x ≥-,由余弦函3+2cos x 332数的图象,得在一个周期[-π,π]上,不等式cos x ≥-的解集为,32{x |-5π6≤x ≤56π}所以,在实数集上不等式的解集为,{x |-56π+2k π≤x ≤56π+2k π,k ∈Z}即函数的定义域为.{x |-56π+2k π≤x ≤56π+2k π,k ∈Z}答案:{x |-56π+2k π≤x ≤56π+2k π,k ∈Z}8.(2019·鄂伦春自治旗一模)若函数f (x )=1+a sin (ax +(a >0))的最大值为3,则f (x )π6的最小正周期为______.解析:函数f (x )=1+a sin 的最大值为3,(ax +π6)∴1+a =3,解得a =2.∴f (x )=1+2sin,(2x +π6)∴f (x )的最小正周期为T ==π.2πω答案:π9.(2019·玉溪市模拟)设函数f (x )=2sin x cos x -cos 2x +1(1)求f (π2)(2)求f (x )的最大值和最小正周期.解:(1)函数f (x )=2sin x cos x -cos 2x +1=sin 2x -cos 2x +1=sin+1,2(2x -π4)∴f =sin+1=×+1=2.(π2)2(2×π2-π4)222(2)由f (x )=sin+1,2(2x -π4)当2x -=+2k π,k ∈Z ,即x =+k π,k ∈Z 时,π4π23π8f (x )取得最大值为+1,2最小正周期为T ==π.2πω10.(2019·泸州市模拟)已知函数f (x )=sin x cos x -cos 2x +a 的最大值为.22(1)求a 的值;(2)求使f (x )≥0成立的x 的集合.解:(1)∵f (x )=sin x cos x -cos 2x +a =sin 2x -+a =sin+a -,121+cos 2x222(2x -π4)12∴f (x )max =+a -=,∴a =.22122212(2)由(1)知,f (x )=sin.22(2x -π4)由f (x )≥0,得sin≥0,22(2x -π4)即2k π≤2x -≤π+2k π,k ∈Z ,π4∴+k π≤x ≤+k π,k ∈Z ,π85π8∴f (x )≥0成立的x 的集合为,k ∈Z .[π8+k π,5π8+k π]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 第3节
1.(2018·全国卷Ⅲ)函数f (x )=tan x 1+tan 2x
的最小正周期为( ) A.π4 B.π2
C .π
D .2π 解析:C [f (x )=tan x 1+tan 2x =sin x
cos x 1+sin 2x cos 2x
=sin x cos x sin 2x +cos 2x =sin x cos x =12sin 2x ,∴f (x )的周期T =2π2=π.故选C.]
2.(2017·全国Ⅲ卷)函数f (x )=15
sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6的最大值为( ) A.65 B .1 C.35
D.15 解析:A [由诱导公式得cos ⎝⎛⎭
⎫x -π6= cos ⎣⎡⎦
⎤π2-⎝⎛⎭⎫x +π3=sin ⎝⎛⎭⎫x +π3,则f (x )= 15sin ⎝⎛⎭⎫x +π3+sin ⎝⎛⎭⎫x +π3=65sin ⎝⎛⎭⎫x +π3,所以函数f (x )的最大值为65
.故选A.] 3.函数f (x )=1-2sin 2⎝⎛⎭
⎫x -π4是( ) A .最小正周期为π的偶函数
B .最小正周期为π的奇函数
C .最小正周期为π2
的偶函数 D .最小正周期为π2
的奇函数 解析:B [因为函数y =1-2sin 2⎝⎛⎭
⎫x -π4= cos ⎝
⎛⎭⎫2x -π2=sin 2x ,所以该函数是最小正周期为π的奇函数.故选B.] 4.(2019·昆明市一模)若直线x =a π(0<a <1)与函数y =tan x 的图象无公共点,则不等式tan x ≥2a 的解集为( )
A.⎩⎨⎧⎭
⎬⎫x |k π+π6≤x <k π+π2,k ∈Z B.⎩
⎨⎧⎭⎬⎫x |k π+π4≤x <k π+π2,k ∈Z C.⎩⎨⎧⎭⎬⎫x |k π+π3≤x <k π+π2,k ∈Z
D.⎩⎨⎧⎭
⎬⎫x |k π-π4≤x ≤k π+π4,k ∈Z 解析:B [直线x =a π(0<a <1)与函数y =tan x 的图象无公共点,∴a =12
,∴不等式化为tan x ≥1,解得k π+π4≤x <k π+π2,k ∈Z ;∴所求不等式的解集为{x |k π+π4≤x <k π+π2
,k ∈Z }.] 5.(2019·长春市一模)已知函数f (x )=2sin (2x +φ)(0<φ<π),且f (0)=1,则下列结论中正确的是( )
A .f (φ)=2
B.⎝⎛⎭⎫π6,0是f (x )图象的一个对称中心
C .∅=π3
D .x =-π6
是f (x )图象的一条对称轴 解析:A [函数f (x )=2sin (2x +φ),且f (0)=
2sin φ=1,∴sin φ=12.又0<φ<π,∴φ=π6或5π6
; 当φ=π6时,f ⎝⎛⎭⎫π6=2sin ⎝⎛⎭⎫2×π6+π6=2,当φ=5π6
时,f ⎝⎛⎭⎫5π6=2sin ⎝⎛⎭⎫2×5π6+5π6=2,故A 正确.] 6.(2018·全国Ⅲ卷)函数f (x )=cos ⎝
⎛⎭⎫3x +π6在[0,π]的零点个数为________. 解析:由f (x )=cos ⎝⎛⎭⎫3x +π6=0,有3x +π6=k π+π2(k ∈Z ),解得x =k 3π+π9,由0≤k 3π+π9
≤π得k 可取0,1,2,∴f (x )=cos ⎝
⎛⎭⎫3x +π6在[0,π]上有3个零点. 答案:3
7.函数f (x )=3+2cos x 的定义域为________.
解析:要使函数f (x )=
3+2cos x 有意义,则3+2cos x ≥0即cos x ≥-32,由余弦函数的图象,得在一个周期[-π,π]上,
不等式cos x ≥-32的解集为⎩⎨⎧⎭
⎬⎫x |-5π6≤x ≤56π, 所以,在实数集上不等式的解集为
⎩⎨⎧⎭
⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z ,
即函数的定义域为
⎩⎨⎧⎭
⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z . 答案:⎩⎨⎧⎭
⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z 8.(2019·鄂伦春自治旗一模)若函数f (x )=1+a sin (ax +π6
(a >0))的最大值为3,则f (x )的最小正周期为______.
解析:函数f (x )=1+a sin ⎝
⎛⎭⎫ax +π6的最大值为3, ∴1+a =3,解得a =2.
∴f (x )=1+2sin ⎝
⎛⎭⎫2x +π6, ∴f (x )的最小正周期为T =2πω
=π. 答案:π
9.(2019·玉溪市模拟)设函数f (x )=2sin x cos x -cos 2x +1
(1)求f ⎝⎛⎭⎫π2
(2)求f (x )的最大值和最小正周期.
解:(1)函数f (x )=2sin x cos x -cos 2x +1=
sin 2x -cos 2x +1=2sin ⎝
⎛⎭⎫2x -π4+1, ∴f ⎝⎛⎭⎫π2=2sin ⎝⎛⎭⎫2×π2-π4+1=2×22
+1=2. (2)由f (x )=2sin ⎝
⎛⎭⎫2x -π4+1, 当2x -π4=π2+2k π,k ∈Z ,即x =3π8
+k π,k ∈Z 时, f (x )取得最大值为2+1,
最小正周期为T =2πω
=π. 10.(2019·泸州市模拟)已知函数f (x )=sin x cos x -cos 2x +a 的最大值为
22
. (1)求a 的值;
(2)求使f (x )≥0成立的x 的集合.
解:(1)∵f (x )=sin x cos x -cos 2x +a =12sin 2x -1+cos 2x 2+a =22sin ⎝⎛⎭⎫2x -π4+a -12,
∴f (x )max =22+a -12=22,∴a =12
. (2)由(1)知,f (x )=
22sin ⎝⎛⎭⎫2x -π4. 由f (x )≥0,得22
sin ⎝⎛⎭⎫2x -π4≥0, 即2k π≤2x -π4
≤π+2k π,k ∈Z , ∴π8+k π≤x ≤5π8
+k π,k ∈Z , ∴f (x )≥0成立的x 的集合为⎣⎡⎦⎤π8+k π,5π8+k π,k ∈Z .。
