垂直与平行练习题
平行与垂直练习题

平行与垂直练习题一、选择题1. 在同一平面内,两条直线的位置关系有几种?A. 1种B. 2种C. 3种D. 4种2. 以下哪组线段是平行线?A. AB与CDB. EF与GHC. MN与OPD. PQ与RS3. 如果两条直线相交成90度角,这两条直线的关系是什么?A. 垂直B. 平行C. 相交D. 异面4. 已知直线a和直线b平行,直线c垂直于直线a,那么直线c与直线b的关系是什么?A. 平行B. 垂直C. 相交D. 异面5. 在平面几何中,平行线的性质不包括以下哪项?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 以上都不是二、填空题1. 如果两条直线相交,那么它们相交所成的角叫做______。
2. 两条直线相交所成的角中,有一个角是直角,那么这两条直线的关系是______。
3. 在同一平面内,不相交的两条直线叫做______。
4. 如果两条直线都与第三条直线平行,那么这两条直线的关系是______。
5. 两条直线相交所成的角中,如果有一个角是锐角,那么这两条直线的关系是______。
三、判断题1. 两条直线不相交,则它们一定平行。
(对/错)2. 垂直线段是最短的线段。
(对/错)3. 两条直线相交,所成的角中,锐角和钝角的和为180度。
(对/错)4. 两条平行线之间的距离处处相等。
(对/错)5. 如果两条直线相交成锐角,则它们一定不是平行线。
(对/错)四、计算题1. 已知直线AB和直线CD平行,直线EF垂直于直线AB,求证:直线EF也垂直于直线CD。
2. 已知直线m和直线n相交于点O,且∠AOM=90°,求证:直线m垂直于直线n。
3. 已知直线a和直线b平行,直线c和直线d平行,且直线c与直线a相交,求证:直线d与直线b也相交。
4. 已知直线PQ和直线RS垂直,直线PQ和直线ST平行,求证:直线RS和直线ST垂直。
5. 已知直线x和直线y相交成锐角,直线x和直线z平行,求证:直线y和直线z不平行。
数的平行线与垂直线练习题及答案

数的平行线与垂直线练习题及答案题一:数的平行线与垂直线(选择题)1. 下图中,哪条线和直线l平行?A. aB. bC. cD. d2. 在平面上,两条直线互相垂直,那么它们之间的夹角为:A. 90°B. 45°C. 180°D. 360°3. 在平面上,若m∥n,n⊥o,则m和o之间的关系是:A. 平行B. 垂直C. 交于一点D. 无法确定4. 下图中,哪个图形与直线l垂直?A. △ABCB. △DEFC. △GHID. △JKL5. 在平面上,若直线m与直线n垂直,m与直线p平行,则直线n 和直线p之间的关系是:A. 平行B. 垂直C. 交于一点D. 无法确定题二:数的平行线与垂直线(填空题)1. 平面上的两条直线互相垂直,则它们的斜率之积为_________。
2. 在平面上,若直线a垂直于直线b,直线b垂直于直线c,则直线a和直线c之间的关系是_________。
3. 直线AB和直线CD互相垂直,直线EF和直线CD平行,那么直线AB和直线EF之间的关系是_________。
4. 平面上有一条直线l垂直于直线m,直线l与直线n平行,则直线m和直线n之间的关系是_________。
题三:数的平行线与垂直线(计算题)1. 已知直线l1的斜率为3,过点A(1, 2)并且平行于直线l1的直线l2的方程是_________。
2. 已知直线l1过点A(2, 4),直线l2过点B(3, 6),且直线l1和直线l2互相垂直,直线l2的斜率为_________。
3. 有一条直线l通过点A(1, 2),斜率为-2,直线m通过点B(3, 4),斜率为2,直线l和直线m互相垂直吗?_________。
4. 已知直线l经过点A(-2, 3)和点B(1, 0),垂直于直线m,且与直线m交于点C(-1, -1)。
直线m的斜率为_________。
题四:数的平行线与垂直线(应用题)1. 甲、乙、丙三个小朋友站在一条平行线上的不同位置,如下图所示:甲站在直线的端点A,丙站在直线的端点B,乙站在直线的中点C。
数的平行线与垂直线练习题

数的平行线与垂直线练习题题目一:平行线1. 请判断以下直线是否平行:a) AB与CDb) EF与GHc) IJ与KL2. 已知折线ABCDEF,其中AB∥CD,EF∥GH,请判断以下直线是否平行:a) AD与GHb) EF与KJc) BC与DE3. 在平面直角坐标系中,已知直线y=2x+3和y=-3x+5,请判断它们是否平行。
4. 已知线段AB和线段CD,其中AB∥CD。
若线段EF∥AB且EF 与CD相交于点G,请问线段EF与CD是否平行。
题目二:垂直线1. 请判断以下直线是否垂直:a) AB与CDb) EF与GHc) IJ与KL2. 已知线段AC和线段BD,其中AC⊥BD。
若线段EF⊥AC且EF与AB相交于点G,请问线段EF与AB是否垂直。
3. 在平面直角坐标系中,已知直线y=2x+3和y=-1/2x+2,请判断它们是否垂直。
4. 已知线段AB和线段CD,其中AB⊥CD。
若线段EF⊥AB且EF与CD相交于点G,请问线段EF与CD是否垂直。
题目三:平行线和垂直线的综合运用1. 在直角坐标系中,已知点A(-1, 2),B(3, 5),C(6, 7),D(3, 1),请判断线段AB和线段CD是否平行,线段AB是否垂直于线段CD。
2. 在平面直角坐标系中,已知直线y=-2x+3,点E(-4, -5)和点F(1, 1),请判断直线EF与直线y=-2x+3是否平行,直线EF是否垂直于直线y=-2x+3。
3. 在平面直角坐标系中,已知点A(2, 4),B(5, 6),C(7, 8),D(4, 2),请判断线段AB和线段CD是否平行,线段AB是否垂直于线段CD。
4. 在直角坐标系中,已知直线y=x+1与直线y=-x+1,请判断这两条直线是否平行,是否垂直。
注意:题目中的直线均指直线段,平行线指两条直线段在同一平面内没有交点,垂直线指两条直线段的斜率乘积为-1。
人教版四年级上册数学平行与垂直同步练习
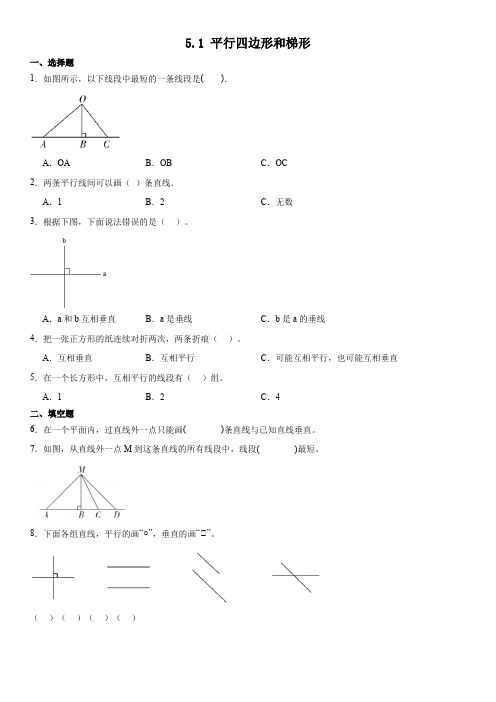
5.1 平行四边形和梯形一、选择题1.如图所示,以下线段中最短的一条线段是().A.OA B.OB C.OC2.两条平行线间可以画()条直线.A.1B.2C.无数3.根据下图,下面说法错误的是()。
A.a和b互相垂直B.a是垂线C.b是a的垂线4.把一张正方形的纸连续对折两次,两条折痕()。
A.互相垂直B.互相平行C.可能互相平行,也可能互相垂直5.在一个长方形中,互相平行的线段有()组。
A.1B.2C.4二、填空题6.在一个平面内,过直线外一点只能画( )条直线与已知直线垂直。
7.如图,从直线外一点M到这条直线的所有线段中,线段( )最短。
8.下面各组直线,平行的画“○”,垂直的画“△”。
()()()()()()()()9.在两条平行线间画垂直线段,如果第一条垂直线段长4厘米,那么第三条垂直线段长厘米。
10.(1)上图中,已知AB//CD,你还发现:( )//( ),( )△( )。
(2)线段EF和线段GH的长度( ),理由是( )。
(不能用量长度的方法说明理由)三、判断题11.3时整,时针和分针互相垂直。
( )12.数学课本封面相邻的两边互相垂直,相对的两边互相平行。
( )13.两个腰分别一样长的梯形一定能拼成一个平行四边形.( )14.不相交的两条直线一定互相平行。
( )15.图中有1组线段互相平行,3组线段互相垂直。
( )四、作图题16.小兔要去河边钓鱼。
请你帮小兔设计一条最短的路线,并在图上画出来。
17.过点D画线段AB的平行线,画线段BC的垂线。
五、解答题18.在下图中找出已学过的图形,并数一数,每种图形各有多少个?19.根据下图形作答。
(1)新校区到太仓北路的距离是()。
(2)计划从新校区铺一条排水管到太仓南路,怎么铺才能使所用的水管长度最短?并在图上画出来。
20.如图是一组平行线,请你在一条直线上任意选几个点,过这些点分别向另一条直线画垂线,量一量点到垂足间的距离,有什么发现吗?把你的发现写下来。
平行垂直练习题

平行垂直练习题一、选择题1. 在同一平面内,如果两条直线相交成90度角,那么这两条直线是:A. 平行线B. 垂直线C. 异面直线D. 相交线2. 下列说法正确的是:A. 平行线永远不会相交B. 垂直线是相交的C. 垂直线永远不会平行D. 两条直线要么平行,要么相交3. 如果一条直线与另一条直线相交,但不是垂直的,那么它们的关系是:A. 平行B. 垂直C. 斜交D. 异面4. 在平面几何中,两条直线的位置关系不包括:A. 平行B. 垂直C. 重合D. 相交5. 如果直线a和直线b在同一平面内,且不相交,那么直线a和直线b是:A. 平行线B. 垂直线C. 异面直线D. 重合直线二、填空题6. 在同一平面内,如果两条直线不相交,则它们是_________。
7. 如果两条直线相交所成的角是90度,则这两条直线是_________。
8. 两条直线相交成30度角,它们是_________。
9. 在平面几何中,两条直线的位置关系有_________、_________和_________。
10. 如果直线a与直线b垂直,那么直线a的斜率与直线b的斜率的乘积是_________。
三、判断题11. 平行线之间的距离处处相等。
()12. 垂直线之间的距离是固定的。
()13. 两条直线相交,它们的位置关系只能是垂直或平行。
()14. 两条直线可以同时是平行的和垂直的。
()15. 在同一平面内,两条直线不相交则它们一定是平行的。
()四、简答题16. 解释什么是平行线,并给出一个例子。
17. 描述垂直线的定义,并解释为什么两条垂直线相交所成的角是90度。
18. 如果两条直线相交,但不是垂直的,它们的位置关系是什么?请给出一个例子。
19. 在平面几何中,两条直线的位置关系有哪些?请列举并简要解释。
20. 为什么说两条直线在同一平面内,如果不相交,则它们一定是平行的?五、应用题21. 已知直线L1的方程为y=2x+3,直线L2的方程为y=-x+1,判断这两条直线是否平行或垂直,并说明理由。
平行线与垂直线的判定练习题

平行线与垂直线的判定练习题一、选择题1. 在平面P上,AB和CD是两条直线,若直线AB与直线CD平行,则下列命题中正确的是:A. AB与CD存在唯一交点B. AB与CD不存在交点C. AB与CD相交于一点D. AB与CD相交于两个不同的点2. 给定平面上的两条直线l和m,下列命题中不可能为真的是:A. l与m平行B. l与m相交于一点C. l与m相交于两个点D. l与m垂直3. 在平面上,如果两条直线互相垂直,则可以推出下列哪条命题?A. 这两条直线在同一平面上B. 这两条直线平行于同一直线C. 这两条直线夹角为90度D. 这两条直线夹角为180度4. 若两条直线的斜率互为倒数,且其中一条直线的斜率为k,则这两条直线为:A. 平行线B. 垂直线C. 相交于一点D. 无法判断5. 在平面上,如果两条直线分别与同一直线平行,则这两条直线互相平行。
A. 正确B. 错误二、填空题1. 设直线l1的斜率为k1,直线l2的斜率为k2,则当k1 * k2 = -1时,直线l1与l2为______。
2. 若两条直线之间的夹角为90度,则这两条直线是___________。
3. 设过点A(2,1)的直线l1的斜率为3,直线l2与l1垂直,求直线l2的斜率。
4. 若平面上AB与CD分别为两条相交直线的交点,且AB与CD互相垂直,则线段AB与线段CD的交点为__________。
5. 两条直线的斜率相等且不为0,则这两条直线平行。
A. 正确B. 错误三、计算题1. 已知平面上直线l1过点A(1,2),斜率为k1;直线l2过点B(-1,3),斜率为k2。
求证:若k1=k2,则线段AB垂直于直线l1。
证明:首先,计算直线l1的斜率:直线l1经过点A(1,2)和B(-1,3),设l1的斜率为k1。
k1 = (3-2)/(-1-1) = -1/2然后,计算直线l2的斜率:直线l2经过点A(1,2)和B(-1,3),设l2的斜率为k2。
平行垂直练习题及答案

平行垂直练习题及答案在数学学科中,平行和垂直是基本的几何概念。
理解和掌握平行和垂直的性质对于解决几何问题至关重要,因此平行和垂直的练习题是学习过程中必不可少的。
本文将提供一些平行和垂直的练习题,并附上详细的解答。
练习题一:判断平行关系1. 已知线段AB和线段CD的中点分别为E和F,若AE=CF且BE=DF,试判断AB和CD的关系。
2. ∠ABC = ∠PQR,∠BCD = ∠QRS,若线段AB和线段PQ平行,试判断线段CD和线段RS的关系。
3. 已知线段AB平行于线段CD,∠EAC = 70°,若∠ACD = x°,试判断∠ECA和∠ADC的大小关系。
答案一:1. 根据条件可知AE=CF,BE=DF,又根据中点划分线段的性质,且E和F分别是线段AB和线段CD的中点,所以EF=EF。
根据SAS准则可得△AEB≌△CFD,根据三角形的等边性质可知线段AB和线段CD平行。
2. 根据条件可知∠ABC = ∠PQR,∠BCD = ∠QRS,又根据等角定理可得△ABC ≌△PQR。
根据三角形的等边性质可知线段AB和线段PQ平行,所以线段CD和线段RS平行。
3. 已知线段AB平行于线段CD,所以利用平行线性质可得∠ECA = ∠ACD。
又根据答案一的证明可知线段AB和线段CD平行,所以△EAC ≌△ACD。
根据三角形的等边性质可知∠ECA = ∠ADC。
练习题二:判断垂直关系1. 线段AB与线段CD相交于点O,若∠AOB = 70°,∠COB = 110°,试判断线段AB和线段CD的关系。
2. 直线l与平面P相交于点A,若直线l垂直于线段AB,试判断直线l与平面P的关系。
3. 已知直线l垂直于平面P,线段AB在平面P内且与直线l相交于点C,试判断线段AB与平面P的关系。
答案二:1. ∠AOB = 70°,∠COB = 110°,根据角和定理可知∠AOB +∠COB = 180°。
四年级数学上册《平行与垂直》练习+答案,学习必备

四年级数学上册《平行与垂直》练习+答案,学习必备选择题1.关于下图,下列说法错误的是( A )。
A.直线a比直线c短B.直线a与直线b不平行C.直线c与直线d之间距离都相等D.直线c与直线d都垂直于直线a【详解】A.直线无法测量长度,所以直线a比直线c短2.体育课中大家分组玩夺宝游戏,宝藏在A点,如果让你选择出发点,你会选择( B )路线。
A.①B.②C.③【详解】根据分析可知,选A点到直线的垂线段,即②路线。
3.观察如图,点M表示笑笑所在的位置,AB表示河边的一条路,笑笑要到河边去,她沿着( C )走最近。
A.道路MAB.道路MBC.道路MC【详解】笑笑要到河边去,她沿着道路MC走最近。
填空题4.在下图中线段AB,AC, AD, AE中最短的一条线段是(线段AC)。
【详解】图中,线段AB,AC,AD,AE中,因为线段AC⊥BE,所以最短的一条线段是线段AC。
5.在纸上画两条直线,这两条直线可能(平行),也可能(相交)。
【详解】在同一平面内,两条直线只有两种位置关系;即平行和相交。
如图:平行相交6.下图中直线a与c互相(垂直),记作(a⊥c);直线a与b互相(平行),记作(a//b)。
【详解】根据题意可知:图中直线a与c互相垂直,记作a⊥c或c⊥a;直线a与b互相平行,记作a//b或b//a。
7.三条直线相交,最多有(3)个交点,最少有(1 )个交点。
【详解】由分析可知,三条线相交情况如下:所以三条直线相交,最多有3个交点,最少有1个交点。
作图题8.操作。
如图:已知直线L和直线L外的一点P。
过P点作出与直线L的平行线。
解答题9.如图。
如果A点挖一条水渠和小河相通,应该怎样挖才能使水渠的长度最短?在图上画出。
根据分析,过A点作小河的垂线段,如下:【点睛】根据垂直的性质:从直线外一点到这条直线可以画无数条线段,其中垂线段最短;由此解答即可。
10.(1)过P点分别画出线段AB的平行线和垂线。
如图:(2)量出∠1和∠2的度数,并填一填。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
垂直与平行、画垂线练习题
一、填空
1、在()平面内不相交的两条直线叫做(),也可以说这两条直线()。
2、如果两条直线相交成直角,就说这两条直线(),其中的一条()叫做另一条直线的(),这两条直线的交点叫做()。
3、从直线外一点到这条直线所画的()最短,它的长度叫做这点到直线的()。
4、经过直线外一点可以画()条与这条直线垂直的直线。
二、判断题。
1、永不相交的两条直线叫做平行线。
2、两条直线互相垂直,这两条直线相交的角一定是直角。
3、小明在纸上画了一条平行线。
4、两条直线不是平行就是相交。
三、选择题。
1.如果两条直线在同一平面内垂直于同一条直线,那么这两条直线()
A、相交
B、互相垂直
C、互相平行
2、在正方形中,每组对边(),相邻的两条边()
A、互相平行
B、互相垂直
C、互相交叉
四、他们说得对吧一?(对的在□里打“√”,错的打“×”。
)
五、画一画。
1、过A 点画已知直线的垂线。
.
2、过A 点画已知直线的平行线。
. .
3、画一个边长是3厘米的正方形。
4、A 、B 两村要安装自来水,怎样
自来水总管 B 村。
