matlab仿真报告
线性系统理论Matlab实践仿真报告

线性系统理论Matlab实验报告1、本题目是在已知状态空间描述的情况下要求设计一个状态反馈控制器,从而使得系统具有实数特征根,并要求要有一个根的模值要大于5,而特征根是正数是系统不稳定,这样的设计是无意义的,故而不妨设采用状态反馈后的两个期望特征根为-7,-9,这样满足题目中所需的要求。
(1)要对系统进行状态反馈的设计首先要判断其是否能控,即求出该系统的能控性判别矩阵,然后判断其秩,从而得出其是否可控;判断能控程序设计如下:>> A=[-0.8 0.02;-0.02 0];B=[0.05 1;0.001 0];Qc=ctrb(A,B)Qc =0.0500 1.0000 -0.0400 -0.80000.0010 0 -0.0010 -0.0200Rc=rank(Qc)Rc =2Qc =0.0500 1.0000 -0.0400 -0.80000.0010 0 -0.0010 -0.0200得出结果能控型判别矩阵的秩为2,故而该系统是完全可控的,故可以对其进行状态反馈设计。
(2)求取状态反馈器中的K,设的期望特征根为-7,-9;其设计程序如下:>> A=[-0.8 0.02;-0.02 0];B=[0.05 1;0.001 0];P=[-7 -9];k=place(A,B,P)k =1.0e+003 *-0.0200 9.00000.0072 -0.4500程序中所求出的k即为所求状态反馈控制器的状态反馈矩阵,即由该状态反馈矩阵所构成的状态反馈控制器能够满足题目要求。
2、(a)要求求该系统的能控型矩阵,并验证该系统是不能控的。
设计程序:>> A=[0 1 0 0 0;-0.1 -0.5 0 0 0;0.5 0 0 0 0;0 0 10 0 0;0.5 1 0 0 0];>> B=[0;1;0;0;0];>> C=[0 0 0 1 0];>> Qc=ctrb(A,B)Qc =0 1.0000 -0.5000 0.1500 -0.02501.0000 -0.5000 0.1500 -0.0250 -0.00250 0 0.5000 -0.2500 0.07500 0 0 5.0000 -2.50000 1.0000 0 -0.1000 0.0500>> Rc=rank(Qc)Rc =4从程序运行的结果可得,系统能控型判别矩阵的秩为4,而系统为5阶系统,故而就验证了该系统为不可控的。
matlab软件仿真实验(信号与系统)(1)
matlab软件仿真实验(信号与系统)(1)《信号与系统实验报告》学院:信息科学与⼯程学院专业:物联⽹⼯程姓名:学号:⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的:学习MATLAB的基本⽤法,了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
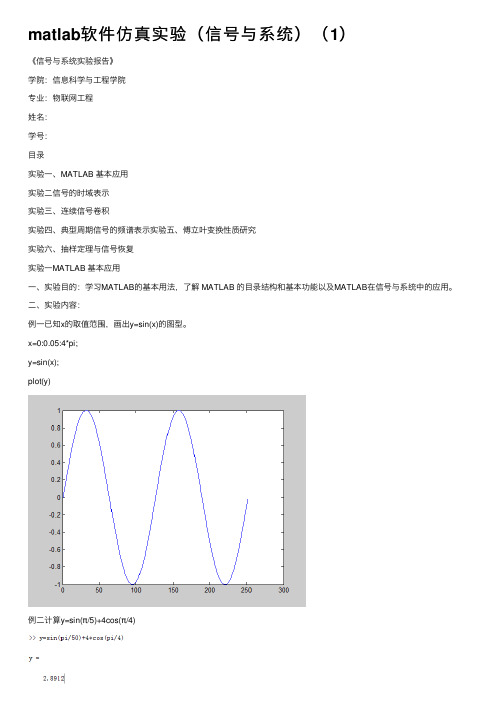
⼆、实验内容:例⼀已知x的取值范围,画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,⽤subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号:指数信号Ae at在MATLAB中可⽤exp函数表⽰,其调⽤形式为:y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号:正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰,其调⽤形式为:A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1,w0=2π,?=π/6) 参考程序:A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数:抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰,其定义为:sinc(t)=sin(πt)/( πt)其调⽤形式为:y=sinc(t)参考程序:t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号:在MATLAB中⽤rectpuls函数来表⽰,其调⽤形式为:y=rectpuls(t,width),⽤以产⽣⼀个幅值为1,宽度为width,相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,是以t=0为中⼼向左右各展开width/2的范围,width的默认值为1。
MATLAB系统仿真报告——有阻尼受迫振动系统

dx dt
Kx
F0
sin
wt
(2)
(2)式是一个线性非齐次方程。令B/M = 2n(n为阻尼系数)),K/M= wn2 ( wn
n 为固有振动频率),ξ = wn 为相对阻尼系数或阻尼比,则(2)式可写为:
dx 2 dt 2
2n
dx dt
wn2 x
h sin( wt )
(3)
根据阻尼对系统振动的影响,振动响应分为弱阻尼(ξ<1)、(强阻尼ξ>1)和 临界阻尼(ξ=1)三种情况。这里仅讨论弱阻尼的情况。在弱阻尼情况下的振动 为响应:x=Ae-ξwnt sin ( 1-ξ2wn t +φ ) +A1 sin (wt+θ) (4) 谐迫振动的主要特性有: (1)式(4)包括瞬态与稳态响应两部分,其中瞬态响应是一个有阻尼的谐振。振
0
0
50
100
15
20
25
184.
184.
184.
184.
184.
184.
18
185.
185.
185.
有图可以看出盐水浓度达到 0.2 kg / m 3 ,需要 184.82 分钟。
2、 脚本文件的方法: t=0:250; v1=6; v2=4; c1=0.5; c2=0.2; c=(2+3*t)./(2000+6*t); plot(t,c); xlabel('t'); ylabel('C'); title('浓度随时间的变化曲线'); grid on
入响应并画出波形。(1 用 simlink 的方法,2 用脚本文件的方法)
matlab电路仿真报告

matlab电路仿真报告一. 仿真背景和目的在电路设计和验证过程中,电路仿真技术是非常重要的。
Matlab这一强大的仿真软件,可快速有效地在仿真环境中进行电路设计验证,确保电路设计在实际应用中的可靠性和稳定性。
二. 仿真内容介绍本次仿真实验主要涉及四个方面的内容:交流电路、直流电路、半导体器件、功率放大器。
1. 交流电路仿真交流电路仿真是电路设计的基础。
本次仿真实验中,我们构建了简单的交流电路,通过仿真计算得到了交流电流、交流电压以及电路功率等参数。
2. 直流电路仿真直流电路仿真实验中,我们建立了稳定的直流电源和直流电路,在仿真环境中模拟了直流电路的工作状态,包括电流、电压、功率等参数。
通过仿真结果可以得到直流电路的性能评估。
3. 半导体器件仿真半导体器件在现代电子电路中广泛应用。
本次仿真中,我们针对开关电路的应用设计了半导体管,通过仿真计算得到了开关电路在不同工作状态下的输出特性,包括开关电压、开通电流等。
4. 功率放大器仿真功率放大器是实际应用中常见的一种电路结构。
仿真实验中,我们设计了基本的功率放大器电路,在仿真环境中计算得到了频率响应、增益、输出功率等参数,用于评估该功率放大器的性能和稳定性。
三. 仿真结果分析通过仿真计算和实验结果分析,可以得出以下几点结论:1. 交流电路仿真结果表明,输入交流电源的电流和电压随时间变化而变化,同时可以计算得到电路的功率和电阻等参数。
2. 直流电路仿真结果表明,直流电路的电流和电压稳定,可以计算得到直流电路的电流、电压和功率等参数。
3. 半导体器件仿真结果表明,半导体器件可以有效地用于开关电路应用,可以计算得到器件的开通电流、开关电压等参数。
4. 功率放大器仿真结果表明,功率放大器可以在一定的频率范围内实现较大的增益和输出功率。
同时,该电路还具有一定的稳定性和可靠性。
四. 总结和展望通过对电路仿真实验的分析和总结,我们可以发现,电路仿真技术在电路设计和验证过程中具有不可替代的作用。
自动实验一——典型环节的MATLAB仿真 报告
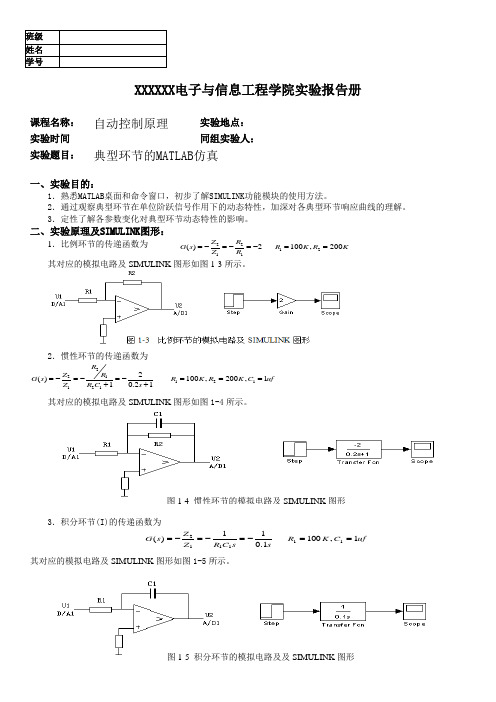
班级 姓名 学号XXXXXX 电子与信息工程学院实验报告册课程名称:自动控制原理 实验地点: 实验时间同组实验人: 实验题目: 典型环节的MATLAB 仿真一、实验目的:1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理及SIMULINK 图形:1.比例环节的传递函数为 221211()2100,200Z R G s R K R K Z R =-=-=-==其对应的模拟电路及SIMULINK 图形如图1-3所示。
2.惯性环节的传递函数为2211211212()100,200,110.21R Z R G s R K R K C uf Z R C s =-=-=-===++其对应的模拟电路及SIMULINK 图形如图1-4所示。
3.积分环节(I)的传递函数为uf C K R s s C R Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图1-5所示。
图1-5 积分环节的模拟电路及及SIMULINK 图形 图1-4 惯性环节的模拟电路及SIMULINK 图形4.微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图1-6所示。
5.比例+微分环节(PD )的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<=== 其对应的模拟电路及SIMULINK 图形如图1-7所示。
6.比例+积分环节(PI )的传递函数为)11(1)(11212s R s C R Z Z s G +-=+-=-= uf C K R R 10,100121===其对应的模拟电路及SIMULINK 图形如图1-8所示。
自动控制原理MATLAB仿真实验报告

实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性; 二、预习要点1、 系统的典型响应有哪些2、 如何判断系统稳定性3、 系统的动态性能指标有哪些 三、实验方法(一) 四种典型响应1、 阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、 脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为:)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式: ① )(sys impulse ; ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =(二) 分析系统稳定性 有以下三种方法:1、 利用pzmap 绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果: p =+ - + -P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
基于MATLAB控制系统仿真实验报告

tf 4
y0
0 1
6、求出 G1(s)
2 (s2 2s 1) 与 G2 (s)
1 (2s3
3s2
1)
的单位阶跃响应,并分别
求出状态空间模型。
解:(1) G1(s) 2 (s2 2s 1) 的状态空间模型求解如下:
function shiyan2 b1=[2];
D(z)
0.62(1 0.136z 1)(1 0.183z (1 0.045z 1)(1 0.53z 1)
1 )
分别用仿真算法得到系统在单位阶跃输入作用下的响应,系统在单位速度输
入是的输出响应。
解:(1)首先将 W1(s)转换为 W1(z),采样周期 T=0.2s,程序清单如下: function shiyan42 num=[10];den=[0.005 0.15 1 0]; ts=0.2;[nc,dc]=c2dm(num,den,ts)
INTRO(注意:intro 为一个用 MATLAB 语言编写的幻灯片程序,主要演示
常用的 MATLAB 语句运行结果。)
然后,根据现实出来的幻灯片右面按钮进行操作,可按 START——NEXT—
—NEXT 按钮一步步运行,观察。
3、自编程序并完成上机编辑,调试,运行,存盘:
(1)用 MATLAB 命令完成矩阵的各种运算,例如:
5、利用 ode23 或 ode45 求解线性时不变系统微分方程 y(t) Ay(t) ,并绘制出 y(t)
曲线,式中
A
0.5
1
1 0.5
t t0 t 如下: function xdot=fun21(t,x) A=[-0.5 1;-1 -0.5]; xdot=A*x; function fzsy22 t0=0;tf=4;tol=1e-6; x0=[0;1];trace=1; [t,x]=ode23('fun21',t0,tf,x0,tol,trace); plot(t,x) 得到的实验结果如下图所示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)根據數學模型建立計算機仿真模型(編程) 計算機仿真就是對數學模型的數值求解。我們將微分方程進行形式上的 變換以便於數值 求解。由(1.2)和(1.3)式得 v(t+ dt) =v(t) + dv=v(t) +adt (1.9) 和 s(t+ dt) =s(t) + ds=s(t) +v(t)dt (1.10) 注意,這種變形僅僅是將方程轉換為一種在自變量(時間)上的「遞 推」表達式,並沒有進行 解析求解。利用(1.9)和(1.10),在已知當前時刻t 的瞬時位移,瞬 時速度和加速度的情況下,我們就可以推知下一個無限鄰近的時刻t+ dt 上物體新的瞬時位移,瞬時速度和加速度,這也就是微分方程數值求解 的基本思想。在數值求解中,無窮小量dt 需要用一個很小的數量¢t來近 似,¢t 稱為微分方程的數值求解步長,通常也稱為仿真步進。顯然,這 種微分方程的遞推求解總是近似的,求解精度與步長有關。下面我們就 用程序來實現這個求解過程。仿真時間範圍設置為0到2秒,為了使得仿 真計算的誤差明顯一些,我們故意採用了較大的仿真步長¢t = 0:1。讀者 可以自己修改仿真步長來觀察計算精度的變化情況。我們將瞬時位移作 為仿真輸出變量,並同時通過(1.8)式計算出解析結果以相互對照。 (4)執行仿真和結果分析 g=9.8; % 重力加速度 v=0; % 設定初始速度條件 s=0; % 設定初始位移條件 t=0; % 設定起始時間 dt=0.1; % 設置計算步長 N=20; % 設置仿真遞推次數. 仿真時間等於N與dt的乘積 for k=1:N v=v+g*dt; % 計算新時刻的速度 s(k+1)=s(k)+v*dt; % 新位移 t(k+1)=t(k)+dt; % 時間更新
畫」仿真的效果。當然,這樣是以犧牲計算速度為代價的。修改後的程 序文件代碼如下。 〔程序代碼〕ch1example1prg2.m % ch1example1prg2.m g=9.8; % 重力加速度 for L=1:5 % 仿真重複5次以便於觀察 v=0; % 初始速度 s=0; % 初始位置 t=0; dt=0.01;% 計算步長 for k=1:200 v=v+g*dt; % 速度 s=s+v*dt; % 位移 t=t+dt; % 時間 plot(0,-s,'o'); axis([-2 2 -20 0]); % 坐標範圍固定 text(0.5,-1,['当前时间:t=',num2str(t)]); text(0.5,-2,['当前速度:v=',num2str(v)]); text(0.5,-3,['当前位置:s=',num2str(s)]); set(gcf,'DoubleBuffer','on');% 雙緩衝避免作圖閃爍 drawnow; % 立即作圖 end end 在程序中,計算步進重新設置為0:01,並且重複仿真多次以便於演示。 在作圖語句之後設 置了固定的顯示坐標範圍,並通過text語句在圖上動態顯示當前計算時 刻的結果值。語句 set(gcf,'DoubleBuffer','on'); 將顯示設備雙緩衝開啟,以避免屏幕刷新引起的閃爍。而 drawnow 是立即執行繪圖指令。在仿真中途可按鍵Ctrl+C來終止程序執行。程序 執行過程中將顯示出物體墜落的動畫效果,其中的一個幀如圖1.2所 示。
பைடு நூலகம்
用Matlab常微分方程求解器重新仿真實例1.2的乒乓球彈跳模型,要求也 能 夠在仿真過程中動態顯示球的墜落和反彈過程,在仿真結束後輸出小球 位移和速度的變化曲 線。設小球的初始位置距離水平面1米,由靜止狀態開始自由墜落,並 設反彈瞬間的速度衰減 係數為K= 0:85。 數學模型與實例1.2完全相同,為了利用標準求解器進行求解,首先將 模型中的方程改寫 為標準的狀態方程形式,小球在空中時,有運動方程
並注意小球碰撞水平面瞬間(在反彈之前)的條件是y60且v60。碰撞瞬 間速度發生反向 並以係數K衰減。據此編寫程序,程序中以x1(t)表示速度狀態變量v(t), 以x2(t)表示位移 狀態變量y(t),並以矩陣形式描述,代碼如下。 v0=0; y0=1; %球的初始狀態 x_state=[v0,y0];%將初始狀態賦值到狀態變量中
下面我們通過對自由落體的仿真試驗來說明計算機仿真的過程。 〔實例1.1〕試對空氣中在重力作用下不同質量物體的下落過程進行建 模和仿真。已知重 力加速度g= 9:8m/s^2,在初始時刻t0= 0s時物體由靜止開始墜落。空氣 對落體的影響可以 忽略不計。 (1)建立數學模型 首先,我們根據物理原理建立自由落體的數學模型。在空氣阻力可忽略 不計時,質量為m 的物體在自由墜落過程中受到豎直向下的恆定重力的作用,由牛頓第二 定律,我們知道,重 力F,加速度a以及物體質量m之間的關係是: F=ma (1.1) 其中加速度就是重力加速度,即a=g。根據題設,初始時刻為t0= 0,物 體的初始速度 為v(t0) = 0,並設物體下落的瞬時速度為v(t)。設物體在t 時刻的位移為 s(t),並設初始位移為零,即s(t0) = 0。根據加速度、速度、位移三者之 間的微積分關係,我們得到一組數學方程 a =dv/dt v =ds/dt F = ma 以及初始條件(也稱為方程的邊界條件) v(t0) = 0 (1.5) s(t0) = 0 m (1.6 我們需要得出不同時刻物體的運動狀態,即物體的瞬時速度和瞬時位 移。至此,我們得到 了自由落體的數學描述。 (2)數學模型的解析分析 數學模型建立之後,可以嘗試對其進行解析求解。解析結果可以幫助我 們驗證仿真數值 結果。對於這個數學模型,其求解十分簡單。只要對加速度方程、速度 方程進行積分並代入初始條件,就能得到我們熟知的結果:
實例1.2〕對乒乓球的彈跳過程進行仿真。忽略空氣對球的影響,乒乓 球垂直下落,落點 為光滑的水平面,乒乓球接觸落點立即反彈。如果不考慮彈跳中的能量 損耗,則反彈前後的瞬時速率不變,但方向相反。如果考慮撞擊損耗, 則反彈速率有所降低。我們希望通過仿真得出乒乓球位移隨時間變化的 關係曲線,並進行彈跳過程的「實時」動畫顯示。 (1)數學模型 首先對乒乓球彈跳過程進行一些理想化假設。設球是剛性的,質量為 m,垂直下落。碰 擊面為水平光滑平面。在理想情況下碰擊無能量損耗。如果考慮碰擊面 損耗,則碰擊前後速 度方向相反,大小按比例係數K;0< K<1下降。在t 時刻的速度設為 v=v(t),位移設 為y=y(t),並以碰擊點為坐標原點,水平方向為坐標橫軸建立直角坐標 系。球體的速度以豎 直向上方向為正方向。重力加速度為g= 9:8m=s2。初始條件假設:設初 始時刻t0= 0球體的初始速度為v0=v(t0),初始位移為y0=y(t0)。受力分 析:在空中時小球受重力F=mg作用,其中,g=-dv/dt。則在t+ dt 時刻小 球的速度為(注意其中負號是考慮了速度的方向) v(t+ dt) =v(t)¡gdt (1.11) 在t+ dt 時刻小球的位移為 y(t+ dt) =y(t) +v(t)dt (1.12) 在小球撞擊水平面的瞬間,即y(t) = 0的時刻,它的速度方向改變,大小 按比例K衰減。 當K= 1時,就是無損耗彈跳情況。因此,小球反彈瞬間(t+ dt 時刻)的
function xdot=ch2example6statefun(t, x, flag) % 乒乓球彈跳模型的標準狀態方程 % x(1)為小球速度,x(2)為小球位移 xdot=zeros(2,1); % 狀態變量矩陣初始化 xdot(1)=-9.8; % 速度加速度方程 xdot(2)=x(1); % 位移速度方程
end % 理論計算, 以便與仿真結果對照 t_theory=0:0.01:N*dt; % 設置解析計算的時間點 v_theory=g*t_theory; % 解析計算的瞬時速度 s_theory=1/2*g*t_theory.^2; % 解析計算的瞬時位移 % 作圖: 仿真結果與解析結果對比 t=0:dt:N*dt; plot(t,s,'o', t_theory,s_theory, '-'); xlabel('時間t'); ylabel('位移s'); legend('仿真結果','理論結果'); 仿真程序編寫完成並調試正確之後,運行得到的結果如圖1.1所示。從 圖中可見,仿真得 出的位移與理論結果之間存在差別,這種差別是由於微分方程數值求解 的算法和採用步長較 大而引起的。事實上,我們這裡採用的數值求解算法是最簡單的矩形積 分的方法,精度不高, 僅僅是為了說明仿真過程而已。現代仿真技術和數值計算方法中已經開 發出許多更好的微分 方程求解算法,可供直接利用。 (5)仿真程序的功能擴展 從ch1example1prg1.m的程序代碼中可見,我們採用了循環語句來實現對 微分方程的遞 推求解,每次循環就將計算時刻向前推進一個步長。全部循環執行完畢 後,就得到了一系列時刻上物體的瞬時速度和瞬時位移值,最後通過繪 圖語句將結果數據用曲線表達出來。 如果我們希望以動態方式來觀察物體墜落的過程,可以這樣設計仿真程 序:使得在數值求 解的過程中能將求解結果以圖形方式輸出出來。這樣,在數值求解不斷 更新的過程中輸出圖 形也隨之同步更新,形成一種「動畫」的效果。這種一邊計算一邊輸出 可視化結果的方式更 加形象直觀,更便於理解物理系統的工作過程,同時也方便演示,教學 講解和學術交流。 我們可以將作圖語句放在遞推計算循環內,並設置即時作圖刷新方式, 從而得到這種「動
...... legend('K=0.85','K=1'); 圖1.3中分別作出了是碰擊衰減係數K= 1和K= 0:85兩種情況下的小球彈 跳位移曲 線。對程序稍加修改就可以得到顯示小球彈跳過程的動畫。修改後的程 序文件代碼如下,讀者可運行該程序觀察不同的碰擊衰減係數下的小球 彈跳過程。 〔程序代碼〕ch1example2prg2.m % ch1example2prg2.m g=9.8; % 重力加速度 v0=0; % 初始速度 y0=1; % 初始位置 m=1; % 小球質量 t0=0; % 起始時間 K=0.85; % 彈跳的損耗係數 N=5000; % 仿真的總步進數 dt=0.005; % 仿真步長 v=v0; % 初狀態 y=y0; for k=1:N if y >0 % 小球在空中的動力方程計算 v =v -g*dt; y =y +v*dt; else % 碰擊瞬間的計算 y =-K.*v*dt; v =-K.*v-g*dt; end plot(0,y,'o'); axis([-2 2 0 1]); % 坐標範圍固定 set(gcf,'DoubleBuffer','on'); % 雙緩衝避免作圖閃爍 drawnow; end
