高考复习专题---立体几何平行关系证明
立体几何(平行线的证明)

立体几何(平行线的证明)在立体几何中,平行线是一种非常重要的概念。
平行线可以定义为在同一个平面内没有交点的两条直线。
证明两条直线平行的方法有很多种,下面将介绍一种简单而常用的方法。
方法一:使用平行线的性质平行线有很多性质,其中一个性质是平行线与横截线之间的夹角相等。
根据这个性质,我们可以通过检查两条线的夹角来证明它们是否平行。
具体步骤如下:1. 给定两条直线AB和CD,我们要证明这两条直线平行。
2. 构建一条横截线EF,该直线与AB和CD相交于点E和F。
3. 使用量角器或直尺测量∠AED和∠CFD的夹角。
如果这两个夹角相等,即∠AED = ∠CFD,那么我们可以得出结论AB与CD平行。
这种方法的好处是简单直观,只需要测量夹角即可。
然而,这种方法并不适用于所有情况,因为有些情况下无法构建合适的横截线。
方法二:使用等边三角形的性质等边三角形是一个有趣的几何形状,所有边都相等。
在等边三角形中,对角线之间的直线也是平行线。
具体步骤如下:1. 给定两条直线AB和CD,我们要证明这两条直线平行。
2. 构建一个等边三角形BCD,在这个等边三角形中,BC = CD。
3. 连接线段AD,我们可以发现线段AD与线段BC平行。
这种方法的好处是不需要测量夹角,只需要利用等边三角形的性质即可。
然而,这种方法也有局限性,因为有些情况下无法构建等边三角形。
综上所述,证明平行线的方法有很多种,其中一些常用的方法是使用平行线的性质和使用等边三角形的性质。
选择合适的方法取决于具体的几何形状和问题要求。
高中数学专项提升——立体几何中平行与垂直证明
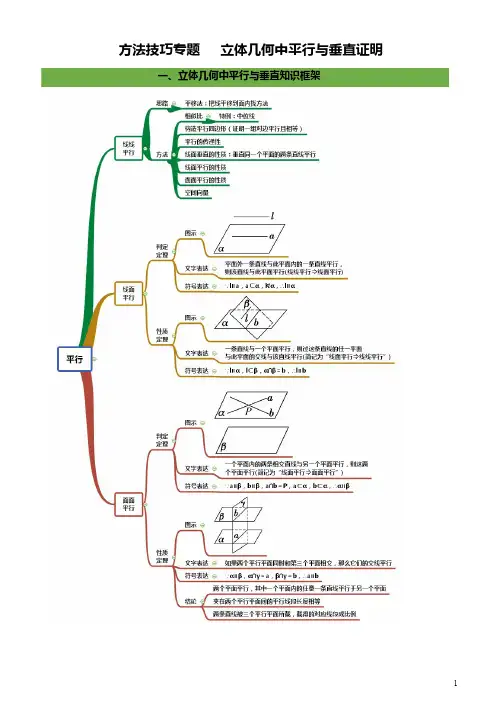
方法技巧专题立体几何中平行与垂直证明一、立体几何中平行与垂直知识框架cc∥∥b a ba ∥⇒二、立体几何中的向量方法【一】“平行关系”常见证明方法1.1直线与直线平行的证明1.1.1利用某些平面图形的特性:如平行四边形的对边互相平行等1.1.2利用三角形中位线性质1.1.3利用空间平行线的传递性(即公理4):平行于同一条直线的两条直线互相平行。
1.1.4利用直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
1.1.5利用平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.1.1.6利用直线与平面垂直的性质定理:垂直于同一个平面的两条直线互相平行。
1.1.7利用平面内直线与直线垂直的性质:在同一个平面内,垂直于同一条直线的两条直线互相平行。
1.1.8利用定义:在同一个平面内且两条直线没有公共点1.2直线与平面平行的证明1.2.1利用直线与平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
αbaabαβb a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒b∥a b a αα⊂⊄α∥a ⇒αab1.2.2利用平面与平面平行的性质推论:两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
βαaβαα∥⊂a β∥a ⇒1.2.3利用定义:直线在平面外,且直线与平面没有公共点1.3平面与平面平行的证明1.3.1利用平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
ααββ////∩⊂⊂ba Pb a b a =αβ//⇒αβbaP1.3.2利用某些空间几何体的特性:如正方体的上下底面互相平行等1.3.3利用定义:两个平面没有公共点1.例题【例1】如图,已知菱形ABCD ,其边长为2,60BAD ∠=,ABD ∆绕着BD 顺时针旋转120得到PBD∆,M 是PC 的中点.(1)求证://PA 平面MBD ;(2)求直线AD 与平面PBD 所成角的正弦值.证明(1)连结AC 交BD 于点O ,连结OM在菱形ABCD 中,O 为AC 中点, M 为PC 的中点∴OM 为∆APC 的中位线,∴OM ∥AP---------------(利用1.1.2中位线性质)又 OM ⊂面MBD ,且PA ⊄面MBD∴//PA 平面MBD----------------(利用1.2.1直线与平面平行的判定定理)【例2】已知四棱锥P-ABCD ,底面ABCD 是60=∠A 、边长为a 的菱形,又ABCD PD 底⊥,且PD=CD ,点M 、N 分别是棱AD 、PC 的中点.证明:DN//平面PMB 。
专题4:立体几何中平行关系的证明(解析版)

专题4:立体几何中平行关系的证明(解析版)1.直线和平面平行的判定(1)定义:直线和平面没有公共点,则称直线平行于平面;(2)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号: ////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭例1.如图所示,在底面为平行四边形的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点.求证://PB 平面AEC .【答案】证明见解析 【分析】根据图像,连接BD ,与AC 相交与O ,连接EO ,ABCD 是平行四边形,O 是BD 的中点,根据中位线的性质即可得证. 【详解】如图,连接BD ,与AC 相交与O ,连接EO , ∵ABCD 是平行四边形, ∴O 是BD 的中点, 又E 是PD 的中点, ∴//EO PB ,又PB ⊄平面AEC ,EO ⊂平面AEC , ∴//PB 平面AEC .例2.如图所示,在四棱锥P ABCD -中,22PA AD CD AB ====,AB AD ⊥,CD AD ⊥,PA ⊥底面ABCD , M 为PC 的中点。
求证://BM 平面PAD【答案】证明见解析. 【分析】取PD 的中点E ,连接,AE ME ,由三角形的中位线定理可得ME ∥CD ,12ME CD =,而已知AB ∥CD ,12AB CD =,从而得AB ∥ME ,AB ME =,所以四边形ABME 为平行四边形,从而得//BM EA ,再利用线面平行的判定定理可证明 【详解】证明:取PD 的中点E ,连接,AE ME 因为M 为PC 的中点,所以ME ∥CD ,12ME CD =, 因为AB ∥CD ,12AB CD =,所以AB ∥ME ,AB ME =,所以四边形ABME 为平行四边形,所以//BM EA , 又因为BM ⊄平面PAD ,EA ⊂平面PAD ,所以//BM平面PAD.注:证明线面垂直1,找中位线 2,找平行四边形 3,正两个面平行2.直线和平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
高考立体几何证明知识点

高考立体几何证明知识点立体几何是数学中的一个重要分支,旨在研究空间中的图形和物体的性质及其相互关系。
在高考中,立体几何是一个重要的考点,其中涉及到很多证明题。
本文将介绍几个高考常见的立体几何证明知识点,帮助考生更好地理解和掌握这些内容。
一、平行关系证明在立体几何中,平行关系是经常需要证明的一个知识点。
首先,我们需要了解平行的定义:若两条直线在同一个平面内,且不相交,则称这两条直线平行。
为了证明两条直线平行,我们可以利用以下几个常见的方法:1.同位角相等法:如果两条直线被平行线所截,那么可以利用同位角的性质来确定这两条直线平行。
同位角是指两条直线被平行线所截时,对应角或内错角两对角,它们的度数相等。
在证明过程中,我们需要找到直线间的对应角或内错角,将它们的度数相等证明出来,从而得出两条直线平行的结论。
2.共线错角相等法:如果两条直线被平行线所截,可以利用共线错角相等的性质来确定这两条直线平行。
共线错角是指两条直线被平行线所截时,同侧的内错角,它们的度数相等。
在证明过程中,我们需要找到两条直线间的共线错角,将它们的度数相等证明出来,从而得出两条直线平行的结论。
二、相似三角形证明相似三角形是立体几何中另一个重要的证明知识点。
首先,我们需要了解相似三角形的定义:若两个三角形的对应角相等,那么这两个三角形是相似的。
证明相似三角形的方法主要有以下几个:1.对应边成比例法:若两个三角形的两对对应边成比例,那么可以证明这两个三角形相似。
在证明过程中,我们需要找到两个三角形中对应的边,并运用对应边成比例的性质来证明它们相似。
2.三角形内相等角法:若两个三角形中,其中一个三角形的两个角与另一个三角形的两个角相等,那么可以证明这两个三角形相似。
在证明过程中,我们需要找到这两个相等的角,并证明它们与其他角的关系,从而得出两个三角形相似的结论。
三、垂直关系证明垂直关系也是立体几何中常见的一个证明知识点。
首先,我们需要了解垂直的定义:两条直线或线段在平面或空间中互相垂直,即两条直线或线段相交且相交的角度为90度。
立体几何平行证明题常见模型及方法

立体几何平行证明题常见模型及方法立体几何中的平行证明题常见的模型和方法有很多。
下面我将介绍一些常见的模型和方法,以帮助你更好地理解和应用立体几何的平行证明。
一、常见模型1.平面与平面的平行证明:常见的模型有两条平行线或两个平行四边形,通过证明平面与平面内对应的直线或四边形是平行的,即可得证。
2.直线与直线的平行证明:常见的模型有平行四边形和交叉角等,通过证明两直线间的对应角相等或同位角互补,即可得证。
3.平面与直线的平行证明:常见的模型有平行四边形的一对对角线、三角形的高、垂足、垂线等,通过证明直线与平面内的直线或线段互相垂直,即可得证。
4.空间中的平面与平面的平行证明:常见的模型有两个平行四边形的高度等、点到平面的垂直距离等,通过证明两个平面内的垂直线的相互平行性,即可得证。
二、常见方法1.剪影法:利用平行关系特殊的剪影形状进行证明。
例如,通过剪影的形状可以直观地判断两根线段平行。
2.联立法:通过建立适当的方程组,将待证的平行条件与已知条件进行联立,最终得到结论。
常见的方法有正投影、平行投影等。
3.直角法:利用直角关系进行证明。
通过找到合适的垂线、垂足等直角线段,可以推导出平行关系。
4.反证法:假设不平行,然后找到与之矛盾的证据,从而推出平行的结论。
5.三角形法:构造适当的三角形,通过三角形的性质和形状关系进行证明。
6.同增减法:通过分析多个角度相应的同增减性质,推导出平行的结论。
7.通道法:利用另一个已经知道的已知命题,构造合适的通道来推导出平行的结论。
以上仅是常见的模型和方法,实际的平行证明题在解题过程中可能会遇到各种不同的情况和策略。
解决此类问题的关键是要有良好的几何直观和分析能力,熟练掌握几何定理和性质,并能够合理运用不同的方法解决问题。
专题01 平行问题的证明(原卷版)
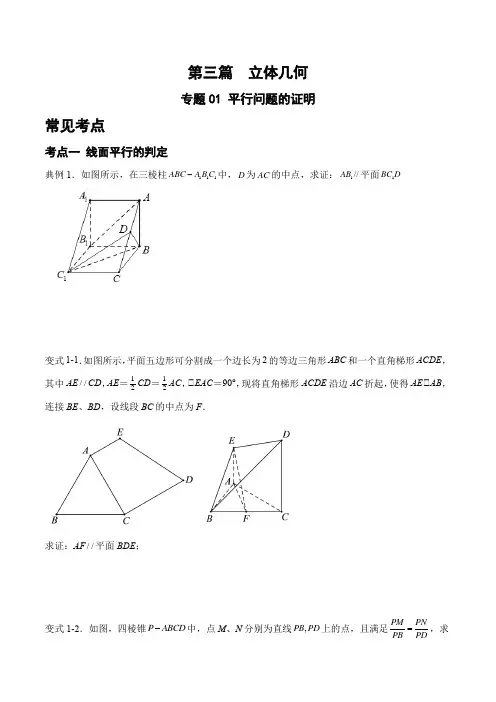
第三篇 立体几何专题01 平行问题的证明常见考点考点一 线面平行的判定典例1.如图所示,在三棱柱111ABC A B C -中,D 为AC 的中点,求证:1//AB 平面1BC D变式1-1.如图所示,平面五边形可分割成一个边长为2的等边三角形ABC 和一个直角梯形ACDE ,其中AE //CD ,AE =12CD =12AC ,∠EAC =90°,现将直角梯形ACDE 沿边AC 折起,使得AE ∠AB ,连接BE 、BD ,设线段BC 的中点为F .求证:AF //平面BDE ;变式1-2.如图,四棱锥P ABCD -中,点M 、N 分别为直线,PB PD 上的点,且满足PM PN PB PD=,求证://MN 平面ABCD .变式1-3.如图所示,已知正方形ABCD .E 、F 分别是AB 、CD 的中点,将ADE 沿DE 折起.证明//BF 平面ADE .考点二 面面平行的判定典例2.如图,在四棱锥P -ABCD 中,E ,F ,G 分别是PC ,PD ,BC 的中点,DC //AB ,求证:平面P AB //平面EFG .变式2-1.已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M 分别是A 1C 1,A 1D 和B 1A 上任意一点.求证:平面1//A EF 平面1B MC .变式2-2.如图,在斜三棱柱ABC A 1B 1C 1中,点D , D 1分别在AC , A 1C 1上,那么当点D 在什么位置时,平面BC 1D ∠平面AB 1D 1变式2-3.如图为一简单组合体,其底面ABCD 为正方形,棱PD 与EC 均垂直于底面ABCD ,2PD EC =,求证:平面//EBC 平面PDA .考点三 线面平行的性质典例3.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,四边形ABCD 是正方形,24AB PA ==,点E 在棱PA 上,//PC 平面BDE .求证:E为PA的中点;变式3-1.四面体ABCD如图所示,过棱AB的中点E作平行于AD,BC的平面,分别交四面体的棱,,于点F G H,,.证明:四边形EFGH是平行四边形.BD DC CA变式3-2.如图所示,已知三棱柱ABC-A'B'C'中,D是BC的中点,D'是B'C'的中点,设平面A'D'B∩平面ABC=a,平面ADC'∩平面A'B'C'=b,判断直线a,b的位置关系,并证明.被一平面所截,截面为平行四边形EFGH,求证:CD∥平面EFGH.变式3-3.如图,三棱锥A BCD考点四 面面平行的性质典例4.如图,在三棱锥P -ABC 中,D ,E ,F 分别是PA ,PB ,PC 的中点.M 是AB 上一点,连接MC ,N 是PM 与DE 的交点,连接FN ,求证:FN∠CM .变式4-1.如图,在棱锥中,:1:3AE AB =,截面EFG ∥底面BDC .已知BDC 的周长是18,求EFG的周长.变式4-2.如图,已知平面//α平面β,点P 是平面α,β外一点,且直线PB ,PD 分别与α,β相交于点A ,B 和点C ,D .如果4cm PA =,5cm AB =,3cm PC =,求PD 的长.变式4-3.如图所示,两条异面直线BA,DC与两平行平面α,β分别交于点B,A和D,C,点M,MN平面αN分别是AB,CD的中点,求证://巩固练习练习一线面平行的判定1.如图,四棱锥A DBCE-中,O为底面平行四边形DBCE对角线的交点,F为AE的中点.求证:AB∥平面DCF.2.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点.求证:EF//平面ABC1D1.3.如图所示,在四棱锥P ABCD -中,22PA AD CD AB ====,AB AD ⊥,CD AD ⊥,PA ⊥底面ABCD , M 为PC 的中点。
(完整版)立体几何中平行与垂直证明方法归纳
c c ∥∥b a ba ∥⇒本文档系统总结归纳了立体几何中平行与垂直证明方法,特别适合于高三总复习时对学生构建知识网络、探求解题思路、归纳梳理解题方法。
是一份不可多得的好资料。
一、“平行关系”常见证明方法(一)直线与直线平行的证明1) 利用某些平面图形的特性:如平行四边形的对边互相平行 2) 利用三角形中位线性质3) 利用空间平行线的传递性(即公理4):平行于同一条直线的两条直线互相平行。
4)利用直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
5) 利用平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.6) 利用直线与平面垂直的性质定理:垂直于同一个平面的两条直线互相平行。
abαβba a =⋂⊂βαβα∥ba ∥⇒b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒αab7) 利用平面内直线与直线垂直的性质:在同一个平面内,垂直于同一条直线的两条直线互相平行。
8) 利用定义:在同一个平面内且两条直线没有公共点(二)直线与平面平行的证明1) 利用直线与平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
2) 利用平面与平面平行的性质推论:两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
3) 利用定义:直线在平面外,且直线与平面没有公共点(三)平面与平面平行的证明常见证明方法:1) 利用平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
αbaβαaβαα∥⊂a β∥a ⇒ααββ////∩⊂⊂b a P b a b a =αβ//⇒αβbaPb∥a b a αα⊂⊄α∥a ⇒2)利用某些空间几何体的特性:如正方体的上下底面互相平行等3)利用定义:两个平面没有公共点二、“垂直关系”常见证明方法(一)直线与直线垂直的证明1)利用某些平面图形的特性:如直角三角形的两条直角边互相垂直等。
高中数学-立体几何位置关系-平行与垂直证明方法汇总
高中数学-立体几何位置关系-平行与垂直证明方法汇总(一)立体几何中平行问题证明直线和平面平行的方法有:①利用定义采用反证法;②平行判定定理;③利用面面平行,证线面平行。
主要方法是②、③两法在使用判定定理时关键是确定出面内的与面外直线平行的直线.常用具体方法:中位线和相似例1、P是平行四边形ABCD所在平面外一点,Q是PA的中点.求证:PC∥面BDQ.证明:如图,连结AC交BD于点O.∵ABCD是平行四边形,∴A O=O C.连结O Q,则O Q在平面BDQ内,且O Q是△APC的中位线,∴PC∥O Q.∵PC在平面BDQ外,∴PC∥平面BDQ.例2、在棱长为a的正方体ABCD-A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.求证:(1)E、F、B、D四点共面;(2)面AMN∥面EFBD.证明:(1)分别连结B 1D 1、ED 、FB ,如图, 则由正方体性质得 B 1D 1∥BD. ∵E 、F 分别是D 1C 1和B 1C 1的中点, ∴EF ∥21B 1D 1.∴EF ∥21BD. ∴E 、F 、B 、D 对共面.(2)连结A 1C 1交MN 于P 点,交EF 于点Q ,连结AC 交BD 于点O ,分别连结PA 、Q O . ∵M 、N 为A 1B 1、A 1D 1的中点, ∴MN ∥EF ,EF ⊂面EFBD. ∴MN ∥面EFBD. ∵PQ ∥A O ,∴四边形PA O Q 为平行四边形. ∴PA ∥O Q.而O Q ⊂平面EFBD ,∴PA ∥面EFBD.且PA ∩MN=P ,PA 、MN ⊂面AMN , ∴平面AMN ∥平面EFBD.例3如图(1),在直角梯形P 1DCB 中,P 1D//BC ,CD ⊥P 1D ,且P 1D=8,BC=4,DC=46,A 是P 1D 的中点,沿AB 把平面P 1AB 折起到平面PAB 的位置(如图(2)),使二面角P —CD —B 成45°,设E 、F 分别是线段AB 、PD 的中点. 求证:AF//平面PEC ;证明:如图,设PC 中点为G ,连结FG ,则FG//CD//AE ,且FG=21CD=AE , ∴四边形AEGF 是平行四边形 ∴AF//EG ,又∵AF ⊄平面PEC ,EG ⊂平面PEC , ∴AF//平面PEC例4、 正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP=DQ.求证:PQ ∥面BCE.证法一:如图(1),作PM ∥AB 交BE 于M ,作QN ∥AB 交BC 于N,连接MN, 因为面ABCD ∩面ABEF=AB,则AE=DB. 又∵AP=DQ, ∴PE=QB.又∵PM ∥AB ∥QN, ∴AE PE AB PM =,BD BQDC QN =. ∴DCQNAB PM =. ∴PM ∥QN.四边形PMNQ 为平行四边形. ∴PQ ∥MN.又∵MN ⊂面BCE ,PQ ⊄面BCE , ∴PQ ∥面BCE.证法二:如图(2),连结AQ 并延长交BC 或BC 的延长线于点K ,连结EK. ∵AD ∥BC, ∴QKAQQB DQ =. 又∵正方形ABCD 与正方形ABEF 有公共边AB ,且AP=DQ ,∴PEAPQK AQ =.则PQ ∥EK. ∴EK ⊂面BCE ,PQ ⊄面BCE. ∴PQ ∥面BCE.例5、正方形ABCD 交正方形ABEF 于AB (如图所示)M 、N 在对角线AC 、FB 上且AM= FN 。
完整)高中立体几何证明平行的专题
完整)高中立体几何证明平行的专题在此文章中,存在一些格式错误和明显有问题的段落,需要进行修改和删除。
修改后的文章如下:立体几何——平行的证明例1】如图,四棱锥P-ABCD的底面是平行四边形,点E、F分别为棱AB、PD的中点。
求证:AF∥平面PCE。
分析:取PC的中点G,连EG,FG,则易证AEGF是平行四边形。
例2】如图,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+3,过A作AE⊥CD,垂足为E,G、F分别为AD、CE的中点,现将△ADE沿AE折叠,使得DE⊥EC。
Ⅰ)求证:BC⊥面CDE;(Ⅱ)求证:FG∥面BCD。
分析:取DB的中点H,连GH、HC,则易证FGHC是平行四边形。
例3】已知直三棱柱ABC-A1B1C1中,D、E、F分别为A1A、C1C、AB的中点,M为BE的中点,AC⊥BE。
求证:(Ⅰ)C1D⊥BC;(Ⅱ)C1D∥平面B1FM。
分析:连EA,易证C1EAD是平行四边形,于是MF//EA。
例4】如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,E为PC的中点。
证明:EB//平面PAD。
分析:取PD的中点F,连EF、AF,则易证ABEF是平行四边形。
例5】如图,已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点,求证:AM∥平面EFG。
分析:连MD交GF于H,易证EH是△AMD的中位线。
例6】如图,ABCD是正方形,O是正方形的中心,E是PC的中点。
求证:PA∥平面BDE。
AEBGMFCD例7】如图,三棱柱ABC-A1B1C1中,D为AC的中点。
求证:AB1//面BDC1.分析:连B1C交BC1于点E,易证ED是△B1AC的中位线。
例8】如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90,BC//AD,BE//AF,G、H分别为FA、FD的中点。
Ⅰ)证明:四边形BCHG是平行四边形;Ⅱ)C、D、F、E四点是否共面?为什么?例9】正方体ABCD-A1B1C1D1.例10:在四棱锥P-ABCD中,AB∥CD,AB=DC,E为PD中点。
高考大题专项(四) 立体几何
| || |
所以异面直线 PC 与 BQ
=
2
,
3
2
所成角的余弦值为 3 .
解题心得用向量法求异面直线所成角的一般步骤
(1)选择三条两两垂直的直线建立空间直角坐标系.
(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量.
(3)利用向量的夹角公式求出向量夹角的余弦值.
(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.
高考大题专项(四) 立体几何
【考情分析】
从近五年的高考试题来看,立体几何是历年高考的重点,约占整个试卷的
15%,通常以一大两小的模式命题,以中、低档难度为主.简单几何体的表面
积与体积、点、线、面位置关系的判定与证明以及空间角的计算是考查
的重点内容,前者多以客观题的形式命题,后者主要以解答题的形式命题考
【例题】 (2020安徽高三三模)如图,边长为2的等边三角形ABC所在平面与
菱形A1ACC1所在平面互相垂直,且BC∥B1C1,BC=2B1C1,A1C=
(1)求证:A1B1∥平面ABC;
(2)求多面体ABC-A1B1C1的体积.
3 1.
AC
(1)证明∵四边形A1ACC1是菱形,
∴AC∥A1C1.
对点训练2(2020辽宁高三三模)如图,在直棱柱ABCDA1B1C1D1中,底面ABCD为菱形,AB=BD=2,BB1=2,BD
与AC相交于点E,A1D与AD1相交于点O.
(1)求证:AC⊥平面BB1D1D;
(2)求直线OB与平面OB1D1所成的角的正弦值.
(1)证明∵底面ABCD为菱形,∴AC⊥BD.
查.着重考查推理论证能力和空间想象能力,而且对数学运算的要求有加强
