浙江大学城市学院线性代数11
线性代数及应用PPT课件

上列各式出现的运算皆可行的前提是:矩阵的维数满 足运算要求。
证明矩阵乘法结合律:(AB)C=A(BC)=ABC 证:设
记
证明DC=AG。 因为 元为:
A的 i 行乘以B的 l 列
,
, 则DC的第i,j
得到DC的第i,j元等于AG的第i,j元。
证明 (AB)T =BTAT
证:
即
。
剩下的要证明它们的第i, j元都对应相等。设
通大学出版社
第一章 矩阵
§1.1 矩阵概念 1.1.1 矩阵概念 定义1 m × n元,排成m行n列的矩形阵列:
称作为:维是m × n的矩阵。 一般用黑体大写字母 A,B,C等表示。
简记为:
确定一个矩阵的两要素:
1.元:a ij 的值; 2.维:m,n的值。
矩阵的例: 问题:A的元和维是什么?
广矩阵进行一系列行初等变换,使得
R1R2 ••• R s [A |b]= [R1R2 ••• R s A | R1R2 ••• R s b ]=[ I n | Rb ]
(R= R1R2 ••• R s)。事实上R=A-1
可见只要将增广矩阵中A对应的那一块通过行初等变换化成 单位阵,对应b的那一块变成Rb= A-1 b,即
1.1.2 一些特殊矩阵 对于矩阵
本课程仅限于实矩阵。
n阶方阵:m=n时的矩阵,
a11 a12 a1n
A
a21 a22 a2n
或 An n
an1 an2 ann
列矩阵(列向量):n=1,
行矩阵(行向量):m=1,
数或标量:m=n=1。 向量的元称为分量,分量的个数称为向量的维。
例:
分别是3维列向量和4维行向量。
学习参考书目
城院 ZUCC 浙江大学城市学院线性代数2010—2011学年第一学期期末试卷及答案详解

浙江大学城市学院线性代数 2010—2011学年第一学期期末试卷一,填空题(每空2分,共20分)1.已知3阶行列式111532101||=ij a ,则12a 的代数余子式_______|| _______,==A2.设3阶方阵A 的行列式2||-=A ,则________|| _______,|2|2==A A 3.已知向量()()()TTT432,301,021321=-==ααα,则___________32321=-+ααα4.设非齐次线性方程组2)( ,34==⨯A R b X A ,且()()T T 231,01221-=-=ξξ是该方程组的解,则此非齐次线性方程组的通解为______________________5.已知3阶方阵A 与B 相似,且A 的秩2)(=A R ,则____|| ____,)(==B B R 6.矩阵⎪⎪⎪⎭⎫⎝⎛-=152543231A 所对应的二次型为____________________________,且此二次型的秩为_______ 二,问答题(每题5分,共20分)1.5阶行列式的项5344312512a a a a a 的符号为_________,请说明理由。
2.⎪⎪⎪⎭⎫ ⎝⎛=100210001F 是初等矩阵吗?(正确说明理由,错误请举反例)3.n 阶实对称矩阵A 一定有n 个不同的特征值吗?(正确说明理由,错误请举反例)4.向量组()()()TTT323,202,121321===ααα是不是3维向量空间3R 的一组基?请说明理由。
三,简单计算题(每题5分,共30分,只写答案无过程不得分)1.已知⎪⎪⎭⎫ ⎝⎛=4221A ,求92 ,A A 。
2.用初等行变换法求方程组⎪⎩⎪⎨⎧=-+=+-=-+0403202321321321x x x x x x x x x 的通解,并将通解用基础解系表示。
3.已知向量组()()()TTTt 12,113,202321===ααα,则t 取何值时该向量组线性相关,并在线性相关时求此向量组的一个极大线性无关组。
浙江大学城市学院创新实验班实施方案(初稿)

附件2浙江大学城市学院创新实验班(微电子)实施方案为推进浙江大学城市学院应用型专业建设,有效对接浙江大学工程师学院、浙江大学微电子学院的专业学位研究生培养,打造专业学位研究生优质生源基地,提升学生的工程应用能力,构建高素质、适合社会需求的工程应用型人才及本科-硕士应用型人才培养通道,创办创新实验班(微电子),并制订实施方案如下。
一、实施目标创新实验班主要招收对电子、信息与自动化技术有浓厚兴趣的学生,强化其专业基础课程学习,扎实其理论基础;提供良好的创新实践技能训练条件,通过系统的、有针对性的实践活动增强学生的动手实践能力,培养学生在集成电路与集成系统设计、智能系统的开发与应用等领域的应用能力和创新精神;有效对接研究生阶段学习,为浙江大学工程师学院提供优质生源,同时提升学生继续深造的能力和就业竞争力。
二、教学模式2016级、2015级和2014级创新实验班采用特色课程模块的教学形式,创新实验班的学生需修读该模块的必选课程,其中部分课程可免修所在专业相关的专业必修课程,其它课程可作为学生所在专业的专业选修课程。
2017级创新实验班的组建及培养模式另行制订。
创新实验班的课程特点:基础课程:强化与考研相关的公共基础课程学习,如数学、英语等,夯实基础,提升教学质量。
特色课程模块:强调学生工程实践能力培养,加强专业深造能力训练,可共享工程师学院的教学资源及实践平台。
三、管理模式参照浙江大学城市学院博学班管理模式。
2014级、2015级、2016级主要面向信息与电气工程学院的学生进行选拔。
1.选拔由浙江大学城市学院、浙江大学工程师学院、浙江大学微电子学院共同组织选拔,并在第一学期第13周末之前完成最终选拔工作。
对于2016级学生,采用高考成绩(20%),线性代数、微积分(I)与大学英语期中成绩(40%),以及面试成绩(40%)核计总成绩,择优录取不超过30人;对于2015级学生,采用已修课程平均分(60%)、面试(40%)核计总成绩,择优录取不超过20人;对于2014级学生,采用已修课程平均分(60%)、面试(40%)核计总成绩,择优录取不超过20人。
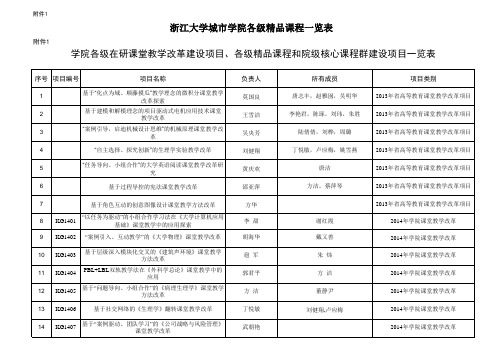
学院各级在研课堂教学改革建设项目、各级精品课程和院级核心课程群建设项目一览表.
负责人
刘加海 黄敏 李向荣 潘建平 王皓白 韩振华 李亚雄 傅乐群 赛来西· 阿不都拉 阮可 董曾珊
所有成员
徐洁,杨锆,方志刚,陈忠宝, 沈剑峰,戴又善,张锐波,曹小华,周艳 微,胡海华,凌俐,杜金潮, 曾玲晖,李杰,赵岚,孙晓译,吕燕萍,张 翀,卢应梅,杜阳龙,楼雪芳, 张立煌,刘健翔,张薇,丁悦敏,陈伟平, 王慧煜,李纪明,胡卫中,吴迪,叶正虹, 肖庆国,陈业玮,徐林强,陈勇, 蒋文杰,潘天芹,周蔚,赖勤,程宏, 杨晓云,徐娴,苏歆海,邵杨,韩燕 , 张健康,梁赫,卫军英, 孙福轩,唐濛,戴红红,张梦新, 李小兰,程菱,李珏,朱琳,
附件1
浙江大学城市学院各级精品课程一览表
附件1
学院各级在研课堂教学改革建设项目、各级精品课程和院级核心课程群建设项目一览表
序号 项目编号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 KG1401 KG1402 KG1403 KG1404 KG1405 KG1406 KG1407
项目名称
项目类别
2012年学院课堂教学改革 2012年学院课堂教学改革 2012年学院课堂教学改革 2012年学院课堂教学改革 院级七期精品课程(2013) 院级七期精品课程(2013) 院级七期精品课程(2013) 院级七期精品课程(2013) 院级七期精品课程(2013) 院级七期精品课程(2013) 院级四期核心课程群(2014) 院级四期核心课程群(2014) 院级四期核心课程群(2014) 院级三期核心课程群(2013) 院级三期核心课程群(2013) 院级三期核心课程群(2013)
负责人
莫国良 王雪洁 吴央芳 刘健翔 黄庆欢 邵亚萍 方华 李 甜 胡海华 扈 军 郭君平 方 洁 丁悦敏 武朝艳
11浙大高等代数

浙江大学
攻读硕士学位研究生入学考试试题
考试科目高等代数(A卷)编号 601 注意:答案必须写在答题纸上,写在试卷或者草稿纸上均无效。
本试卷共计十道试题,每题满分15分;用E表示单位矩阵,矩
阵A的转置矩阵表示为.
1.如果),且n阶方阵A有一个
特征值等于1,证明都不是可逆矩阵。
2.解下列方程组:
3.设n阶方阵A的伴随矩阵为,当时,证明
.
4.设n阶方阵A满足证明是不可逆矩
阵。
5.设是欧式空间的常用基,
一个矩阵P被称为置换矩阵假如存在一个全排列阶
使得矩阵,例如
就是一个四阶置换矩阵,假如n方阵A的秩等于r,证明存在置换矩阵使得,其中的秩等于r。
6.设是实数域上三维线性空间,定
义,证明T是V上的线性变换,并求其特征值和特征向量。
7.设B是实数域上矩阵,,对任意一个大于零的
常数a,证明定义了一个内积使得成为欧式空间,其中表示列向量的转置,E表示单位矩阵。
8.试证明满足的n阶方阵A都相似于一个对角矩阵。
9.假设是半正定矩阵,证明满足的所有
组成的维子空间。
10.已知矩阵,求矩阵,使为
若当()标准型。
线性代数 浙大版 第一章第二节

1 1 2 3 1
r3 r2
0 0
2 0
1 1
5 1
3 2
0 0 1 0 2
0 0 2 2 2
2
r4 r3 r5 2r3
4 1 1 2 3 1 3
0 0 1 0 2
r3 2r1 0 2 0 4 1
3 5 7 14 6 4 4 10 10 2
4 1 1 2 3 1 3
0 0 1 0 2
r3 2r1 0 2 0 4 1
an1 ani ann an1 an i ann
性质5 把行列式的某一列(行)的各元素乘以 同一数然后加到另一列(行)对应的元素上去, 行列式不变.
例如
a11 a1i a1 j a1n
a21 a2i k a2 j a2 j
an1 ani anj anj
0 ab
3111
例3
计算
1 D
3
1
1
1131
例4 计算
1113
=48
a a D a a
b ab 2a b 3a b
c abc 3a 2b c 6a 3b c
d abcd 4a 3b 2c d
10a 6b 3c d a4
注意:上述各例都用到把几个运算写在一起的省 略写法,要注意各个运算次序一般不能颠 倒,因为后一次运算是作用在前一次运算 结果上.
1 1 2 3 1
0 2 1 5 3
浙江大学线代解题指导

《线性代数》常见计算题型及常用思路一、 计算题题型1.解线性方程组(必须掌握)(1) 最常用方法:先用高斯消元法化为阶梯形,从而得出自由未知量(设为1,,t i i x x ),然后对自由未知量赋予任意值,即设11,,t i i t x k x k ==,这儿1,,t k k 为任意常数。
把赋予自由未知量的值带入方程组,解除方程组的解(是关于1,,t k k 的一些表达式)(2) 方法(1)的变形:先用高斯消元法化为阶梯形,从而得出自由未知量(设为1,,t i i x x )。
设1,,t t F αα∈是t F 的一组基(常取自然基)。
然后令1(,,),1,2,t i i j x x j t α==,分别解得方程组的解:1,,t X X (这是一个基础解系)。
则可知方程组的解为11t t X k X k X =++,这儿1,,t k k 为任意常数。
(一般解)(3) C ramer 法则。
注意:Cramer 法则只对系数矩阵可逆的情形适用。
题型2.将()V F β∈用1,,()m V F αα∈线性表示(或求坐标) 常用思路:待定系数法。
设1,,m x x 使得11m m x x βαα=++。
然后根据题设条件得到关于1,,m x x 的一个方程组。
解方程组。
方法二:利用课本定理4.10(如果已知在某一组基下的矩阵) 题型3.判断1,,()m V F αα∈的线性相关性常用思路:待定系数法。
设1,,m x x 使得110m m x x αα=++。
然后根据题设条件得到关于1,,m x x 的一个方程组。
解方程组。
如果方程组只有零解,则1,,()m V F αα∈线性相关。
反之,线性无关。
题型4.求1,,()m V F αα∈的极大无关组及秩常用思路:待定系数法。
设1,,m x x 使得110m m x x αα=++。
然后根据题设条件得到关于1,,m x x 的一个方程组。
用高斯消元法化简方程组,得到自用未知量。
浙江大学城市学院线性代数期中考试试卷汇集

城院线性代数期中试卷汇集浙江大学姜豪汇编2012年3月目录第一部分:试卷真题11—12学年第一学期期中试卷 (2)10—11学年第二学期期中试卷 (4)10—11学年第一学期期中试卷 (6)09—10学年第二学期期中试卷 (9)09—10学年第一学期期中试卷 (13)第二部分:答案与评估11—12学年第一学期期中试卷答案 (15)11—12学年第一学期期中试卷难度与题量评估 (16)10—11学年第二学期期中试卷答案 (16)10—11学年第二学期期中试卷难度与题量评估 (18)10—11学年第一学期期中试卷答案 (18)10—11学年第一学期期中试卷难度与题量评估 (19)09—10学年第二学期期中试卷答案 (20)09—10学年第二学期期中试卷难度与题量评估 (21)09—10学年第一学期期中试卷答案 (21)09—10学年第一学期期中试卷难度与题量评估 (22)第三部分:试题详解11—12学年第一学期期中试卷详解 (22)10—11学年第二学期期中试卷详解 (28)10—11学年第一学期期中试卷详解 (34)09—10学年第二学期期中试卷详解 (39)09—10学年第一学期期中试卷详解 (44)第一部分:试卷真题城院线代2011—2012学年第一学期期中试卷一,填空题(每空2分,共20分)1. 5阶行列式||ij a 的项2532511344a a a a a 的符号是_______ .2. _____002013112, _____21501102=-=-.3. 已知⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-=100030002 ,200010001B A ,则==AB A , ____||4. 若矩阵[]42⨯=ija A ,且j i a ij 2-=,则=A5. 已知⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-=22111602 ,51240321B A ,则=+B A 2 ,=-B A 26. ()()=-⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-211223 , _____223211二,问答题(每题5分,共25分)1. 排列)12(135)2(246-n n 的逆序数是多少?请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
城院线代11—12学年第二学期期末试卷一,填空题(每空2分,共20分)1.3阶行列式. ___________________111222=b c a b c a2.设B A ,均为3阶方阵,且6|| ,3||==B A ,则_____|)2(| , _____||1==-A AB3.已知⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛13422312X ,则 , 23121==⎪⎪⎭⎫ ⎝⎛-X4. 若齐次线性方程组O X A =⨯33有非零解,则系数矩阵的秩)(A R 最大可取_____ 5.已知3阶方阵A 有一特征值为5,则A 4必有一特征值为_____,2A 必有一特征值为_____ 。
6.设向量()()TT1132,1121-=-=βα,那么内积_____),(=βα,α的长度为______。
二,问答题(每题4分,共20分)1.设A 是一个可逆矩阵,则A 的特征值全不为零吗?说明理由。
2.已知向量组()()()TTT402,520,32121-=-=-=βαα,β能否由21,αα线性表示?说明理由。
3.已知321,,ααα线性无关,则133221 , ,αααααα-++线性无关吗?说明理由。
4.矩阵⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=5632 , 6251B A 是否相似?说明理由。
5.()()()TTT563,012,321321--=-==ααα是否是标准正交向量组?说明理由。
三,简单计算题(每题5分,共30分。
只写答案无过程不得分。
)1.计算行列式 2421012344022211-----2.求矩阵⎪⎪⎪⎭⎫ ⎝⎛---=111013221A 的逆矩阵。
3.求非齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=-+=++-=-+--=-+337713434234213214321431x x x x x x x x x x x x x 的通解,并用向量形式表示。
4.t 取何值时,向量组()()()TTTt 31,321,111321===ααα线性相关?5.求向量组()()()TTT2431,0213,1312321-=-=-=ααα,()T11344-=α的一个极大线性无关组。
6.已知矩阵⎪⎪⎪⎭⎫ ⎝⎛=32020002x A 与⎪⎪⎪⎭⎫⎝⎛=y B 00020001相似,求x 与y 的值。
四,计算题(第1题10分,第2题14分,共24分。
只写答案无过程不得分。
) 1.已知向量组()()()TTT0201,0011,2021321===ααα,将此向量组改造成为一组标准正交向量组。
2.设矩阵⎪⎪⎪⎭⎫ ⎝⎛=101020101A ,求(1) A 的特征值和特征向量;(2) 矩阵2)(A kE B +=,其中k 为实数,求一个对角矩阵Λ,使得B 与Λ相似。
五,证明题(本题6分)设B A ,均为n 阶实对称矩阵,证明:A 与B 相似||||E B E A λλ-=-⇔ 。
城院线代11—12学年第二学期期末试卷试题详解一,填空题(每空2分,共20分)1.3阶行列式. ___________________111222=b c a b c a解:这是范德蒙行列式,直接用公式即可。
参见教材P20例2。
这行列式的值为))()((a c a b c b --- 。
2.设B A ,均为3阶方阵,且6|| ,3||==B A ,则_____|)2(| , _____||1==-A AB 解:由矩阵乘法性质(4)(教材P38)1863||||||=⨯==⇒B A AB 。
再由教材P49可逆矩阵性质(5)和教材P35矩阵数乘性质(5)=⇒-|)2(|1A241381||21|2|13=⨯==A A 。
3.已知⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛13422312X ,则 , 23121==⎪⎪⎭⎫⎝⎛-X解:当0≠-bc ad 有⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫⎝⎛-a c b d bc ad d c b a 11,用此公式⇒ ⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫⎝⎛-231223121。
由⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛13422312X ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=⇒-134223121X ⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=14129713422312 。
4. 若齐次线性方程组O X A =⨯33有非零解,则系数矩阵的秩)(A R 最大可取_____ 解:由教材P87定理3.2的推论知:当O X A =⨯33有非零解3)(0||<⇒=⇒A R A2)(≤⇒A R ,故)(A R 最大可取2 。
5.已知3阶方阵A 有一特征值为5,则A 4必有一特征值为_____,2A 必有一特征值为_____ 。
解:由教材P117定理4.3A 4⇒必有一特征值为2054=⨯,2A 必有一特征值为2552= 。
6.设向量()()TT1132,1121-=-=βα,那么内积_____),(=βα,α的长度为______。
解:由教材P129定义4.41162)1(11)1(3221),(--+=-⋅+⋅-+⋅+⋅=⇒βα6=. 由教材P129定义4.571)1(21||||2222=+-++=⇒α .二,问答题(每题4分,共20分)1.设A 是一个可逆矩阵,则A 的特征值全不为零吗?说明理由。
答:是的。
根据教材P117推论4.1得出。
2.已知向量组()()()TTT402,520,32121-=-=-=βαα,β能否由21,αα线性表示?说明理由。
答:设()βαααα2121~), (==A A ,则⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---=0002102011050420201453022201~A ,所以2)()~(==A R A R ,故由教材P79定理3.1知线性方程组β=AX 有解,即β能由21,αα线性表示。
3.已知321,,ααα线性无关,则133221 , ,αααααα-++线性无关吗?说明理由。
答:解法1:()()13321332210321αααααααααα-+−−−→−-++=+-cc c A B =由教材P70定理2.6)()(B R A R =⇒, 但B 的第1列是零向量,故3)(<B R ,所以3)(<A R ,由教材P94定理3.3推出133221 , ,αααααα-++线性相关。
解法2:用观察法)()(213213αααααα+-+=-⇒,由此式和教材P96定理3.4推出133221 , ,αααααα-++线性相关。
(注:以上两种解法都没有用到“321,,ααα线性无关”这一条件。
也就是说,把这条件去掉,结论仍成立。
)解法3:()()⎪⎪⎪⎭⎫ ⎝⎛-=-++110011101321133221ααααααααα而⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-−−→−⎪⎪⎪⎭⎫ ⎝⎛-=-00011010111011010111001110112r r A D =, 由2)()(==D R A R 知A 的列向量组线性相关,故由命题3.3.10推出133221 , ,αααααα-++线性相关。
(注:引用命题3.3.10要用到“321,,ααα线性无关”这一条件。
) 解法4:设 ⇒=-++++O k k k )()()(133322211αααααα O k k k k k k =++++-332221131)()()(ααα 由于321,,ααα线性无关,故⇒⎪⎩⎪⎨⎧=+=+=-000322121k k k k k k 系数矩阵⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-=000110101110110101110011101A 32)(<=⇒A R ,所以由教材P87定理3.2 知这个齐次线性方程组有非零解,故133221 , ,αααααα-++线性相关。
4.矩阵⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=5632 , 6251B A 是否相似?说明理由。
答:B A B A tr tr 352 tr ,761tr ≠⇒=+-==+=,所以由教材P120定理4.6A ⇒与B 不相似。
5.()()()TTT563,012,321321--=-==ααα是否是标准正交向量组?说明理由。
答:114321||||2221>=++=α,所以1α不是单位向量,故这个向量组不是标准正交向量组。
三,简单计算题(每题5分,共30分。
只写答案无过程不得分。
)1.计算行列式 2421012344022211-----解:原式242101230124402102,4241------+r r r r 按第4列展开03234440102 21231244210223=-+---=c c 。
(第1列与第3列相同)2.求矩阵⎪⎪⎪⎭⎫ ⎝⎛---=111013221A 的逆矩阵。
解:⎪⎪⎪⎭⎫ ⎝⎛---−−−→−⎪⎪⎪⎭⎫ ⎝⎛---=+-101110013650001221100111010013001221) (1312,3r r r r E A⎪⎪⎪⎭⎫ ⎝⎛-----−−−→−⎪⎪⎪⎭⎫ ⎝⎛---−−−−→−⎪⎪⎪⎭⎫ ⎝⎛---−−→−-++-↔512100613010201001512100101110201001013650101110001221332232132)1(,5,2r r r r r r r r r所以, ⎪⎪⎪⎭⎫ ⎝⎛-----=-5126132011A 。
3.求非齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=-+=++-=-+--=-+337713434234213214321431x x x x x x x x x x x x x 的通解,并用向量形式表示。
解:⎪⎪⎪⎪⎪⎭⎫⎝⎛-----→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------→⎪⎪⎪⎪⎪⎭⎫⎝⎛------383700122000212103111244770103210212103110133077101134341231101⎪⎪⎪⎪⎪⎭⎫⎝⎛---→⎪⎪⎪⎪⎪⎭⎫⎝⎛-----→⎪⎪⎪⎪⎪⎭⎫⎝⎛-----→610003837006210705940076100038370014714702177071220003837002121031101 ⎪⎪⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎪⎪⎭⎫⎝⎛-→6100080100800105000161000560700560070350007,所以,本题有唯一解:⎪⎪⎩⎪⎪⎨⎧===-=68854321x x x x 向量形式的唯一解:()T6885- 。
本方程组的导出组只有零解,故通解形式为:()()TTk X 00006885+-=,其中k 为任意常数。
4.t 取何值时,向量组()()()TTTt 31,321,111321===ααα线性相关?解:()D t t t A r r r r r r =⎪⎪⎪⎭⎫ ⎝⎛-−−→−⎪⎪⎪⎭⎫ ⎝⎛-−−−→−⎪⎪⎪⎭⎫ ⎝⎛==---500210111120210111313211112313122,321ααα所以,当5=t 时⇒=-⇒05t 秩⇒<===32)()(},,{321D R A R ααα321,,ααα线性相关。
