立体几何2
立体几何2-角与距离
立体几何(Ⅱ)——角与距离一、知识网络二、高考考点1.异面直线所成的角;异面直线间的距离.其中,异面直线所成的角是重点,也是难点。
2.直线和平面所成的角;直线与平面的距离.其中,在计算题中,直线和平面所成的角或距离问题为高考命题热点,它不但所占比例大,而且几乎年年有,次次出。
3.二面角、以二面角为载体引出的平行、垂直以及其它的角和距离问题。
三、知识要点1.异面直线所成的角异面直线间的距离(见专题26)2.直线和平面所成的角(1)斜线在平面内的射影(Ⅰ)有关概念:①过一点向平面引垂线,垂足叫做这点在这个平面内的射影;这点与垂足间的线段叫做这点到这个平面的垂线段。
②一条直线和一个平面相交,但不和这个平面垂直时,这条直线叫做这个平面的斜线;斜线和平面的交点叫做斜足;从平面外一点向平面引斜线,这点与斜足间的线段叫做这点到这个平面的斜线段。
③从斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影,垂足与斜足间的线段叫做这点到平面的斜线段在这个平面内的射影。
(Ⅱ)定理:从平面外一点向平面所引的垂线段和斜线段中①射影等长斜线段等长;②射影较长斜线段较长;③斜线段长大于垂线段。
(2)直线和平面所成的角(Ⅰ)定义与命题①定义:平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条直线和这个平面所成的角。
特例:若直线与平面垂直,则说直线和平面所成的角是直角;若直线与平面平行或在平面内,则说直线与平面所成角是0°的角。
认知:设斜线l与平面所成角为θ,则θ∈(0°,90°);设直线l与平面所成角为θ,则θ∈[0°,90°]。
②命题(最小角定理):斜线和平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角。
(3)三垂线定理及其逆定理三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
高二选必一数学人教B版章节第一章空间向量与立体几何(2)+答案解析(附后)

bbgxxbj高二选必一数学人教B版章节第一章空间向量与立体几何1.2空间向量在立体几何中的应用1.2.4二面角第1课时二面角及其度量一、单选题(本大题共6小题,共30分。
在每小题列出的选项中,选出符合题目的一项)1.已知平面内有一个以AB为直径的圆,,点C在圆周上异于点A,,点D,E分别是点A在PC,PB上的射影,则 ( )A. 是二面角的平面角B. 是二面角的平面角C. 是二面角的平面角D. 是二面角的平面角2.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,则这两个二面角的大小关系是 ( )A. 相等B. 互补C. 相等或互补D. 不能确定3.已知和均为边长为a的等边三角形,且,则二面角的大小为 ( )A. B. C. D.4.如图所示,点P是二面角棱上的一点,分别在,平面内引射线PM,PN,若,,则二面角的大小为 ( )A. B. C. D.5.正方形ABCD所在平面外有一点P,平面ABCD,若,则平面PBC与平面ABCD的夹角为 ( )A. B. C. D.6.如图,在正方体ABCD中,棱长为1,过AB作平面交棱,分别为E,若平面与底面ABCD所成的角为,则截面ABEF的面积为 ( )A. B. C. D.二、填空题(本大题共3小题,共15分)7.若P是所在平面外一点,且和都是边长为2的正三角形,,则二面角的大小为__________.8.四边形ABCD是边长为2的正方形,MA和PB都与平面ABCD垂直,且,则平面PMD 与平面ABCD所成角的余弦值为__________.9.在正方体中,截面与底面ABCD所成的二面角的正切值为__________.三、解答题(本大题共1小题,共12分。
解答应写出文字说明,证明过程或演算步骤)10.本小题12分已知在三棱锥中,平面ABC,,求二面角的余弦值.答案和解析1.【答案】B【解析】【分析】本题考查二面角,线面垂直的判定,属于中档题;根据题意做出图形,证明平面PAC继而证明平面PBC,所以有平面ADE即可得结果.【解答】解:因为,,所以,因为AB为圆的直径,所以,,所以平面PAC,所以,因为D为A在PC上的射影,所以,又,所以平面PBC,所以,又,,所以平面ADE,所以是二面角的平面角 .故选2.【答案】C【解析】【分析】本题考查二面角的概念,属于基础题.根据二面角的概念可知,当这两个二面角的两个面均同向或均异向时,它们相等;当这两个二面角的两个面中,一组同向,另一组异向时,它们互补,即可求解.【解答】解:当这两个二面角的两个面均同向或均异向时,它们相等;当这两个二面角的两个面中,一组同向,另一组异向时,它们互补.故选3.【答案】C【解析】【分析】本题主要考查了二面角的大小计算,属于基础题.取BC的中点E,连结EA,ED,得到,,得到二面角的平面角,利用等边三角形的性质计算即可.【解答】解:如图,取BC的中点E,连接、,根据等边三角形的性质得,,即为所求,又,,所以是等边三角形,则故选4.【答案】D【解析】【分析】本题考查的知识点是二面角及其度量,属于基础题,我们要根据二面角的定义,在两个平面的交线上取一点Q,然后向两个平面引垂线,构造出二面角的平面角,然后根据平面几何的性质,求出含二面角的平面角的三角形中相关的边长,解三角形即可得到答案.【解答】解:过AB上一点Q分别在,内做AB的垂线,交PM,PN于M点和N点,则即为二面角的平面角,如下图所示:设,,,,又由,易得为等边三角形,则,解三角形QMN易得,故答案为5.【答案】B【解析】【分析】本题主要考查线面垂直的判定及性质,利用空间向量求二面角,属于中档题.以A点为原点,建立空间直角坐标系,不妨设,写出各点的坐标,由线面垂直的判定及性质得到为平面PAB的法向量,过A作,可证明平面PCD,故为平面PCD的法向量,利用〈,〉可得平面PAB与平面PCD所成的二面角的大小.【解答】解:由题意可以A点为原点,建立如图所示的空间直角坐标系,不妨设,则,,,平面ABCD,平面ABCD,,又,,面PAB,平面PAB,为平面PAB的法向量,即,过A作,,则E为PD中点,由题意,,,PA,面PAD,面PAD,面PAD,,,PD,面PCD,则平面PCD,故为平面PCD的法向量,且,,平面PAB与平面PCD所成的二面角的大小为故答案选6.【答案】D【解析】【分析】本题考查二面角与空间几何体的截面问题,为基础题.【解答】解:由图可知,平面与底面ABCD所成的角等同于,可得,且截面ABEF为矩形,可得截面面积为7.【答案】【解析】【分析】本题主要考查了二面角及其度量,考查空间想象能力、运算能力和推理论证能力,属于基础题.取BC的中点D,连接PD、AD,根据二面角的平面角的定义可知为二面角的平面角,在三角形PDA中求出此角即可.【解答】解:取BC的中点D,连接PD、AD,、均为正三角形,,,为二面角的平面角.又,,故答案为8.【答案】或【解析】【分析】本题考查二面角的求法,解题时要认真审题,注意面积法的合理运用.考虑在平面ABCD同侧或异侧,结合,能求出【解答】解:设平面PMD与平面ABCD所成角的大小为,在平面ABCD上的射影为,易得当在平面ABCD同侧时,如图所示:,,当在平面ABCD异侧时,如图所示:,,,,所以平面PMD与平面ABCD所成角的余弦值为或故答案为或9.【答案】【解析】【分析】本题考查了二面角的求法,考查了转化思想,属于基础题.连接AC交BD于点O,连接,根据条件可知为所求的角,再求出即可.【解答】解:如图所示,连接AC交BD于点O,连接,则,,为二面角的平面角,设,则,所以10.【答案】方法一:如图,过点B作于点E,则E为AC的中点,过点E作于点F,连接因为平面ABC,平面PAC,所以平面平面又因为,平面ABC,平面平面,所以平面由三垂线定理有,所以是二面角的平面角.设,由E是AC的中点,得,,所以,所以方法二:利用射影面积公式如图,过点B作于点E,连接因为平面ABC,平面PAC,所以平面平面ABC,又因为,平面ABC,平面平面,所以平面PAC,所以是在平面PAC上的射影.设,则,,所以在中,AB边上的高,所以又设二面角的大小为,由射影面积公式有【解析】本题考查二面角的求解,为一般题.。
(高中段)大题考法立体几何第二课时空间向量与空间角3
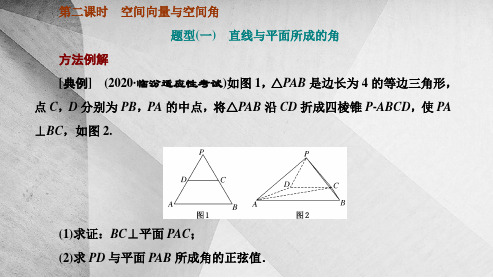
[解] (1)证明:在△ABC 中,BC=2,AB=4,∠ABC=60°,所以 AC2= BC2+AB2-2BC·AB·cos B=12,
则有 AC2+BC2=AB2,即 AC⊥BC. 又因为 PA⊥BC,PA∩AC=A,PA⊂平面 PAC,AC⊂平面 PAC,所以 BC ⊥平面 PAC. (2)由(1)知 AC⊥BC,以点 C 为坐标原点,CA,CB 所在 直线分别为 x,y 轴建立如图所示的坐标系 C-xyz. 则 C(0,0,0),A(2 3,0,0),B(0,2,0),D( 3,-1,0), 易知 P 在底面的射影为 AC 与 BD 的交点, 所以 P233,0,236,―PD→= 33,-1,-2 36,
由(1)知―A→P =0,1, 22是平面 PCB 的一个法向量,
记 n =―A→P ,则
n ,m
n ·m =
|n |·|m
|=2 5
5 .
所以二面角
B-PC-E
的余弦值为2 5
5 .
融通方法 利用空间向量求二面角的解题模型
应用体验 (2020·河北“五个一”名校联考)在四棱锥 P-ABCD 中,AD ∥BC,AB=BC=CD=12AD,G 是 PB 的中点,△PAD 是 等边三角形,平面 PAD⊥平面 ABCD. (1)求证:CD⊥平面 GAC; (2)求二面角 P-AG-C 大小的正弦值.
设平面 AEF 的一个法向量为 n =(x1,y1,z1),
n ·―AE→=0,
则 n
·―AF→=0,
即x21x+1+z1λ=y1=0,0.
令 y1=2,则zx11==λ-. λ, ∴n =(-λ,2,λ).
设平面 PCD 的一个法向量为 m =(x2,y2,z2),
2021版理科数学全国通用版备战一轮复习(课件 课时跟踪检测):第八章 立体几何 (2)

第八章立体几何第二节空间几何体的表面积与体积A级·基础过关|固根基|1.如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为()A.312B.34C.612D.64解析:选A易知三棱锥B1-ABC1的体积等于三棱锥A-B1BC1的体积,又三棱锥A-B1BC1的高为32,底面积为12,故其体积为13×12×32=312.2.(2020届大同调研)某几何体的三视图如图所示,则该几何体外接球的表面积为()A.11πB.14π3C.28π3D.16π解析:选C由三视图可知,该几何体的直观图为三棱锥,记为三棱锥A-BCD,将该三棱锥放在长方体中,如图所示,其中AB⊥平面BCD,AB=2,△BCD为边长为2的正三角形.设O 1为正△BCD 的中心,O 为三棱锥A -BCD 外接球的球心,R 为外接球的半径.连接OO 1,OB ,O 1B ,则OO 1⊥平面BCD ,OO 1=1,BO 1=23×2×32=233,则OB 2=R 2=12+2332=73,所以该几何体外接球的表面积S =4πR 2=4π×73=28π3,故选C .3.如图是一个实心金属几何体的直观图,它的中间是高l 为6124的圆柱,上、下两端均是半径r 为2的半球,若将该实心金属几何体在熔炉中高温熔化(不考虑过程中的原料损失),熔成一个实心球,该球的直径为( )A .3B .4C .5D .6解析:选C 实心金属几何体的体积V =43πr 3+πr 2l =43π×8+π×4×6124=1256π.设实心球的半径为R ,由体积相等得43πR 3=1256π,所以R =52,所以该球的直径为2R =5.4.如图,圆柱的底面半径为1,平面ABCD 为圆柱的轴截面,从A 点开始,沿着圆柱的侧面拉一条绳子到C 点,若绳子的最短长度为3π,则该圆柱的侧面积为( )A .42π2B .22π2C .52π2D .4π2解析:选A 沿AD 将圆柱的侧面展开,绳子的最短长度即侧面展开图中A ,C 两点间的距离,连接AC ,所以AC =3π,展开后AB 的长度为π.设圆柱的高为h ,则AC 2=AB 2+h 2,即9π2=π2+h 2,解得h =22π,所以圆柱的侧面积为2×π×1×22π=42π2.5.(2020届贵阳摸底)某几何体的三视图如图所示,则它的体积为()A.23B.43C.13D.16解析:选A根据三视图可知,该几何体为三棱锥,记为A-BCD,放在正方体中如图所示,则该几何体的体积V=13·S△BCD×2=13×12×2×1×2=23.故选A.6.(2019届合肥市二检)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图由两个半圆和两条线段组成,则该几何体的表面积为()A.17π+12 B.12π+12C.20π+12 D.16π+12解析:选C由三视图知,该几何体是一个由大半圆柱挖去一个小半圆柱得到的,两个半圆柱的底面半径分别为1和3,高均为3,所以该几何体的表面积为12×2π×3×3+12×2π×1×3+2×⎝⎛⎭⎪⎫12π×32-12π×12+2×2×3=20π+12,故选C.7.(2019届福州市质检)如图,以棱长为1的正方体的顶点A为球心,以2为半径作一个球面,则该正方体的表面被球面所截得的所有弧长之和为()A.3π4B.2πC.3π2D.9π4解析:选C正方体的表面被该球面所截得的弧长是相等的三部分,如图,上底面被球面截得的弧长是以A1为圆心,1为半径的圆周长的14,所以所有弧长之和为3×2π4=3π2.故选C.8.(2019届洛阳市第二次联考)已知正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面圆面积的最小值是()A.7π4B.2πC.9π4D.3π解析:选C设正三角形ABC的中心为O1,连接OO1,OA,O1A,由题意得O1O⊥平面ABC,O1O=1,OA=2,∴在Rt△O1OA中,O1A=OA2-O1O2=3,∴AB=3.∵E为AB的中点,∴AE=3 2.连接OE,则OE⊥AB.过点E作球O的截面,当截面与OE垂直时,截面圆的面积最小,此时截面圆的半径r =32,可得截面圆面积的最小值为πr 2=9π4,故选C .9.(2019届南昌市二模)已知圆锥的侧面展开图为四分之三个圆面,设圆锥的底面半径为r ,母线长为l ,有以下结论:①l ∶r =4∶3;②圆锥的侧面积与底面面积之比为4∶3;③圆锥的轴截面是锐角三角形.其中所有正确结论的序号是( )A .①②B .②③C .①③D .①②③解析:选A 设圆锥的母线长l =1.因为圆锥的侧面展开图为四分之三个圆面,所以圆锥的侧面积为34π.又圆锥的底面半径为r ,所以由2πr =34×2π,得r =34,所以l r =43,故①正确;圆锥的侧面积与底面积之比为34ππ·⎝ ⎛⎭⎪⎫342=43,故②正确;设圆锥的轴截面三角形的顶角为θ,因为圆锥的底面直径为2×34=32,所以cos θ=12+12-⎝ ⎛⎭⎪⎫3222×1×1=-18,所以角θ为钝角,所以圆锥的轴截面是钝角三角形,故③错误.故选A .10.(2019届惠州模拟)已知三棱锥S -ABC 的底面是以AB 为斜边的等腰直角三角形,AB =2,SA =SB =SC =2,则三棱锥S -ABC 的外接球的球心到平面ABC 的距离是( )A .33B .1C . 3D .332解析:选A ∵三棱锥S -ABC 的底面是以AB 为斜边的等腰直角三角形,SA =SB =SC =2,∴S 在底面ABC 内的射影为AB 的中点.设AB 的中点为H ,连接SH,CH,∴SH⊥平面ABC,∴SH上任意一点到A,B,C的距离相等,易知SH=3,CH=1,∴在Rt△SHC中,∠HSC=30°.在面SHC内作SC的垂直平分线MO,交SH于点O,交SC于点M,则O为三棱锥S-ABC的外接球的球心.∵SC=2,∴SM=1.又∠OSM=30°,∴SO=233,OH=33,∴球心O到平面ABC的距离为33,故选A.11.如图,在直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将该直角梯形绕BC边旋转一周,则所得的几何体的表面积为________.解析:根据题意可知,所得几何体的上半部分为圆锥(底面半径为1,高为1),下半部分为圆柱(底面半径为1,高为1),如图所示,则所得几何体的表面积为圆锥侧面积、圆柱的侧面积以及圆柱的下底面面积之和,即表面积为π×1×12+12+2π×1×1+π×12=(2+3)π.答案:(2+3)π12.(2020届贵阳摸底)在四面体ABCD中,若AB=CD=5,AC=BD=6,AD=BC=3,则四面体ABCD的外接球的表面积为________.解析:如图所示,将四面体补形为长方体,则四面体的四个顶点均为长方体的顶点,四面体的外接球即长方体的外接球.设长方体的长、宽、高分别为a,b,c,则⎩⎪⎨⎪⎧a2+b2=9,a2+c2=6,b2+c2=5,三个等式相加得2(a2+b2+c2)=20⇒a2+b2+c2=10,设该四面体外接球的半径为R,则2R=a2+b2+c2=10,即R=102,所以该四面体外接球的表面积为4πR2=4π×104=10π.答案:10πB级·素养提升|练能力|13.(2019届合肥市二检)我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是多少.如果我们把求截去的正四棱锥的高改为求剩下的正四棱台的体积,则该正四棱台的体积是(注:1丈=10尺)()A.1 946立方尺B.3 892立方尺C.7 784立方尺D.11 676立方尺解析:选B解法一:如图,记正四棱台为A1B1C1D1-ABCD.该正四棱台由正四棱锥S-ABCD截得,O为正方形ABCD的中心,E为BC的中点,E1为B1C1的中点.设正四棱台的高为x,则由图中△SO1E1∽△SOE,得SO1SO=O1E1OE,即30-x30=310,解得x=21,所以该正四棱台的体积V=13×(62+6×20+202)×21=3 892(立方尺),故选B.解法二:如解法一中图,记正四棱台为A1B1C1D1-ABCD.该正四棱台由正四棱锥S-ABCD截得,O为正方形ABCD的中心,E为BC的中点,E1为B1C1的中点.设截去的正四棱锥的高为x,则由图中△SO1E1∽△SOE,得SO1SO =O1E1OE,即x 30=310,解得x=9,所以该正四棱台的体积V=V正四棱锥S-ABCD-V正四棱锥S-A1B1C1D1=13×202×30-13×62×9=3 892(立方尺),故选B.14.(2019届郑州市第二次质量预测)在长方体ABCD-A1B1C1D1中,AD=DD1=1,AB=3,E,F,G分别是棱AB,BC,CC1的中点,P是底面ABCD 内一动点,若直线D1P与平面EFG没有公共点,则△PBB1面积的最小值为()A.32B.1C.34D.12解析:选C记△PBB1的面积为S.因为P在底面ABCD上,所以PB⊥BB1,即△PBB1为直角三角形.又BB1=DD1=1,所以S=12×BB1×PB=12PB,所以当线段PB的长最小时,S取得最小值.因为D1P与平面EFG无公共点,所以D1P∥平面EFG.如图①,连接AD1,D1C,AC,易证GF∥AD1,EF∥AC,又GF∩EF =F,AD1∩AC=A,所以平面AD1C∥平面EFG,所以D1P⊂平面AD1C,又点P 是底面ABCD内一动点,所以点P一定在线段AC上运动.如图②,当PB⊥AC时,线段PB的长最小,此时PB=AB·BCAC=32,故S min=12×32=34,故选C.15.在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB.9π2C.6πD.32π3解析:选B由题意可得,若V最大,则球与直三棱柱的部分面相切,若与三个侧面都相切,可求得球的半径为2,球的直径为4,超过直三棱柱的高,所以这个球放不进去,则球可与上下底面相切,此时半径R=32,故该球的体积最大,V max=43πR3=4π3×278=9π2.16.(2020届惠州调研)在三棱锥A-BCD中,底面BCD是直角三角形且BC⊥CD,斜边BD上的高为1,三棱锥A-BCD的外接球的直径是AB,若该外接球的表面积为16π,则三棱锥A-BCD体积的最大值为________.解析:如图,过点C作CH⊥BD于H.由外接球的表面积为16π,可得外接球的半径为2,则AB=4.因为AB为外接球的直径,所以∠BDA=90°,∠BCA =90°,即BD⊥AD,BC⊥CA,又BC⊥CD,CA∩CD=C,所以BC⊥平面ACD,所以BC⊥AD,又BC∩BD=B,所以AD⊥平面BCD,AD⊂平面ABD,所以平面ABD⊥平面BCD,又平面ABD∩平面BCD=BD,所以CH⊥平面ABD.设AD=x(0<x<4),则BD=16-x2.在△BCD中,BD边上的高CH=1,所以V三棱锥A-BCD=V三棱锥C-ABD=13×12×x×16-x2×1=16-x4+16x2,当x2=8时,V三棱锥A-BCD有最大值,故三棱锥A-BCD体积的最大值为4 3.答案:4 3。
学生版立体几何(2)

立体几何(2)一、基础训练1. 一条直线和平面所成角为θ,那么θ的取值范围是_________2. 已知点E ,F ,G ,H 分别为空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,且直线EF ⋂直线GH=P ,那么P 在直线___________上. (填以A ,B ,C ,D 为起点和终点的直线)3. 在正方形1111D C B A ABCD -中,对角线D B 1与对角线AC 所成的角的大小为_______.4. 若直线a ∥直线b ,直线b ∥平面α,则a 与α的位置关系是_____________.5. 正三棱锥底面三角形的边长为3,侧棱长为2,则其体积为____________ 6.已知m ,n 是两条不同的直线,α,β是两个不同的平面.①若m ⊂α,m ⊥β,则α⊥β; ②若m ⊂α,α∩β=n ,α⊥β,则m ⊥n ; ③若m ⊂α,n ⊂β,α∥β,则m ∥n ; ④若m ∥α,m ⊂β,α∩β=n ,则m ∥n . 上述命题中为真命题的是___________(填写所有真命题的序号).二、例题1. 已知四边形ABCD 是矩形,PA ⊥平面ABC ,,M N 分别是,AB PC 的中点. (1)求证:MN AB ⊥;(2)若PA AD =,求证:MN ⊥平面PCD .2.已知:正方体1111ABCD-A B C D ,边长为1,E 为棱1CC 的中点. (1)求证:AE BD ⊥;(2)求二面角E-AD-C 的正切值A BC DD 1C 1B 1A 1 3.如图,在棱长均为4的三棱柱111ABC ABC -中,D 、1D 分别是BC 和11B C 的中点. (1)求证:11A D ∥平面1AB D ;(2)若平面ABC ⊥平面11BCC B ,160O B BC ∠=,求三棱锥 1B ABC -的体积.4. 直四棱柱1111A B C D A B C D -中,底面ABCD 是直角梯形,∠BAD =∠ADC =90°,222AB AD CD ===.11=BB(1)求证:AC ⊥平面BB 1C 1C ;(2)在A 1B 1上是否存一点P ,使得DP 与平面BCB 1与平面ACB 1都平行?证明你的结论.三、作业1. 已知P 为ABC ∆所在平面外一点,点O 为点P 在平面ABC 上的射影,若PA ,PB ,PC 与底面成等角,则O 是ABC ∆的________心.2. 三个平面两两垂直,它们的交线交于一点O ,若点P 到三个平面的距离分别为3,4,5,则OP 的长为________.3. 已知直线m 、n 及平面α,其中m ∥n ,那么在平面α内到两条直线m 、n 距离相等的点的集合可能是:①一条直线;②一个平面;③一个点;④空集。
2020版高考数学人教版理科一轮复习第七章 立体几何 (2)

1.(方向 1)(2019·洛阳市第一次统考)某几何体的三视图如图所示,
则该几何体的体积是( B )
15π A. 2
17π C. 2
B.8π D.9π
解析:依题意,题中的几何体是由两个完全相同的圆柱各自 用一个不平行于其轴的平面去截后所得的部分拼接而成的组合 体(各自截后所得的部分也完全相同),其中一个截后所得的部分 的底面半径为 1,最短母线长为 3、最长母线长为 5,将这两个截 后所得的部分拼接,恰好可以形成一个底面半径为 1,母线长为 5+3=8 的圆柱,因此题中的几何体的体积为 π×12×8=8π,故 选 B.
又平面 B1D1D∩平面 B1EDF=B1D,
所以 O1H⊥平面 B1EDF,
所以 O1H 等于四棱锥 C1-B1EDF 的高.
因为△B1O1H∽△B1DD1,
Байду номын сангаас
所以
O1H=B1OB11·DDD1=
6 6 a.
方向 3 利用体积法求点面距离 【例 4】 如图,在四棱锥 P-ABCD 中,底面 ABCD 是矩形,PD ⊥底面 ABCD,M,N 分别为 AB,PC 的中点,PD=AD=2,AB=4.
如图,连接 AB′,AD′,B′D′,因为三棱锥 A′-AB′D′ 是正三棱锥,所以 A′A,A′B′,A′D′与平面 AB′D′所成 的角都相等.分别取 C′D′,B′C′,BB′,AB,AD,DD′ 的中点 E,F,G,H,I,J,连接 EF,FG,GH,IH,IJ,JE, 易得 E,F,G,H,I,J 六点共面,平面 EFGHIJ 与平面 AB′D′ 平行,且截正方体所得截面的面积最大.又 EF=FG=GH=IH =IJ=JE= 22,所以该正六边形的面积为 6× 43×( 22)2=343, 所以 α 截此正方体所得截面面积的最大值为34 3,故选 A.
高二数学寒假作业立体几何2

立体几何22作业(文科)知识回顾一、旋转体和多面体 1.旋转体的形成几何体 旋转图形 旋转轴 圆柱 矩形 任一边所在的直线 圆锥 直角三角形 任一直角边所在的直线 圆台 直角梯形 垂直于底边的腰所在的直线球半圆直径所在的直线2.多面体的结构特征3.直观图(1)画法:常用斜二测画法. (2)规则:①在已知图形中建立直角坐标系xOy ,画直观图时,它们分别对应x ′轴和y ′轴,两轴交于点O ′,使∠x ′O ′y ′=45°,它们确定的平面表示水平平面;②已知图形中平行于x 轴或y 轴的线段,在直观图中分别画成平行于x ′轴和y ′轴的线段; ③已知图形中平行于x 轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的12.4.三视图(1)三视图的画法规则:主、俯视图长对正,主、左视图高平齐;俯、左视图宽相等,前后对应. (2)画简单组合体的三视图应注意的两个问题:①首先,确定主视、俯视、左视的方向,同一物体放置的位置不同,所画的三视图可能不同.②其次,简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置.典例1、如图,某几何体的主视图与左视图都是边长为1的正方形,且体积为12,则该几何体的俯视图可以是 ( )二、空间图形的基本关系与公理 1.空间图形的公理(1)公理1:过不在一条直线上的三点,有且只有一个平面(即可以确定一个平面). (2)公理2:如果一条直线上的两点在一个平面内,那么这条直线在此平面内(即直线在平面内).(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.(4)公理4:平行于同一条直线的两条直线平行. 2.空间中两直线的位置关系(1)空间中两直线的位置关系⎩⎨⎧共面直线⎩⎪⎨⎪⎧相交直线平行直线异面直线:不同在任何一个平面内(2)异面直线所成的角①定义:过空间任意一点P 分别引两条异面直线a ,b 的平行线l 1,l 2(a ∥l 1,b ∥l 2),这两条相交直线所成的锐角(或直角)就是异面直线a ,b 所成的角.②范围:⎝⎛⎦⎤0,π2. (3)定理(等角定理)空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补. 3.空间中直线与平面、平面与平面的位置关系(1)空间中直线与平面的位置关系位置关系图形表示符号表示公共点直线a在平面α内aα有无数个公共点直线在平面外直线a与平面α平行a∥α没有公共点直线a与平面α斜交a∩α=A有且只有一个公共点直线a与平面α垂直a⊥α(2)空间中两个平面的位置关系位置关系图形表示符号表示公共点两平面平行α∥β没有公共点两平面相交斜交α∩β=l有一条公共直线垂直α⊥β且α∩β=a典例2、如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是()A B C D三、线面平行1.线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(简记为“线线平行⇒线面平行”)∵l∥a,aα,lα,∴l∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)∵l∥α,lβ,α∩β=b,∴l∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)∵a∥β,b∥β,a∩b=P,aα,bα,∴α∥β性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行∵α∥β,α∩γ=a,β∩γ=b,∴a∥b 1111①AD1∥BC1;②平面AB1D1∥平面BDC1;③AD1∥DC1;④AD1∥平面BDC1.四、线面垂直1.直线与平面垂直(1)定义:如果一条直线和一个平面内的任意一条直线都垂直,那么称这条直线和这个平面垂直.(2)定理文字语言图形语言符号语言判定定理如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直⎭⎪⎬⎪⎫aαbαl⊥al⊥ba∩b=A⇒l⊥α性质定理如果两条直线同垂直于一个平面,那么这两条直线平行⎭⎬⎫a⊥αb⊥α⇒ a∥b2.二面角(1)定义:从一条直线出发的两个半平面所组成的图形叫作二面角.这条直线叫作二面角的棱,这两个半平面叫作二面角的面.(2)二面角的度量——二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角.平面角是直角的二面角叫作直二面角.3.平面与平面垂直(1)定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.(2)定理文字语言图形语言符号语言判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直⎭⎬⎫l⊥αlβ⇒α⊥β性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直⎭⎬⎫α⊥βlβα∩β=al⊥a⇒l⊥αA.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面βB.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βC .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βD .如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l ,那么l ⊥γ 五、空间几何体的表面积与体积 1.多面体的表(侧)面积因为多面体的各个面都是平面,所以多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式 S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l三者关系S 圆柱侧=2πrl ――→r ′=r S 圆台侧=π(r +r ′)l ――→r ′=0S 圆锥侧=πrl名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =Sh 锥体(棱锥和圆锥) S 表面积=S 侧+S 底 V =13Sh台体(棱台和圆台)S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 31.正四面体的表面积与体积棱长为a 的正四面体,其表面积为3a 2,体积为212a 3. 2.几个与球有关的切、接常用结论 (1)正方体的棱长为a ,球的半径为R , ①若球为正方体的外接球,则2R =3a ; ②若球为正方体的内切球,则2R =a ;③若球与正方体的各棱相切,则2R =2a .(2)若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.(3)正四面体的外接球与内切球的半径之比为3∶1,棱长为a 的正四面体,其内切球半径R 内=612a ,外接球半径R 外=64a . 典例5、如图,将一个长方体用过相邻三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为________.强化训练一、单选题1.正四棱台的上、下底面边长分别为1cm,3cm 2cm ,则棱台的侧面积为( ) A .24cmB .28cmC .243cmD .23cm2.设a ,b 是两条不同的直线,,αβ是两个不同的平面,给出下列命题: ①若,,a b a b αβ⊥⊂⊂,则αβ⊥ ②若,,a b αβαβ⊂⊂∥,则a b ∥ ③若,,a b αβαβ⊂⊥∥,则a b ⊥ ④若,,a b a b αβ⊥⊥∥,则αβ∥ 其中为真命题的是( ) A .①②B .②③C .③④D .①④3.正方体1111ABCD A B C D -中,点M 在棱1DD 上,过点C 作平面1BMC 的平行平面α,记平面α与平面11BCC B 的交线为l ,则1A C 与l 所成角的大小为( )A .6πB .4π C .3π D .2π 4.如图,正方体1111ABCD A B C D -中,若E ,F ,G 分别是棱AD ,1C C ,11B C 的中点,则下列结论中正确的是( ) A .BE ⊥平面DFGB .1//A E 平面DFGC .//CE 平面DFGD .平面1//A EB 平面DFG5.以下结论中错误的是( ) A .经过不共面的四点的球有且仅有一个 B .平行六面体的每个面都是平行四边形 C .正棱柱的每条侧棱均与上下底面垂直D .棱台的每条侧棱均与上下底面不垂直6.已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为( ) A .4π B .2π C .23π D .π7.如图是一个长方体的展开图,如果将它还原为长方体,那么线段AB 与线段CD 所在的直线( )A .平行B .相交C .是异面直线D .可能相交,也可能是异面直线8.如图为一个三棱锥的三视图,则该三棱锥的体积为( )A .13B .23C .12D .439.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A .5B .4C .3D .210.“圆柱容球”是指圆柱形容器里放了一个球,且球与圆柱的侧面及上、下底面均相切,则该圆柱的体积与球的体积之比为( ) A .2 B .32C .3D .π3二、填空题11.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的外接球的表面积为________.12.已知圆锥的顶点为P ,母线PA ,PB 所成角的余弦值为34,PA 与圆锥底面所成角为60°,若PAB △的面积为7,则该圆锥的体积为______.13.某圆柱的侧面展开图是面积为8的正方形,则该圆柱一个底面的面积为___________. 14.如图,在棱长为2的正方体1111ABCD A B C D -中,E 是侧面11BB C C 内的一个动点,则三棱锥1D AED -的体积为_________.三、解答题15.如图,在三棱锥P ABC -中,底面ABC 是直角三角形,2AC BC ==,PB PC =,D 为AB 的中点.(1)证明:BC PD ⊥;(2)若3PA =,5PB =,求点A 到平面PDC 的距离.16.如图1,菱形ABCD 中,60A ∠=︒,4AB =,DE AB ⊥于E ,将AED 沿DE 翻折到A ED ',使A E BE '⊥,如图2.(1)求三棱锥C A BD -'的体积;(2)在线段A D '上是否存在一点F ,使EF ∥平面A BC '?若存在,求DFFA '的值;若不存在,说明理由.17.如图,在三棱锥P -ABC 中,底面ABC 是直角三角形,AC =BC =2,PB =PC ,D 为AB 的中点.(1)证明:BC⊥PD;(2)若AC⊥PB,PA=3,求直线PA与平面PBC所成的角的正弦值.。
专题二 第2讲 立体几何中的算、证、求问题

(3) 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD
=3,E为棱CD上一点,若三棱锥E-PAB的体积为4,则PA的长为____4____.
【解析】
(例1(3)))
因为△EAB的面积为S=
1 2
×2×3=3,所以三棱锥E-PAB的体积为V=
13×3×PA=4,所以PA=4.
第27页
栏目导航
(变式(2))
二轮提优导学案 ·数学
(2) 求证:平面BDM⊥平面ADEF. 【解答】 设DC=1,由题意知DC⊥BC,BC=1,BD= 2. 在梯形ABCD中,AB∥CD,所以∠ABD=∠BDC=45°. 因为AB=2DC=2, 所以在△ABD中,由余弦定理知 AD= AB2+BD2-2AB·BDcos∠ABD= 2. 因为AB=2,所以AD2+BD2=AB2, 所以∠ADB=90°,所以AD⊥BD.
【解析】 设圆柱的底面半径为R,则圆锥的底面半径也为R,圆柱和圆锥的高均为
h=2R.因为S1=2πR×2R=4πR2,圆锥的母线长为 R2+2R2= 5R,所以S2=12×2πR
×
5R=
5πR2,所以SS21=
5 4.
第10页
栏目导航
二轮提优导学案 ·数学
专题二 立体几何
(2) (2019·南方凤凰台密题)若正方体的棱长为 2,则以该正方体各个面的中心为顶
第31页
栏目导航
专题二 立体几何
二轮提优导学案 ·数学
专题二 立体几何
(2) 若∠ABC=60°,求证:平面PAB⊥平面PAE; 【解答】 因为底面ABCD是菱形且∠ABC=60°,所以△ACD为正三角形,又E为 CD的中点,所以AE⊥CD. 因为AB∥CD,所以AE⊥AB. 因为PA⊥平面ABCD,AE⊂ 平面ABCD, 所以AE⊥PA. 因为PA∩AB=A,PA,AB⊂ 平面PAB, 所以AE⊥平面PAB. 又AE⊂ 平面PAE,所以平面PAB⊥平面PAE.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何21. (2010 全国I 理)如图,四棱锥S-ABCD 中,SD ⊥底面ABCD ,2. AB ∥DC ,AD ⊥DC ,12AB AD DC SD ====,,E 为棱3. SB 上的一点,平面EDC ⊥平面SBC . (Ⅰ)证明:2SE EB =;(Ⅱ)求二面角--A DE C 的大小.2. (2010 全国II 理)如图,直棱柱111ABC A B C -中,AC BC =,1A A AB =,D 为1BB 的中点,E 为1AB 上的一点,13AE EB =. (I )证明:DE 为异面直线1AB 与CD 的公垂线;(II )设异面直线1AB 与CD 的夹角为45°, 求二面角111A AC B --的大小. 3. (2010 四川理) (本小题满分12分)已知正方体ABCD A B C D -''''的棱长为1,点M 是 棱AA '的中点,点O 是对角线BD '的中点. (Ⅰ)求证:OM 为异面直线AA '和BD '的公垂线; (Ⅱ)求二面角M BC B -'-'的大小; (Ⅲ)求三棱锥M OBC -的体积.4. (2010 天津理) 如图,在长方体1111ABCD A B C D -中,E 、F 分别是棱BC ,1CC 上的点,2CFAB CE ==,1::1:2:4AB AD AA =.(Ⅰ)求异面直线EF 与1A D 所成角的余弦值; (Ⅱ)证明AF⊥平面1A ED ;(Ⅲ)求二面角1A ED F --的正弦值. 5. (2006 安徽理) (本小题满分12分)如图,P 是边长为1的正六边形ABCDEF 所在平面外一点,1PA =,P 在平面ABC 内的射影为BF 的中点O .(1)证明PA BF ⊥;(2)求面APB 与面DPB 所成二面角的大小. 6. (2006 北京理) (本小题共14分) 如图,在底面为平行四边形的四棱 锥P ABCD -中,AB AC ⊥,SCABEDCAE D C 1BB 1A 1D 'A BCDMOA 'B 'C 'A 1B 1C 1D 1 A BCD EFCAP EDBF O P BCAEDPA ⊥平面ABCD ,且PA AB =, 点E 是PD 的中点.(Ⅰ)求证:AC PB ⊥;(Ⅱ)求证:PB ∥平面AEC ;(Ⅲ)求二面角E AC B --的大小.7. (2006 四川理)如图,在长方体1111ABCD A B C D -中,E P ,分别是11BC A D ,的中点,M N ,分别是1AE CD ,的中点,1AD AA a ==,2AB a =.(I )求证:1ADD MN A 1面∥; (II )求二面角P AE D --的大小; (III )求三棱锥P DEN -的体积. 111ABC A B C -8. (2006 全国II 理)如图,在直三棱柱中,AB BC =,D ,E 分别为11BB AC ,的中点.(I )证明:ED为异面直线1BB 与1AC 的公垂线;(II )设12AA AC AB ==,求二面角11A AD C --的大小.9. (2006 浙江理) 如图,在四棱锥P ABCD -中,底面为直角梯形,AD BC ∥,90BAD ∠=,PA ⊥底面ABCD ,且2PA AD AB BC ===,M N ,分别为PC PB ,的中点. (Ⅰ)求证:PB DM ⊥;(Ⅱ)求CD 与平面ADMN 所成的角.10. (2007 天津理)如图,在四棱锥P ABCD -中 ,PA ⊥底面ABCD , 60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点. (Ⅰ)证明CD AE ⊥;(Ⅱ)证明PD ⊥平面ABE ; (Ⅲ)求二面角A PD C --的大小.11. (2009 全国II 理) (本小题满分12分) 如图,直三棱柱ABC,,D 、E 分别为、的中点,平面.(Ⅰ)证明:=; (Ⅱ)设二面角为,求与平面BCD 所成角的大小.10}2B -=<+A B ={}2|log 2A x x =≤()B a =-∞,A B ⊆a()c +∞,c ={|1}A x x =≤{|}B x x a =≥A B R=aA =-≤B xx =-+≥A B =∅A B ⊆ABCDEA 1 C 1B 1DEC BA12. (2009 海南理)如图,四棱锥S-ABCD 的底面是正方形 ,每条侧棱的长都是地面边长的2倍,P 为侧棱SD 上的点.(Ⅰ)求证:AC ⊥SD ;(Ⅱ)若SD ⊥平面PAC ,求二面角P-AC-D 的大小; (Ⅲ)在(Ⅱ)的条件下,侧棱SC 上是否存在一点E ,使得BE ∥平面PAC .若存在,求SE ∶EC 的值;若不存在,试说明理由.13. (2008 全国I 理) (本小题满分12分) (注意:在试题卷上作答无效.........) 四棱锥A BCDE -中,底面BCDE 为矩形,侧面ABC ⊥底面BCDE ,2BC =,2CD =,AB AC =.(Ⅰ)证明:AD CE ⊥;(Ⅱ)设CE 与平面ABE 所成的角为45,求二面角C AD E --的大小.14. (2008 全国II 理)如图,正四棱柱1111ABCD A B C D -中,124AA AB ==,点E 在1CC 上且EC E C 31=.(Ⅰ)证明:1A C ⊥平面BED ;(Ⅱ)求二面角1A DE B --的大小.15. (2009 湖南理) (本小题满分12分) 如图,在正三棱柱111ABC A B C -中,12AB AA =,点D 是11A B 的中点,点E 在11A C 上,且DE AE ⊥.(I )证明:平面ADE平面;(II )求直线AD 和平面1ABC 所成角的正弦值.16. (2009 江苏) 如图,在直三棱柱111ABC A B C -中,E F ,分别是11A B A C ,的中点,点D在11B C 上,11A D B C ⊥. 求证:(1)EF ∥平面ABC ;xx ,≤{}|1x x ≥CDE AB SPDCA BAB CD EA 1B 1C 1D 1 A 1B 1C 1CBA E DACA 1BC EFD(2)111A FD BB C C ⊥平面平面.17. (2009 山东理) 如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为等腰梯形,AB CD ∥,4AB =,2BC CD ==,12AA =,E ,1E ,F 分别为棱AD ,1AA ,AB 的中点.(Ⅰ)证明:直线1EE ∥平面1FCC ; (Ⅱ)求二面角1B FC C --的余弦值.18. (2009 陕西理)如图,在直三棱柱111ABC A B C -中,1AB =,13AC AA ==,60ABC ∠=°.(Ⅰ)证明:1AB A C ⊥;(Ⅱ)求二面角1A A C B --的大小.19. (2009 上海理) 如图,在直三棱柱111ABC A B C -中,12AA BC AB ===,AB BC ⊥,求二面角111B AC C --的大小.20. (2009 天津理) 如图,在五面体ABCDEF 中,FA ⊥平面ABCD ,AD BC FE AB AD M ⊥∥∥,,为EC 的中点,1.2AF AB BC FE AD ====(Ⅰ)求异面直线BF 与DE 所成的角的大小; (Ⅱ)证明平面AMD ⊥平面CDE ; (Ⅲ)求二面角A CD E --的余弦值.21. (2009 重庆理)如题(19)图,在四棱锥中,且;平面平面,;为的中点,.求:(Ⅰ)点到平面的距离; (Ⅱ)二面角的大小.{}|()0M x f x =<{}|()0P x f x '=>MP a(1)-,∞(01),(1)+,∞[)1+,∞|2xxa xxb -<∈->∈R R ,,,⊆3a b +≤||3a b +≥||3a b -≤A 1 D 1C 1B 1BAED CFE 1A CBA 1 C 1B 1A 1B 1C 1CBA FEDCMA BEA DSCB22. (2009 全国I 理) (本小题满分12分) 如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD =,2DC SD ==,点M 在侧棱SC 上,60ABM ∠=°.(Ⅰ)证明:M 是侧棱SC 的中点; (Ⅱ)求二面角S AM B --的大小.23. (2008 天津理) 如图,在四棱锥P ABCD -中,底面ABCD 是矩形.已知3AB=,2AD =,2PA =,22PD =,60PAB =∠.(Ⅰ)证明AD ⊥平面PAB ;(Ⅱ)求异面直线PC 与AD 所成的角的大小; (Ⅲ)求二面角P BD A --的大小. 24. (2008 浙江理) 如图,矩形ABCD 和梯形BEFC 所在平面互相垂直,BE CF ∥,90BCF CEF ∠=∠=,3AD =,2EF =.(Ⅰ)求证:AE ∥平面DCF ; (Ⅱ)当AB 的长为何值时,二面角A EF C --的大小为60?25. (2007 海南宁夏理)如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形,90BAC ∠=°,O 为BC 中点. (I )证明:SO ⊥平面ABC ;(II )求二面角A SC B --的余弦值.26. (2007 全国I 理) 四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD .已知45ABC =∠,2AB =,22BC =,3SA SB ==.(Ⅰ)证明SA BC ⊥;(Ⅱ)求直线SD 与平面SAB 所成角的大小.27. (2007 全国II 理) (本小题满分12分)如图,在四棱锥S ABCD -中,底面ABCD 为正方形, 侧棱SD ⊥底面ABCD E F ,,分别为AB SC ,的中点. (1)证明EF ∥平面SAD ;(2)设2SD DC =,求二面角A EF D --的大小.28. (2007 陕西理) (本小题满分12分)如图,在底面为直角梯形的四棱锥P ABCD -中,90AD BC ABC ∠=,∥°,PA ⊥平面SMCB A DA BCDP DABE FCDBCASABCD .42236PA AD AB BC ====,,,.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)求二面角P BD A --的大小.29. (2007 四川理) (本小题满分12分)如图,PCBM 是直角梯形,9012PCB PM BC PM BC ∠===,∥,,,又1AC =,120ACB AB PC ∠=,⊥,直线AM 与直线PC 所成的角为60.(Ⅰ)求证:平面PAC ⊥平面ABC ; (Ⅱ)求二面角M AC B --的大小;(Ⅲ)求三棱锥P MAC -的体积.30. (2007 浙江理) (本题14分)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点. (I )求证:CM EM ⊥;(II )求CM 与平面CDE 所成的角.ACBMP。
