电路理论基础课后答案(哈工大陈希有)第11章
哈工大电路理论基础课后习题答案1

i2 3A 0.5A 2.5A
节点②:
i1 i2 i3 2.5A 2A 4.5A
对回路 l 列 KVL 方程:
10 i2 5 3A u 8V
得
u 32V 电压源发出的功率
P US 8V i1 8V 4.5A 36W
得
u2 280V
网络 N 吸收的功率
PN uN 3A 30W
电流源发出的功率
P iS u2 5A 1400W
注释:根据电流源的特性, 图中与电流源串联的电阻只影响电流源端电压或者说 只影响电流源提供的功率。 答案 1.11 解:设各元件电压电流方向如图所示。
i2 3A 0.5A 2.5A
i2 8A 3A 1A 2A 4A
① 1A
A
⑤
i2
3A
8A
i1
i3 ④ ② i4
2A
B
③ (b)
答案 1.5 解:如下图所示
5V i1
②
l3 1A
①
2A
l1 l2
7V
1A
i4
⑤ 1A ③
6V
l4 8V
i2
④
i3
(1)由 KCL 方程得 节点①:
i1 2A 1A 3A
①
i1 10 + 5A 5 u2 l2 10V l1 -
3A
50
N
25V
对节点①列 KCL 方程
i1 5A 3A 2A
对回路列 KVL 方程 回路 l1 :
i1 10 3A 5 uN 25V 10V
电路理论基础(陈希有)习题解答10-14

uC (0 ) uC (0 ) 24V iL (0 ) iL (0 ) 2A
由 KVL 得开关电压:
6
6 3
Ri
u(0 ) uC (0 ) 8 iL (0 ) (24 8 2)V 8V
(b)
答案 10.3 解: t 0 时电容处于开路, i 0 ,受控源源电压 4i 0 ,所以 等 效 电 阻
由换路定律得:
t0
4 4
时 电 感 处 于 短 路 , 故
Ri
(b)
8
3 i L (0 ) 9A 3A ,由换路定律得: 63 iL (0 ) iL (0 ) 3A
求等效电阻的电路如图(b)所示。 ,
等效电阻
Ri (4 // 4) // 8 1.6
时间常数
求稳态值的电路如图(b)所示。 i ( ) 2 2 10V 3 3 4 Ri iL ( ) 4 2 2
(b) (c)
(b)
Ri (
时间常数
6 3 3 1.5 )k 3k 6 3 3 1.5
3 6 3
答案 10.13
解:当 t 0 , r 列 KVL 方程得:
-1-
答案 10.1
解: t
0 时,电容处于开路,故 uC (0 ) 10mA 2k 20V
t 0 时,求等效电阻的电路如图(b)所示。
i 6 3 4i
iL (t ) iL (0 )e t / 3e 2t A (t 0)
电感电压
由换路定律得:
u1 (t ) L
由换路定律得
L / Ri 0.5s
由三要素公式得: 解 得 A 答案 10.9 解:当 t 原始值
(整理)电路理论基础(梁贵书)第11章答案

第十一章习题解答11-1周期性矩形脉冲如图所示,试求其傅立叶级数展开形式。
t解:02212w T πππ=== 00011()22T m m U a f t dt U dt T πππ===⎰⎰ 00002211()cos 2cos sin 0Tm k m U a f t kw tdt U ktdt ktT kππππ=⋅===⎰⎰0002()sin 12sin 2211()cos ()(cos 1)21cos 41,3,5,00,2,4,Tk m mm m mb f t kw tdtT U ktdt U U kt k k k U k k U k k k πππππππππ=⋅===⋅⋅----=⎧=⎪=⎨⎪=⎩⎰⎰ ∴14mU b π=,343m U b π=,54,5mU b π=0135()sin sin 3sin 5444sin sin 3sin 5354111(sin sin 3sin 5sin 7)357mmm m m m f t a b t b t b t U U U Ut t t U U t t t t ππππππ=++++=++++=+++++11-3在图示电路中,无源一端口网络N 的 端口电压和端口电流分别为()100cos31450cos(94230)V u t t t ︒=+- 3()10cos314 1.75cos(942)A i t t t θ=++若把N 看作为RLC 串连电路,试求:(1)R,L,C 之值;(2)3θ之值;(3)电路消耗的功率。
解:(1)13()100cos31450cos(94230)()()u t t t u t u t ︒=+-=+313()10cos314 1.75cos(942)()()i t t t i t i t θ=++=+∵1()100cos314u t t =,∴.10V U ︒=∵1()10cos314i t t =,∴.10A I ︒=∵.1U 与.1I 同相,∴LC 串连分支对基波而言发生 串连谐振,∴.1.1100U R I ︒===Ω21314314C L =⇒= ∵3()50cos(94230)V u t t ︒=-,∴.330U ︒=-,3U = 33() 1.75cos(942)i t t θ=+,∴.33A I θ=∴333501.75U Z I ==== ∴22110(942)816.33942L C+-= 21(942)716.33942L C -= 194226.76942L C -=(∵w 时谐振,∴3w 时呈感性)∵21314C L =∴2194226.761942314L L -= 31494226.763LL -=∴31.9mH L =231317.94F 31431.910C μ-==⨯⨯(2)∵.330V U ︒=-,.33I θ= 33611(942)10(94231.910)942942317.941010(30 3.34)28.4769.44Z R j L j C j --︒=+-=+⨯⨯-⨯⨯=+-=∠Ω .3333.333028.4769.44U U Z I I θ︒︒==∠--≈∠ ∴33069.44θ︒︒--=∴33069.4499.44θ︒︒︒=--=-(3)1︒1()100cos314V u t t =单独作用时,1()10cos314A i t t =∴221110500W P I R =⨯=⨯= 2︒ 3()50cos(94230)V u t t ︒=-单独作用时,3() 1.75cos(94299.44)A i t t ︒=-2233101015.31W P I =⨯=⨯=1350015.31515.31W P P P =+=+=11-10图示电路为滤波电路,要求14w 的谐波电流传至负载,而使基波电流无法达到负载。
哈工大电路原理基础课后习题集

第一章习题1.1 图示元件当时间t<2s时电流为2A,从a流向b;当t>2s时为3A,从b流向a。
根据图示参考方向,写出电流的数学表达式。
1.2图示元件电压u=(5-9e-t/τ)V,τ>0。
分别求出t=0 和t→∞时电压u的代数值及其真实方向。
图题1.1 图题1.21.3 图示电路。
设元件A消耗功率为10W,求;设元件B消耗功率为-10W,求;设元件C发出功率为-10W,求。
图题1.31.4求图示电路电流。
若只求,能否一步求得?1.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压u14、u15、u52、u53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知,,,。
求各元件消耗的功率。
1.7 图示电路,已知,。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压。
1.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N吸收的功率和电流源发出的功率。
1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W,求r的值。
1.14 求图示电路受控源和独立源各自发出的功率。
1.15图示电路为独立源、受控源和电阻组成的一端口。
试求出其端口特性,即关系。
1.16 讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响,加深对独立源特性的理解。
第二章习题2.1 图(a)电路,若使电流A,,求电阻;图(b)电路,若使电压U=(2/3)V,求电阻R。
2.2 求图示电路的电压及电流。
2.3 图示电路中要求,等效电阻。
求和的值。
2.4求图示电路的电流I。
2.5 求图示电路的电压U。
2.6 求图示电路的等效电阻。
2.7 求图示电路的最简等效电源。
图题2.72.8 利用等效变换求图示电路的电流I。
电工电子学第十一章习题答案
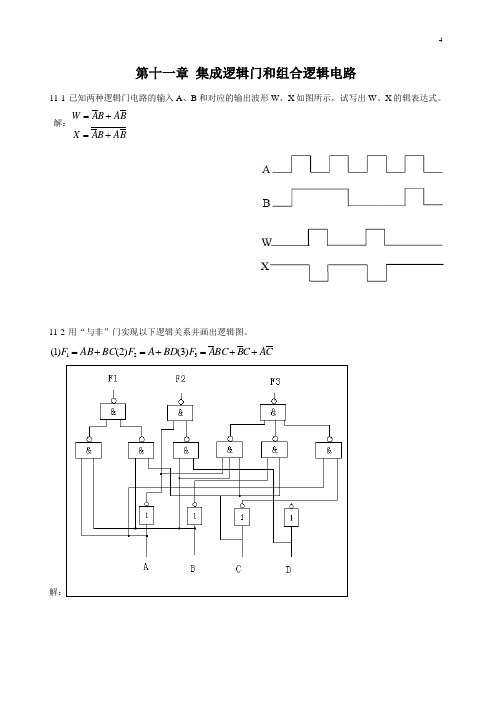
第十一章 集成逻辑门和组合逻辑电路11-1 已知两种逻辑门电路的输入A 、B 和对应的输出波形W 、X 如图所示,试写出W 、X 的辑表达式。
解:BA B A X B A B A W +=+=11-2 用“与非”门实现以下逻辑关系并画出逻辑图。
C A C B BC A F BD A F BC AB F ++=+=+=321)3()2()1(解:CA CB BC A C A C B BC A F BDA BD A F BC AB BC AB F ••=++=•=+=•=+=32111-3 用代数法化简下列逻辑函数:① F=A B +AB+BC ,② F=B A C+A+B+C ,③ F=ABC+A B+AB C 解:① F=A+BC② F=B A C+A+B+C=A+B+C③ F=ABC+A B+AB C =B 11-4 试分析图示电路的逻辑功能解:(1)0=•=B A B A F(2)B A B A B A B B A A AB B AB A AB B AB A F +=+•++•=•+•=•••=)()(此为异或门,其真值表为 右图(3)C B A L ⊕⊕==m 0+m 3+m 5+m 6 逻辑功能为 :全加器和的反码的逻辑表达式 (4)7421m m m m C B A F +++=⊕⊕= 逻辑功能为 :全加器和的逻辑表达式 此两式的真值表图如右下图11-5 组合逻辑电路如图所示,试求输出函数的最简逻辑表达式并画出改用“与非”门实现的逻辑电路图 解:C B A C A C A B A C A AB F ++=+++=⊕+= ;改成与非门:C B A C B A F ••=++=11-6 按少数服从多数的原则,试设计一个三人表决电路,并用“或非”门实现。
解:(1)按题意:输入变量有三个分别为、B、C;输出变量有一个为F。
列出真值表如下图(2)写出逻辑表达式上弟即或非-或非蠨达弟ȍH11-7 用耳线-8线译码周74LS138和适当的“与非”门设计一个奇偶校验电路,要籂弓输入三个变量䨭有偶数个1时输出为1,否则为0解:(1)按题意:输入变量有三个分别为A、B、C;输出变量有一个为F。
电路理论基础课后习题答案 陈希有主编 第十到十四章

答案10.1解:0<t时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A3)363685(V45)0(=Ω+⨯++=-i,A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得:V24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i由KVL 得开关电压:V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解:<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
电路理论习题答案第11章

第十一章习题解答11-1周期性矩形脉冲如图所示,试求其傅立叶级数展开形式。
t解:02212w T πππ=== 00011()22T m mU a f t dt U dt T πππ===⎰⎰ 00002211()cos 2cos sin 0T m k m U a f t kw tdt U ktdt ktT kππππ=⋅===⎰⎰0002()sin 12sin 2211()cos ()(cos 1)21cos 41,3,5,00,2,4,Tk m mm m mb f t kw tdtT U ktdtU U kt k k k U k k U k k k πππππππππ=⋅===⋅⋅----=⎧=⎪=⎨⎪=⎩⎰⎰ ∴14mU b π=,343mU b π=,54,5mU b π=0135()sin sin 3sin 5444sin sin 3sin 5354111(sin sin 3sin 5sin 7)357mmm m m m f t a b t b t b t U U U Ut t t U U t t t t ππππππ=++++=++++=+++++11-3在图示电路中,无源一端口网络N 的 端口电压和端口电流分别为()100cos31450cos(94230)V u t t t ︒=+-3()10cos314 1.75cos(942)A i t t t θ=++若把N 看作为RLC 串连电路,试求:(1)R,L,C 之值;(2)3θ之值;(3)电路消耗的功率。
解:(1)13()100cos31450cos(94230)()()u t t t u t u t ︒=+-=+313()10cos314 1.75cos(942)()()i t t t i t i t θ=++=+∵1()100cos314u t t =,∴.10V U ︒=∵1()10cos314i t t =,∴.10A I ︒=∵.1U 与.1I 同相,∴LC 串连分支对基波而言发生 串连谐振,∴.1.1100U R I ︒===Ω21314314C L =⇒= ∵3()50cos(94230)V u t t ︒=-,∴.330U ︒=-,3U = 33() 1.75cos(942)i t t θ=+,∴.33A I θ=∴333501.75U Z I ====∴22110(942)816.33942L C+-=21(942)716.33942L C -=194226.76942L C -=(∵w 时谐振,∴3w 时呈感性)∵21314C L =∴2194226.761942314L L -= 31494226.763LL -=∴31.9mH L =231317.94F 31431.910C μ-==⨯⨯(2)∵.330V U ︒=-,.33I θ=33611(942)10(94231.910)942942317.941010(30 3.34)28.4769.44Z R j L j C j --︒=+-=+⨯⨯-⨯⨯=+-=∠Ω .3333.333028.4769.44U U Z I I θ︒︒==∠--≈∠ ∴33069.44θ︒︒--=∴33069.4499.44θ︒︒︒=--=-(3)1︒1()100cos314V u t t =单独作用时,1()10cos314A i t t =∴221110500W P I R =⨯=⨯=3()50cos(94230)V u t t ︒=-单独作用时,3() 1.75cos(94299.44)A i t t ︒=-2233101015.31W P I =⨯=⨯=1350015.31515.31W P P P =+=+=11-10图示电路为滤波电路,要求14w 的谐波电流传至负载,而使基波电流无法达到负载。
电路分析第十一章习题参考答案
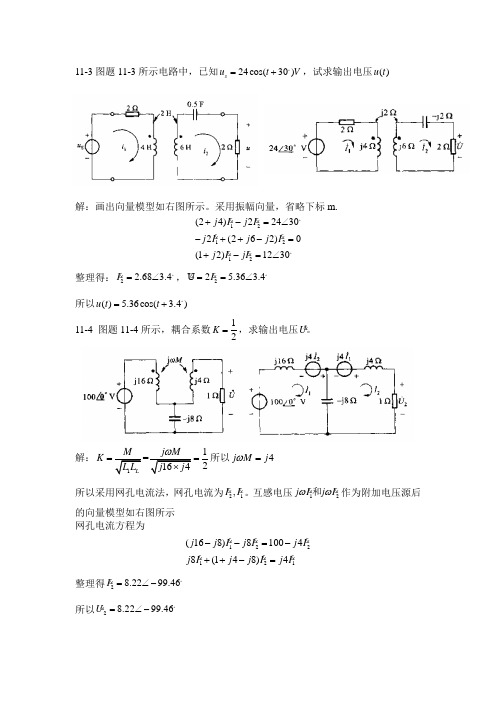
11-3图题11-3所示电路中,已知24cos(30)s u t V =+。
,试求输出电压()u t解:画出向量模型如右图所示。
采用振幅向量,省略下标m.121212(24)224302(262)0(12)1230j I j I j I j j I j I jI +-=∠-++-=+-=∠ 。
整理得:2 2.68 3.4I =∠ 。
,2U 2 5.36 3.4I ==∠ 。
所以() 5.36cos( 3.4)u t t =+。
11-4 图题11-4所示,耦合系数12K =,求输出电压U 。
解:12K ==所以4j M j ω= 所以采用网孔电流法,网孔电流为21,I I 。
互感电压12j I j I ωω 和作为附加电压源后的向量模型如右图所示网孔电流方程为122121(168)810048(148)4j j I j I j I j I j j I j I --=-++-= 整理得28.2299.46I =∠- 。
所以28.2299.46U =∠- 。
11-8电路图题11-8所示,试求对电源端的输入阻抗、电流12I I 和。
解:列网孔方程1212(24)21202(22)0j I j I j I j I +-=∠-++= 。
整理得12(22),2I j A I A =-= 所以12Z (33)22i j j =Ω=+Ω- 11-9 已知空心变压器的参数:1122L =9H,R =200,L =4H,R =1000.5.k ΩΩ=及所接负载为800Ω电阻和1F μ电容串联,所接正弦电压源频率为400rad/s, 电压有效值为300V ,内阻为500,Ω内电感为0.25H .试求传送给负载的功率P 和空心变压器的功率传输效率。
解:(1)可以画出电路如上图所示。
M=3H =做出向量模型后可以列出网孔方程为1212(500200100300)12003001200(10080016002500)0j j I j I j I j j I +++-=-+++-=整理得1271.56A 0.0596116.6A 50I I -==∠- 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题11.1 根据定义求和的象函数。
解: (1)(2)题11.2设求的象函数。
解:由拉氏变换的微分、线性和积分性质得:题11.3设(t 为纯数)。
分别求对应象函数、、,验证卷积定理。
解:设 , 则与的卷积为)()(t t t f ε=)(e )(t t t f atε-=2020001e 1e 1e e )()(-ss dt s s t dt t t s F stst st st=-=+-==∞-∞-∞-∞----⎰⎰ε20)(20)(00)(1e )(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dt s s t dt t t s F t s t s st st t ξξετd f c t bf tt f a t f f t A t f t t )()(d )(d )(,0)0(),()e 1()(011121/1⎰-++==-=--)(2t f )(2s F )/1(//1)(1τττ+=+-=s s A s A s A s F )/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F )()()(,e 2)(,e 5)(215221t f t f t f t f t f tt *===--)(1s F )(2s F )(s F 25)}({)(11+==s t f s F L 52)}({)(22+==s t f L s F )5)(2(10)()(21++=s s s F s F )(1t f )(2t f对上式取拉氏变换得:由此验证。
题11.4求下列函数的原函数。
(a) (b)(c)解:(a), 所以(b)所以)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221tt t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L )()()}(*)({2121s F s F t f t f =L 6512)(2+++=s s s s F)2)(1(795)(23+++++=s s s s s s F 623)(2++=s s s F 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A 3|31221-=++=-=s s s A tt s s t f 321e 5e 3}3523{)(---+-=+++-=L )2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A tt t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)查表得题11.5分别求图示(a)、(b)电路的等效运算阻抗或等效运算导纳。
图题11.5解:(a) 由运算电路(略)求得端口等效运算阻抗为:, (b) 画出运算电路如图11.5(c)所示在端口加电流,列写节点电压方程如下由式(2)解得代入式(1)得所以623)(2++=s s s F 22)5()1(5)5/3(++⨯=s )5sin(e 53)(t t f t -=H5.011262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z 112611430)(22++++=s s s s s Z i U )(2s __⎩⎨⎧-==++-=-+)2()]()([3)(3)()]5.0/(11[)()1()()()()1(2122s U s U s U s U s s U s I s U s U s )(144)(2s U s s s U ⨯+=)()()1221(s I s U s ss =+-+1212)(2i+++=s s s s Y题11.6图(a)所示电路,设电感电压零状态响应象函数为,求电源电压[用表示]。
图题11.6解:运算电路如图11.6(b)所示。
化简得题11.7图示电路,已知V ,求零状态响应。
解:)(s U L )(S s U )(s U LL u)(s U L (S s U bss U s I L L 3)()(=)()/21()()(6)(1s U s s U s I s U L L L +=+=)(/5.04/21)2/(14)()(12s U ss s s U s I L++=+=)(]/5.04/212132[)()]()([2)(12S s U sss s s U s I s I s U LL +++++=++=)()18(389136)(2S s U s s s s s U L+++=)(e 2S t u tε-=u u -+u 图题11.7由运算电路 (略)并利用分压公式求得电容电压象函数为:式中, 所以V题11.8图(a)所示电路,已知,求零状态响应。
图题11.8解:电容和电感的初始储能均为零,,画出运算电路如图11.8 (b) 所示。
由分流公式求得电容电压象函数为:式中21)](e [)(2+==-s t s U tSεL 23/1)2)(3/1()3/2()(222212222)(21+++=++=⨯+⨯++⨯=s A s A s s s s U ss s ss U SVs 152|2)3/2(3/11-=+=-=s s s A Vs 8.0|3/1)3/2(22=+=-=s s sA ]e )15/2(e 8.0[)(3/2t t t u ---=A )(S t i ε=C u.0s s I /1)(S=(b )(sU C )(s 233)()5.0/(133)(2S ++=⨯++=s s s I s s s I C )2)(1(65.01)()(++=⨯=s s s s s I s U CC 21321++++=s A s A s A Vs 3|)2)(1(61=++==s s s A所以V 题11.9图(a)所示电路,开关接通前处于稳态。
已知, 。
求开关接通后电容电压u 。
图题11.9解:由图(a)得:, 运算电路如图11.9(b)所示。
列写节点电压方程如下:解得:各待定系数为Vs 6|)2(612-=+=-=s s s A Vs 3|)1(623=+=-=s s s A )()e 3e 63()}({)(21t s U t u tt CC ε---+-==L ,2,V 2,V 1121Ω===R U U Ω==432R R F 2.0,H )6/5(==C L1U 2V 1)0(1==-U u A 25.0/)0(21==-R U iL s/(b)6/524/5/5/14/21)6/5121()()6/512.0414121(s s s s s s s U s s ++=⨯+-++++32)65(625.6)(32122++++=++++=s A s A s A s s s s s s U Vs 1|)3)(2(625.6021=++++==s s s s s A所以V题11.10图示电路在零状态下,外加电流源,已知G =2S ,L =1H ,C =1F 。
试求电压。
解:由运算电路(略)求得并联电路运算导纳电流源象函数电压象函数反变换得题11.11图(a)所示电路中外加阶跃电压,已知C 1=0.3F ,C 2=0.7F ,R =10Ω。
求零状态响应电压及电流。
Vs 25.1|)3(625.6222=+++=-=s s s s s A Vs 1|)3)(2(625.6021=++++==s s s s s A )e 25.1e 25.11()}({)(321tt s U t u ----+==L A )(e )(3St t i tε-=)(t u )图题11.10ss s s s sC sL G s Y 12121)(2++=++=++=31)}(e {)(3S+==-s t s I tεL 3Vs 75.01Vs 75.0)1(Vs 5.0)3)(12()()()(22S+-++++-=+++==s ss s s s s s Y s I s U V )()]e e (75.0e 5.0[)}({3-1t t s U u tt t ε----+-==L V )(9)(St t u ε=)(2t u )(2t i图题11.11解:运算电路如图(b)所示图中由节点电压法得解得反变换得题11.12图(a)所示电路开关断开前处于稳态。
求开关断开后电路中、及的变化规律。
)(t )(2s (S s U ss U 9)(S =)()()1(S 1221s U sC s U sC sC R=++1.07.2)(2+=s s U 1.0189.089.11.089.1)()(222+-=+==s s s s U sC s I V )(εe 7.2)}({)(1.0212t s U t u t--==L A )](e 189.0)(δ89.1[)}({)(1.0212t t s I t i tε---==L 1i 1u 2u (a)图题11.12解:时电路处于直流稳态,由图(a)求得:, t >0时的运算电路如图(b)所示。
对回路列KVL 方程得解得所以反变换得(t >0)题11.13图(a)所示电路A ,,V , A 求的变化规律。
0<t A 210V 20)0(1=Ω=-i A 110V10)0(2=Ω=-i (b)ss s I s s 103420)()103210(1--+=+++43.05.0)4(2.02)(1+-=++=s s s s s s I 44.26.34)(2)(11++-=-=s s sI s U 46.36.33)(3)(12++=+=s s sI s U A )e 3.05.0()}({)(4111ts I t i ---==L V )(e 4.2)(δWb 6.3)}({)(41-11t t s U t u t ε-+⨯-==L V)(e 6.3)(δWb 6.3)}({)(4212t t s U t u tε--+⨯==L )(3S t i ε=)(Wb 2S t u δ⨯=1)0(=-C u 2)0(=-L i C u图 题11.13解:画出运算电路如图(b)所示,列写节点电压方程如下:解得:式中, 反变换得题11.14图(a)所示电路开关接通前处于稳态,已知,,,。
