Dependence of critical level statistics on the sample shape
索引中的页码为英文原书页码

索引索引中的页码为英文原书页码,与书中页边标注的页码一致AA.R.E.(asymptotic relative efficiency)(渐近相对效率),112of Cox and Stuart test(Cox 和Stuart检验), 175, 323of Daniel test(Daniel检验), 322of Durbin test(Durbin检验), 394of Frieaman test(Frieaman检验), 379of Kendall’s tau, 327of Kruskal-Wallis test(Kruskal-Wallis检验), 287of Mann-Whitney test(Mann-Whitney检验), 284of median test(中位数检验), 285, 297of paired t test(配对t检验), 364of Quade test(Quade检验), 380of quantile test vs. one-sample t test(分位数检验对一样本t检验), 148of rank test for slope(斜率的秩检验), 342of sign test(符号检验), 363of sign test vs. t test(符号检验vs. t检验), 164,175of sign test vs. Wilcoxon signed ranks test(符号检验vs. Wilcoxon符号秩检验),164, 175 of Spearman’s rho,327of squared ranks test(平方秩检验), 309of two-sample t test(两样本t检验), 284of Wilcoxon signed ranks test(Wilcoxon符号秩检验), 363acceptance region(接受域), 98aligned-rank methods(秩排列方法),384, 385alternative hypothesis(备择假设),95alternatives, ordered(备择的,次序的), 297analysis of covariance(方差分析), 297analysis of covariance,one-way(方差分析,一种方式), 222, 297approximate confidence interval for μ(μ的近似置信区间), 85approximation formulas for tolerance limits(容忍限逼近公式), 151, 155 approximation, normal(逼近,正态):to binomial distribution(二项分布), 58to sum of ranks(秩和), 58approximations to chi-squared distribution(χ2分布近), 62asymptotic relative efficiency, (see also A. R. E)(渐近相对效率), 112asymptotically distribution-free methods(渐近分布自由方法), 117Bbiased estimators for σ, 85 σ的有偏估计量biased test, 108 有偏检验binomial coefficient, 9, 11 二项系数binomial distribution, 28 二项分布mean and variance in, 49 均值和方差normal approximation to, 58 正态逼近tables of the, 513-524 表格tests based on the, 123 基于…的检验binomial expansion, 11 二项展开binomial test, 104, 124 二项检验power of, 127 功效bioassay, 119 生物鉴定bivariate random variable, 72 二维随机变量block design, incomplete, 387 区组设计,不完全的randomized complete, 251, 368 完全随机化blocks, multiple comparisons with complete, 371, 375 区组, 完全多重比较bootstrap, 349 bootstrapbootstrap method of estimation, 86 估计的bootstrap方法censored data, 297 删失数据censored sample, 155, 285 删失样本central limit theorem, 57, 85 中心极限定理centroid, 36 重心chi-squared approximation to Kruskal-Wallis test, 295 χ2近似Kruskal-Wallis检验chi-squared approximation distribution function, 54, 59 分布函数的χ2逼近approximations to, 62 逼近到…tables, 512 表格chi-squared goodness-of-fit test, 239, 240, 429, 430, 442, 443 χ2拟合优度检验chi-squared random variables, sum of, 62 χ2随机变量,和chi-squared test: χ2检验for differences in probabilities, 180, 199 概率差异with fixed marginal totals, 209 固定边缘总和for independence, 204 独立性circular distributions, 285, 364 圆周分布cluster analysisi, 419 聚类分析Cochran test, 250 Cochran检验Cochran’s criteria for small expected values, 202 对小期望值的Cochran准则confidence, 83 置信multinomial, 9, 12 多项式coefficient of concordance, Kendall’s, 328, 380 一致性系数,Kendall’s comparisons, multiple: 对比,多重with complete blocks, 371, 375 完全区组incomplete blocks, 390 不完全区组with independent sample, 290, 297, 398 独立样本in test for variances, 304 方差检验complete block design, randomized, 368 完全区组设计,随机化completely randomized design,222 完全随机化设计composite hypothesis, 97 复合假设computer simulation to find null distribution, 446, 447 计算机模拟求零假设分布concordance between blocked rankings, 385 区组秩间的一致性condorance, Kendall’s coefficient of, 328, 382 一致性, Kendall 系数concordant pairs, 319 不和谐配对conditional probability, 17, 23, 24 条件概率conditional probability function, 29 条件概率函数confidence band for a distribution function,438 分布函数置信界confidence coefficient, 83, 114, 129 置信系数for the difference between two means, 281 两均值差异for a mean, parametric, 149 均值,参数for the median difference, 360 中位差异for μ, approximate, 85 对于μ, 逼近for a probability or population proportion, 130 对于概率或总体比例exact tables for, 525-536 精确表格for a quantile, 135, 143 分位数one-sided, 153 单边for a slope, 335 斜率conservative test, 113 保守检验consistent, 117 相合的consisitent sequence of tests, 106, 108, 160 检验的相合序列consistent, sign test, 163 相合,符号检验contingency coefficient 列联系数:Cramér’s, 229 CramérPearson’s, 231 PearsonContingency table, 166, 179, 199, 292 列联表fourfold, 180 四重的multi-dimenional, 215 多维的r×c, 199 r×c维three-way, 214 三种方式的two-way, 214 两种方式的continuity correction, 126, 127, 135, 138, 159, 190, 192, 194, 195 连续修正in Kendall’s tau, 322 Kendall’s tauin Mann-Whitney test, 274, 275 Mann-Whitney 检验in Wilcoxon signed ranks test, 359 Wilcoxon符号秩检验continuous distribution function, 53 连续分布函数continuous random variable, 52, 53 连续型随机变量control, sign test for comparing several treatments with a, 175 控制,几种处理比较的符号检验convenience sample, 69 方便样本correction for continuity, 126, 127, 135, 138, 159, 190, 192, 194, 195 连续修正correction, Sheppard’s, 248 修正,Sheppard correlation: 相关性quick test for, 196 快速检验rank, 312 秩sign test for, 172 符号检验correlation coefficient: 相关系数Kendall’s partial,327 Kendall 偏Kendall’s rank, 318, 319, 325, 326 Kendall 秩Pearson’s product moment, 313,318 Pearson 乘积矩Spearman’s rank, 314, 325, 326 Spearmn秩correlation coefficient between two random variables, 43 两随机变量的相关系数correlation test: 相关性检验Kendall’s rank, 175, 321 Kendall秩Spearman’s rank, 175, 316 Spearma秩counting rules, 5 计数法则covariance, 39 协方差analysis of, 297 分析of two random variables, 41, 42, 46 两随机变量of two ranks, 45 两秩Cox and Stuart test for trend, 169, 170 Cox 和Stuart趋势检验A.R. E. of, 175Cramér’s coefficient, 230, 234 Cramér系数Cramér’s contingency coefficient, 229 Cramér列联系数Cramér’s-von Mises goodness-of –fit test, 441 Cramér’s-von Mises拟合优度检验Cramér’s-von Mises two-sample test, 463 Cramér’s-von Mises两样本检验tables for, 464 表格critical region, 97, 98, 101 临界区域size of, 100 大小curves, survival, 119 曲线, 生存Daniel’s test for trend, 323 Daniel趋势检验decile, 33, 34 十分位数(的)decision rule, 98 决策法则degrees of freedom, 59 自由度dependence, measure of, 227 相依,度量design: 设计completely randomized, 222 完全随机化experimental, 419 经验incomplete block, 387 不完全区组randomized complete block, 368 随机化完全区组deviates, random normal, 404 偏离,正态随机difference between two means, confidence interval for the, 281 两均值差异,置信区间difference, confidence interval for the median, 360 差异,中位数置信区间discordant pairs, 319 不和谐配对discrete distribution function, 52 离散分布函数discrete random variable, 52 离散型随机变量discrete uniform distribution, 28, 437 离散均匀分布discriminant analysis, 119, 419 判别分析dispersion, sign test for trends in, 175 散布,趋势的符号检验distribution: 分布binomial, 27 二项discrete uniform, 28 离散均匀exponential, 447 指数hypergeometric, 30 超几何分布lognormal, 453 对数正态分布null, 99 零假设uniform, 433 均匀distribution-free, 114 分布自由distribution-free methods, asymptoticall, 117 分布自由方法,渐近的distribution function, 26 分布函数chi-squared, 54, 59 χ2confidence band for, 438 置信界continuous, 53 连续discrete, 52 离散empirical, 79, 428 经验joint, 29 联合normal, 54, 55 正态of order statistics, 146, 147, 153 次序统计量sample, 79, 80 样本distributions with heavytails, 116, 148, 164 重尾分布distributions with light tails, 116, 164 轻尾分布dose-response curves, 349 剂量响应曲线Durbin test, 387, 388 Durbin检验efficiency of, 394 效率efficiency, 106 效率asymptotic, 112 渐近的of the Durbin test,394 Durbin检验of the Friedman test, 379 Friedman检验of the paired t-test, 364 配对t检验的relative, 110, 111, 112 相关的of the sign test, 364 符号检验of the Smirnov test, 465 Smirnov检验of the Wilcoxon test, 364 Wilcoxon检验empirical distribution function, 79, 428 经验分布函数empirical survival function, 89 经验生存函数empty set, 14 空集error: 误差standard, 85, 88 标准type Ⅰ, 98 Ⅰ类typeⅡ,98, 99 Ⅱ类estimate: 估计interval, 83 区间point, 83 点of the standard deviation, 443 标准差estimation, 79, 88 估计of parameters in chi-squared goodness-of-fit test, 243, 245, 249 参数χ2拟合度估计estimator, 79, 81 估计量of population mean, 115 样本均值of population standard deviation, 115 样本标准差unbiased, 74 无偏for μ, 84 μfor σ2, 85 σ2 event, 7, 14 事件probability of, 14 概率sure, 14 必然事件events, independent, 18, 19 事件,独立joint, 17 联合mutually exclusive, 18, 19 互不相容exact test, Fisher’s, 188, 213 精确检验,Fisher exclusive, mutually, 14 不相容,相互expected normal scores, 404 期望正态得分expected value, 35, 39 期望(值) expected values, small: 期望(值),小in contingency tables, 201, 220 列联表in goodness-of-fit test, 241, 249 拟合优度检验experiment, 6, 69 试验experimental design, 419 试验设计experiments, independent, 15, 19, 20 试验,独立exponential distribution, 447 指数分布Lilliefors test for the, 448 Lilliefors检验extension of the median test, 224 中位数检验的扩展F-distribution: F分布in Friedman test, 370 Friedman检验in incomplete block analysis, 389 不完全区组分析in Quade test, 374 Quade检验table of the, 562-571 表格F statistic, 297, 300 F统计量computed on scores, 312 得分计算F test, 297, 300 F检验for equal variances, 308, 309 等方差for randomized complete blocks, 379 随机完全区组factorial notation, 8 阶乘记号families of distributions, goodness-of-fit tests for, 442 分布族,拟合优度检验Fisher’s: Fisherexact test, 188, 213 精确检验least significant difference, 296 最小显著差异LSD procedure on ranks, 379method of randomization,407 随机化方法four-fold contingency table, 180, 233 四重列联表freedom, degrees of, 59 自由,度Friedman test, 367, 369 Friedman检验efficiency of, 379 效率extension of, 383 推广function: 函数distribution, 26 分布powder, 163 功效probability, of a random variable, 25 概率, 随机变量probability, on a sample space, 15 概率,样本空间random, 80 随机step, 52 阶梯survival, 80 生存gamma coefficient, 320 gamma 系数goodness-of-fit test: 拟合优度chi-squared, 239, 240 χ2Cramér-von Mises, 441 Cramér-von Mises kolmgorov, 428,430, 435 Kolmgorov goodness-of-fit tests for families of distributions,442 分布族拟合优度检验grand median, 218 全中位数heavy tails, distributions with, 116, 148, 164 重尾,分布Hodges-Lahman estimate of shift, 282, 361 Hodges-Lahman 漂移估计hypergeometric distribution, 30, 188, 191 超几何分布mean of, 188, 191 均值standard deviation of, 188, 191 标准差hypothesis: 假设alternative, 95 备择的composite, 97 复合的null, 95 零假设simple, 97 简单testing, 95 检验tests, properties of, 106 检验,性质incomplete block design, 368, 387 不完全区组设计incomplete block, multiple comparisons, 390 不完全区组, 多重比较independence, the chi-squared test for, 204 独立,χ2检验independent: 独立events, 18, 19 事件experiments, 15, 19, 20 试验random variables, 31, 46, 72 随机变量samples, multiple comparisons with, 290, 296, 398 样本,多重比较samples, randomization test for two, 409 样本,随机化检验inference, statistical, 68 推断,统计的interaction: 交互rank transformation test for, 419 秩变换检验test for, 384 检验intercept, 333 截距Internet websites, v 因特网,网址interquartile range, 37 四分位数极差interval, confidence, 83 区间,置信interval estimate, 83, 129 区间估计interval scale of measurement, 74 测量的区间尺度joint distribution function, 28, 29 联合分布函数joint event, 17 联合事件joint probability function, 28 联合概率函数Jonckheere-Terpstra test for ordered alternatives, 325 Jonckheere-Terpstra顺序备择检验Kaplan-Meier estimator, 89 Kaplan-Meier估计量Kendall’s: Kendall coefficient of concordance, 328 一致性系数partial correlation coefficient, 327 偏相关系数rank correlation test, 175, 321 秩相关检验tau, 318, 319, 325, 326, 335exact tables, 545-546 精确表tau, A. R. E. of, 327 tautau for ordered alternatives,381 顺序备择tau Klotz test, 401 Klotz检验Kolmogorov goodness-of-fit test, 428, 430 Kolmogorov 拟合优度检验exact tables, 549 精确表Kolmogorov goodness-of-fit test for discrete distributions, 435离散分布的Kolmogorov拟合优度检验Kolmogorov-Smirnov tests, 428 Kolmogorov-Smirnov检验Kruskal-Wallis test, 288 Kruskal-Wallis检验exact tables for, 541 精确表least significant difference, Fisher’s, 296 最小显著差异, Fisher’s least squares estimates, 334 最小二乘估计least squares method, 333 最小二乘方法Let’s make a deal, 66 让我们和妥协level of significance, 99 显著水平life testing, 148 寿命检验light tails, distributions with, 116, 164 轻尾,分布likelihood ratio statistic, 258 似然比统计量likelihood ratio test, 259 似然比检验Liliefors test for the exponential distribution, 448 指数分布的Liliefors检验table, 551 表格Liliefors test for normality, 443 Liliefors 正态性检验tables, 551 表格limits, tolerance, 150 极限,容忍linear regression, 333 线性回归location estimates, robust, 362 位置估计,稳健location measure of, 36 位置度量loglinear models, 215, 259 对数线性模型lognormal distribution, 453 对数正态分布longitudinal studies, 119 纵向研究lottery game, Texas Lotto, 66 彩票游戏,Texas Lotto lower-tailed test, 98 左边检验Mann-Whitney test, 103, 203, 271 Mann-Whitney检验tables, 538-540 表格Mantel-Haenszel test, 192 Mantel-Haenszel检验marginal totals, chi-squared test with fixed, 209 边缘和,固定的χ2检验matched pairs,350 配对randomization test for, 412 随机化检验McNemar test, 166, 180, 252, 255, 256 McNemar检验compared with paired t test, 178 与配对t检验比较mean, 36, 51 均值of hypergeometric distribution, 188, 191 超几何分布population, estimator of, 115 总体,估计量in rank test using scores, 306 得分的秩检验sample, 81, 83 样本of sum of random variables, 39 随机变量和of sum of ranks, 41, 49 秩和and variance in binomial distribution, 49 二项分布的方差means: 均值confidence interval for the difference between two, 281 两差异的置信区间sign test for equal, 160 对相等的符号检验measurement scale, 73 度量尺度interval, 74 区间nominal, 73 名义ordianal, 74 有序的ratio, 75 比率measures of dependence, 227 相依度量median, 33, 34 中位数difference, confidence interval for, 360 差异,置信区间grand, 218 总的sample, 82 样本test, 218, 352, 355 检验comparison with Kruskal-Wallis test,291 与Kruskal-Wallis检验的比较an extension of, 224 一个推广medians, sign test for equal, 160 中位数,对相等的符号检验meta-analysis, 452 无-分析minimum chi-squared method, 243, 245 最小χ2距离方法Minitab, v, 91, 107, 127, 130, 139, 144, 161, 182, 201, 205, 210, 220, 241, 276, 282, 290, 318, 322, 328, 336, 355, 361, 371, 382, 390, 444, 451model, 6 模型models,loglinear,215, 259 模型,对数线性monotonic regression, 344 单调回归Mood test for variances, 309, 312 Mood 方差检验multi-dimensional contingency table, 215 多维列联表multinomial: 多项式的coefficient, 9, 12, 系数distribution, 203, 207, 249 分布proportions, simultaneous confidence intervals for, 133 比例,联合置信区间multiple comparisons: 多重比较complete block design, 371, 375 完全区组设计incomplete blocks design,390 不完全区组设计independent samples, 290,297,398 独立样本in one-way layout, 220,222,252 以一种方式设计variance, 304 方差multiple regression, 419 多元回归multivariate data, randomization test for, 416 多元数据,随机化检验multivariate observations,385 多元观察multivariate random variable, 71, 72 多元随机变量confidence region for, 362, 364 置信区间mutually exclusive, 14 互不相容events, 19 事件NCSS, vnominal scale data, 117, 118 名义尺度数据nominal scale of measurement, 73 测量的名义尺度nonparametric methods, 116 非参数方法nonparametric statistics, 2, 114 非参数统计definition, 118 定义normal approximation: 正态逼近to binomial distribution, 58 二项分布to chi-squared distribution, 62 χ2分布to hypergeometric, 188, 194 超几何in Mann-Whitney test, 301, 302 Mann-Whitney检验to sum of ranks, 58 秩和in Wilcoxon signed ranks test, 301, 302 Wilcoxon秩和检验normal deviates, random, 404 正态偏差,随机normal distribution function, 54, 55 正态分布函数standard, 55 标准正态分布函数tables of, 508-511 标准正态分布函数表normal scores, 396 标准得分expected,404 期望的in matched pairs test, 400 配对检验in one-way layout, 397 以一种方式设计in test for correlation, 403 相关检验in test for variance, 401 方差检验in two-way layout, 403 以两种方式设计normality: 正态Lilliefors test for, 443 Lilliefors正态检验Shapiro-Wilk test for, 450 Shapiro-Wilk检验normalized sample, 443 标准化样本null distribution, 99 零假设分布null hypothesis,96 零假设one-sample case, 350 一样本情形one-sample t test, 363, 418 一样本t 检验one-tailed test,98 单边检验one-to-one correspondence, 52 一一对应one-way analysis of variance, 222, 297 一种方式的方差分析one-way layout, 227 一种方式的设计order statistic of rank k, 77, 82 秩的次序统计量order statistics, 143 次序统计量distribution function of,146, 147, 153 分布函数ordered alternatives, 297, 385 有序备择Jonckheere-Terpstra test for, 325 Jonckheere-Terpstra检验Page test for, 380 Page检验ordered categories, analysis of contingency table with, 292 有序分类,列联表分析ordered observation, 77 次序观察ordered random sample, 77 次序随机样本ordinal data, 117, 118, 271, 272 有序数据ordinal scale of measurement, 74 测量的顺序尺度outcomes, 6 结果outliers, 117, 284, 297 离群值p-value, 101 p-值Page test for ordered alternatives, 380 顺序备择的Page检验paired t test, 363 配对t检验efficiency of,364 效率McNemar test compared with, 178 McNemar检验的比较parallelism of two regression lines, 364 两回归直线的平行parameter estimation, 88 参数估计parametric confidence interval for mean, 149 均值的参数置信区间parametric methods, 115 参数方法parametric statistics, 2, 114 参数统计partial correlation coefficient: 偏相关系数Kendall’s, 327 Kendall’Spearman’s, 328 SpearmanPASS, v, 107Pearson product moment correlation coefficient, 313 Pearson乘积矩相关系数Pearson’s Pearsoncontingency coefficient, 231 列联系数mean-square contingency coefficient, 231 均方列联系数product moment correlation coefficient, 313, 318 乘积矩相关系数percentile, 33, 34 百分位点phi coefficient, 234, 239 phi系数Pitman’s efficiency, 112 Pitman有效性point estimate, 83 点估计point in the sample space, 13 样本空间中的点population, 68, 69 总体sampled, 69, 70 抽样target, 69, 70 目标power, 3, 100, 106, 116 功效of the binomial test, 127 二项检验function, 106, 163 函数probabilities, chi-squared test for differences in, 180, 199 概率,差异的χ2检验probability, 5, 13 概率conditional, 17, 23 条件的confidence interval for, 130 置信区间of the event, 14 事件function, 15 函数conditional, 29 条件的joint, 28 联合of the point, 14 点的sample, 69 样本properties of random variables, 33 随机变量的性质proportion, confidence interval for population, 130 比例,总体的置信区间Quade test, 367, 373 Quade检验efficiency of, 380 效率power of, 380 功效quantile, 27, 33, 34 分位数confidence interval for, 135, 143 置信区间population, 136 总体sample, 81 样本test, 135, 136, 222 检验A.R.E. vs.one-sample t test, 148 A.R.E. vs.一样本t检验quartile, 33, 34 四分位数random function, 80 随机函数random normal deviates, 404 随机正态偏差random sample, 69, 70, 71 随机样本random variable, 22, 23, 76 随机变量bivariate, 72 二维continuous, 52, 53 连续discrete, 52 离散distribution function of, 26 分布函数multivariate, 71, 72 多元probability function of, 25 概率函数random variables: 随机变量correlation coefficient between two, 43 两随机变量的相关系数covariance of two, 41, 42, 46 两随机变量的协方差independent, 31, 46, 72 独立properties of, 33 性质randomization, Fisher’s method of, 407 随机化,Fisher方法randomization test for two independence samples, 409 独立样本的随机化检验randomized complete block design, 251, 368 随机化完全区组设计randomness, test for, 242 随机,检验range, 37 极差interquartile, 37 四分位数间的rank correlation, 312 秩相关Kendall’s test for, 175, 321 Kendall检验spearman’s test for, 175, 316 Spearman检验rank of an order statistic, 77 次序统计量的秩rank transformation, 417 秩变换ranks: 秩covariance of two, 45 两随机变量的协方差mean of sum of, 41, 49 和的均值ratio scale of measurement, 75 测量的比率尺度region: 域acceptance, 98 接受critical, 97, 98, 101 临界rejection, 98 拒绝regression, 328, 332 回归equation, 332 方程linear, 333 线性monotonic, 344 单调multiple, 419 多元parallelism of two lines, 364 两线平行rejection region, 98 拒绝域relative efficiency, 110, 111, 112 相对效率asymptotic, 112 渐近Resampling Stats, v, 88 重抽样research hypothesis, 95 假设研究rho, Spearman’s, 314, 325, 326, 335 rho, Spearman relationship with Friedman’s test, 382 与Friedman检验的关系robust, 419, 420 稳健location estimates, 362 局部估计methods, 115, 119 方法runs tests, 3 游动检验S-Plus, v, 88, 91, 127, 130, 168, 182189, 193, 201, 205, 210, 241, 276, 290, 318, 322, 355, 371, 432, 444, 449sample, 68, 69 样本censored, 155, 285 删失convenience, 69 方便distribution function, 79, 80 分布函数mean, 81, 83 均值mean, unbiased for μ, 84 均值,对μ无偏median, 82 中位数normalized,443 正则化probability, 69 概率quantile,81 分位数sequential, 362 序贯space, 13 空间point in the, 13 样本空间中的点standard deviation, 83 标准差variance, 81, 83 方差unbiased for σ2, 85 对σ2无偏sampled population, 69, 70 抽样总体SAS, v, 168, 182, 189, 193, 201, 205, 210, 230, 259, 276, 290, 322, 325, 355, 371, 390, 451 scale,measure of, 37 刻度(尺度), 度量scale,tests for, 309, 310 刻度,检验scale, measurement, 73 刻度, 测量scorses, 306 得分expected normal, 404 期望正态F statistic computed on, 312 计算F统计量mean in rank test using, 306 均值的秩检验normal, 396 正态variance in rank test using, 307 方差的秩检验sequential sampling, 362 序贯抽样sequential testing, 285 序贯检验set, empty, 14 集合,空集Shapiro-Wilk test for normality, 450 Shapiro-Wilk正态检验Siegel-Tukey test, 312 Siegel-Tukey检验sign test, 157 符号检验consistent, 163 相合for correlation, 172 相关性efficiency of, 364 效率for equal means, 160 等均值for equal medians, 160 等中位数extension to k samples of, 367 推广到k样本unbiased, 163 无偏variations of, 166, 175 方差vs. t test, A.R.E. of, 164, 175 vs. t检验,A.R.E. vs. Wilcoxon signed ranks test, A.R.E of, 164, 175 vs. Wilcoxonf符号秩检验,A.R.E signed ranks test, Wilcoxon, 352 符号秩检验,Wilcoxon significance, level of, 99 显著,水平simple hypothesis, 97 简单假设simulation, computer, to find null distribution, 446, 447 模拟,计算机, 求零假设分布size of the critical region, 100 临界域的大小slope, A.R.E. of rank test for, 335 斜率, A.R.E.秩检验slope in linear regression, 333 线性回归的斜率confidence interval for, 335 置信区间testing the, 335 检验Smirnov test, 456, Smirnov检验efficiency of, 465 效率exact tables, 558-560 精确表Smirnov-type tests for several samples, 462 多样本Smirnov型检验Spearman’s foottrule, 331 Spearman 脚规则Spearman’s rank correlation test, 175, 316 Spearman秩相关检验A.R.E. of, 327 A.R.E.exact tables, 544 精确表Spearman’s rho, 314, 325, 326, 335 Spearman’s rhofor ordered alternatives, 380 顺序备择relationship with Friedman’s test, 382 与Friedman检验的关系split plots, 385 裂区SPSS, v, 382, 390squared ranks test for variances, 300 方差的平方秩检验exact tables for, 542-543 精确表standard deviation, 37, 38 标准差estimation of, 443 估计of hypergeometric distribution, 188, 191 超几何分布population, estimator of, 115 总体,估计量sample, 83 样本standard error, 85, 88 标准差standard normal distribution, 55 标准正态分布STA TA, v, 88statistic, 75, 76 统计量order, 77, 82 次序test, 35,96, 97 检验STA TISTUICA, vstatistical inference, 68 统计推断statistics, 68 统计学StatMost, v, 259StatXact, v, 104, 127, 130, 144, 161, 168, 182, 189, 201, 205, 210, 220, 230, 241, 252, 276, 282, 290, 303, 318, 322, 325, 355, 361, 371, 375, 380, 382, 387, 399, 400, 401, 408, 409, 413, 432, 435, 444, 451, 459stem and leaf method, 270 茎叶方法step function, 52 阶梯函数stratified samples, 362 分层样本sum of chi-squared random variables, 62 χ2随机变量的和sum of integers formula, 40 整数和公式sum of random variables: 随机变量和mean of, 39 均值variance of, 48 方差sum of squared integers formula,43 整数平方和公式sure event, 14 必然事件survival curves, 119 生存曲线survival function, 89 生存函数empirical, 89 经验symmetric distributions, 350, 351 对称分布symmetry, Smirnov test for, 465 对称性,Smirnov检验symmetry, tests for, 364 对称性,检验SYSTA T, v, 88, 91, 259t distribution, table, 561 t分布,表格t statistic computed on ranks, 367 基于秩计算的t统计量t test: t检验,efficiency of paired, 364 配对效率one sample, 363, 418 一样本paired, 363 配对two sample, 284, 417 两样本table,contingency, 166, 179, 292 表,列联target population, 69, 70 目标总体tau, Kendall’s, 318, 319, 325, 326, 335 tau, Kendall test, conservative, 113 检验, 保守的test, hypothesis, 95 检验,假设test, one tailed, 98 检验,单边test, statistic, 3, 96, 97 检验,统计量test,unbiased, 106, 108, 160 检验,无偏testing hypotheses, 95 假设检验tests, consistent sequence of, 106, 108, 160 检验,相合序列three-way contingency table, 214 三种方式列联表tolerance limits, 150 容忍限approximation formulas for, 151, 155 逼近公式exact tables for, 537 精确表tansformation, rank, 417 变换,秩trend: 趋势Cox and Stuart test for, 169, 170 Cox和Stuart检验Daniel’s test for, 232 Daniel检验trials, 6 基本试验Tschuprow’s coefficient, 232 Tschuprow系数two independent samples, randomization test for, 409 两独立样本,随机化检验two-sample Cramér-von Mises test, 463 两样本Cramér-von Mises检验two-sample t test, 198 两样本t检验two-tailed test, 98 双边t检验two-way contingency table, 214 两种方式列联表typ eⅠerror , 98 一类错误typ eⅡerror, 98, 99 二类错误unbiased estimator, 84, 94 无偏估计量unbiased, sign test, 163 无偏,符号检验unbiased test, 106, 108, 160 无偏检验uniform distribution: 均匀分布continuous, 433 连续discrete, 28, 437 离散upper-tailed test, 98 右边检验value, expected,35, 39 值,期望van der Waerden test, 397 van der Waerden检验variable, random, 22, 23, 76 变量,随机variance, 36, 37 方差in binomial distribution, 49 二项分布multiple comparisons for test for, 304 检验的多重比较in rank test using scores, 307 得分秩检验sample, 81, 83 样本squared ranks test for, 300 平方秩检验of sum of random variables, 48 随机变量的和of sum of ranks, 48, 49 秩和tests for, 309 检验variations of the sign test, 166, 175 符号检验的变差Walsh test, 364 Walsh检验websites, Internet, v 网址,因特耐特网Wilcoxon signed ranks test, 164, 352, 411 Wilcoxon符号秩检验continuity correction in, 359 连续相关efficiency of, 364 效率extension to k samples of, 367 推广到k个样本normal approximation in, 353, 359 正态逼近tables, 547-548 表格Wilcoxon test, 103 Wilcoxon检验Wilcoxon two-sample test, 271 Wilcoxon两样本检验。
《统计学》_各章关键术语(中英文对照)

定比尺度数据(ratio scale level data)
分类变量(categorical variable) 定性变量、属性变量(qualitative variable)
数值变量(numerical variable) 定量变量、数量变量(quantitative variable)
定距尺度(interval scale)
定距尺度变量(interval scale level variable)
定距尺度数据(interval scale level data)
定比尺度(ratio scale)
定比尺度变量(ratio scale level variable)
推断统计学(inferential statistics)
总体(population) 母体(parent)(parent population)
样本、子样(sample)
调查对象总体(respondents population) 有限总体(finite population)
后验概率(posterior probability)
随机变量(random variable)
离散型随机变量(discrete type random variable)
连续型随机变量(continuous type random variable)
概率分布(probability distribution)
复合事件(union of event)
必然事件(certain event)
不可能事件(impossible event)
基本事件空间(elementary event space)
互不相容事件(mutually exclusive events)
英文版概率论与数理统计重点单词
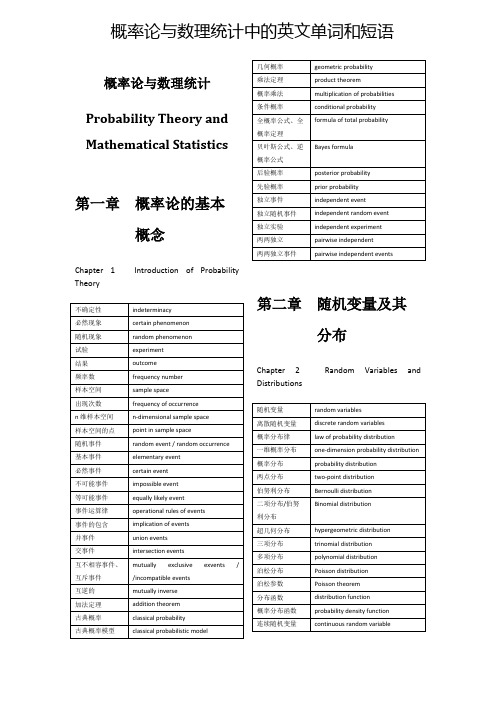
概率论与数理统计Probability Theory and Mathematical Statistics第一章概率论的基本概念Chapter 1 Introduction of Probability Theory不确定性indeterminacy必然现象certain phenomenon随机现象random phenomenon试验experiment结果outcome频率数frequency number样本空间sample space出现次数frequency of occurrencen维样本空间n-dimensional sample space样本空间的点point in sample space随机事件random event / random occurrence基本事件elementary event必然事件certain event不可能事件impossible event等可能事件equally likely event事件运算律operational rules of events事件的包含implication of events并事件union events交事件intersection events互不相容事件、互斥事件mutually exclusive exvents / /incompatible events互逆的mutually inverse加法定理addition theorem古典概率classical probability古典概率模型classical probabilistic model 几何概率geometric probability乘法定理product theorem概率乘法multiplication of probabilities条件概率conditional probability全概率公式、全概率定理formula of total probability贝叶斯公式、逆概率公式Bayes formula后验概率posterior probability先验概率prior probability独立事件independent event独立随机事件independent random event独立实验independent experiment两两独立pairwise independent两两独立事件pairwise independent events第二章随机变量及其分布Chapter 2 Random Variables and Distributions随机变量random variables离散随机变量discrete random variables概率分布律law of probability distribution一维概率分布one-dimension probability distribution 概率分布probability distribution两点分布two-point distribution伯努利分布Bernoulli distribution二项分布/伯努利分布Binomial distribution超几何分布hypergeometric distribution三项分布trinomial distribution多项分布polynomial distribution泊松分布Poisson distribution泊松参数Poisson theorem分布函数distribution function概率分布函数probability density function连续随机变量continuous random variable概率论与数理统计中的英文单词和短语概率密度probability density概率密度函数probability density function 概率曲线probability curve均匀分布uniform distribution指数分布exponential distribution指数分布密度函数exponential distribution density function正态分布、高斯分布normal distribution标准正态分布standard normal distribution正态概率密度函数normal probability density function正态概率曲线normal probability curve标准正态曲线standard normal curve柯西分布Cauchy distribution分布密度density of distribution第三章多维随机变量及其分布Chapter 3 Multivariate Random Variables and Distributions二维随机变量two-dimensional random variable联合分布函数joint distribution function二维离散型随机变量two-dimensional discrete random variable二维连续型随机变量two-dimensional continuous random variable联合概率密度joint probability variablen维随机变量n-dimensional random variablen维分布函数n-dimensional distribution functionn维概率分布n-dimensional probability distribution 边缘分布marginal distribution边缘分布函数marginal distribution function边缘分布律law of marginal distribution边缘概率密度marginal probability density二维正态分布two-dimensional normal distribution二维正态概率密two-dimensional normal probability 度density二维正态概率曲线two-dimensional normal probabilitycurve条件分布conditional distribution条件分布律law of conditional distribution条件概率分布conditional probability distribution条件概率密度conditional probability density边缘密度marginal density独立随机变量independent random variables第四章随机变量的数字特征Chapter 4 Numerical Characteristics fo Random Variables数学期望、均值mathematical expectation期望值expectation value方差variance标准差standard deviation随机变量的方差variance of random variables均方差mean square deviation相关关系dependence relation相关系数correlation coefficient协方差covariance协方差矩阵covariance matrix切比雪夫不等式Chebyshev inequality第五章大数定律及中心极限定理Chapter 5 Law of Large Numbers and Central Limit Theorem大数定律law of great numbers切比雪夫定理的special form of Chebyshev theorem特殊形式依概率收敛convergence in probability伯努利大数定律Bernoulli law of large numbers同分布same distribution列维-林德伯格定理、独立同分布中心极限定理independent Levy-Lindberg theorem辛钦大数定律Khinchine law of large numbers利亚普诺夫定理Liapunov theorem棣莫弗-拉普拉斯定理De Moivre-Laplace theorem第六章样本及抽样分布Chapter 6 Samples and Sampling Distributions统计量statistic总体population个体individual样本sample容量capacity统计分析statistical analysis统计分布statistical distribution统计总体statistical ensemble随机抽样stochastic sampling / random sampling 随机样本random sample简单随机抽样simple random sampling简单随机样本simple random sample经验分布函数empirical distribution function样本均值sample average / sample mean样本方差sample variance样本标准差sample standard deviation标准误差standard error样本k阶矩sample moment of order k样本中心矩sample central moment样本值sample value样本大小、样本容量sample size样本统计量sampling statistics随机抽样分布random sampling distribution抽样分布、样本分布sampling distribution自由度degree of freedomZ分布Z-distributionU分布U-distribution第七章参数估计Chapter 7 Parameter Estimations统计推断statistical inference参数估计parameter estimation分布参数parameter of distribution参数统计推断parametric statistical inference点估计point estimate / point estimation总体中心距population central moment总体相关系数population correlation coefficient总体分布population covariance总体协方差population covariance点估计量point estimator估计量estimator无偏估计unbiased estimate / unbiasedestimation估计量的有效性efficiency of estimator矩法估计moment estimation总体均值population mean总体矩population moment总体k阶矩population moment of order k总体参数population parameter极大似然估计maximum likelihood estimation极大似然估计量maximum likelihood estimator极大似然法maximum likelihood method /maximum-likelihood method似然方程likelihood equation似然函数likelihood function区间估计interval estimation置信区间confidence interval置信水平confidence level置信系数confidence coefficient单侧置信区间one-sided confidence interval置信上限confidence upper limit置信下限confidence lower limitU估计U-estimator正态总体normal population总体方差的估计estimation of population variance 置信度degree of confidence方差比variance ratio第八章假设检验Chapter 8 Hypothesis Testings参数假设parametric hypothesis假设检验hypothesis testing两类错误two types of errors统计假设statistical hypothesis统计假设检验statistical hypothesis testing检验统计量test statistics显著性检验test of significance统计显著性statistical significanceone-sided test单边检验、单侧检验one-sided hypothesis单侧假设、单边假设双侧假设two-sided hypothesis双侧检验two-sided testing显著水平significant levelrejection region拒绝域/否定区域接受区域acceptance regionU检验U-testF检验F-test方差齐性的检验homogeneity test for variances 拟合优度检验test of goodness of fit。
综述Representation learning a review and new perspectives

explanatory factors for the observed input. A good representation is also one that is useful as input to a supervised predictor. Among the various ways of learning representations, this paper focuses on deep learning methods: those that are formed by the composition of multiple non-linear transformations, with the goal of yielding more abstract – and ultimately more useful – representations. Here we survey this rapidly developing area with special emphasis on recent progress. We consider some of the fundamental questions that have been driving research in this area. Specifically, what makes one representation better than another? Given an example, how should we compute its representation, i.e. perform feature extraction? Also, what are appropriate objectives for learning good representations?
USP统计Permutation测试的独立性测试(离散、连续和无限维度数据)说明书

Package‘USP’October12,2022Title U-Statistic Permutation Tests of Independence for all Data TypesVersion0.1.2Author Thomas B.Berrett<**********************.uk>[aut,cre],Ioannis Kontoyian-nis<*****************>[aut],Richard J.Sam-worth<***********************>[aut]Maintainer Thomas B.Berrett<**********************.uk>Description Implements various independence tests for discrete,continuous,and infinite-dimensional data.The tests are based on a U-statistic permutation test,the USP of Berrett,Kon-toyiannis and Samworth(2020)<arXiv:2001.05513>,and shown to be minimax rate opti-mal in a wide range of settings.As the permutation principle is used,all tests have exact,non-asymptotic Type I error control at the nominal level.License MIT+file LICENSEEncoding UTF-8LazyData trueRoxygenNote7.1.1Imports stats,RdpackRdMacros RdpackNeedsCompilation noRepository CRANDate/Publication2021-01-2709:30:21UTCR topics documented:coeffs (2)DiscStat (3)FourierBasis (3)FourierKernel (4)InfKern (5)KernStat (6)sumbasis (6)USP (7)12coeffs USP.test (8)USPFourier (9)USPFourierAdapt (10)USPFunctional (11)Index13 coeffs Calculate coefficients of a function’s series expansionDescriptionThis function is used in InfKern to produce the kernel matrix from functional data defined on the interval[0,1].For further details see Section7.4of(Berrett et al.2021).Usagecoeffs(X,Ntrunc)ArgumentsX The discretised functions whose coefficients are required.This should be a ma-trix with one row per function,and with Ndisc columns,where Ndisc is thegrid size of the discretisation.Ntrunc The number of coefficients that are required.The function returns coefficients 1,...,Ntrunc.ValueThe coefficients of X in its expansion in terms of sine functions.See(Berrett et al.2021)for more detail.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplest=seq(from=0,to=1,length.out=1000);X=t^2U=coeffs(X,100)[1,];L=5plot(t,X,type="l")approx=rep(0,1000)for(l in1:L){approx=approx+qnorm(U[l])*sqrt(2)*sin((l-1/2)*pi*t)/((l-1/2)*pi)lines(t,approx,col=l+1)}DiscStat 3DiscStat Test statistic for dependence in contingency tableDescriptionThis function computes the value of the test statistic T n measuring the strength of dependence in a contingency table.See Section 3.1of (Berrett et al.2021)for a defiageDiscStat(freq)Argumentsfreq Two-way contingency table whose strength of dependence is to be measured.ValueA list containing the value of the test statistic T n ,the table of expected null counts,and the table of contributions to T n .ReferencesBerrett TB,Kontoyiannis I,Samworth RJ (2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear .Examplesfreq=r2dtable(1,rep(10,5),rep(10,5))[[1]];DiscStat(freq)freq=diag(1:5);DiscStat(freq)freq=r2dtable(1,rep(10,5),rep(10,5))[[1]]+4*diag(rep(1,5))DiscStat(freq)FourierBasis Fourier basis functionsDescriptionComputes the values of the one-dimensional Fourier basis functions at a vector of locations x and with a vector of frequencies m .The scaling factor of 2πis included,so that the function returns,e.g.,√2cos(2πmx ).UsageFourierBasis(a,m,x)4FourierKernelArgumentsa Sine or cosine;a=0gives cosine and a=1gives sine.m Vector of frequencies m.x Vector of locations x.ValueReturns the values of √2cos(2πmx).ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplese=FourierBasis(1,1:100,0.01);plot(0.01*(1:100),e,type="l")e=FourierBasis(0,1,0.01*(1:100));plot(0.01*(1:100),e,type="l")FourierBasis(1,1:3,0.1*(1:10))FourierKernel Kernel matrix for Fourier basisDescriptionCalculates the kernel matrix,described in(Berrett et al.2021)for univariate continuous data when using the Fourier basis.This function is used in USPFourier.UsageFourierKernel(x,M)Argumentsx A vector in[0,1]n for some n,containing the observations.M The maximum frequency of Fourier basis functions to compute.ValueThe kernel matrix K,to be used in independence testing.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.InfKern5Examplesn=10;x=runif(n)FourierKernel(x,5)InfKern Kernel for infinite-dimensional exampleDescriptionFunction to produce the kernel matrices in the infinite dimensional example described in Section7.4of(Berrett et al.2021).Here,a random function is converted to a sequence of coefficients andwe use the Fourier basis on these coefficients.This function is an essential part of USPFunctional.UsageInfKern(X,Ntrunc,M)ArgumentsX Matrix giving one of the samples to be tested.Each row corresponds to a dis-cretised function,with each column giving the values of the functions at thecorresponding grid point.Ntrunc The total number of coefficients to look at in the basis expansion of the func-tional data.M The maximum frequency to look at in the Fourier basis.ValueThe kernel matrix for the sample X.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesn=10#number of observationsNdisc=1000;t=1/Ndisc#functions represented at grid points1/Ndisc,2/Ndisc,...,1X=matrix(rep(0,Ndisc*n),nrow=n)for(i in1:n){x=rnorm(Ndisc,mean=0,sd=1)X[i,]=cumsum(x*sqrt(t))}InfKern(X,2,2)6sumbasis KernStat Test statistic calculated from two kernel matricesDescriptionCalculate the U-statistic measure of dependence given two kernel matrices J and K,as described in Section7.1of(Berrett et al.2021).For the featured examples considered these matrices can be calculated using FourierKernel or InfKern.Alternatively,if a different basis is to be used,then the kernels can be entered separately.UsageKernStat(J,K)ArgumentsJ n×n kernel matrix corresponding tofirst sample.K n×n kernel matrix corresponding to second sample.ValueTest statistic measure the strength of dependence between the two samples.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesx=runif(100);y=runif(100);M=3J=FourierKernel(x,M);K=FourierKernel(y,M)KernStat(J,K)sumbasis Kernel entries in infinite dimensional caseDescriptionFunction to calculate each entry of the kernel matrix in the infinite dimensional example described in Section7.4of(Berrett et al.2021).Here,a random function is converted to a sequence of coefficients and we use the Fourier basis on these coefficients.This function is only used in the function InfKern.Usagesumbasis(Ntrunc,M,x1,x2)USP7 ArgumentsNtrunc The total number of coefficients to look at.M The maximum frequency to look at in the Fourier basis.x1The coefficients of thefirst data point.x2The coefficients of the second data point.ValueThe entry of the kernel corresponding to the two data points.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesx1=runif(5);x2=runif(5);sumbasis(5,2,x1,x2)USP Permutation test of independence.DescriptionCarry out an independence test of the independence of two samples,give two kernel matrices J and K,as described in Section7.1of(Berrett et al.2021).We calculate the test statistic and null statistics using the function KernStat,before comparing them to produce a p-value.For the featured examples considered these matrices can be calculated using FourierKernel or InfKern.Alternatively,if a different basis is to be used,then the kernels can be entered separately.UsageUSP(J,K,B=999,ties.method="standard",nullstats=FALSE)ArgumentsJ n×n kernel matrix corresponding tofirst sample.K n×n kernel matrix corresponding to second sample.B The number of permutation used to calibrate the test.ties.method If"standard"then calculate the p-value as in(5)of(Berrett et al.2021),which is slightly conservative.If"random"then break ties randomly.This preservesType I error control.nullstats If TRUE,returns a vector of the null statistic values.8USP.testValueReturns the p-value for this independence test and the value of the test statistic,D n,as defined in (Berrett et al.2021).If nullstats=TRUE is used,then the function also returns a vector of the null statistics.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesx=runif(100);y=runif(100);M=3J=FourierKernel(x,M);K=FourierKernel(y,M)USP(J,K,999)n=50;r=0.6;Ndisc=1000;t=1/NdiscX=matrix(rep(0,Ndisc*n),nrow=n);Y=matrix(rep(0,Ndisc*n),nrow=n)for(i in1:n){x=rnorm(Ndisc,mean=0,sd=1)se=sqrt(1-r^2)#standard deviation of errore=rnorm(Ndisc,mean=0,sd=se)y=r*x+eX[i,]=cumsum(x*sqrt(t))Y[i,]=cumsum(y*sqrt(t))}J=InfKern(X,2,1);K=InfKern(Y,2,1)USP(J,K,999)USP.test Independence test for discrete dataDescriptionCarry out a permutation independence test on a two-way contingency table.The test statistic is T n, as described in Sections3.1and7.1of(Berrett et al.2021).This also appears as Un in(Berrett and Samworth2021).The critical value is found by sampling null contingency tables,with the same row and column totals as the input,via Patefield’s algorithm,and recomputing the test statistic. UsageUSP.test(freq,B=999,ties.method="standard",nullstats=FALSE)Argumentsfreq Two-way contingency table whose independence is to be tested.B The number of resampled null tables to be used to calibrate the test.ties.method If"standard"then calculate the p-value as in(5)of(Berrett et al.2021),which is slightly conservative.If"random"then break ties randomly.This preservesType I error control.nullstats If TRUE,returns a vector of the null statistic values.ValueReturns the p-value for this independence test and the value of the test statistic,T n,as defined in (Berrett et al.2021).The third element of the list is the table of expected counts,and thefinal element is the table of contributions to T n.If nullstats=TRUE is used,then the function also returnsa vector of the null statistics.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Berrett TB,Samworth RJ(2021).“USP:an independence test that improves on Pearson’s chi-squared and the G-test.”Submitted,available at arXiv:2101.10880.Examplesfreq=r2dtable(1,rep(10,5),rep(10,5))[[1]]+4*diag(rep(1,5))USP.test(freq,999)freq=diag(1:5);USP.test(freq,999)freq=r2dtable(1,rep(10,5),rep(10,5))[[1]];test=USP.test(freq,999,nullstats=TRUE)plot(density(test$NullStats,from=0,to=max(max(test$NullStats),test$TestStat)),xlim=c(min(test$NullStats),max(max(test$NullStats),test$TestStat)),main="Test Statistics")abline(v=test$TestStat,col=2);TestStats=c(test$TestStat,test$NullStats)abline(v=quantile(TestStats,probs=0.95),lty=2)USPFourier Independence test for continuous dataDescriptionPerforms a permutation test of independence between two univariate continuous random variables, using the Fourier basis to construct the test statistic,as described in(Berrett et al.2021).UsageUSPFourier(x,y,M,B=999,ties.method="standard",nullstats=FALSE)Argumentsx A vector containing thefirst sample,with each entry in[0,1].y A vector containing the second sample,with each entry in[0,1].M The maximum frequency to use in the Fourier basis.B The number of permutation to use when calibrating the test.ties.method If"standard"then calculate the p-value as in(5)of(Berrett et al.2021),whichis slightly conservative.If"random"then break ties randomly.This preservesType I error control.nullstats If TRUE,returns a vector of the null statistic values.ValueReturns the p-value for this independence test and the value of the test statistic,D n,as defined in(Berrett et al.2021).If nullstats=TRUE is used,then the function also returns a vector of the nullstatistics.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesx=runif(10);y=x^2USPFourier(x,y,1,999)n=100;w=2;x=integer(n);y=integer(n);m=300unifdata=matrix(runif(2*m,min=0,max=1),ncol=2);x1=unifdata[,1];y1=unifdata[,2]unif=runif(m);prob=0.5*(1+sin(2*pi*w*x1)*sin(2*pi*w*y1));accept=(unif<prob);Data1=unifdata[accept,];x=Data1[1:n,1];y=Data1[1:n,2]plot(x,y)USPFourier(x,y,2,999)x=runif(100);y=runif(100)test=USPFourier(x,y,3,999,nullstats=TRUE)plot(density(test$NullStats,from=min(test$NullStats),to=max(max(test$NullStats),test$TestStat)), xlim=c(min(test$NullStats),max(max(test$NullStats),test$TestStat)),main="Test Statistics") abline(v=test$TestStat,col=2);TestStats=c(test$TestStat,test$NullStats)abline(v=quantile(TestStats,probs=0.95),lty=2)USPFourierAdapt Adaptive permutation test of independence for continuous data.DescriptionWe implement the adaptive version of the independence test for univariate continuous data usingthe Fourier basis,as described in Section4of(Berrett et al.2021).This applies USPFourier with arange of values of M,and a properly corrected significance level.UsageUSPFourierAdapt(x,y,alpha,B=999,ties.method="standard")Argumentsx The vector of data points from thefirst sample,each entry belonging to[0,1].y The vector of data points from the second sample,each entry belonging to[0,1].alpha The desired significance level of the test.B Controls the number of permutations to be used.With a sample size of n eachtest uses B log2n permutations.If B+1<1/αthen it is not possible to rejectthe null hypothesis.ties.method If"standard"then calculate the p-value as in(5)of(Berrett et al.2021),which is slightly conservative.If"random"then break ties randomly.This preservesType I error control.ValueReturns an indicator with value1if the null hypothesis of independence is rejected and0otherwise.If the null hypothesis is rejected,the function also outputs the value of M at the which the null was rejected and the value of the test statistic.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesn=100;w=2;x=integer(n);y=integer(n);m=300unifdata=matrix(runif(2*m,min=0,max=1),ncol=2);x1=unifdata[,1];y1=unifdata[,2]unif=runif(m);prob=0.5*(1+sin(2*pi*w*x1)*sin(2*pi*w*y1));accept=(unif<prob);Data1=unifdata[accept,];x=Data1[1:n,1];y=Data1[1:n,2]plot(x,y)USPFourierAdapt(x,y,0.05,999)USPFunctional Independence test for functional dataDescriptionWe implement the permutation independence test described in(Berrett et al.2021)for functional data taking values in L2([0,1]).The discretised functions are expressed in a series expansion,and an independence test is carried out between the coefficients of the functions,using a Fourier basis to define the test statistic.UsageUSPFunctional(X,Y,Ntrunc,M,B=999,ties.method="standard")ArgumentsX A matrix of the discretised functional data from thefirst sample.There are n rows,where n is the sample size,and Ndisc columns,where Ndisc is the gridsize such that the values of each function on1/Ndisc,2/Ndisc,...,1are given.Y A matrix of the discretised functional data from the second sample.The dis-cretisation grid may be different to the grid used for X,if required.Ntrunc The number of coefficients to retain from the series expansions of X and Y.M The maximum frequency to use in the Fourier basis when testing the indepen-dence of the coefficients.B The number of permutations used to calibrate the test.ties.method If"standard"then calculate the p-value as in(5)of(Berrett et al.2021),which is slightly conservative.If"random"then break ties randomly.This preservesType I error control.ValueA p-value for the test of the independence of X and Y.ReferencesBerrett TB,Kontoyiannis I,Samworth RJ(2021).“Optimal rates for independence testing via U-statistic permutation tests.”Annals of Statistics,to appear.Examplesn=50;r=0.6;Ndisc=1000;t=1/NdiscX=matrix(rep(0,Ndisc*n),nrow=n);Y=matrix(rep(0,Ndisc*n),nrow=n)for(i in1:n){x=rnorm(Ndisc,mean=0,sd=1)se=sqrt(1-r^2)#standard deviation of errore=rnorm(Ndisc,mean=0,sd=se)y=r*x+eX[i,]<-cumsum(x*sqrt(t))Y[i,]<-cumsum(y*sqrt(t))}USPFunctional(X,Y,2,1,999)Indexcoeffs,2DiscStat,3FourierBasis,3FourierKernel,4InfKern,5KernStat,6sumbasis,6USP,7USP.test,8USPFourier,9USPFourierAdapt,10USPFunctional,1113。
f critical value表

一、什么是临界值表?临界值表又称为临界值参考表,是一种统计学工具,用于确定统计检验的显著水平。
统计检验是指通过对样本数据进行分析,判断总体特征的假设是否成立的过程。
在进行统计检验的过程中,需要将所得的检验统计量与临界值进行比较,以确定是否拒绝原假设。
临界值表中包含了不同显著水平下的临界值,可供统计学家和研究人员进行参考。
二、临界值表的作用及意义1. 帮助确定统计检验的显著水平在进行统计检验时,显著水平是一个重要的参数,它表示了当假设成立时,观察到一个给定结果的概率。
临界值表中的数值就是以不同显著水平为基础,确定了在特定条件下能否拒绝原假设的临界值。
2. 提供了统计推断的依据在实际研究和分析中,经常需要进行统计推断,即从样本推断总体特征。
临界值表提供了一种客观、标准化的依据,可以帮助研究人员作出准确的统计推断。
3. 为统计研究提供了参考标准对于很多统计研究,临界值表是一个非常重要的参考标准。
在实际进行统计分析时,可以通过对临界值表的应用,来确定所得结果的显著性,进而进行正确的统计推断。
三、临界值表的编制和使用1. 编制临界值表是通过数理统计学的理论和方法得出的,通常由专业的统计学家和研究人员进行编制。
在编制过程中,会考虑到不同的显著水平、样本容量、自由度等因素,以确保临界值的准确性和可靠性。
2. 使用在进行统计检验时,需要根据具体情况选择合适的显著水平,并查阅相应的临界值表。
以 t 分布的临界值表为例,当自由度和显著水平确定后,可以从表中查找对应的临界值,然后将所得的检验统计量与之比较,以作出统计推断。
四、临界值表的局限性及注意事项1. 局限性临界值表是在一定条件下得出的理论数值,因此在实际应用中可能无法完全适用于所有情况。
特别是在样本容量较小或者样本分布不满足正态分布假设的情况下,临界值表的准确性可能会受到影响。
2. 注意事项在使用临界值表时,需要确保所用的表格与具体的统计方法和条件相匹配。
另外,还需要注意样本容量、显著水平、自由度等参数的选择,以及对临界值的正确理解和应用等方面的注意事项。
最小抑菌浓度测定方法

Agar and broth dilution methods to determine the minimal inhibitory concentration (MIC)of antimicrobial substancesIrith Wiegand,Kai Hilpert &Robert E W HancockCentre for Microbial Diseases and Immunity Research,University of British Columbia,2259Lower Mall Research Station,Vancouver,British Columbia,V6T 1Z4,Canada.Correspondence should be addressed to R.E.W.H.(bob@cmdr.ubc.ca).Published online 17January 2008;doi:10.1038/nprot.2007.521The aim of broth and agar dilution methods is to determine the lowest concentration of the assayed antimicrobial agent (minimal inhibitory concentration,MIC)that,under defined test conditions,inhibits the visible growth of the bacterium being investigated.MIC values are used to determine susceptibilities of bacteria to drugs and also to evaluate the activity of new antimicrobial agents.Agar dilution involves the incorporation of different concentrations of the antimicrobial substance into a nutrient agar medium followed by the application of a standardized number of cells to the surface of the agar plate.For broth dilution,often determined in 96-well microtiter plate format,bacteria are inoculated into a liquid growth medium in the presence of different concentrations of an antimicrobial agent.Growth is assessed after incubation for a defined period of time (16–20h)and the MIC value is read.This protocol applies only to aerobic bacteria and can be completed in 3d.INTRODUCTIONAgar dilution and broth dilution are the most commonly used techniques to determine the minimal inhibitory concentration (MIC)of antimicrobial agents,including antibiotics and other substances that kill (bactericidal activity)or inhibit the growth (bacteriostatic activity)of bacteria.The methods described here are targeted for testing susceptibility to antibiotic agents as opposed to other antimicrobial biocides such as preservatives and disinfectants.However,there are no major reasons why they cannot be used for these other antimicrobials.For agar dilution,solutions with defined numbers of bacterial cells are spotted directly onto the nutrient agar plates that have incorporated different antibiotic concentrations.After incubation,the presence of bacterial colonies on the plates indicates growth of the organism.Broth dilution uses liquid growth medium containing geometrically increasing concentrations (typi-cally a twofold dilution series)of the antimicrobial agent,which is inoculated with a defined number of bacterial cells.The final volume of the test defines whether the method is termed macro-dilution,when using a total volume of 2ml,or microdilution,if performed in microtiter plates using r 500m l per well.After incubation,the presence of turbidity or a sediment indicates growth of the organism.In both the agar and the broth dilution approaches,the MIC is defined as the lowest concentration (in mg l À1)of the antimicrobial agent that prevents visible growth of a microorganism under defined conditions.In clinical practice,this in vitro parameter is used to classify the tested microorganism as either clinically susceptible,intermediate or resistant to the tested drug.The interpretative standards for these classifications are published by different national organi-zations such as the Clinical and Laboratory Standards Institute (CLSI)1in the USA and the European Committee on Antimicrobial Susceptibility T esting (EUCAST)2.Breakpoints (the particular MIC that differentiates susceptible,and assumingly treatable,from resistant and assumingly untreatable organisms)are derived from microbiological and clinical experience,and can vary according to the particular species being examined and the particularantimicrobial agent.Features that define these breakpoints are MIC distributions of relevant species,pharmacodynamics and pharmacokinetics of the antimicrobial agent,and clinical outcome data.Resistance (above the breakpoint)is associated with a high likelihood of therapeutic failure,whereas susceptibility is associated with a greater probability of therapeutic success.For isolates classified as intermediate,the therapeutic effect is uncertain 3.MIC determinations can be used for monitoring the develop-ment of antibiotic drug resistance.MIC wild-type distribution databases are available for relevant species–drug combinations ().The highest MIC of the wild-type popu-lation is defined as the ‘epidemiological cut-off value’or wild-type (WT)cut-off value 3(Fig.1).Organisms with acquired resistance can be easily identified by showing higher MIC values than the epidemiological cut-off value.As even slight changes may become clinically relevant,the determination of MIC is a valuable means for resistance surveillance,as well as providing a valuable comparatorp u o r G g n i h s i l b u P e r u t a N 8002©n a t u r e p r o t o c o l s/m o c .e r u t a n .w w w //:p t thN u m b e r o f t e s t e d i s o l a t e sFigure 1|Distribution of MIC values for different isolates for given species (modified from Wiegand and Wiedemann 27).NATURE PROTOCOLS |VOL.3NO.2|2008|163for variants of a given antimicrobial agent and/or species with differential susceptibility.Indeed for new drug candidates,the MIC determination is one of the first steps to evaluate the antimicrobial potential.Specialized protocols can also allow inferences to be drawn regarding resistance mechanisms.For example,results from broth dilution MIC determination with certain b -lactam antibiotics (cefotaxime,cefpodoxime and/or ceftazidime)in the presence or absence of an inhibitor (clavulanic acid)can indicate the produc-tion of extended-spectrum b -lactamases when MICs are at least three twofold concentration steps lower in the presence of the b -lactamase inhibitor 1.Epidemiological resistance data further-more provide the basis for appropriate first-line therapy recom-mendations for empirical treatment.Dilution methods are considered as reference methods for in vitro susceptibility testing and are also used to evaluate the performance of other methods of susceptibility testing.Crucial parametersAs the test results vary widely under different test conditions,the procedures have to be standardized for intra-and inter-laboratory reproducibility.The protocols described here are adjusted to a step-by-step format and follow the guidelines of the two established organizations and committees,the CLSI 1and EUCAST 2.Modifica-tions are introduced for testing the susceptibility to cationic antimicrobial peptides and other cationic agents that tend to bind to surfaces.If implemented rigorously according to the procedures described herein,these modifications allow the generation of reliable data that will be comparable between different laboratories.The use of all methods of this protocol is limited to aerobic bacteria that grow well within 24h in the CLSI and EUCAST recommended test Mueller–Hinton growth medium.Mueller–Hinton broth (MHB)is a general purpose medium that can be used for cultivation of a wide variety of nonfastidious microorgan-isms.For growth of fastidious organisms,such as Streptococcus spp.,Haemophilus influenzae ,Neisseria gonorrheae ,Helicobacter pylori and Campylobacter spp.,the broth needs to be supplemented;furthermore,enrichment of the incubation atmosphere with CO 2and an extension of the incubation time may be necessary for growth.For these species,specific recommendations for medium composition and for test conditions can be found in the CLSI guidelines 1.MediumT o produce accurate and reproducible results,a number of addi-tional requirements must be fulfilled by the test medium for certain antibiotics or antibiotic/species combinations:Correct susceptibility testing of tetracyclines 4,5,daptomycin for gram-positive bacteria 6and aminoglycosides for Pseudomonas aeruginosa 5in broth medium is dependent on the content of Ca 2+and Mg 2+ions.Non-cation-adjusted (unsupplemented)MHB contains in general inadequate amounts of Ca 2+and Mg 2+ions (information given by manufacturer).The broth,therefore,needs to be supplemented with divalent cations when testing the abovementioned antibiotics and/or antibiotic-species combina-tions.The final concentration should be 20–25mg Ca 2+and 10–12.5mg Mg 2+per liter 1,which reflects the divalent cation concentration in blood.Cation-adjusted MHB is commerciallyavailable and only needs to be further supplemented with Ca 2+in case of daptomycin susceptibility testing,as the recommended calcium concentration for testing this antibiotic is 50mg l À1(ref.1).Please note however that cation-adjusted MHB should not be used when testing the activity of cationic antimicrobial peptides,as the presence of Ca 2+and Mg 2+ions causes a substantial inhibition of the cationic peptides’activity 7,8.Mueller–Hinton agar (MHA)needs to be supplemented with 2%(wt/vol)sodium chloride for testing susceptibility of Staphylococcus aureus to methicillin,oxacillin and nafcillin 1.Methicillin-resistant S.aureus (MRSA)are often heteroresistant with resistant and susceptible cells in the same culture and supplementation with NaCl enhances the expression of hetero-geneous resistance 9.T o avoid the adsorption of dalbavancin to plastic surfaces,the addition of polysorbate 80to broth at a final concentration of 0.002%(vol/vol)is recommended.Refer to the CLSI guidelines 1when testing this antibiotic.High levels of thymidine and thymine interfere with suscept-ibility testing of sulfonamides and trimethoprim 10.Contrary to the Difco MHB (not cation-adjusted),the BBL MHB (not cation-adjusted)is not explicitly formulated to have a low thymine and thymidine content.So,according to the manufac-turer,only the former may be used for broth dilution antimi-crobial susceptibility testing.Tigecycline is prone to oxidation,and it seems that its activity is affected by the amount of dissolved oxygen in the medium,which increases with the age of the broth.So,for broth dilution MIC tests with tigecycline,it is necessary to use fresh cation-adjusted MHB (o 12h after autoclaving)11.BacteriaThe bacteria subjected to antimicrobial susceptibility testing must be isolated in pure culture and should have been identified at the genus and species level.Most organisms are available from hospital laboratories,the American Type Culture Collection or other national collections (see Table 1).InoculumThe standardization of the bacterial cell number used for suscept-ibility testing is of critical importance for obtaining accurate and reproducible results.The recommended final inoculum size for broth dilution is 5Â105colony-forming units (cfu)ml À1;thep u o r G g n i h s i l b u P e r u t a N 8002©n a t u r e p r o t o c o l s/m o c .e r u t a n .w w w //:p t t h TABLE 1|Control organisms for antimicrobial susceptibility testing.Identical to ATCC strain Escherichia coli ATCC 25922NCTC 12241,CIP 76.24,DSM 1103Pseudomonas aeruginosa ATCC 27853NCTC 12934,CIP 76.110,DSM 1117Staphylococcus aureus ATCC 29213NCTC 12973,CIP 103429,DSM 2569Enterococcus faecalis ATCC 29212NCTC 12697,CIP 103214,DSM 2570ATCC,American Type Culture Collection,P.O.Box 1549,Manassas,VA 20108,USA;NTCT,NationalCollection of Type Cultures,Health Protection Agency,61Colindale Avenue,London NW95EQ,UK;CIP,Collection de l’Institut Pasteur,25–28Rue de Docteur Roux,75724Paris Cedex 15,France;DSMZ,Deutsche Sammlung von Mikroorganismen und Zellkulturen,Inhoffenstra e 7B,38124Braunschweig,Germany.164|VOL.3NO.2|2008|NATURE PROTOCOLSappropriate cell number in agar dilution experiments is set at 104cfu per spot.Higher inocula can lead to an increase in the MIC particularly if the tested bacterium produces an enzyme capable of destroying the antibiotic.An inoculum effect (e.g.,an eightfold or greater MIC increase upon testing with a 100-fold higher inoculum than recommended)is frequently seen when testing b -lactam suscept-ibility for isolates that produce b -lactamases that are able to inactivate b -lactam antibiotics 12.Lighter inocula than recom-mended may give artificially lower e of inocula with o 5Â105cfu ml À1in broth microdilution can lead to false-susceptible results as described for the detection of methicillin resistance in S.aureus 13and for resistance to certain b -lactams in b -lactamase overproducing Klebsiella oxytoca isolates 14.A fresh pure culture should be used for the preparation of the inoculum.T o avoid the selection of an atypical variant clone,bacteria from four to five normal-appearing colonies are taken to prepare a bacterial suspension with a density equivalent to 108cfu ml À1,which is later used for inoculation.Several options are available for the generation of the bacterial suspension (direct colony suspension into liquid and growth methods using either fresh or overnight cultures).The density of the cell suspension can be assessed spectrophotometri-cally for testing a small number of different bacterial isolates (n o 5).For a larger number of different bacterial isolates,to save time,a turbidity standard can be used as a visual parison between the standards and the turbidity of the bacterial suspensions will in fact point the researcher toward the appropriate dilution for the suspension.The turbidity of a so-called McFarland 0.5standard is equal to 1–2Â108cfu ml À1.McFarland 0.5turbidity standards are commercially available from several manufacturers (e.g.,bioMerieux,cat.no.70900or Scientific Device Laboratory).Alternatively,a BaSO 4turbidity standard equaling the McFarland 0.5standard can be prepared as described below.Once the bacterial suspension is adjusted,it must be used within 30min to avoid changes in the cell number 2.All protocols described here contain a paragraph on how to determine whether the correct inoculum density was used for the susceptibility testing.If the MIC tests are carried out in a laboratory on a routine basis,the cell counts of the inoculum need to be determined only periodically.For all other users,we recommend validating the accuracy of procedures for every test.Quality controlT o verify that the susceptibility results are accurate,it is necessary to include at least one control organism with every batch of MIC determinations.Control organisms are available from different strain collections (Table 1).The MICs for routinely used antibiotics for the quality control organisms are published 1,2and the test values for the control strains should be within the published range to be considered acceptable.LimitationsThe MIC value does not give an indication of the mode of action (cidal or static)of the antimicrobial agent.Within the MIC well or tube or on the agar plate with no visible growth,there may still be viable cells if the drug had a bacteriostatic effect on the bacterial species tested.Growth may resume after the removal of the drug.Alternatively,there may be partial inhibition resulting in impaired and reduced growth rates and consequently no visible growth within the time given.Both phenomena are different from the action of a bactericidal drug,which causes irreversible damage leading to cell death.Furthermore,even with the knowledge of the mode of action of an antimicrobial agent,the MIC value alone is a poor predictor of the efficacy of the drug in vivo .Factors that affect the response to therapy are far more complex and include host defense mechan-isms,underlying diseases of the patient,the site of infection,and the pharmacokinetic and pharmacodynamic properties of the drugs 15.Alternative method for determining MIC valuesMICs for commonly used antibiotics can be obtained using an agar diffusion method with commercially available strips containing an exponential gradient of antibiotic (Etest;AB Biodisk).The antibiotic diffuses into the agar medium inoculated with a lawn culture of the test organism.After overnight incubation,the MIC is read at the point of intersection of an elliptical growth inhibition zone with the strip that has an MIC scale printed on it.This test has been evaluated for a variety of bacteria/antibiotic combinations 16–21and is rapid and easy to use;however,it is limited to the antibiotic range supplied by the manufacturer and is an expensive test to use for screening.Several automated systems for antimicrobial susceptibility test-ing and identification of clinically relevant bacteria are now commercially available,e.g.,Phoenix Automated MicrobiologySystem (BD Diagnostic Systems),the VITEK 2System (bioMe ´r-ieux)and the MicroScan WalkAway-96System (Dade Behring).These systems are cost effective for clinical laboratories with a high throughput of clinical specimens.Fully automated systems reduce the time for setup and,depending on the system,also reduce the time to produce results compared to conventional tests.Moreover,they offer convenient interfaces with laboratory and hospital information systems.However,when testing certain organism-antimicrobial combinations limitations on the accuracy of the assessment of MIC values by these systems are known 22,23.Experimental designAs there are alternative routes for generating the bacterial suspen-sion with different time requirements and alternative methods to determine MIC values with potential pause point options that require advance planning of the workflow,the experiment should be carefully designed by the user before starting the protocol.The flowchart in Figure 2illustrates how the different stages are coordinated.Please examine this figure carefully to make an informed choice as to which experimental approach to embark on.MATERIALSREAGENTS.MHB (Difco;BD Diagnostics,cat.no.275730)sterilized by autoclaving .Mueller–Hinton II broth (cation-adjusted (CAMHB);BBL,BD Diagnostics,cat.no.212322)sterilized by autoclaving.MHA (Difco;BD Diagnostics).Agar,T echnical (Difco;BD Diagnostics,cat.no.281230).Solution A:0.02%acetic acid (Fisher)containing 0.4%BSA (BoehringerMannheim)p u o r G g n i h s i l b u P e r u t a N 8002©n a t u r e p r o t o c o l s/m o c .e r u t a n .w w w //:p t t h NATURE PROTOCOLS |VOL.3NO.2|2008|165.Solution B:0.01%acetic acid containing 0.2%BSA.Preparation of McFarland Standard 0.5:BaCl 2Á2H 2O (Sigma-Aldrich,cat.no.B0750),H 2SO 4(Fluka,cat.no.84721)!CAUTION H 2SO 4is very corrosive/toxic;handling must be performed under the hood;wear acid-resistant gloves and protective clothing (see REAGENT SETUP)..Cation adjustment:MgCl 2Á6H 2O (Fluka,cat.no.63072),CaCl 2Á2H 2O (Fluka,cat.no.21101).Physiological saline [0.9%(wt/vol)NaCl]sterilized by autoclaving EQUIPMENT.Spectrophotometer suitable for measuring at wave lengths of 600and 625nm.For antibiotics:sterile 96-well microtiter plates.We recommend polystyrene plates (BD Falcon;Fisher Scientific,cat.no.351177)for most antimicrobials as these are easier to read at the end of the experiment.For cationic antimicrobial agents such as peptides:96-well polypropylene microtiter plates (Costar,cat.no.3790)!CAUTION Avoid tissue culture treated or polystyrene plates as these are strongly negatively charged and will nonspecifically bind peptides..Eppendorf polypropylene microcentrifuge tubes,1.5ml (Fisher Scientific,cat.no.05-402-24B),sterilized.Screw-capped glass tubes,13Â100mm (Fisher Scientific,cat.no.14-930-10A).48-Pin replicator (Boekel Scientific,cat.no.140501)for inoculating agar dilution plates.Shaker,suitable for test tubes 13Â100mm.Parafilm (Pechiney Plastic Packaging;Fisher Scientific,cat.no.13-374-10).Glass tubes,13Â100mm (VWR International,cat.no.47729-572)with cap (Utech Products,cat.no.1017622),sterilized .Erlenmeyer flasks.Sterile petri dishes,15Â100mm (Fisherbrand;Fisher Scientific,cat.no.08-75-712).0.2-m m pore size cellulose acetate filters (Nalgene;Fisher Scientific,cat.no.190-2520).Cell spreader (Fisherbrand;Fisher Scientific,cat.no.08-100-11).Inoculation loop or cotton swabs (sterilized by autoclaving).Vortex mixerREAGENT SETUPPreparation of McFarland 0.5BaSO 4turbidity standard Prepare a 1.175%(wt/vol)barium chloride dihydrate (BaCl 2Á2H 2O)solution (0.048mol l À1BaCl 2)and a 1%(vol/vol)sulfuric acid (H 2SO 4)solution (0.18mol l À1,0.36N).Add 0.5ml of the 1.175%BaCl 2solution to 99.5ml of the 1%H 2SO 4solution with constant stirring to get a suspension.Measure the optical density of the turbidity standard using a spectrophotometer with a 1cm light path length.The correct absorbance at 625nm should be 0.08–0.13.Aliquot 4–6ml into screw-capped glass tubes.The tubes should have the same size as those for preparing the bacterial suspension for inoculation.Seal tubes tightly withParafilm and store in the dark at room temperature (20–23.51C).Standards are p u o r G g n i h s i l b u P e r u t a N 8002©n a t u r e p r o t o c o l s/m o c .e r u t a n .w w w //:p t t h Pure cultures of bacterial isolates (test and control)Day 1Day 2orPrior to testing (2 d required)Prepare overnight culturesPrepare media (store at 4 °C) and antibioticstock solutions (freeze)Antimicrobial susceptibility testing— part I Determine the cell count inovernight culturesPreparation of bacterial suspensionIncubate on nonselectiveagar overnightoror orSuspension with 1–2 × 108cfu/mlTake sample for cell count (ifused for agar dilution)Colony suspensionAdjust turbidity using a McFarland Standard 0.54–6 h growth methodPrepare overnight cultures inliquidGrowth method using overnight culturesAdjust turbidity using a spectrophotometerPrepare agar plates with antibiotics[Day 1 may be possibledepending on the antibiotic (store at 4 °C)]orororPreparebroth macro dilutions of antibioticPrepare broth micro dilutions of antibioticPrepare broth micro dilutions of peptideAntimicrobial susceptibility testing— part ll[Day 1 may be possible (freeze)]Inoculate agarplatesorInoculate broth macro dilutions of antibioticororTake sample for cell countRead MICsInoculate broth micro dilutions of peptideInoculate broth micro dilutions of antibioticDetermine cell countDay 3Figure 2|Flowchart for antimicrobial susceptibility testing.166|VOL.3NO.2|2008|NATURE PROTOCOLSstable for at least a month.!CAUTION H 2SO 4is corrosive/toxic;wear appro-priate safety clothing when handling concentrated H 2SO 4.Preparation of antibiotic-free nutrient-rich agar plates Prepare agar med-ium according to the manufacturer’s instructions.Alternatively,use nutrient-rich broth according to the manufacturer’s instructions and add 1.7%agar (17g agar per liter)before autoclaving.Approximately 20–25ml is necessary to pour one 15Â100mm petri dish.After autoclaving (e.g.,1211C,15min,1bar),cool the medium to 50–601C.Pour agar into the petri dishes and allow to set.Dry the surface of the agar plates either in an incubator or in a laminar air flow hood for 30min with the lid ajar.Store agar plates in plastic bags in inverted position (bottom facing up)at 41C.Adjustment of cation content of MHB medium (20–25mg Ca 2+and 10–12.5mg Mg 2+per liter)Prepare a 10mg ml À1Mg 2+stock solution by dissolving 8.36g of MgCl 2Á6H 2O in 100ml deionized water.Prepare a 10mg ml À1Ca 2+stock solution by dissolving 3.68g of CaCl 2Á2H 2O in 100ml deionized water.Filter-sterilize both stock solutions using 0.2-m m pore size cellulose-acetate filters.Prepare MHB according to the manufacturer’s instructions,autoclave and cool the medium to 2–81C before the addition of the cation solutions.Add 100m l of stock solution per 1mg l À1needed for 1l of medium.For example,add 2ml of Ca 2+stock solution if 20mg needs to be added to 1l MHB.Stock solution of the antimicrobial agent Antimicrobial agents should be stored in the dark at 41C in sealed containers containing a desiccant unless recommended otherwise by the manufacturer.We advise the storage ofantimicrobial peptides at 201C.Before weighing the antimicrobial agent,let the container warm at room temperature for B 2h to avoid condensation of water on the powder.Antibiotics are generally supplied by the manufacturer with the information about the potency (m g per mg powder)that needs to be taken into consideration when weighing the agent.For antibiotics,prepare a stock solution at 10mg ml À1when planning to use it for agar dilution (Step 4A).For broth dilution tests (Steps 4B and 4C)set up a stock solution with a concentration atleast ten times higher than the highest concentration to be tested.For testing antimicrobial peptides (Steps 4D and 4E),prepare a 20-fold concentrated stock e the following formula for calculating the right amount of antibiotic to be weighed (this does not apply to antimicrobial peptides):W ¼ðC ÂV ÞPwhere,W ¼weight of antimicrobial agent in milligram to be dissolved;V ¼desired volume (ml);C ¼final concentration of stock solution (m g ml À1);P ¼potency given by the manufacturer (m g mg À1).Use sterile containers and spatula for weighing the antimicrobial agent and dissolve in sterile distilled water or in the recommended solvent.A list ofsolvents for frequently used antibiotics is found in ref.24.Antibiotic solutions can be filter-sterilized using a 0.2-m m pore size cellulose-acetate filter.However,it has to be ascertained that the antibiotic does not bind to cellulose acetate (information that is sometimes given by the manufacturer).Do not filter-sterilize antimicrobial peptides,which tend to bind to anionic surfaces like cellulose acetate.Always use the fresh antibiotic stock solution for broth microdilution if it is planned to freeze the antibiotic containing microtiter plates at 701C for later usage.For other applications,aliquot the stocksolution.The volume of the aliquots depends on the downstream applications and in general one aliquot should contain the volume needed for one test.Containers need to be sterile,cold resistant and should seal tightly (e.g.,for smaller volumes sterile Eppendorf tubes can be used).Store the aliquots at 201C or below unless it is instructed otherwise by the manufacturer.Most antimicrobial agents are stable at À601C for at least 6months.Stability and storage information for frequently used antibiotics can be found in ref.24.Do not refreeze thawed stock solutions.Some antimicrobials,particularly b -lactams antibiotics,can degrade when thawed and refrozen repeatedly 1.PROCEDUREPreparation of the bacterial suspensionTIMING B 5min per isolate/overnight pause point1|Streak the bacterial isolates to be tested (including a control organism)onto nutrient-rich (e.g.,Mueller–Hinton)agar plates without inhibitor to obtain single colonies.2|Incubate plates for 18–24h at 371C.3|Different methods for the preparation of the inoculum can be used.Direct suspension of overnight colonies into broth or sterile saline solution (option A)is a very convenient method that can be used for most bacterial species.It is particularlyrecommended for fastidious organisms such as Streptococcus spp.,Haemophilus spp.and Neisseria spp.For some strains within a species,unpredictable clumping can occur with option A.Consequently,when colonies are difficult to suspend and an even suspension is difficult to achieve,freshly grown broth cultures can be diluted (option B).As an alternative to a freshly grown culture,an overnight broth culture can also be used (option C)according to the user’s preference.This method is not part of CLSI or EUCAST recommendations;however,the option to use overnight cultures is given in the guide to antimicrobial susceptibility testing of the British Society of Antimicrobial Chemotherapy 24.(A)Colony suspension methodTIMING B 5min per isolate (i)Prepare the antibiotic or peptide dilutions.(ii)For each isolate,select three to five morphologically similar colonies from the fresh agar plate from Step 2and touchthe top of each selected colony using a sterile loop or cotton swab.Transfer the growth into a sterile capped glass tube containing sterile broth or saline solution.Mix using a vortex mixer.(iii)Turbidity can be assessed visually by comparing the test and the McFarland Standard.Mix the McFarland 0.5BaSO 4stan-dard vigorously using a vortex mixer.Please note that commercially available standards containing latex particles should not be vortexed,but gently inverted several parison against a white background with contrasting black lines and good lighting are helpful.Alternatively,the turbidity can be verified measuring the absorbance of the suspension spectrophotometrically.The absorbance should be in the same range as that of the McFarland standard 0.5(OD625nm should be at 0.08–0.13).(iv)Adjust the suspension’s turbidity to that of a McFarland Standard 0.5by adding sterile distilled water,saline or broth,ifthe turbidity is too high,or by adding more bacterial material if is too low.m CRITICAL STEP After turbidity adjustment,the bacterial suspension should be used within 30min,as the cell number might otherwise change.p u o r G g n i h s i l b u P e r u t a N 8002©n a t u r e p r o t o c o l s/m o c .e r u t a n .w w w //:p t t h NATURE PROTOCOLS |VOL.3NO.2|2008|167。
心理学术语+

汉英心理学常用词汇[人格]表面特质 surface traitⅠ型错误 type Ⅰ error Ⅱ型错误 type Ⅱ errorF 分布 F distributionF 检验 F testt 分布 t distributiont 检验 t testz 分数 z scorez 检验 z testφ系数 φ coefficientχ2分布 chi-square distributionχ2检验 chi-square testχ2可加性 additivity of chi-square艾森克人格问卷 Eysenck Personality Questionnaire, EPQ爱德华兹个人爱好量表 Edwards Personal Preference Schedule, EPPS 白板说 theory of tabula rasa百分等级 percentile rank贝利婴儿发展量表 Bayley Scales of Infant Development贝叶斯定理 Bayes’ theorem备择假设 alternative hypothesis比率量表 ratio scale比率智商 ratio intelligence quotient比内-西蒙智力量表 Binet-Simon Scale of Intelligence变异系数 coefficient of variation标准差 standard deviation标准分数 standard score标准化测验 standardized test标准九分 stanine标准误差 standard error标准正态分布 standard normal distribution表面效度 face validity参数 parameter参数估计 parameter estimation参数统计检验 parametric statistical test操作测验 performance test测量误差 measurement error测验标准化 test standardization测验法 test method测验分数 test score测验焦虑test anxiety测验偏向test bias测验手册test manual测验特征函数test characteristic function测验项目test item差异量数measure of difference差异显著性significance of difference常模norm常模参照测验norm-referenced test场独立性field independence场依存性field dependence称名量表nominal scale成就测验achievement test抽样sampling抽样分布sampling distribution处理均方mean square of treatment创造性人格creative personality次要特质secondary trait丹佛儿童发展筛选测验Denver Development Screening Test 单尾检验one-tailed test单因素方差分析one-factor analysis of variance导出分数derived score等距量表interval scale等值复本equivalent forms邓肯多重范围检验Duncan multiple-range test地位人格status personality点二列相关point biserial correlation调和平均数harmonic mean独立性检验test of independence多项选择法multiple choice method多元分析multiple analys is多元回归multiple regression多重比较multiple comparison多重相关multiple correlation儿童统觉测验Children’s Apperception Test二列相关biserial correlation二项分布binomial distribution二元论dualism泛心[灵]论panpsychism方差variance方差分析analysis of variance, ANOVA方差齐性homogeneity of variance非参数检验non-parametric test费希尔Z转换Fisher’s Z transform ation分半信度split-half reliability分层抽样stratified sampling符号检验sign test负相关negative correlation副现象论epiphenomenalism概化理论generalizability theory, GT感觉主义sensationalism格塞尔发展测验Gesell Development Test个别测验individual test构想效度construct validity古迪纳夫-哈里斯画人测验Goodenough-Harries Drawing Test合成分数composite score机能系统理论theory of functional system积差相关product-moment correlation极大似然法maximum likelihood method集中量数measure of central tendency集中趋势central tendency几何平均数geometric average计算机化适应性测验computerized adaptive test加权平均数weighted mean家庭调查表home inventory假设检验hypothesis testing间接测量indirect measurement检验能力power of test检验统计量statistic of test鉴别指数discrimination index交叉效度分析cross validation交互作用interaction焦虑anxiety教师自编测验teacher-made test进攻性aggresiveness经典测验理论classical test theory, CTT经验心理学empirical psychology警察心理测验mental test for police拒绝域rejection region聚类分析cluster analysis均方mean square考夫曼儿童评估测验Kaufman Assessment Battery for Children, K-ABC 克龙巴赫α系数Cronbach’s α coefficien t客观测验objective test客观题objective item肯德尔和谐系数Kendall’s concordance coefficient肯德尔一致性系数Kendall’s consistency coefficient控制源locus of control库德-理查森信度Kuder-Richardson reliability跨文化测验cross-cultural test雷文推理测验Raven’s Progressive Matrices Test类型论type theory离差deviation离差平方和sum of deviation square离差智商deviation intelligence quotient离中趋势divergence tendency理论心理学theoretical psychology理性心理学rational psychology理性主义rationalism利克特量表Likert Scale连续变量continuous variable联想主义associationism两阶段抽样法two-stage sampling量表值scale value列联表contingency table临床测验clinical test临界值critical value零相关zero correlation陆军甲种测验Army Alpha Test罗杰斯自我论Rogers’ self theory马尔计算理论Marr’s computational theory马克思主义心理学Marxist psychology曼-惠特尼U检验Mann-Whitney U test描述统计descriptive statistics明尼苏达多相人格调查表Minnesota Multiphas ic Personality Inventory, MMPI 墨迹测验inkblot test目标参照测验criterion referenced test内容效度content validity纳格尔图片测验Nagel Chart Test难度测验power test能力测验ability test能力倾向测验aptitude test纽曼-科伊尔斯检验Newman-Keuls test判别分析discriminant analysis皮尔逊相关系数Pearson’s correlation coefficient偏回归partial regression偏态分布skewed distribution平行测验parallel test平行复本parallel forms评定法rating method评定量表rating scale评定者误差rater’s error评分者信度scorer reliability迫选测验forced-choice test潜在特质理论latent trait theory, LTT情境测验situational test区分能力倾向测验Differential Aptitude Test, DAT区分效度discrimination validity趋势检验trend test全距range人格personality人格测验personality test人格结构personality structure人格理论theory of personality人格面具persona人格心理学personality psychology认识论epistemology散点图scatterplot色盲测验color blindness test神经心理测验neuropsychological test生活事件量表life event scale剩余标准差residual standard deviation十六种人格因素问卷Sixteen Personality Factor Questionnaire, 16PF 时限time limit实验控制experimental control实证效度empirical validity适合度检验goodness of fit test双峰分布bimodal distribution双盲double blind双尾检验two-tailed test顺序量表ordinal scale思维型thinking type斯皮尔曼-布朗公式Spearman-Brown formula斯皮尔曼等级相关Spearman’s rank correl ation斯泰尔-克劳福德效应Stile-Crawford effect斯坦福-比内智力量表Stanford-Binet Intelligence Scale斯特朗-坎贝尔兴趣调查表Strong-Campbell Interest Inventory四分[位]差quartile deviation, Q速度测验speed test算术平均数arithmetic mean, AM随机抽样random sampling随机化randomization随机区组设计randomized block design态度量表attitude scale特质trait特质论trait theory填充测验completion test同时效度concurrent validity同质性homogeneity统计分析statistical analysis统计概率statistical probability统计决策statistical decision统计显著性statistical significance投射测验projective test团体测验group test推论统计inferential statistics完全随机化设计completely randomized design威尔科克森符号秩次检验Wilcoxon’s sign rank test韦克斯勒成人智力量表Wechsler Adult Intelligence Scale, WAIS韦克斯勒儿童智力量表Wechsler Intelligence Scale for Children, WISC 文化公平测验culture fair test无偏估计量unbiased estimator误差均方error mean square析因设计方差分析analysis of variance of factorial design系统误差systematic error显著性水平significance level线性关系linear relationship线性回归linear regression相关correlation相关矩阵correlation matrix相关系数coefficient of correlation相容效度congruent validity项目反应理论item response theory, IRT项目分析item analysis项目难度item difficulty项目区分度item discrimination项目特征函数item characteristic function项目特征曲线item characteristic curve项目选择item selection小概率事件small probability event效标criterion效标关联效度criterion-related validity效度validity校正数correction协方差分析analysis of covariance心理测量学psychometrics心理测验mental test, psychological test心理分析mental analys is心理量表mental scale心理年龄mental age心理统计学psychological statistics心理物理量表psychophysical scale心理现象系统system of mental phenomena心理学方法论methodology in psychology心理学史history of psychology心理学体系system of psychology心理学系统观systematic approach in psychology心理主义mentalism心身平行论mind-body parallelism心身问题mind-body problem心身相互作用论mind-body interactionism新生儿行为评价量表Neonatal Behavioral Assessment Scale 信度reliability信息函数information function兴趣测验interest test虚无假设null hypothesis选拔与安置测验selection and placement test学业成就测验academic achievement test延迟满足delay of gratification样本sample一般能力测验general ability test一元论monism因变量dependent variable因素分析factor analys is因素负荷factor loading因素效度factorial validity英国经验主义British empiricism又称“变异数”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :c o n d -m a t /9804312v 1 [c o n d -m a t .d i s -n n ] 29 A p r 1998Dependence of critical level statistics on the sample shape H.Potempa and L.Schweitzer Physikalisch-Technische Bundesanstalt,Bundesallee 100,D-38116Braunschweig,Germany Abstract The level-spacing distribution of consecutive energy eigenvalues is calculated numerically at the metal insulator transition for 3d systems with different cuboid shapes.It is found that the scale independent critical P c (s )changes as a function of the aspect ratio of the samples while the critical disorder W c /V =16.4remains the same.We use our data to test whether an expression for the small-s behaviour of the level statistics proposed by Kravtsov and Mirlin for the metallic regime is applicable also at the critical point.For this reason,a shape dependent dimensionless critical conductance g c has been extracted from the small-s behaviour of the critical level statistics.Our result for a cubic sample,g c =0.112±0.005,is in good agreement with a value obtained previously from calculations using the Kubo-formula.1Introduction Energy eigenvalue correlations provide general tools for the statistical description of disordered materials.Among them,the nearest neighbour level spacing distribution P (s )represents one of the simplest statistics.Here,s =|E i +1−E i |/∆is the energy difference of consecutive eigenvalues E i divided by the mean level spacing ∆.Nevertheless,knowing P (s ),it is possible to tell whether a given system exhibits metallic or insulating behaviour at temperature T =0K.Considerable attention has recently focused on the special case of critical statistics which were found at the metal insulator transition in disordered 3d [1,2,3,4,5,6,7,8,9]and 2d [10,11,12,13]systems.In all cases,the numerically obtained critical level statistics were noticed to be independent of the system size L .This is different in the metallic and insulating regimes where a size dependence has been observed.In the limit L →∞,the nearest neighbour spacing distribution follows the Poissonian decay,P (s )=exp(−s ),for disorder strength W larger than the critical disorder W c .The metallic side,W/W c <1,is well described by random matrix theory (RMT)[14,15,16,17].As in the metallic phase,the critical P c (s )depends on the symmetry of the Hamiltonian describing the system under consideration.In addition,and in contrast to the universal RMT description for the metallic phase,the critical P c (s )depends alsoon the spatial dimension.The respective forms of P c (s )are known only from numerical studies.In Ref.[7]using the Anderson model,the application of an Aharonov-Bohm-flux was shown not only to change the universality class of the level statistics due to breaking of time reversal symmetry.It has also been demonstrated that,depending on the strength of the flux,there exists a set of scale independent critical spacing distributions.These are associated with a continuous crossover from orthogonal to unitary symmetry [7,18].It is well known that the corresponding Hamilton matrix can be transformed such that the AB-flux is completely absorbed into the boundary conditions.So the question arises,whether or not P c (s )does in general depend on the boundary conditions applied.Recently,it has been shown [19]that P c (s )is in fact sensitive to a change of the periodic boundary conditions,which were always applied previously,to Dirichlet boundary conditions in one,two and three directions.Figure1:The critical level spacing distribution P c(s,q)versus the level spacing s for aspect ratios q=1(⋆,L0=L z=30a),q=1/7(◦,L0=56a,L z=8a),and q=20(•,L0= 10a,L z=200a).The solid line is the Poissonian decay exp(−s).The insert displays the semi-logarithmic plot of the large-s behaviour.In this paper we show that P c(s)is sensitive to the shape of the sample,too.We present results of a numerical investigation on variousfinite size cuboids with square base L20and height L z,characterized by the aspect ratio q=L z/L0.Assuming that a formula for the small-s behaviour of P(s),proposed by Kravtsov and Mirlin[20]for the metallic regime,may approxi-mately be used at the metal-insulator transition,a dimensionless critical conductance g c can be extracted from the small-s behaviour of the calculated P c(s).Wefind that g c also depends on the sample shape and that the value obtained for the cubic system is in close agreement with a result obtained by a different method.2ModelWe investigate the conventional3d Anderson model which is described by the HamiltonianH= mεm c†m c m+V <m=n>(c†m c n+c†n c m).(1) The creation,c†m,and annihilation,c m,operators act on the states of non-interacting electrons at the sites{m,n}of a3d simple cubic lattice.The disorder energiesεm are chosen to be a set of independent random numbers distributed in the interval[−W/2,W/2]with probability 1/W,where W denotes the disorder strength measured in units of V.We consider only transfer between nearest neighbour sites.Periodic boundary conditions are applied in all directions.The size of the different systems investigated are described by a quadratic base L20and a height L z ranging from8to200lattice constants a.The shape of the system is conveniently denoted by the dimensionless aspect ratio q=L z/L0.For all shapes,a size independent metal insulator transition is found at a critical disorder of W c/V=16.4.The eigenvalues used in our study have been taken from an interval[−0.5V,0.5V]around the band centre.They are obtained by direct diagonalization using a Lanczos algorithm.For each aspect ratio,several system sizes are computed with a large number of different realizations<ρ>2<ρ(E)ρ(E+ω)>,(3) whereρ(E)is the density of states at energy E,s=ω/∆,and<...>denotes averaging over realizations of the disorder potential.In the metallic regime and for small s,R(s)becomes[20]R(s)=π2π6g2)s.(4)∞ n x,n y,n z=−∞n2x+n2y+n2z=01(2+q2)2In conclusion,a dependence of the scale independent critical level statistics on the shape of the samples has been detected at the Anderson transition in3d ing a formula which has been proposed for the metallic regime[20]tofit our data obtained at the critical point,we find a shape dependence of the scale independent conductance g c.Provided that this method of extracting the conductance is justified also at the critical point,the various experimentally obtained critical conductances reported in the literature can possibly be attributed to different shapes of the samples investigated.AcknowledgmentsWe would like to thank G.Montambaux and I.Kh.Zharekeshev for useful discussions. References[1]B.I.Shklovskii et al.,Phys.Rev.B47,11487(1993).[2]E.Hofstetter and M.Schreiber,Phys.Rev.B48,16979(1993).[3]E.Hofstetter and M.Schreiber,Phys.Rev.Lett.73,3137(1994).[4]A.G.Aronov,V.E.Kravtsov,and I.V.Lerner,JETP Lett.59,39(1994).[5]A.G.Aronov,V.E.Kravtsov,and I.V.Lerner,Phys.Rev.Lett.74,1174(1995).[6]I.K.Zharekeshev and B.Kramer,Jap.Journ.Appl.Phys.34,4361(1995).[7]M.Batsch,L.Schweitzer,I.Kh.Zharekeshev,and B.Kramer,Phys.Rev.Lett.77,1552(1996).[8]J.T.Chalker,V.E.Kravtsov,and I.V.Lerner,JETP Lett.64,386(1996).[9]I.Kh.Zharekeshev and B.Kramer,Phys.Rev.Lett.79,717(1997).[10]L.Schweitzer and I.Kh.Zharekeshev,J.Phys.:Condens.Matter7,L377(1995).[11]S.N.Evangelou,Phys.Rev.Lett.75,2550(1995).[12]T.Ohtsuki and Y.Ono,J.Phys.Soc.Jpn.64,4088(1995).[13]M.Batsch and L.Schweitzer,in High Magnetic Fields in the Physics of Semiconductors II:Proceedings of the International Conference,W¨u rzburg1996,edited by ndwehr and W.Ossau(World Scientific Publishers Co.,Singapore,1997),pp.47–50.[14]E.P.Wigner,Ann.Math.65,203(1957).[15]F.J.Dyson,Journal of Mathematical Physics3,140(1962).[16]M.L.Mehta,Random Matrices,2nd ed.(Academic Press,San Diego,1991).[17]K.B.Efetov,Adv.Phys.32,53(1983).[18]G.Montambaux,Phys.Rev.B55,12833(1997).[19]D.Braun,G.Montambaux,and M.Pascaud,cond-mat/9712256(1997).[20]V.E.Kravtsov and A.D.Mirlin,JETP-Lett.60,645(1994).[21]mbrianides and H.B.Shore,Phys.Rev.B50,7268(1994).[22]M.Kaveh and N.F.Mott,Phil.Mag.B55,9(1987).。
