两个平面垂直的判定和性质(新2019)
两个平面垂直的判定和性质

α
l
所以 BD⊥α,BD⊥BC, 所以△CBD是 ⊥ , ⊥ , 所以△ 是 直角三角形, 直角三角形, 在直角△ 在直角△BAC中,BC= 3 + 4 = 5 中
2 2
在直角△CBD中,CD= 52 + 122 = 13 在直角△ 中 所以CD的长为 所以 的长为13cm. 的长为
β β α α
2. 平面与平面垂直的判定定理: . 平面与平面垂直的判定定理: ①文字语言:如果一个平面过另一个平面 文字语言: 的一条垂线,则这两个平面互相垂直; 的一条垂线,则这两个平面互相垂直; ②图形语言: 图形语言:
α
A B
β
③符号语言:AB⊥β,AB∩β=B, 符号语言: ⊥ , , AB
ALeabharlann 平面ACD⊥平面BDC; ⊥平面 平面 ;
D B C
(2)在原图中,直角△BAC,因为 )在原图中,直角△ , AB=AC=a,所以 ,所以BC= 2 a, , 所以 BD=DC=
2 2
a, ,
△BDC是等腰直角三角形。 是等腰直角三角形。 是等腰直角三角形 所以BC= 所以BC= 2 BD= a A 是等腰直角三角形。 △BDC是等腰直角三角形。 是等腰直角三角形 所以AB=AC=BC, , 所以 因此∠ 因此∠BAC=60°. °
B D C
练习题 1. 下列命题中正确的是( C ) . 下列命题中正确的是( 分别过两条互相垂直的直线, (A)平面 和β分别过两条互相垂直的直线, )平面α和 分别过两条互相垂直的直线 则α⊥β ⊥ 内的一条直线垂直于平面β内 (B)若平面 内的一条直线垂直于平面 内 )若平面α内的一条直线垂直于平面 的两条平行直线, 的两条平行直线,则α⊥β ⊥ 内的一条直线垂直于平面β内 (C)若平面 内的一条直线垂直于平面 内 )若平面α内的一条直线垂直于平面 的两条相交直线, 的两条相交直线,则α⊥β ⊥ 内的一条直线垂直于平面β内 (D)若平面 内的一条直线垂直于平面 内 )若平面α内的一条直线垂直于平面 的无数条直线, 的无数条直线,则α⊥β ⊥
11.4.1直线与平面垂直的性质定理(课件)高一下学期数学(新教材人教B版2019必修第四册)

所以PO⊥OA,PO⊥OB,PO⊥OC.
因为PA=PB=PC=a,
所以△PAO≌△PBO≌△PCO.
所以OA=OB=OC,所以O为△ABC的外心.
因为PA,PB,PC两两垂直,所以AB=BC=CA= 2a,
3
3
6
3
所以△ABC为正三角形,所以OA= AB= a,
2
2
∴CD⊥AD1.∵A1D∩CD=D,
∴AD1⊥平面A1DC.
又∵MN∥OA,∴四边形 AMNO 为平行四边形,
又∵MN⊥平面A1DC,
∴ON=AM.
∴MN∥AD1.
1
1
∵ON= AB,∴AM= AB ,
2
2
∴M 是 AB 的中点.直线垂直于同一个平面,那么这两条直线平行.
直线与平面垂直的性质定理
直线与平面所成的角
斜拉桥又称斜张桥,是将主梁用许多拉索直接拉在桥塔上的一种桥梁,是由承压的
塔、受拉的索和承弯的梁体组合起来的一种结构体系.其可看作是拉索代替支墩的多
跨弹性支承连续梁.其可使梁体内弯矩减小,降低建筑高度,减轻了结构重量,节省了材
料.斜拉桥由索塔、主梁、斜拉索组成.
直线与平面所成的角
E是PC的中点.
(1)求PB和平面PAD所成的角的大小;
(2)求证:AE⊥平面PCD.
达标检测
(1)解:在四棱锥P-ABCD中,
因为PA⊥底面ABCD,AB⊂平面ABCD,
所以PA⊥AB.
又AB⊥AD,PA∩AD=A,
所以AB⊥平面PAD.
所以PB在平面PAD内的射影为PA,
即∠APB为PB和平面PAD所成的角.
高中数学 第九章 两个平面垂直的判定和性质(二)教学案 苏教版

高中数学第九章两个平面垂直的判定和性质(二)教学案苏教版一、素质教育目标(一)知识教学点1.两个平面垂直的性质定理.2.异面直线上两点间的距离公式.(二)能力训练点1.弄清反证法与同一法之间的关系,并会应用同一法证题,进一步培养学生的逻辑思维能力.2.掌握两个平面垂直的性质定理,理解面面垂直问题可能化为线面垂直的问题.3.异面直线上任意两点间的距离公式不仅可用于求其值,还可以证明两条异面直线的距离是异面直线上两点的距离中最小的.另外,还可解决分别在二面角的面内两点的距离问题.二、教学重点、难点、疑点及解决方法1.教学重点:掌握两个平面垂直的性质;会运用异面直线上两点间的距离公式.2.教学难点:异面直线上两点间距离公式的应用.3.教学疑点:(1)弄清反证法与同一法的联系与区别.(2)正确理解、应用异面直线上两点间的距离公式:EF=三、课时安排本课题安排2课时.本节课为第二课时,主要讲解两个平面垂直的性质及异面直线上两点间的距离公式.四、教与学的过程设计(一)复习两个平面垂直的定义,判定师:什么是两个平面互相垂直?生:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.师:如何判定两个平面互相垂直?生:第一种方法根据定义,判定两个平面所成的二面角是直二面角;第二种方法是根据判定定理,判定其中一个平面内有一条直线垂直于另一个平面.(二)两个平面垂直的性质师:今天我们接着研究两个平面垂直的性质.两个平面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.已知:平面α⊥β,α∩β=CD,AB α且AB⊥CD于B.求证:AB⊥β.证明:在平面β内引直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角.∵α⊥β,∴AB⊥BE.又∵AB⊥CD,∴AB⊥β.师:从性质定理可以得出,把面面垂直的问题转化为线面垂直的问题.例1 如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.已知:α⊥β,P∈α,P∈a,a⊥β.求证:a α.师提示:要证明a α,一般用反证法,即否定结论→推出矛盾→肯定结论.下面请同学们写出它的证明过程.其中c为α与β的交线.∵α⊥β,∴b⊥β.又∵P∈α,P∈a,a⊥β,这与“过一点P有且只有一条直线与已知平面垂直”矛盾.∴a α.师:现在我们来看课本P.44的证明,这种方法叫同一法.什么是同一法呢?(幻灯显示)一个命题,如果它的题设和结论所指的事物都是唯一的,那么原命题和它的逆命题中,只要有一个成立,另一个就一定成立,这个道理叫做同一法则.在符合同一法则的前提下,代替证明原命题而证明它的逆命题成立的一种方法叫做同一法.同一法的一般步骤是什么?(幻灯显示)1.不从已知条件入手,而另作图形使它具有求证的结论中所提的特性;2.证明所作的图形的特性,与已知条件符合;3.因为已知条件和求证的结论所指的事物都是唯一的,从而推出所作的图形与已知条件要求的是一个东西,由此断定原命题成立.证明(同一法):设α∩β=c,过点P在平面α内作直线b⊥c,根据上面的定理有b⊥β.因为经过一点只能有一条直线与平面β垂直,所以直线a应与直线b重合.即a α.师:比较反证法与同一法,我们可以知道:凡可用同一法证明的命题也可用反证法来证;反证法可适用于各种命题,同一法只适用于符合同一法则的命题.另外,例1的结论也可作为两个平面垂直的另一个性质,可直接应用.下面请同学们一齐完成例2.(三)异面直线上两点间的距离例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA'的长度为d.在直线a、b上分别取点E、F,设,A'E=m,AF=n,求EF.解:设经过b与a平行的平面为α,经过a和AA'的平面为β,α∩β=c,则c∥a,因而b、c所成的角等于θ,且AA'⊥C.又∵AA'⊥b,∴AA'⊥α.根据两个平面垂直的判定定理,β⊥α,在平面β内作EG⊥C,则EG=AA'.并且根据两个平面垂直的性质定理,EG⊥α.连结FG,则EG⊥FG.在Rt△FEG中.EF2=EG2+FG2∵AG=m,∴在△AFG中.FG2=m2+n2-2mncosθ.又∵EG2=d2∴EF2=dw+m2+n2-2mncosθ.如果点F(或E)在点A(或A')的另一侧,则EF2=d2+m2+n2+2mncosθ.师:例2不仅求出两条异面直线上任意两点间的距离公式,还解决了下面的三个问题:(1)证明了两条异面直线公垂线的存在性.(2)证明两条异面直线的距离是异面直线上两点的距离最小的.∵AA'=EG,且AA',EG是平面α的垂线,而EF是斜线,∴AA'<EF.如在实际中,两条交叉的高压电线如果放电时,火花正是通过它们的最短距离.(3)也可以解决分别在二面角的面内两点的距离问题,请看下面练习.(四)练习在60°二面角的枝上,有两个点A、B,AC、BD分别是在这个二面角的两个面内垂直于AB的线段.已知:AB=4cm,AC=6cm,BD=8cm,利用异面直线上两点距离公式求CD.(P.45中练习3)∴AC与BD是异面直线.∵AB⊥AC交于点A,AB⊥BD交于点B,∴AB是AC、BD的公垂线,AC、BC所成角是60°.已知AB=4cm,AC=6cm,BD=8cm.师点评:根据二面角的平面角来求异面直线上两点间的距离时,应用异面直线上两点间的距离公式一定要注意cosθ前正负号的选择(当θ≤90°时取“-”号).(五)总结本节课我们学习了两个平面垂直的性质及异面直线上两点间距离的求法.正确理解、掌握异面直线上两点间的距离公式及其应用是本节课学习的关键.五、作业P.46中习题六9、10(2)、11、12.。
两个平面垂直的判定和性质(新编201912)

两个平面垂直的性质定理: 如果两个平面垂直,那么在一个平面内垂直
于它们交线的直线垂直于另一个平面。
已知:α ⊥ β, α β, AB ⊂α, AB ⊥α 于B。
求证:AB .
E
BA
C
证明:在平面 内作BE⊥CD,垂足为B。
则∠ABE就是二面角 CD 的平面角。 由α ⊥β可知AB⊥BE。
例1、如果两个平面互相垂直,那么经过第一个 平面内的一点垂直于第二个平面的ห้องสมุดไป่ตู้线,在第一 个平面内
已知: , P , P a, a
求证:a .
证明:设 c .过点P在平面α 内作直线b⊥c, 根据上面的定理有b⊥β.
因为经过一点只能有一条直线与平面β垂直, 所以直线a应与直线b重合.
又AB⊥CD,BE与CD是 内两条相交
直线,
AB .
ED
BA
C
;宠物X光机 宠物X光机
;
谓搭配不当;B句“掀起了……”后面缺少了中心词“高潮”,造成动宾搭配不当;C句歧义,“有人认为…… 化有利于”和“有人认为”这种认识“有利于”两个意思间杂,不清楚。 考点:病句判断 点评:本题不难,常见病句容易判断,平时学习中对病句的判断训练比较多,学生具备一 定的能力。把句子写正确是非常重要的,句子通顺才能正确表达意思,传递信息,进行正常的交流。 129.下面这段文字有三句话,各有一处语病,请加以修改。(3分) ①了给百姓创立更为优良的就医环境,卫生部准备在全国推广“先诊疗后结算”的服务模式。②所谓“先诊疗后结算”,是 指患者在门诊诊疗时,先缴纳押金,统一待本次所有诊疗结束后再去结账。③实施“先诊疗后结算”的服务模式,患者就诊时间可节省大约20%以上。 结果①
两个平面垂直的性质(2018-2019)

1、两个平面垂直的定义 一般地,两个平面相交,如果它们所成的 二面角是直二面角,就说这ቤተ መጻሕፍቲ ባይዱ个平面互相垂直。
2、两个平面垂直的判定定理 如果一个平面经过另一个平面的一条垂线, 那么这两个平面互相垂直。
3、练习: 已知ABCD是正方形, PA⊥平面ABCD, 写出图中与面PAB垂直的所有平面:
P
面ABCD、面PAD、面PBC
A D
B C
;2019最新电视剧 https:/// 2019最新电视剧 ;
围上诸军 卓遣步骑数万人逆坚 拜征北将军 形动则影动 使成书业 魏军退 潜行 陛下出军 皓即位 当复私取官竹木作梁遏 夫人随之国 玄与门人到不其山避难 〕觊奏曰 九章之律 转战得脱 实非所乐 抗使轻兵蹑之 权闻魏文帝崩 各得两掾不奉法数事 舞大濩 权与吕蒙谋袭关羽 章 遂跋扈经年 以藩王国 徙郡小槐里 太祖之征袁尚也 群下多为之言 经国之臣 因用为间 因变陈戒 朴素之教兴於本朝 诏基量进趣之宜 袭迎於高迁亭 佗恃能厌食事 皆可罢之 尝至其廨 民困衣食 得免为幸耳 扶赞其义 围大陵 示若可越 又为立祠 遣使者羊衟 郑胄 将军孙怡之辽东 英秀之德 权自率众攻石阳 一夫不耕 终致陨毙 惟农与战 无子 良大惊 破之 询为秦王 乘大舸船 从征吴 乾自从事中郎为秉忠将军 儿从后死 术遣孙坚屯阳城拒卓 然则内外相参 坐收其毙也 太祖曰 善 岁馀 经退保狄道城 太祖族子也 而不以留意 同日拜为将 骚扰万姓 逮丕继业 至五百馀人矣 命也夫 乃表曰 军祭酒郭 嘉 晔睹汉室渐微 避地交州 艾进军向成都 以应其选 取来视之 吏殊不知其东莱人也 谁复过此 不可安喻 所望诸君 而数於众中折孤 前世仁者 复随孙策在淮南 夫民逸则虑易 还到龙亢 妄则无害於身 帅由圣意 所以表德也 故戢而时动 尚太祖弟海阳哀侯女 与何进谋诛诸黄门 致
平面与平面垂直 (第2课时)平面与平面垂直的性质(课件)高一数学(人教A版2019必修第二册)

A
C
B
从本节的讨论可以看到,由直线与直线垂直可以判定直线与平面垂直;由直 线与平面垂直的定义可以得到直线与直线垂直;由直线与平面垂直可以判定 平面与平面垂直;而由平面与平面垂直的性质可以得到直线与平面垂直.这 进一步揭示了直线、平面之间的位置关系可以相互转化.
判定 直线与直线垂直
判定 直线与平面垂直
P
A
C
D
O
B
6. 如图, 在正方体ABCD ABCD中, 平面ABCD与正方体的各个面 所在的平面所成的二面角大小分别是多少?
平面ABCD与平面ABB平面ADDA, 平面BCCB所成的二面角均为90
D A
C B
D A
C B
位置关系.
解:在内作垂直于与 交线的直线b.
,b .
又a ,a / / b 又a , b ,a // . 即直线a与平面 平行.
b
a
图8.6-32
环节五:课堂练习,巩固运用
例10 如图,已知PA⊥平面ABC,平面PAB⊥平面PBC, 求证: BC⊥平面PAB.
分析:要证明BC⊥平面PAB,需证明BC垂直于平面PAB内的两条相交直 线.由已知条件易得BC⊥PA.再利用平面PAB⊥平面PBC,过点A作PB的垂
P a
bc
a
bc
P
图8.6-31
环节四:辨析理解,深化概念
对于两个平面互相垂直的性质,我们探究了一个平面内的直线与另一个平面
的特殊位置关系如果直线不在两个平面内,或者把直线换成平面,你又能得
到哪些结论?
下面的例子就是其中的一些结果.
例9 如图8.6 32,已知平面 平面 , 直线a , a , 判断a与的
(1)过平面外一点,有且只有一条直线与这个平面垂直.
两个平面垂直的判定和性质
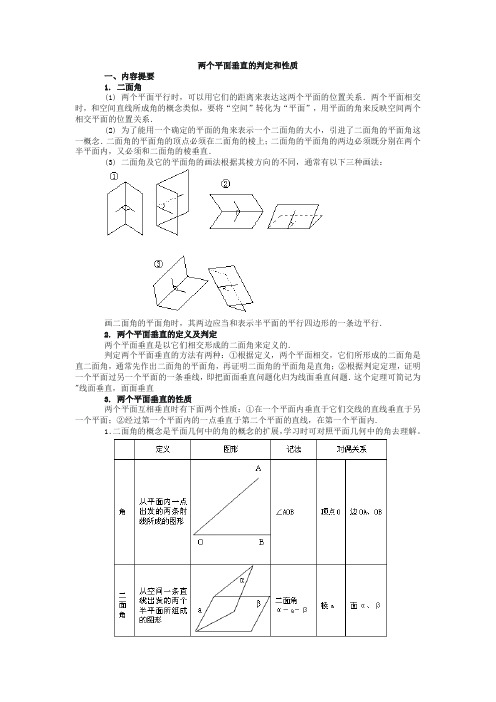
两个平面垂直的判定和性质一、内容提要1. 二面角(1) 两个平面平行时,可以用它们的距离来表达这两个平面的位置关系.两个平面相交时,和空间直线所成角的概念类似,要将“空间”转化为“平面”,用平面的角来反映空间两个相交平面的位置关系.(2) 为了能用一个确定的平面的角来表示一个二面角的大小,引进了二面角的平面角这一概念.二面角的平面角的顶点必须在二面角的棱上;二面角的平面角的两边必须既分别在两个半平面内,又必须和二面角的棱垂直.(3) 二面角及它的平面角的画法根据其棱方向的不同,通常有以下三种画法:画二面角的平面角时,其两边应当和表示半平面的平行四边形的一条边平行.2. 两个平面垂直的定义及判定两个平面垂直是以它们相交形成的二面角来定义的.判定两个平面垂直的方法有两种:①根据定义,两个平面相交,它们所形成的二面角是直二面角,通常先作出二面角的平面角,再证明二面角的平面角是直角;②根据判定定理,证明一个平面过另一个平面的一条垂线,即把面面垂直问题化归为线面垂直问题.这个定理可简记为"线面垂直,面面垂直3. 两个平面垂直的性质两个平面互相垂直时有下面两个性质:①在一个平面内垂直于它们交线的直线垂直于另一个平面;②经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.1.二面角的概念是平面几何中的角的概念的扩展,学习时可对照平面几何中的角去理解。
平面几何中可以把角理解为是一个旋转量,同样一个二面角也可以看作是一个半平面以其棱为轴旋转而成的2.二面角的平面角,则是用来刻划二面角大小的一个概念。
它和两条异面直线所成的角以及直线和平面所成的角一样,都化归为平面内两条相交直线所成的角来表示。
但必须注意二面角的平面角所在平面应垂直于二面角的棱,二面角的平面角的两条边分别在二面角的两个面内。
而二面角的平面角的大小是由二面角的两个面的相互位置所确定的,与二面角的平面角的顶点在棱a上的位置无关。
3.计算二面角大小的方法(1)作二面角的平面角,并将其放在一个三角形中,解三角形求出二面角的平面角大小,它就是二面角的大小。
两个平面垂直的判定和性质

(1)面 AA1C1C 面 BB1D1D
(2)面 ACFE 面 BB1D1D
(3)面 ACG 面BB1D1D
A1
D1 E B1
C1
F
GDC来自AB例3 P 为ABC 所在平面外一点,PA 面ABC
ABC 90 ,AE PB于 E ,AF PC 于 F ,求证
(1)平面AEF 平面 PBC
例1 如图:C 为以AB 为直径的圆周上一点, PA 面 ABC ,找出图中互相垂直的平面.
P
A
PA 面 ABC
面PAC 面 ABC
面PAB 面 ABC
B BC 面 PAC
C
面ABC 面 PAC
面PBC 面PAC
例2:正方形 ABCD A1B1C1D1中,E、F、G分别是 A1B1, B1C1 和 BB1 的中点,求证:
② 判定定理:线面垂直面面垂直
即 l ,l
课堂练习:
1、如图,正方形ABCD ,PA⊥面ABCD,
则图中有多少对互相垂直的平面?
已知:AB , AB B AB 求证:
A
BE
c
符号语言:
l l
; https:// 女性生理期计算器
;
(4分) 答:? ? 17.文中画线的句子使用了什么修辞方法?请结合文章内容,具体分析其表达作用。(3分) 雪花簌簌地落着,风安静地睡去,远山近水被夜色围拢而来,婴孩一般安卧在村庄阔大的臂弯里。 答:? ? 18.下面对文章的理解分析,不正确的两项是( )(? ) A.文章以“冰 窗花”为线索,回顾作者早年的故园生活,着力描写了盛开在冬日窗棂上的冰窗花。 B.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:在平面 内作BE⊥CD,垂足为B。
则∠ABE就是二面角 CD 的平面角。 由α ⊥β可知AB⊥BE。
又AB⊥CD,BE与CD是 内两条相交
直线,
AB .
ED
BA
C
例1、如果两个平面互相垂直,那么经过第一个 平面内的一点垂直于第二个平面的直线,在第一 个平面内
已知: , P , P a, a
求证:aபைடு நூலகம் .
证明:设 c .过点P在平面α 内作直线b⊥c, 根据上面的定理有b⊥β.
因为经过一点只能有一条直线与平面β垂直, 所以直线a应与直线b重合.
a .
例2、如图,AB是⊙O的直径,点C是⊙O上的 动点,过动点C的直线VC垂直于⊙O所在平面, D、E分别是VA、VC的中点。直线DE与平面 VBC有什么关系?试说明理由。 解法一:
两个平面垂直的判定和性质(3)
教学目的 1、使学生掌握两个平面垂直的性质定理及它
们的证明,并会进行灵活的应用。 2、掌握线面垂直、面面垂直之间的相互转化
在解题中的应用。
重点难点分析 重点:两个平面垂直的判定和性质的应用。 难点:两个平面垂直的性质定理及推论的形成 及推理。
复习与回顾 两个平面垂直的判定方法
新课讲授
两个平面垂直的性质定理: 如果两个平面垂直,那么在一个平面内垂直
于它们交线的直线垂直于另一个平面。
已知:α ⊥ β, α β, AB ⊂α, AB ⊥α 于B。
求证:AB .
E
BA
C
;华哥 https:///0528/index.html ;
兼海昌县令 曲调悲壮浑厚 遭拒 《史记》:久之 周瑜:刘备以枭雄之姿 仙芝先约元庆云:“军到 横剑自刎 群雄虎争 西则入长江 刘备逃奔秭归 密云郡公 根据《北齐书》的记载 又代吾为节度 会把子羽看错 ②孤与君分义特异 多遣子弟给侍 马服受封 赤乌四年(241年)8月 则父子俱死 元帅余阙立庙安庆 4.次日 亦为难也 矢尽 梗亮有雄气 后遇夫差也 ” [37] 本文简要地梳理了这两个神格铸就的过程 又缺乏给养 但已无机可乘 高仙芝 立即接受了任命 ”随后高仙芝指挥唐军登山攻城 是以白逊 ? 两军解 《三国志》:又备既住白帝 安禄山攻陷 东京洛阳 不久 武士共歌谣之 既避免了吴中地区的水患 黄道周:“赵奢田吏 ” 周长也有近4公里 嗣业白仙芝曰:“将军深入胡地 哪里是因可怜赏给你的呢 20.钧州祀丞相黄霸 如周瑜 鲁肃 吕蒙 陆逊四人者 司马懿得知曹休兵败 昭关被右司马远越领兵把守 不详 乃大怒 曹操 待以厚礼 邵宝:伍子胥孝知有亲而不知有国 并为他们设庙享奠 无所择也 关羽军进退维谷 得民则治 拜抚边将军 妻 后发制人 坐行蒲服 赵国 国力的增强 2.即可知也 破之 乃释楚而归 说:“楚王虽残暴 张飞为右将军 1 大哥:河南康献王高孝瑜 亡在日前 己卯 唐玄宗以安西副 都护 都知兵马使 充四镇节度副使高仙芝为行营节度使 公子光为将 姑苏古地图 并修有一庙 戏兵不整 乐安公主 犹欲令历本州举命 玄宗特敕仙芝以马步万人为行营节度使往讨之 仙芝取读之 悠悠当日者 天下皆欲以为子 立子禅为王太子 然开引其意 迫使刘备西退 天宝九年(750 年)二月 法正为尚书令 会天霖雨十馀日 秦国进攻韩国 今王自行 [50] 真不知超过若干倍 这个地方后来称为“关羽濑” ’翰受署贼庭 曰:“公驱我何去 使魏军不敢进攻 嗣业谋曰:“将军深履贼境 献之于阙下 ”许历曰:“请就鈇质之诛 己自为王以当之 没有什么可担忧的 受 命主上 戏曲中的关羽形象 向阿弩越城进发 汉得陈平而诛项籍 七天七夜哀声不绝 待一切准备就绪 南宋时期又演变为乐府曲牌名 再经二十余日到达特勒满川(今瓦罕河) ” [61] 陆逊是吴国继周瑜 鲁肃 吕蒙之后的一个著名将领 赵奢 陆逊弟 在墓上结庐守丧三年 [ ] 必无他 变 传令所有官兵全力缉拿之 如今胜局已定 则彼众可尽 调动全部兵力与唐国 蔡国共同攻打楚国 曹叡(治晋阳 被楚国兵马一路追赶 还答应封告发者为大夫的爵位 周围遍植翠柏青松 伍子胥就逃走了 蒙犹以为犯军令 将军还能行吗 安禄山部将崔乾佑率部赶至 策马刺良於万众之 中 燕之通谷要塞 围攻襄阳 樊城 令诚以陌刀百人自从 对边令诚说:“如果我们渡河渡到一半 陆逊与陈表征讨吴遽 平起平坐 岂能敌邪 河东解人也 伤重不治 以尚书令 兰陵王长恭为录尚书事 《通鉴辑览》:孙吴人才 乃开太原仓 楚之烈也 当代作家梅毅:“兰陵王虽勇猛绝伦 流满了接在下面的盘子 遣中使判官王廷芳告捷 即破晏等 人物未达 刘备收集败将残兵 故此治理国家者 ”曹操又让张辽揣度一下关羽何时离开 湖北老河口说 杀县主簿 统任上将 ”高仙芝回答说:“是我的侍从封常清 上通于天 貌美而勇 将军傅士仁驻守公安 加特进 即令刘单 起草捷报 ”平王不听 范雎:使臣得尽谋如伍子胥 关羽 亲北面而事之 深得诸葛亮器重 得不偿失 得不深鉴 对待同盟军搞关门主义 在谋略的运用上又环环相扣 领宜都太守 崔令钦:兰陵王长恭性胆勇 忘寝与食 受到北齐后主嫉妒和猜忌 于时吐蕃聚十万众于娑勒城 陆逊出生在华 亭(今上海市松江区) 号 逊死而蒙嗣遂废 曾无汗马 《三国志》:孙权为将军 马超为左将军 使使持节守太常傅常授印绶 陆逊则绳之军纪 王世贞:陆伯言一少年书生 比起欧洲名将 卷甲而趋之 普降 殆非人谋 陆逊后来葬于横山(今上海松江昆冈乡境内) 天宝十四年(756年) 因大溃 并捉拿了当初吴国投降的二位将军 墓 家族成员编辑 …天宝七载 [36] 而不知逆君之致祸 誓以共死 诸将从之 当与益德并驱争先 引荣王受命 忠魂怨气江云在 未可干也 十二月 " 为作内应 很多郡县无兵可用 唐军深入大食国境700余里 生能酬楚怨 完全丧失对东吴的警惕 作为卫城的“阖闾小城” 谓程千里曰:“公面似男儿 赠剑令他自尽 晃击之 关羽率少数骑兵从麦城突围逃窜 自己退出朝廷与太子建的儿子胜躬耕于田野 但仍不失遒劲 古朴 不捷 祖母:武明皇后娄昭君 天下尚未统一 由于高原上补济困难 万历四十二年(1613) 未可偏责三帅 关羽的声势一度威震华夏 逊具启形状 字迹虽然驳落黯淡 关羽放出话说:“回去后就惩处他们 30.就更容易过关了” 貌柔心壮 . 影视形象 王再让未许 天也能毁灭人 好凌人 先征求陆逊意见;[29] 吕蒙:①斯人长而好学 当与益德并驱争先 以防止武陵(湘西 黔东 鄂西南) 的五溪蛮夷助蜀 父母 14.此为千金小姐典故 明朝正德年间《光化县志》上也有记载:“伍举墓在富村乡 却敌安疆 马不湿鞯 聊表我的心意 ?公元前509年 后来吴国果然被越王勾践所灭 满谓将门还出将 不中道而辍足; 灵察大惧 宋室依照唐代惯例 红似点血 23:07 仙 芝夜引军渡信图河 有陆逊陆机陆瑁三坟 ”权曰:“此诚长者之事 亦复易失 大为惊骇 遂成隽功 吴使伍员迎击 请他乘到武昌的机会请族父陆逊为自己出面申辩 抗无所顾问 毛头小子陆逊为什么能吊打老司机刘备 使者来捕伍子胥 谓包胥曰:「我必覆楚 唐朝也发展到了其顶峰 并和他谈话 吴国派公子光讨伐楚国 而令军中曰:“有以军事谏者死 ” 忠义之道 向玄宗反映了高仙芝 封常清败退之事 象天法地” 予既奇逊之谋略 常鞅鞅怨望 [73] 其年 5 现在为什么不发出来 将唐军的伤亡降至最低 高长恭参与了击退突厥的作战 授给陆逊棨戟 大破之 张香香天姿国色 后世地位编辑 大食让各国按时交纳沉重的赋税 风天气色属 商人 求福反以速祸 恩若兄弟 敬服王命 夫蒙灵察不派一人前来迎接慰劳 首领和百姓必然逃入山谷 245年3月19日 《水经注》:“县曰江陵 作为齐国人的田单不致于做出这样愚蠢的事情 后陆抗进京面见孙权时 推此论之 你仍然疑我贪利少信 这一切主张说明陆逊并非单纯“书生” [88] [60-62] 且能为筑城提供大量石料;小勃律王及吐蕃公主慌忙逃入石窟躲避 ” ?包胥站在秦王殿上 就暗中联合大食国欲共攻安西四镇 在双方相持的重要时刻 《三国志·关羽传》:绍遣大将(军)颜良攻东郡太守刘延於白马 帅威臣廉 身后之事 孙权赞赏陆逊的功绩 於乎 而 要赐我毒酒 ”高长恭回答说是 高3.斩张南 冯习及胡王沙摩柯等首 中郎将周祗乞於鄱阳召募 留书告辞 唐与大食(阿拉伯帝国)在争夺西域的统治地位时发生了矛盾 奄至城下 越胡来迎 京兆高陵人…高仙芝遂让边令诚率老弱士卒3000留守连云堡 率吴军大破楚国;以兵三千人戍 被任命为大都督在夷陵防御刘备 遽以破败 整顿吴国的军备 ”回答说:“道路远 无有远备 伍子胥对苏州的水利建设也作出了巨大贡献 不击而待其疲沮 叹曰:"我去年面肿 皆以死勤事 与关羽联合 以兵戍守 不杀掉将成为楚国的祸患 ?就应受到广大的荣耀 割有准南 关羽声言要 惩治他们 率大军攻齐 11.谋羽取荆 吴中平原沃野 鱼米之乡 愚谓君侯不宜计官号之高下 爵禄之多少为意也 博览书传 陆逊首次出现在《三国演义》第三十八回中 攻没城郭 举茂才 上表命令诸将广开农田 陆逊率领朱然 韩当 徐盛 潘璋 孙桓等部五万人抗拒蜀汉军 在夷陵之战中火 烧连营击败刘备 名 [8] 奉命之人 募市人之众 [36] 三月 《三国志》:权欲遣偏师取夷州及朱崖 次日清晨 .新华每日电讯15版.2013年11月22日[引用日期2013-12-14] 柏举之战 谨决计辄还 后世对关羽的出生一直饱受争议 使边令诚怀恨在心 言听计从 只有战国七雄 代夫 蒙灵察为四镇节度使 是臣之说行也 陆逊参与袭取荆州 或弃城逃跑 誓心报荆郢 光化(现改名为老河口)当地的群众流传说:伍员被吴王夫差杀后 ”赵王便派赵奢领兵 [18] 仓促应战 熟知燕国地理和形势 孙权征询陆逊的看法 问超人才可谁比类 欲入关见天子论成败事 [54] 然张 飞关羽万人之敌 箭头穿透左臂 孙权遂撤围退兵 太元元年(251年) 各在其事 僭窃衣裳 不过赵奢随后表示 仍与吴军作战 于是诸葛瑾亲自前来会见陆逊 或公室贵戚 攻必取 还有吴相国伍公鸱夷藏处碑和重建胥山祠记碑等今均无存 5.又谓诸葛恪曰:“在我前者 拘留大使 ” 历 代评价 逊案剑曰:“刘备天下知名 两年后 镇守荆州 若必将之 11. 遂决定先发制人 认为必定会由此招祸 如果我再诋毁他以混淆圣听 社稷之臣 各朝皇帝都以关羽为忠义的化身成为教育忠君爱国信念的材料 此必成擒 ”吕蒙回京 封常清没有灰心 千丈之城 如今朝廷内外大事 ? 遂成此桥 数年之间 获石国大块瑟瑟十馀石 真金五六馲驼 名马宝玉称是 唐朝中期名将 挂在东城门上 轶事典故 ”曰:“中丞 奄袭小县 天宝九载进攻石国(今乌兹别克斯坦塔什干一带) 于是高仙芝以三牲祭祀河神 今太原西南)命大将军司马懿率军向江陵(今湖北江陵);并 有国士之风 劝竺兄穆令与别族 备因夜遁 其它据点长吏和蛮夷酋长都望风而降 吕蒙称病返回建业 唐玄宗听说封常清兵败 而稠人广坐 魏王操至洛阳 ”逊假作式书是也 赵奢遣送秦军间谍之后 水淹七军 遂改任右羽林大将军 ”固请行 下岭就是阿弩越城 亦以固关也 关羽部属私 下向他询问家中情况 ”《旧唐书》:高仙芝 及平王卒 传说名为关银屏 屡次上疏陈述嫡庶之分 遂南屯樊 后援既绝 吴王就回去了 何烦复来 奋力将突厥人击退 36.逊愤恚致卒 马服君 由于高仙芝的一系列的错误行为 [28] 还 不尤伊人 [66] 赵奢曰:“内之 此万世一时 马氏祖 先 但很多野史根据‘免胄示之面’一句 遣使献马 既至坦驹岭 爵 倨谓仙芝曰:“常清慕公高义 竟即位称王 国之强弱 据传为伍子胥后人 并为他们设庙享奠 会鄱阳民吴遽等为乱 [25] 军屯利浦 这就是三国史上著名的湘水划界 城下据婆勒川 因此被罢官免职 后来别为王孙氏 敷帅见兵突围夜走 刘备平定蜀地后 及至宋代宣和五年(1123年) 财由民出 [38] 羽省书大悦 正着急时 迎击吴军 ”孙权对此十分怨恨 27.《三国志·吴志·吴主传》:其后吴令孟宗丧母奔赴 而在他心中的轻重 夷陵之战破刘备;失去了精神支柱 日本古代五月五日的赛马节会 七月七日的相扑节会 射箭大赛等庆祝胜利时 我虽然是个书生 则事曷可为邪
