2010-2011(2)线性代数A卷
线性代数试题A及答案
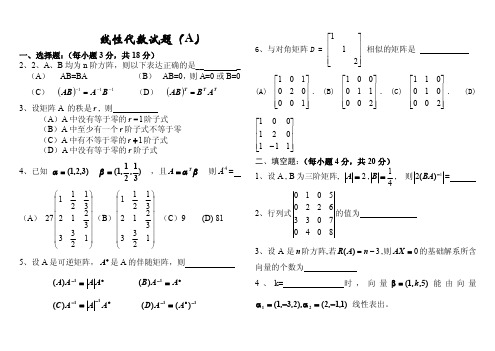
线性代数试题(A )一、选择题:(每小题3分,共18分)2、2、A 、B 均为n 阶方阵,则以下表达正确的是__ _ (A ) AB=BA (B ) AB=0,则A=0或B=0 (C ) ()111---=B A AB (D ) ()T T TA B AB =3、设矩阵A 的秩是r , 则(A )A 中没有等于零的1-r 阶子式 (B )A 中至少有一个r 阶子式不等于零 (C )A 中有不等于零的1+r 阶子式 (D )A 中没有等于零的r 阶子式4、已知 )3,2,1(=a )31,21,1(=b ,且b a T A = 则4A =(A ) 27÷÷÷÷÷÷øöççççççèæ1233321231211(B )÷÷÷÷÷÷øöççççççèæ1233321231211 (C )9 (D) 81 5、设A 是可逆矩阵,*A 是A 的伴随矩阵,则*-=A A A A 1)( *-=A A B 1)( *--=A AA C 11)( 11)()(-*-=A A D6、与对角矩阵D = úúúûùêêêëé211 相似的矩阵是 (A) úúúûùêêêëé100020101. (B) úúúûùêêêëé200110001. (C) úúúûùêêêëé200010011. (D) úúúûùêêêëé-111021001 二、填空题:(每小题4分,共20分)1、设A , B 为三阶矩阵, 2=A ,41=B , 则12-)(BA = 2、行列式8040703362205010的值为 3、设A 是n 阶方阵,若3-=n A R )(,则0=AX 的基础解系所含向量的个数为4、k= 时,向量)5,,1(k =b 能由向量)1,1,2(),2,3,1(21-=a -=a 线性表出。
《线性代数》-期终A卷

杭州电子科技大学继续教育学院学生考试卷( A )卷A 表示方阵A 的行列式,r (A )表示矩阵A 的秩。
一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.3阶行列式011101110---=ij a 中元素a 21的代数余子式A 21=( ) A .-2 B .-1 C .-1D .22.若120231101λλ=0,则12λλ、必须满足( )A .1220λλ==,B 122λλ==C 122λλ=,可为任意数D 12λλ、均可为任意数 3.有矩阵3223,33,A B C ⨯⨯⨯,下列矩阵运算可行的是( ) A AC B ABC C BAC D AB BC -4.如果线性方程组12323331223(1)(3)(1)x x x x x x x λλλλλλ++=-⎧⎪-=-⎪⎨=-⎪⎪-=---⎩有唯一解,则λ=( )A 1或2B —1或3C 1或3D 1-或3- 5.设向量组α1, α2, α3, α4线性相关,则向量组中( ) A .必有一个向量可以表为其余向量的线性组合 B .必有两个向量可以表为其余向量的线性组合 C .必有三个向量可以表为其余向量的线性组合 D .每一个向量都可以表为其余向量的线性组合6.设A=1243⎛⎫⎪⎝⎭, B=12x y ⎛⎫ ⎪⎝⎭,则A 与B 可交换的充分必要条件是( ) A 1x y -= B 1x y -=- C x y = D 2x y = 7.下列矩阵不是初等矩阵的是( )A 100001010⎛⎫⎪⎪ ⎪⎝⎭ B001010100⎛⎫⎪- ⎪ ⎪⎝⎭ C 1001002001⎛⎫⎪⎪- ⎪ ⎪⎝⎭D100014001⎛⎫ ⎪- ⎪ ⎪⎝⎭8.已知向量组 123(1,2,1,1),(2,0,,0),(0,4,5,2)t ααα=-==--,的秩为2,则t =( ) A 3 B 3- C 2 D 2-9.四元线性方程组 1421400x x x x x ⎧+=⎪=⎨⎪-=⎩的基础解系是( )A (0,0,0,0)TB (0,0,2,0)TC (1,0,1)T- D (0,0,2,0)T和 (0,0,0,1)T10.三阶矩阵A 的特征值为 2,1,3.-则下列矩阵中非奇异矩阵是( ) A 2I -A B 2I+A C I -A D A -3I 二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
线性代数10-01真题(A) 定稿版

上海水产大学试卷姓名: 学号: 专业班名: 一、填空题(每空3分,共42分)1. 排列41325的逆序数是_____.2. 行列式A=31402301-的值为_____. 3. 矩阵A=⎪⎪⎭⎫ ⎝⎛5321, B=⎪⎪⎭⎫ ⎝⎛9173,则 2A-B=_________ , TB =_________ ,AB=______________ , BA=______________.4. 矩阵A=⎪⎪⎪⎭⎫ ⎝⎛--161502623的秩是_____ ,最高阶非零子式为________. 5. 设向量1α=(1,2,3,4)2α=(3,6,9,k )线性相关,则k =_____.6. 向量组1α=(3,1,1),2α=(2,1,0),3α=(1,3,1), 4α=(1,2,5)是线性相关还是线性无关, _____________.7. 矩阵A=⎪⎪⎭⎫⎝⎛4312的伴随矩阵是__________. 8. 矩阵A=⎪⎪⎭⎫⎝⎛9503的两个特征值为_____和______. 9. 设A 是3⨯4矩阵,其秩为3, 若1η、2η是非齐次线性方程组b AX =的两个不同的解,则它的通解为____________________.二、解答题,按要求解答下列各题1. 计算行列式 (1).2165103012014312----(5分) (2).ab b bb a b b bb a bb b b a (8分)2. 设⎪⎪⎪⎭⎫ ⎝⎛--=420131201A ,⎪⎪⎪⎭⎫ ⎝⎛=621013401B 求X 使AX B =(10分)3. 求出向量组 1α=(1,1,-1,0),2α=(2,3,-1,1),3α=(1,0,-1,2),4α=(1,2,1,4)中的一个极大无关组,并把不属于极大无关组的向量用极大无关组表示。
(12分)4. 问n 为何值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0020421431321x nx x nx x x x x x 有非零解? (8分)5. 求非其次线性方程组⎪⎩⎪⎨⎧=++-=-+=+++33215314214324321x x x x x x x x x x 的基础解系与通解。
线性代数考试试卷

线性代数考试试卷一.单选题:(2510)''⨯=1.设A 、B 为同阶方阵,下列等式中恒正确的是( )A. AB=BAB ()111---+=+B A B A C. B A B A +=+D. ()T T T B A B A +=+2.设A 为3阶方阵,且已知22A -=,则|A |=( )A .1-B .14-C .41D .13..设矩阵A =⎪⎪⎪⎭⎫ ⎝⎛--500043200101,则A 中( )A .所有2阶子式都不为零B .所有2阶子式都为零C .所有3阶子式都不为零D .存在一个3阶子式不为零4.设行列式2211b a b a =1,2211c a c a =2,则222111c b a c b a ++=( )A .3B .1-C .1D .3-5.线性方程组12233121x x x x x x αα-=⎧⎪-=⎨⎪-=⎩有解的充分必要条件是α=( )A 、1-B 、13C 、13- D 、1 二、填空题(4520)''⨯=1.行列式122305403--中元素3的代数余子式是 . 2.设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-=21031231B A ,,则 BA AB -= ;3.设⎪⎪⎪⎭⎫ ⎝⎛--=A 200012011,则=A -1 ;4.若向量组T T T t t )1,0,0(,)0,2,1(,)0,1,1(2321+==+=ααα线性相关,则t = .5. 设A 为n 阶方阵,0=Ax 有非零解,则A 必有一个特征值为 ;三、计算题)(06601'=⨯'1.计算行列式的值12342341=34124123D2.设⎪⎪⎪⎭⎫ ⎝⎛---=433312120A ,⎪⎪⎭⎫ ⎝⎛-=132321B ,求X 使B XA =. 3.求齐次线性方程组⎪⎩⎪⎨⎧=+--=+--=-+-02200432143214321x x x x x x x x x x x x 的基础解系.4.求向量组T T T T )1,2,2,2(,)1,1,3,2(,)1,1,2,3(,)1,3,2,1(4321-==-=-=αααα的秩和一个最大线性无关组,并把不属于最大无关组的向量用最大无关组线性表示.5. 设三阶矩阵A 的特征值为1,0,1321-===λλλ,对应的特征向量为⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=212,122,221321p p p ,求A .6. 判断二次型312123222132144465),,(x x x x x x x x x x f ++---=的正定性.四、证明题)(01'若21αα,是n 阶矩阵A 属于不同特征值21λλ,的特征向量,证明21αα+不是A 的特征向量.。
全校各专业《线性代数》课程试卷及答案A卷

全校各专业《线性代数》课程试卷及答案A 卷试卷 A 考试方式 闭卷 考试时间(120分钟)一、选择题(本题共4小题,每小题4分,满分16分。
每小题给出的四个选项中,只有一项符合题目要求) 1、设A ,B 为n 阶方阵,满足等式0=AB,则必有( ) (A)0=A 或0=B ; (B)0=+B A ; (C )0=A 或0=B ; (D)0=+B A 。
2、A 和B 均为n 阶矩阵,且222()2A B A AB B +=++,则必有( ) (A) A E =; (B)B E =; (C ) A B =. (D) AB BA =。
3、设A 为n m ⨯矩阵,齐次方程组0=Ax 仅有零解的充要条件是( )(A) A 的列向量线性无关; (B) A 的列向量线性相关; (C ) A 的行向量线性无关; (D) A 的行向量线性相关. 4、 n 阶矩阵A 为奇异矩阵的充要条件是( ) (A) A 的秩小于n ; (B) 0A ≠;(C) A 的特征值都等于零; (D) A 的特征值都不等于零; 二、填空题(本题共4小题,每题4分,满分16分)5、若4阶矩阵A 的行列式5A =-,A *是A 的伴随矩阵,则*A = 。
6、A 为n n ⨯阶矩阵,且220A A E --=,则1(2)A E -+= 。
7、已知方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-+43121232121321x x x a a 无解,则a = 。
8、二次型2221231231213(,,)2322f x x x x x tx x x x x =++++是正定的,则t 的取值范围是 。
三、计算题(本题共2小题,每题8分,满分16分)9、计算行列式1111111111111111x x D y y+-=+-10、计算n 阶行列式121212333n n n n x x x x x x D x x x ++=+四、证明题(本题共2小题,每小题8分,满分16分。
2010-2011-1线性代数试卷A卷

(B) 的通解是 ;
(C) 的通解是 ;
(D) 的通解是 .
8.下列二阶矩阵可对角化的是.
(A) ;(B) ;(C) ;(D) .
三、(10分)计算行列式 的值.
四、好题(10分)设向量组 线性相关,向量组 线性无关,问
(1) 能否由 线性表出?先证明a2a3线性无关
(2) 能否由 线性表出?(请证明以上两点)
二、选择题(每小题4分,共32分)
1.设A为n阶方阵则 的必要条件是b .
(A) 中有两行(列)元素对应成比例;(B) 中必有一行为其余行的线性组合;
(C) 中有一行元素全为零;(D) 中任意一行为其余行的线性组合.
2.设A,B均为n阶非零方阵,且AB=0,则 ?????.
(A)必有一个等于0;(B)都小于n;
(A)A的列向量线性无关;(B)A的列向量线性相关;
(C)A的行向量线性无关;(D)A的行向量线性相关.
6.对非齐次线性方程组 及其导出组 ,c.
(A)若 仅有零解,则 无解;
(B)若 有非零解,则 有无穷多解;
(C)若 有无穷多解,则 有非零解;
(D)若 有惟一解,则 有非零解.
7.设A为 矩阵,若 有解, 是其两个特解, 的基础解系是 ,则b.
(C)一个小于n,一个等于n;(D)都等于n.
3.设A为m阶方阵,B为n阶方阵,且 , , ,则 =c .
(A) ;(B) ;(C) ;(D) .
4.A,B,C均为n阶方阵,下面正确的是d.
(A)AB=BA;(B)若AB=AC,则B=C;
(C)若AB=0,则A=0或B=0;(D)若 ,则 .
5.设A为 矩阵,齐次方程组 仅有零解的充分条件是a.
完整版)线性代数试卷及答案

完整版)线性代数试卷及答案线性代数A试题(A卷)试卷类别:闭卷考试时间:120分钟考试科目:线性代数学号:______ 姓名:______题号得分阅卷人一.单项选择题(每小题3分,共30分)1.设A经过初等行变换变为B,则(B)。
(下面的r(A),r(B)分别表示矩阵A,B的秩)。
A) r(A)。
r(B);(D)2.设A为n(n≥2)阶方阵且|A|=,则(C)。
A) A中有一行元素全为零;(B) A中必有一行为其余行的线性组合;(C) A有两行(列)元素对应成比例;(D) A的任一行为其余行的线性组合。
3.设A,B是n阶矩阵(n≥2),AB=O,则下列结论一定正确的是: (D)A) A=O或B=O。
(B) B的每个行向量都是齐次线性方程组AX=O的解。
(C) BA=O。
(D) R(A)+R(B)≤n.4.下列不是n维向量组α1,α2.αs线性无关的充分必要条件是(A)A) 存在一组不全为零的数k1,k2.ks使得k1α1+k2α2+。
+ksαs≠O;(B) 不存在一组不全为零的数k1,k2.ks使得k1α1+k2α2+。
+ksαs=O(C) α1,α2.αs的秩等于s;(D) α1,α2.αs 中任意一个向量都不能用其余向量线性表示。
5.设n阶矩阵(n≥3)A=,若矩阵A的秩为n-1,则a必为()。
11;(C) -1;(D)。
(A) 1;(B)6.四阶行列式a1a2a3a4b1b2b3b4的值等于()。
A) a1a2a3a4+b1b2b3b4;(B) (a1a2-b1b2)(a3a4-b3b4);(C)a1a2a3a4-b1b2b3b4;(D) (a2a3-b2b3)(a1a4-b1b4)。
1.设A为四阶矩阵且A=b,则A的伴随矩阵A的行列式为b^3.(C)2.设A为n阶矩阵满足A+3A+In=O,In为n阶单位矩阵,则A=−A−3In。
(C)9.设A,B是两个相似的矩阵,则下列结论不正确的是A与B的行列式相同。
线性代数试卷A
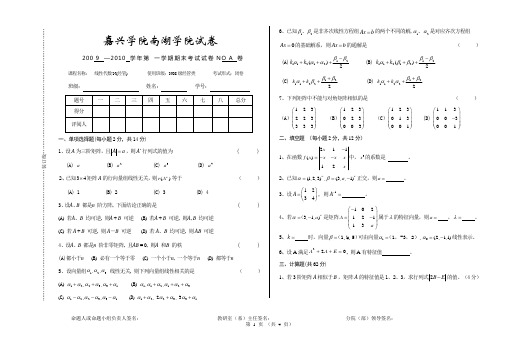
嘉兴学院南湖学院试卷200 9 —2010 学年第 一学期期末考试试卷N O A 卷 课程名称: 线性代数N(经管) 使用班级:N08级经管类 考试形式:闭卷班级: 姓名: 学号:一、单项选择题(每小题2分,共14分)1、设A 为三阶矩阵,且A a =,则*A 行列式的值为 ( ) (A) a (B) 2a (C) 3a (D) 4a2、已知34⨯矩阵A 的行向量组线性无关,则()T r A 等于 ( ) (A) 1 (B) 2 (C) 3 (D) 43、设A 、B 都是n 阶方阵, 下面结论正确的是 ( ) (A ) 若A 、B 均可逆, 则A + B 可逆 (B ) 若A + B 可逆, 则A , B 均可逆 (C ) 若A + B 可逆, 则A -B 可逆 (D ) 若A 、B 均可逆, 则AB 可逆4、设A 、B 都是n 阶非零矩阵, 且AB = 0, 则A 和B 的秩 ( )(A)都小于n (B ) 必有一个等于零 (C ) 一个小于n , 一个等于n (D ) 都等于n5、设向量组123,,ααα 线性无关, 则下列向量组线性相关的是 ( )(A ) 122331,,αααααα+++ (B ) 112123,,αααααα+++(C ) 122331,,αααααα--- (D ) 122331, 2, 3αααααα+++6、已知12ββ、是非齐次线性方程组A x b =的两个不同的解,12αα、是对应齐次方程组0A x =的基础解系,则A x b=的通解是 ( ) (A)1211212()2k k ββααα-+++ (B) 1211212()2k k ββαββ-+++(C) 1211222k k ββαβ+++(D) 1211222k k ββαα+++7、下列矩阵中不能与对角矩阵相似的是 ( )(A )123223333⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B )123023003⎛⎫ ⎪ ⎪ ⎪⎝⎭ (C )123013001⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D) 113003001⎛⎫⎪- ⎪ ⎪⎝⎭二、填空题 (每小题2分,共12分)1、在函数211()12xf x xx x x-=--中,3x 的系数是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010-2011
2 线性代数(必修) A 卷
数理学院 全校本科生(答案写在答题纸上,写在试题纸上无效) 一、填空题(每小题3分,共15分) 1.设A 为4阶矩阵,且5-=A ,则=-A ,=-T A 2 ,=-T A 2 . 2.设C B A ,,均为n 阶方阵,且E ABC =,则=T T A BC )( . 3. 设矩阵3)(,111111111111=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A R k k k k A ,则=k _________. 4.设3阶矩阵A 的特征值为5,2,1-,23A A B -=,则=B . 5.若二次型32312123222142244x x x x x x x x x f +-λ+++=为正定二次型,则λ的取值范 围是 . 二、选择题(每小题3分,共15分) 1. 设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=y x B A 21,3421,则A 与B 可交换的充要条件是( ). (A ) 1+=y x ; (B ) 1-=y x ; (C )y x =; (D ) y x 2=. 2. 设A 为n 阶矩阵,且A A =2,则下列命题正确的是( ). )(A O A =; )(B E A =; )(C 若A 不可逆则O A =; )(D 若A 可逆则E A =. 3. 线性方程组b x A n m =⨯有解的充要条件是( ) A. 0=b B. n m < C. n m = D. ),()(b A R A R = 4. 已知向量组s a a a A ,,:21,r s s a a a a B + ,,,:21则必有( ) (A )A 组线性相关⇒ B 组线性相关; (B )A 组线性无关⇒ B 组线性无关; (C )B 组线性相关⇒ A 组线性相关; (D )B 组线性相关⇒ A 组线性无关. 课程考试试题 学期学年拟题学院(系): 适 用 专 业:
5. n 阶矩阵A 的n 个特征值互异是A 与对角阵相似的( )
(A )充分条件;(B )必要条件;(C )充分必要条件;(D )既非充分又非必要条件.
三、 计算题(本题20分)
1.(10分)已知x
x x x
x f 3232
23321)(111=,求)4(f . 2.(10分)设⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=410011103A ,且满足A X AX +=2,求X. 四、(本题25分)
1.(15分)λ取何值时,线性方程组⎪⎩
⎪⎨⎧-λ-=λ-+--=-λ-+=-+λ-1)5(42,24)5(2,122)2(321321321x x x x x x x x x 有唯一解?无解?
有无穷多解?在无穷多解时求其通解.
2.(10分)设向量组,1412,1012,31407,02314321⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛-=α⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=α⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=α⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=α,求 (1)向量组的秩; (2)向量组的一个最大无关组.
五、(15分)设矩阵⎪⎪⎪⎭
⎫ ⎝⎛----=442442221A ,求一个正交矩阵P ,使AP P 1-为对角阵.
六、证明题(10分).
(1)(5分)设方阵A 满足O E A A =--22,证明A 与E A 2+都可逆,并求出它们的
逆矩阵;
(2)(5分)设向量组s ααα,,,21 线性无关,s s αλ++αλ+αλ=β 2211,其中
),2,1(0s i i =≠λ,证明:β代替i α后的向量组s i i ααβααα+-,,,,,,1121 也是线性无关.。
